A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids
Abstract
:1. Introduction
2. The Descriptions of Mathematical Models
3. The Coupled LBM of Viscoelastic Fluids
3.1. Incompressible LBGK Model with the Extra Force
3.2. Solving the Oldroyd-B Constitutive Model
3.3. The Temporal Marching of Coupled Solvers
| Algorithm 1. The coupled algorithm using a homogeneous time step. |
| Require: , , , , (is a dimension less terminal time) |
| Do |
| ; |
| ; |
| ; |
| ; |
| ; |
| ; |
| While |
| Algorithm 2. Generalized asynchronously coupling method. |
| Require: , , , , (is a dimension less terminal time) |
| Do |
| For (k = 1; k++; k ≤ N) |
| { |
| ; |
| } |
| ; |
| ; |
| ; |
| ; |
| While |
4. Numerical Results and Discussions
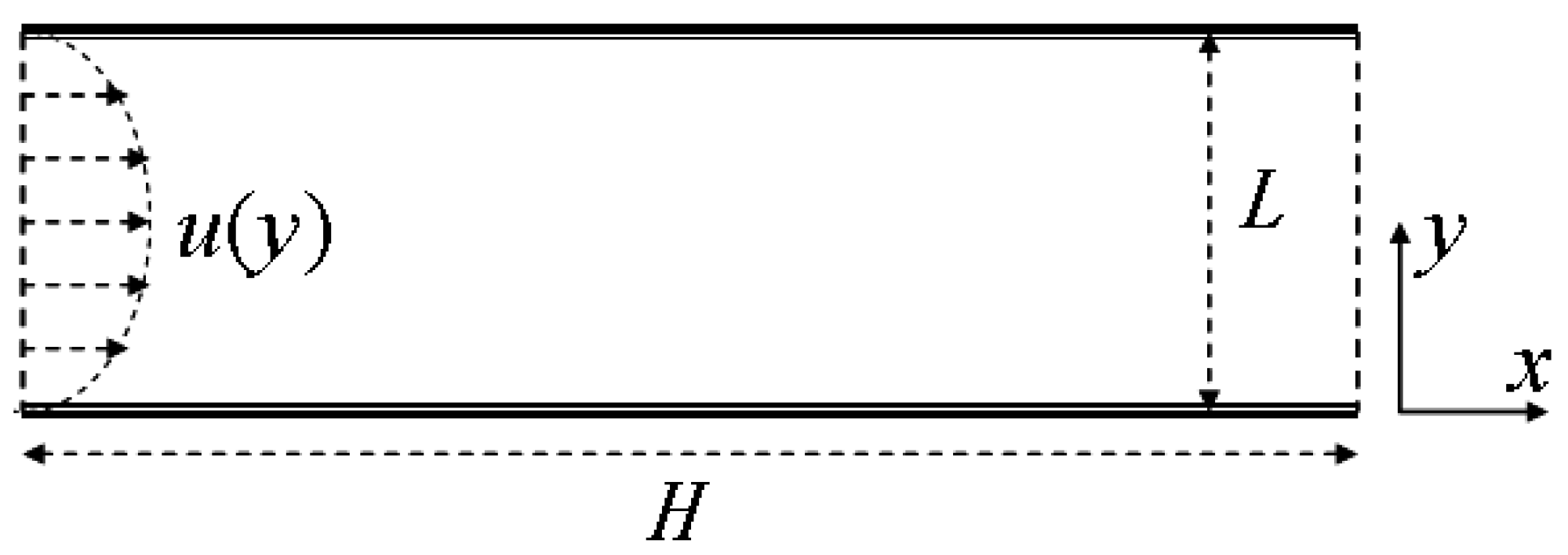
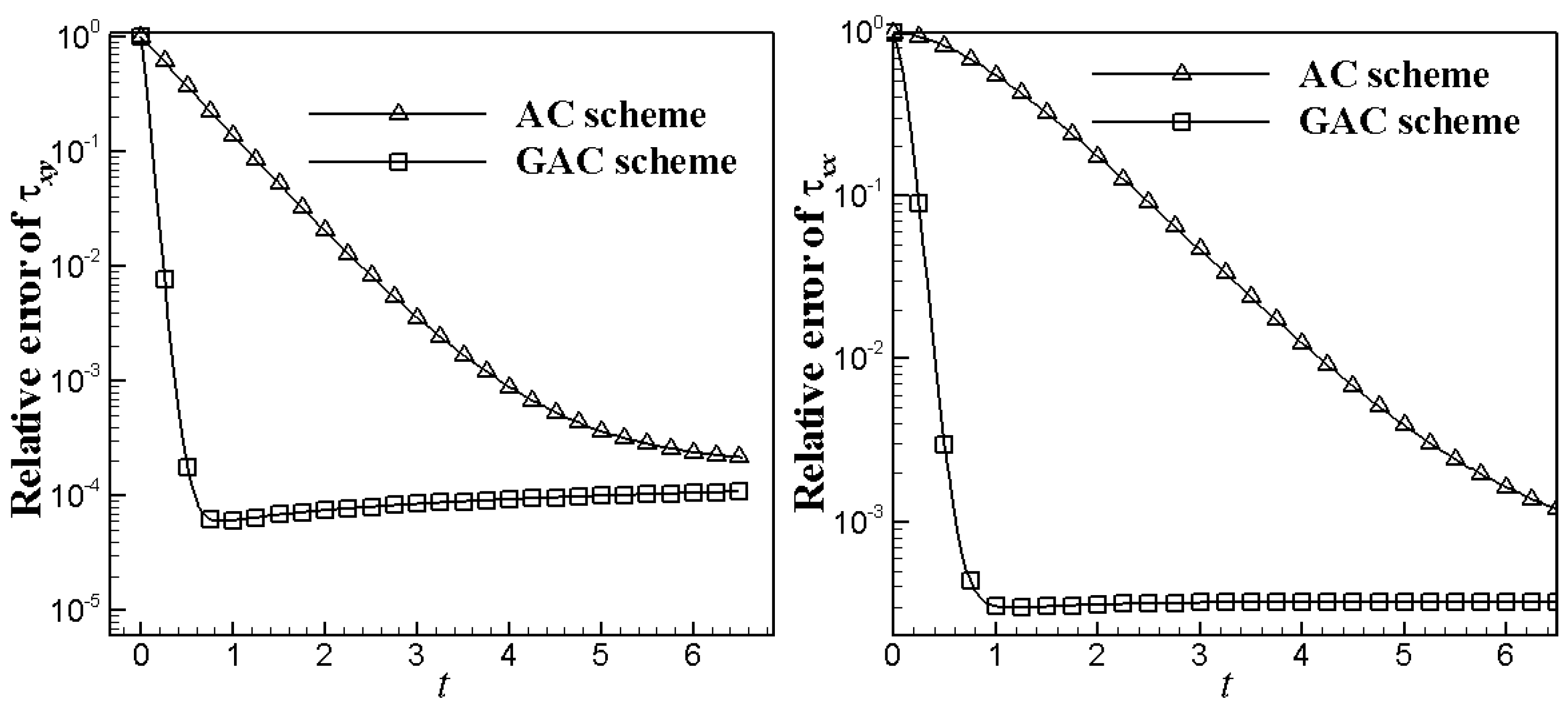
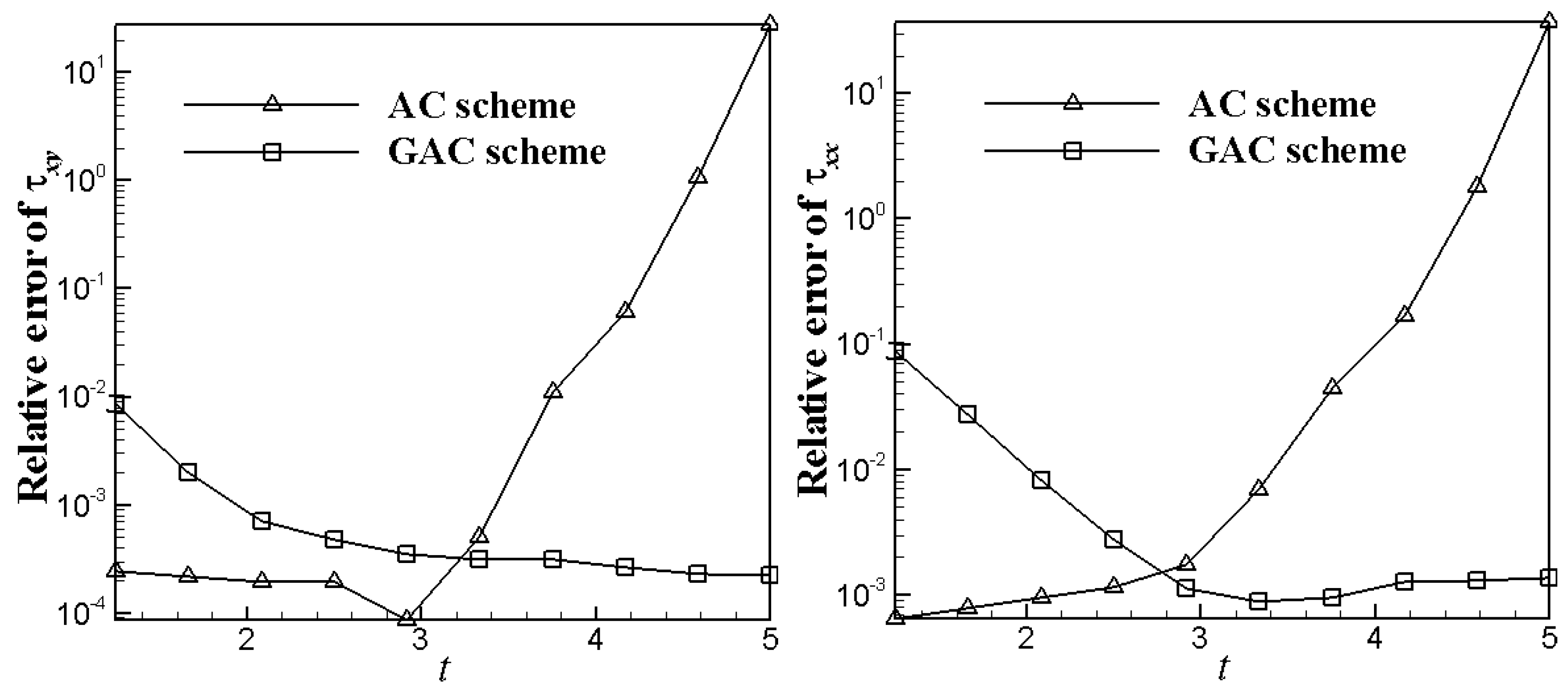
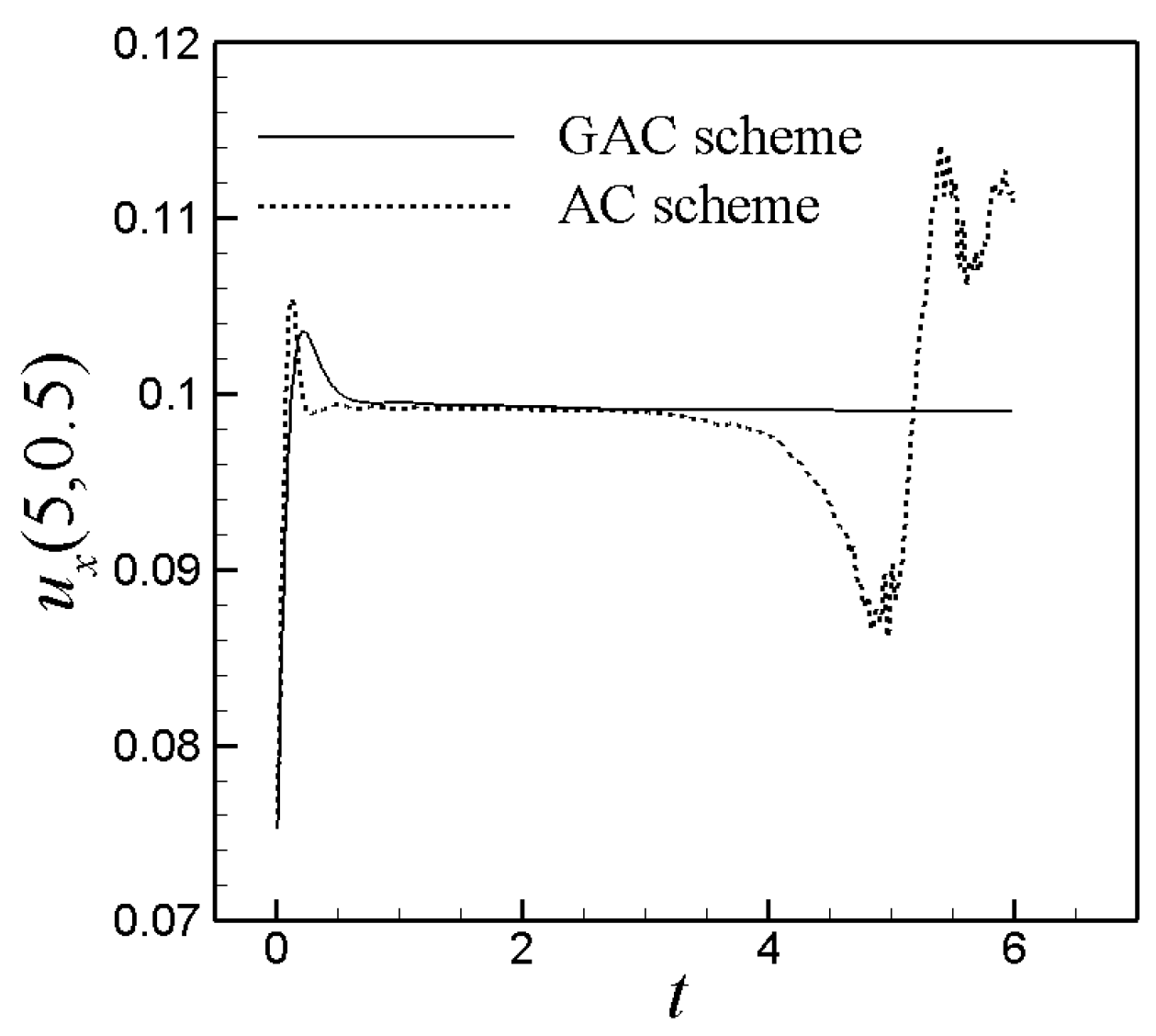
4.1. 2D Channel Flows
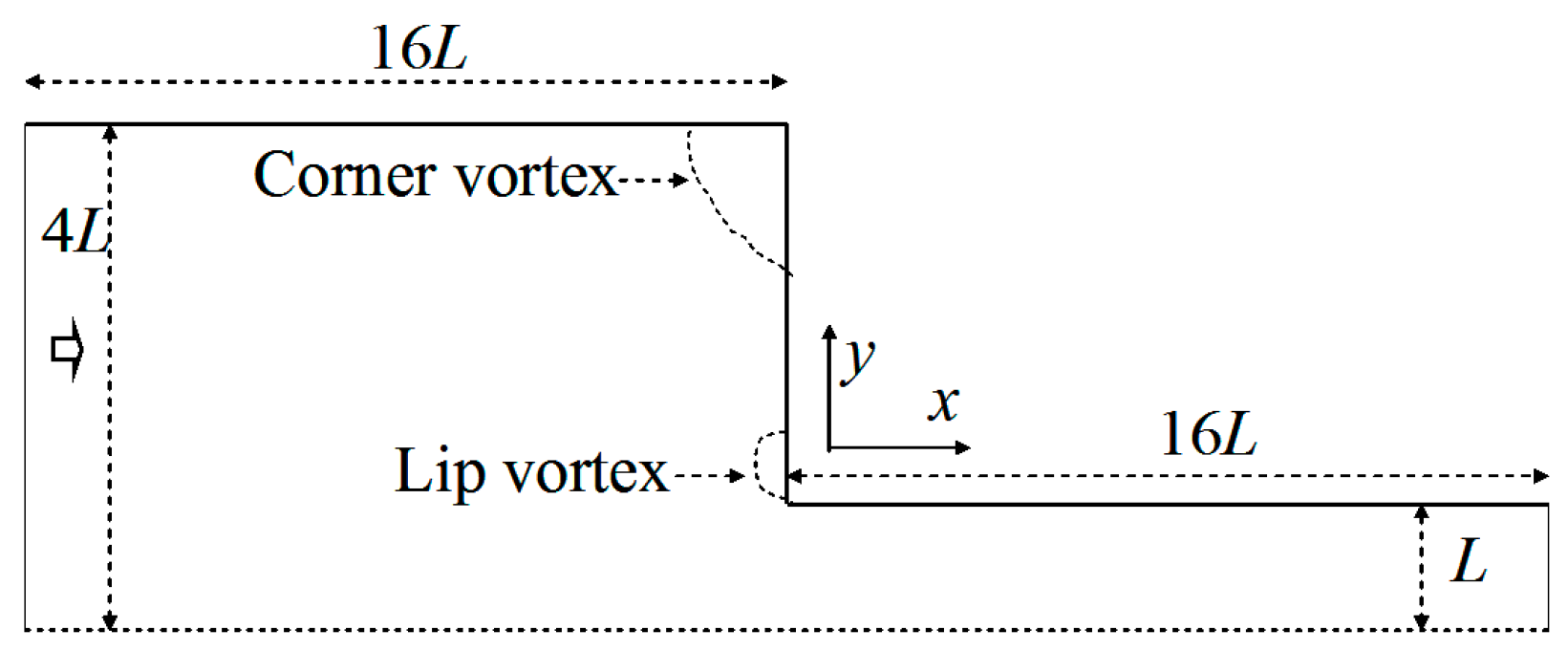
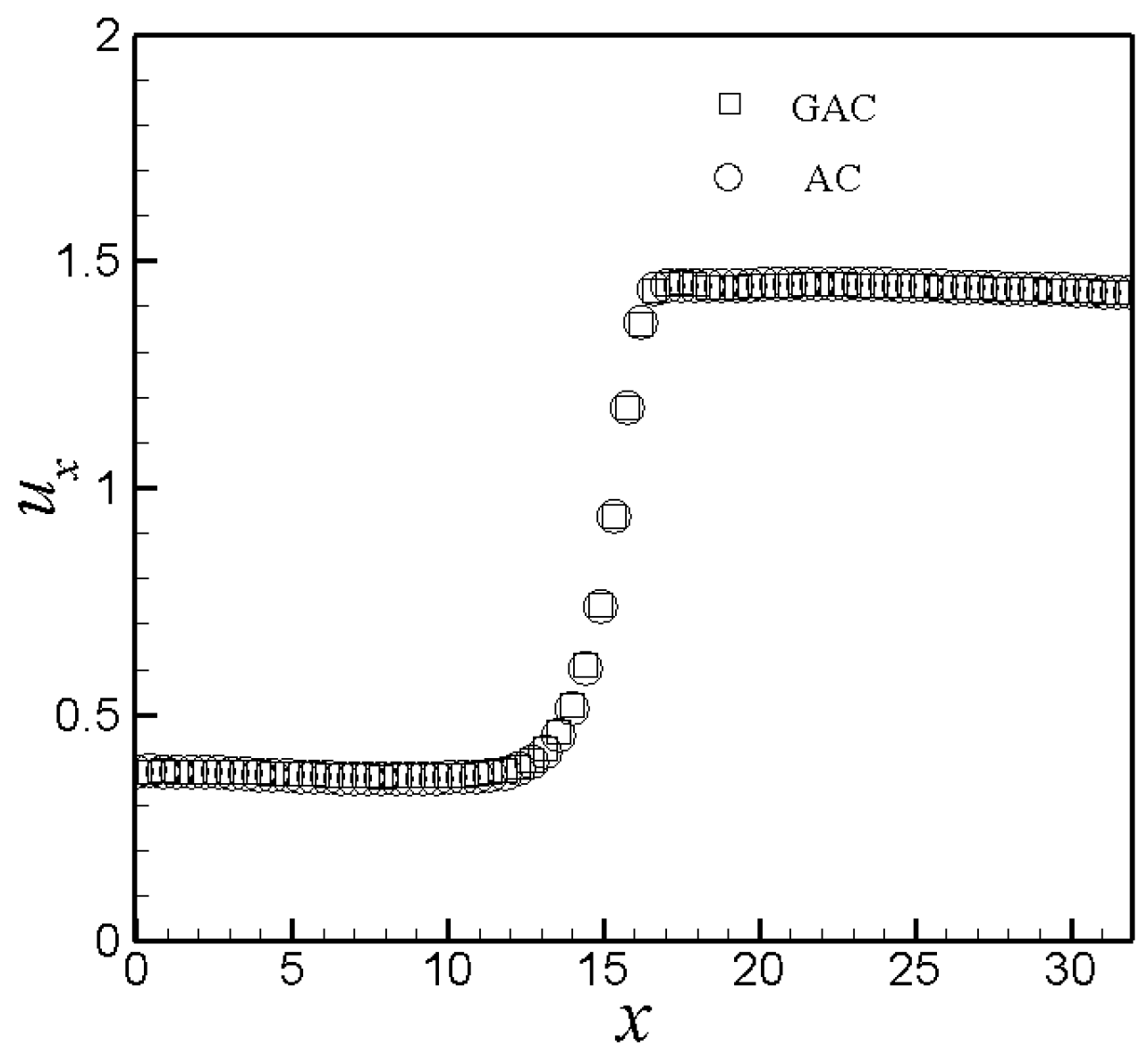
4.2. Contraction Flows
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Recovering Incompressible Naveier-Stokes Equation with Elastic Force
References
- Keunings, R. On the high Weissenberg number problem. J. Non-Newton. Fluid Mech. 1986, 20, 209–226. [Google Scholar] [CrossRef]
- Walters, K.; Webster, M.F. The distinctive CFD challenges of computational rheology. Int. J. Numer. Methods Fluids 2003, 43, 577–596. [Google Scholar] [CrossRef]
- Renardy, M. Current issues in non-Newtonian flows: A mathematical perspective. J. Non-Newton. Fluid Mech. 2000, 90, 243–259. [Google Scholar] [CrossRef]
- Mirzakhalili, E.; Nejat, A. High-order solution of viscoelastic fluids using the discontinuous Galerk in method. J. Fluids Eng. 2015, 137, 031205. [Google Scholar] [CrossRef]
- Comminal, R.; Hattel, J.H.; Alves, M.A.; Spangenberg, J. Vortex behavior of the Oldroyd-B fluid in the 4-1 planar contraction simulated with the stream function–log-conformation formulation. J. Non-Newton. Fluid Mech. 2016, 237, 1–15. [Google Scholar] [CrossRef]
- Niethammer, M.; Marschall, H.; Kunkelmann, C.; Bothe, D. A numerical stabilization framework for viscoelastic fluid flow using the finite volume method on general unstructured meshes. Int. J. Number. Methods Fluids 2017, 86, 131–166. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, MS, USA, 2001. [Google Scholar]
- Qian, Y.H.; Deng, Y.F. A lattice BGK model for viscoelastic media. Phys. Rev. Lett. 1997, 79, 2742–2745. [Google Scholar] [CrossRef]
- Giraud, L.; d’Humières, D.; Lallemand, P. A lattice Boltzmann model for Jeffreys viscoelastic fluid. Euro Phys. Lett. 1998, 42, 625–630. [Google Scholar] [CrossRef]
- Ammar, A. Lattice Boltzmann method for polymer kinetic theory. J. Non-Newton. Fluid Mech. 2010, 165, 1082–1092. [Google Scholar] [CrossRef]
- Gupta, A.; Sbragaglia, M.; Scagliarini, A. Hybrid Lattice Boltzmann/Finite Difference simulations of viscoelastic multicomponent flows in confined geometries. J. Comput. Phys. 2015, 291, 177–197. [Google Scholar] [CrossRef] [Green Version]
- Su, J.; Ouyang, J.; Wang, X. Lattice Boltzmann method for the simulation of viscoelastic fluid flows over a large range of Weissenberg numbers. J. Non-Newton. Fluid Mech. 2013, 194, 42–59. [Google Scholar] [CrossRef]
- Zou, S.; Yuan, X.F.; Yang, X. An integrated lattice Boltzmann and finite volume method for the simulation of viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2014, 211, 99–113. [Google Scholar] [CrossRef]
- Phillips, T.N.; Roberts, G.W. Lattice Boltzmann models for non-Newtonian flows. J. Appl. Math. 2011, 76, 790–816. [Google Scholar] [CrossRef]
- Papenkort, S.; Voigtmann, T. Lattice Boltzmann simulations of a viscoelastic shear-thinning fluid. J. Chem. Phys. 2015, 143, 044512. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shu, C.; Yang, L.M.; Yuan, H.Z. A decoupling multiple-relaxation-time lattice Boltzmann flux solver for non-Newtonian power-law fluid flows. J. Non-Newton. Fluid Mech. 2016, 235, 20–28. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, J.; Bertola, V.; Wang, M. Lattice Boltzmann modeling for multiphase viscoplastic fluid flow. J. Non-Newton. Fluid Mech. 2016, 234, 118–128. [Google Scholar] [CrossRef]
- Su, J.; Ouyang, J.; Wang, X. Lattice Boltzmann method coupled with Oldroyd-B constitutive model for a viscoelastic fluid. Phys. Rev. E 2013, 88, 053304. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E.; Ren, W.Q.; Vanden-Eijnden, E. A general strategy for designing seamless multiscale methods. J. Comput. Phys. 2009, 228, 5437–5453. [Google Scholar] [CrossRef]
- Ren, W. Seamless multiscale modeling of complex fluids using fiber bundle dynamics. Commun. Math. Sci. 2007, 5, 1027–1037. [Google Scholar] [CrossRef]
- Bird, R.; Curtiss, C.; Armstrong, R. Dynamics of Polymeric Liquids; Wiley: New York, NY, USA, 1987; Volume 1 and 2. [Google Scholar]
- Guo, Z.L.; Shi, B.C.; Wang, N.C. Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Guo, Z.L.; Zheng, C.G.; Shi, B.C. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Lockerby, D.A.; Duque-Daza, C.A.; Borg, M.K. Time-step coupling for hybrid simulations of multiscale flows. J. Comput. Phys. 2013, 237, 344–365. [Google Scholar] [CrossRef] [Green Version]
- Hassager, O. Working group on numerical techniques. J. Non-Newton. Fluid Mech. 1988, 29, 2–5. [Google Scholar]
- Afonso, A.; Oliveira, P.J.; Pinho, F.T. Dynamics of high-Deborah number entry flows: A numerical study. J. Fluid Mech. 2011, 677, 272–304. [Google Scholar] [CrossRef]

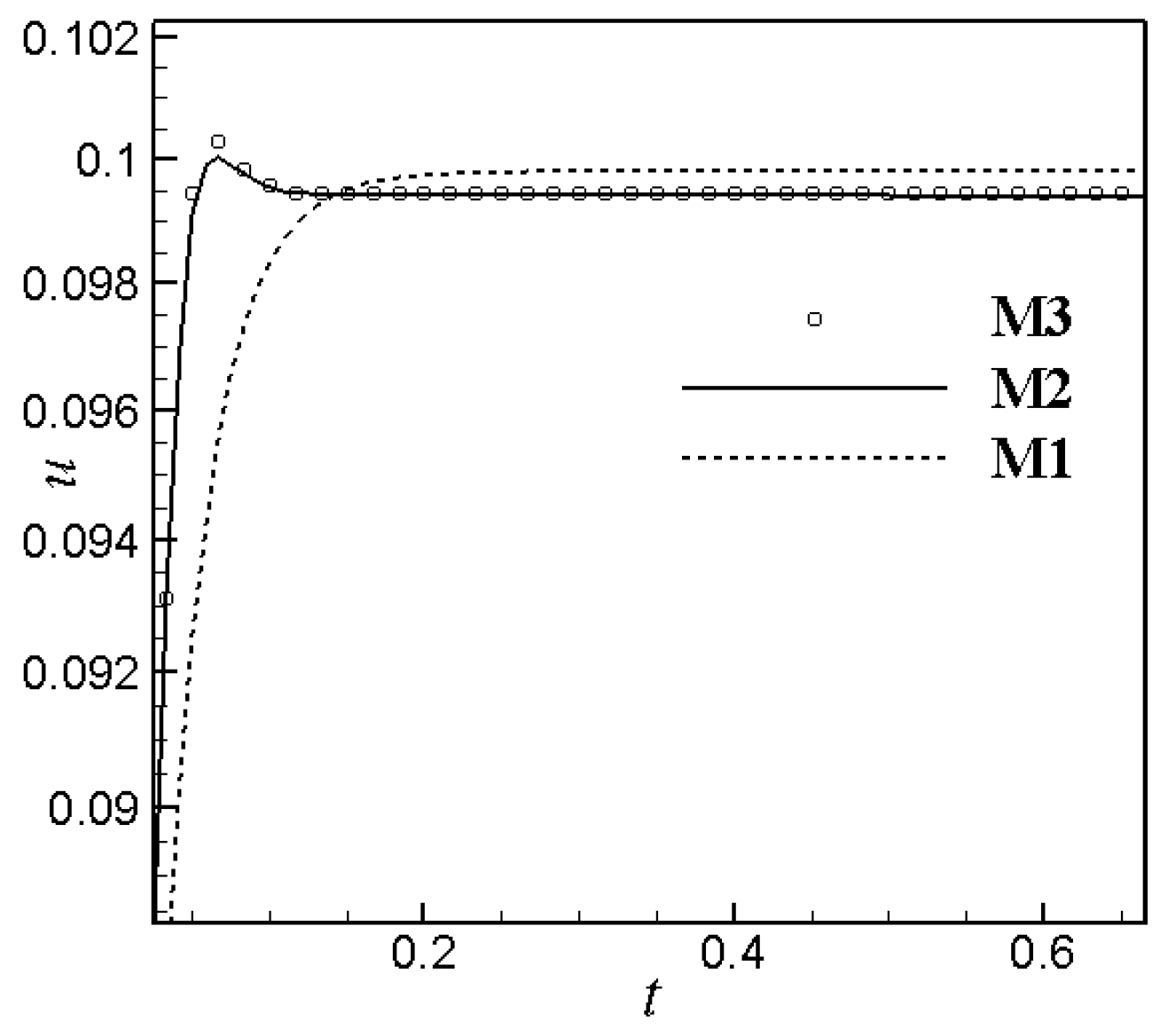

| Mesh | Total Cell | (x/L) |
|---|---|---|
| M1 | 120,000 | 0.05 |
| M2 | 392,000 | 0.0142 |
| M3 | 512,000 | 0.0125 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Ouyang, J.; Lu, J. A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids. Appl. Sci. 2018, 8, 352. https://doi.org/10.3390/app8030352
Su J, Ouyang J, Lu J. A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids. Applied Sciences. 2018; 8(3):352. https://doi.org/10.3390/app8030352
Chicago/Turabian StyleSu, Jin, Jie Ouyang, and Junxiang Lu. 2018. "A Lattice Boltzmann Method and Asynchronous Model Coupling for Viscoelastic Fluids" Applied Sciences 8, no. 3: 352. https://doi.org/10.3390/app8030352





