Pressure Transient Model of Water-Hydraulic Pipelines with Cavitation
Abstract
:1. Introduction
2. Mathematical Models
2.1. Basic Equations without Cavitation
2.2. Continuity Equation under Vaporous Cavitation Condition
2.3. Frictional Items
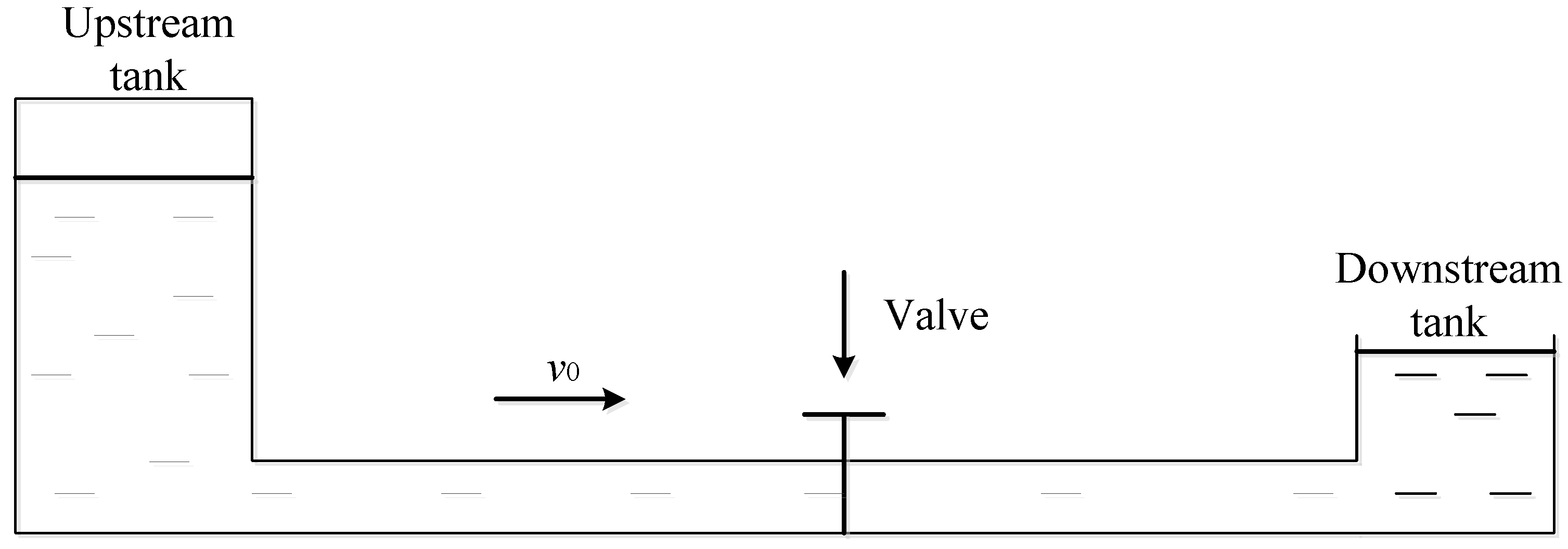
3. Simulation Methods
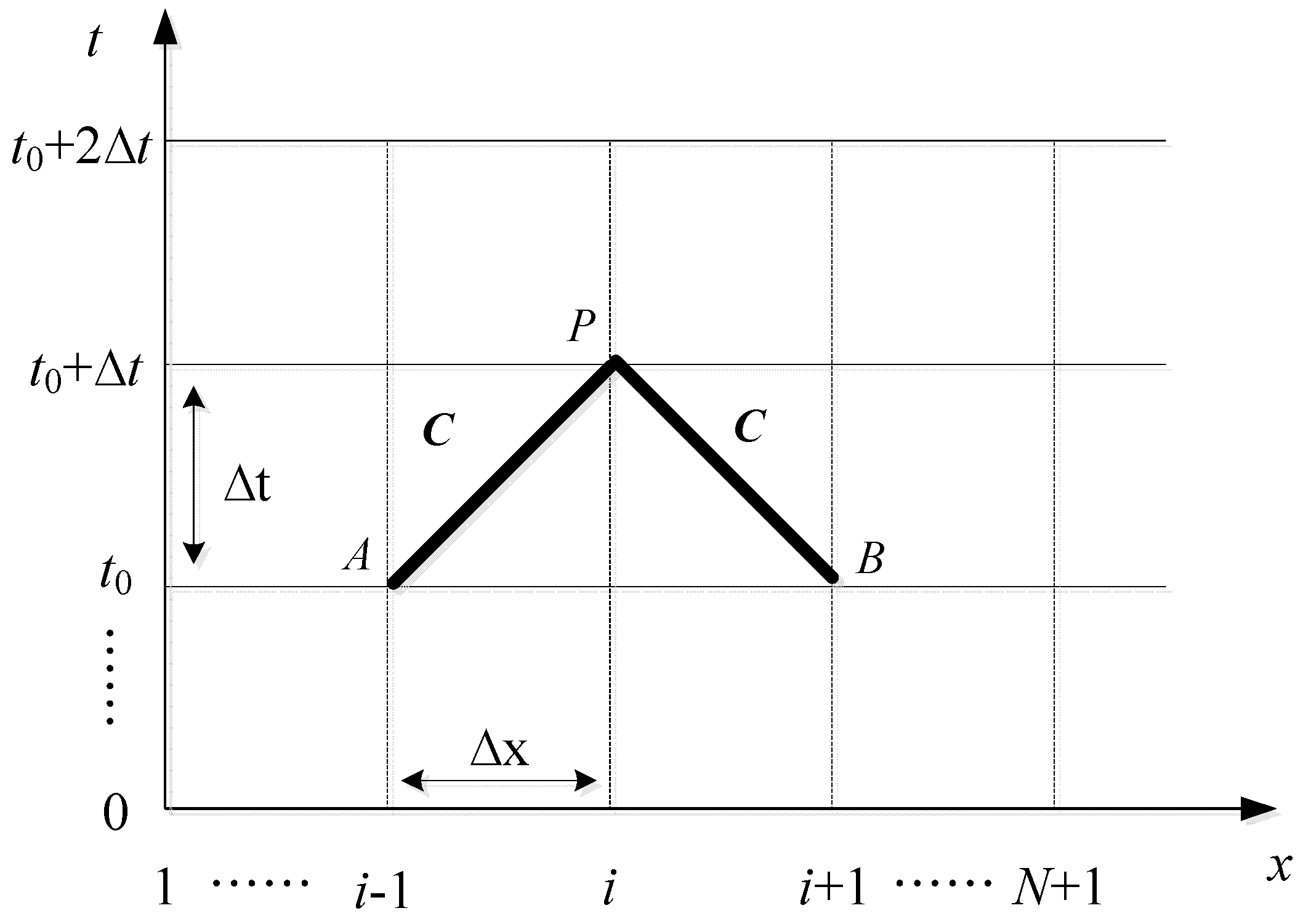
3.1. Method of Characteristics
3.2. Finite Difference Method
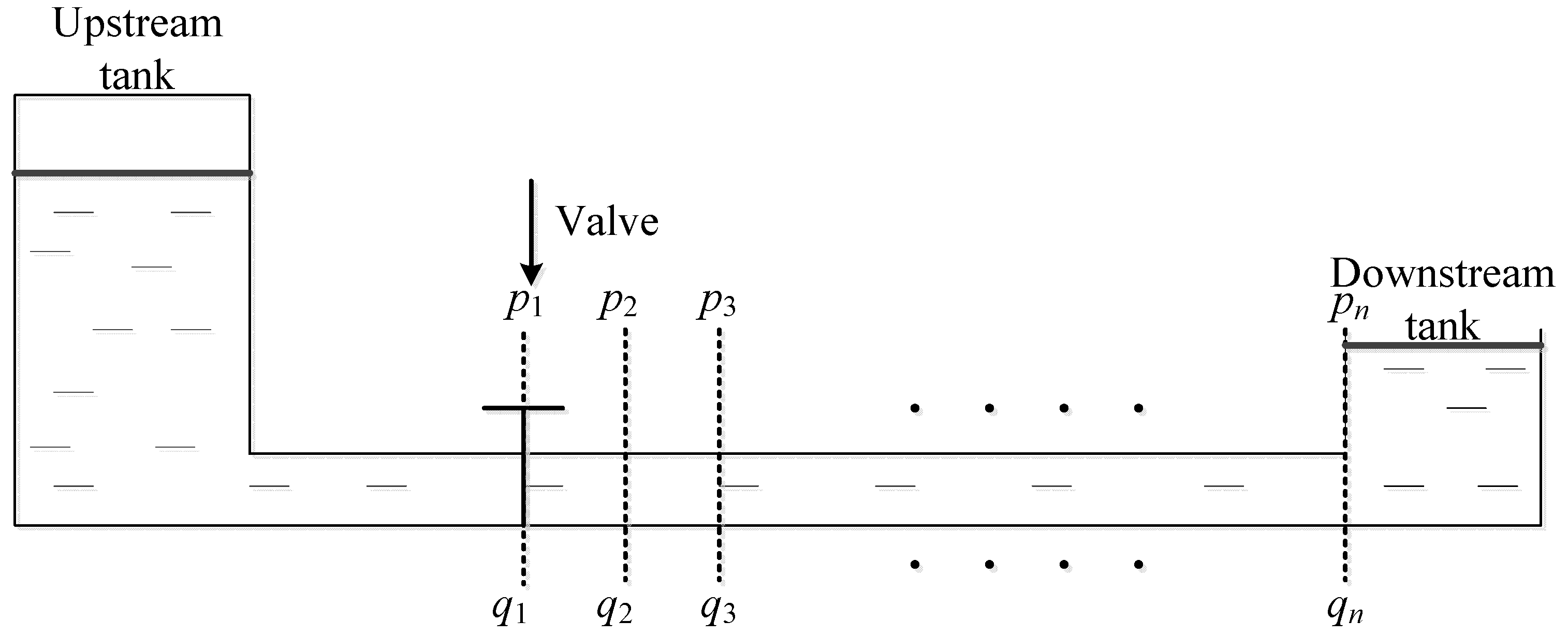
3.2.1. The Downstream Side of the Valve
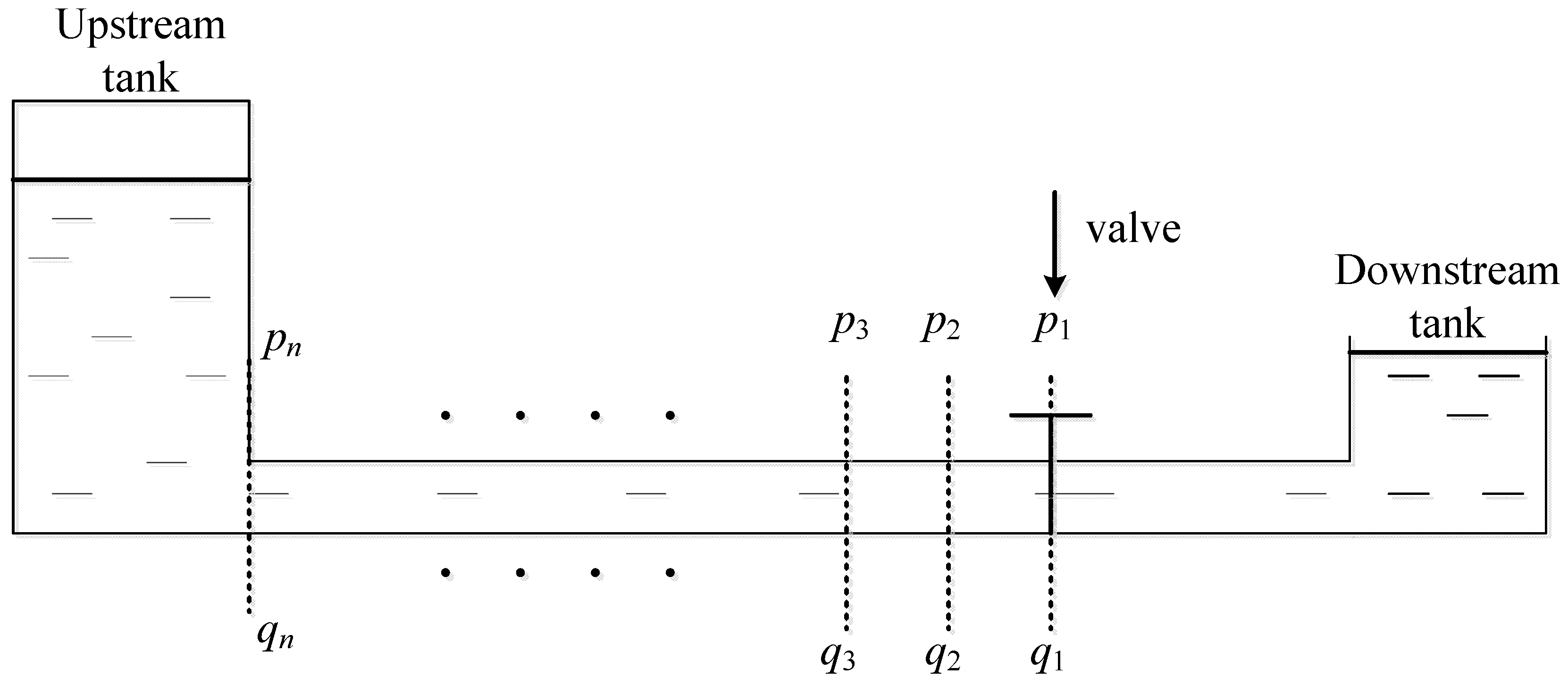
3.2.2. The Upstream Side of the Valve
4. Simulation Results
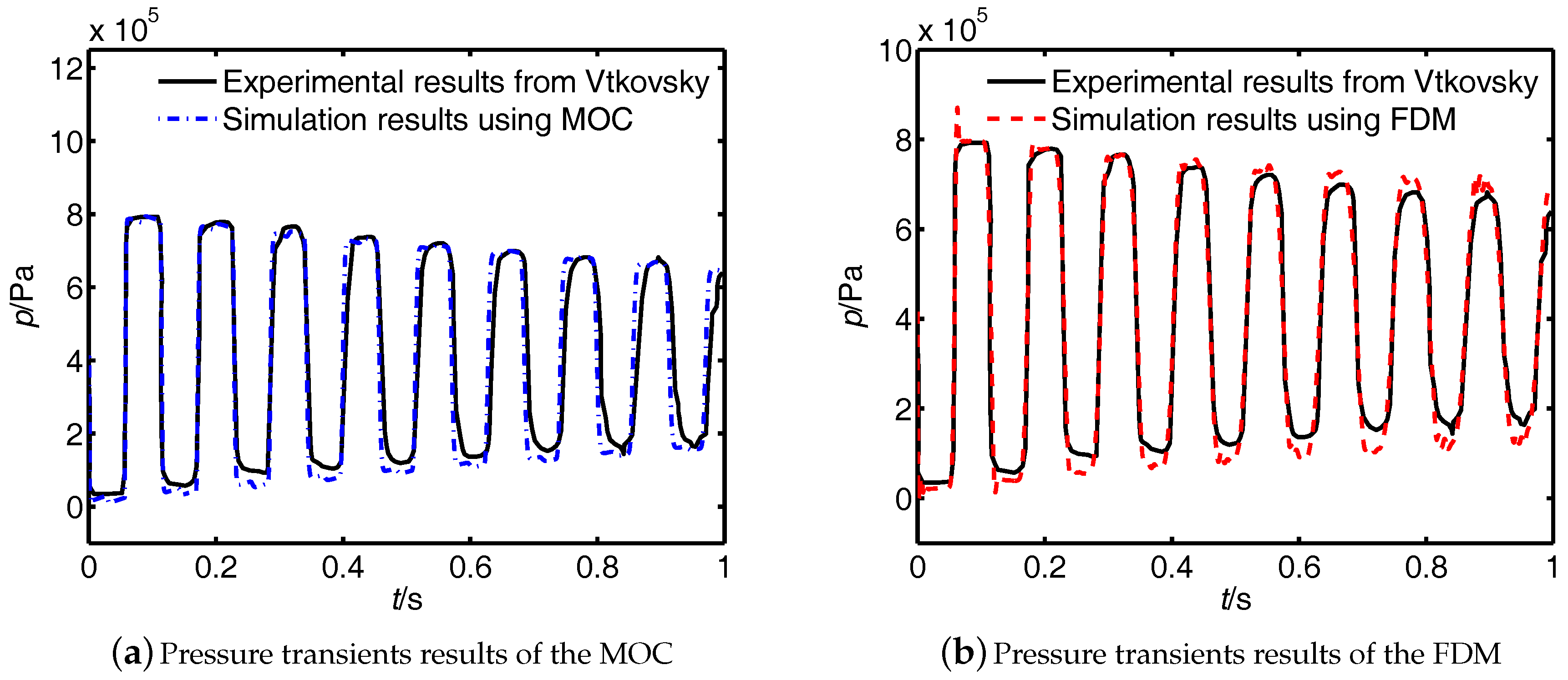
4.1. Case 1: Pressure Transients without Cavitation on the Downstream Side of Valve
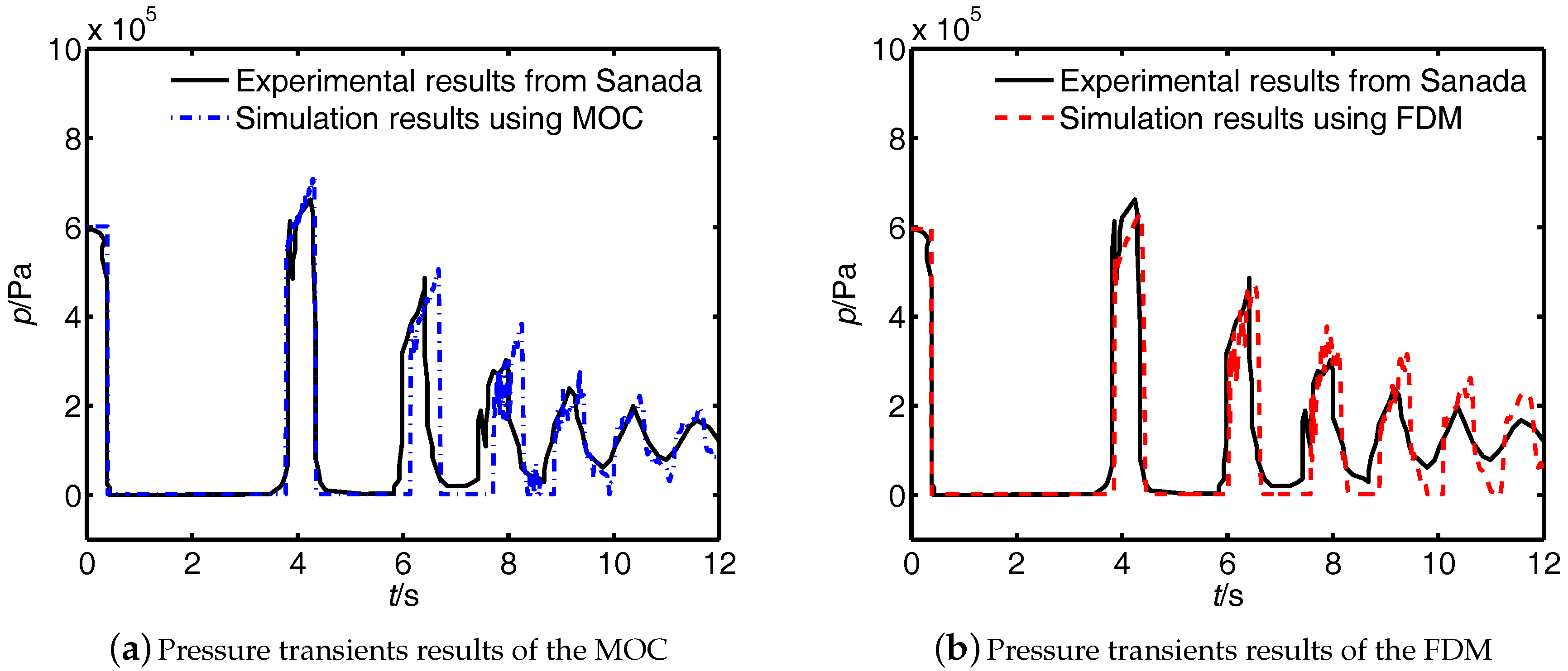
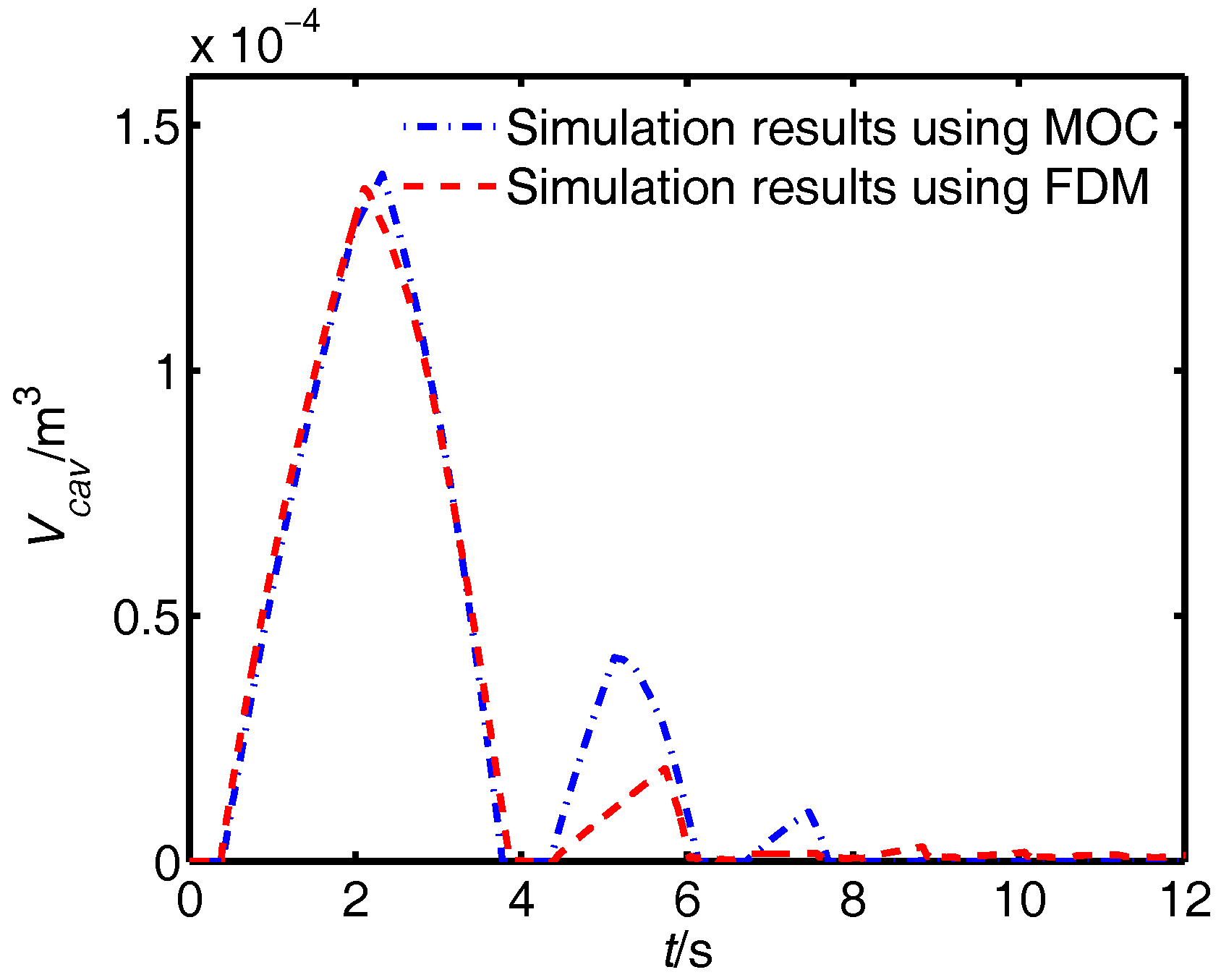
4.2. Case 2: Pressure Transients with Cavitation on the Downstream Side of Valve
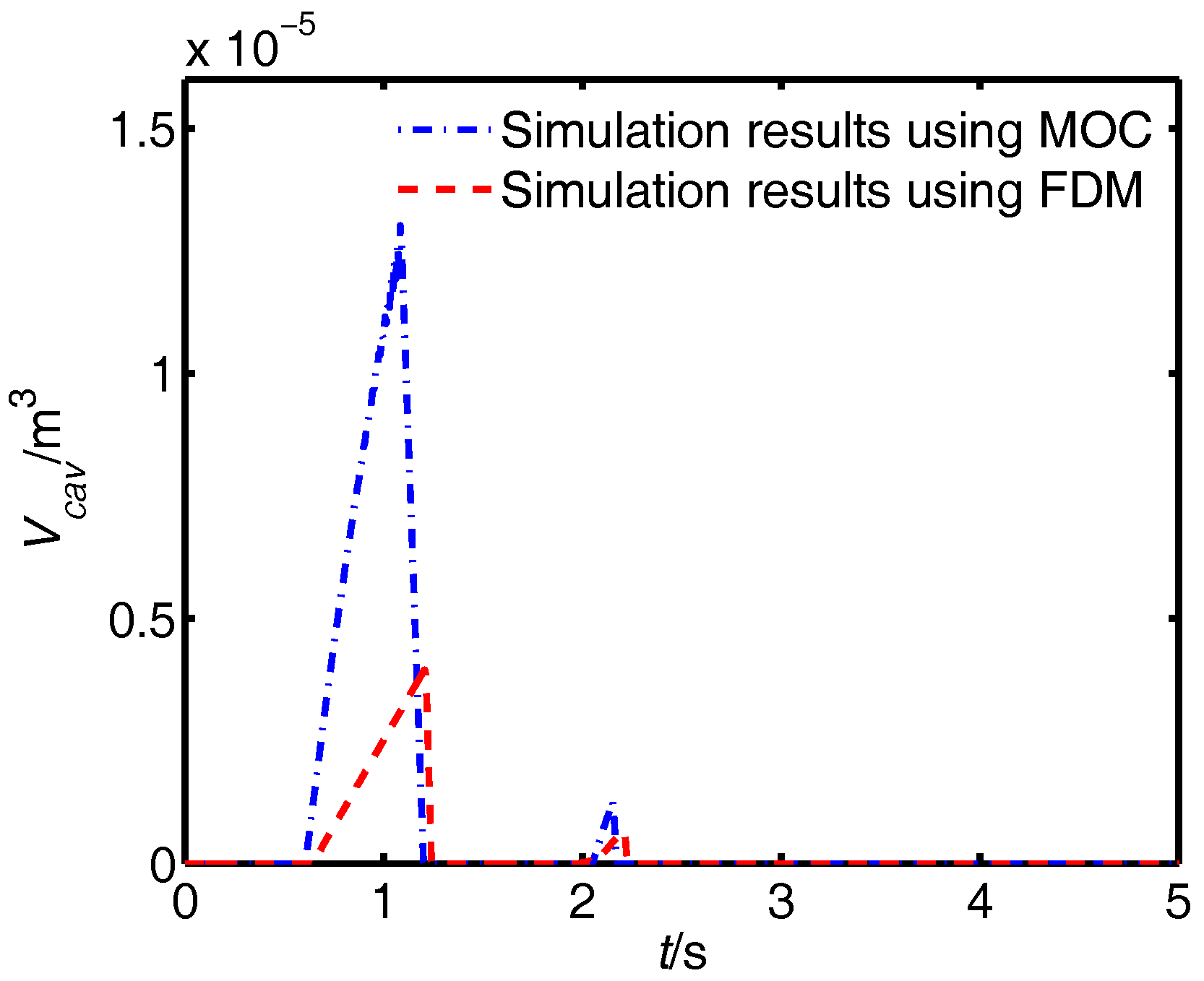
4.3. Case 3: Pressure Transients with Cavitation on the Upstream Side of the Valve
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IAD | Integral of absolute difference |
| (Pa) | Effective bulk modulus |
| (m/s) | Acoustic velocity in the fluid |
| f | Coefficient of Darcy–Weisbach |
| (N) | Steady friction |
| (N) | Friction |
| Weighting constant | |
| Weighting constant | |
| p | Vector of pressures at nodes |
| (Pa) | Pressure at points A, B, and P |
| (Pa) | Pressure in the upstream tank |
| (Pa) | Pressure in the downstream tank |
| New vector of pressures at nodes | |
| Experimental results of pressure transients at the valve | |
| Steady-state pressure at the valve | |
| Simulation results of pressures transients at the valve | |
| q | Vector of flow rate at nodes |
| () | Flow rate at points A, B, and P |
| New vector of flow rate at nodes | |
| () | Inflow rate |
| () | Outflow rate |
| (m) | Radius of the pipeline |
| v (m/s) | Velocity in the fluid |
| (m/s) | Initial velocity in the fluid |
| () | Cavitation volume |
| (N) | Weighting function |
| () | Density of fluid |
| () | Viscosity of fluid |
References
- Kojima, E.; Shinada, M.; Shindo, K. Fluid transient phenomena accompanied with column separation in fluid power pipeline. Bull. JSME 1984, 27, 2421–2429. [Google Scholar] [CrossRef]
- Chaudhry, M.H.; Bhallamudi, S.M.; Martin, C.S.; Naghash, M. Analysis of transient pressures in bubbly, homogeneous, gas-liquid mixtures. J. Fluids Eng.-Trans. ASME 1990, 112, 225–231. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Backstepping control of electro-hydraulic system based on extended-state-observer with plant dynamics largely unknown. IEEE Trans. Ind. Electron. 2016, 63, 6909–6920. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. State-constrained control of single-rod electrohydraulic actuator with parametric uncertainty and load disturbance. IEEE Trans. Control Syst. Technol. 2017. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, Q.; Liu, Y. Anti-windup control of electro-hydraulic system with load disturbance and modeling uncertainty. IEEE Trans. Ind. Inform. 2017. [Google Scholar] [CrossRef]
- Guo, Q.; Yu, T.; Jiang, D. Robust H∞ positional control of 2-DOF robotic arm driven by electro-hydraulic servo system. ISA Trans. 2015, 59, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.J.; Burrows, C.R.; Edge, K.A. Pressure pulsation in reciprocating pump piping systems Part 1: Modelling. Proc. Inst. Mech. Eng. Part I 1997, 211, 229–237. [Google Scholar] [CrossRef]
- Shu, J.J. A finite element model and electronic analogue of pipeline pressure transients with frequency-dependent friction. J. Fluids Eng. 2003, 125, 194–199. [Google Scholar] [CrossRef]
- Shu, J.J. Modeling vaporous cavitation on fluid transient. Int. J. Press. Vessels Pip. 2003, 80, 187–195. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R. Pipeline column separation flow regimes. J. Hydraul. Eng. 1999, 125, 835–848. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Waterhammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Jiang, D.; Li, S.J. Simulation of hydraulic pipeline pressure transients accompanying cavitation and gas bubbles using Matlab/Simulink. In Proceedings of the 2006 ASME Joint U.S.-European Fluids Engineering Summer Meeting, Miami, FL, USA, 17–20 July 2006; pp. 657–665. [Google Scholar]
- Jiang, D.; Li, S.J.; Bao, G. Parameter identification of gas bubble model in pressure pulsations using genetic algorithms. Acta Phys. Sin. 2008, 57, 5072–5080. [Google Scholar]
- Jiang, D.; Li, S.J.; Edge, K.A.; Zeng, W. Modeling and simulation of low pressure oil-hydraulic pipeline transients. Comput. Fluids 2012, 67, 79–86. [Google Scholar] [CrossRef] [Green Version]
- Jiang, D.; Li, S.J.; Yang, P.; Zhao, T.Y. Frequency-dependent friction in pipelines. Chin. Phys. B 2015, 24, 034701. [Google Scholar]
- Shi, Y.; Wang, Y.; Cai, M.; Zhang, B.; Zhu, J. An aviation oxygen supply system based on a mechanical ventilation model. Chin. J. Aeronaut. 2018, 31, 197–204. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, B.; Cai, M.; Zhang, D. Numerical Simulation of volume-controlled mechanical ventilated respiratory system with two different lungs. Int. J. Numer. Methods Biomed. Eng. 2016, 33, 2852. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhang, B.; Cai, M.; Xu, W. Coupling Effect of Double Lungs on a VCV Ventilator with Automatic Secretion Clearance Function. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, T.; Cai, M.; Wang, Y.; Xu, W. Energy conversion characteristics of a hydropneumatic transformer in a sustainable-energy vehicle. Appl. Energy 2016, 171, 77–85. [Google Scholar] [CrossRef]
- Sadafi, M.; Riasi, A.; Nourbakhsh, S.A. Cavitating flow during water hammer using a generalized interface vaporous cavitation model. J. Fluids Struct. 2012, 34, 190–201. [Google Scholar] [CrossRef]
- Karadžić, U.; Bulatović, V.; Bergant, A. Valve-Induced Water Hammer and Column Separation in a Pipeline Apparatus. J. Mech. Eng. 2014, 60, 742–754. [Google Scholar] [CrossRef]
- Iglesias-Rey, P.L.; Fuertes-Miquel, V.S.; Garcia-Mares, F.J.; Martínez-Solano, F.J. Characterization of Commercial Air Intake and Exhaust Valves. Tecnol. Cienc. Agua 2016, 7, 57–69. [Google Scholar]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical modelling of pipelines with air pockets and air valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef]
- Majd, A.; Ahmadi, A.; Keramat, A. Investigation of Non-Newtonian Fluid Effects during Transient Flows in a Pipeline. J. Mech. Eng. 2016, 62, 105–115. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Liu, D.Y.; Ma, J.J.; Wang, P.; Xia, L. A second-order Finite Volume Method for pipe flow with water column separation. J. Hydro-Environ. Res. 2017, 17, 47–55. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Liu, D.Y.; Karney, B.; Wang, P.; Xia, L.; Ma, J.J.; Xu, C. CFD Approach for column separation in water pipelines. J. Hydraul. Eng. 2016, 142, 04016036. [Google Scholar] [CrossRef]
- Himr, D. Investigation and numerical simulation of a water hammer with column separation. J. Hydraul. Eng. 2016, 141, 04014080. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L.S. Fluid Transients in Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Pettersson, M.; Weddfelt, K.; Palmberg, J.O. Modelling and measurement of cavitation and air release in a fluid power piston pump. In Proceedings of the Third Scandinavian International Conference on Fluid Power, Linköping, Sweden, 25–26 May 1993; p. 113. [Google Scholar]
- Harris, R.M.; Edge, K.A.; Tillley, D.G. The suction dynamics of positive displacement axial piston pumps. J. Dyn. Syst. Meas. Control 1994, 116, 281–287. [Google Scholar] [CrossRef]
- Zielke, W. Frequency-dependent Friction in Transient Liquid Flow. J. Basic Eng. 1968, 90, 109–115. [Google Scholar] [CrossRef]
- Trikha, A.K. Efficient Method for Simulation Frequency-dependent Friction in Transient Liquid Flow. J. Fluids Eng. 1975, 97, 97–105. [Google Scholar] [CrossRef]
- Taylor, S.E.M.; Johnston, D.N.; Longmore, D.K. Modeling of transient flow in hydraulic pipelines. Proc. Inst. Mech. Eng. Part I 1997, 211, 447–456. [Google Scholar]
- Vitkovsky, J.P.; Bergant, A.; Simpson, A.R.; Martin, M.A.; Lambert, F. Systematic evaluation of one-dimensional unsteady friction models in simple pipelines. J. Hydraul. Eng. 2006, 132, 696–708. [Google Scholar] [CrossRef]
- Rabie, M.G.; Rabie, M. Fluid Power Engineering; McGraw-Hill Education: New York, NY, USA, 2009. [Google Scholar]
- Sanada, K.; Kitagawa, A.; Takenaka, T. A study on analytical methods by classification of column separations in a water pipeline. Bull. JSME 1990, 56, 585–593. [Google Scholar] [CrossRef]

| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 2.0141 | 5.3946 |
| Parameter | Value |
|---|---|
| Upstream tank pressure (bar) | 4.25 |
| Downstream tank pressure (bar) | 4.22 |
| Pipe radius (mm) | 11.05 |
| Pipe length L (m) | 37.2 |
| Water density () | 1000 |
| Initial velocity (m/s) | 0.3 |
| Acoustic velocity in the fluid (m/s) | 1319 |
| Case | (bar) | IAD of MOC | IAD of FDM |
|---|---|---|---|
| 1 | 0.91% | 0.05% | |
| 2 | 2.75% | 2.47% | |
| 3 | 12.39% | 10.84% |
| Parameter | Value |
|---|---|
| Upstream pressure (bar) | 6.55164 |
| Downstream pressure (bar) | 0.98065 |
| Pipe radius (mm) | 7.6 |
| Pipe length L (m) | 200 |
| Water density () | 1000 |
| Initial velocity (m/s) | 1.5 |
| Viscosity of the fluid (cP) | 1 |
| Times | Method | MOC (case 1) | FDM (case 1) | MOC (case 2) | FDM (case 2) | MOC (case 3) | FDM (case 3) |
|---|---|---|---|---|---|---|---|
| 1st time | start time (s) | – | – | 0.40 | 0.38 | 0.60 | 0.65 |
| end time (s) | 3.77 | 3.87 | 1.21 | 1.24 | |||
| duration (s) | 3.37 | 3.49 | 0.61 | 0.59 | |||
| maximum volume time (s) | 2.32 | 2.11 | 1.08 | 1.21 | |||
| maximum volume () | |||||||
| 2nd time | start time (s) | – | – | 4.34 | 4.37 | 2.05 | 1.98 |
| end time (s) | 6.14 | 6.03 | 2.17 | 2.23 | |||
| duration (s) | 1.80 | 1.66 | 0.12 | 0.25 | |||
| maximum volume time (s) | 5.12 | 5.73 | 2.15 | 2.21 | |||
| maximum volume () | |||||||
| 3rd time | start time (s) | – | – | 6.72 | 6.54 | – | – |
| end time (s) | 7.71 | 7.62 | |||||
| duration (s) | 0.99 | 1.08 | |||||
| maximum volume time (s) | 7.46 | 6.76 | |||||
| maximum volume () |
| Parameter | Value |
|---|---|
| Upstream pressure (bar) | 4.90325 |
| Downstream pressure (bar) | 0.98065 |
| Pipe radius (mm) | 7.6 |
| Pipe length L (m) | 200 |
| Water density () | 1000 |
| Initial velocity (m/s) | 1.45 |
| Viscosity of fluid (cP) | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Ren, C.; Zhao, T.; Cao, W. Pressure Transient Model of Water-Hydraulic Pipelines with Cavitation. Appl. Sci. 2018, 8, 388. https://doi.org/10.3390/app8030388
Jiang D, Ren C, Zhao T, Cao W. Pressure Transient Model of Water-Hydraulic Pipelines with Cavitation. Applied Sciences. 2018; 8(3):388. https://doi.org/10.3390/app8030388
Chicago/Turabian StyleJiang, Dan, Cong Ren, Tianyang Zhao, and Wenzhi Cao. 2018. "Pressure Transient Model of Water-Hydraulic Pipelines with Cavitation" Applied Sciences 8, no. 3: 388. https://doi.org/10.3390/app8030388
APA StyleJiang, D., Ren, C., Zhao, T., & Cao, W. (2018). Pressure Transient Model of Water-Hydraulic Pipelines with Cavitation. Applied Sciences, 8(3), 388. https://doi.org/10.3390/app8030388




