CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods
Abstract
:Featured Application
Abstract
1. Introduction
2. Risers’ Geometries and Materials and FE Modeling
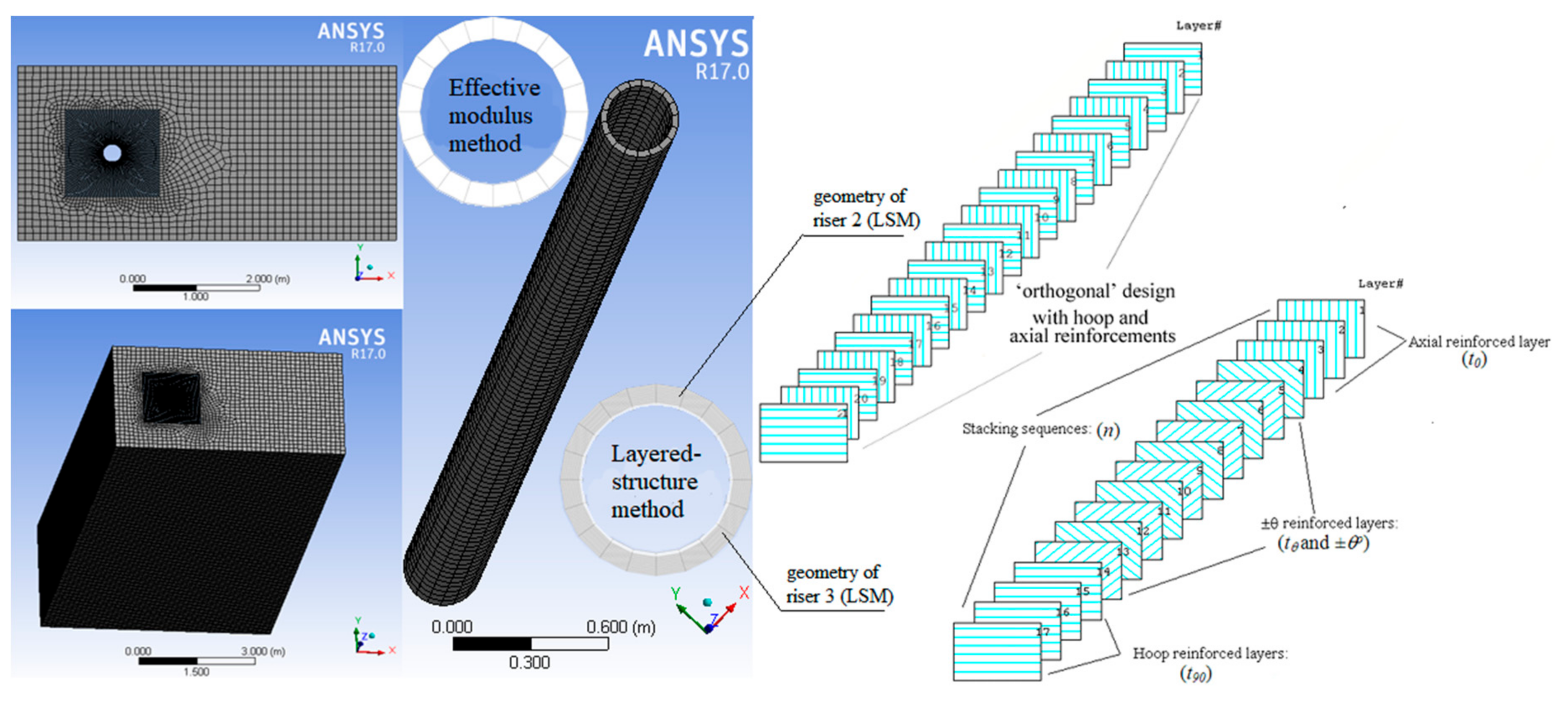
2.1. Riser Geometries
2.2. Materials for the Risers
2.3. FE Modeling
3. Results and Comparison
3.1. Properties for Different Risers
3.2. Effects of 2D and 3D Models
3.3. Effects of the Models with/without FSI
3.4. Results for 3D VIV with FSI Using Different Modeling Methods
- (1)
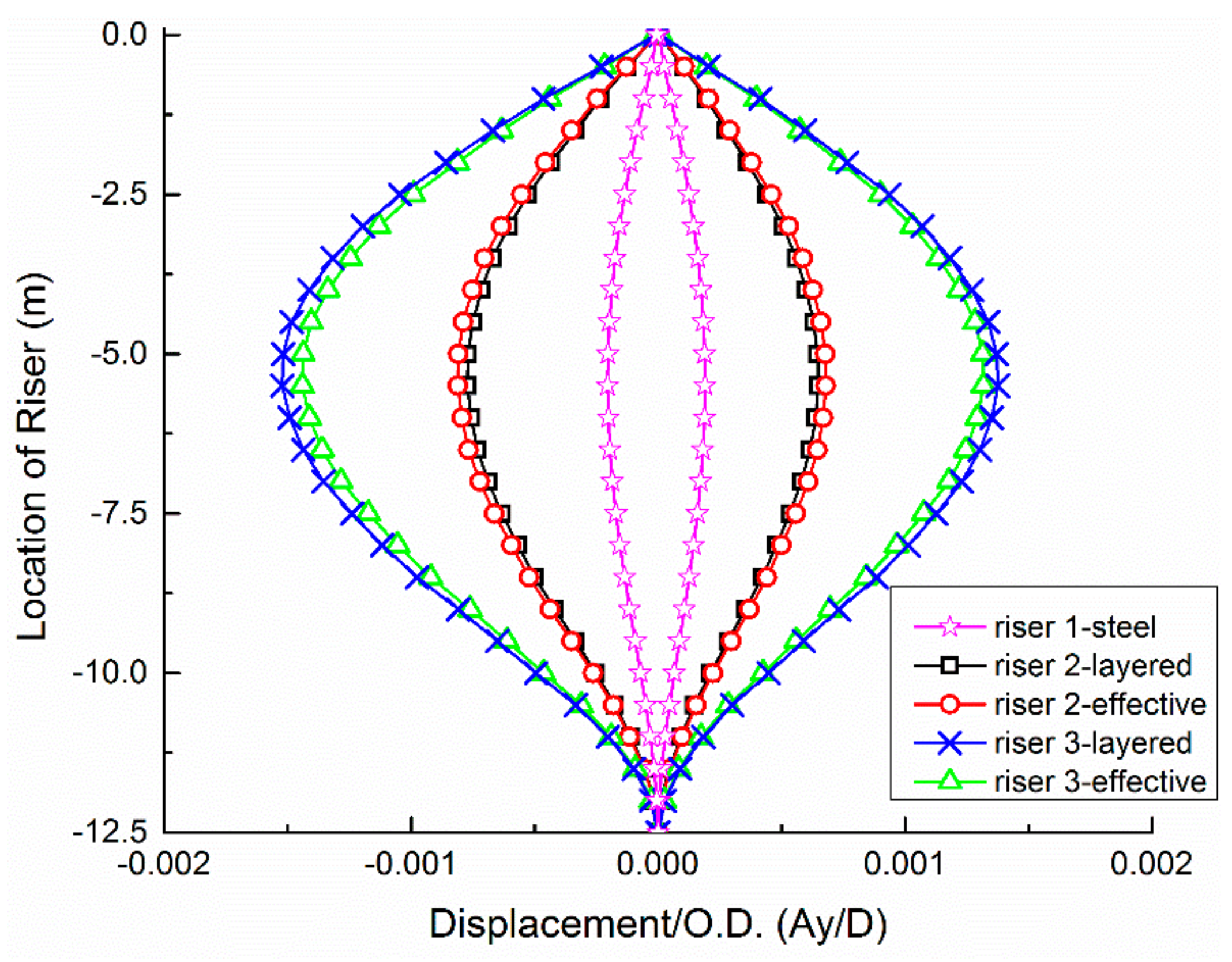
- For the same riser: (i) different modeling methods lead to similar results for riser’s displacement time history; (ii) the deformation in the middle part of the riser is larger than that in both ends, and the deformation close to the fixed end is the minimum; (iii) the deformation in the flow-direction is relatively stable at a specific value while the deformation in the cross-flow direction increases and decreases periodically; and (iv) the vibration in cross-flow direction is more obvious than that in flow direction.
- (2)
- For the different risers, Riser 1’s displacement is less than Riser 2’s displacement, which is less than Riser 3’s displacement, due to their different bending modulus and tension forces.
- (1)
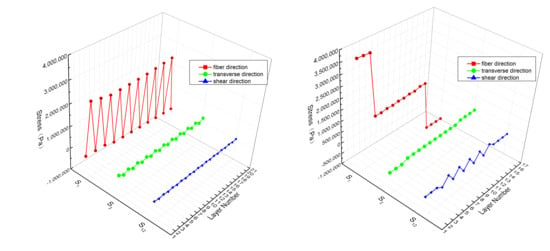
- Stress in fiber direction (S1): S1 is smaller in hoop reinforced fiber layers than that in axial reinforced fiber layers for composite Riser 2 while S1 is largest in axial reinforced fiber layers, medium in inclined reinforced fiber layers and smallest in hoop reinforced fiber layers for composite Riser 3.
- (2)
- Stress in transverse direction (S2): S2 is larger in hoop reinforced fiber layers than that in axial reinforced fiber layers for composite Riser 2, while S2 is largest in hoop reinforced fiber layers, medium in inclined reinforced fiber layers and smallest in axial reinforced fiber layers for composite Riser 3.
- (3)
- Stress in shear (S12): Riser 2 only contains orthorhombic fiber reinforcements, and therefore almost no shear stress S12 is produced; contrarily, composite Riser 3 includes shear stress S12 in the inclined composite layers.
4. Conclusions
- (1)
- Both 2D and 3D models lead to 2S vortex shedding modes for all three risers and VIV of a riser has obvious 3D characteristics and is affected by the depth of the flow field as well as the effect of FSI. As a result, a 3D model with FSI for the VIV is more accurate and realistic.
- (2)
- The amplitude of the cross-flow vibration is much larger than that of the flow-direction vibration, and the cross-flow vibration has a distinct periodicity while the flow-direction vibration tends to be at a relatively stable value. The deformation of the three risers are different due to their geometries, material properties, top-tension force, constraints, etc.
- (3)
- Different risers have different stress distributions, i.e., the stresses of composite risers are generally smaller than those of steel riser and occur in the middle and fixed end of the composite risers.
- (4)
- For the composite risers modeled by EMM and LSM: (i) EMM and LSM lead to similar VIV results for the same composite riser and both can be utilized to obtain the global performance of the composite risers; and (ii) EMM is easier and more efficient for the global calculation; however, to show the response of the each composite lamina, LSM is compulsory.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ochoa, O.O.; Salama, M.M. Offshore composites: Transition barriers to an enabling technology. Compos. Sci. Technol. 2005, 65, 2588–2596. [Google Scholar] [CrossRef]
- Salama, M.M.; Martinussen, E.; Spencer, B.; Hanna, S.; Hsu, T.M.; Stjern, G.; Franco, E.; Storhaug, T.; Echtermeyer, A. Composite risers are ready for field applications-status of technology, field demonstration and life cycle economics. In Proceedings of the 13th Annual Deep Offshore Technology Conference, Rio de Janeiro, Brazil, 17–19 October 2001. [Google Scholar]
- Sparks, C.P.; Odru, P.; Bono, H.; Metivaud, G. Mechanical testing of high-performance composite tubes for TLP production risers. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 1988. [Google Scholar]
- Salama, M.M.; Johnson, D.B.; Long, J.R. Composite production riser-testing and qualification. SPE Prod. Facil. 1998, 13, 170–177. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration, 2nd ed.; Krieger Publishing Company: Malabar, FL, USA, 2001. [Google Scholar]
- Wang, C.; Shankar, K.; Morozov, E.V. Tailored local design of deep sea FRP composite risers. Adv. Compos. Mater. 2015, 24, 375–397. [Google Scholar] [CrossRef]
- Wang, C.; Shankar, K.; Morozov, E.V. Global design and analysis of deep sea FRP composite risers under combined environmental loads. Adv. Compos. Mater. 2017, 26, 79–98. [Google Scholar] [CrossRef]
- Salama, M.M.; Stjern, G.; Storhaug, T.; Spencer, B.; Echtermeyer, A. The first offshore field installation for a composite riser joint. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2002. [Google Scholar]
- Smith, K.L.; Leveque, M.E. Ultra-Deepwater Production Systems Technical-Progress Report; Conoco Phillips Company: Houston, TX, USA, 2003. [Google Scholar]
- Wang, C.; Shankar, K.; Morozov, E.V. Tailored design of top-tensioned composite risers for deep-water applications using three different approaches. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Smith, K.L.; Leveque, M.E. Ultra-Deepwater Production Systems Technical-Final Report; Conoco Phillips Company: Houston, TX, USA, 2005. [Google Scholar]
- Picard, D.; Hudson, W.; Bouquier, L.; Dupupet, G.; Zivanovic, I. Composite carbon thermoplastic tubes for deepwater application. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2007. [Google Scholar]
- Wang, C.; Shankar, K.; Ashraf, M.A.; Morozov, E.V.; Ray, T. Surrogate-assisted optimisation design of composite riser. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2016, 230, 18–34. [Google Scholar] [CrossRef]
- Feng, C.C. The Measurement of Vortex Induced Effects in Flow Past Stationary and Oscillating Circular and D-Section Cylinders; University of British Columbia: Vancouver, BC, Canada, 1968. [Google Scholar]
- Sarpkaya, T. Fluid forces on oscillating cylinders. J. Waterw. Port. Coast. Ocean Div. 1978, 104, 275–290. [Google Scholar]
- Gopalkrishnan, R. Vortex Induced Forces on Oscillating Bluff Cylinders; Department of Ocean Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 1993. [Google Scholar]
- Khalak, A.; Williamson, C.H.K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 1999, 13, 813–851. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C.H.K. Resonance forever: Existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluids Mech. 2002, 473, 147–166. [Google Scholar] [CrossRef]
- Hartlen, R.T.; Currie, I.G. Lift-oscillator model of vortex-induced vibration. J. Eng. Mech. Div. 1970, 96, 577–591. [Google Scholar]
- Skop, R.A.; Griffin, O.M. On a theory for the vortex-excited oscillations of flexible cylindrical structures. J. Sound Vib. 1975, 41, 263–274. [Google Scholar] [CrossRef]
- Kim, W.J.; Perkins, N.C. Two-dimensional vortex-induced vibration of cable suspensions. J. Fluids Struct. 2002, 16, 229–245. [Google Scholar] [CrossRef]
- Facchinetti, M.L.; de Langre, E.; Biolley, F. Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 2004, 19, 123–140. [Google Scholar] [CrossRef]
- Wu, X.; Huang, W. A new model for predicting vortex-induced vibration of a long flexible riser with large deformation. J. Vib. Shock 2013, 32, 21–25, 30. [Google Scholar]
- Guo, H.; Zhao, W.; Wang, F. Experimental investigation of the effect of internal flow on top tension of the riser. J. Ocean Univ. China 2015, 45, 102–109. [Google Scholar]
- Lou, M.; Yu, C. Dynamic responses of a riser under combined excitation of internal waves and background currents. Int. J. Naval Arch. Ocean 2014, 6, 685–699. [Google Scholar] [CrossRef]
- Tang, Y.; Shao, W.; Zhang, J.; Wang, L.Y.; Gui, L. Dynamic response analysis for coupled parametric vibration and vortex-induced vibration of top-tensioned riser in deep-sea. Eng. Mech. 2013, 30, 282–286. [Google Scholar]
- Huang, X.; Wang, J. Simulation of flow around a circular cylinder and vortex-induced vibraiont using the discrete vortex method. In Proceedings of the 11th National Symposium on Hydrodynamics, Zhejiang, China, 4–7 July 2013. [Google Scholar]
- Liu, J.; Guo, H.; Zhao, J. Numerical simulaiton of flow around two tandem circular cylinder of equal dimeter. J. Ocean Univ. China 2013, 43, 92–97. [Google Scholar]
- Ji, C.; Xiao, Z.; Wang, Y.; Wang, H. Numerical investigation on vortex-induced vibration of an elastically mounted circular cylinder at low Reynolds number using the fictitious domain method. Int. J. Comput. Fluid Dyn. 2011, 25, 207–221. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, H.; Tang, W. VIV fatigue reliability and fatigue safety factor analysis of deep-water riser. Ocean Eng. 2014, 32, 17–23. [Google Scholar]
- Tan, L.B.; Chen, Y.; Jaiman, R.K.; Sun, X.; Tan, V.B.C.; Tay, T.E. Coupled fluid–structure simulations for evaluating a performance of full-scale deepwater composite riser. Ocean Eng. 2015, 94, 19–35. [Google Scholar] [CrossRef]
- Huang, K.Z. Composite TTR design for an ultradeepwater TLP. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2005. [Google Scholar]
- Chen, Y.; Tan, L.B.; Jaiman, R.K.; Sun, X.; Tay, T.E.; Tan, V.B.C. Global-local analysis of a full-scale composite riser during vortex-induced vibration. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Bogetti, T.A.; Hoppel, C.P.R.; Drysdale, W.H. Three-Dimensional Effective Property and Strength Prediction of Thick Laminated Composite Media; Aberdeen Proving Ground, United States Army Research Laboratory: Adelphi, MD, USA, 1995. [Google Scholar]
- Sun, C.T.; Li, S. Three-dimensional effective elastic constant for thick laminates. J. Compos. Mater. 1988, 22, 629–639. [Google Scholar] [CrossRef]
- Chakrabarti, S.K. Handbook of Offshore Eengineering, 1st ed.; Elsevier: Plainfield, IL, USA, 2005. [Google Scholar]
















| Riser | I.D. (m) | O.D. (m) | Length (m) | Lay-Ups | t_liner (mm) | t_0° (mm) | t_±θ° (mm) | t_90° (mm) | ±θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Riser 1 | 0.25 | 0.3 | 12.5 | Monolithic steel | |||||
| Riser 2 | 0.25 | 0.326 | 12.5 | [liner/90/(0/90)10] | 6 | 1.165 | 1.85 | ||
| Riser 3 | 0.25 | 0.31 | 12.5 | [liner/03/(+52,−52)5/904] | 6 | 1.48 | 1.30 | 1.64 | 52 |
| Material | Density (kg/m3) | E1 (GPa) | E2 = E3 (GPa) | G12 = G13 (GPa) | ν12 = ν13 | G23 (GPa) | ν23 | (MPa) | (MPa) | (MPa) | (MPa) | τ12 (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Steel | 7850 | 207 | 0.3 | 625 | ||||||||
| PEEK | 1300 | 3.64 | 0.4 | 120 | ||||||||
| AS4-PEEK | 1561 | 131 | 8.7 | 5 | 0.28 | 2.78 | 0.48 | 1648 | 864 | 62.4 | 156.8 | 125.6 |
| Riser | ρeffective (kg/m3) | Ex (GPa) | Ey (GPa) | Ez (GPa) | Gxy (GPa) | Gxz (GPa) | Gyz (GPa) | νxy | νxz | νyz |
|---|---|---|---|---|---|---|---|---|---|---|
| Riser 2 | 1524.4 | 45.7 | 73.8 | 9.83 | 4.42 | 2.87 | 2.95 | 0.0316 | 0.479 | 0.453 |
| Riser 3 | 1513.3 | 30.4 | 50.28 | 9.59 | 16.44 | 2.46 | 2.75 | 0.251 | 0.378 | 0.284 |
| Flow Parameters | Riser Type | Re | Tension Force (N) | |
|---|---|---|---|---|
| density (kg/m3) | 1024 | Riser 1 | 101,887 | 31,145 |
| velocity (m/s) | 0.36 | Riser 2 | 110,716 | 12,838 |
| υ | 1.06 × 10−6 | Riser 3 | 105,283 | 9776 |
| Type | Riser 1 | Riser 2 Effective | Riser 2 Layered | Riser 3 Effective | Riser 3 Layered | |
|---|---|---|---|---|---|---|
| natural frequency /(Hz) | 7.87 | 8.64 | 8.85 | 6.98 | 6.82 | |
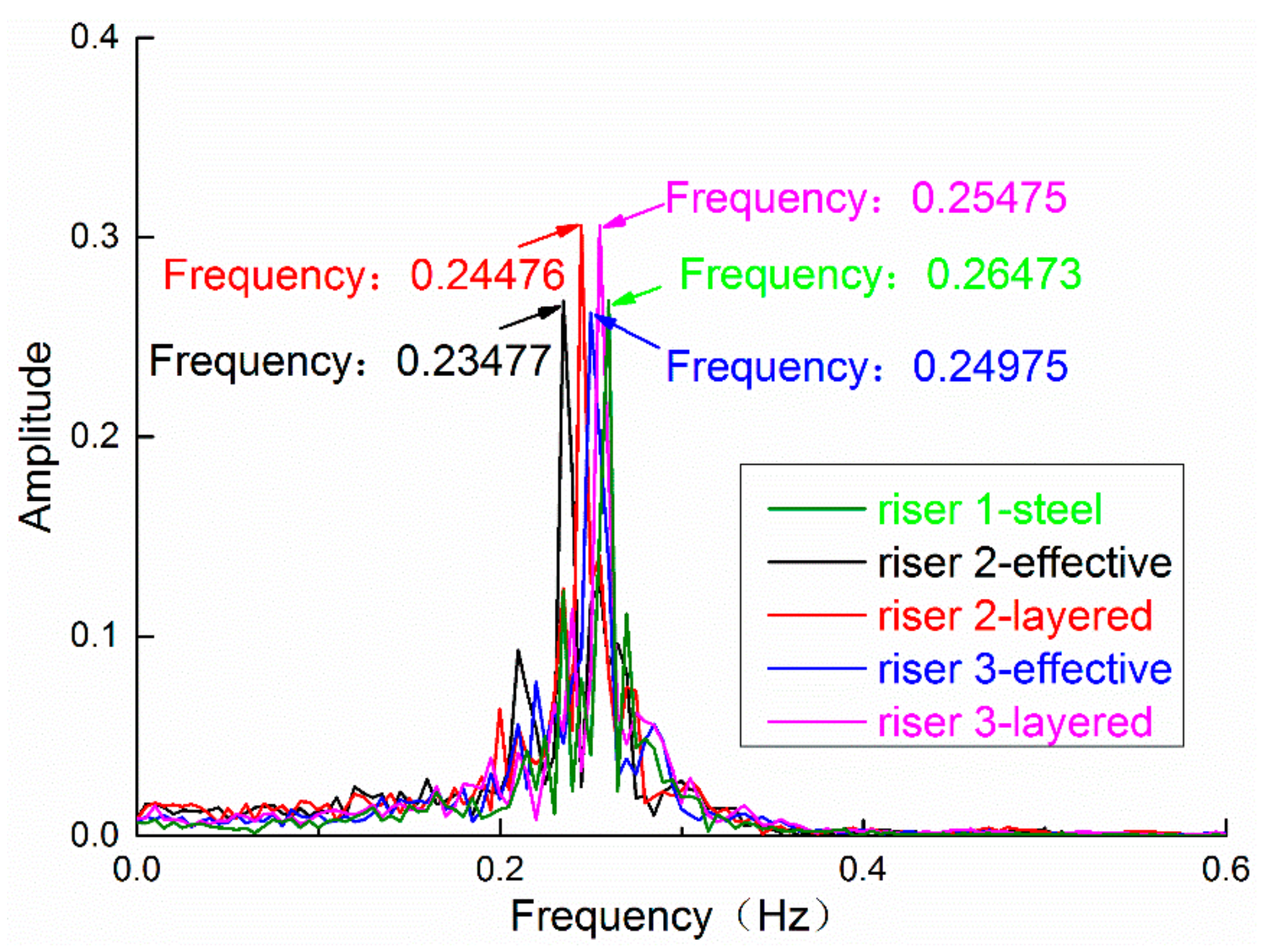
| vortex shedding frequency fs/(Hz) | Equation (9) | 0.25 | 0.23 | 0.23 | 0.24 | 0.24 |
| FFT of CL | 0.26 | 0.23 | 0.24 | 0.25 | 0.25 | |
| reduced velocity Ur | 0.153 | 0.13 | 0.12 | 0.17 | 0.17 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Sun, M.; Shankar, K.; Xing, S.; Zhang, L. CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods. Appl. Sci. 2018, 8, 684. https://doi.org/10.3390/app8050684
Wang C, Sun M, Shankar K, Xing S, Zhang L. CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods. Applied Sciences. 2018; 8(5):684. https://doi.org/10.3390/app8050684
Chicago/Turabian StyleWang, Chunguang, Mingyu Sun, Krishnakumar Shankar, Shibo Xing, and Lu Zhang. 2018. "CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods" Applied Sciences 8, no. 5: 684. https://doi.org/10.3390/app8050684
APA StyleWang, C., Sun, M., Shankar, K., Xing, S., & Zhang, L. (2018). CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods. Applied Sciences, 8(5), 684. https://doi.org/10.3390/app8050684