Comparison of CO2 Flow Behavior through Intact Siltstone Sample under Tri-Axial Steady-State and Transient Flow Conditions
Abstract
:1. Introduction
2. Experimental Methodology
2.1. Sample Description
2.2. Experimental Procedure
2.3. Permeability Calculation
3. Results and Discussion
3.1. Permeability Behavior of CO2 under Steady-State Conditions
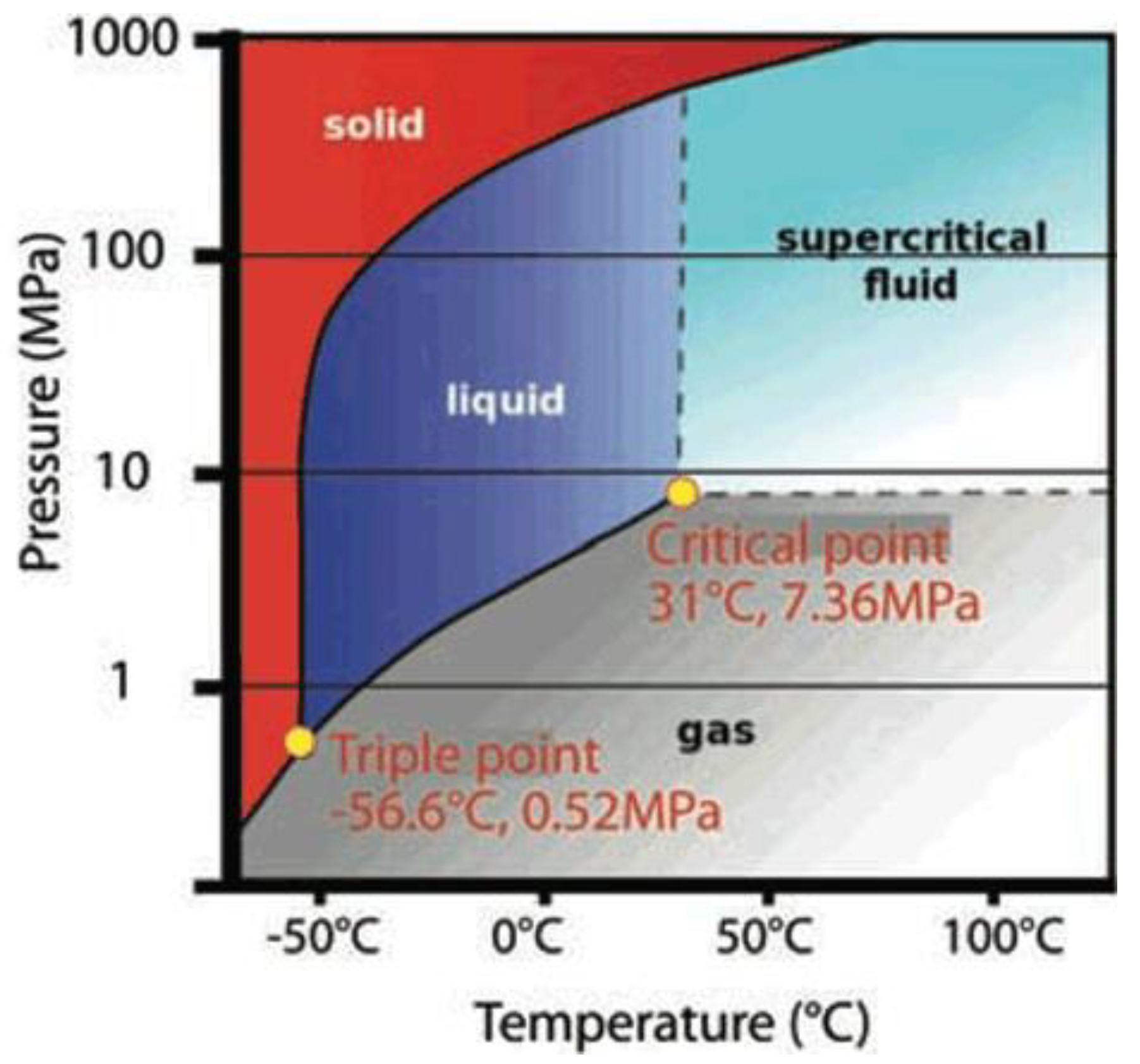
3.2. Considering Thermodynamic Properties Variation of CO2 Flow
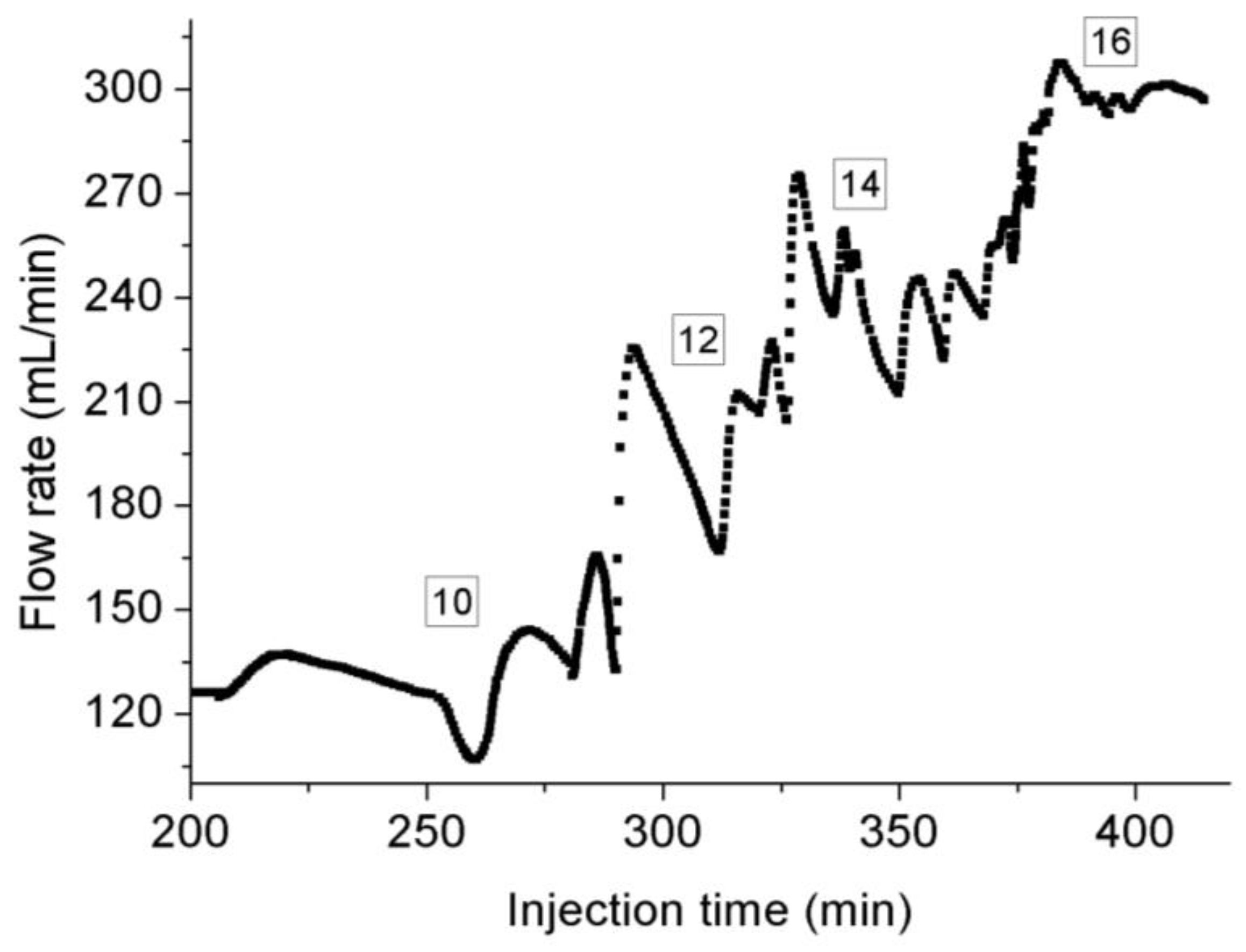
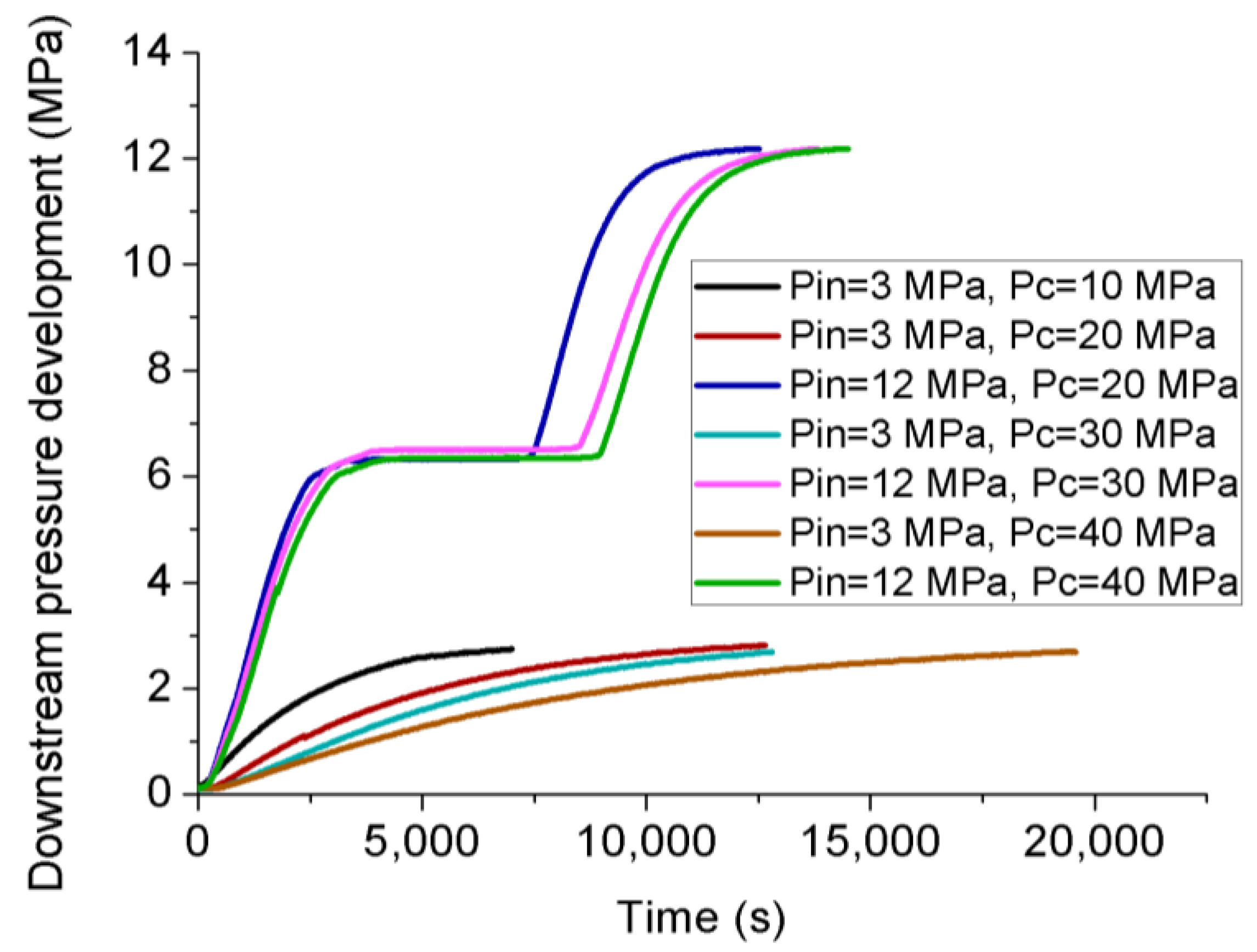
3.3. Permeability Behavior of CO2 under Transient Conditions
3.4. Effect of Effective Stress Law on Permeability Behavior of CO2
4. Conclusions
- (1).
- Much lower permeability values for liquid CO2 compared to gaseous CO2 were observed under transient conditions, due to the reduced slip-flow effect. Considering the significant difference of density between two phases, the mass flow rate of liquid CO2 is much higher than that of gaseous CO2.
- (2).
- Under steady-state conditions, the heat exchange with the decrease of pore pressure can greatly decrease the flow temperature due to the unique thermodynamic properties of CO2, which can liquefy the gaseous CO2 and extend the length of liquid CO2 along the sample, and much higher density of liquid CO2 can lead to higher flow rate recorded by flowmeter at room temperature. Faster temperature variation at higher injection pressure than 9 MPa can results in the presence of small drikold particles, which is responsible for the unstable flow rate at higher injection pressure.
- (3).
- Permeability calculated under transient conditions is much lower than that under steady-state conditions, except the reason that the slip-flow effect under steady-state conditions increased the flow behavior of CO2 through the tested sample with ultralow permeability, the influence of temperature variation can be excluded under transient conditions due to its much lower flow rate. During the field fracturing process, liquid CO2 is injected into the formation matrix at high pore pressure, and the conditions are closer to transient laboratory conditions. Therefore, the transient permeability calculation approach is more reliable for the shale fracturing process.
- (4).
- The variation of apparent permeability with injection pressure is affected by the combined effects of slip-flow effect, temperature variation and effective stress. Under transient conditions without any temperature variation, increasing the injection pressure caused an opposite trend of apparent permeability for gaseous and liquid CO2, because the slip-flow effect dominates the downward of permeability for gaseous CO2 and the effect of effective stress dominates the upward of permeability for liquid CO2, respectively. However, under steady-state conditions, although liquid CO2 showed a similar upward trend to that under transient conditions, gaseous CO2 permeability also exhibited an upward trend with the increase of injection pressure, which is opposite to that under transient conditions, because the influence of temperature variation becomes stronger with the increase of flow rate and increases the apparent permeability with the increase of injection pressure.
- (5).
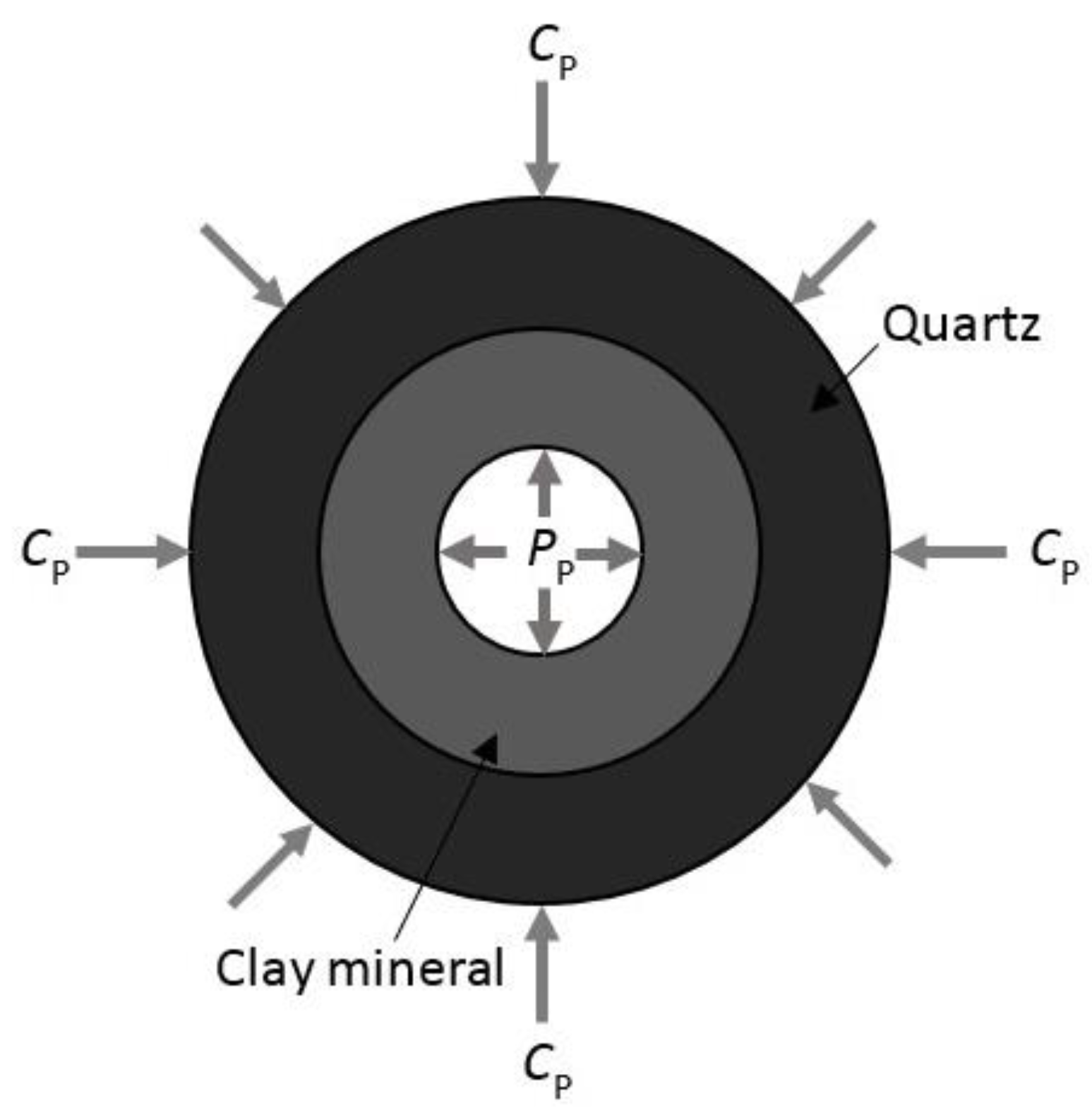
- Increasing the confining pressure causes the internal natural micro-fractures or preferential flow pathways in the rock matrix to close, which significantly reduces its flow capacity or permeability. A greater than 1 effective stress coefficient () for permeability confirms the greater sensitivity of CO2 to pore pressure compared to confining pressure due to the abundance of clay minerals.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- US Energy Information Administration. International Energy Outlook; US Energy Information Administration: Washington, DC, USA, 2011.
- Conti, J.; Holtberg, P.; Diefenderfer, J.; Napolitano, S.; Schaal, A.; Turnure, J.; Westfall, L. Annual Energy Outlook 2014 with Projections to 2040; US Energy Information Administration: Washington, DC, USA, 2014.
- Heller, R.; Vermylen, J.; Zoback, M. Experimental investigation of matrix permeability of gas shales. AAPG Bull. 2014, 98, 975–995. [Google Scholar] [CrossRef]
- Kumar, H.; Elsworth, D.; Mathews, J.; Marone, C. Permeability evolution in sorbing media: Analogies between organic-rich shale and coal. Geofluids 2015, 16, 43–55. [Google Scholar] [CrossRef]
- Liu, H.; Ranjith, P.; Georgi, D.; Lai, B. Some key technical issues in modelling of gas transport process in shales: A review. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 231–243. [Google Scholar] [CrossRef]
- Arnold, D. Liquid CO2 and sand: An alternative to water-based stimulation fluids. Pet. Eng. Int. 1998, 71, 89–92. [Google Scholar]
- Ghahremani, N.; Clapp, L. Feasibility of using brackish groundwater desalination concentrate as hydraulic fracturing fluid in the eagle ford shale. In Proceedings of the Shale Energy Engineering Conference 2014: Technical Challenges, Environmental Issues, and Public Policy, Pittsburgh, PA, USA, 21–23 July 2014; pp. 23–32. [Google Scholar]
- Gallegos, T.J.; Varela, B.A.; Haines, S.S.; Engle, M.A. Hydraulic fracturing water use variability in the United States and potential environmental implications. Water Resour. Res. 2015, 51, 5839–5845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birkle, P. Geochemical fingerprinting of hydraulic fracturing fluids from qusaiba hot shale and formation water from paleozoic petroleum systems, Saudi Arabia. Geofluids 2016, 16, 565–584. [Google Scholar] [CrossRef]
- Li, X.; Feng, Z.; Han, G.; Elsworth, D.; Marone, C.; Saffer, D.; Cheon, D.-S. Breakdown pressure and fracture surface morphology of hydraulic fracturing in shale with H2O, CO2 and N2. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 63–76. [Google Scholar] [CrossRef]
- Lillies, A.T.; King, S.R. Sand fracturing with liquid carbon dioxide. In Proceedings of the SPE Production Technology Symposium, Hobbs, NM, USA, 8–9 November 1982. [Google Scholar]
- Sinal, M.; Lancaster, G. Liquid CO2 fracturing: Advantages and limitations. J. Can. Pet. Technol. 1987, 26, 26–30. [Google Scholar] [CrossRef]
- Zhou, X.; Burbey, T. Fluid effect on hydraulic fracture propagation behavior: A comparison between water and supercritical CO2-like fluid. Geofluids 2014, 14, 174–188. [Google Scholar] [CrossRef]
- Perera, M.; Ranjith, P.; Choi, S.; Airey, D.; Weniger, P. Estimation of gas adsorption capacity in coal: A review and an analytical study. Int. J. Coal Prep. Util. 2012, 32, 25–55. [Google Scholar] [CrossRef]
- Ong, S.; Ramos, R.; Zheng, Z. Sand production prediction in high rate, perforated and open-hole gas wells. In Proceedings of the SPE International Symposium on Formation Damage Control, Lafayette, LA, USA, 23–24 February 2000. [Google Scholar]
- Godec, M.; Koperna, G.; Petrusak, R.; Oudinot, A. Potential for enhanced gas recovery and CO2 storage in the Marcellus Shale in the Eastern United States. Int. J. Coal Geol. 2013, 118, 95–104. [Google Scholar] [CrossRef]
- De Silva, P.; Ranjith, P. A study of methodologies for CO2 storage capacity estimation of saline aquifers. Fuel 2012, 93, 13–27. [Google Scholar] [CrossRef]
- Rushing, J.; Newsham, K.; Lasswell, P.; Cox, J.; Blasingame, T. Klinkenerg-corrected permeability measurements in tight gas sands: Steady-state versus unsteady-state techniques. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar]
- Perera, M.S.A.; Ranjith, P.G.; Choi, S.K.; Airey, D. Numerical simulation of gas flow through porous sandstone and its experimental validation. Fuel 2011, 90, 547–554. [Google Scholar] [CrossRef]
- Perera, M.; Ranjith, P.; Choi, S.; Airey, D. Investigation of temperature effect on permeability of naturally fractured black coal for carbon dioxide movement: An experimental and numerical study. Fuel 2012, 94, 596–605. [Google Scholar] [CrossRef]
- Carles, P.; Egermann, P.; Lenormand, R.; Lombard, J. Low permeability measurements using steady-state and transient methods. In Proceedings of the International Symposium of the SCA, Calgary, AB, Canada, 10–12 September 2007. [Google Scholar]
- Boulin, P.; Bretonnier, P.; Gland, N. Comparison of steady state method and transient methods for water permeability measurement in low permeability rocks. In Proceedings of the SPE Low Perm Symposium, Denver, CO, USA, 5–6 May 2016; p. 1234. [Google Scholar]
- Ranathunga, A.S.; Perera, M.S.A.; Ranjith, P.G.; Ju, Y.; Vishal, V.; De Silva, P.N.K. A macro-scale experimental study of sub- and super-critical CO2 flow behaviour in Victorian brown coal. Fuel 2015, 158, 864–873. [Google Scholar] [CrossRef]
- Zhang, C.; Ranjith, P.; Perera, M.; Zhao, J.; Zhang, D.; Wanniarachchi, W. A novel approach to precise evaluation of carbon dioxide flow behaviour in siltstone under tri-axial drained conditions. J. Nat. Gas Sci. Eng. 2016, 34, 331–340. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Jensen, J.L.; Pedersen, P.K.; Freeman, M. Innovative methods for flow-unit and pore-structure analyses in a tight siltstone and shale gas reservoir. AAPG Bull. 2012, 96, 355–374. [Google Scholar] [CrossRef]
- Burnham, A.K. Porosity and permeability of Green River oil shale and their changes during retorting. Fuel 2017, 203, 208–213. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, Q. Estimating permeability using median pore-throat radius obtained from mercury intrusion porosimetry. J. Geophys. Eng. 2013, 10, 25014. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Mostaghimi, P.; Armstrong, R.T.; Saadatfar, M.; Pinczewski, W.V. Porosity and permeability characterization of coal: A micro-computed tomography study. Int. J. Coal Geol. 2016, 154, 57–68. [Google Scholar] [CrossRef]
- Husain, R.A.; Zayed, A.S.; Ahmed, W.M.; Elhaji, H.S. Image segmentation with improved watershed algorithm using radial bases function neural networks. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 121–126. [Google Scholar]
- Bergaya, F.; Lagaly, G. Handbook of Clay Science; Newnes: Oxford, UK, 2013; Volume 5. [Google Scholar]
- Kuila, U.; Prasad, M. Specific surface area and pore-size distribution in clays and shales. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Kuila, U.; Prasad, M. Specific surface area and pore-size distribution in clays and shales. Geophys. Prospect. 2013, 61, 341–362. [Google Scholar] [CrossRef]
- Wu, T.; Li, X.; Zhao, J.; Zhang, D. Mutiscale pore structure and its effect on gas transport in organic-rich shale. Water Resour. Res. 2017, 7, 5438–5450. [Google Scholar] [CrossRef]
- Ranjith, P.; Perera, M. A new triaxial apparatus to study the mechanical and fluid flow aspects of carbon dioxide sequestration in geological formations. Fuel 2011, 90, 2751–2759. [Google Scholar] [CrossRef]
- Darabi, H.; Ettehad, A.; Javadpour, F.; Sepehrnoori, K. Gas flow in ultra-tight shale strata. J. Fluid Mech. 2012, 710, 641–658. [Google Scholar] [CrossRef]
- Klinkenberg, L. The permeability of porous media to liquids and gases. In Drilling and Production Practice; American Petroleum Institute: Tulsa, OK, USA, 1941; pp. 200–213. [Google Scholar]
- Kollek, J. The determination of the permeability of concrete to oxygen by the Cembureau method—A recommendation. Mater. Struct. 1989, 22, 225–230. [Google Scholar] [CrossRef]
- Lemmon, E.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: NIST Reference Fluid Thermodynamic and Transport Properties, REFPROP; Version 9.0; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010.
- Webster, C. The Discovery of Boyle’s Law, and the Concept of the Elasticity of Air in the Seventeenth Century. Arch. Hist. Exact Sci. 1965, 2, 441–502. [Google Scholar] [CrossRef]
- Bustin, R.M.; Bustin, A.M.; Cui, A.; Ross, D.; Pathi, V.M. Impact of shale properties on pore structure and storage characteristics. In Proceedings of the SPE Shale Gas Production Conference, Fort Worth, TX, USA, 16–18 November 2008. [Google Scholar]
- Tanikawa, W.; Shimamoto, T. Klinkenberg effect for gas permeability and its comparison to water permeability for porous sedimentary rocks. Hydrol. Earth Syst. Sci. Discussions 2006, 3, 1315–1338. [Google Scholar] [CrossRef]
- Ghabezloo, S.; Sulem, J.; Guédon, S.; Martineau, F. Effective stress law for the permeability of a limestone. Int. J. Rock Mech. Min. Sci. 2009, 46, 297–306. [Google Scholar] [CrossRef] [Green Version]
- Rathnaweera, T.; Ranjith, P.; Perera, M.; Yang, S. Determination of effective stress parameters for effective CO2 permeability in deep saline aquifers: An experimental study. J. Nat. Gas Sci. Eng. 2015, 24, 64–79. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Pruess, K. On CO2 fluid flow and heat transfer behavior in the subsurface, following leakage from a geologic storage reservoir. Environ. Geol. 2008, 54, 1677–1686. [Google Scholar] [CrossRef]
- Mungan, C.E. Irreversible Adiabatic Compression of an Ideal Gas; Naval Postgraduate School, Monterey CA Department of Physics: Monterey, CA, USA, 2003. [Google Scholar]
- Terzaghi, K.V. The shearing resistance of saturated soils and the angle between the planes of shear. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Cambridge, MA, USA, 22–26 June 1936; pp. 54–56. [Google Scholar]
- Biot, M.; Willis, D. The theory of consolidation. J. Appl. Elast. Coeff. Mech. 1957, 24, 594–601. [Google Scholar]
- Zoback, M.D.; Byerlee, J. Permeability and effective stress: Geologic notes. AAPG Bull. 1975, 59, 154–158. [Google Scholar]
- Walls, J.; Nur, A. Pore pressure and confining pressure dependence of permeability in sandstone. In Proceedings of the Transactions of the 7th Formation Evaluation Symposium, Calgary, AB, Canada, 21–24 October 1979; pp. 1–8. [Google Scholar]
- Al-Wardy, W.; Zimmerman, R.W. Effective stress law for the permeability of clay-rich sandstones. J. Geophys. Res. Solid Earth 2004, 109, 1029–1039. [Google Scholar] [CrossRef]






















| Confining Pressure(MPa) | Injection Pressure (MPa) | |
|---|---|---|
| Gaseous State | Liquid State | |
| 10 | 3, 4, 5, 6 | 7, 8, 9 |
| 20, 30, 40 | 3, 4, 5, 6 | 7, 8, 9, 10, 12, 14, 16 |
| Injection Pressure (MPa) | Confining Pressure (MPa) | |||
|---|---|---|---|---|
| 10 | 20 | 30 | 40 | |
| 7 | 23.96 | 26.74 | 34.18 | 28.99 |
| 8 | 40.16 | 41.67 | 47.47 | 45.56 |
| 9 | 48.59 | 49.60 | 54.78 | 53.33 |
| 10 | 56.55 | 60.00 | 58.12 | |
| 12 | 70.00 | 68.48 | 67.33 | |
| 14 | 75.29 | 76.79 | 77.31 | |
| 16 | 79.00 | 80.74 | 81.15 | |
| Confining Pressure (MPa) | Injection Pressure (MPa) | |
|---|---|---|
| Gaseous State | Liquid State | |
| 10 | 3, 6 | 9 |
| 20, 30, 40 | 3, 6 | 9, 12, 15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Pathegama Gamage, R.; Anne Perera, M.S. Comparison of CO2 Flow Behavior through Intact Siltstone Sample under Tri-Axial Steady-State and Transient Flow Conditions. Appl. Sci. 2018, 8, 1092. https://doi.org/10.3390/app8071092
Zhang C, Pathegama Gamage R, Anne Perera MS. Comparison of CO2 Flow Behavior through Intact Siltstone Sample under Tri-Axial Steady-State and Transient Flow Conditions. Applied Sciences. 2018; 8(7):1092. https://doi.org/10.3390/app8071092
Chicago/Turabian StyleZhang, Chengpeng, Ranjith Pathegama Gamage, and Mandadige Samintha Anne Perera. 2018. "Comparison of CO2 Flow Behavior through Intact Siltstone Sample under Tri-Axial Steady-State and Transient Flow Conditions" Applied Sciences 8, no. 7: 1092. https://doi.org/10.3390/app8071092
APA StyleZhang, C., Pathegama Gamage, R., & Anne Perera, M. S. (2018). Comparison of CO2 Flow Behavior through Intact Siltstone Sample under Tri-Axial Steady-State and Transient Flow Conditions. Applied Sciences, 8(7), 1092. https://doi.org/10.3390/app8071092







