Improving Stability Prediction in Peripheral Milling of Al7075T6
Abstract
:1. Introduction
2. Materials and Methods
2.1. Milling Stability Prediction with the EMHP Method
2.2. Effect of Runout and Cutting Speed
3. Results
3.1. Experimental Validation of Stability Prediction
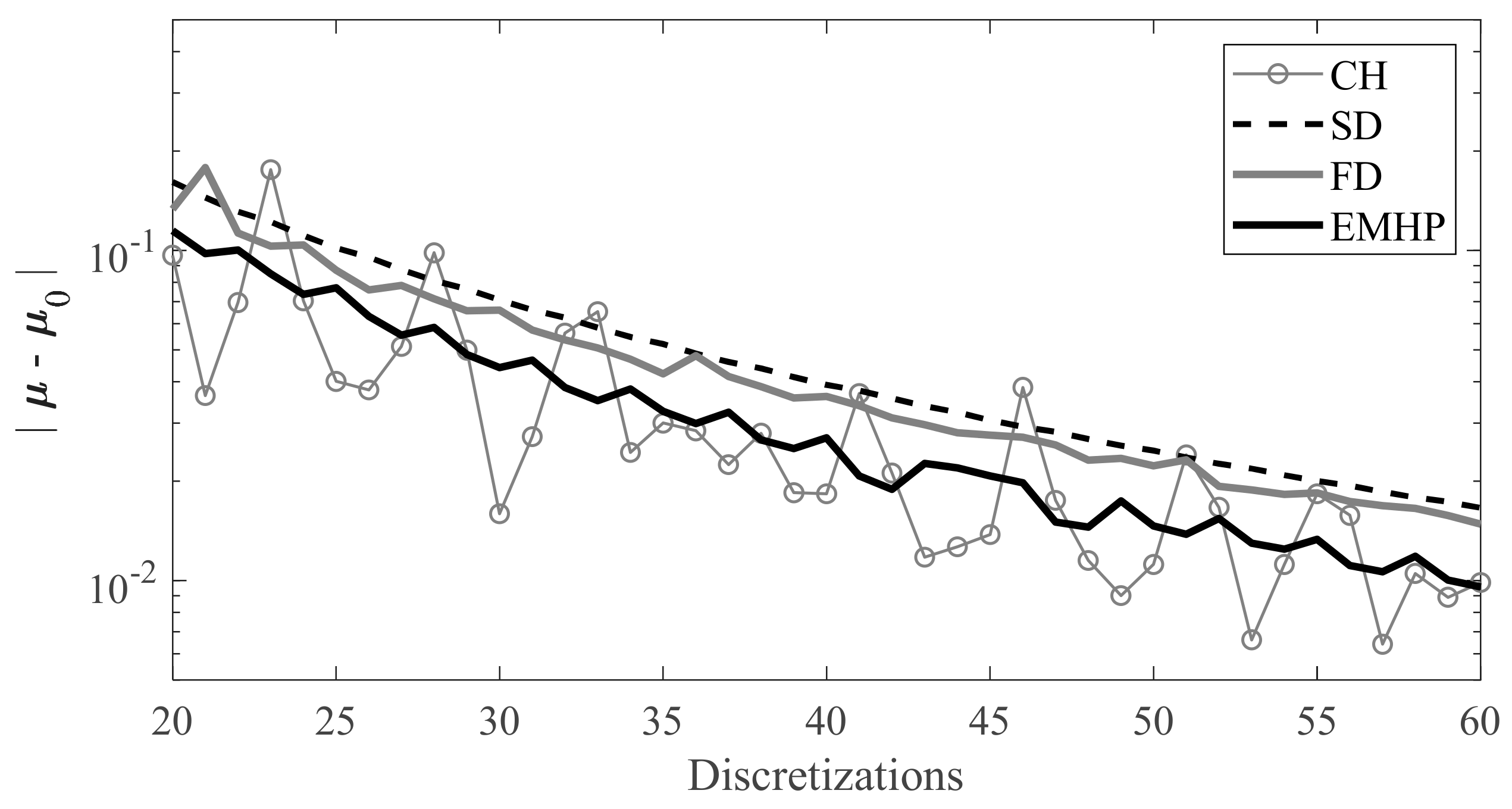
3.2. Accuracy and Computation Times
4. Discussion
5. Conclusions
- We observed a significant variation in the cutting forces depending on cutting speeds, and a model was thus proposed where the cutting-force coefficients varied depending on the cutting speed. Using an exponential cutting speed model, we described how the cutting-force coefficient decreased as a function of the increase in cutting speed.
- It was experimentally demonstrated that inclusion of the effects of the helix angle, runout, and characterization dependent on the cutting speed allowed for much more precise stability boundaries. Furthermore, typical stability lobes with constant cutting coefficients were found to only be valid for a narrow spindle speed range, meaning that their applicability is not valid in real practice.
- The convergence of the EMHP was compared with other efficient methods, such as the semi-discretization and full-discretization methods. When considering numeric convergence and computation times, the EMHP and Chebyshev proved to be the most efficient methods.
Author Contributions
Funding
Conflicts of Interest
References
- Smith, S.; Tlusty, J. Efficient Simulation Programs for Chatter in Milling. CIRP Ann. 1993, 42, 463–466. [Google Scholar] [CrossRef]
- Altintas, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Davies, M.A.; Pratt, J.R.; Dutterer, B.; Burns, T.J. Stability prediction for low radial immersion milling. J. Manuf. Sci. Eng. 2002, 124, 217–225. [Google Scholar] [CrossRef]
- Merdol, S.D.; Altintas, Y. Multifrequency solution of chatter stability for low immersion milling. J. Manuf. Sci. Eng. 2004, 126, 459–466. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Analytical prediction of chatter stability in milling—Part 1: General formulation. J. Dyn. Syst. Meas. Control 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Bayly, P.V.; Halley, J.E.; Mann, B.P.; Davies, M.A. Stability of interrupted cutting by temporal finite element analysis. J. Manuf. Sci. Eng. 2003, 125, 220–225. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G. Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G.; Turi, J. Comparison of zeroth-and first-order semi-discretizations, for the delayed Mathieu equation. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 3, pp. 2625–2629. [Google Scholar]
- Insperger, T.; Stepan, G.; Turi, J. On the higher-order semi-discretizations for periodic delayed systems. J. Sound Vib. 2008, 313, 334–341. [Google Scholar] [CrossRef]
- Butcher, E.A.; Nindujarla, P.; Bueler, E. Stability of up-and down-milling using Chebyshev collocation method. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005; Volume 6, pp. 841–850. [Google Scholar]
- Urbikain, G.; López de Lacalle, L.N.; Fernández, A. Regenerative vibration avoidance due to tool tangential dynamics in interrupted turning operations. J. Sound Vib. 2014, 333, 3996–4006. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; López de Lacalle, L.N.; Elías-Zúñiga, A. Spindle speed variation technique in turning operations: Modeling and real implementation. J. Sound Vib. 2016, 383, 384–396. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; López de Lacalle, L.N.; Elías-Zúñiga, A. Stability and vibrational behaviour in turning processes with low rotational speeds. Int. J. Adv. Manuf. Technol. 2015, 80, 871–885. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Insperger, T. Full-discretization and semi-discretization for milling stability prediction: Some comments. Int. J. Mach. Tools Manuf. 2010, 50, 658–662. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Second-order full-discretization method for milling stability prediction. Int. J. Mach. Tools Manuf. 2010, 50, 926–932. [Google Scholar] [CrossRef]
- Compeán, F.I.; Olvera, D.; Campa, F.J.; López de Lacalle, L.N.; Elías-Zúñiga, A.; Rodríguez, C.A. Characterization and stability analysis of a multivariable milling tool by the enhanced multistage homotopy perturbation method. Int. J. Mach. Tools Manuf. 2012, 57, 27–33. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Couey, J.; Marsh, E.; Mauntler, N.; Hughes, D. Runout effects in milling: Surface finish, surface location error, and stability. Int. J. Mach. Tools Manuf. 2007, 47, 841–851. [Google Scholar] [CrossRef]
- Engin, S.; Altintas, Y. Mechanics and dynamics of general milling cutters. Part I: Helical end mills. Int. J. Mach. Tools Manuf. 2001, 41, 2195–2212. [Google Scholar] [CrossRef]
- Mann, B.P.; Insperger, T.; Bayly, P.V.; Stepan, G. Stability of up-milling and down-milling, part 2: Experimental verification. Int. J. Mach. Tools Manuf. 2003, 43, 35–40. [Google Scholar] [CrossRef]
- Astakhov, V.P. Tribology of Metal Cutting, 1st ed.; Elsevier Science: New York, NY, USA, 2006; Volume 52. [Google Scholar]
- Kumme, R.; Mack, O.; Bill, B.; Gossweiler, C.; Haab, H.R. Dynamic Properties and Investigations of Piezoelectric Force Measuring Devices. VDI BERICHTE 2002, 1685, 161–172. [Google Scholar]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olvera, D.; Urbikain, G.; Elías-Zuñiga, A.; López de Lacalle, L.N. Improving Stability Prediction in Peripheral Milling of Al7075T6. Appl. Sci. 2018, 8, 1316. https://doi.org/10.3390/app8081316
Olvera D, Urbikain G, Elías-Zuñiga A, López de Lacalle LN. Improving Stability Prediction in Peripheral Milling of Al7075T6. Applied Sciences. 2018; 8(8):1316. https://doi.org/10.3390/app8081316
Chicago/Turabian StyleOlvera, Daniel, Gorka Urbikain, Alex Elías-Zuñiga, and Luis Norberto López de Lacalle. 2018. "Improving Stability Prediction in Peripheral Milling of Al7075T6" Applied Sciences 8, no. 8: 1316. https://doi.org/10.3390/app8081316
APA StyleOlvera, D., Urbikain, G., Elías-Zuñiga, A., & López de Lacalle, L. N. (2018). Improving Stability Prediction in Peripheral Milling of Al7075T6. Applied Sciences, 8(8), 1316. https://doi.org/10.3390/app8081316







