Thin Cap Fibroatheroma Detection in Virtual Histology Images Using Geometric and Texture Features
Abstract
1. Introduction
2. Related Works
3. Proposed Approach
3.1. Segmentation
3.1.1. Proposed KMPSO-mED Model and Its Adaptation to VH-IVUS Image Segmentation
3.1.2. Pre-Processing
3.1.3. K-Means Algorithm
3.1.4. Particle Swarm Optimisation (PSO)
3.1.5. Hybrid K-Means and PSO (KMPSO) Model
3.1.6. Pixel-Wise Classification Using Minimum the Euclidian Distance (mED) Algorithm
3.1.7. Cluster Validity
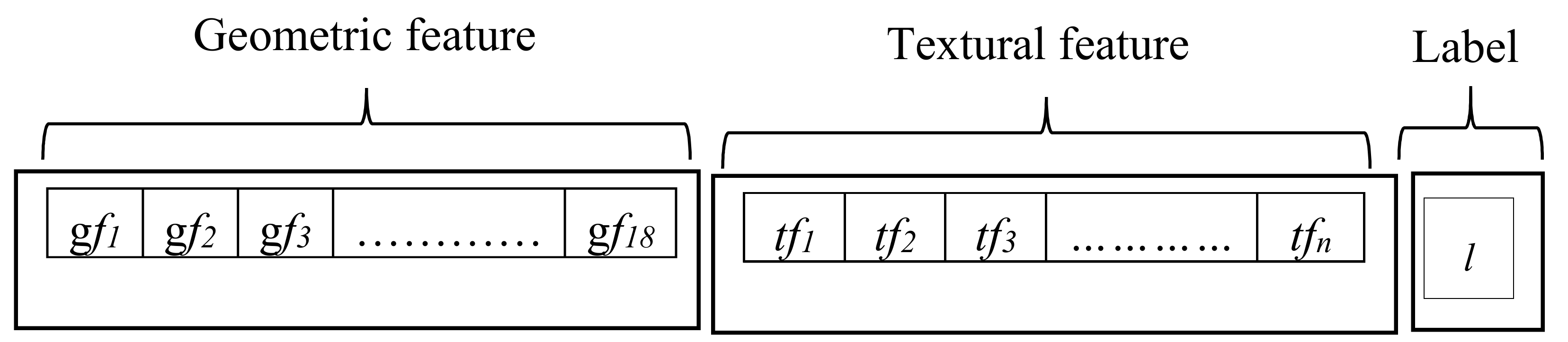
3.2. Feature Extraction
3.2.1. Geometric-Based Features
3.2.2. Texture-Based Features
3.2.3. Local Binary Patterns (LBP)
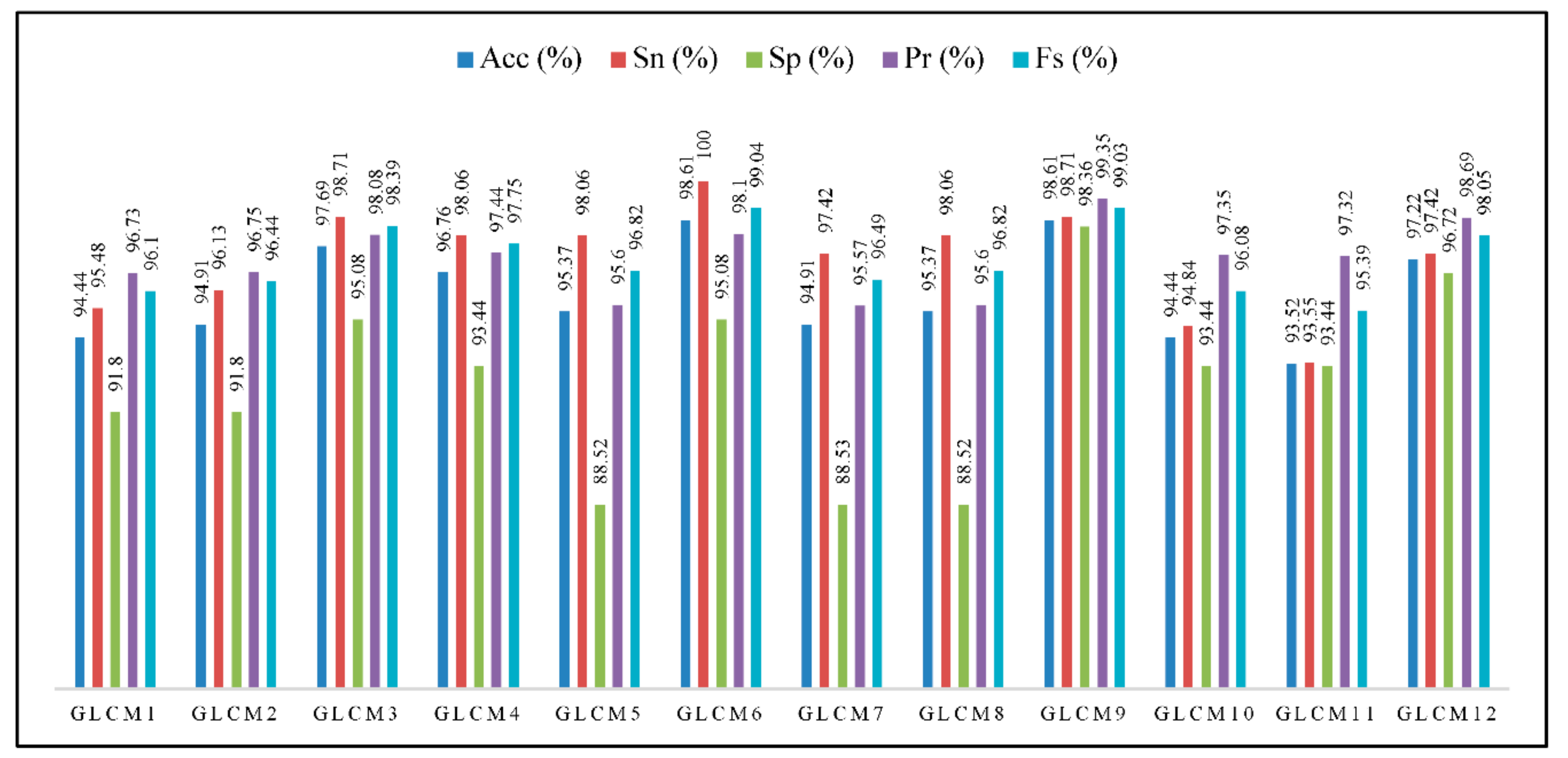
3.2.4. Grey Level Co-Occurrence Matrix (GLCM)
3.2.5. Modified Run Length Matrix (MRL)
3.2.6. Feature Selection
3.3. Classification
3.3.1. Machine Learning Algorithms
3.3.2. Evaluation
K-Fold Cross Validation
Performance Measures
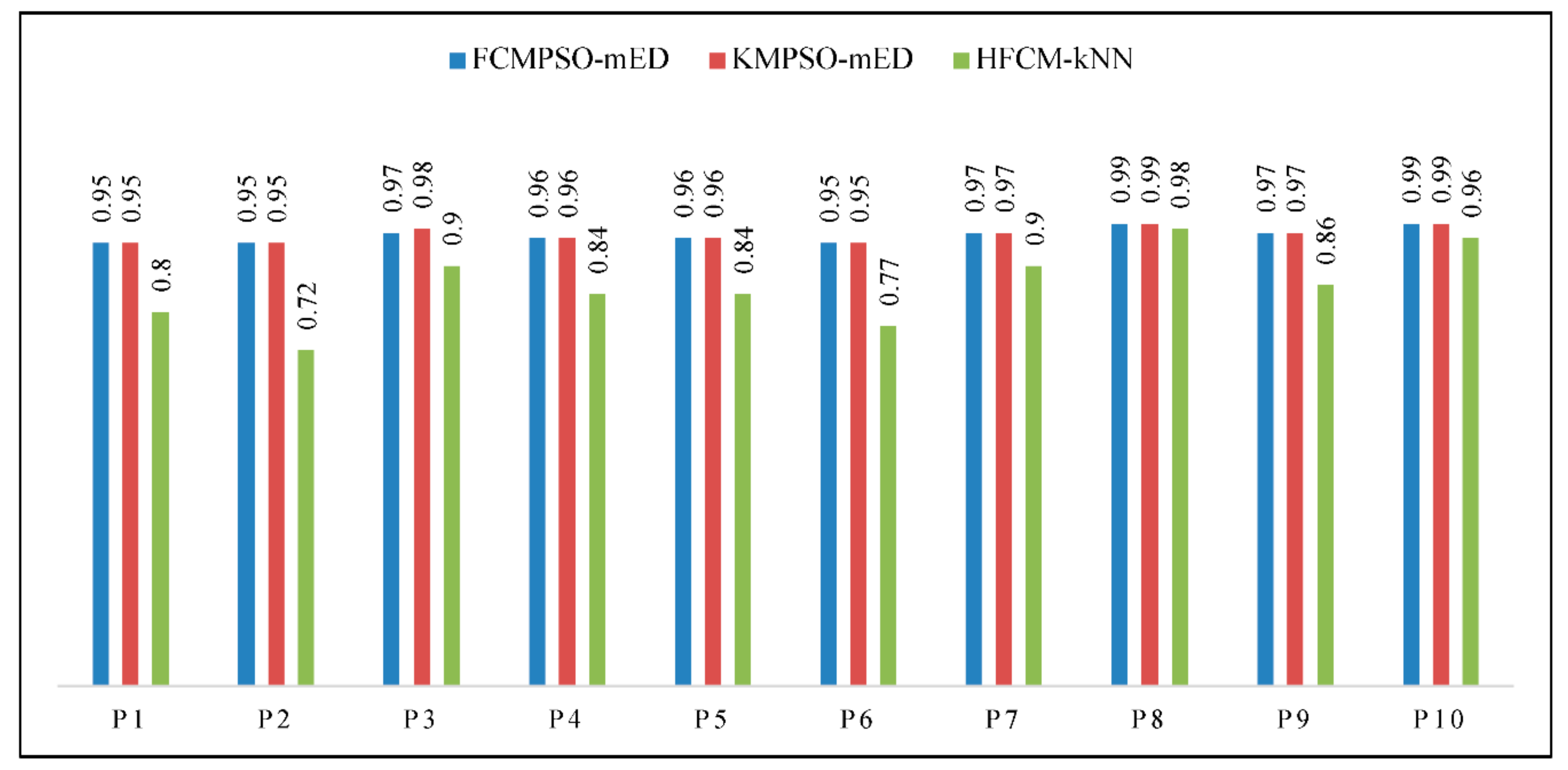
3.3.3. TCFA Detection Using Geometric Features
3.3.4. TCFA Detection Using Geometric and Texture Features
Combination of Geometric and LBP Features
Combination of Geometric and GLCM Features
Combination of Geometric and MRL Features
4. Validation
4.1. Validation by OCT
4.2. Validation Using VH-IVUS and IVUS Images
4.3. Validation Using VH-IVUS Images
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| ANN | Artificial Neural Network |
| CDC | Confluent DC |
| CLBT | Close Lumen Tracing |
| CNC | Confluent NC |
| DC | Dense Calcium |
| DCCL | Dense Calcium in Contact with the Lumen |
| DCL | DC Layering |
| DWPF | Discrete Wavelet Packet Frame |
| ECC | Extracting Confluent Component |
| ECG | Electrocardiogram |
| FCM | Fuzzy C-means |
| FCMPSO | Fuzzy C-means with Particle Swarm Optimisation |
| FF | Fibro-Fatty Tissue |
| FI | Fibrotic Tissue |
| FO | First Order |
| GLCM | Grey-Level Co-occurrence Matrix |
| HOG | Histogram of Oriented Gradients |
| IVUS | Intravascular Ultrasound |
| KMPSO | K-means and PSO |
| k-NN | K-Nearest Neighbour |
| LBP | Local Binary Patterns |
| mED | minimum Euclidean Distance |
| MRL | Modified Run Length |
| NC | Necrotic Core |
| NCCL | Necrotic Core in Contact with the Lumen |
| NCL | Necrotic Core Layering |
| NGL | Neighbouring Grey- Level |
| OCT | Optical Coherence Tomography |
| OLBT | Open Lumen Tracing |
| PBA | Plaque Burden Assessment |
| PSO | Particle Swarm Optimisation |
| ROI | Region of Interest |
| ST | Scattering Transforms |
| SOM | Self-Organising Maps |
| SVM | Support Vector Machine |
| SW | Silhouette Weight |
| TCFA | Thin cap fibroatheroma |
| VH-IVUS | Virtual Histology—Intravascular Ultrasound |
| VIAS | Volcano Corporation, San Diego, CA, USA |
| WF | Wavelet Features |
References
- Sun, S. An innovative intelligent system based on automatic diagnostic feature extraction for diagnosing heart diseases. Knowl.-Based Syst. 2015, 75, 224–238. [Google Scholar] [CrossRef]
- Konig, A.; Bleie, O.; Rieber, J.; Jung, P.; Schiele, T.M.; Sohn, H.Y.; Leibig, M.; Siebert, U.; Klauss, V. Intravascular ultrasound radiofrequency analysis of the lesion segment profile in ACS patients. Clin. Res. Cardiol. 2010, 99, 83–91. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.J.; Obaid, D.R.; Costopoulos, C.; Parker, R.A.; Calvert, P.A.; Teng, Z.; Hoole, S.P.; West, N.E.; Goddard, M.; Bennett, M.R. Direct comparison of virtual-histology intravascular ultrasound and optical coherence tomography imaging for identification of thin-cap fibroatheroma. Circ. Cardiovasc. Imaging 2015, 8, e003487. [Google Scholar] [PubMed]
- Cascón-Pérez, J.D.; de la Torre-Hernández, J.M.; Ruiz-Abellón, M.C.; Martínez-Pascual, M.; Mármol-Lozano, R.; López-Candel, J.; Cano, P.; Fernández, C.; Ramos, J.L.; Villegas, M. Characteristics of culprit atheromatous plaques obtained in vivo by intravascular ultrasound radiofrequency analysis: Results from the CULPLAC study. Am. Heart J. 2013, 165, 400–407. [Google Scholar] [CrossRef] [PubMed]
- Liang, M.; Puri, A.; Devlin, G. The vulnerable plaque: The real villain in acute coronary syndromes. Open Cardiovasc. Med. J. 2011, 5, 123–129. [Google Scholar] [CrossRef] [PubMed]
- Akasaka, T.; Kubo, T. Identification of Vulnerable Plaques with Optical Coherence Tomography. In Atherosclerotic Cardiovascular Disease; Pesek, D.K., Ed.; InTech: Tokyo, Japan, 2011. [Google Scholar]
- Escalera, S.; Pujol, O.; Mauri, J.; Radeva, P. Intravascular ultrasound tissue characterization with sub-class error-correcting output codes. J. Signal Process. Syst. 2009, 55, 35–47. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, P.; Shao, J.; Cheng, Y.; Zhang, Y.; Bai, J. A snake-based method for segmentation of intravascular ultrasound images and its in vivo validation. Ultrasonics 2011, 51, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Nair, A.; Kuban, B.D.; Obuchowski, N.; Vince, D.G. Assessing spectral algorithms to predict atherosclerotic plaque composition with normalized and raw intravascular ultrasound data. Ultrasound Med. Biol. 2001, 27, 1319–1331. [Google Scholar] [CrossRef]
- Katouzian, A. Quantifying Atherosclerosis: IVUS Imaging for Lumen Border Detection and Plaque Characterization. Ph.D. Thesis, Columbia University, New York, NY, USA, 2011. [Google Scholar]
- Papaioannou, T.G.; Schizas, D.; Vavuranakis, M.; Katsarou, O.; Soulis, D.; Stefanadis, C. Quantification of new structural features of coronary plaques by computational post-hoc analysis of virtual histology-intravascular ultrasound images. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 643–651. [Google Scholar] [CrossRef] [PubMed]
- Giannoglou, V.G.; Stavrakoudis, D.G.; Theocharis, J.B.; Petridis, V. Genetic fuzzy rule-based classification systems for tissue characterization of intravascular ultrasound images. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Czopek, K.; Legutko, J.; Jąkała, J. Quantitative assessment for confluent plaque area related to diagnostic IVUS/VH images. In Proceedings of the Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 717–720. [Google Scholar]
- Szczypiński, P.; Klepaczko, A.; Pazurek, M.; Daniel, P. Texture and color based image segmentation and pathology detection in capsule endoscopy videos. Comput. Methods Programs Biomed. 2014, 113, 396–411. [Google Scholar] [CrossRef] [PubMed]
- Ain, Q.; Jaffar, M.A.; Choi, T.-S. Fuzzy anisotropic diffusion based segmentation and texture based ensemble classification of brain tumor. Appl. Soft Comput. 2014, 21, 330–340. [Google Scholar] [CrossRef]
- Dagher, I.; Issa, S. Subband effect of the wavelet fuzzy C-means features in texture classification. Image Vis. Comput. 2012, 30, 896–905. [Google Scholar] [CrossRef]
- Nanni, L.; Brahnam, S.; Ghidoni, S.; Menegatti, E.; Barrier, T. Different approaches for extracting information from the co-occurrence matrix. PLoS ONE 2013, 8, e83554. [Google Scholar] [CrossRef] [PubMed]
- Raveaux, R.; Burie, J.-C.; Ogier, J.-M. Structured representations in a content based image retrieval context. J. Vis. Commun. Image Represent. 2013, 24, 1252–1268. [Google Scholar] [CrossRef]
- Xu, D.-H.; Kurani, A.S.; Furst, J.D.; Raicu, D.S. Run-length encoding for volumetric texture. Heart 2004, 27, 25–30. [Google Scholar]
- Taki, A.; Roodaki, A.; Setarehdan, S.K.; Avansari, S.; Unal, G.; Navab, N. An IVUS image-based approach for improvement of coronary plaque characterization. Comput. Boil. Med. 2013, 43, 268–280. [Google Scholar] [CrossRef] [PubMed]
- Pazinato, D.V.; Stein, B.V.; de Almeida, W.R.; Werneck, R.D.O.; Júnior, P.R.M.; Penatti, O.A.; Torres, R.D.S.; Menezes, F.H.; Rocha, A. Pixel-level tissue classification for ultrasound images. IEEE J. Biomed. Health Inform. 2016, 20, 256–267. [Google Scholar] [CrossRef] [PubMed]
- Giannoglou, V.; Theocharis, J. Decision Fusion of Multiple Classifiers for Coronary Plaque Characterization from IVUS Images. Int. J. Artif. Intell. Tools 2014, 23, 1460005. [Google Scholar] [CrossRef]
- Zhang, L.; Jing, J.; Zhang, H. Fabric Defect Classification Based on LBP and GLCM. J. Fiber Bioeng. Inform. 2015, 8, 81–89. [Google Scholar] [CrossRef]
- Athanasiou, L.S.; Karvelis, P.S.; Tsakanikas, V.D.; Naka, K.K.; Michalis, L.K.; Bourantas, C.V.; Fotiadis, D.I. A Novel Semiautomated Atherosclerotic Plaque Characterization Method Using Grayscale Intravascular Ultrasound Images: Comparison with Virtual Histology. Inf. Technol. Biomed. IEEE Trans. 2012, 16, 391–400. [Google Scholar] [CrossRef] [PubMed]
- Giannoglou, V.G.; Stavrakoudis, D.G.; Theocharis, J.B. IVUS-based characterization of atherosclerotic plaques using feature selection and SVM classification. In Proceedings of the 12th International Conference on Bioinformatics & Bioengineering (BIBE), Larnaca, Cyprus, 11–13 November 2012; pp. 715–720. [Google Scholar]
- Katouzian, A.; Karamalis, A.; Sheet, D.; Konofagou, E.; Baseri, B.; Carlier, S.G.; Eslami, A.; Konig, A.; Navab, N.; Laine, A.F. Iterative self-organizing atherosclerotic tissue labeling in intravascular ultrasound images and comparison with virtual histology. IEEE Trans. Biomed. Eng. 2012, 59, 3039–3049. [Google Scholar] [CrossRef] [PubMed]
- Dehnavi, S.M.; Babu, M.; Yazchi, M.; Basij, M. Automatic soft and hard plaque detection in IVUS images: A textural approach. In Proceedings of the 2013 IEEE Conference on Information & Communication Technologies (ICT), Thuckalay, India, 11–12 April 2013; pp. 214–219. [Google Scholar]
- Kannan, S.; Devi, R.; Ramathilagam, S.; Takezawa, K. Effective FCM noise clustering algorithms in medical images. Comput. Boil. Med. 2013, 43, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Jodas, D.S.; Pereira, A.S.; Tavares, J.M.R. A review of computational methods applied for identification and quantification of atherosclerotic plaques in images. Expert Syst. Appl. 2016, 46, 1–14. [Google Scholar] [CrossRef]
- Downe, R.W. Predictive Analysis of Coronary Plaque Morphology and Composition on a One Year Timescale. Ph.D. Thesis, University of Iowa, Iowa, IA, USA, 2013. [Google Scholar]
- Dhawale, P.; Rasheed, Q.; Griffin, N.; Wilson, D.L.; Hodgson, J.M. Intracoronary ultrasound plaque volume quantification. In Proceedings of the Computers in Cardiology, London, UK, 5–8 September 1993; pp. 121–124. [Google Scholar]
- Sonka, M.; Zhang, X.; Siebes, M.; Bissing, M.S.; DeJong, S.C.; Collins, S.M.; McKay, C.R. Segmentation of intravascular ultrasound images: A knowledge-based approach. IEEE Trans. Med. Imaging 1995, 14, 719–732. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Sonka, M.; Beichel, R.R. Graph-based IVUS segmentation with efficient computer-aided refinement. IEEE Trans. Med. Imaging 2013, 32, 1536–1549. [Google Scholar] [PubMed]
- Jones, J.-L.; Essa, E.; Xie, X.; Smith, D. Interactive segmentation of media-adventitia border in ivus. In Proceedings of the Computer Analysis of Images and Patterns, York, UK, 27–29 August 2013; pp. 466–474. [Google Scholar]
- Ciompi, F.; Pujol, O.; Gatta, C.; Alberti, M.; Balocco, S.; Carrillo, X.; Mauri-Ferre, J.; Radeva, P. HoliMAb: A holistic approach for Media–Adventitia border detection in intravascular ultrasound. Med. Image Anal. 2012, 16, 1085–1100. [Google Scholar] [CrossRef] [PubMed]
- Essa, E.; Xie, X.; Sazonov, I.; Nithiarasu, P. Automatic IVUS media-adventitia border extraction using double interface graph cut segmentation. In Proceedings of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 69–72. [Google Scholar]
- Katouzian, A.; Angelini, E.; Angelini, D.; Sturm, B.; Andrew, N.; Laine, F. Automatic detection of luminal borders in IVUS images by magnitude-phase histograms of complex brushlet coefficients. In Proceedings of the 32nd Annual International Conference of the IEEE EMBS, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 3073–3076. [Google Scholar]
- Lazrag, H.; Aloui, K.; Naceur, M.S. Automatic segmentation of lumen in intravascular ultrasound images using fuzzy clustering and active contours. In Proceedings of the International Conference on Control, Engineering and Information Technology Proceedings Engineering and Technology, Sousse, Tunisia, 4–7 June 2013; pp. 58–63. [Google Scholar]
- Mendizabal-Ruiz, E.G.; Rivera, M.; Kakadiaris, I.A. Segmentation of the luminal border in intravascular ultrasound B-mode images using a probabilistic approach. Med. Image Anal. 2013, 17, 649–670. [Google Scholar] [CrossRef] [PubMed]
- Sofian, H.; Ming, J.T.C.; Noor, N.M. Detection of the lumen boundary in the coronary artery disease. In Proceedings of the IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Dhaka, Bangladesh, 19–20 December 2015; pp. 143–146. [Google Scholar]
- Plissiti, M.E.; Fotiadis, D.I.; Michalis, L.K.; Bozios, G.E. An automated method for lumen and media-adventitia border detection in a sequence of IVUS frames. IEEE Trans. Inf. Technol. Biomed. 2004, 8, 131–141. [Google Scholar] [CrossRef] [PubMed]
- Giannoglou, G.D.; Chatzizisis, Y.S.; Koutkias, V.; Kompatsiaris, I.; Papadogiorgaki, M.; Mezaris, V.; Parissi, E.; Diamantopoulos, P.; Strintzis, M.G.; Maglaveras, N. A novel active contour model for fully automated segmentation of intravascular ultrasound images: In vivo validation in human coronary arteries. Comput. Boil. Med. 2007, 37, 1292–1302. [Google Scholar] [CrossRef] [PubMed]
- Taki, A.; Najafi, Z.; Roodaki, A.; Setarehdan, S.K.; Zoroofi, R.A.; Konig, A.; Navab, N. Automatic segmentation of calcified plaques and vessel borders in IVUS images. Int. J. Comput. Assist. Radiol. Surg. 2008, 3, 347–354. [Google Scholar] [CrossRef]
- Athanasiou, L.S.; Karvelis, P.S.; Sakellarios, A.I.; Exarchos, T.P.; Siogkas, P.K.; Tsakanikas, V.D.; Naka, K.K.; Bourantas, C.V.; Papafaklis, M.I.; Koutsouri, G. A hybrid plaque characterization method using intravascular ultrasound images. Technol. Health Care 2013, 21, 199–216. [Google Scholar] [PubMed]
- Rezaei, Z.; Selamat, A.; Taki, A.; Rahim, M.S.M.; Kadir, M.R.A. Automatic Plaque Segmentation based on hybrid Fuzzy Clustering and k Nearest Neighborhood using Virtual Histology Intravascular Ultrasound Images. Appl. Soft Comput. 2016. [Google Scholar] [CrossRef]
- Nanni, L.; Lumini, A.; Brahnam, S. Local binary patterns variants as texture descriptors for medical image analysis. Artif. Intell. Med. 2010, 49, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Taki, A. Improvement and Automatic Classification of IVUS-VH (Intravascular Ultrasound—Virtual Histology) Images; Technical University of Munich (TUM): Munich, Germany, 2010. [Google Scholar]
- Hassan, M.; Chaudhry, A.; Khan, A.; Kim, J.Y. Carotid artery image segmentation using modified spatial fuzzy c-means and ensemble clustering. Comput. Methods Programs Biomed. 2012, 108, 1261–1276. [Google Scholar] [CrossRef] [PubMed]
- Nair, A.; Kuban, B.D.; Tuzcu, E.M.; Schoenhagen, P.; Nissen, S.E.; Vince, D.G. Coronary plaque classification with intravascular ultrasound radiofrequency data analysis. Circulation 2002, 106, 2200–2206. [Google Scholar] [CrossRef] [PubMed]
- Mishra, T.; Mishra, C.; Das, B. An approach to the classification, diagnosis and management of vulnerable plaque. J. Indian Coll. Cardiol. 2013, 3, 57–66. [Google Scholar] [CrossRef]
- Katouzian, A.; Baseri, B.; Konofagou, E.E.; Laine, A.F. Texture-driven coronary artery plaque characterization using wavelet packet signatures. In Proceedings of the 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; pp. 197–200. [Google Scholar]
- Wang, X.-Y.; Wang, T.; Bu, J. Color image segmentation using pixel wise support vector machine classification. Pattern Recognit. 2011, 44, 777–787. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Wang, W.; Ma, J.; Qian, J.; Ge, J. Automatic segmentation of calcifications in intravascular ultrasound images using snakes and the contourlet transform. Ultrasound Med. Boil. 2010, 36, 111–129. [Google Scholar] [CrossRef] [PubMed]
- Foster, B.; Bagci, U.; Mansoor, A.; Xu, Z.; Mollura, D.J. A review on segmentation of positron emission tomography images. Comput. Boil. Med. 2014, 50, 76–96. [Google Scholar] [CrossRef] [PubMed]
- Hanmandlu, M.; Verma, O.P.; Susan, S.; Madasu, V.K. Color segmentation by fuzzy co-clustering of chrominance color features. Neurocomputing 2013, 120, 235–249. [Google Scholar] [CrossRef]
- El-Dahshan, E.-S.A.; Mohsen, H.M.; Revett, K.; Salem, A.-B.M. Computer-aided diagnosis of human brain tumor through MRI: A survey and a new algorithm. Expert Syst. Appl. 2014, 41, 5526–5545. [Google Scholar] [CrossRef]
- Zhao, F.; Xie, X.; Roach, M. Computer Vision Techniques for Transcatheter Intervention. IEEE J. Transl. Eng. Health Med. 2015, 3, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Mesejoa, P.; Ibánezd, Ó.; Cordónd, Ó.; Cagnonia, S. A survey on image segmentation using metaheuristic-based deformable models: State of the art and critical analysis. Appl. Soft Comput. 2016, 44, 1–29. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S. Image segmentation by fuzzy c-means clustering algorithm with a novel penalty term. Comput. Inform. 2012, 26, 17–31. [Google Scholar]
- Bora, D.J.; Gupta, A.K.; Khan, F.A. Comparing the Performance of L* A* B* and HSV Color Spaces with Respect to Color Image Segmentation. Int. J. Emerg. Technol. Adv. Eng. 2015, 5, 192–203. [Google Scholar]
- Beaumont, R.; Bhaganagar, K.; Segee, B.; Badak, O. Using fuzzy logic for morphological classification of IVUS-based plaques in diseased coronary artery in the context of flow-dynamics. Soft Comput. 2010, 14, 265–272. [Google Scholar] [CrossRef]
- Yang, M.-S.; Hu, Y.-J.; Lin, K.C.-R.; Lin, C.C.-L. Segmentation techniques for tissue differentiation in MRI of ophthalmology using fuzzy clustering algorithms. Magn. Reson. Imaging 2002, 20, 173–179. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, D. Locality sensitive C-means clustering algorithms. Neurocomputing 2010, 73, 2935–2943. [Google Scholar] [CrossRef]
- Sigut, M.; Alayón, S.; Hernández, E. Applying pattern classification techniques to the early detection of fuel leaks in petrol stations. J. Clean. Prod. 2014, 80, 262–270. [Google Scholar] [CrossRef]
- Kroon, D.-J. Segmentation of the Mandibular Canal in Cone-Beam CT Data; Citeseer: Enschede, The Netherlands, 2011. [Google Scholar]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Level set evolution without re-initialization: A new variational formulation. In Proceedings of the CVPR 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 430–436. [Google Scholar]
- Idris, I.; Selamat, A.; Nguyen, N.T.; Omatu, S.; Krejcar, O.; Kuca, K.; Penhaker, M. A combined negative selection algorithm–particle swarm optimization for an email spam detection system. Eng. Appl. Artif. Intell. 2015, 39, 33–44. [Google Scholar] [CrossRef]
- Saini, G.; Kaur, H. A Novel Approach towards K-Mean Clustering Algorithm with PSO. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 5978–5986. [Google Scholar]
- Mookiah, M.R.K.; Acharya, U.R.; Lim, C.M.; Petznick, A.; Suri, J.S. Data mining technique for automated diagnosis of glaucoma using higher order spectra and wavelet energy features. Knowl.-Based Syst. 2012, 33, 73–82. [Google Scholar] [CrossRef]
- Kalyani, S.; Swarup, K.S. Particle swarm optimization based K-means clustering approach for security assessment in power systems. Expert Syst. Appl. 2011, 38, 10839–10846. [Google Scholar] [CrossRef]
- Van der Merwe, D.; Engelbrecht, A.P. Data clustering using particle swarm optimization. In Proceedings of the 2003 Congress on Evolutionary Computation, CEC’03, Canberra, Australia, 8–12 December 2003; pp. 215–220. [Google Scholar]
- Mira, A.; Bhattacharyya, D.; Saharia, S. RODHA: Robust outlier detection using hybrid approach. Am. J. Intell. Syst. 2012, 2, 129–140. [Google Scholar] [CrossRef]
- Mala, C.; Sridevi, M. Color Image Segmentation Using Hybrid Learning Techniques. IT Converg. Pract. 2014, 2, 21–42. [Google Scholar]
- Saha, S.; Alok, A.K.; Ekbal, A. Brain image segmentation using semi-supervised clustering. Expert Syst. Appl. 2016, 52, 50–63. [Google Scholar] [CrossRef]
- Sowmya, B.; Rani, B.S. Colour image segmentation using fuzzy clustering techniques and competitive neural network. Appl. Soft Comput. 2011, 11, 3170–3178. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Arumugadevi, S.; Seenivasagam, V. Comparison of clustering methods for segmenting color images. Indian J. Sci. Technol. 2015, 8, 670–677. [Google Scholar] [CrossRef]
- Ai, L.; Zhang, L.; Dai, W.; Hu, C.; Kirk Shung, K.; Hsiai, T.K. Real-time assessment of flow reversal in an eccentric arterial stenotic model. J. Biomech. 2010, 43, 2678–2683. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Garcia, H.M.; Costa, M.A.; Serruys, P.W. Imaging of coronary atherosclerosis: Intravascular ultrasound. Eur. Heart J. 2010, 31, 2456–2469. [Google Scholar] [CrossRef] [PubMed]
- Depeursinge, A.; Fageot, J.; Al-Kadi, O.S. Fundamentals of Texture Processing for Biomedical Image Analysis: A General Definition and Problem Formulation. In Biomedical Texture Analysis; Elsevier: London, UK, 2018; pp. 1–27. [Google Scholar]
- Brunenberg, E.; Pujol, O.; ter Haar Romeny, B.; Radeva, P. Automatic IVUS segmentation of atherosclerotic plaque with stop & go snake. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Copenhagen, Denmark, 1–6 October 2006; pp. 9–16. [Google Scholar]
- Reddy, R.O.K.; Reddy, B.E.; Reddy, E.K. An Effective GLCM and Binary Pattern Schemes Based Classification for Rotation Invariant Fabric Textures. Int. J. Comput. Eng. Sci. 2014, 4. [Google Scholar] [CrossRef]
- Mookiah, M.R.K.; Acharya, U.R.; Martis, R.J.; Chua, C.K.; Lim, C.M.; Ng, E.; Laude, A. Evolutionary algorithm based classifier parameter tuning for automatic diabetic retinopathy grading: A hybrid feature extraction approach. Knowl.-Based Syst. 2013, 39, 9–22. [Google Scholar] [CrossRef]
- Acharya, U.R.; Faust, O.; Molinari, F.; Sree, S.V.; Junnarkar, S.P.; Sudarshan, V. Ultrasound-based tissue characterization and classification of fatty liver disease: A screening and diagnostic paradigm. Knowl.-Based Syst. 2015, 75, 66–77. [Google Scholar] [CrossRef]
- Aujol, J.-F.; Chan, T.F. Combining geometrical and textured information to perform image classification. J. Vis. Commun. Image Represent. 2006, 17, 1004–1023. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distribution. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Wang, R.; Dai, J.; Zheng, H.; Ji, G.; Qiao, X. Multi features combination for automated zooplankton classification. In Proceedings of the OCEANS—Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–5. [Google Scholar]
- Pietikäinen, M. Image analysis with local binary patterns. In Proceedings of the Scandinavian Conference on Image Analysis, Joensuu, Finland, 19–22 June 2005; pp. 115–118. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Sree, V.S.; Eugene, L.W.J.; Ghista, D.N.; San Tan, R. An integrated index for detection of Sudden Cardiac Death using Discrete Wavelet Transform and nonlinear features. Knowl.-Based Syst. 2015, 83, 149–158. [Google Scholar] [CrossRef]
- Taki, A.; Hetterich, H.; Roodaki, A.; Setarehdan, S.; Unal, G.; Rieber, J.; Navab, N.; König, A. A new approach for improving coronary plaque component analysis based on intravascular ultrasound images. Ultrasound Med. Boil. 2010, 36, 1245–1258. [Google Scholar] [CrossRef] [PubMed]
- Giannoglou, V.G.; Stavrakoudis, D.G.; Theocharis, J.B.; Petridis, V. Genetic fuzzy rule based classification systems for coronary plaque characterization based on intravascular ultrasound images. Eng. Appl. Artif. Intell. 2015, 38, 203–220. [Google Scholar] [CrossRef]
- Kennedy, R.L.; Lee, Y.; Roy, B.V.; Reed, C.D.; Lippmann, R.P. Solving Data Mining Problems through Pattern Recognition; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1998; Chapter 19; pp. 11–16. [Google Scholar]
- Falasconi, M.; Gutierrez, A.; Pardo, M.; Sberveglieri, G.; Marco, S. A stability based validity method for fuzzy clustering. Pattern Recognit. 2010, 43, 1292–1305. [Google Scholar] [CrossRef]
- Liu, Z.-G.; Pan, Q.; Dezert, J. Classification of uncertain and imprecise data based on evidence theory. Neurocomputing 2014, 133, 459–470. [Google Scholar] [CrossRef]
- Wu, C.-H.; Lai, C.-C.; Chen, C.-Y.; Chen, Y.-H. Automated clustering by support vector machines with a local-search strategy and its application to image segmentation. Opt. Int. J. Light Electron Opt. 2015, 126, 4964–4970. [Google Scholar] [CrossRef]
- Ren, J. ANN vs. SVM: Which one performs better in classification of MCCs in mammogram imaging. Knowl.-Based Syst. 2012, 26, 144–153. [Google Scholar] [CrossRef]
- Antkowiak, M. Artificial Neural Networks vs. Support Vector Machines for Skin Diseases Recognition. Master’s Thesis, Department of Computing Science, Umea University, Umeå, Sweden, 2006. [Google Scholar]
- Zanaty, E. Support vector machines (SVMs) versus multilayer perception (MLP) in data classification. Egypt. Inform. J. 2012, 13, 177–183. [Google Scholar] [CrossRef]
- Ciompi, F.; Gatta, C.; Pujol, O.; Rodrıguez-Leor, O.; Ferré, J.M.; Radeva, P. Reconstruction and Analysis of Intravascular Ultrasound Sequences. Recent Adv. Biomed. Signal Process. 2010, 1, 223–243. [Google Scholar]
- Anooj, P. Clinical decision support system: Risk level prediction of heart disease using weighted fuzzy rules. J. King Saud Univ. Comput. Inf. Sci. 2012, 24, 27–40. [Google Scholar] [CrossRef]
- Selvathi, D.; Emimal, N. Statistical modeling for the characterization of atheromatous plaque in Intravascular Ultrasound images. In Proceedings of the 2012 International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 15–16 March 2012; pp. 320–324. [Google Scholar]
- Obaid, D.R.; Calvert, P.A.; McNab, D.; West, N.E.; Bennett, M.R. Identification of coronary plaque sub-types using virtual histology intravascular ultrasound is affected by inter-observer variability and differences in plaque definitions. Circ. Cardiovasc. Imaging 2012, 5, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Selamat, A.; Subroto, I.M.I.; Ng, C.-C. Arabic script web page language identification using hybrid-KNN method. Int. J. Comput. Intell. Appl. 2009, 8, 315–343. [Google Scholar] [CrossRef]
- Gonzalo, N.; Garcia-Garcia, H.M.; Regar, E.; Barlis, P.; Wentzel, J.; Onuma, Y.; Ligthart, J.; Serruys, P.W. In vivo assessment of high-risk coronary plaques at bifurcations with combined intravascular ultrasound and optical coherence tomography. JACC Cardiovasc. Imaging 2009, 2, 473–482. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T.; Ino, Y.; Tanimoto, T.; Kitabata, H.; Tanaka, A.; Akasaka, T. Optical coherence tomography imaging in acute coronary syndromes. Cardiol. Res. Pract. 2011. [Google Scholar] [CrossRef] [PubMed]
- Kermani, A.; Ayatollahi, A.; Taki, A. Full-Automated 3D Analysis of Coronary Plaque using Hybrid Intravascular Ultrasound (IVUS) and Optical Coherence (OCT). In Proceedings of the 2nd Conference on Novel Approaches of Biomedical Engineering in Cardiovascular Diseases; Available online: https://www.researchgate.net/publication/306094665_Full-Automated_3D_Analysis_of_Coronary_Plaque_using_Hybrid_Intravascular_Ultrasound_IVUS_and_Optical_Coherence_OCT (accessed on 9 September 2018).
- Calvert, P.A.; Obaid, D.R.; O’Sullivan, M.; Shapiro, L.M.; McNab, D.; Densem, C.G.; Schofield, P.M.; Braganza, D.; Clarke, S.C.; Ray, K.K. Association between IVUS findings and adverse outcomes in patients with coronary artery disease: The VIVA (VH-IVUS in Vulnerable Atherosclerosis) Study. JACC Cardiovasc. Imaging 2011, 4, 894–901. [Google Scholar] [CrossRef] [PubMed]
- König, A.; Klauss, V. Virtual histology. Heart 2007, 93, 977–982. [Google Scholar] [CrossRef] [PubMed]
- Chavan, N.V.; Jadhav, B.; Patil, P. Detection and classification of brain tumors. Int. J. Comput. Appl. 2015, 112, 48–53. [Google Scholar]














| Source | Segmentation | Technique | Advantages | Disadvantages |
|---|---|---|---|---|
| Dhawale, Rasheed, Griffin, Wilson and Hodgson [31] | Dynamic search algorithm | Semi-automatic |
|
|
| Sonka, Zhang, Siebes, Bissing, DeJong, Collins and McKay [32] | Heuristic graph searching and global image information | Semi-automatic |
|
|
| Plissiti, Fotiadis, Michalis and Bozios [41] | Deformable model | Automatic |
|
|
| Giannoglou, Chatzizisis, Koutkias, Kompatsiaris, Papadogiorgaki, Mezaris, Parissi, Diamantopoulos, Strintzis and Maglaveras [42] | Deformable model | Automatic |
|
|
| Taki, Najafi, Roodaki, Setarehdan, Zoroofi, Konig and Navab [43] | Active contours and level sets | Automatic |
|
|
| Katouzian, Angelini, Angelini, Sturm, Andrew and Laine [37] | Brushlet Analysis and Fourier Domain | Automatic |
|
|
| Zhu, Zhang, Shao, Cheng, Zhang and Bai [8] | Gradient vector flow snake model | Automatic |
|
|
| Essa, Xie, Sazonov and Nithiarasu [36] | Graph cut | Automatic |
|
|
| Ciompi, Pujol, Gatta, Alberti, Balocco, Carrillo, Mauri-Ferre and Radeva [35] | Holistic approach | Automatic |
|
|
| Athanasiou, Karvelis, Sakellarios, Exarchos, Siogkas, Tsakanikas, Naka, Bourantas, Papafaklis and Koutsouri [44] | deformable models | Automatic |
|
|
| Sun, Sonka and Beichel [33] | Graph-based | Automatic segmentationanduser-guided refinement |
|
|
| Lazrag, Aloui and Naceur [38] | FCM algorithm and active contours | Automatic |
|
|
| Mendizabal-Ruiz, Rivera and Kakadiaris [39] | Deformable curve | Automatic |
|
|
| Jones, Essa, Xie and Smith [34] | Graph-cut | User-assisted |
|
|
| Sofian, Ming and Noor [40] | Otsu threshold | Automatic |
|
|
| Parameters | Description |
|---|---|
| Particle | Candidate solution to a problem |
| Velocity | Rate of position change |
| Fitness | The best solution achieved |
| pbest | Best value obtained in previous particle |
| gbest | Best value obtained so far by any particle in the population |
| No | VH-IVUS | Plaque | FF | FI | NC | DC | SW |
|---|---|---|---|---|---|---|---|
| 1 |  |  | 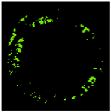 |  |  |  | 0.95 |
| 2 | 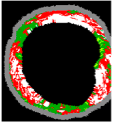 | 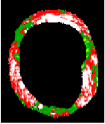 |  |  |  |  | 0.95 |
| 3 | 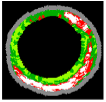 |  |  |  |  |  | 0.95 |
| 4 |  |  |  |  |  |  | 0.93 |
| 5 | 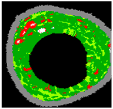 | 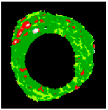 |  |  |  |  | 0.95 |
| 6 | 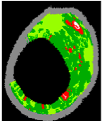 | 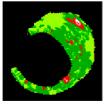 |  |  |  |  | 0.96 |
| 7 | 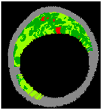 |  |  | 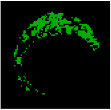 |  | - | 0.97 |
| 8 | 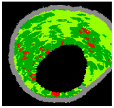 | 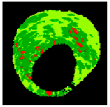 |  |  |  | - | 0.94 |
| 9 |  |  |  | 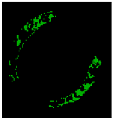 | - | - | 0.98 |
| Class | Classified as Positive | Classified as Negative |
|---|---|---|
| + | TP: The number of correctly predicted positives. | FN: The number of incorrectly predicted negatives. |
| − | FP: The number of incorrectly predicted positives. | TN: The number of correctly predicted negatives. |
| Classifiers | Acc (%) | Sn (%) | Sp (%) | Pr (%) | FS (%) |
|---|---|---|---|---|---|
| BPNN | 87.04 | 98.91 | 18.75 | 87.50 | 92.86 |
| KNN_5 | 95.37 | 98.37 | 78.13 | 96.28 | 97.31 |
| KNN_10 | 92.59 | 97.83 | 62.50 | 93.75 | 95.74 |
| KNN_15 | 93.06 | 96.20 | 75.00 | 95.68 | 95.94 |
| KNN_20 | 87.50 | 96.74 | 34.38 | 89.45 | 92.95 |
| KNN_25 | 88.43 | 97.83 | 34.38 | 89.55 | 93.51 |
| KNN_30 | 88.43 | 97.83 | 34.38 | 89.55 | 93.51 |
| SVM_MLP | 82.87 | 85.81 | 75.41 | 89.86 | 87.79 |
| SVM_Linear | 95.83 | 96.77 | 93.44 | 97.40 | 97.09 |
| SVM_Poly_1 | 96.71 | 98.71 | 91.80 | 96.84 | 97.76 |
| SVM_Poly_2 | 96.76 | 97.42 | 95.08 | 98.05 | 97.73 |
| SVM_Poly_3 | 97.69 | 99.35 | 93.44 | 97.47 | 98.40 |
| SVM_rbf_0.80 | 95.83 | 98.71 | 88.52 | 95.63 | 97.14 |
| SVM_rbf_0.90 | 96.76 | 99.35 | 90.16 | 96.25 | 97.78 |
| SVM_rbf_1 | 95.83 | 98.06 | 90.16 | 96.20 | 97.12 |
| SVM_rbf_1.10 | 97.69 | 100 | 91.80 | 96.88 | 98.41 |
| SVM_rbf_1.20 | 97.22 | 98.06 | 95.08 | 98.06 | 98.06 |
| Feature | Description |
|---|---|
| GF_LBP | Combined geometric and LBP features. |
| GF_LBP_PCA | Combined geometric and the first principle components of LBP |
| GF_GLCM | Combined geometric and GLCM features. |
| GF_GLCM_PCA | Combined geometric and first principle components of GLCM |
| GF_MRL | Combined geometric and MRL features. |
| GF_MRL_PCA | Combined geometric and the first principle components of MRL |
| TP | TN | FP | FN | Accuracy | Sensitivity | Specificity | Precision | F-Score |
|---|---|---|---|---|---|---|---|---|
| 11 | 2 | 0 | 1 | 92.85% | 91.67% | 100% | 100% | 95.65% |
| Method | TP | TN | FP | FN | Accuracy | Sensitivity | Specificity | Precision | F-Score |
|---|---|---|---|---|---|---|---|---|---|
| CA&CD | 9 | 38 | 2 | 9 | 81.03 | 50 | 95 | 81.81 | 62.07 |
| CA&SVM | 11 | 35 | 5 | 7 | 79.31 | 61.11 | 87.50 | 68.75 | 64.70 |
| CD&SVM | 8 | 39 | 3 | 8 | 81.03 | 84.81 | 84.81 | 84.81 | 75.78 |
| TP | TN | FP | FN | Accuracy | Sensitivity | Specificity | Precision | F-Score |
|---|---|---|---|---|---|---|---|---|
| 41 | 33 | 0 | 2 | 97.36 | 95.34 | 100 | 100 | 97.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaei, Z.; Selamat, A.; Taki, A.; Mohd Rahim, M.S.; Abdul Kadir, M.R.; Penhaker, M.; Krejcar, O.; Kuca, K.; Herrera-Viedma, E.; Fujita, H. Thin Cap Fibroatheroma Detection in Virtual Histology Images Using Geometric and Texture Features. Appl. Sci. 2018, 8, 1632. https://doi.org/10.3390/app8091632
Rezaei Z, Selamat A, Taki A, Mohd Rahim MS, Abdul Kadir MR, Penhaker M, Krejcar O, Kuca K, Herrera-Viedma E, Fujita H. Thin Cap Fibroatheroma Detection in Virtual Histology Images Using Geometric and Texture Features. Applied Sciences. 2018; 8(9):1632. https://doi.org/10.3390/app8091632
Chicago/Turabian StyleRezaei, Zahra, Ali Selamat, Arash Taki, Mohd Shafry Mohd Rahim, Mohammed Rafiq Abdul Kadir, Marek Penhaker, Ondrej Krejcar, Kamil Kuca, Enrique Herrera-Viedma, and Hamido Fujita. 2018. "Thin Cap Fibroatheroma Detection in Virtual Histology Images Using Geometric and Texture Features" Applied Sciences 8, no. 9: 1632. https://doi.org/10.3390/app8091632
APA StyleRezaei, Z., Selamat, A., Taki, A., Mohd Rahim, M. S., Abdul Kadir, M. R., Penhaker, M., Krejcar, O., Kuca, K., Herrera-Viedma, E., & Fujita, H. (2018). Thin Cap Fibroatheroma Detection in Virtual Histology Images Using Geometric and Texture Features. Applied Sciences, 8(9), 1632. https://doi.org/10.3390/app8091632









