Numerical Study on the Seismic Response of Fluid-Saturated Porous Media Using the Precise Time Integration Method
Abstract
:1. Introduction
2. The u-p Dynamic Formulation for Wave Motion in FSPM
2.1. Basic Assumptions
2.2. Expressions of u-p Dynamic Formulation
3. Time-Stepping Explicit Algorithm for Numerical Solution to u-p Dynamic Formulation
3.1. Algorithm Implementation
3.2. Algorithm Validation
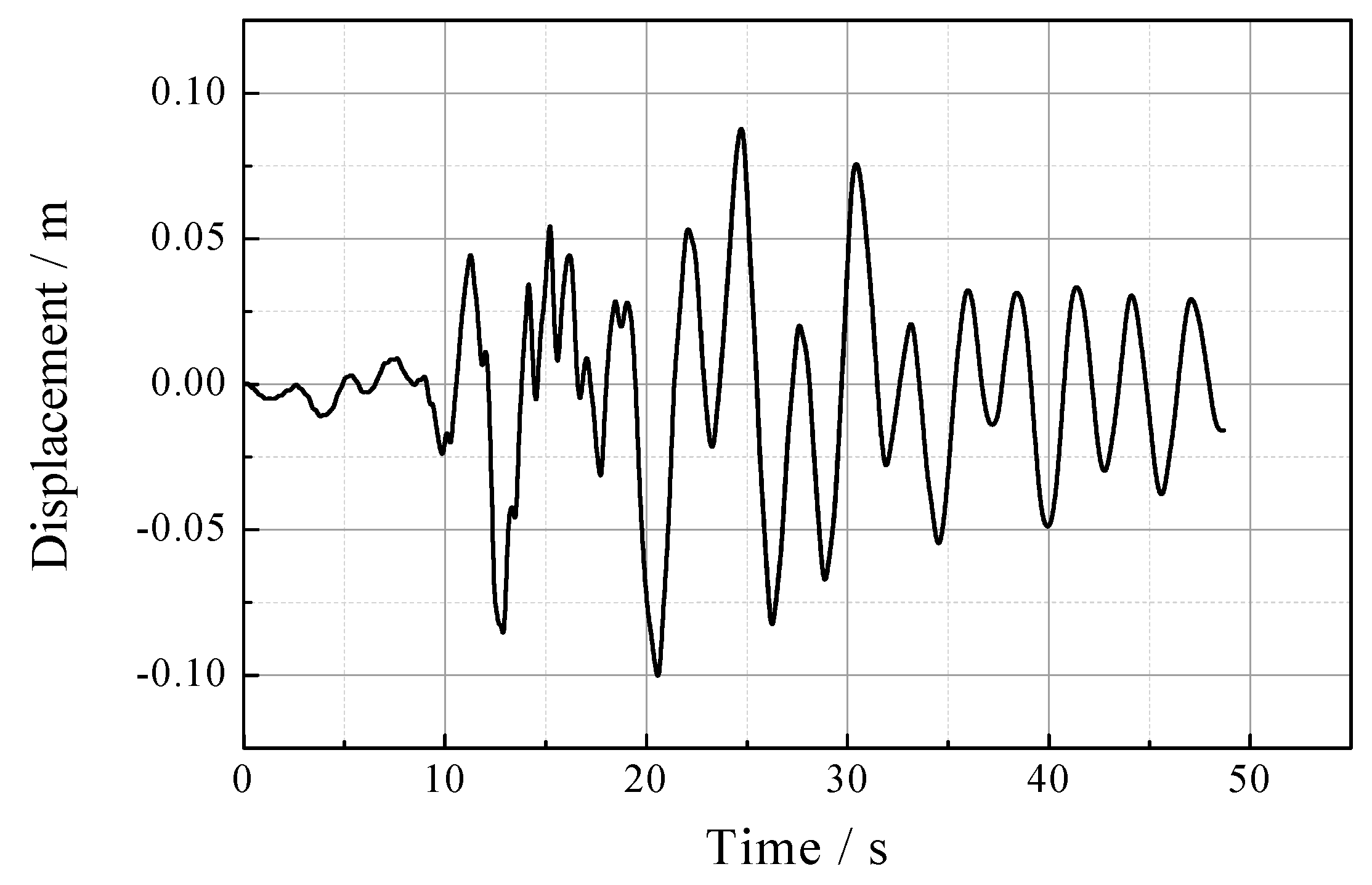
4. Numerical Study on Seismic Response of FSPM
5. Sensitivity of the Material Properties of the FSPM
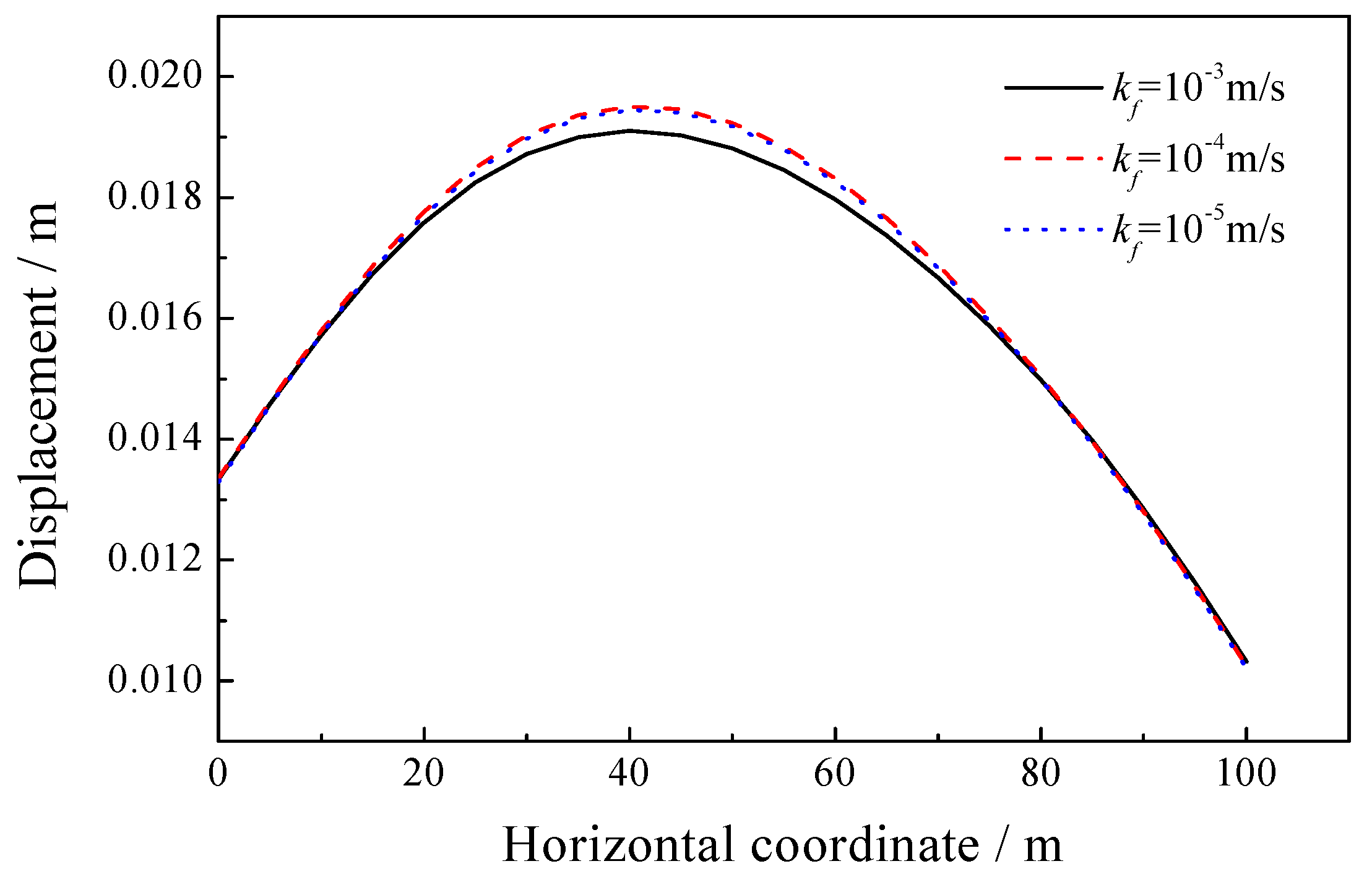
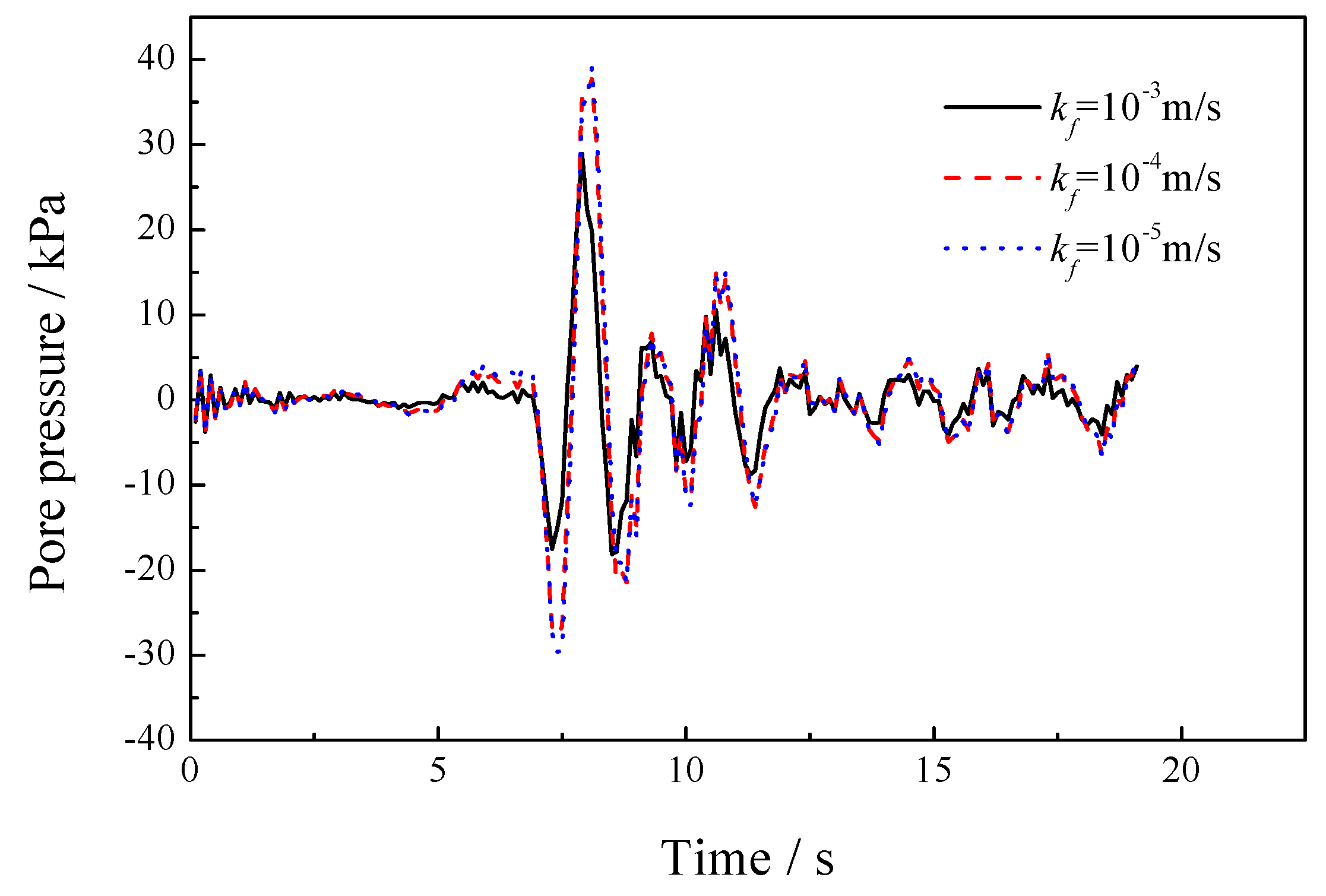
5.1. Sensitivity of the Permeability Coefficient
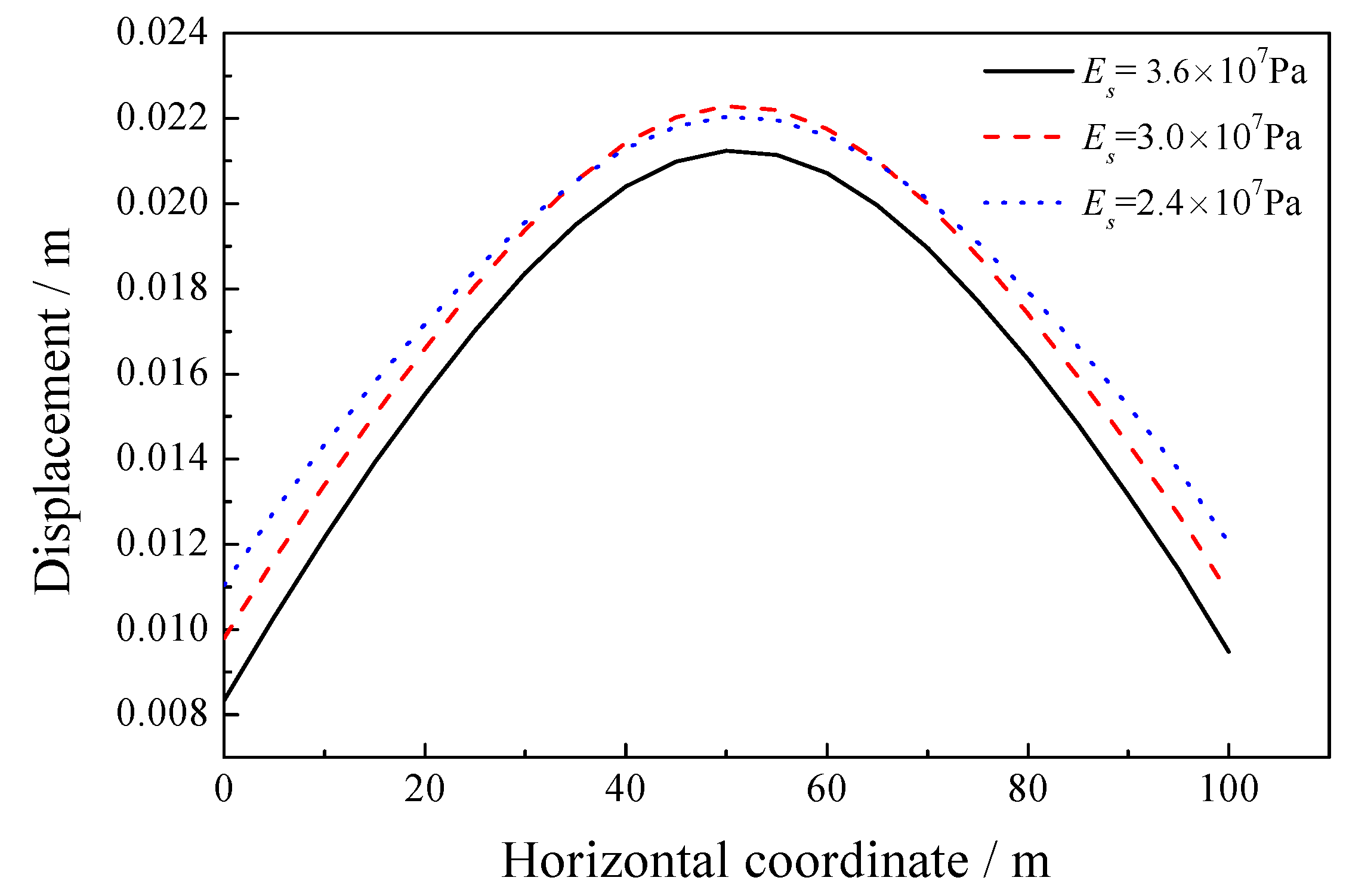
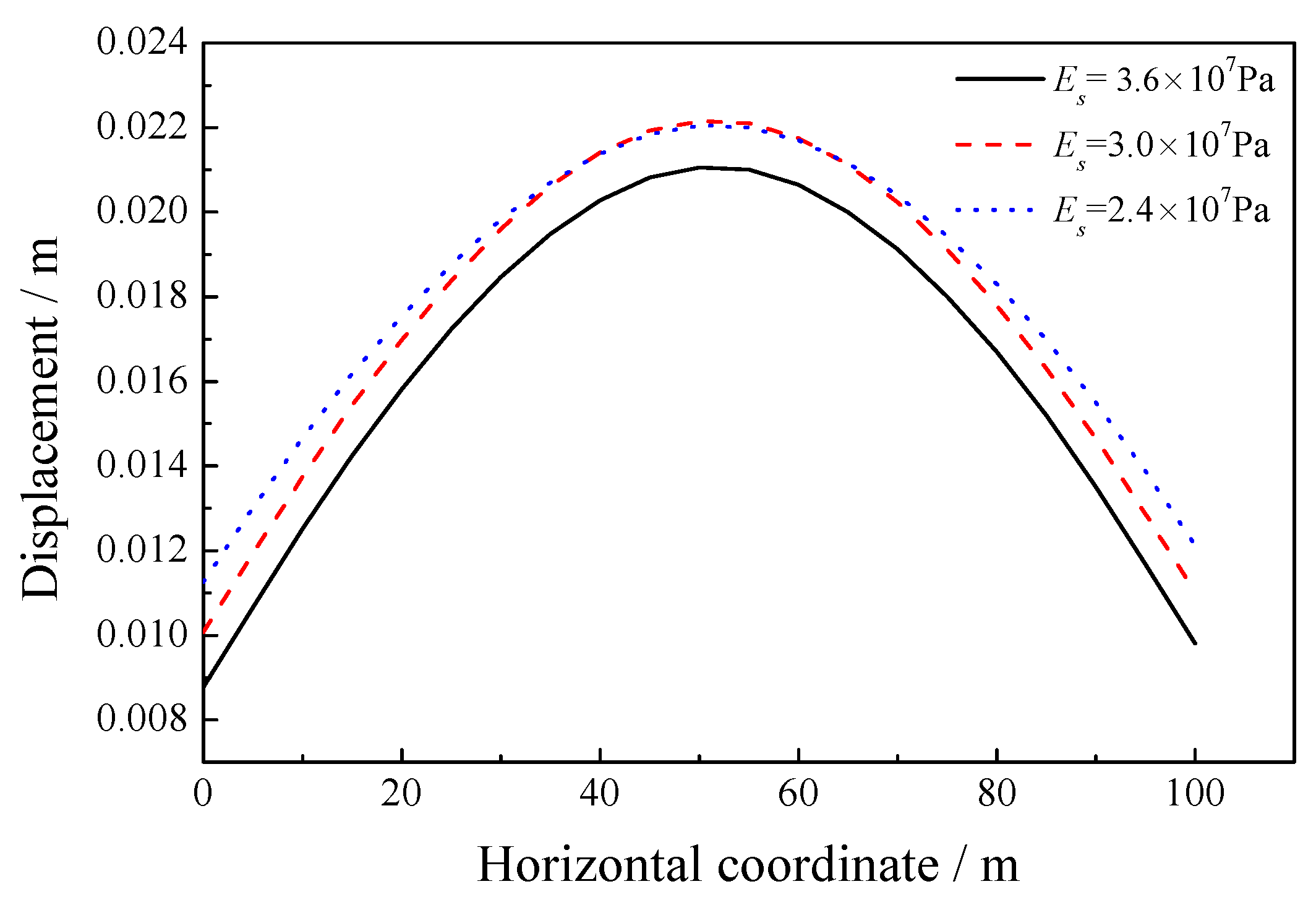
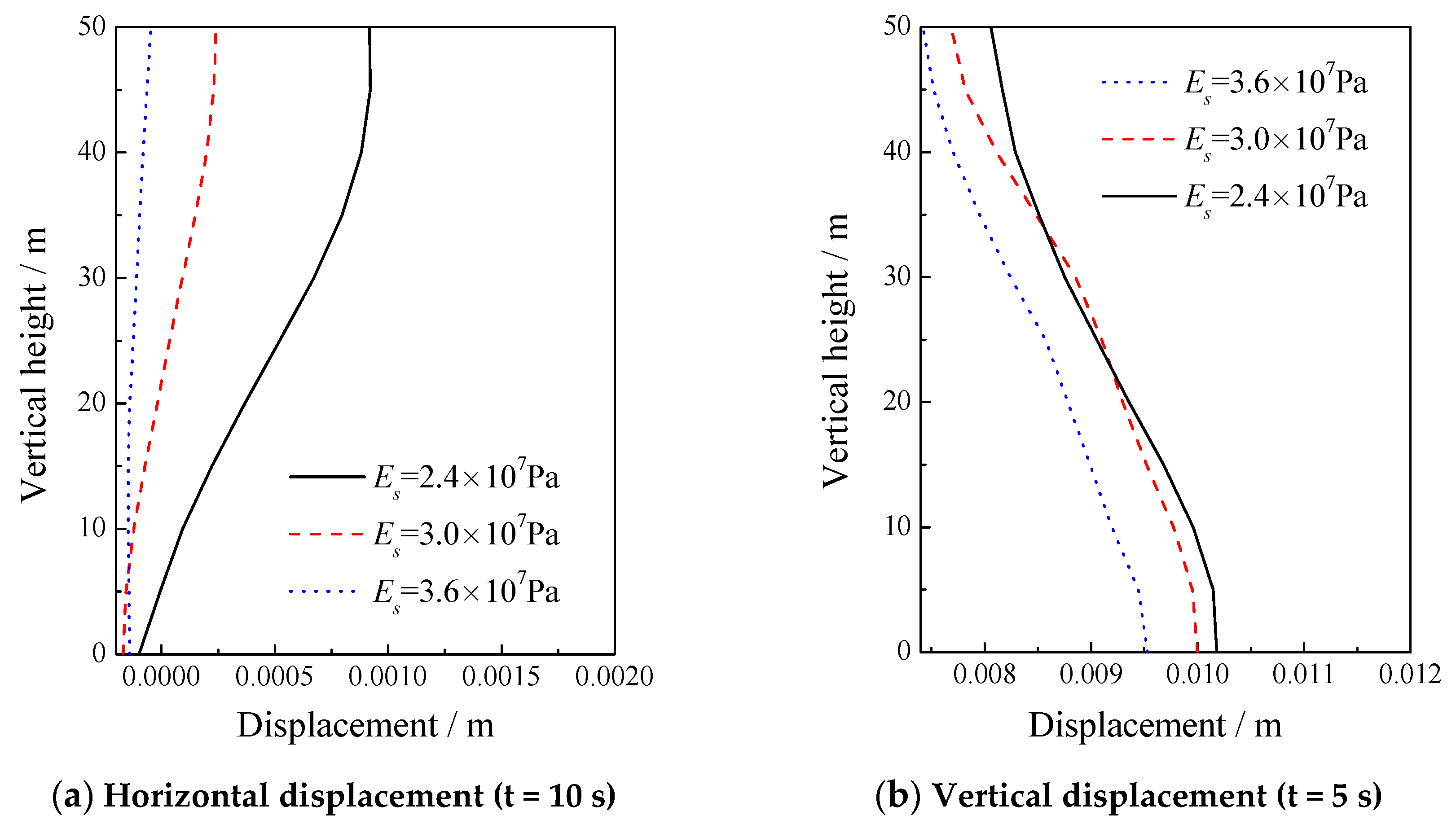
5.2. Sensitivity of the Elastic Modulus of the Solid Skeleton
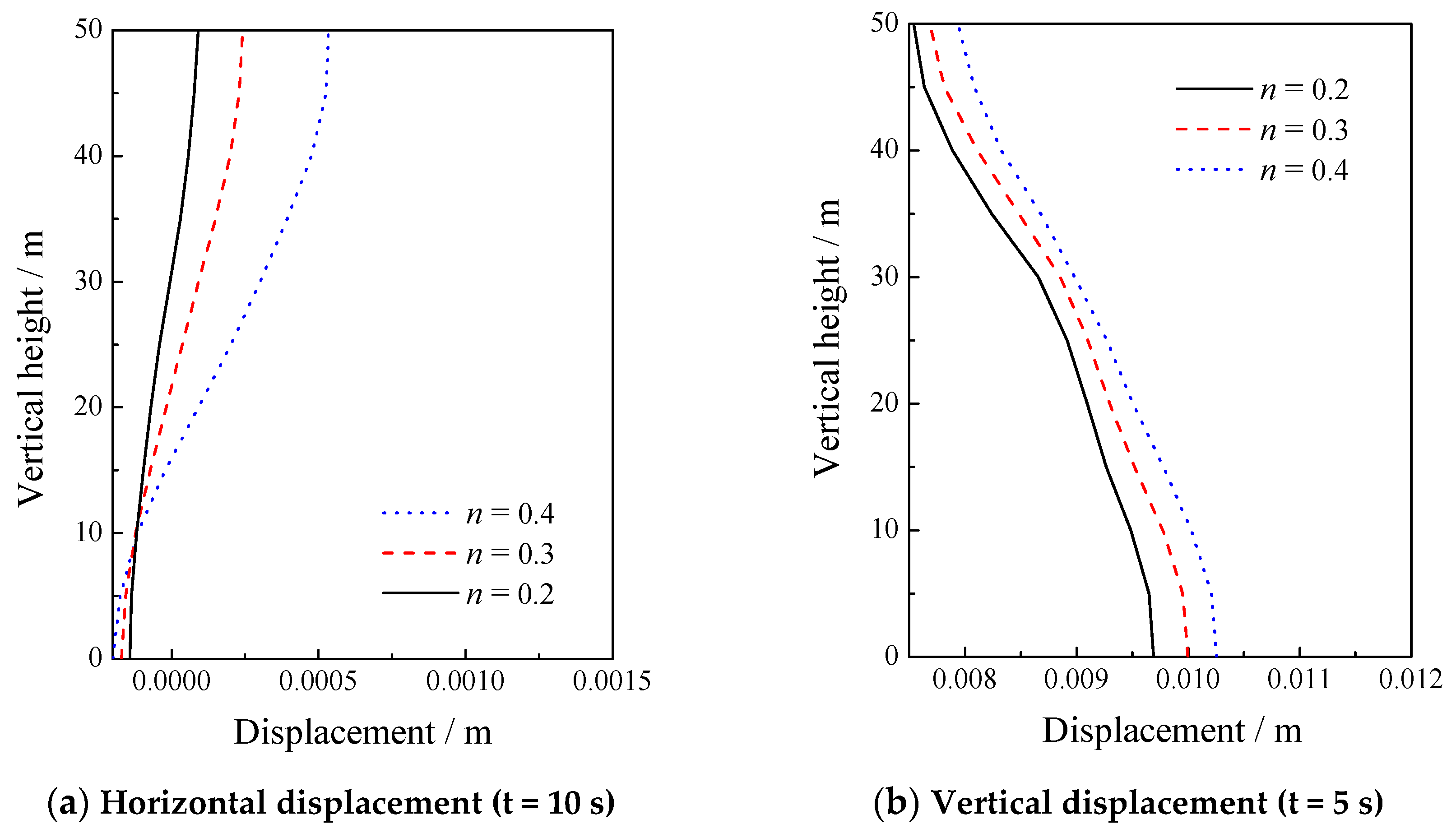
5.3. Sensitivity of the Porosity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. J. Acoust. Soc. Am. 1956, 28, 168–191. [Google Scholar] [CrossRef]
- Biot, M.A. Generalized Theory of Acoustic Propagation in Porous Dissipative Media. J. Acoust. Soc. Am. 1962, 34, 1254–1264. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Chang, C.T.; Bettess, P. Drained, Undrained, Consolidating and Dynamic Behaviour Assumptions in Soils. Geotechnique 1980, 30, 385–395. [Google Scholar] [CrossRef]
- Park, K.C. Stabilization of Partitioned Solution Procedure for Pore Fluid-Soil Interaction Analysis. Int. J. Numer. Methods Eng. 1983, 19, 1669–1673. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Paul, D.K.; Chan, A.H.C. Unconditionally Stable Staggered Solution Procedure for Soil-Pore Fluid Interaction Problems. Int. J. Numer. Methods Eng. 1988, 26, 1039–1055. [Google Scholar] [CrossRef]
- Huang, M.S.; Zienkiewicz, O.C. New Unconditionally Stable Staggered Solution Procedures for Coupled Soil-Pore Fluid Dynamic Problems. Int. J. Numer. Methods Eng. 1998, 43, 1029–1052. [Google Scholar] [CrossRef]
- Huang, M.S.; Wu, S.M.; Zienkiewicz, O.C. Incompressible or Nearly Incompressible Soil Dynamic Behaviour-A New Staggered Algorithm to Circumvent Restrictions of Mixed Formulation. Soil Dyn. Earthq. Eng. 2001, 21, 169–179. [Google Scholar] [CrossRef]
- Li, X.X.; Li, L.; Du, X.L. An Implicit-Implicit Staggered Algorithm for Dynamic Problems of Saturated Soil. Chin. J. Undergr. Space Eng. 2008, 4, 806–809. [Google Scholar]
- Zienkiewicz, O.C.; Huang, M.S.; Wu, J.; Wu, S.M. A New Algorithm for The Coupled Soil-Pore Fluid Problem. Shock Vib. 1993, 1, 3–14. [Google Scholar] [CrossRef]
- Pastor, M.; Zienkiewicz, O.C.; Li, T.C.; Xiaoqing, L.; Huang, M.S. Stabilized Finite Elements with Equal Order of Interpolation for Soil Dynamics Problems. Arch. Comput. Method Eng. 1999, 6, 3–33. [Google Scholar] [CrossRef]
- Li, X.K.; Han, X.H.; Pastor, M. An Iterative Stabilized Fractional Step Algorithm for Finite Element Analysis in Saturated Soil Dynamics. Comput. Meth. Appl. Mech. Eng. 2003, 192, 3845–3859. [Google Scholar] [CrossRef]
- Song, J.; Xu, C.S.; Du, X.L.; Li, L. An Explicit Integrator Method for The Dynamic Problem of Fluid-Saturated Porous Medium in Time Domain. Chin. J. Comput. Mech. 2017, 34, 579–585. [Google Scholar]
- Zhong, W.X. On Precise Time-Integration Method for Structural Dynamics. J. Dalian Univ. Technol. 1994, 34, 131–136. [Google Scholar]
- Duan, X.M.; Li, L.; Du, X.L.; Song, J. A Precise Time-Integration Method for Wave Propagation of Fluid-Saturated Porous Media. Rock Soil Mech. 2015, 36, 2702–2707. [Google Scholar]
- Du, X.L.; Song, J.; Li, L. Explicit-Implicit Staggered Algorithm of u–p Formulation for Dynamic Problems of Fluid-Saturated Porous Media. Chin. J. Geotech. Eng. 2016, 38, 395–403. [Google Scholar]
- Song, J.; Xu, C.S.; Du, X.L.; Li, L. A Temporal Explicit-Explicit Algorithm Based on The Precise Time-Integration for Solving the Dynamic Problems of Fluid-Saturated Porous Media in u-p Form. Eng. Mech. 2017, 34, 9–17. [Google Scholar]
- Liao, Z.P.; Wong, H.L. A Transmitting Boundary for The Numerical Simulation of Elastic Wave Propagation. Soil Dyn. Earthq. Eng. 1984, 3, 174–183. [Google Scholar] [CrossRef]
- Huang, M.S.; Yue, Z.Q.; Tham, L.G.; Zienkiewicz, O.C. On The Stable Finite Element Procedures for Dynamic Problems of Saturated Porous Media. Int. J. Numer. Methods Eng. 2004, 61, 1421–1450. [Google Scholar] [CrossRef]
- Simon, B.R.; Zienkiewicz, O.C.; Paul, D.K. An Analytical Solution for the Transient Response of Saturated Porous Elastic Solids. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 381–398. [Google Scholar] [CrossRef]
- Du, X.L. Theories and Methods of Wave Motion for Engineering; Science Press: Beijing, China, 2009; pp. 18–21. ISBN 978-7-03-024589-2. [Google Scholar]




























| (Pa) | (Pa) | (Pa) | (kg/m3) | (kg/m3) | (m/s) | |
| 8.33 × 106 | 1.25 × 107 | 1.0 × 105 | 1000 | 1700 | 1.0 × 10−2 | 0.3 |
| (Pa) | (Pa) | (Pa) | (kg/m3) | (kg/m3) | (m/s) | |
| 8.33 × 106 | 1.25 × 107 | 1.0 × 105 | 1000 | 1700 | 1.0 × 10−3, 1.0 × 10−4, 1.0 × 10−5 | 0.3 |
| (Pa) | (Pa) | (kg/m3) | (kg/m3) | (m/s) | ||
| 2.4 × 107, 3.0 × 107, 3.6 × 107 | 0.2 | 1.0 × 105 | 1000 | 1700 | 1.0 × 10−2 | 0.3 |
| (Pa) | (Pa) | (Pa) | (kg/m3) | (kg/m3) | (m/s) | |
| 8.33 × 106 | 1.25 × 107 | 1.0 × 105 | 1000 | 1700 | 1.0 × 10−2 | 0.2, 0.3, 0.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhou, S.; Du, X.; Song, J.; Gao, C. Numerical Study on the Seismic Response of Fluid-Saturated Porous Media Using the Precise Time Integration Method. Appl. Sci. 2019, 9, 2037. https://doi.org/10.3390/app9102037
Li L, Zhou S, Du X, Song J, Gao C. Numerical Study on the Seismic Response of Fluid-Saturated Porous Media Using the Precise Time Integration Method. Applied Sciences. 2019; 9(10):2037. https://doi.org/10.3390/app9102037
Chicago/Turabian StyleLi, Liang, Shuo Zhou, Xiuli Du, Jia Song, and Chao Gao. 2019. "Numerical Study on the Seismic Response of Fluid-Saturated Porous Media Using the Precise Time Integration Method" Applied Sciences 9, no. 10: 2037. https://doi.org/10.3390/app9102037




