Model-Free Identification of Nonlinear Restoring Force with Modified Observation Equation
Abstract
:1. Introduction
1.1. Background
1.2. Literature Survey
1.3. Scope
2. Formulas of the Proposed Approach
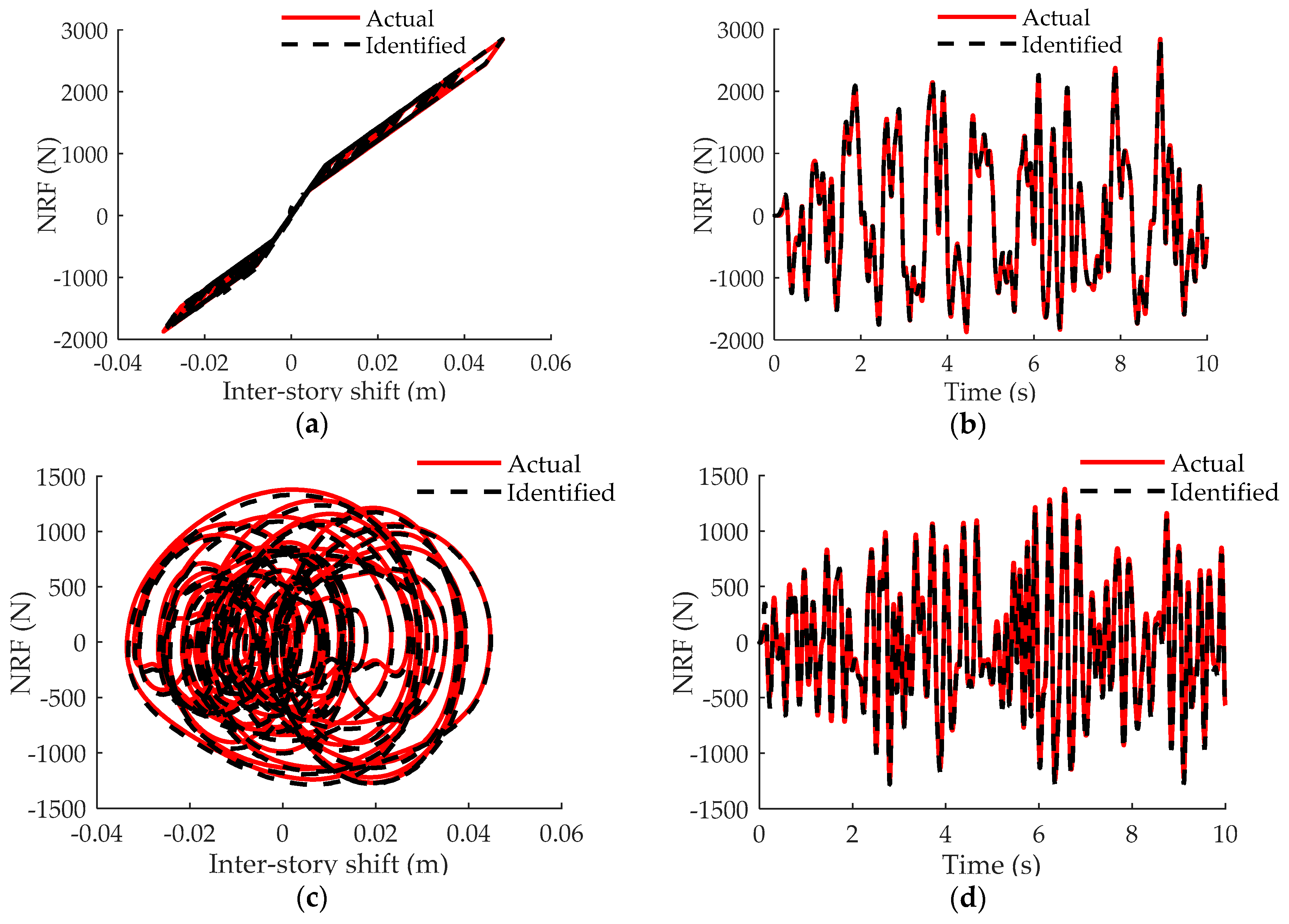
3. Numerical Application
3.1. Building Structure Equipped with MR Damper
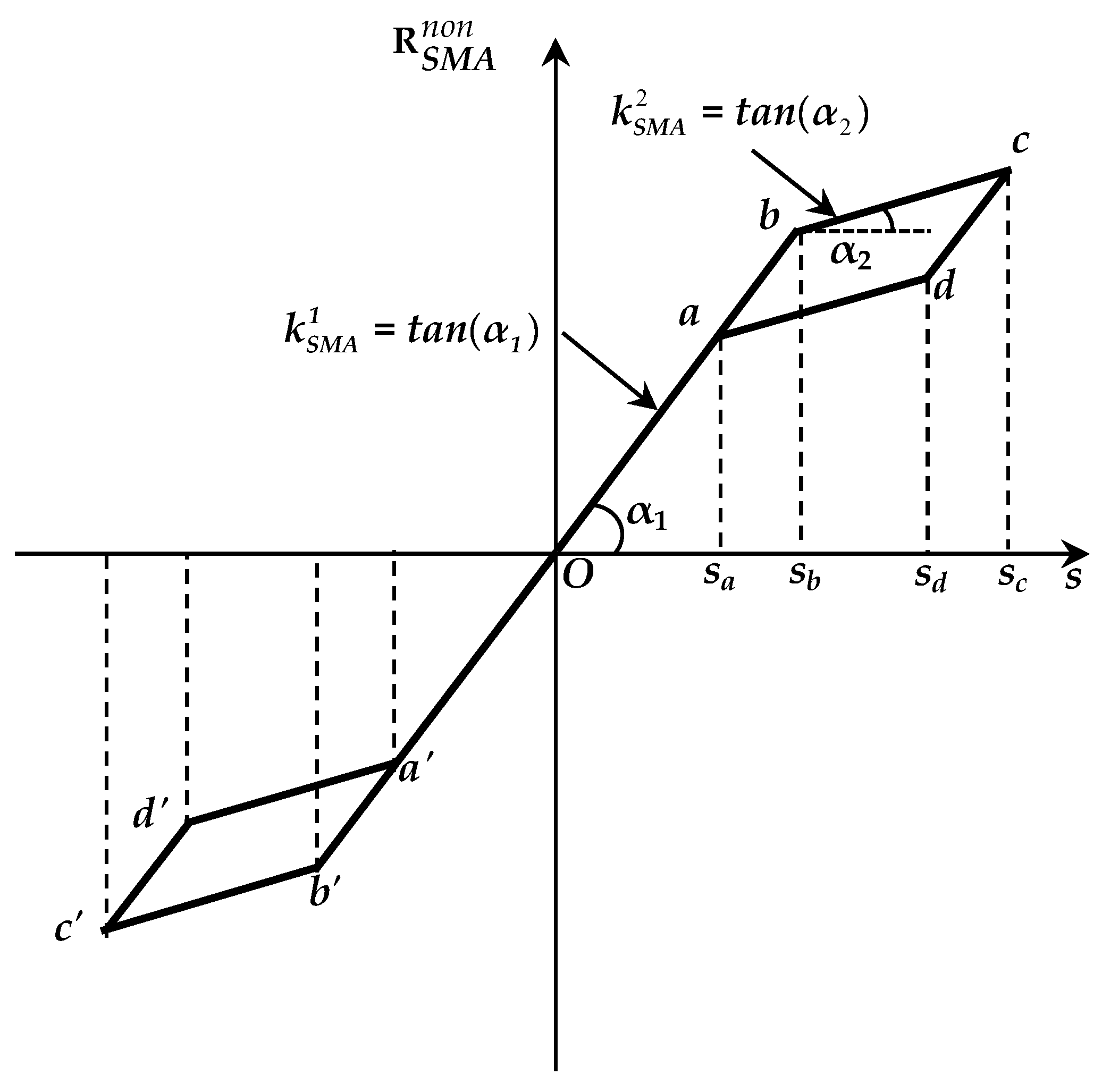
3.2. Building Structure Equipped with SMA Damper
3.3. Building Structure Equipped with SMA and MR Damper
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fan, W.; Qiao, P.Z. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Xu, Y.L.; He, J. Smart Civil Structures; CRC Press: Boca Raton, FL, USA, 2017; pp. 333–389. [Google Scholar]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Proc. 2006, 20, 505–592. [Google Scholar] [CrossRef]
- Kerschen, G.; Noël, J.P. Nonlinear system identification in structural dynamics: 10 more years of progress. Mech. Syst. Signal Proc. 2017, 83, 2–35. [Google Scholar]
- Worden, K.; Tomlinson, G.R. Nonlinearity in Structural Dynamics; IOP Publishing Ltd.: Bristol, UK, 2001; pp. 301–350. [Google Scholar]
- Di Massa, G.; Russo, R.; Strano, S.; Terzo, M. System structure identification and adaptive control of a seismic isolator test rig. Mech. Syst. Signal Proc. 2013, 40, 736–753. [Google Scholar] [CrossRef]
- Pagano, S.; Russo, R.; Strano, S.; Terzo, M. Non-linear modelling and optimal control of a hydraulically actuated seismic isolator test rig. Mech. Syst. Signal Proc. 2013, 35, 255–278. [Google Scholar] [CrossRef]
- Zaghari, B.; Rustighi, E.; Tehrani, M.G. Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation. Vibration 2018, 1, 157–171. [Google Scholar] [CrossRef]
- Zhang, P.; Huo, L.; Song, G. Impact fatigue of viscoelastic materials subjected to pounding. Appl. Sci. 2018, 8, 117. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W.; Bigdeli, Y. Identification of the response of a controlled building structure subjected to seismic load by using nonlinear system models. Appl. Sci. 2016, 6, 301. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, S.; Huang, H.W.; Zhou, L. An adaptive extended Kalman filter for structural damage identification. Struct. Control Health Monit. 2006, 13, 849–867. [Google Scholar] [CrossRef]
- Wu, M.; Smyth, A.W. Application of the unscented Kalman filter for real-time nonlinear structural system identification. Struct. Control Health Monit. 2007, 14, 971–990. [Google Scholar] [CrossRef]
- Lei, Y.; Wu, Y.; Li, T. Identification of nonlinear structural parameters under limited input and output measurements. Int. J. Nonlinear Mech. 2012, 47, 1141–1146. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, B.Y.; Wu, B. Structural system identification with extended Kalman filter and orthogonal decomposition of excitation. Math. Probl. Eng. 2014, 2014, 987694. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Rodrigo Astroza, R.; Conte, J.P. Extended Kalman filter for material parameter estimation in nonlinear structural finite element models using direct differentiation method. Earth. Eng. Struct. Dyn. 2015, 44, 1495–1522. [Google Scholar] [CrossRef]
- Lei, Y.; Hua, W.; Luo, S.; He, M. Detection and parametric identification of structural nonlinear restoring forces from partial measurements of structural responses. Struct. Eng. Mech. 2015, 54, 291–304. [Google Scholar] [CrossRef]
- Liu, J.; Lei, Y.; He, M. A two-stage parametric identification of strong nonlinear structural systems with incomplete response measurements. Int. J. Struct. Stab. Dyn. 2016, 16, 1640022. [Google Scholar] [CrossRef]
- Jin, C.; Jang, S.; Sun, X. An integrated real-time structural damage detection method based on extended Kalman filter and dynamic statistical process control. Adv. Struct. Eng. 2017, 20, 549–563. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Y.; Wang, Z. An adaptive three-stage extended Kalman filter for nonlinear discrete-time system in presence of unknown inputs. ISA Trans. 2018, 75, 101–117. [Google Scholar] [CrossRef]
- Astroza, R.; Alessandri, A.; Conte, J.P. A dual adaptive filtering approach for nonlinear finite element model updating accounting for modeling uncertainty. Mech. Syst. Signal Proc. 2019, 115, 782–800. [Google Scholar] [CrossRef]
- Astroza, R.; Ebrahimian, H.; Conte, J.P. Performance comparison of Kalman−based filters for nonlinear structural finite element model updating. J. Sound Vib. 2019, 438, 520–542. [Google Scholar] [CrossRef]
- Masri, S.F.; Caughey, T.K. A nonparametric identification technique for nonlinear dynamic problems. J. Appl. Mech. 1979, 46, 433–447. [Google Scholar] [CrossRef]
- Masri, S.F.; Sassi, H.; Caughey, T.K. A nonparametric identification of nearly arbitrary nonlinear systems. J. Appl. Mech. 1982, 49, 619–628. [Google Scholar] [CrossRef]
- Masri, S.F.; Miller, R.K.; Saud, A.F.; Caughey, T.K. Identification of nonlinear vibrating structures; part I: Formulation. J. Appl. Mech. 1987, 109, 918–922. [Google Scholar] [CrossRef]
- Masri, S.F.; Miller, R.K.; Saud, A.F.; Caughey, T.K. Identification of nonlinear vibrating structures; part II: Application. J. Appl. Mech. 1987, 109, 923–929. [Google Scholar] [CrossRef]
- Worden, K. Data processing and experiment design for the restoring force surface method, part I: Integration and differentiation of measured time data. Mech. Syst. Signal Proc. 1990, 4, 295–319. [Google Scholar] [CrossRef]
- Worden, K. Data processing and experiment design for the restoring force surface method, part II: Choice of excitation signal. Mech. Syst. Signal Proc. 1990, 4, 321–344. [Google Scholar] [CrossRef]
- Masri, S.F.; Tasbihgoo, F.; Caffrey, J.P.; Smyth, A.W.; Chassiakos, A.G. Data-based model-free representation of complex hysteretic MDOF systems. Struct. Control Health Monit. 2006, 13, 365–387. [Google Scholar] [CrossRef]
- Xu, B.; He, J.; Masri, S.F. Data-based Identification of nonlinear restoring force under spatially incomplete excitations with power series polynomial model. Nonlinear Dyn. 2012, 67, 2063–2080. [Google Scholar] [CrossRef]
- He, J.; Xu, B.; Masri, S.F. Restoring force and dynamic loadings identification for a nonlinear chain-like structure with partially unknown excitations. Nonlinear Dyn. 2012, 69, 231–245. [Google Scholar] [CrossRef]
- Xu, B.; He, J.; Dyke, S.J. Model-free nonlinear restoring force identification for SMA dampers with double Chebyshev polynomials: Approach and validation. Nonlinear Dyn. 2015, 82, 1507–1522. [Google Scholar] [CrossRef]
- Cesarano, C.; Fornaro, C. Operational identities on generalized two-variable Chebyshev polynomials. Int. J. Pure Appl. Math. 2015, 100, 59–74. [Google Scholar] [CrossRef]
- Cesarano, C.; Fornaro, C. A note on two-variable Chebyshev polynomials. Georgian Math J. 2017, 24, 339–349. [Google Scholar]
- Xu, B.; He, J.; Masri, S.F. Data-based model-free hysteretic restoring force and mass identification for dynamic systems. Comput. Aided Civ. Infrastruct. Eng. 2015, 30, 2–18. [Google Scholar] [CrossRef]
- Lei, Y.; Luo, S.J.; He, M.Y. Identification of model-free structural nonlinear restoring forces using partial measurements of structural responses. Adv. Struct. Eng. 2017, 20, 69–80. [Google Scholar] [CrossRef]
- Su, H.; Yang, X.; Liu, L.; Lei, Y. Identifying nonlinear characteristics of model-free MR dampers in structures with partial response data. Measurement 2018, 130, 362–371. [Google Scholar] [CrossRef]
- Yuan, T.C.; Yang, J.; Chen, L.Q. Nonparametric identification of nonlinear piezoelectric mechanical systems. J. Appl. Mech. 2018, 85, 111008. [Google Scholar] [CrossRef]
- Ondra, V.; Sever, I.A.; Schwingshackl, C.W. A method for non-parametric identification of non-linear vibration systems with asymmetric restoring forces from a resonant decay response. Mech. Syst. Signal Proc. 2019, 114, 239–258. [Google Scholar] [CrossRef]
- Worden, K.; Staszewski, W.J.; Hensman, J.J. Natural computing for mechanical systems research: A tutorial overview. Mech. Syst. Signal Proc. 2011, 25, 4–111. [Google Scholar] [CrossRef]
- Zhou, Q.; Qu, W.L. Two mechanic models for magnetorheological damper and corresponding test verification. Earthq. Eng. Eng. Vib. 2002, 22, 144–150. [Google Scholar]

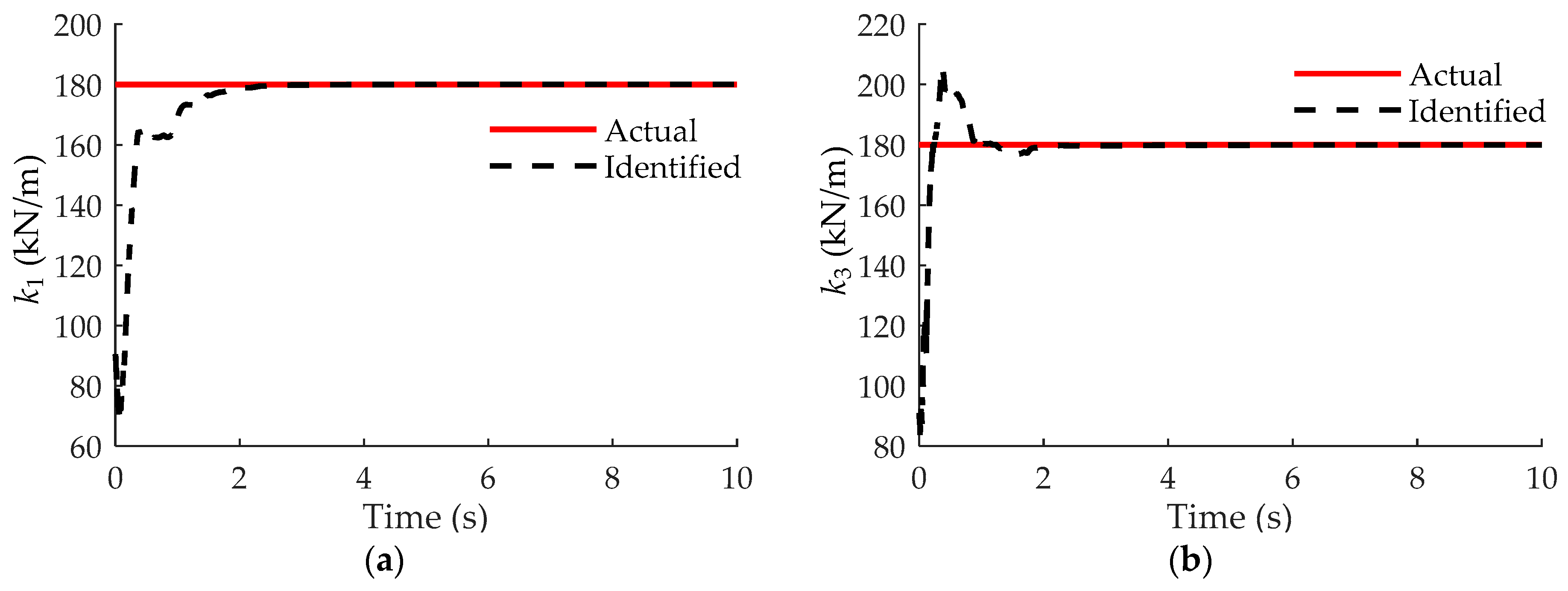
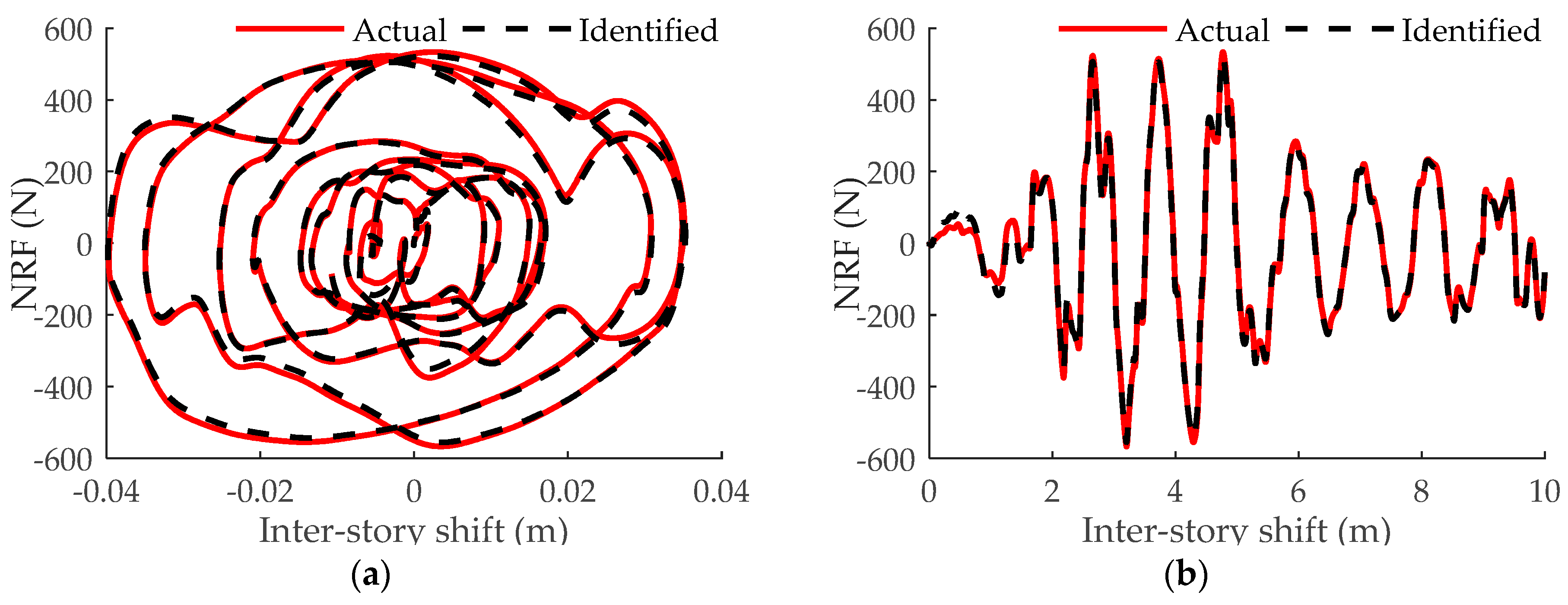


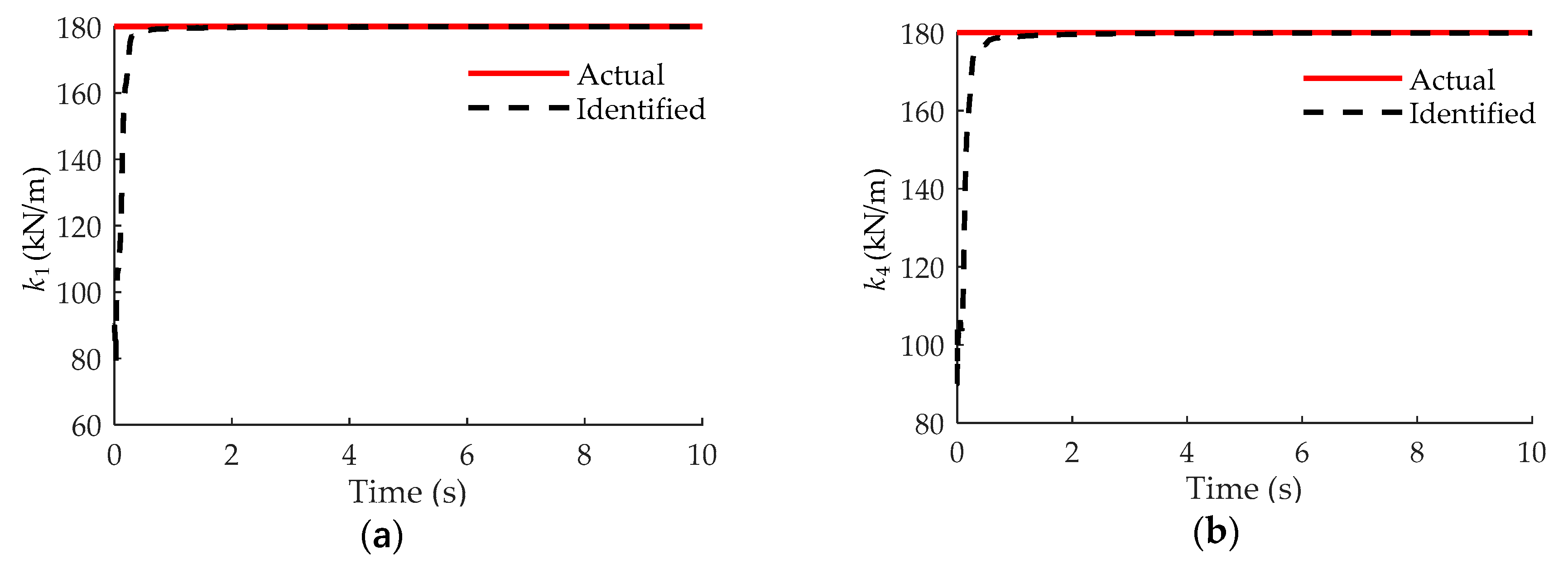
| Parameters | Actual | Identified | Error (%) | Parameters | Actual | Identified | Error (%) |
|---|---|---|---|---|---|---|---|
| k1 (kN/m) | 180.00 | 180.05 | 0.03 | k5 (kN/m) | 180.00 | 179.47 | −0.29 |
| k2 (kN/m) | 180.00 | 180.76 | 0.42 | k6 (kN/m) | 180.00 | 179.84 | −0.09 |
| k3 (kN/m) | 180.00 | 179.94 | -0.04 | α | 0.2644 | 0.2662 | 0.67 |
| k4 (kN/m) | 180.00 | 180.24 | 0.13 | β | 2.578 × 10−3 | 2.565 × 10−3 | −0.30 |
| Parameters | Actual | Identified | Error (%) | Parameters | Actual | Identified | Error (%) |
|---|---|---|---|---|---|---|---|
| k1 (kN/m) | 180.00 | 179.92 | −0.05 | k5 (kN/m) | 180.00 | 179.94 | −0.04 |
| k2 (kN/m) | 180.00 | 179.88 | −0.06 | k6 (kN/m) | 180.00 | 179.83 | −0.10 |
| k3 (kN/m) | 180.00 | 179.84 | −0.09 | α | 0.2644 | 0.2643 | −0.04 |
| k4 (kN/m) | 180.00 | 179.90 | −0.06 | β | 2.578 × 10−3 | 2.591 × 10−3 | 0.55 |
| Parameters | Actual | Identified | Error (%) | Parameters | Actual | Identified | Error (%) |
|---|---|---|---|---|---|---|---|
| k1 (kN/m) | 180.00 | 179.96 | −0.02 | k5 (kN/m) | 180.00 | 179.98 | −0.01 |
| k2 (kN/m) | 180.00 | 179.94 | −0.03 | k6 (kN/m) | 180.00 | 179.86 | −0.08 |
| k3 (kN/m) | 180.00 | 179.95 | −0.03 | α | 0.2644 | 0.2642 | −0.07 |
| k4 (kN/m) | 180.00 | 179.92 | −0.05 | β | 2.578 × 10−3 | 2.589 × 10−3 | 0.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Zhang, X.; Qi, M.; Xu, B. Model-Free Identification of Nonlinear Restoring Force with Modified Observation Equation. Appl. Sci. 2019, 9, 306. https://doi.org/10.3390/app9020306
He J, Zhang X, Qi M, Xu B. Model-Free Identification of Nonlinear Restoring Force with Modified Observation Equation. Applied Sciences. 2019; 9(2):306. https://doi.org/10.3390/app9020306
Chicago/Turabian StyleHe, Jia, Xiaoxiong Zhang, Mengchen Qi, and Bin Xu. 2019. "Model-Free Identification of Nonlinear Restoring Force with Modified Observation Equation" Applied Sciences 9, no. 2: 306. https://doi.org/10.3390/app9020306





