A New Model for Constant Fuel Utilization and Constant Fuel Flow in Fuel Cells
Abstract
:1. Introduction
2. A Brief Review of the Literature
- Direct methanol fuel cell (DFMC), about 60 C
- Proton exchange membrane (or polymer electrolyte membrane) fuel cell (PEMFC), less than 120 C, typically about 80 C
- Alkaline fuel cell (AFC), about 100 C or less
- Phosphoric acid fuel cell (PAFC), about 150–200 C
- Molten carbonate fuel cell (MCFC), about 600–700 C
- Solid oxide fuel cell (SOFC), about 600–1000 C
- mechanistic (theoretical)
- empirical (experimental)
- semi-empirical
- data-driven (machine-learning-based)
3. The Problem
- activation loss
- concentration loss
- ohmic loss
- losses due to fuel crossover and internal current.
- The gases used in the chemical reactions are ideal and uniformly distributed.
- The fuel cell is considered a single “lumped” system; the species enter the cell through one end and exit through the other end.
- The only reaction that contributes to voltage takes place between hydrogen and oxygen. There is no parasitic reaction.
- All reactants generate their ideal number of electrons.
- No fuel or oxidant crosses the electrolyte.
- The gases have a uniform concentration in the supply channels; there are no pressure losses.
- The flows are incompressible.
- The fuel and oxidant are available as soon as they are needed (no delays).
- The partial pressures of the gases in the bulk of the anode and the cathode channels are assumed to be the same as those at the triple-phase-boundaries.
- The temperature is fixed (stable) at all times, and temperature variations across the cell are ignored.
- The operating voltage is uniform over the cell.
- Heat losses are negligible (the fuel cell is well insulated).
- There is no gas leakage.
- The Nernst equation can be applied.
4. Constant Fuel Utilization
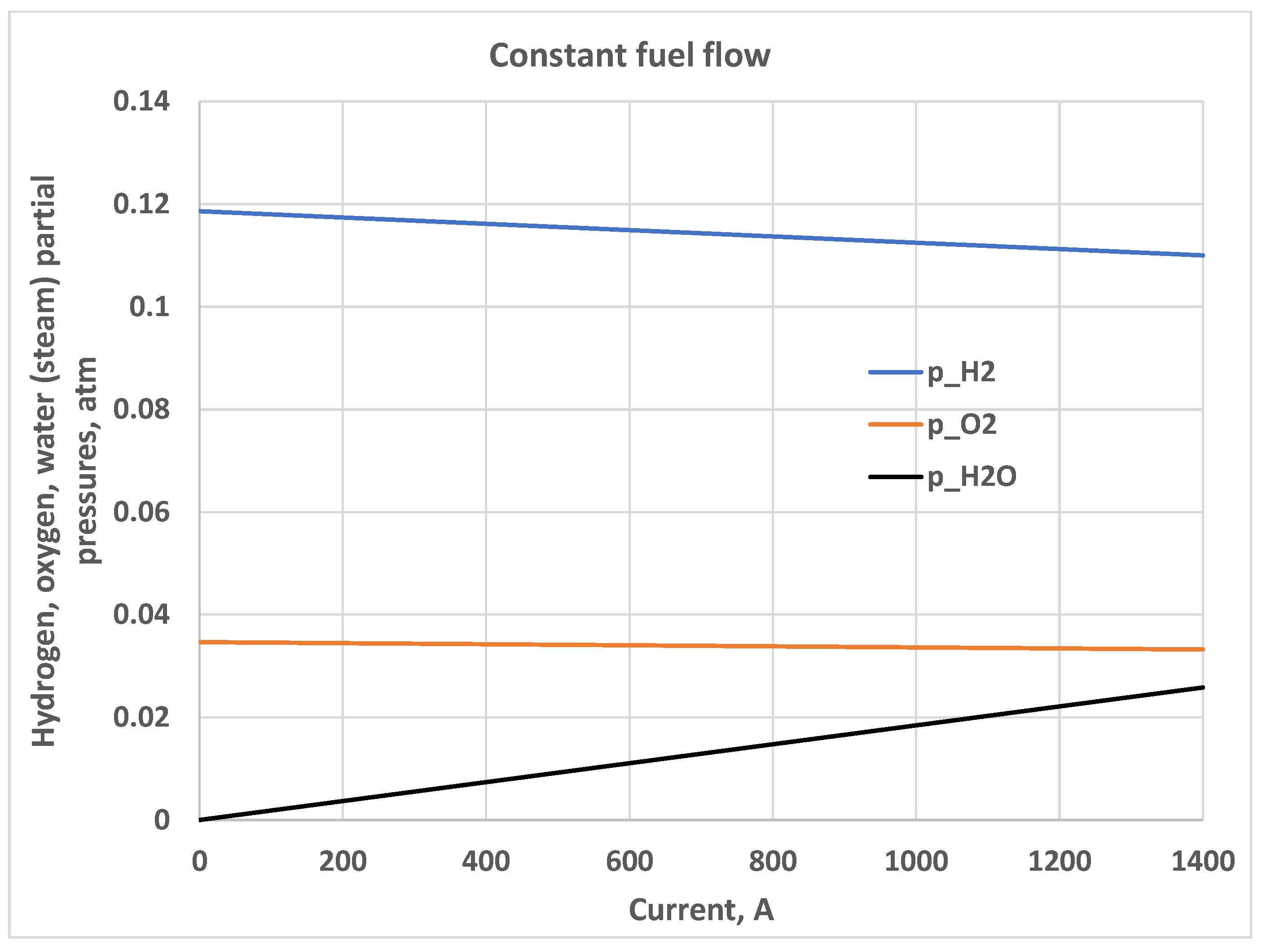
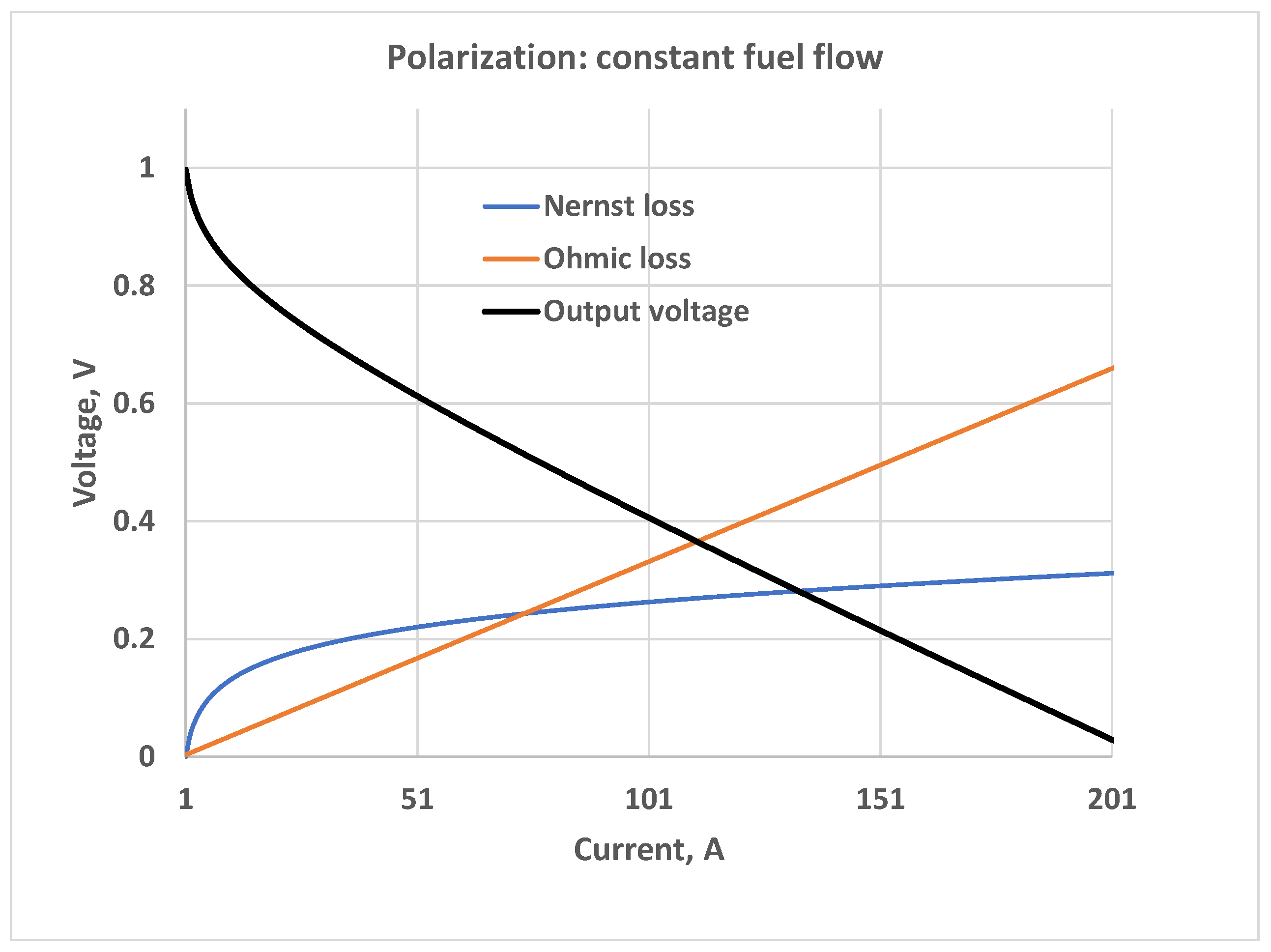
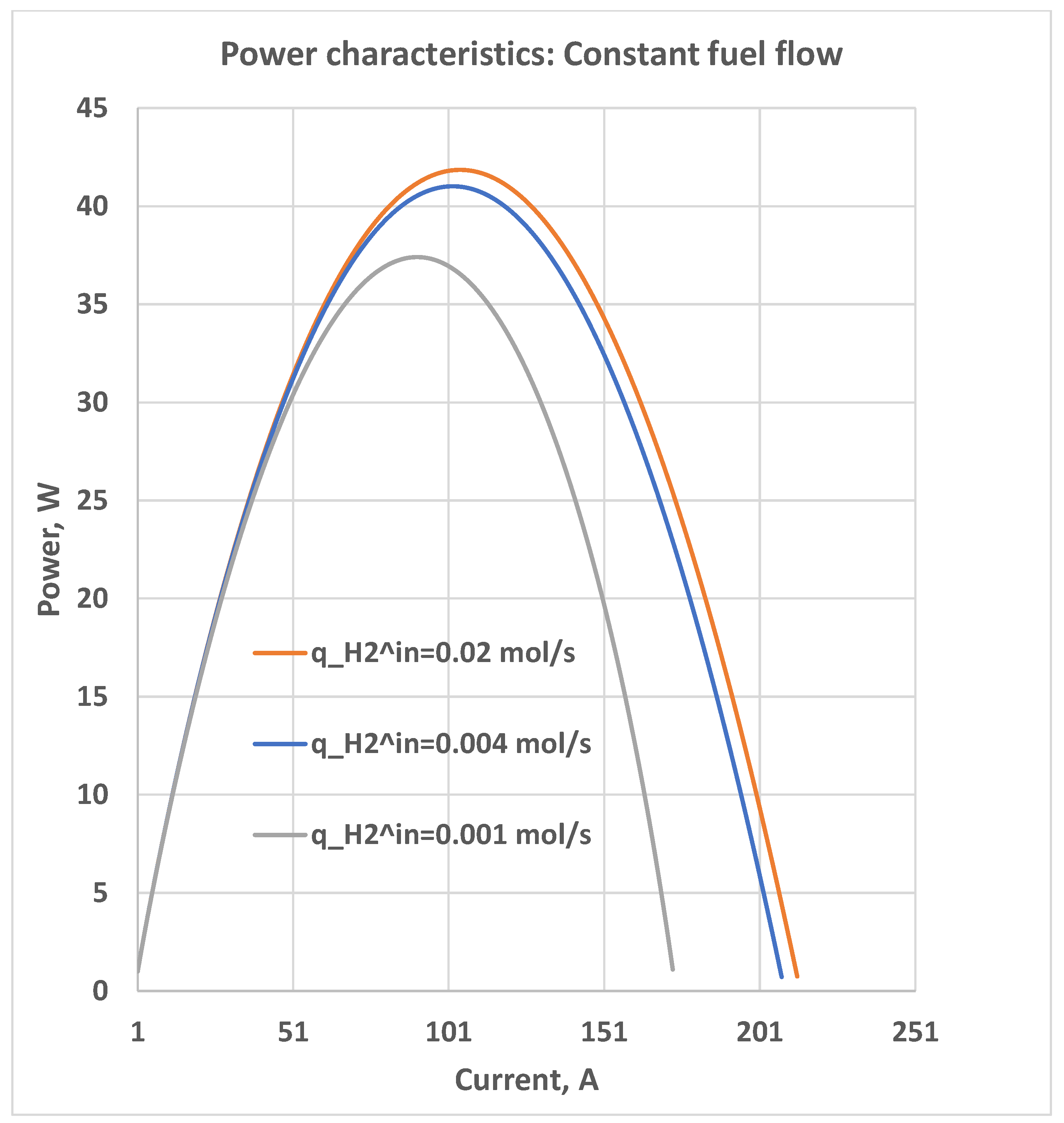
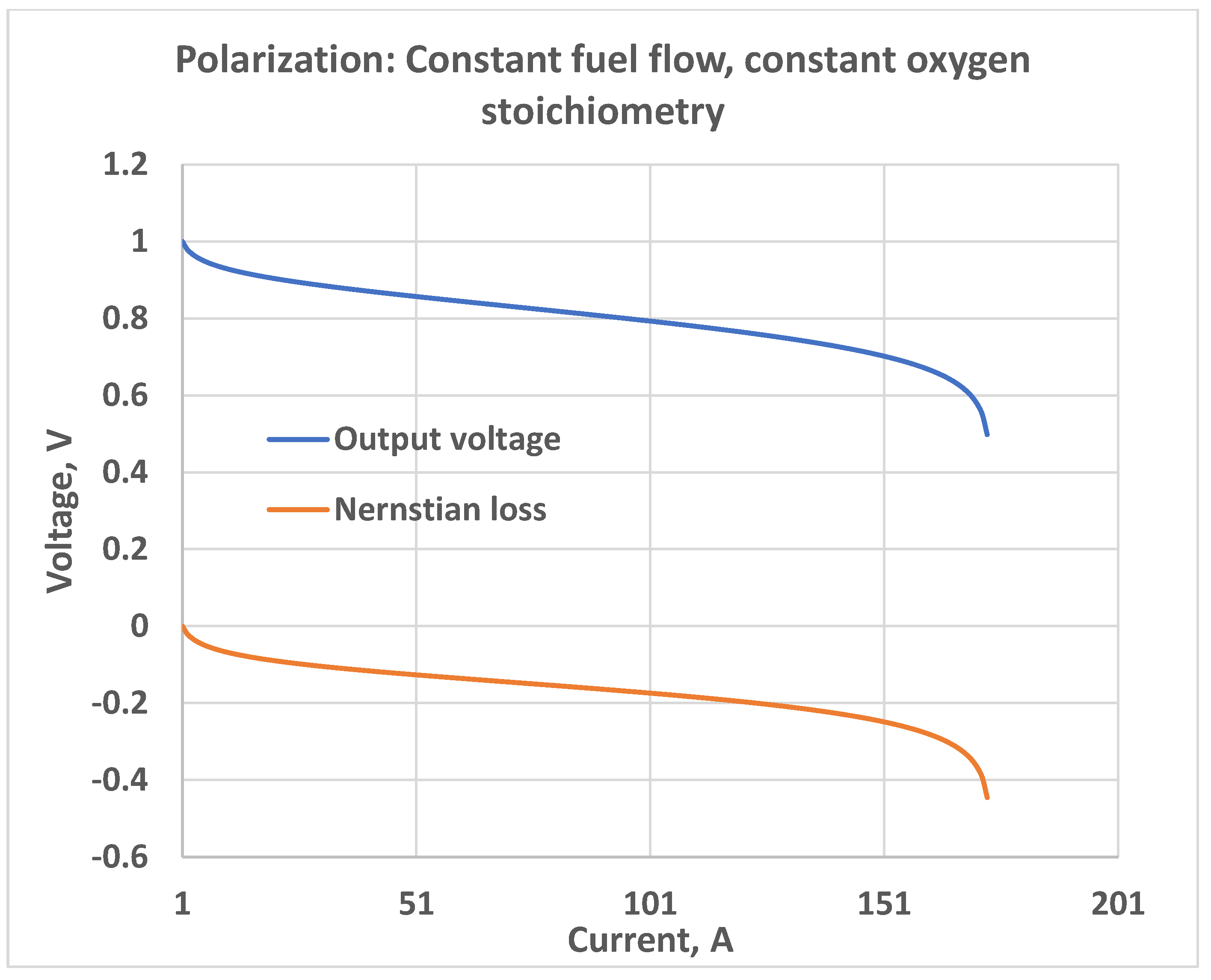
5. Constant Fuel Flow
5.1. Constant Hydrogen-Oxygen Input Flow Ratio
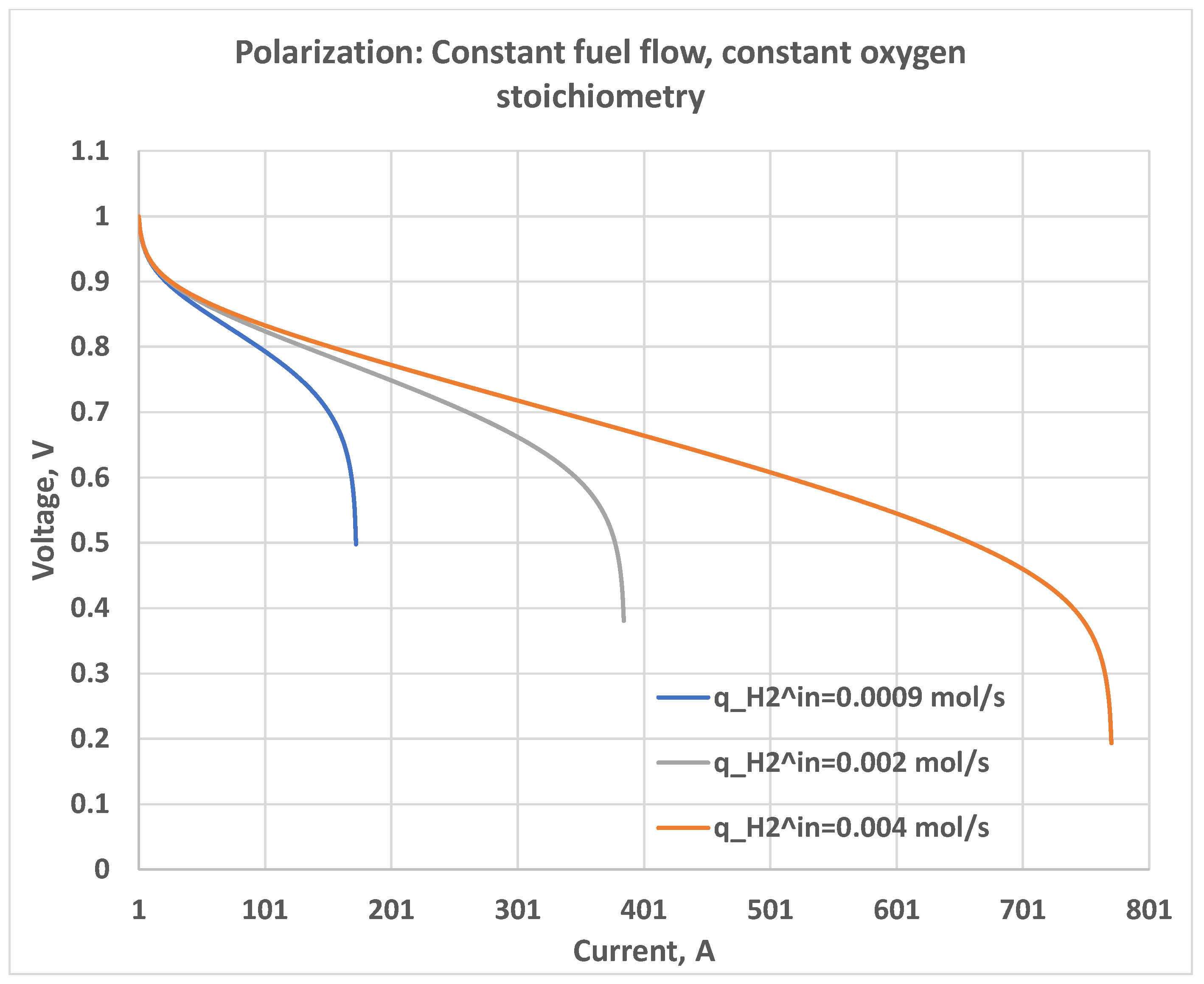
5.2. Constant Oxygen Stoichiometry Ratio
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SOFC | Solid oxide fuel cell |
| PEMFC | Proton exchange membrane fuel cell |
| EMF | Electromotive force |
| Nomenclature | |
| Nernst potential (open-circuit EMF) of a single cell, V | |
| Standard (reference) EMF of a single cell, V | |
| Standard (reference) EMF of a single cell at temperature , V | |
| V | Output terminal voltage of a single cell, V |
| T | Temperature, K |
| n | Number of electrons transferred |
| a | Activity |
| Activity of hydrogen | |
| Activity of oxygen | |
| Activity of water vapor (steam) | |
| Change in entropy, J/(mol K) | |
| p | Pressure or partial pressure, atm |
| Standard-state pressure, atm | |
| Partial pressure of hydrogen, atm | |
| Partial pressure of oxygen, atm | |
| Partial pressure of water vapor, atm | |
| Fuel cell current, A | |
| u | Fuel utilization ratio |
| Ratio of hydrogen-to-oxygen input flow rates | |
| Valve molar constant for hydrogen, mol/(s atm) | |
| Valve molar constant for oxygen, mol/(s atm) | |
| Valve molar constant for water vapor, mol/(s atm) | |
| Modeling constant, mol/(s A) | |
| Hydrogen input flow rate, mol/s | |
| Hydrogen output flow rate, mol/s | |
| Hydrogen flow rate that takes part in the reaction, mol/s | |
| Oxygen input flow rate, mol/s | |
| Oxygen output flow rate, mol/s | |
| Oxygen reacting flow rate, mol/s | |
| Water vapor output flow rate, mol/s | |
| Water vapor flow rate produced in the reaction, mol/s | |
| r | Ohmic resistance of a single cell, Ohm |
| R | Universal gas constant, J/(mol K) |
| F | Faraday’s constant, Coulombs/mol |
References
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained, 2nd ed.; Wiley: Chichester, UK, 2003. [Google Scholar]
- Singhal, S.C.; Kendall, K. (Eds.) High-Temperature Solid Oxide Fuel Cells: Fundamentals, Design and Applications; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Barbir, F. PEM Fuel Cells: Theory and Practice, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- O’Hayre, R.; Cha, S.W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Cavallaro, A.; Pramana, S.S.; Ruiz-Trejo, E.; Sherrell, P.C.; Ware, E.; Kilner, J.A.; Skinner, S.J. Amorphous- cathode-route towards low temperature SOFC. Sustain. Energy Fuels 2018, 2, 862–875. [Google Scholar] [CrossRef]
- Radisavljevic, V. On controllability and system constraints of the linear models of proton exchange membrane and solid oxide fuel cells. J. Power Sources 2011, 196, 8549–8552. [Google Scholar] [CrossRef]
- Li, Y.H.; Choi, S.S.; Rajakaruna, S. An analysis of the control and operation of a solid oxide fuel-cell power plant in an isolated system. IEEE Trans. Energy Convers. 2005, 20, 381–387. [Google Scholar] [CrossRef]
- Chakraborty, U.K. Reversible and irreversible potentials and an inaccuracy in popular models in the fuel cell literature. Energies 2018, 11, 1851. [Google Scholar] [CrossRef]
- Kakac, S.; Pramuanjaroenkij, A.; Zhou, X.Y. A review of numerical modeling of solid oxide fuel cells. Int. J. Hydrogen Energy 2007, 32, 761–786. [Google Scholar] [CrossRef]
- Comparison of Fuel Cell Technologies, Fuel Cell Technologies Office, U.S. Department of Energy. Available online: https://www.energy.gov/eere/fuelcells/comparison-fuel-cell-technologies (accessed on 16 February 2019).
- Ito, H.; Miyazaki, N.; Ishida, M.; Nakano, A. Efficiency of unitized reversible fuel cell systems. In. J. Hydrogen Energy 2016, 41, 5803–5815. [Google Scholar] [CrossRef]
- Santoro, C.; Arbizzani, C.; Erable, B.; Ieropoulos, I. Microbial fuel cells: From fundamentals to applications. A review. J. Power Sources 2017, 356, 225–244. [Google Scholar] [CrossRef] [PubMed]
- Cheddie, D.; Munroe, N. Review and comparison of approaches to proton exchange membrane fuel cell modeling. J. Power Sources 2005, 147, 72–84. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef]
- Wang, K.; Hissel, D.; Péra, M.C.; Steiner, N.; Marra, D.; Sorrentino, M.; Pianese, C.; Monteverde, M.; Cardone, P.; Saarinen, J. A Review on solid oxide fuel cell models. Int. J. Hydrogen Energy 2011, 36, 7212–7228. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Hussain, M.A.; Daud, W.A.W.; Soroush, M.; Shamiri, A. Mathematical modeling of solid oxide fuel cells: A review. Renew. Sustain. Energy Rev. 2011, 15, 1893–1917. [Google Scholar] [CrossRef]
- Saadi, A.; Becherif, M.; Aboubou, A.; Ayad, M.Y. Comparison of proton exchange membrane fuel cell static models. Renew. Energy 2013, 56, 64–71. [Google Scholar] [CrossRef]
- Wu, H.-W. A review of recent development: Transport and performance modeling of PEM fuel cells. Appl. Energy 2016, 165, 81–106. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew. Sustain. Energy Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Blal, M.; Benatiallah, A.; NeÇaibia, A.; Lachtar, S.; Sahouane, N.; Belasri, A. Contribution and investigation to compare models parameters of (PEMFC), comprehensives review of fuel cell models and their degradation. Energy 2019, 168, 182–199. [Google Scholar] [CrossRef]
- Radisavljević-Gajić, V.; Milanović, M.; Rose, P. Modeling and System Analysis of PEM Fuel Cells. In Multi-Stage and Multi-Time Scale Feedback Control of Linear Systems with Applications to Fuel Cells; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Qin, Y.; Li, X.; Jiao, K.; Du, Q.; Yin, Y. Effective removal and transport of water in a PEM fuel cell flow channel having a hydrophilic plate. Appl. Energy 2014, 113, 116–126. [Google Scholar] [CrossRef]
- Cheddie, D.; Munroe, N.D.H. A dynamic 1D model of a solid oxide fuel cell for real time simulation. J. Power Sources 2007, 171, 634–643. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Toffolo, A.; Zanon, F. Parameter Setting for a Tubular SOFC Simulation Model. J. Energy Resour. Technol. 2004, 126, 40–46. [Google Scholar] [CrossRef]
- Göll, S.; Samsun, R.C.; Peters, R. Analysis and optimization of solid oxide fuel cell-based auxiliary power units using a generic zero-dimensional fuel cell model. J. Power Sources 2011, 196, 9500–9509. [Google Scholar] [CrossRef]
- Badur, J.; Lemański, M.; Kowalczyk, T.; Ziółkowski, P.; Kornet, S. Verification of zero-dimensional model of SOFC with internal fuel reforming for complex hybrid energy cycles. Chem. Process Eng. 2018, 39, 113–128. [Google Scholar] [CrossRef]
- Zabihian, F.; Fung, A.S. Macro-level modeling of solid oxide fuel cells, approaches, and assumptions revisited. J. Renew. Sustain. Energy 2017, 9, 054301. [Google Scholar] [CrossRef]
- Padulles, J.; Ault, G.W.; McDonald, J.R. An integrated SOFC plant dynamic model for power systems simulation. J. Power Sources 2000, 86, 495–500. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Development of models for analyzing the load-following performance of microturbines and fuel cells. Electr. Power Syst. Res. 2002, 62, 1–11. [Google Scholar] [CrossRef] [Green Version]
- El-Sharkh, M.Y.; Rahman, A.; Alam, M.S.; Byrne, P.C.; Sakla, A.A.; Thomas, T. A dynamic model for a stand-alone PEM fuel cell power plant for residential applications. J. Power Sources 2004, 138, 199–204. [Google Scholar] [CrossRef]
- Jurado, F.; Valverde, M. Multiobjective genetic algorithms for fuzzy inverter in solid oxide fuel cell system. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Dubrovnik, Croatia, 20–23 June 2005. [Google Scholar]
- Jurado, F.; Valverde, M. Genetic fuzzy control applied to the inverter of solid oxide fuel cell for power quality improvement. Electr. Power Syst. Res. 2005, 76, 93–105. [Google Scholar] [CrossRef]
- Li, Y.H.; Rajakaruna, S.; Choi, S.S. Control of a solid oxide fuel cell power plant in a grid-connected system. IEEE Trans. Energy Convers. 2007, 22, 405–413. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.; Shaw, S.R. Dynamic models and model validation for PEM fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H. A physically based dynamic model for solid oxide fuel cells. IEEE Trans. Energy Convers. 2007, 22, 887–897. [Google Scholar] [CrossRef]
- Huo, H.-B.; Zhong, Z.-D.; Zhu, X.-J.; Tu, H.-Y. Nonlinear dynamic modeling for a SOFC stack by using a Hammerstein model. J. Power Sources 2008, 175, 441–446. [Google Scholar] [CrossRef]
- Wu, X.-J.; Zhu, X.-J.; Cao, G.-Y.; Tu, H.-Y. Predictive control of SOFC based on a GA-RBF neural network. J. Power Sources 2008, 179, 232–239. [Google Scholar] [CrossRef]
- Chakraborty, U.K. Static and dynamic modeling of solid oxide fuel cell using genetic programming. Energy 2009, 34, 740–751. [Google Scholar] [CrossRef]
- Chakraborty, U.K. An error in solid oxide fuel cell stack modeling. Energy 2011, 36, 801–802. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T. A new method for dynamic performance improvement of a hybrid power system by coordination of converter’s controller. J. Power Sources 2011, 196, 4033–4043. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T.; Adabi, J. Power management, dynamic modeling and control of wind/FC/battery-bank based hybrid power generation system for stand-alone application. Eur. Trans. Electr. Power 2012, 22, 271–293. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; García, P.; Fernández, L.M.; Jurado, F. Predictive control for the energy management of a fuel-cell–battery–supercapacitor tramway. IEEE Trans. Ind. Inform. 2014, 10, 276–285. [Google Scholar] [CrossRef]
- Fedakar, S.; Bahceci, S.; Yalcinoz, T. Modeling and simulation of grid connected solid oxide fuel cell using PSCAD. J. Renew. Sustain. Energy 2014, 6, 053118. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Hoseintabar, M.; Faiz, J. Frequency control of isolated WT/PV/SOFC/UC network with new control strategy for improving SOFC dynamic response. Int. Trans. Electr. Energy Syst. 2015, 25, 1748–1770. [Google Scholar] [CrossRef]
- Chettibi, N.; Mellit, A.; Sulligoi, G.; Massi Pavan, A. Fuzzy-based power control for distributed generators based on solid oxide fuel cells. In Proceedings of the IEEE International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 580–585. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Ottaviano, A. Solid oxide fuel cell modelling: Electrochemical performance and thermal management during load-following operation. Energy 2016, 115, 107–119. [Google Scholar] [CrossRef]
- Vigneysh, T.; Kumarappan, N. Autonomous operation and control of photovoltaic/solid oxide fuel cell/battery energy storage based microgrid using fuzzy logic controller. Int. J. Hydrogen Energy 2016, 41, 1877–1891. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, W.; Li, D.; He, T.; Xue, Y.; Han, M.; Zheng, S. The disturbance rejection design based on physical feedforward for solid oxide fuel cell. In Proceedings of the 17th IEEE International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 18–21 October 2017. [Google Scholar] [CrossRef]
- Pan, L.; Xue, Y.; Sun, L.; Li, D.; Wu, Z. Multiple model predictive control for solid oxide fuel cells. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE 2017), Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Wu, G.; Sun, L.; Lee, K.Y. Disturbance rejection control of a fuel cell power plant in a grid-connected system. Control Eng. Pract. 2017, 60, 183–192. [Google Scholar] [CrossRef]
- Sun, L.; Hua, Q.; Shen, J.; Xue, Y.; Li, D.; Lee, K.Y. A combined voltage control strategy for fuel cell. Sustainability 2017, 9, 1517. [Google Scholar] [CrossRef]
- Triwiyatno, A.; Thalib, H. The design of connection solid oxide fuel cell (SOFC) integrated grid with three-phase inverter. IOP Conf. Ser. Mater. Sci. Eng. 2018, 316, 012057. [Google Scholar] [CrossRef]
- Sun, L.; Wu, G.; Xue, Y.; Shen, J.; Li, D.; Lee, K.Y. Coordinated control strategies for fuel cell power plant in a microgrid. IEEE Trans. Energy Convers. 2018, 33, 1–9. [Google Scholar] [CrossRef]
- Chettibi, N.; Mellit, A. Intelligent control strategy for a grid connected PV/SOFC/BESS energy generation system. Energy 2018, 147, 239–262. [Google Scholar] [CrossRef]
- Safari, A.; Shahsavari, H.; Salehi, J. A mathematical model of SOFC power plant for dynamic simulation of multi-machine power systems. Energy 2018, 149, 397–413. [Google Scholar] [CrossRef]
- Adair, D.; Jaeger, M. Quasistatic modelling of PEM fuel cell humidification system. Mater. Today Proc. 2018, 5, 22776–22784. [Google Scholar] [CrossRef]
- Gebregergis, A.; Pillay, P.; Bharracharyya, D.; Rengaswemy, R. Solid oxide fuel cell modeling. IEEE Trans. Ind. Electron. 2009, 56, 139–148. [Google Scholar] [CrossRef]
- Karcz, M. From 0D to 1D modeling of tubular solid oxide fuel cell. Energy Convers. Manag. 2009, 50, 2307–2315. [Google Scholar] [CrossRef]
- Shen, S.; Kuang, Y.; Zheng, K.; Gao, Q. A 2D model for solid oxide fuel cell with a mixed ionic and electronic conducting electrolyte. Solid State Ion. 2018, 315, 44–51. [Google Scholar] [CrossRef]
- Aydın, Ö.; Nakajima, H.; Kitahara, T. Reliability of the numerical SOFC models for estimating the spatial current and temperature variations. Int. J. Hydrogen Energy 2016, 41, 15311–15324. [Google Scholar] [CrossRef]
- Conti, B.; Bosio, B.; McPhail, S.; Santoni, F.; Pumiglia, D.; Arato, E. A 2-D model for Intermediate Temperature Solid Oxide Fuel Cells Preliminarily Validated on Local Values. Catalysts 2019, 9, 36. [Google Scholar] [CrossRef]
- Ramesh, P.; Duttagupta, S.P. Effect of Channel Dimensions on Micro PEM Fuel Cell Performance Using 3D Modeling. Int. J. Renew. Energy Res. 2013, 3, 353–358. [Google Scholar]
- Tang, S.; Amiri, A.; Vijay, P.; Tadé, M.O. Development and validation of a computationally efficient pseudo 3D model for planar SOFC integrated with a heating furnace. Chem. Eng. J. 2016, 290, 252–262. [Google Scholar] [CrossRef]
- Ghorbani, B.; Vijayaraghavan, K. 3D and simplified pseudo-2D modeling of single cell of a high temperature solid oxide fuel cell to be used for online control strategies. Int. J. Hydrogen Energy 2018, 43, 9733–9748. [Google Scholar] [CrossRef]
- Amiri, A.; Vijay, P.; Tadé, M.O.; Ahmed, K.; Ingram, G.D.; Pareek, V.; Utikar, R. Planar SOFC system modelling and simulation including a 3D stack module. Int. J. Hydrogen Energy 2016, 41, 2919–2930. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, J.; Yue, D.; Yang, G.; Ye, S.; He, C.; Wang, W.; Yuan, J.; Huang, N. Three-dimensional CFD modeling of transport phenomena in a cross-flow anode-supported planar SOFC. Energies 2014, 7, 80–98. [Google Scholar] [CrossRef]
- Osafi, M.R.; Ani, A.B.; Kalbasi, M. Numerical modeling of solid acid fuel cell performance with CsH2PO4- AAM (anodic alumina membrane) composite electrolyte. Int. J. Heat Mass Transf. 2019, 129, 1086–1094. [Google Scholar] [CrossRef]
- He, Z.; Birgersson, E.; Li, H. Reduced non-isothermal model for the planar solid oxide fuel cell and stack. Energy 2014, 70, 478–492. [Google Scholar] [CrossRef]
- Timurkutluk, B.; Mat, M.D. A review on micro-level modeling of solid oxide fuel cells. Int. J. Hydrogen Energy 2016, 41, 9968–9981. [Google Scholar] [CrossRef]
- Grew, K.N.; Chiu, W.K.S. A review of modeling and simulation techniques across the length scales for the solid oxide fuel cell. J. Power Sources 2012, 199, 1–13. [Google Scholar] [CrossRef]
- Haraldsson, K.; Wipke, K. Evaluating PEM fuel cell system models. J. Power Sources 2004, 126, 88–97. [Google Scholar] [CrossRef]
- Hissel, D.; Turpin, C.; Astier, S.; Boulon, L.; Bouscayrol, A.; Bultel, Y.; Candusso, D.; Caux, S.; Chupin, S.; Colinart, T.; et al. A Review on Existing Modeling Methodologies for PEM Fuel Cell Systems. Available online: https://www.researchgate.net/publication/260401912 (accessed on 16 February 2019).
- Zhang, X.; Yang, D.; Luo, M.; Dong, Z. Load profile based empirical model for the lifetime prediction of an automotive PEM fuel cell. Int. J. Hydrogen Energy 2017, 42, 11868–11878. [Google Scholar] [CrossRef]
- Messing, M. Empirical Modeling of Fuel Cell Durability: Cathode Catalyst Layer Degradation. Master’s Thesis, Simon Fraser University, Burnaby, BC, Canada, 2017. Available online: https://pdfs.semanticscholar.org/0d12/d528b9f915104006c2c77993e94552438806.pdf (accessed on 16 February 2019).
- Nalbant, Y.; Colpan, C.O.; Devrim, Y. Development of a one-dimensional and semi-empirical model for a high temperature proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 5939–5950. [Google Scholar] [CrossRef]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.T. Learning from Data; AMLBook: Chicago, IL, USA, 2012. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Pearson: London, UK, 2009. [Google Scholar]
- Banzhaf, W.; Olson, R.S.; Tozier, W.; Riolo, R. (Eds.) Genetic Programming Theory and Practice XV; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Chakraborty, U.K.; Abbott, T.; Das, S.K. PEM fuel cell modeling using differential evolution. Energy 2012, 40, 387–399. [Google Scholar] [CrossRef]
- Chakraborty, U.K. (Ed.) Advances in Differential Evolution; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Molyneux, P. The Dimensions of Logarithmic Quantities. J. Chem. Educ. 1991, 68, 467–469. [Google Scholar] [CrossRef]
- Mills, I.M. Letters (Dimensions of Logarithmic Quantitites). J. Chem. Educ. 1995, 72, 954–955. [Google Scholar] [CrossRef]
- White, M.A. Quantity Calculus: Unambiguous Designation of Units in Graphs and Tables. J. Chem. Educ. 1998, 75, 607–609. [Google Scholar] [CrossRef]
- Matta, C.F.; Massa, L.; Gubskaya, A.V.; Knoll, E. Can One Take the Logarithm or the Sine of a Dimensioned Quantity or a Unit? Dimensional Analysis Involving Transcendental Function. J. Chem. Educ. 2011, 88, 67–70. [Google Scholar] [CrossRef]
- Fuel Cell Handbook, 7th ed.; EG&G Technical Services, Inc. (U.S. Department of Energy): Gaithersburg, MD, USA, 2004.
- Burstein, G.T. A hundred years of Tafel’s Equation: 1905–2005. Corros. Sci. 2005, 47, 2858–2870. [Google Scholar] [CrossRef]
- DiGiuseppe, G. High Power Density Cell Development at Siemens Westinghouse. In Solid Oxide Fuel Cells IX (SOFC-IX) Vol. 1: Cells, Stacks and Systems; Singhal, S.C., Mizusaki, J., Eds.; Electrochemical Society Proceedings Vol. 2005-07; ECS: Pennington, NJ, USA, 2005; pp. 322–332. [Google Scholar]
- Zhang, L.; Wang, N. An adaptive RNA genetic algorithm for modeling of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2013, 38, 219–228. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, N.; Zhang, L. Circular genetic operators based RNA genetic algorithm for modeling proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 17779–17790. [Google Scholar] [CrossRef]
- Ohenoja, M.; Sorsa, A.; Leiviskä, K. Model structure optimization for fuel cell polarization curves. Computers 2018, 7, 60. [Google Scholar] [CrossRef]
- Ohenoja, M.; Leiviskä, K. Validation of genetic algorithm results in a fuel cell model. Int. J. Hydrogen Energy 2010, 35, 12618–12625. [Google Scholar] [CrossRef]
- Aguiar, P.; Adjiman, C.S.; Brandon, N.P. Anode-supported intermediate-temperature direct internal reforming solid oxide fuel cell II. Model-based dynamic performance and control. J. Power Sources 2005, 147, 136–147. [Google Scholar] [CrossRef]
- Mueller, F.; Brouwer, J.; Jabbari, F.; Samuelsen, S. Dynamic Simulation of an Integrated Solid Oxide Fuel Cell System Including Current-Based Fuel Flow Control. J. Fuel Cell Sci. Technol. 2006, 3, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Vijay, P.; Samantaray, A.K.; Mukherjee, A. On the rationale behind constant fuel utilization control of solid oxide fuel cells. J. Syst. Control Eng. 2009, 223, 229–251. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.; Leung, D.Y. Parametric study of solid oxide steam electrolyzer for hydrogen production. Int. J. Hydrogen Energy 2007, 32, 2305–2313. [Google Scholar] [CrossRef]
- Patcharavorachot, Y.; Arpornwichanop, A.; Chuachuensuk, A. Electrochemical study of a planar solid oxide fuel cell: Role of support structures. J. Power Sources 2008, 177, 254–261. [Google Scholar] [CrossRef]
- Chakraborty, U.K. A simple electrochemical model for constant fuel flow in solid oxide fuel cells. Presented at the IEEE International Conference on Recent Innovations in Electrical, Electronics & Communication Engineering (ICRIEECE), Bhubaneswar, India, 27–28 July 2018. [Google Scholar]








| Parameter | Value |
|---|---|
| T | 1273 K |
| u | 0.8 |
| 0.843 mol/(s·atm) | |
| 0.281 mol/(s·atm) | |
| 2.52 mol/(s·atm) | |
| r | 3.28125 × 10 |
| 1.145 | |
| n | 2 |
| Constants | |
| F | 96,485 Coulombs/mol |
| R | 8.31 J/(mol K) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, U.K. A New Model for Constant Fuel Utilization and Constant Fuel Flow in Fuel Cells. Appl. Sci. 2019, 9, 1066. https://doi.org/10.3390/app9061066
Chakraborty UK. A New Model for Constant Fuel Utilization and Constant Fuel Flow in Fuel Cells. Applied Sciences. 2019; 9(6):1066. https://doi.org/10.3390/app9061066
Chicago/Turabian StyleChakraborty, Uday K. 2019. "A New Model for Constant Fuel Utilization and Constant Fuel Flow in Fuel Cells" Applied Sciences 9, no. 6: 1066. https://doi.org/10.3390/app9061066




