Flutter and Divergence Instability of Axially-Moving Nanoplates Resting on a Viscoelastic Foundation
Abstract
:1. Introduction
2. Basic Equations
3. Solution Method
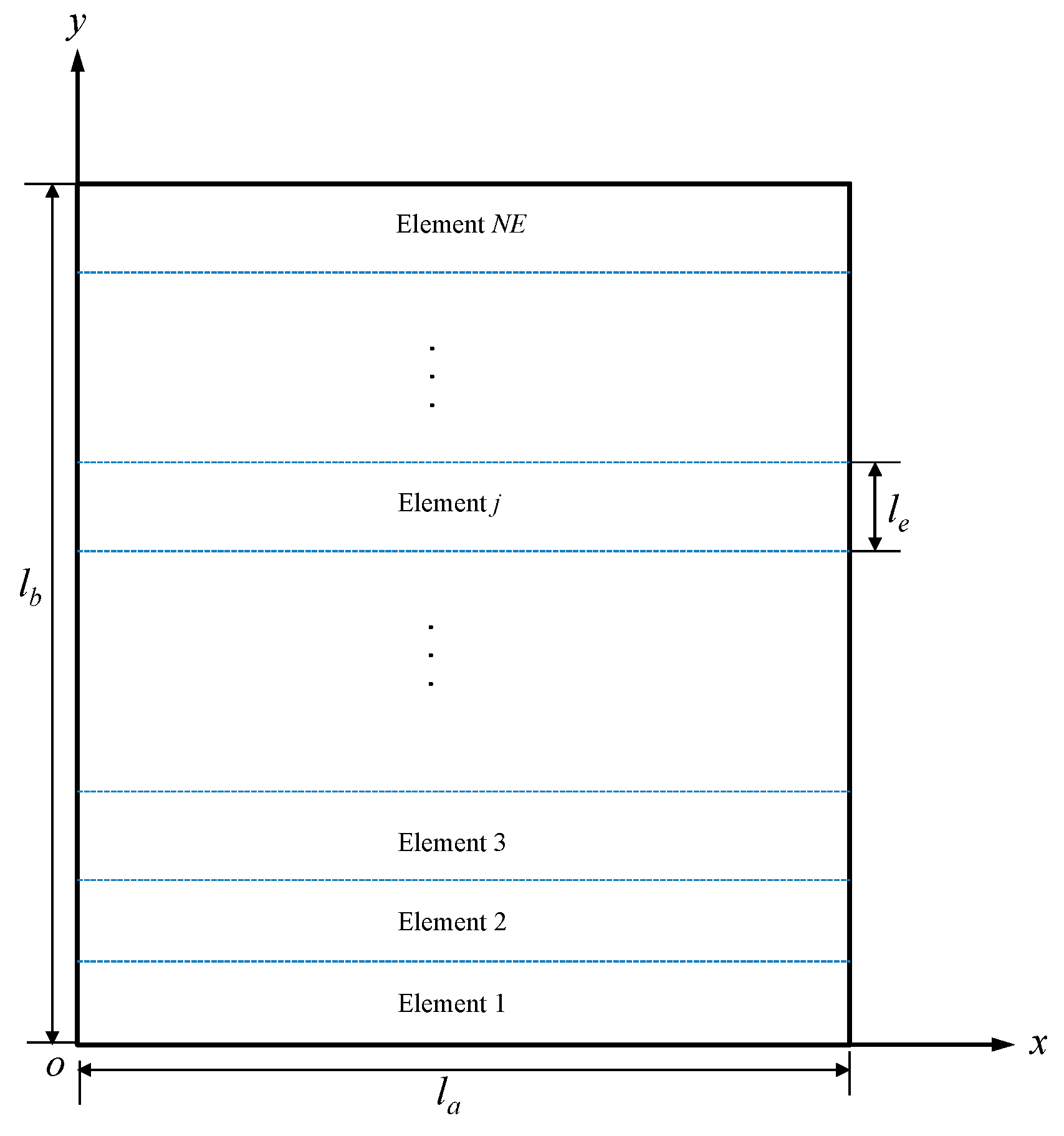
4. Numerical Investigation
4.1. Comparison and Validation
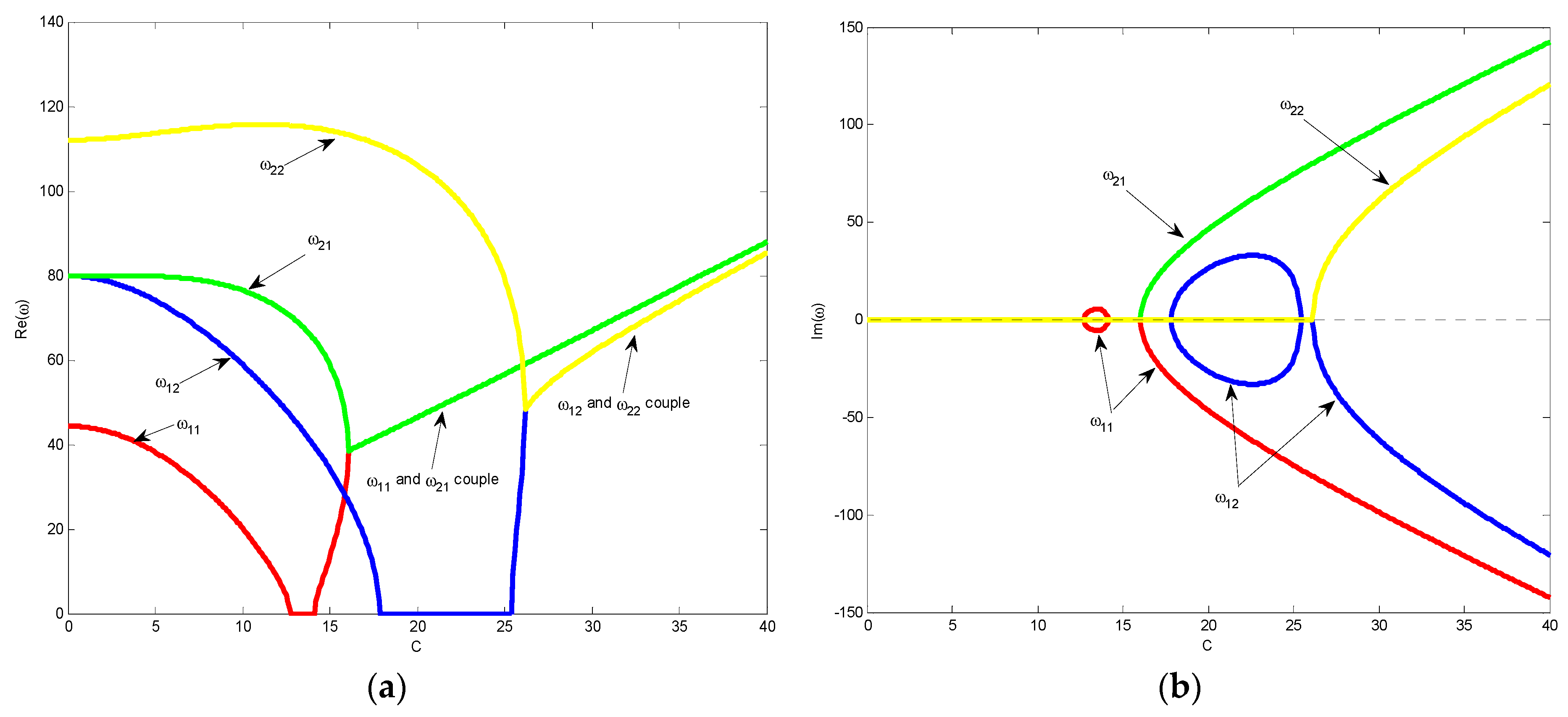
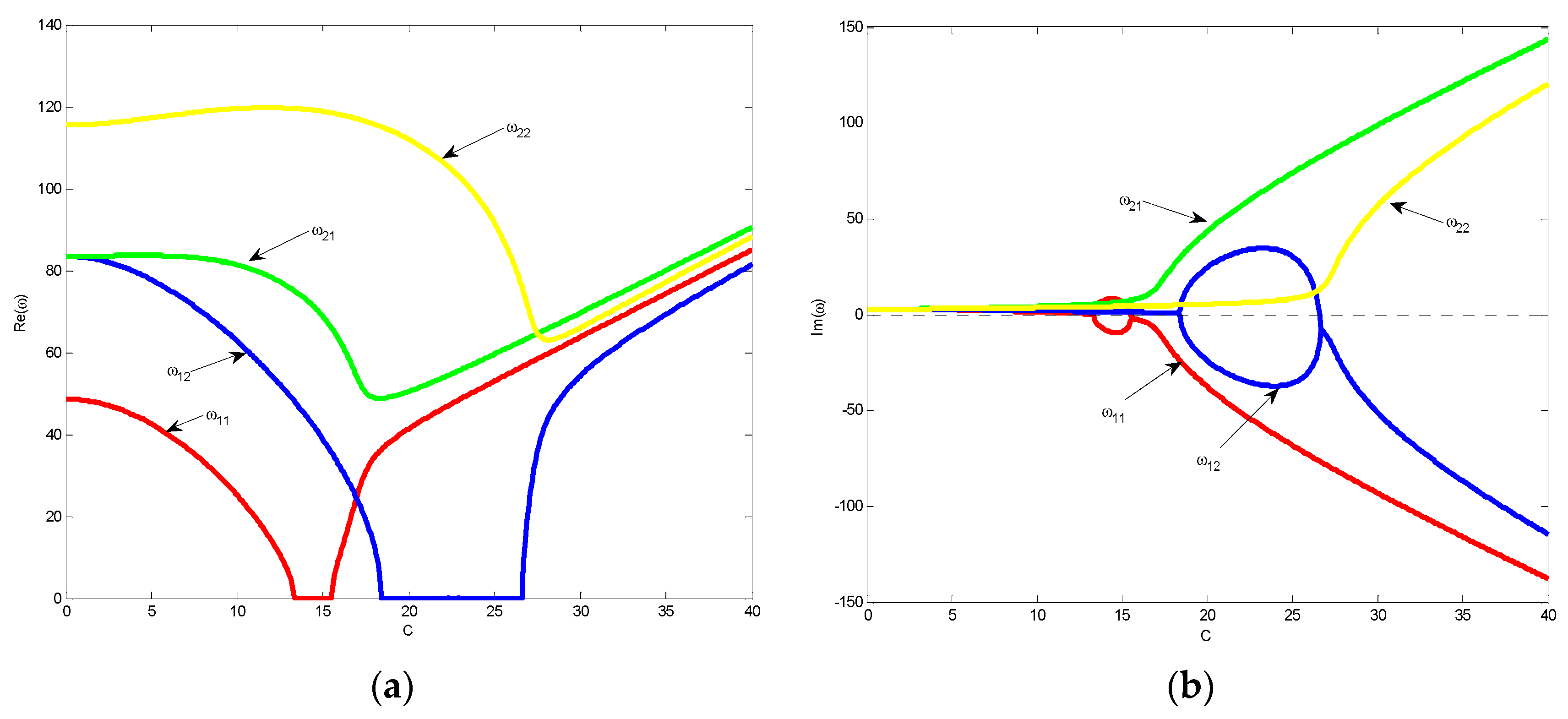
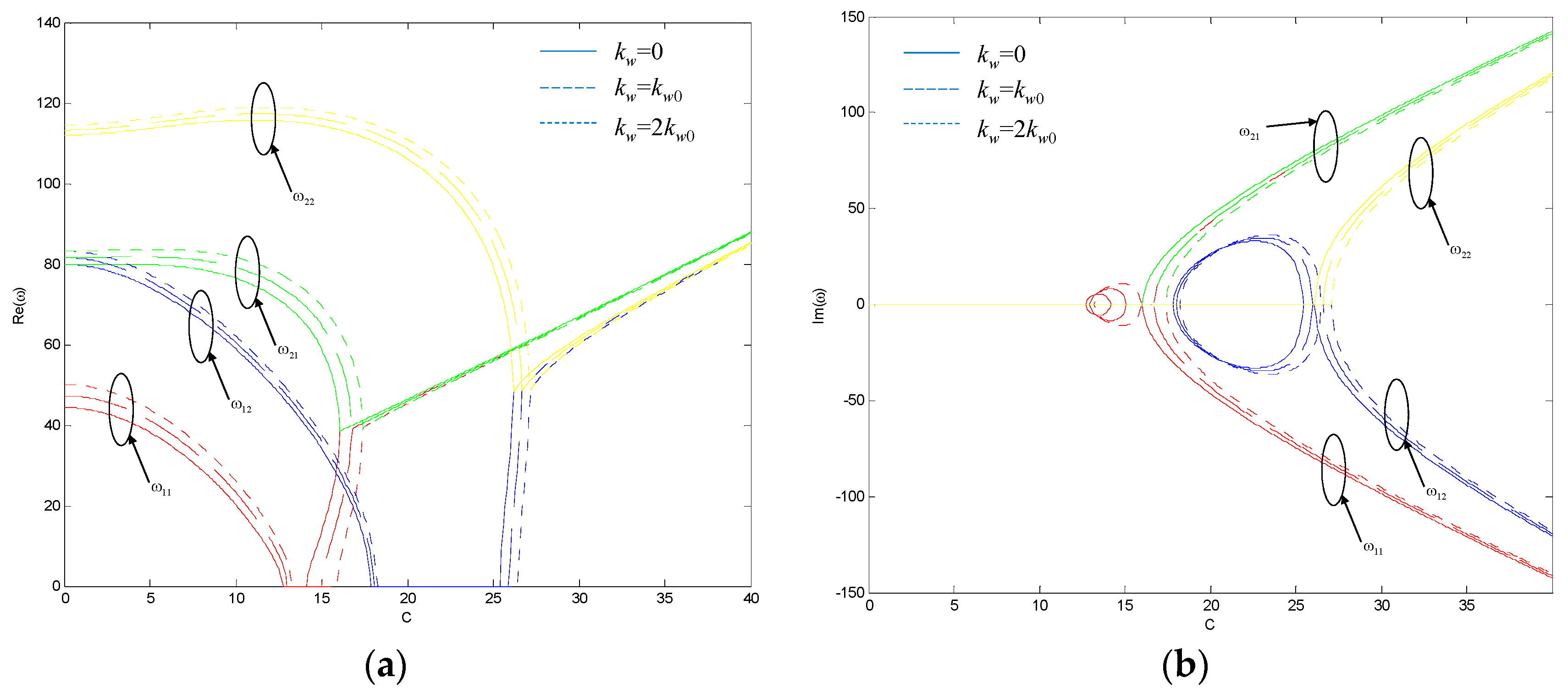
4.2. Flutter and Divergent Instability
5. Conclusions
- (i)
- The viscoelastic foundation has a dominant impact on vibrations of the axially-moving nanoplate. The dimensionless natural frequencies of the axially-moving nanoplate resting on a viscoelastic foundation are complex numbers when the dimensionless moving speed C > 0.
- (ii)
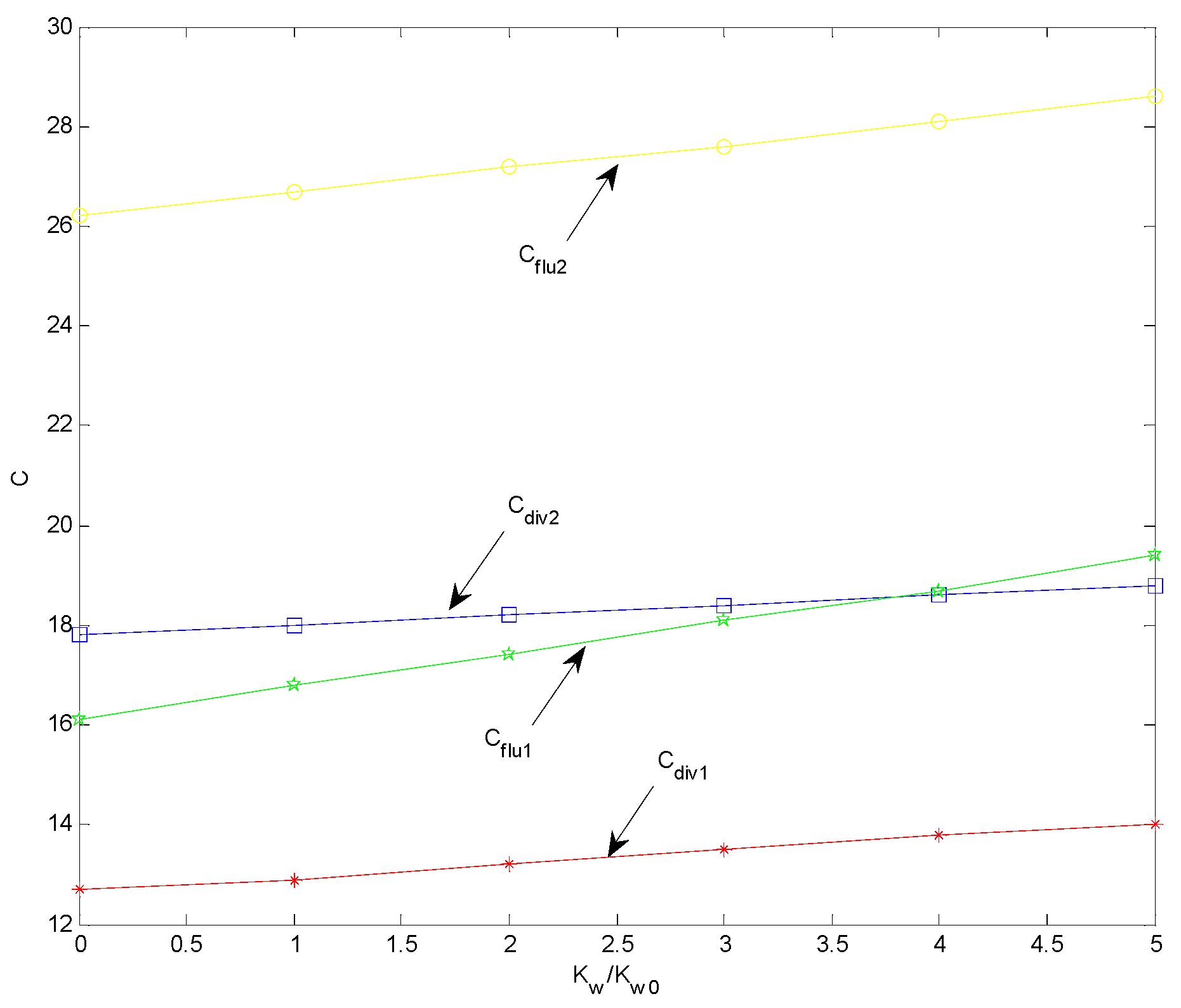
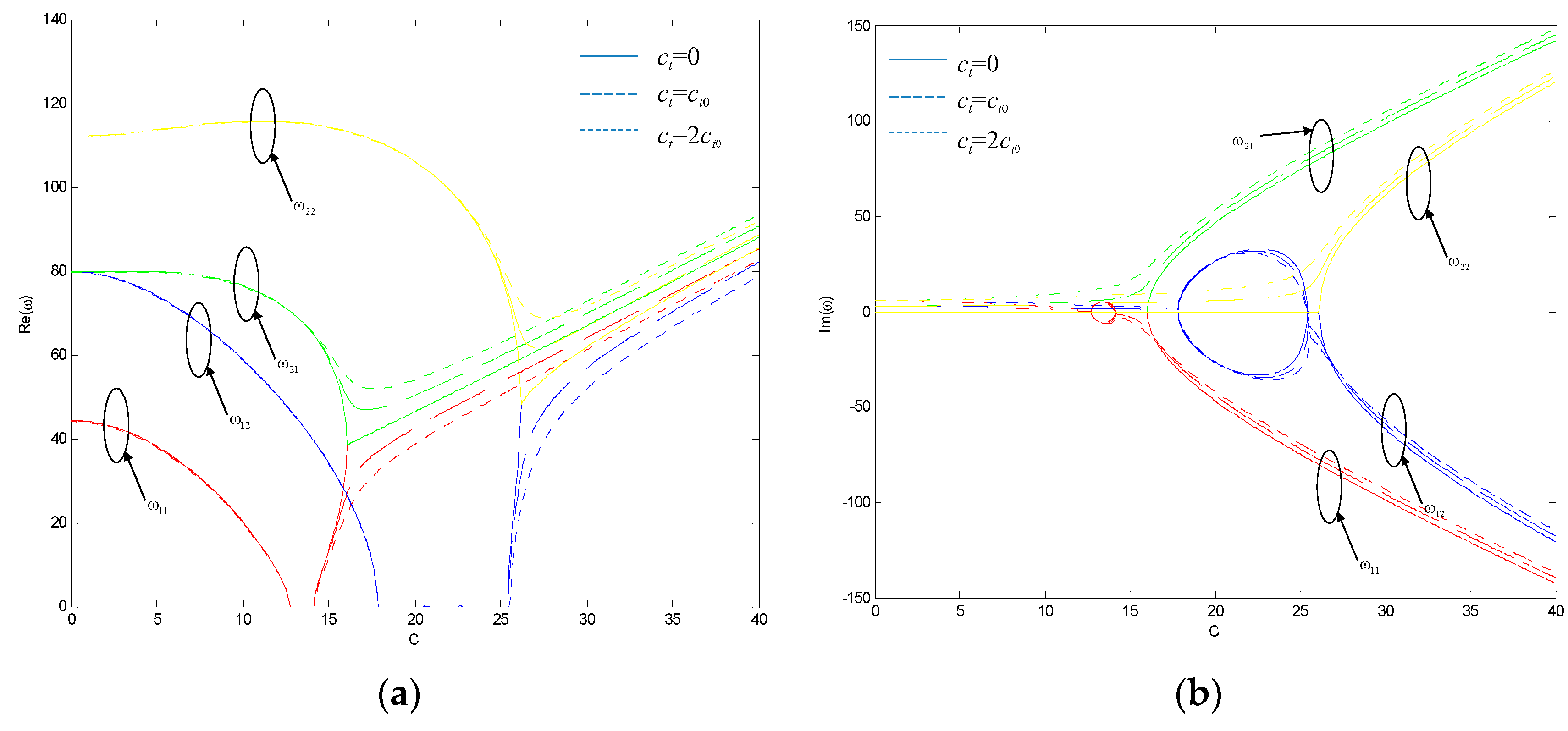
- The Winkler’s modulus kw of the viscoelastic foundation significantly affects both the instability zone and the divergence speed. The Pasternak’s modulus kG of the viscoelastic foundation affects mainly the divergence speed. The damping ct of the viscoelastic foundation has almost no influence on the instability zone or divergence speed.
- (iii)
- Mode-couple flutter disappears when the axially-moving nanoplate rests on a viscoelastic foundation. This change of instability types is mainly influenced by the damping ct of the viscoelastic foundation.
- (iv)
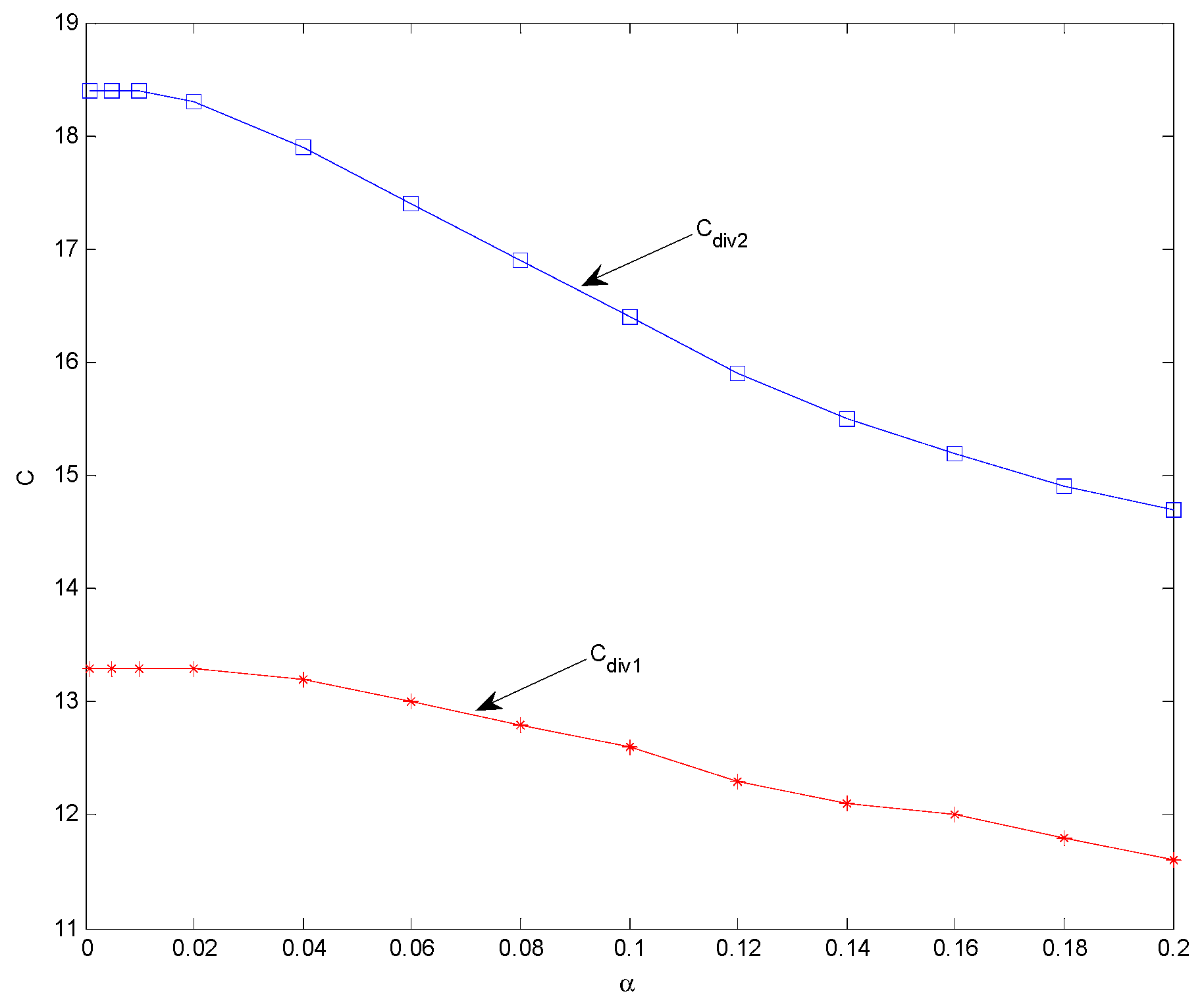
- Small-parameter α affects both the divergence instability zero and the divergence speed of the axially-moving nanoplates resting on a viscoelastic foundation. Such influences become more substantial when α > 0.02.
- (v)
- The divergence instability is also quite sensitive to the biaxial force, which influences the divergence instability zero and the corresponding divergence speed.
Author Contributions
Funding
Conflicts of Interest
References
- Asemi, S.R.; Farajpour, A.; Mohammadi, M. Nonlinear vibration analysis of piezoelectric nanoelectro mechanical resonators based on nonlocal elasticity theory. Compos. Struct. 2014, 116, 703–712. [Google Scholar] [CrossRef]
- Song, S.; Hou, Y.; Guo, M.; Wang, L.; Tong, X.; Wu, J. An investigation on the aggregate-shape embedded piezoelectric sensor for civil infrastructure health monitoring. Constr. Build. Mater. 2017, 131, 57–65. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.P.; Lu, C.; Zhang, P.Q. Dynamic properties of flexural beams using a nonlocal elasticity model. J. Appl. Phys. 2006, 99, 073510. [Google Scholar] [CrossRef]
- Aydogdu, M. A general nonlocal beam theory: Its application to nanobeam bending, buckling and vibration. Physica E 2009, 41, 1651–1655. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Z.; Wright, A.R.; Zhang, C. Orbital magnetization of graphene and graphene nanoribbons. J. Appl. Phys. 2008, 103, 103711. [Google Scholar] [CrossRef] [Green Version]
- Duan, W.H.; Wang, C.M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory. Nanotechnology 2007, 18, 385704. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.M. The constitutive relation and small scale parameter of nonlocal continuum mechanics for modelling carbon nanotubes. Nanotechnology 2007, 18, 75702. [Google Scholar] [CrossRef]
- Li, X.; Bhushan, B. A review of nanoindentation continuous stiffness measurement technique and its applications. Mater. Charact. 2002, 48, 11–36. [Google Scholar] [CrossRef]
- Memarian, F.; Fereidoon, A.; Khodaei, S.; Mashhadzadeh, A.H.; Ganji, M.D. Molecular dynamic stud y of mechanic al propert ies of single/double wall SiCNTs: Consideration temperature, diameter and interlayer distance. Vacuum 2017, 139, 93–100. [Google Scholar] [CrossRef]
- Lei, Y.; Adhikari, S.; Murmu, T.; Friswell, M.I. Asymptotic frequencies of various damped nonlocal beams and plates. Mech. Res. Commun. 2014, 62, 94–101. [Google Scholar] [CrossRef]
- Kolahchi, R.; Bidgoli, A.M.M. Size-dependent sinusoidal beam model for dynamic instability of single-walled carbon nanotubes. Appl. Math. Mech. 2016, 37, 265–274. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solution of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. A unified continuum theory of electrodynamics of liquid crystals. Int. J. Eng. Sci. 1997, 35, 1137–1157. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Shen, Z.B.; Tang, H.L.; Li, D.K.; Tang, G.J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, L.; Rabczuk, T. Binding energy and mechanical stability of single- and multi-walled carbon nanotube serpentines. J. Chem. Phys. 2014, 140, 3846–3855. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.D.; Tang, Y.Q.; Chen, L.Q.; Lim, C.W. Dynamic stability of axially accelerating Timoshenko beam: Average method. Eur. J. Mech. A Solids 2010, 29, 81–90. [Google Scholar] [CrossRef]
- Kiani, K. Longitudinal, transverse and torsional vibrations and stabilities of axially moving single-walled carbon nanotubes. Curr. Appl. Phys. 2013, 13, 1651–1660. [Google Scholar] [CrossRef]
- Mokhtari, A.; Mirdamadi, H.R.; Ghayour, M.; Sarvestan, V. Time wave domain analysis for axially moving pre-stressed nanobeam by wavelet-based spectral element method. Int. J. Mech. Sci. 2016, 105, 58–69. [Google Scholar] [CrossRef]
- Wang, J.; Shen, H.; Zhang, B.; Liu, J.; Zhang, Y. Complex modal analysis of transverse free vibrations for axially moving nanobeams based on the nonlocal strain giadient theory. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 101, 85–93. [Google Scholar] [CrossRef]
- Li, C. Size-dependent thermal behaviors of axially traveling nanobeams based on a strain gradient theory. Struct. Eng. Mech. 2013, 48, 415–434. [Google Scholar] [CrossRef]
- Rezaee, M.; Lotfan, S. Non-linear nonlocal vibration and stability analysis of axially moving nanoscale beams with time-dependent velocity. Int. J. Mech. Sci. 2015, 96, 36–46. [Google Scholar] [CrossRef]
- Oveissi, S.; Ghassemi, A. Longitudinal and transverse wave propagation analysis of stationary and axially moving carbon nanotubes conveying nano-fluid. Appl. Math. Model. 2018, 60, 460–477. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, C.; Fan, X.L.; Tong, L.H. Transverse free vibration and stability of axially moving nanoplates based on nonlocal elasticity theory. Appl. Math. Model. 2017, 45, 65–84. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.J.; Cheng, M.; Fan, X.L. Nonlocal vibrations and stabilities in parametric resonance of axially moving viscoelastic piezoelectric nanoplate subjected to thermo- electro-mechanic al forces. Composites Part B 2017, 116, 153–169. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Kumar, A. Vibration analysis of orthotropic graphene sheets embedded in Pasternak elastic medium using nonlocal elasticity theory and differential quadrature method. Comput. Mater. Sci. 2010, 50, 239–245. [Google Scholar] [CrossRef]
- Jung, W.Y.; Han, S.C.; Park, W.T. A modified couple stress theory for buckling analysis of S-FGM nanoplates embedded in Pasternak elastic medium. Composites Part B 2014, 60, 746–756. [Google Scholar] [CrossRef]
- Radic, N.; Jeremic, D.; Trifkovic, S.; Milutinovic, M. Buckling analysis of double-orthotropic nanoplates embedded in Pasternak elastic medium using nonlocal elasticity theory. Composites Part B 2014, 61, 162–171. [Google Scholar] [CrossRef]
- Asemi, S.R.; Farajpour, A. Thermo-electro-mechanical vibration of coupled piezoelectric nanoplate systems under non-uniform voltage distribution embedded in Pasternak elastic medium. Curr. Appl. Phys. 2014, 14, 814–832. [Google Scholar] [CrossRef]
- Asemi, S.R.; Farajpour, A.; Asemi, H.R.; Mohammadi, M. Influence of initial stress on the vibration of double-piezoelectric-nanoplate systems with various boundary conditions using DQM. Physica E 2014, 63, 169–179. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Shanab, R.A.; Seddek, L.F. Vibration analysis of Euler-Bernoulli nanobeams embedded in an elastic medium by a sixth-order compact finite difference method. Appl. Math. Model. 2016, 40, 2396–2406. [Google Scholar] [CrossRef]
- Arani, A.G.; Jalaei, M.H. Transient behavior of an orthotropic graphene sheet resting on orthotropic visco-Pasternak foundation. Int. J. Eng. Sci. 2016, 103, 97–113. [Google Scholar] [CrossRef]
- Gharib, A.; Karimi, M.S.; Arani, A.G. Vibration analysis of the embedded piezoelectric polymeric nano-composite panels in the elastic substrate. Composites Part B 2016, 101, 64–76. [Google Scholar] [CrossRef]
- Biloueiet, B.S.; Kolahchi, R.; Bidgoli, M.R. Buckling of concrete columns retrofitted with nano-fiber reinforced polymer (NFRP). Comput. Concr. 2016, 18, 1053–1063. [Google Scholar] [CrossRef]
- Jamalpoor, A.; Savadkoohi, A.A.; Hosseini, M.; Hashemi, S.H. Free vibration and biaxial buckling analysis of double magneto-electro-elastic nanoplate-systems coupled by a visco-Pasternak medium via nonlocal elasticity theory. Euro. J. Mech. A/Solids 2017, 63, 84–98. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Arefi, M. Nonlocal transient electrothermomechanical vibration and bending analysis of a functionally graded piezoelectric single-layered nanosheet rest on visco-Pasternak foundation. J. Therm. Stress 2017, 40, 167–184. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Size-dependent free vibration and dynamic analyses of piezoelectromagnetic sandwich nanoplates resting on viscoelastic foundation. Physica B 2017, 521, 188–197. [Google Scholar] [CrossRef]
- Kolahchi, R.; Zarei, M.S.; Hajmohammad, M.H.; Oskouei, A.N. Visco-nonlocal-refined Zigzag theories for dynamic buckling of laminated nanoplates using differential cubature-Bolotin methods. Thin-Walled Struct. 2017, 113, 162–169. [Google Scholar] [CrossRef]
- Zhang, D.P.; Lei, Y.; Shen, Z.B. Thermo-electro-mechanical vibration analysis of piezoelectric nanoplates resting on viscoelastic foundation with various boundary conditions. Int. J. Mech. Sci. 2017, 131–132, 1001–1015. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Yang, J. Vibration of FG magneto-electro-viscoelastic porous nanobeams on visco-Pasternak foundation. Composites Part B 2018, 155, 244–256. [Google Scholar] [CrossRef]
- Liu, H.; Lv, Z. Uncertainty analysis for wave dispersion behavior of carbon nanotubes embedded in Pasternak-type elastic medium. Mech. Res. Commun. 2018, 92, 92–100. [Google Scholar] [CrossRef]

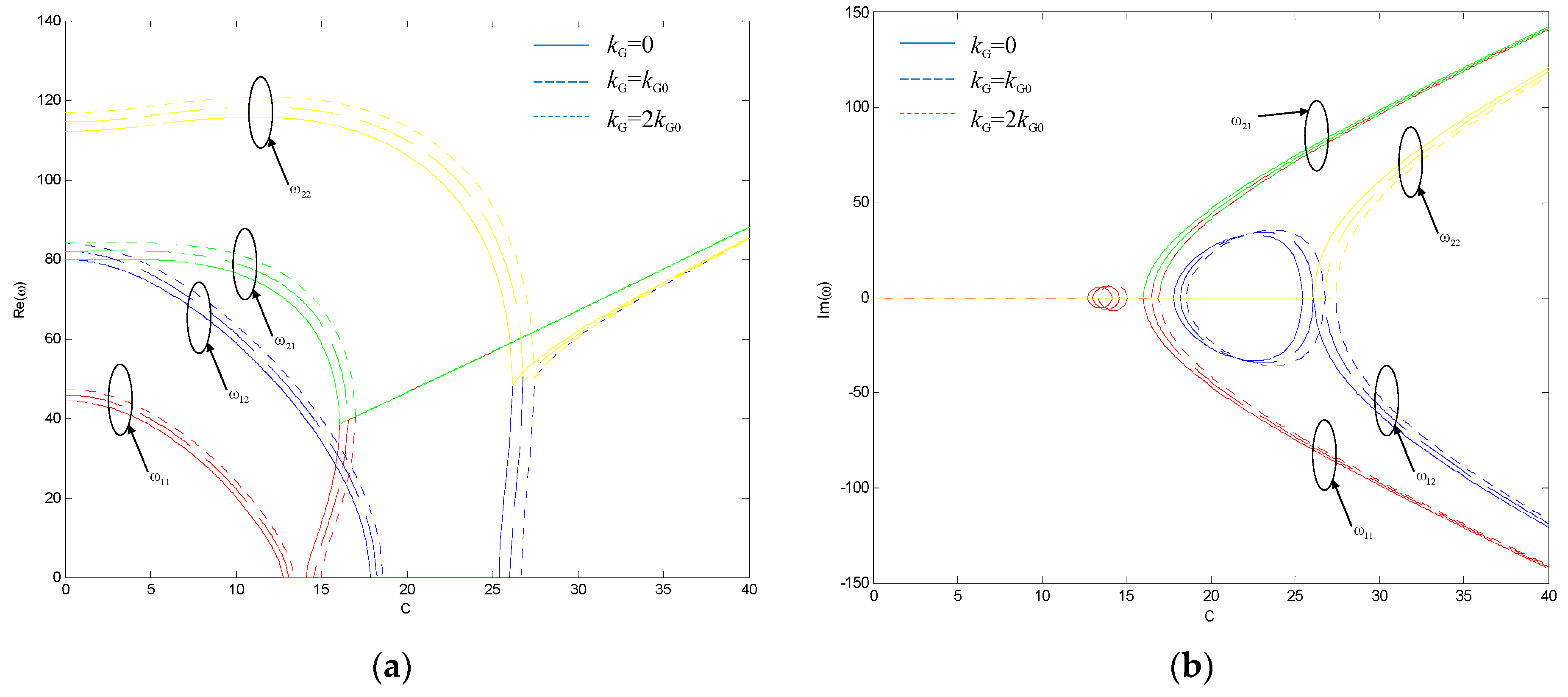



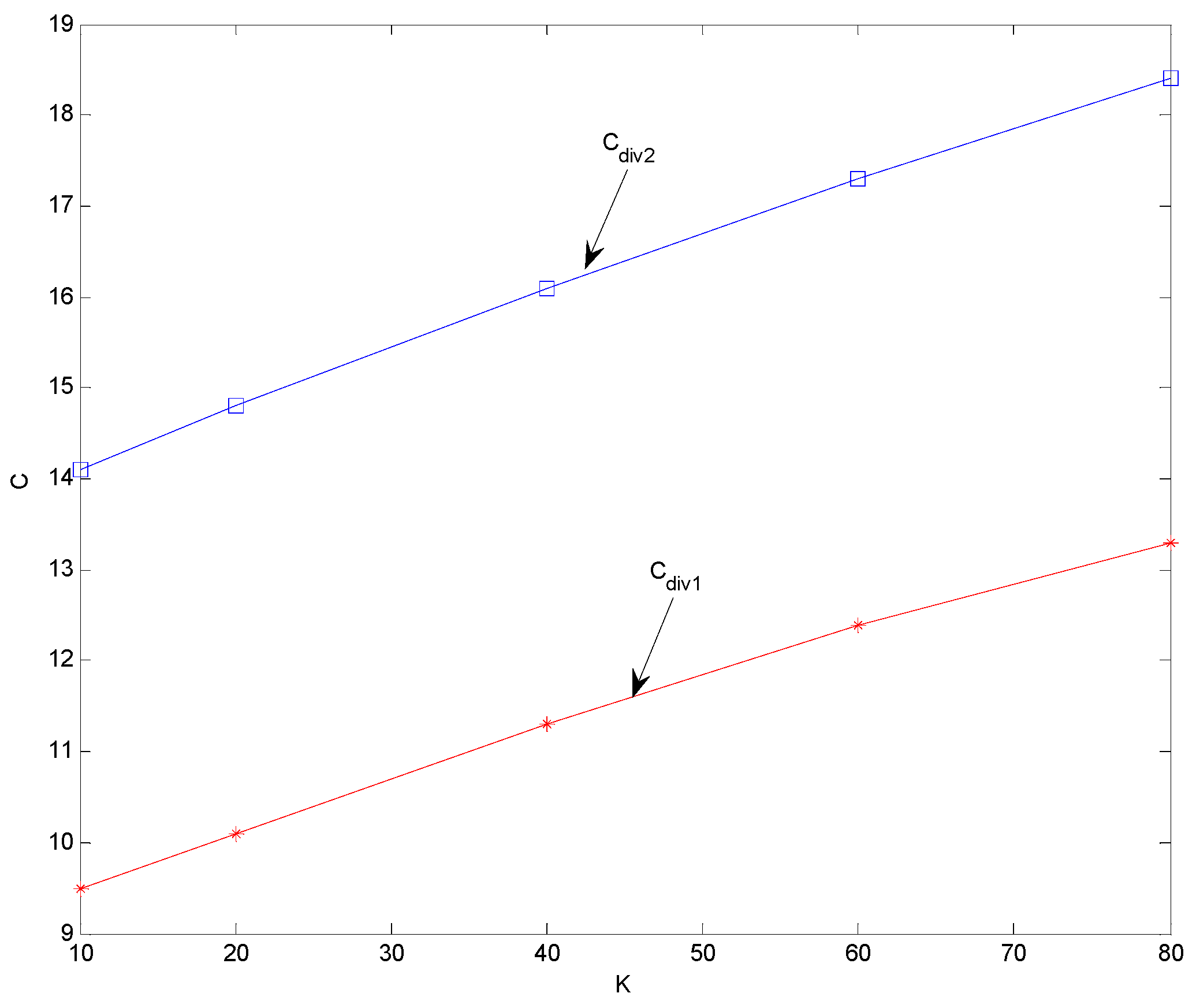
| C | ω11 | ω12 | ||
|---|---|---|---|---|
| α = 0.0 | α = 0.005 | α = 0.0 | α = 0.005 | |
| Pressent/Ref. [24] | Pressent/Ref. [24] | Pressent/Ref. [24] | Pressent/Ref. [24] | |
| 0 | 44.3601/44.3709 | 44.3577/44.3687 | 79.8500/79.8941 | 79.9500/79.8753 |
| 2 | 43.3402/43.3435 | 43.3361/43.3409 | 78.5746/78.5923 | 78.5598/78.5714 |
| 4 | 40.2698/40.2712 | 40.2500/40.2674 | 74.6534/74.6768 | 74.6401/74.6494 |
| 6 | 35.1732/35.1804 | 35.1611/35.1745 | 68.1010/68.1130 | 68.0699/68.0746 |
| 8 | 28.0989/28.1030 | 28.0899/28.0940 | 58.8110/58.8225 | 58.7618/58.7690 |
| 10 | 19.0302/19.0359 | 19.0221/19.0228 | 46.6143/46.6159 | 46.5418/46.5434 |
| C | ω11 | ω12 | ||
|---|---|---|---|---|
| α = 0.01 | α = 0.10 | α = 0.01 | α = 0.10 | |
| 0 | 0.4860 + 0.0297i | 0.4791 + 0.0273i | 0.8345 + 0.0296i | 0.7814 + 0.0219i |
| 2 | 0.4761 + 0.0290i | 0.4680 + 0.0265i | 0.8248 + 0.0291i | 0.7692 + 0.0214i |
| 4 | 0.4467 + 0.0270i | 0.4359 + 0.0244i | 0.7968 + 0.0277i | 0.7350 + 0.0202i |
| 6 | 0.3994 + 0.0240i | 0.3844 + 0.0214i | 0.7532 + 0.0259i | 0.6837 + 0.0186i |
| 8 | 0.3345 + 0.0203i | 0.3143 + 0.0177i | 0.6961 + 0.0238i | 0.6179 + 0.0169i |
| 10 | 0.2509 + 0.0156i | 0.2226 + 0.0129i | 0.6263 + 0.0214i | 0.5380 + 0.0151i |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Zhang, D.; Wang, W. Flutter and Divergence Instability of Axially-Moving Nanoplates Resting on a Viscoelastic Foundation. Appl. Sci. 2019, 9, 1097. https://doi.org/10.3390/app9061097
Duan J, Zhang D, Wang W. Flutter and Divergence Instability of Axially-Moving Nanoplates Resting on a Viscoelastic Foundation. Applied Sciences. 2019; 9(6):1097. https://doi.org/10.3390/app9061097
Chicago/Turabian StyleDuan, Jingbo, Dapeng Zhang, and Wenjie Wang. 2019. "Flutter and Divergence Instability of Axially-Moving Nanoplates Resting on a Viscoelastic Foundation" Applied Sciences 9, no. 6: 1097. https://doi.org/10.3390/app9061097




