Lipid Diffusion in Supported Lipid Bilayers: A Comparison between Line-Scanning Fluorescence Correlation Spectroscopy and Single-Particle Tracking
Abstract
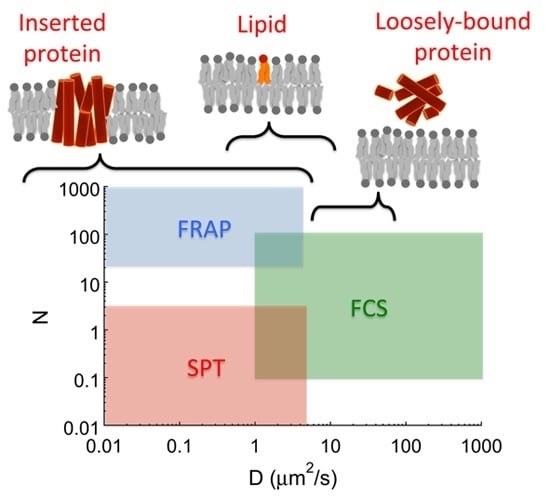
:1. Introduction
2. Results
2.1. Line-Scanning Fluorescence Correlation Spectroscopy


2.2. Single-Particle Tracking


3. Discussion
| Experimental Method | Analysis Method | D (μm2 · s−1) |
|---|---|---|
| Line-scanning FCS | Full images | 3.4 ± 0.4 |
| Cropped images | 3.2 ± 0.4 | |
| SPT | MSD of individual tracks | 2.4 ± 0.3 |
| MSD of combined track | 2.2 ± 0.4 | |
| Distribution of displacements | 1.6 ± 0.2 |
4. Methods
4.1. Supported Lipid Bilayer Preparation
4.2. Line-Scanning Fluorescence Correlation Spectroscopy
4.2.1. Confocal Imaging
4.2.2. Generation and Analysis of Line Autocorrelation Functions
4.3. Single-Particle Tracking
4.3.1. Total Internal Reflection Fluorescence Microscopy
4.3.2. Generation and Analysis of Single-Particle Tracks
5. Conclusion
Acknowledgements
Author Contributions
Conflicts of Interest
References
- So, P.T.; Dong, C.Y.; Masters, B.R.; Berland, K.M. Two-photon excitation fluorescence microscopy. Annu. Rev. Biomed. Eng. 2000, 2, 399–429. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, D. Total internal reflection fluorescence microscopy in cell biology. Traffic 2001, 2, 764–774. [Google Scholar] [CrossRef] [PubMed]
- Lichtman, J.W.; Conchello, J.A. Fluorescence microscopy. Nat. Methods 2005, 2, 910–919. [Google Scholar] [CrossRef] [PubMed]
- Hess, S.T.; Huang, S.; Heikal, A.A.; Webb, W.W. Biological and chemical applications of fluorescence correlation spectroscopy: A review. Biochemistry 2002, 41, 697–705. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, T.; Schütz, G.J.; Baumgartner, W.; Gruber, H.J.; Schindler, H. Imaging of single molecule diffusion. Proc. Natl. Acad. Sci. USA 1996, 93, 2926–2929. [Google Scholar] [CrossRef] [PubMed]
- Leung, B.O.; Chou, K.C. Review of super-resolution fluorescence microscopy for biology. Appl. Spectrosc. 2011, 65, 967–980. [Google Scholar] [CrossRef] [PubMed]
- Singer, S.; Nicolson, G.L. The fluid mosaic model of the structure of cell membranes. In Membranesand Viruses in Immunopathology; Day, S.B., Good, R.A., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1972; pp. 7–47. [Google Scholar]
- Kusumi, A.; Fujiwara, T.K.; Chadda, R.; Xie, M.; Tsunoyama, T.A.; Kalay, Z.; Kasai, R.S.; Suzuki, K.G. Dynamic organizing principles of the plasma membrane that regulate signal transduction: Commemorating the fortieth anniversary of Singer and Nicolson’s fluid-mosaic model. Annu. Rev. Cell Dev. Biol. 2012, 28, 215–250. [Google Scholar] [CrossRef] [PubMed]
- Abu-Arish, A.; Kalab, P.; Ng-Kamstra, J.; Weis, K.; Fradin, C. Spatial distribution and mobility of the Ran GTPase in live interphase cells. Biophys. J. 2009, 97, 2164–2178. [Google Scholar] [CrossRef] [PubMed]
- Shivakumar, S.; Kurylowicz, M.; Hirmiz, N.; Manan, Y.; Friaa, O.; Shamas-Din, A.; Masoudian, P.; Leber, B.; Andrews, D.W.; Fradin, C. The proapoptotic protein tBid forms both superficially bound and membrane-inserted oligomers. Biophys. J. 2014, 106, 2085–2095. [Google Scholar] [CrossRef] [PubMed]
- Petersen, N. Scanning fluorescence correlation spectroscopy. I. Theory and simulation of aggregation measurements. Biophys. J. 1986, 49, 809–815. [Google Scholar] [CrossRef]
- Palmer, A.; Thompson, N. Theory of sample translation in fluorescence correlation spectroscopy. Biophys. J. 1987, 51, 339–343. [Google Scholar] [CrossRef]
- Berland, K.; So, P.; Chen, Y.; Mantulin, W.; Gratton, E. Scanning two-photon fluctuation correlation spectroscopy: Particle counting measurements for detection of molecular aggregation. Biophys. J. 1996, 71, 410–420. [Google Scholar] [CrossRef]
- Ries, J.; Chiantia, S.; Schwille, P. Accurate determination of membrane dynamics with line-scan FCS. Biophys. J. 2009, 96, 1999–2008. [Google Scholar] [CrossRef] [PubMed]
- Digman, M.A.; Brown, C.M.; Sengupta, P.; Wiseman, P.W.; Horwitz, A.R.; Gratton, E. Measuring fast dynamics in solutions and cells with a laser scanning microscope. Biophys. J. 2005, 89, 1317–1327. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.; Dalal, R.; Hebert, B.; Digman, M.; Horwitz, A.; Gratton, E. Raster image correlation spectroscopy (RICS) for measuring fast protein dynamics and concentrations with a commercial laser scanning confocal microscope. J. Microsc. 2008, 229, 78–91. [Google Scholar] [CrossRef] [PubMed]
- Schwille, P.; Korlach, J.; Webb, W.W. Fluorescence correlation spectroscopy with single-molecule sensitivity on cell and model membranes. Cytometry 1999, 36, 176–182. [Google Scholar] [CrossRef]
- Korlach, J.; Schwille, P.; Webb, W.W.; Feigenson, G.W. Characterization of lipid bilayer phases by confocal microscopy and fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. USA 1999, 96, 8461–8466. [Google Scholar] [CrossRef] [PubMed]
- Benda, A.; Beneš, M.; Marecek, V.; Lhotskỳ, A.; Hermens, W.T.; Hof, M. How to determine diffusion coefficients in planar phospholipid systems by confocal fluorescence correlation spectroscopy. Langmuir 2003, 19, 4120–4126. [Google Scholar] [CrossRef]
- Zhang, L.; Granick, S. Lipid diffusion compared in outer and inner leaflets of planar supported bilayers. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef] [PubMed]
- Samiee, K.; Moran-Mirabal, J.; Cheung, Y.; Craighead, H. Zero mode waveguides for single-molecule spectroscopy on lipid membranes. Biophys. J. 2006, 90, 3288–3299. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Har, J.Y.; Sankaran, J.; Hong, Y.; Kannan, B.; Wohland, T. Molecular diffusion measurement in lipid bilayers over wide concentration ranges: A comparative study. Chem. Phys. Chem. 2008, 9, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Macháň, R.; Hof, M. Recent developments in fluorescence correlation spectroscopy for diffusion measurements in planar lipid membranes. Int. J. Mol. Sci. 2010, 11, 427–457. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J.; Jacobson, K. Single-particle tracking: Applications to membrane dynamics. Annu. Rev.Biophys. Biomol. Struct. 1997, 26, 373–399. [Google Scholar] [CrossRef] [PubMed]
- Schütz, G.; Schindler, H.; Schmidt, T. Single-molecule microscopy on model membranes reveals anomalous diffusion. Biophys. J. 1997, 73, 1073–1080. [Google Scholar] [CrossRef]
- Sonnleitner, A.; Schütz, G.; Schmidt, T. Free Brownian motion of individual lipid molecules in biomembranes. Biophys. J. 1999, 77, 2638–2642. [Google Scholar] [CrossRef]
- Dietrich, C.; Yang, B.; Fujiwara, T.; Kusumi, A.; Jacobson, K. Relationship of lipid rafts to transient confinement zones detected by single particle tracking. Biophys. J. 2002, 82, 274–284. [Google Scholar] [CrossRef]
- Kusumi, A.; Nakada, C.; Ritchie, K.; Murase, K.; Suzuki, K.; Murakoshi, H.; Kasai, R.S.; Kondo, J.; Fujiwara, T. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: High-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 351–378. [Google Scholar] [CrossRef] [PubMed]
- Lovell, J.F.; Billen, L.P.; Bindner, S.; Shamas-Din, A.; Fradin, C.; Leber, B.; Andrews, D.W. Membrane binding by tBid initiates an ordered series of events culminating in membrane permeabilization by Bax. Cell 2008, 135, 1074–1084. [Google Scholar] [CrossRef] [PubMed]
- Satsoura, D.; Kučerka, N.; Shivakumar, S.; Pencer, J.; Griffiths, C.; Leber, B.; Andrews, D.W.; Katsaras, J.; Fradin, C. Interaction of the full-length Bax protein with biomimetic mitochondrial liposomes: A small-angle neutron scattering and fluorescence study. Biochim. Biophys. Acta Biomembr. 2012, 1818, 384–401. [Google Scholar] [CrossRef] [PubMed]
- Shamas-Din, A.; Bindner, S.; Zhu, W.; Zaltsman, Y.; Campbell, C.; Gross, A.; Leber, B.; Andrews, D.W.; Fradin, C. tBid undergoes multiple conformational changes at the membrane required for Bax activation. J. Biol. Chem. 2013, 288, 22111–22127. [Google Scholar] [CrossRef] [PubMed]
- Shamas-Din, A.; Satsoura, D.; Khan, O.; Zhu, W.; Leber, B.; Fradin, C.; Andrews, D. Multiple partners can kiss-and-run: Bax transfers between multiple membranes and permeabilizes those primed by tBid. Cell Death Dis. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Cathcart, K.; Patel, A.; Dies, H.; Rheinstädter, M.C.; Fradin, C. Effect of cholesterol on the structure of a five-component mitochondria-like phospholipid membrane. Membranes 2015, 5, 664–684. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, M.; Petersen, N.O. Image cross-correlation spectroscopy: A new experimental biophysical approach to measurement of slow diffusion of fluorescent molecules. Methods Cell Sci. 1996, 18, 47–54. [Google Scholar] [CrossRef]
- Wiseman, P.W.; Squier, J.A.; Ellisman, M.H.; Wilson, K.R. Two-photon image correlation spectroscopy and image cross-correlation spectroscopy. J. Microsc. 2000, 200, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Friaa, O.; Furukawa, M.; Shamas-Din, A.; Leber, B.; Andrews, D.W.; Fradin, C. Optimizing the acquisition and analysis of confocal images for quantitative single-mobile-particle detection. ChemPhysChem 2013, 14, 2476–2490. [Google Scholar] [CrossRef] [PubMed]
- Satsoura, D.; Leber, B.; Andrews, D.W.; Fradin, C. Circumvention of fluorophore photobleaching in fluorescence fluctuation experiments: A beam scanning approach. ChemPhysChem 2007, 8, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Ernst, D.; Köhler, J. Measuring a diffusion coefficient by single-particle tracking: Statistical analysis of experimental mean squared displacement curves. Phys. Chem. Chem. Phys. 2013, 15, 845–849. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.; Sheetz, M.P.; Elson, E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991, 60, 910–921. [Google Scholar] [CrossRef]
- Saxton, M.J. Single-particle tracking: The distribution of diffusion coefficients. Biophys. J. 1997, 72, 1744–1753. [Google Scholar] [CrossRef]
- Bauer, M.; Valiullin, R.; Radons, G.; Kärger, J. How to compare diffusion processes assessed by single-particle tracking and pulsed field gradient nuclear magnetic resonance. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef] [PubMed]
- Heidernätsch, M.; Bauer, M.; Radons, G. Characterizing N-dimensional anisotropic Brownian motion by the distribution of diffusivities. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed]
- Tamm, L.K.; McConnell, H.M. Supported phospholipid bilayers. Biophys. J. 1985, 47, 105–113. [Google Scholar] [CrossRef]
- Vácha, R.; Siu, S.W.; Petrov, M.; Böckmann, R.A.; Barucha-Kraszewska, J.; Jurkiewicz, P.; Hof, M.; Berkowitz, M.L.; Jungwirth, P. Effects of Alkali cations and Halide anions on the DOPC lipid membrane. J. Phys. Chem. A 2009, 113, 7235–7243. [Google Scholar] [CrossRef] [PubMed]
- Mulligan, K.; Jakubek, Z.J.; Johnston, L.J. Supported lipid bilayers on biocompatible polysaccharide multilayers. Langmuir 2011, 27, 14352–14359. [Google Scholar] [CrossRef] [PubMed]
- Petrášek, Z.; Schwille, P. Precise measurement of diffusion coefficients using scanning fluorescence correlation spectroscopy. Biophys. J. 2008, 94, 1437–1448. [Google Scholar] [CrossRef] [PubMed]
- Nie, S.; Chiu, D.T.; Zare, R.N. Probing individual molecules with confocal fluorescence microscopy. Science 1994, 266, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Digman, M.A.; Gratton, E. Analysis of diffusion and binding in cells using the RICS approach. Microsc. Res. Tech. 2009, 72, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J. Wanted: A positive control for anomalous subdiffusion. Biophys. J. 2012, 103, 2411–2422. [Google Scholar] [CrossRef] [PubMed]
- Shakhov, A.; Valiullin, R.; Kärger, J. Tracing molecular propagation in dextran solutions by pulsed field gradient NMR. J. Phys. Chem. Lett. 2012, 3, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Sigaut, L.; Pearson, J.E.; Colman-Lerner, A.; Dawson, S.P. Messages do diffuse faster than messengers: Reconciling disparate estimates of the morphogen bicoid diffusion coefficient. PLoS Comp. Biol. 2014, 10. [Google Scholar] [CrossRef] [PubMed]
- Kubitscheck, U.; Kückmann, O.; Kues, T.; Peters, R. Imaging and tracking of single GFP molecules in solution. Biophys. J. 2000, 78, 2170–2179. [Google Scholar] [CrossRef]
- Soong, R.; Macdonald, P.M. Lateral diffusion of peg-lipid in magnetically aligned bicelles measured using stimulated echo pulsed field gradient 1 h NMR. Biophys. J. 2005, 88, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, K.; Sanders, M.; Grinberg, F.; Galvosas, P.; Vasenkov, S. Application of pulsed field gradient NMR with high gradient strength for studies of self-diffusion in lipid membranes on the nanoscale. Langmuir 2008, 24, 7365–7370. [Google Scholar] [CrossRef] [PubMed]
- Gambin, Y.; Lopez-Esparza, R.; Reffay, M.; Sierecki, E.; Gov, N.; Genest, M.; Hodges, R.; Urbach, W. Lateral mobility of proteins in liquid membranes revisited. Proc. Natl. Acad. Sci. USA 2006, 103, 2098–2102. [Google Scholar] [CrossRef] [PubMed]
- Horvath, S.E.; Daum, G. Lipids of mitochondria. Prog. Lipid Res. 2013, 52, 590–614. [Google Scholar] [CrossRef] [PubMed]
- Cheezum, M.; Walker, W.; Guilford, W. Quantitative comparison of algorithms for tracking single fluorescent particles. Biophys. J. 2001, 81, 2378–2388. [Google Scholar] [CrossRef]
- Thompson, R.E.; Larson, D.R.; Webb, W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002, 82, 2775–2783. [Google Scholar] [CrossRef]
- Crocker, J.; Grier, D. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 1996, 179, 298–310. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rose, M.; Hirmiz, N.; Moran-Mirabal, J.M.; Fradin, C. Lipid Diffusion in Supported Lipid Bilayers: A Comparison between Line-Scanning Fluorescence Correlation Spectroscopy and Single-Particle Tracking. Membranes 2015, 5, 702-721. https://doi.org/10.3390/membranes5040702
Rose M, Hirmiz N, Moran-Mirabal JM, Fradin C. Lipid Diffusion in Supported Lipid Bilayers: A Comparison between Line-Scanning Fluorescence Correlation Spectroscopy and Single-Particle Tracking. Membranes. 2015; 5(4):702-721. https://doi.org/10.3390/membranes5040702
Chicago/Turabian StyleRose, Markus, Nehad Hirmiz, Jose M. Moran-Mirabal, and Cécile Fradin. 2015. "Lipid Diffusion in Supported Lipid Bilayers: A Comparison between Line-Scanning Fluorescence Correlation Spectroscopy and Single-Particle Tracking" Membranes 5, no. 4: 702-721. https://doi.org/10.3390/membranes5040702
APA StyleRose, M., Hirmiz, N., Moran-Mirabal, J. M., & Fradin, C. (2015). Lipid Diffusion in Supported Lipid Bilayers: A Comparison between Line-Scanning Fluorescence Correlation Spectroscopy and Single-Particle Tracking. Membranes, 5(4), 702-721. https://doi.org/10.3390/membranes5040702