Review of Discrete Element Method Simulations of Soil Tillage and Furrow Opening
Abstract
:1. Introduction
2. Modelling Agricultural Soils with DEM
2.1. DEM Contact Models
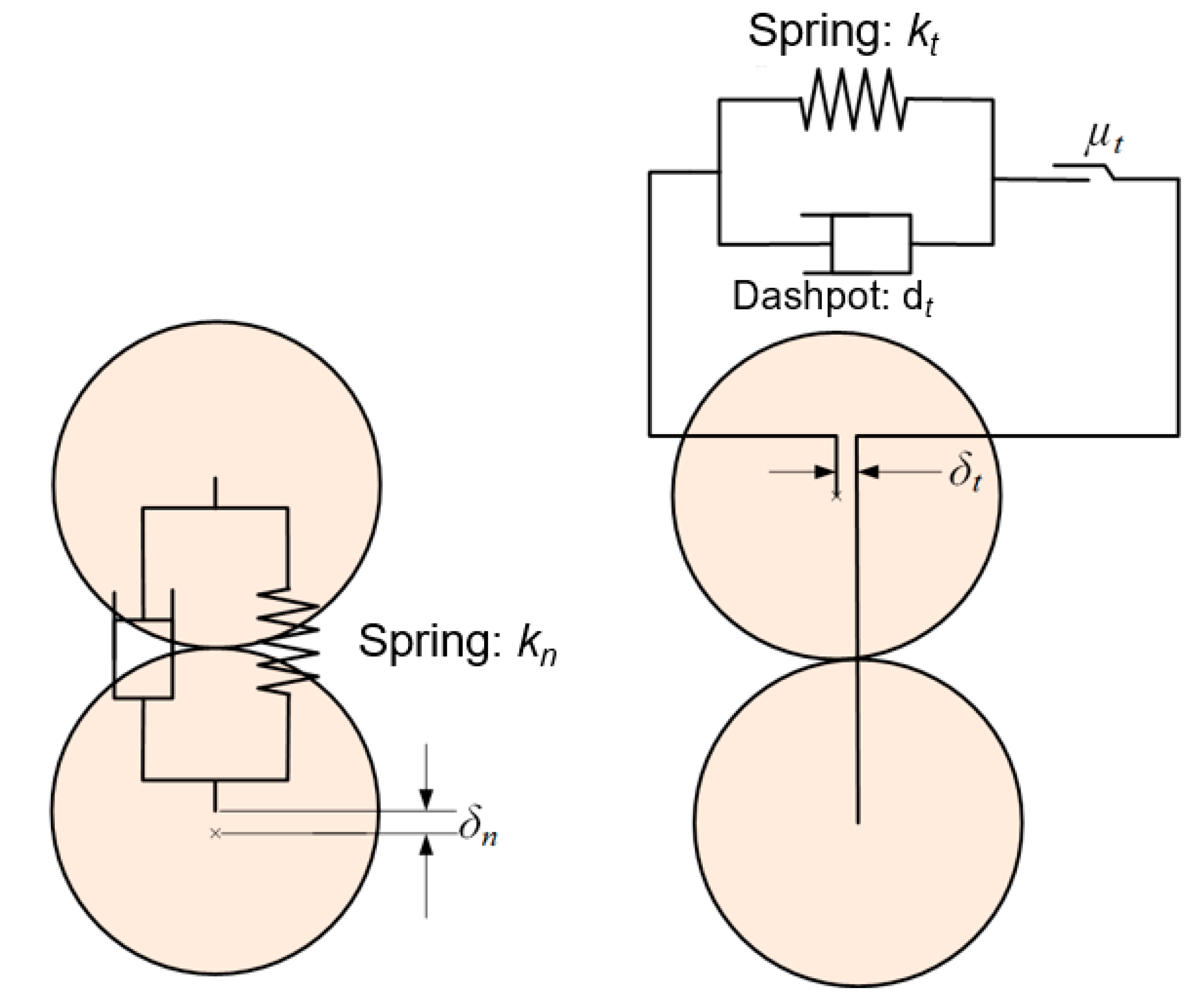
2.1.1. Linear Spring Contact Model
2.1.2. Hertz–Mindlin Contact Model
2.1.3. Hysteretic Spring Contract Model
2.1.4. Accounting for Cohesion with DEM Contact Models
Linear Cohesion Model
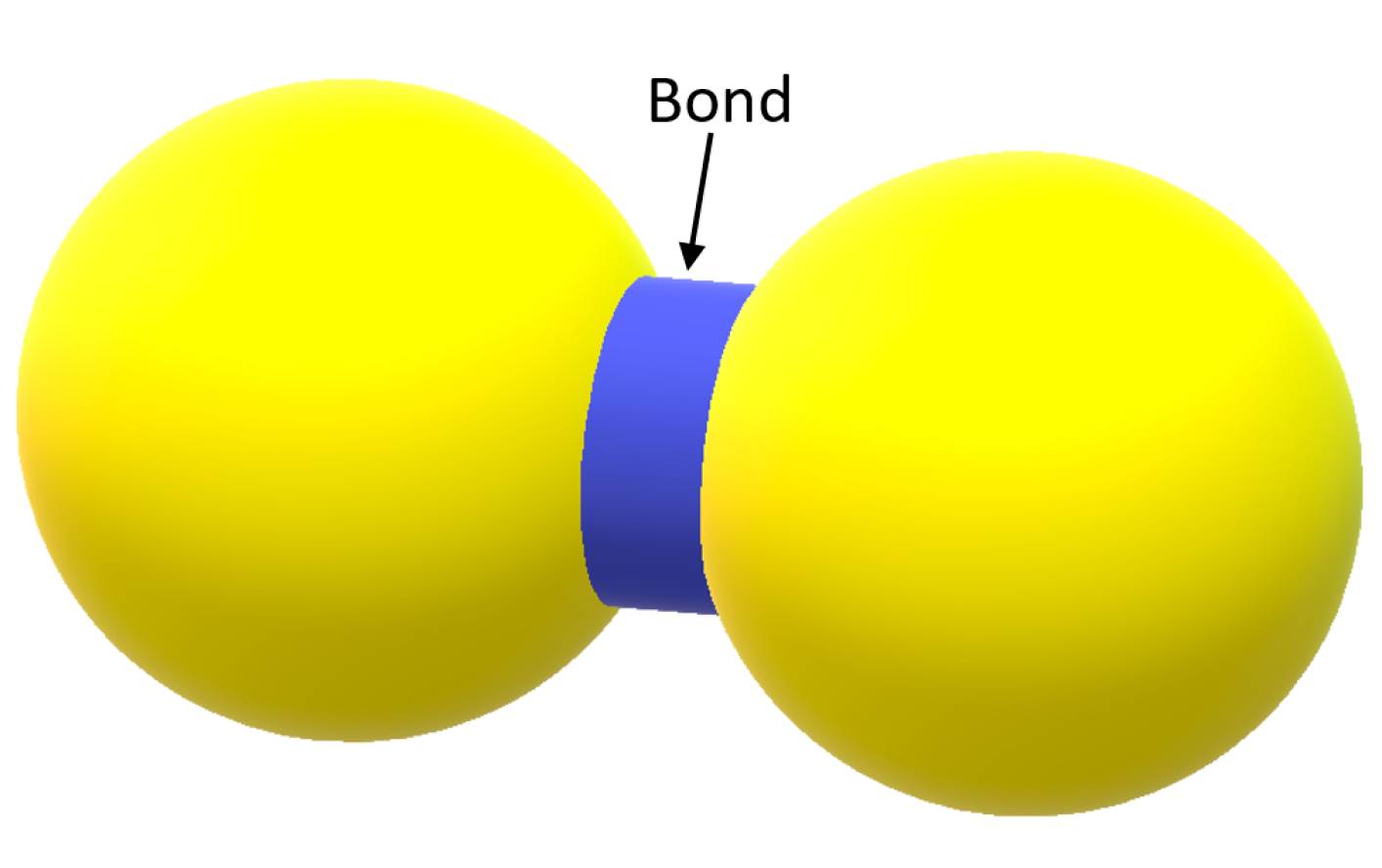
Parallel Bond Model
Johnson–Kendall–Roberts Cohesion
| Reference | Relative Error in DEM Prediction (%) Relative to Measured Data | Travel Speed (km h−1) | Operating Depth (mm) | Tillage Tools | Soil Texture | Dry Bulk Density (kg m−3) | Soil Water Content (%, w/w) | Cohesive Strength (kPa) | Contact Model | |
|---|---|---|---|---|---|---|---|---|---|---|
| Draught | Vertical Force | |||||||||
| Sadek et al. [58] | n/a | n/a | n/a | n/a | n/a | Sandy soil | 990 1280 1360 1500 | 0.02 13 21.5 | 1.23-32.70 | PBM |
| Chen et al. [7] | 4 to 31 | n/a | 3.19 (average) | 100 | Sweep tine | Coarse sand Loamy sand Sandy loam | 1410 1330 1410 | 8.98 14.84 18.2 | 15.7 25.2 36 | PBM |
| Obermayr et al. [52] | n/a | n/a | 2.16–4.5 | 10–200 | Bulldozer blade | n/a | 1900 | n/a | 11.16 | LSCM + cohesion |
| Tamas et al. [30] | 4 to 12 | n/a | 1.8–8.64 | 200 | Sweep tine | Sandy soil | 1850 | 6.33 | 11.86 | PBM |
| Bravo et al. [18] | 9, 24 | n/a | - | 150–500 | Para-plough and mouldboard plough | Clay (Vertosol) | 1000 1200 1400 | 8 18 20 35 | 25–125 | LSCM + cohesion |
| Li et al. [56] | 3 to 15 | n/a | 3.6 | 180–260 | Subsoiler | n/a | n/a | 19 | n/a | PBM |
| Mak and Chen [61] | n/a | n/a | 2.2–6.59 | 50–200 | Sweep tine | Loamy sand | 1320 | 11.3 | 13.9 | PBM |
| Obermayr et al. [72] | n/a | n/a | 100–200 | Straight-vertical blade and bulldozer blade | Sand | 1520 1980 1870 | 10 15 | 6–22.5 | LSCM + cohesion | |
| Ucgul et al. [38] | ≤11.6 | ≤15.2 | 5–12.5 | 70 | Sweep tine | Sandy loam | 1750 | 8 | 6 | HSCM |
| Ucgul et al. [53] | n/a | n/a | 4–12 | 75 | Sweep tine | Sandy loam | 1320 1780 1880 | 1 15 13 | 3 15 22 | HSCM + LCM |
| Kotrocz et al. [60] | n/a | n/a | n/a | 50–150 | Cone penetrometer | Loamy sand | 1632 | 15.8 | 6.61–8.66 | PBM |
| Li et al. [70] | 2.99 | 3–18 | Claw | Sandy loam | 1300 | n/a | 17.5 | PBM | ||
| Murray [69] | 1.86 | 50.7 | 8 | 38 | Disc and hoe openers | Clayey lacustrine | 1560 | 19.6 | n/a | PBM |
| Hang et al. [32] | n/a | n/a | 3 | 300 | Subsoiler | Loamy clay | 1346 | 12.5 | 11.8 | PBM |
| Milkevych et al. [62] | n/a | n/a | 3.2 | 100 | Sweep tine | Coarse sand Loamy sand | 1410 1330 | 9 14.8 | 15.8 25.1 | PBM |
| Tekeste et al. [55] | 9, 12 | -59, -49 | 0.79–9.65 | 102 | Sweep tine | Loam | 1307 | 8.99 | 33 | PBM |
| Tong et al. [73] | <10 | <10 | 7.2 | 300–450 | Subsoiler (straight shank-sweep tine, curved shank-chisel tine, curved shank-sweep tine, bentleg-chisel tine) | n/a | 1230–1420 | n/a | n/a | not stated |
| Kim et al. [44] | 5.16 to 9.9 | n/a | 7.64–7.9 | 5–200 | Mouldboard plough | Loam | 1496–1904 | 24.5–34.02 | n/a | EEPA |
| Aikins et al. [41] | 5 to 31 | 8, 20 and greater | 8 | 100 | Bentleg and narrow point openers | Clay (Vertosol) | 1504 | 23.7 | 46.4 | HSCM + LCM |
| Wang et al. [74] | 15.08 | n/a | 3 | 300 | Winged subsoiler | Sandy loam | 1404–1833 | n/a | n/a | PBM |
| Sadek et al. [75] | ≤20.2 | n/a | 4–16 | 127 | Disc | Sandy loam | 1700 | 16.32 | n/a | PBM |
| Saunders et al. [76] | n/a | n/a | 4.5–10 | 25–100 | Plough skimmers | Sandy loam | 1523.8 | 8.3 | n/a | HSCM + LCM |
| Ma et al. [77] | 2.88 to 5.97 | n/a | 1.08–2.16 | 120 | Scraper | Sandy loam | 1389 | 10 | n/a | not stated |
| Hoseinian et al. [35] | 2 | 2.5 | 0.9 | 150 | Dual sideway-share | Sandy clay loam | 1565 | 11.5 | 15.4 | PBM |
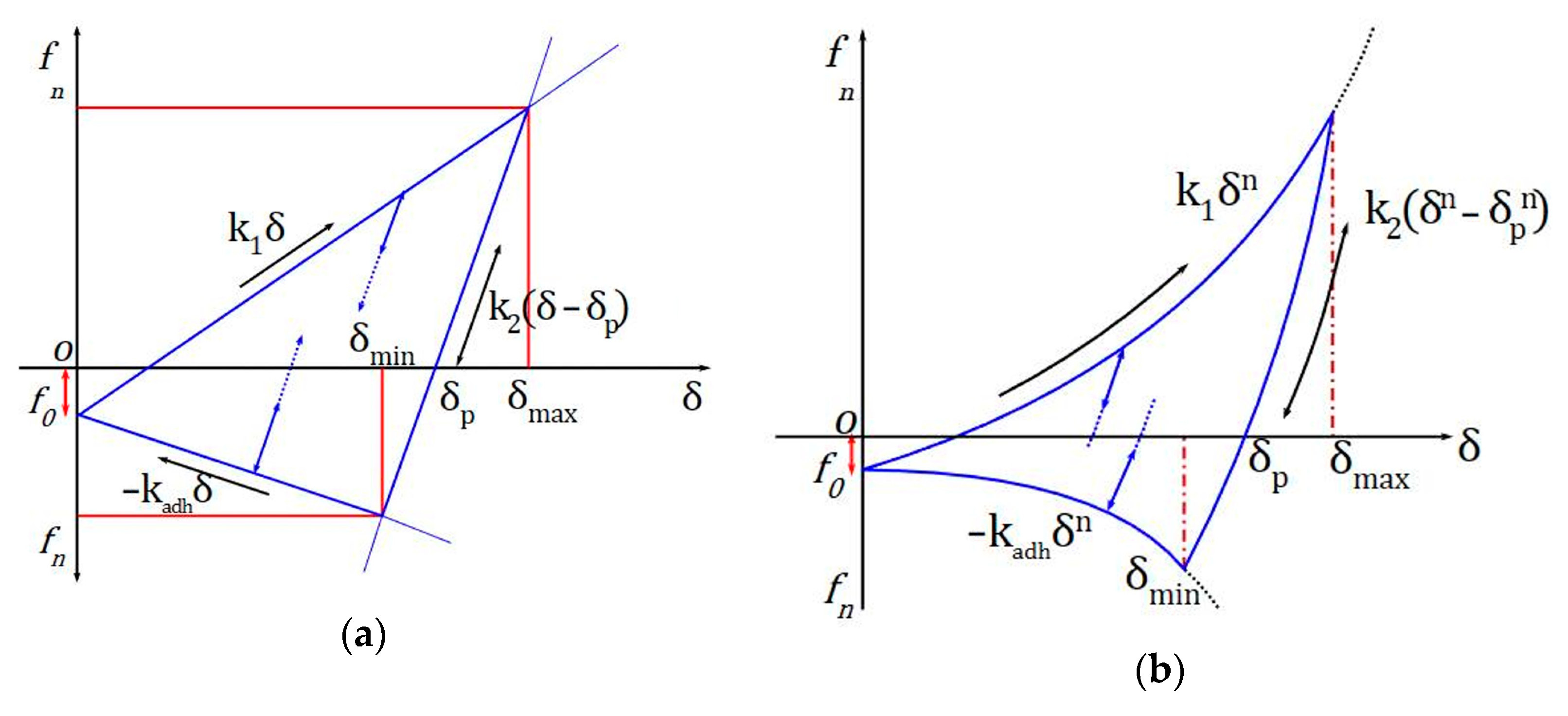
Edinburgh Elasto-Plastic Adhesion Model
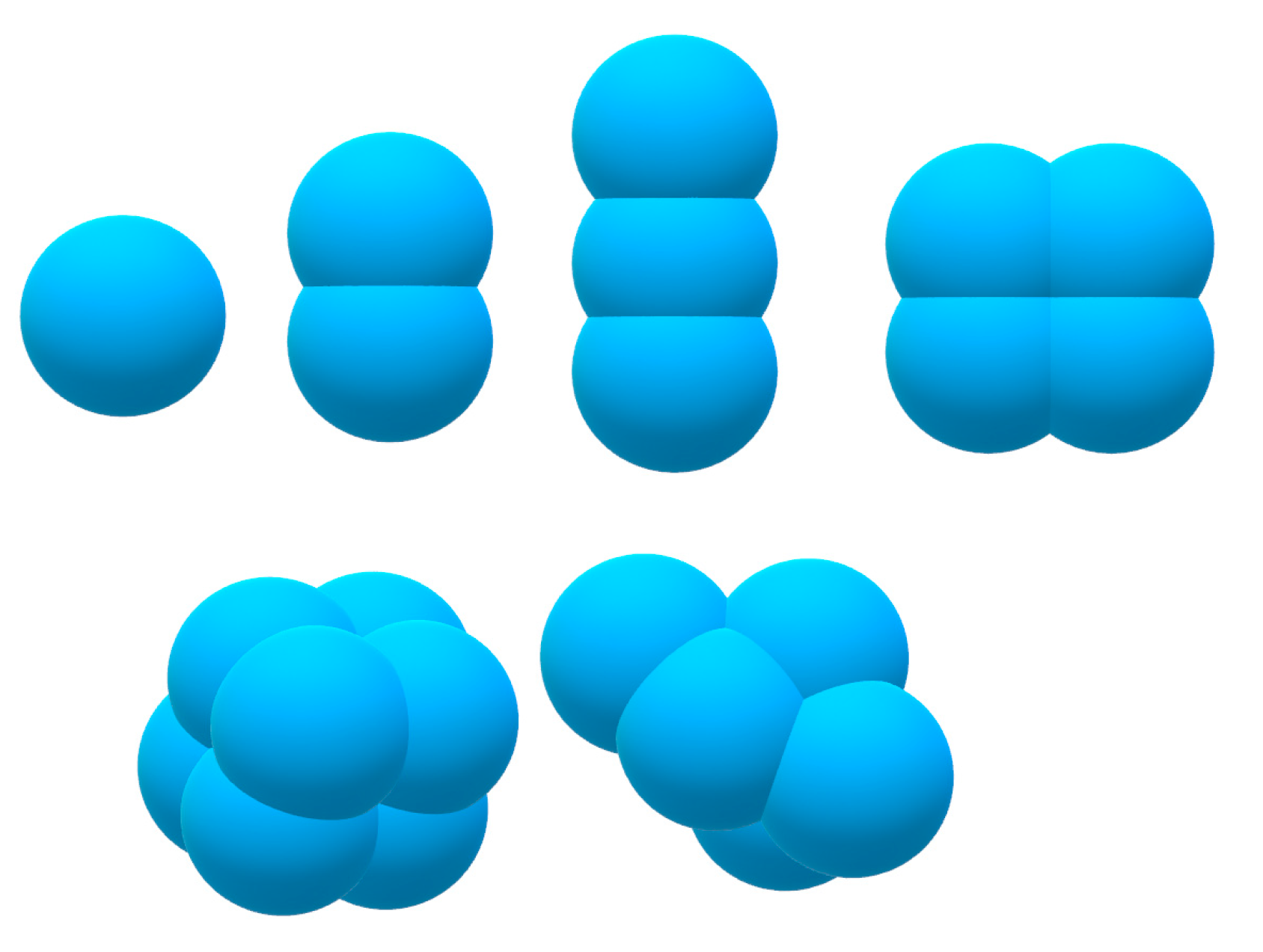
2.2. Particle Size and Shape
3. Calibration Techniques for Determining DEM Input Parameters
3.1. Angle of Repose Test
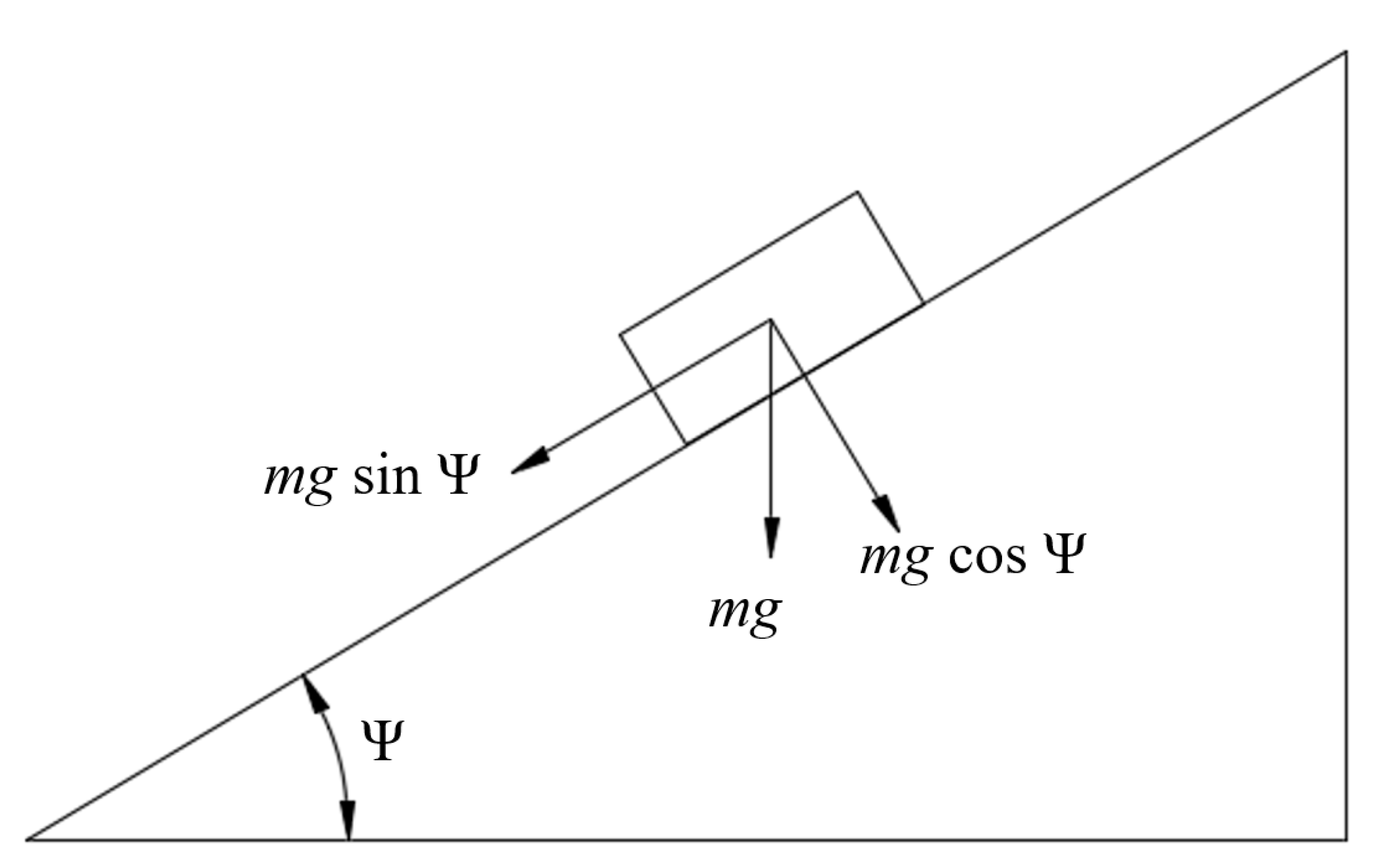
3.2. Inclined Plane Test
3.3. Direct Shear Test
3.4. Triaxial Compression Test
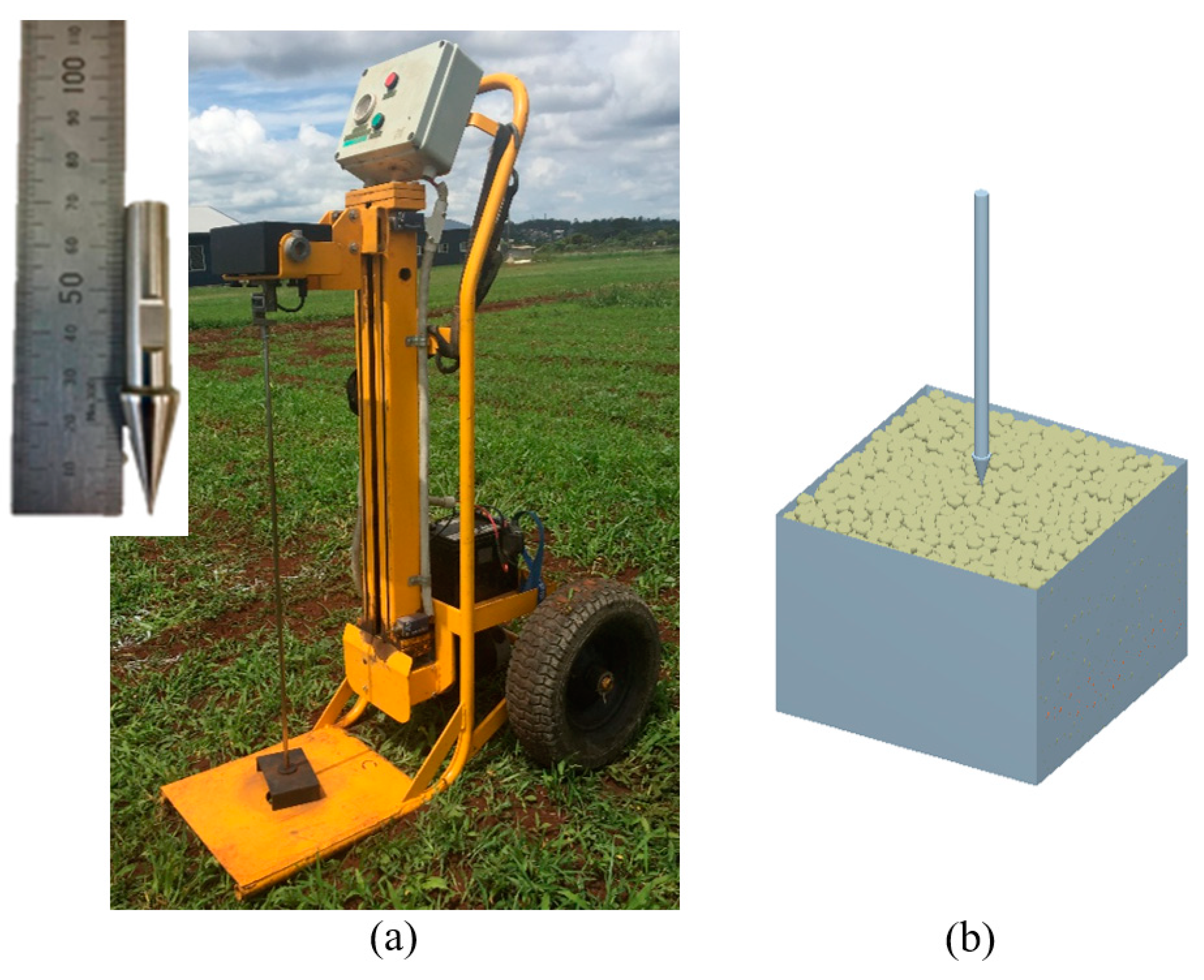
3.5. In Situ Approaches
4. Prediction of Soil Failure, Loosening, and Disturbance Parameters
4.1. Soil Failure and Loosening
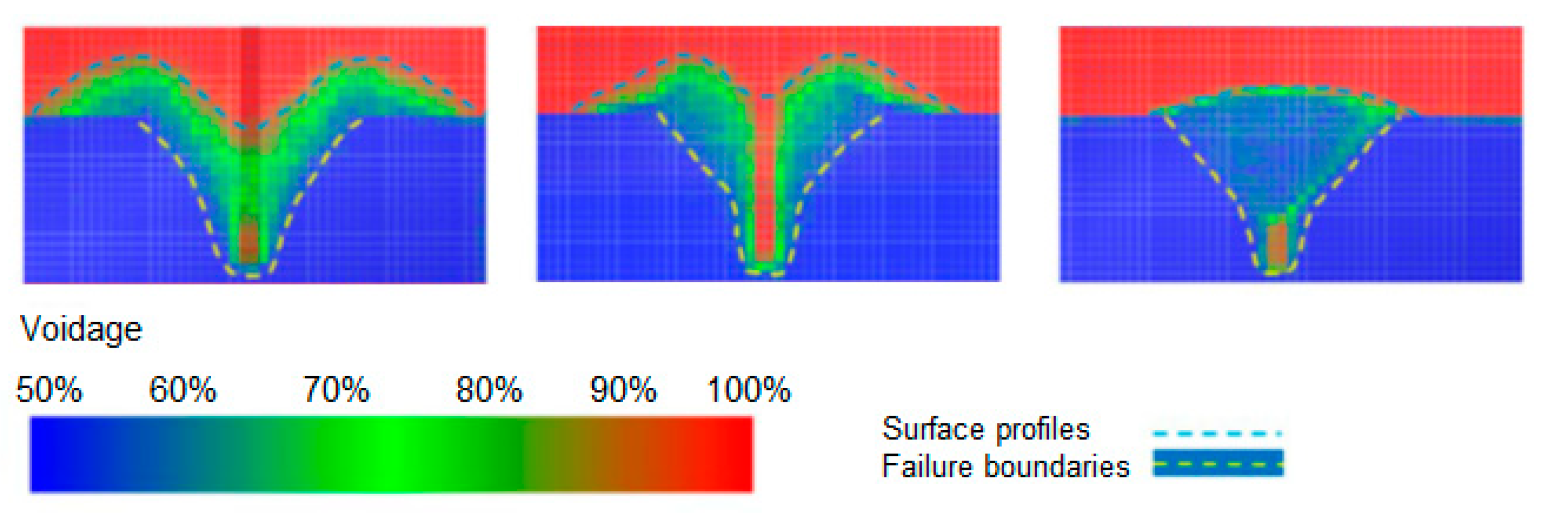
- Minimum particle displacement caused directly by an opener occurs with particles just adjacent to the bottom part of the opener (for wide tines) or particles aligning the walls of the slot below critical depth (for narrow tines).
- To establish a sharp contrast between displaced and undisturbed particles, particle locations immediately after particle loosening (i.e., before the particle settle) has to be used.
4.2. Soil Movement and Disturbance Parameters
5. Prediction of Tillage Forces
6. Soils Modelled in DEM Simulations
7. Conclusions
- Even though the Hertz–Mindlin contact model (HMCM) has been used in most DEM studies of tillage and furrow opening, it consistently fails to predict vertical soil force accurately. The Hysteretic Spring contact model (HSCM) can more accurately predict soil forces and particle movement.
- Angle of repose, inclined plane, direct shear, triaxial compression, and some in situ tests (grouser shear, plate sinkage, and cone penetration tests) have been used to measure and calibrate DEM input parameters. The angle of repose test has been used mainly for cohesionless soils due to the poor flowability of cohesive soils. However, using results from reproducible phases of the angle of repose experiment, successful calibrations for cohesive soils have been achieved.
- Unlike other numerical models, DEM is able to closely predict not only soil forces, but it is also capable of modelling soil failure mechanisms, soil loosening, and soil particle movement. Soil rupture and crack propagation, critical depth, three-dimensional particle movement within the soil profile and lateral particle movement on top of the soil have all been predicted in DEM.
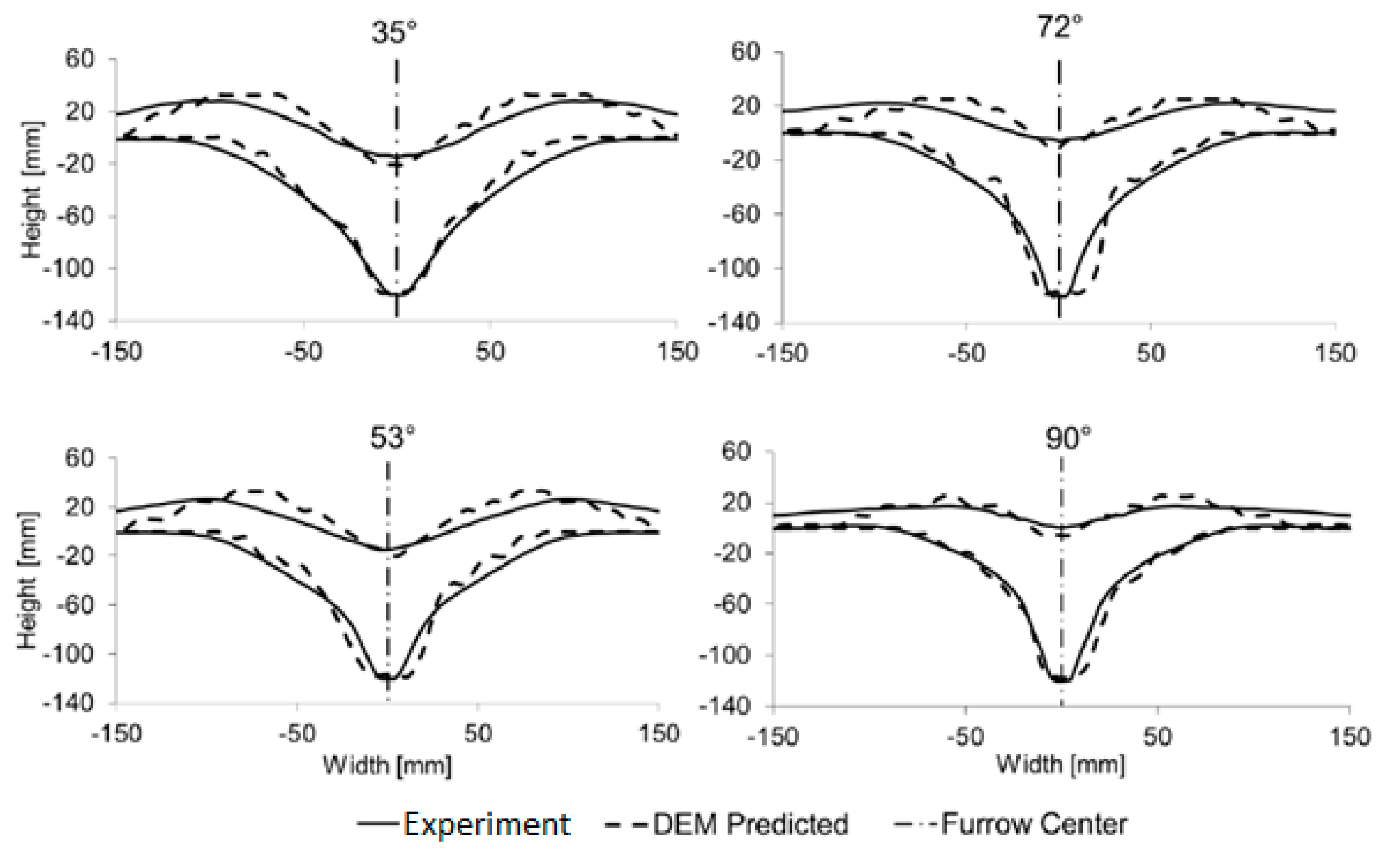
- Using voidage or porosity grids to determine loosened furrow cross-sectional profiles has been found to be superior to using particle velocity and displacement profiles. However, some researchers have successfully used a particle displacement approach to determine accurate furrow profiles with a more objective criteria for defining loosened furrow boundary.
- Close predictions of draught and vertical forces (≤20%) have been obtained with DEM. These predictions can be improved by using smaller particles of a near-real shape. However, this must be balanced with computation time requirements.
- The Edinburgh elasto-plastic adhesion model (EEPA) has been successfully used to model consolidated or cohesive powders. This contact model is recommended to be studied more extensively for cohesive soils, although some researchers have used it.
- Due to pore water pressure within wet and soft soils, coupling DEM and CFD is likely to produce more accurate simulations. This idea can be explored in future research.
- A comprehensive analysis of soil disturbance parameters has been successfully done using voidage grids in EDEM® DEM software. Replication of this approach in other DEM software is recommended.
- The criteria introduced by Aikins et al. [41] for defining particle displacement threshold for DEM furrow profile identification need further investigation with particles of smaller radii than the 5 mm used in the study. This approach can provide greater details on the three-dimensional soil translocation process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| γ | Surface energy (J/m2) |
| Linear overlap | |
| Normal component of relative velocity | |
| Tangential component of relative velocity | |
| Cohesive stress | |
| Linear relative velocity | |
| Tangential component of overlap | |
| Friction coefficient | |
| Internal friction angle between the particles (Degree) | |
| µr | Coefficient of rolling friction |
| µs | Coefficient of static friction |
| A | Cross-sectional area of the shear box |
| a | JKR contact radius |
| c | Soil cohesion (Pa) |
| ca | Soil–metal adhesion (Pa) |
| d | Working depth (m) |
| dn | Damping coefficient |
| dt | Tangential component of damping coefficient |
| e | Coefficient of restitution of the particles |
| E | Young’s modulus |
| Eeq | Equivalent Young’s modulus |
| F | Contact force |
| Fa | Normal force in direct shear test |
| Fb | Horizontal (shearing) force in direct shear test |
| Fca | Cohesive or adhesive force |
| Fd | Damping force |
| Fn | Normal contact force |
| Fs | Spring force |
| Ft | Tangential component of the contact force |
| g | Acceleration due to gravity |
| Geq | Equivalent shear modulus |
| Ii | Moment of inertia of a particle |
| k1 | Loading stiffnesses |
| k2 | Unloading stiffnesses |
| kn | Normal stiffness |
| kt | Tangential component of stiffness |
| meq | Equivalent particle mass |
| mi | Mass of spherical particle |
| mr | Mass of the ball used in inclined plane test |
| ms | Mass of block used in inclined plane test |
| N | N factor. Suffixes: γ = gravitational, c = cohesive, a = adhesive, q = surcharge |
| P | Soil cutting force (N) |
| q | Surcharge stress (Pa) |
| q | Deviator stress in triaxial compression test |
| rc | Contact radius |
| req | Equivalent particle radius |
| ri, | Radius of spherical particle |
| Ti | Torque due to the tangential component of the contact force |
| Vg | Voidage grid volume |
| Vp | Total volume of particles with centroids within voidage grid |
| w | Tool width (m) |
| xi | Location of spherical particle |
| γ | Specific weight of soil (N m−3) |
| εa | Axial strain in triaxial compression test |
| σ1 | Axial stress in triaxial compression test |
| σ3 | Radial stress in triaxial compression test |
| Ψ | Inclined plane tilt angle. Subscripts: s = sliding, r = rolling |
| ωi | Angular velocity of a particle |
References
- Aybek, A.; Baser, E.; Arslan, S.; Ucgul, M. Determination of the effect of biodiesel use on power take-off performance characteristics of an agricultural tractor in a test laboratory. Turk. J. Agric. For. 2011, 35, 103–113. [Google Scholar] [CrossRef]
- Kushwaha, R.L.; Zhang, Z.X. Evaluation of factors and current approaches related to the computerized design of tillage tools: A review. J. Terramechanics 1998, 35, 69–86. [Google Scholar] [CrossRef]
- Aikins, K.A.; Barr, J.B.; Ucgul, M.; Jensen, T.A.; Antille, D.L.; Desbiolles, J.M.A. No-tillage furrow opener performance: A review of tool geometry, settings and interactions with soil and crop residue. Soil Res. 2020, 58, 603–621. [Google Scholar] [CrossRef]
- McKyes, E. Soil Cutting and Tillage; Development in Agricultural Engineering Volume 7; Elsevier: Amsterdam, The Netherlands, 1985; Volume 7. [Google Scholar]
- Godwin, R.J. A review of the effect of implement geometry on soil failure and implement forces. Soil Tillage Res. 2007, 97, 331–340. [Google Scholar] [CrossRef]
- Shmulevich, I.; Asaf, Z.; Rubinstein, D. Interaction between soil and a wide cutting blade using the discrete element method. Soil Tillage Res. 2007, 97, 37–50. [Google Scholar] [CrossRef]
- Chen, Y.; Munkholm, L.J.; Nyord, T. A discrete element model for soil-sweep interaction in three different soils. Soil Tillage Res. 2013, 126, 34–41. [Google Scholar] [CrossRef]
- Hettiaratchi, D.R.P.; Reece, A.R. Symmetrical three-dimensional soil failure. J. Terramechanics 1967, 4, 45–67. [Google Scholar] [CrossRef]
- Godwin, R.J.; Spoor, G. Soil failure with narrow tines. J. Agric. Eng. Res. 1977, 22, 213–228. [Google Scholar] [CrossRef]
- Asaf, Z.; Rubinstein, D.; Shmulevich, I. Determination of discrete element model parameters required for soil tillage. Soil Tillage Res. 2007, 92, 227–242. [Google Scholar] [CrossRef]
- Shmulevich, I. State of the art modeling of soil–tillage interaction using discrete element method. Soil Tillage Res. 2010, 111, 41–53. [Google Scholar] [CrossRef]
- McKyes, E.; Ali, O.S. The cutting of soil by narrow blades. J. Terramechanics 1977, 14, 43–58. [Google Scholar] [CrossRef]
- Godwin, R.J.; O’Dogherty, M.J. Integrated soil tillage force prediction models. J. Terramechanics 2007, 44, 3–14. [Google Scholar] [CrossRef]
- Fielke, J.M. Finite element modelling of the interaction of the cutting edge of tillage implements with soil. J. Agric. Eng. Res. 1999, 74, 91–101. [Google Scholar] [CrossRef]
- Karmakar, S.; Ashrafizadeh, S.R.; Kushwaha, R.L. Experimental validation of computational fluid dynamics modeling for narrow tillage tool draft. J. Terramechanics 2009, 46, 277–283. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Franco, Y.; Rubinstein, D.; Shmulevich, I. Prediction of soil-bulldozer blade interaction using discrete element method. Trans. ASABE 2007, 50, 345–353. [Google Scholar] [CrossRef]
- Bravo, E.L.; Tijskens, E.; Suarez, M.H.; Cueto, O.G.; Ramon, H. Prediction model for non-inversion soil tillage implemented on discrete element method. Comput. Electron. Agric. 2014, 106, 120–127. [Google Scholar] [CrossRef]
- Markauskas, D.; Ramírez-Gómez, Á.; Kačianauskas, R.; Zdancevičius, E. Maize grain shape approaches for DEM modelling. Comput. Electron. Agric. 2015, 118, 247–258. [Google Scholar] [CrossRef]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Barr, J.B.; Ucgul, M.; Desbiolles, J.M.A.; Fielke, J.M. Simulating the effect of rake angle on narrow opener performance with the discrete element method. Biosyst. Eng. 2018, 171, 1–15. [Google Scholar] [CrossRef]
- Peng, B. Discrete Element Method (DEM) Contact Models Applied to Pavement Simulation. Unpublished. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, 2014. [Google Scholar]
- Luding, S. Introduction to discrete element methods: Basics of contact force models and how to perform the micro-macro transition to continuum theory. Eur. J. Environ. Civ. Eng. 2008, 12, 785–826. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials. Biosyst. Eng. 2016, 147, 206–229. [Google Scholar] [CrossRef]
- Tamás, K.; Bernon, L. Role of particle shape and plant roots in the discrete element model of soil–sweep interaction. Biosyst. Eng. 2021, 211, 77–96. [Google Scholar] [CrossRef]
- Ucgul, M. Simulation of Sweep Tillage Using Discrete Element Modelling. Unpublished. Ph.D. Thesis, University of South Australia, Adelaide, Australia, 2014. [Google Scholar]
- Tanaka, H.; Momozu, M.; Oida, A.; Yamazaki, M. Simulation of soil deformation and resistance at bar penetration by the Distinct Element Method. J. Terramechanics 2000, 37, 41–56. [Google Scholar] [CrossRef]
- Ono, I.; Nakashima, H.; Shimizu, H.; Miyasaka, J.; Ohdoi, K. Investigation of elemental shape for 3D DEM modeling of interaction between soil and a narrow cutting tool. J. Terramechanics 2013, 50, 265–276. [Google Scholar] [CrossRef] [Green Version]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil. Biosyst. Eng. 2014, 121, 105–117. [Google Scholar] [CrossRef]
- Tamas, K.; Jori, I.J.; Mouazen, A.M. Modelling soil-sweep interaction with discrete element method. Soil Tillage Res. 2013, 134, 223–231. [Google Scholar] [CrossRef] [Green Version]
- Bo, L.; Rui, X.; Liu, F.Y.; Jun, C.; Han, W.T.; Bing, H. Determination of the draft force for different subsoiler points using discrete element method. Int. J. Agr. Biol. Eng. 2016, 9, 81–87. [Google Scholar] [CrossRef]
- Hang, C.; Gao, X.; Yuan, M.; Huang, Y.; Zhu, R. Discrete element simulations and experiments of soil disturbance as affected by the tine spacing of subsoiler. Biosyst. Eng. 2018, 168, 73–82. [Google Scholar] [CrossRef]
- Cheng, J.; Zheng, K.; Xia, J.; Liu, G.; Jiang, L.; Li, D. Analysis of adhesion between wet clay soil and rotary tillage part in paddy field based on discrete element method. Processes 2021, 9, 845. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, B.; Ding, L.; Li, L.; Chen, X.; Li, J. Soil Particle Modeling and Parameter Calibration for Use with Discrete Element Method. Trans. ASABE 2021, 64, 2011–2023. [Google Scholar] [CrossRef]
- Hoseinian, S.H.; Hemmat, A.; Esehaghbeygi, A.; Shahgoli, G.; Baghbanan, A. Development of a dual sideway-share subsurface tillage implement: Part 1. Modeling tool interaction with soil using DEM. Soil Tillage Res. 2022, 215, 105201. [Google Scholar] [CrossRef]
- Du, J.; Heng, Y.; Zheng, K.; Luo, C.; Zhu, Y.; Zhang, J.; Xia, J. Investigation of the burial and mixing performance of a rotary tiller using discrete element method. Soil Tillage Res. 2022, 220, 105349. [Google Scholar] [CrossRef]
- Zhai, S.; Shi, Y.; Zhou, J.; Liu, J.; Huang, D.; Zou, A.; Jiang, P. Simulation optimization and experimental study of the working performance of a vertical rotary tiller based on the discrete element method. Actuators 2022, 11, 324. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. 3D DEM tillage simulation: Validation of a hysteretic spring (plastic) contact model for a sweep tool operating in a cohesionless soil. Soil Tillage Res. 2014, 144, 220–227. [Google Scholar] [CrossRef]
- Barr, J.; Desbiolles, J.; Ucgul, M.; Fielke, J.M. Bentleg furrow opener performance analysis using the discrete element method. Biosyst. Eng. 2020, 189, 99–115. [Google Scholar] [CrossRef]
- Makange, N.R.; Ji, C.; Torotwa, I. Prediction of cutting forces and soil behavior with discrete element simulation. Comput. Electron. Agric. 2020, 179, 105848. [Google Scholar] [CrossRef]
- Aikins, K.A.; Ucgul, M.; Barr, J.B.; Jensen, T.A.; Antille, D.L.; Desbiolles, J.M.A. Determination of discrete element model parameters for a cohesive soil and validation through narrow point opener performance analysis. Soil Tillage Res. 2021, 213, 105123. [Google Scholar] [CrossRef]
- Awuah, E.; Zhou, J.; Liang, Z.; Aikins, K.A.; Gbenontin, B.V.; Mecha, P.; Makange, N.R. Parametric analysis and numerical optimisation of Jerusalem artichoke vibrating digging shovel using discrete element method. Soil Tillage Res. 2022, 219, 105344. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Huang, Y.; Ji, J. An efficient method for determining DEM parameters of a loose cohesive soil modelled using hysteretic spring and linear cohesion contact models. Biosyst. Eng. 2022, 215, 283–294. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Siddique, M.A.A.; Kim, W.-S.; Kim, Y.-J.; Lee, S.-D.; Lee, D.-K.; Hwang, S.-J.; Nam, J.-S.; Park, S.-U.; Lim, R.-G. DEM simulation for draft force prediction of moldboard plow according to the tillage depth in cohesive soil. Comput. Electron. Agric. 2021, 189, 106368. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Liu, D.; Xie, F.; Ashwehmbom, L.G.; Zhang, Z.; Tang, Q. Calibration of discrete element parameters and experimental verification for modelling subsurface soils. Biosyst. Eng. 2021, 212, 215–227. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, H.; Liu, J.; Yang, S.X. Control method of seedbed compactness based on fragment soil compaction dynamic characteristics. Soil Tillage Res. 2020, 198, 104551. [Google Scholar] [CrossRef]
- Sun, J.; Chen, H.; Wang, Z.; Ou, Z.; Yang, Z.; Liu, Z.; Duan, J. Study on plowing performance of EDEM low-resistance animal bionic device based on red soil. Soil Tillage Res. 2020, 196, 104336. [Google Scholar] [CrossRef]
- Dai, F.; Song, X.; Zhao, W.; Shi, R.; Zhang, F.; Zhang, X. Mechanism analysis and performance improvement of mechanized ridge forming of whole plastic film mulched double ridges. Int. J. Agric. Biol. Eng. 2020, 13, 107–116. [Google Scholar] [CrossRef]
- Barr, J. Optimising bentleg opener geometry for higher speed no-till seeding. Unpublished Ph.D. Thesis, University of South Australia, Mawson Lakes, South Australia, Australia, 2018. [Google Scholar]
- EDEM. EDEM 2020 Documentation; DEM Solutions: Edinburgh, UK, 2020. [Google Scholar]
- Tamás, K.; Kovács, Á.; Jóri, I.J. The evaluation of the parallel bond’s properties in DEM modeling of soils. Period. Polytech. Mech. Eng. 2016, 60, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Obermayr, M.; Vrettos, C.; Eberhard, P. A discrete element model for cohesive soil. In Proceedings of the III International Conference on Particle-Based Methods—Fundamentals and Applications, Stuttgart, Germany, 18–20 September 2013; pp. 783–794. [Google Scholar]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Tekeste, M.Z.; Balvanz, L.R.; Hatfield, J.L.; Ghorbani, S. Discrete element modeling of cultivator sweep-to-soil interaction: Worn and hardened edges effects on soil-tool forces and soil flow. J. Terramechanics 2019, 82, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Liu, F.Y.; Mu, J.Y.; Chen, J.; Han, W.T. Distinct element method analysis and field experiment of soil resistance applied on the subsoiler. Int. J. Agric. Biol. Eng. 2014, 7, 54–59. [Google Scholar] [CrossRef]
- Mak, J.; Chen, Y.; Sadek, M.A. Determining parameters of a discrete element model for soil–tool interaction. Soil Tillage Res. 2012, 118, 117–122. [Google Scholar] [CrossRef]
- Sadek, M.A.; Chen, Y.; Liu, J. Simulating shear behavior of a sandy soil under different soil conditions. J. Terramechanics 2011, 48, 451–458. [Google Scholar] [CrossRef]
- Van der Linde, J. Discrete Element Modeling of a Vibratory Subsoiler. Unpublished MSc. Thesis, University of Stellenbosch, Matieland, South Africa, 2007. [Google Scholar]
- Kotrocz, K.; Mouazen, A.M.; Kerenyi, G. Numerical simulation of soil-cone penetrometer interaction using discrete element method. Comput. Electron. Agric. 2016, 125, 63–73. [Google Scholar] [CrossRef] [Green Version]
- Mak, J.; Chen, Y. Simulation of draft forces of a sweep in a loamy sand soil using the discrete element method. Can.Biosyst.Eng. 2014, 56, 2.1–2.7. [Google Scholar] [CrossRef]
- Milkevych, V.; Munkholm, L.J.; Chen, Y.; Nyord, T. Modelling approach for soil displacement in tillage using discrete element method. Soil Tillage Res. 2018, 183, 60–71. [Google Scholar] [CrossRef]
- Sadek, M.; Chen, Y. Feasibility of using PFC3D to simulate soil flow resulting from a simple soil-engaging tool. Trans. ASABE 2015, 58, 987–996. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, Y. Simulation of soil-micropenetrometer interaction using the discrete element method (DEM). Trans. ASABE 2016, 59, 1157–1163. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, Y.; Zhang, X. Modelling the interaction of a deep tillage tool with heterogeneous soil. Comput. Electron. Agric. 2017, 143, 130–138. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Chen, Y. Simulation of straw movement by discrete element modelling of straw-sweep-soil interaction. Biosyst. Eng. 2019, 180, 25–35. [Google Scholar] [CrossRef]
- Zhang, R.; Li, J. Simulation on mechanical behavior of cohesive soil by Distinct Element Method. J. Terramechanics 2006, 43, 303–316. [Google Scholar] [CrossRef]
- Gupta, V.; Sun, X.; Xu, W.; Sarv, H.; Farzan, H. A discrete element method-based approach to predict the breakage of coal. Adv. Powder Technol. 2017, 28, 2665–2677. [Google Scholar] [CrossRef]
- Murray, S. Modelling of Soil-Tool Interactions Using the Discrete Element Method. Unpublished MSc. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2016. [Google Scholar]
- Li, B.; Chen, Y.; Chen, J. Modeling of soil-claw interaction using the discrete element method (DEM). Soil Tillage Res. 2016, 158, 177–185. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar]
- Obermayr, M.; Vrettos, C.; Eberhard, P.; Dauwel, T. A discrete element model and its experimental validation for the prediction of draft forces in cohesive soil. J. Terramechanics 2014, 53, 93–104. [Google Scholar] [CrossRef]
- Tong, J.; Jiang, X.-H.; Wang, Y.-M.; Ma, Y.-H.; Li, J.-W.; Sun, J.-Y. Tillage force and disturbance characteristics of different geometric-shaped subsoilers via DEM. Adv. Manuf. 2020, 8, 392–404. [Google Scholar] [CrossRef]
- Wang, X.; Li, P.; He, J.; Wei, W.; Huang, Y. Discrete element simulations and experiments of soil-winged subsoiler interaction. Int. J. Agric. Biol. Eng. 2021, 14, 50–62. [Google Scholar] [CrossRef]
- Sadek, M.A.; Chen, Y.; Zeng, Z. Draft force prediction for a high-speed disc implement using discrete element modelling. Biosyst. Eng. 2021, 202, 133–141. [Google Scholar] [CrossRef]
- Saunders, C.; Ucgul, M.; Godwin, R.J. Discrete element method (DEM) simulation to improve performance of a mouldboard skimmer. Soil Tillage Res. 2021, 205, 104764. [Google Scholar] [CrossRef]
- Ma, S.; Niu, C.; Yan, C.; Tan, H.; Xu, L. Discrete element method optimisation of a scraper to remove soil from ridges formed to cold-proof grapevines. Biosyst. Eng. 2021, 210, 156–170. [Google Scholar] [CrossRef]
- Morrissey, J.P.; Thakur, S.C.; Ooi, J.Y. EDEM Contact Model: Adhesive Elasto-Plastic Model; School of Engineering, University of Edinburgh: Edinburgh, UK, 2014. [Google Scholar]
- Thakur, S.C.; Morrissey, J.P.; Sun, J.; Chen, J.F.; Ooi, J.Y. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model. Granul Matter 2014, 16, 383–400. [Google Scholar] [CrossRef]
- Schoeneberger, P.J.; Wysocki, D.A.; Benham, E.C.; Soil Survey Staff. Field Book for Describing and Sampling Soils; version 3.0; Natural Resources Conservation Service, National Soil Survey Center: Lincoln, NE, USA, 2012.
- Morrissey, J.P. Discrete Element Modelling of Iron Ore Pellets to Include the Effects of Moisture and Fines. Unpublished Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2013. [Google Scholar]
- Jang, G.; Lee, S.; Lee, K.J. Discrete element method for the characterization of soil properties in Plate-Sinkage tests. J. Mech. Sci. Technol. 2016, 30, 2743–2751. [Google Scholar] [CrossRef]
- Mousaviraad, M.; Tekeste, M.; Rosentrater, K. Discrete element method (DEM) simulation of corn grain flow in commercial screw auger. In Proceedings of the 2016 American Society of Agricultural and Biological Engineers Annual International Meeting, Orlando, FL, USA, 17–20 July 2016. [Google Scholar]
- Coetzee, C.J. Calibration of the discrete element method and the effect of particle shape. Powder Technol. 2016, 297, 50–70. [Google Scholar] [CrossRef]
- Smith, W.; Melanz, D.; Senatore, C.; Iagnemma, K.; Peng, H.E. Comparison of discrete element method and traditional modeling methods for steady-state wheel-terrain interaction of small vehicles. J. Terramechanics 2014, 56, 61–75. [Google Scholar] [CrossRef]
- Adajar, J.B.; Alfaro, M.; Chen, Y.; Zeng, Z. Calibration of discrete element parameters of crop residues and their interfaces with soil. Comput. Electron. Agric. 2021, 188, 106349. [Google Scholar] [CrossRef]
- Hernández-Vielma, C.; Estay, D.; Cruchaga, M. Response surface methodology calibration for DEM study of the impact of a spherical bit on a rock. Simul. Model. Pract. Theory 2022, 116, 102466. [Google Scholar] [CrossRef]
- Mudarisov, S.; Farkhutdinov, I.; Khamaletdinov, R.; Khasanov, E.; Mukhametdinov, A. Evaluation of the significance of the contact model particle parameters in the modelling of wet soils by the discrete element method. Soil Tillage Res. 2022, 215, 105228. [Google Scholar] [CrossRef]
- Qiu, Y.; Guo, Z.; Jin, X.; Zhang, P.; Si, S.; Guo, F. Calibration and Verification Test of Cinnamon Soil Simulation Parameters Based on Discrete Element Method. Agriculture 2022, 12, 1082. [Google Scholar] [CrossRef]
- Zeng, F.; Li, X.; Zhang, Y.; Zhao, Z.; Cheng, C. Using the discrete element method to analyze and calibrate a model for the interaction between a planting device and soil particles. INMATEH Agric. Eng. 2021, 413–424. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, M.; Liu, Y.; Gao, K.; Su, B.; Qi, Y. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]
- Al-Hashemi, H.M.B.; Al-Amoudi, O.S.B. A review on the angle of repose of granular materials. Powder Technol. 2018, 330, 397–417. [Google Scholar] [CrossRef]
- Qi, L.; Chen, Y.; Sadek, M. Simulations of soil flow properties using the discrete element method (DEM). Comput. Electron. Agric. 2019, 157, 254–260. [Google Scholar] [CrossRef]
- Li, P.; Ucgul, M.; Lee, S.H.; Saunders, C. A new approach for the automatic measurement of the angle of repose of granular materials with maximal least square using digital image processing. Comput. Electron. Agric. 2020, 172, 105356. [Google Scholar] [CrossRef]
- Rackl, M.; Hanley, K.J. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Roessler, T.; Katterfeld, A. DEM parameter calibration of cohesive bulk materials using a simple angle of repose test. Particuology 2019, 45, 105–115. [Google Scholar] [CrossRef]
- Aikins, K.A. Performance of Bentleg Opener for High Speed No-Tillage Sowing in Cohesive Soil. Unpublished. Ph.D. Thesis, University of Southern Queensland, Toowoomba, QLD, Australia, 2020. [Google Scholar]
- Syed, Z.; Tekeste, M.; White, D. A coupled sliding and rolling friction model for DEM calibration. J. Terramechanics 2017, 72, 9–20. [Google Scholar] [CrossRef]
- Rees, S. Introduction to Triaxial Testing: Part 1; GDS Instruments: Hampshire, UK, 2013. [Google Scholar]
- Wang, Y.; Guo, P.; Dai, F.; Li, X.; Zhao, Y.; Liu, Y. Behavior and Modeling of Fiber-Reinforced Clay under Triaxial Compression by Combining the Superposition Method with the Energy-Based Homogenization Technique. Int. J. Geomech. 2018, 18, 04018172. [Google Scholar] [CrossRef]
- Bardet, J.P. Experimental Soil Mechanics; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Ahlinhan, M.F.; Houehanou, E.; Koube, M.B.; Doko, V.; Alaye, Q.; Sungura, N.; Adjovi, E. Experiments and 3D DEM of Triaxial Compression Tests under Special Consideration of Particle Stiffness. Geomaterials 2018, 8, 39–62. [Google Scholar] [CrossRef] [Green Version]
- Das, B.M. Advanced Soil Mechanics, 5th ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Aikins, K.A.; Barr, J.B.; Antille, D.L.; Ucgul, M.; Jensen, T.A.; Desbiolles, J.M.A. Analysis of effect of bentleg opener geometry on performance in cohesive soil using the discrete element method. Biosyst. Eng. 2021, 209, 106–124. [Google Scholar] [CrossRef]
- Barr, J.; Fielke, J. Discrete element modelling of narrow point openers to improve soil disturbance characteristics of no-till seeding systems. In Proceedings of the ASABE Annual International Meeting, Orlando, FL, USA, 17–20 July 2016. [Google Scholar]
- Spoor, G.; Godwin, R.J. An experimental investigation into the deep loosening of soil by rigid tines. J. Agric. Eng. Res. 1978, 23, 243–258. [Google Scholar] [CrossRef]
- Spoor, G.; Fry, R.K. Soil disturbance generated by deep-working low rake angle narrow tines. J. Agric. Eng. Res. 1983, 28, 217–234. [Google Scholar] [CrossRef]
- Conte, O.; Levien, R.; Debiasi, H.; Sturmer, S.L.K.; Mazurana, M.; Muller, J. Soil disturbance index as an indicator of seed drill efficiency in no-tillage agrosystems. Soil Tillage Res. 2011, 114, 37–42. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Hu, X.; Wang, H.; Shi, X.; Ma, X. Simulation of soil cutting and power consumption optimization of a typical rotary tillage soil blade. Appl. Sci. 2022, 12, 8177. [Google Scholar] [CrossRef]
- Hirasawa, K.; Kataoka, T.; Kubo, T. Prediction and evaluation for leveling performance in rotary tiller. In Proceedings of the 4th IFAC Conference on Modelling and Control in Agriculture, Espoo, FL, USA, 27–30 August 2013; pp. 315–320. [Google Scholar]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Defining the effect of sweep tillage tool cutting edge geometry on tillage forces using 3D discrete element modelling. Inf. Process. 2015, 2, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Aikins, K.A.; Antille, D.L.; Ucgul, M.; Jensen, T.A.; Barr, J.B.; Desbiolles, J.M.A. Analysis of effects of operating speed and depth on bentleg opener performance in cohesive soil using the discrete element method. Comput. Electron. Agric. 2021, 187, 106236. [Google Scholar] [CrossRef]
- Karkala, S.; Davis, N.; Wassgren, C.; Shi, Y.; Liu, X.; Riemann, C.; Yacobian, G.; Ramachandran, R. Calibration of Discrete-Element-Method Parameters for Cohesive Materials Using Dynamic-Yield-Strength and Shear-Cell Experiments. Processes 2019, 7, 278. [Google Scholar] [CrossRef] [Green Version]








| Contact Model | Advantages | Disadvantages | Types of Soil Modelled | References | Software Used by Researchers |
|---|---|---|---|---|---|
| Linear spring contact model |
|
| Sandy | Tanaka et al. [27], Asaf et al. [10], Shmulevich et al. [6], Ono et al. [28] | PFC2D, EDEM |
| Linear spring contact model with cohesion |
|
| Vertosol | Bravo et al. [18] | DEMeter++ |
| Hertz–Mindlin contact model |
|
| Sandy | Ucgul et al. [29] | EDEM |
| Parallel bond model (PBM) or Hertz–Mindlin contact model with cohesion |
|
| Coarse sand, loamy, sandy loam, loessal, clay, sandy clay loam, loamy clay | Tamas et al. [30], Chen et al. [7], Bo et al. [31], Hang et al. [32], Cheng et al. [33], Yang et al. [34], Hoseinian et al. [35] | EDEM PFC3D |
| Hertz–Mindlin contact model with Johnson–Kendall–Roberts (JKR) |
|
| Clay, silty clay loam | Cheng et al. [33], Du et al. [36], Zhai et al. [37] | EDEM |
| Hysteric spring contact model |
|
| Sandy | Ucgul et al. [38], Ucgul et al. [29] | EDEM |
| Hysteric spring contact model with linear cohesion contact model |
|
| Sandy loam, clay (Vertosol) | Barr et al. [21], Barr et al. [39], Makange et al. [40], Aikins et al. [41], Awuah et al. [42], Wang et al. [43] | EDEM |
| Edinburgh elasto-plastic adhesion model |
|
| Clay, clay loam, sandy loam, loam, sandy | Kim et al. [44], Wu et al. [45], Zhao et al. [46], Sun et al. [47] | EDEM, PFC3D, LiGGGHTS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aikins, K.A.; Ucgul, M.; Barr, J.B.; Awuah, E.; Antille, D.L.; Jensen, T.A.; Desbiolles, J.M.A. Review of Discrete Element Method Simulations of Soil Tillage and Furrow Opening. Agriculture 2023, 13, 541. https://doi.org/10.3390/agriculture13030541
Aikins KA, Ucgul M, Barr JB, Awuah E, Antille DL, Jensen TA, Desbiolles JMA. Review of Discrete Element Method Simulations of Soil Tillage and Furrow Opening. Agriculture. 2023; 13(3):541. https://doi.org/10.3390/agriculture13030541
Chicago/Turabian StyleAikins, Kojo Atta, Mustafa Ucgul, James B. Barr, Emmanuel Awuah, Diogenes L. Antille, Troy A. Jensen, and Jacky M. A. Desbiolles. 2023. "Review of Discrete Element Method Simulations of Soil Tillage and Furrow Opening" Agriculture 13, no. 3: 541. https://doi.org/10.3390/agriculture13030541
APA StyleAikins, K. A., Ucgul, M., Barr, J. B., Awuah, E., Antille, D. L., Jensen, T. A., & Desbiolles, J. M. A. (2023). Review of Discrete Element Method Simulations of Soil Tillage and Furrow Opening. Agriculture, 13(3), 541. https://doi.org/10.3390/agriculture13030541









