How Much Meteorological Information Is Necessary to Achieve Reliable Accuracy for Rainfall Estimations?

Abstract

This paper reports the study of the effect of the length of the recorded data used for monthly rainfall forecasting. Monthly rainfall data for three periods of 5, 10, and 49 years were collected from Kermanshah, Mashhad, Ahvaz, and Babolsar stations and used for calibration time series models. Then, the accuracy of the forecasting models was investigated by the following year’s data. The following was concluded: In temperate and semi-arid climates, 60 observation data is sufficient for the following year’s rainfall forecasting. The accuracy of the time series models increased with increasing amounts of observation data of arid and humid climates. Time series models are appropriate tools for forecasting monthly rainfall forecasting in semi-arid climates. Determining the most critical rainfall month in each climate condition for agriculture schedules is a recommended aim for future studies.

1. Introduction

More accurate forecasting of monthly rainfall is significantly important in water resource management and crop pattern design. In this study, time series models were used to forecast monthly rainfall in four different climates. After publishing the paper of Box and Jenkins [1], Box–Jenkins models became a general time series model of hydrological forecasting. These models include the Auto Regressive Integrated Moving Average (ARIMA), the AR Moving Average (ARMA), the Auto Regressive (AR), and the Moving Average (MA). Access to basic information requires integration from the series (for a continuous series) or calculating all differences in the series (for a continuous series). Since the constant of integration in derivation or differences are deleted, the probability of using accurate amount in this process is not possible. Therefore, ARIMA models are non-static and cannot be used to reconstruct the missing data. However, these models are very useful for forecasting changes in hydrological processes considering agricultural water management, evapotranspiration, and water crisis issues [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Models of time series analysis (Box–Jenkins models) in various fields of hydrology and rainfall forecasting in irrigation schedules are widely applied, some of which will be described in what follows.

Serinaldi and Kilsby [18] presented a modular class of multisite monthly rainfall generators for water resource management and impact studies. The results of the case study show that the model can capture several characteristics of the rainfall series. In particular, it enables the simulation of low and high rainfall scenarios more extreme than those observed as well as the reproduction of the distribution of the annual accumulated rainfall, and of the relationship between the rainfall and circulation indices such as the North Atlantic Oscillation (NAO) and the Sea Surface Temperature (SST), thus proving the framework to be well-suited for sensitivity analysis under alternative climate scenarios and additional forcing variables. Luc et al. [19] studied an application of artificial neural networks (ANNs) for rainfall forecasting successfully. Wei et al. [20] used weather satellite imagery to forecast rainfall in Taiwan. Andrieu et al. [21] studied the adaptation and application of a quantitative rainfall forecasting model in a mountainous region. This work showed that a limit on forecast lead-time may be related to the response time of the precipitating cloud system. Burlando et al. [22], using ARMA models, forecasted short-term rainfall. The hourly rainfall parameter from two gaging stations in Colorado, USA, and from several stations in Central Italy, was used. Results showed that the event-based estimation approach yields better forecasts. Hu et al. [23] studied rainfall, mosquito density, and the transmission of the Ross River virus using a time-series forecasting model. Their results showed that both rainfall and mosquito density were strong predictors of Ross River virus transmission in simple models. Ramírez et al. [24] used an ANN technique for rainfall forecasting applied to the São Paulo region. The results showed that ANN forecasts were superior to the ones obtained by the linear regression model, thus revealing a great potential for an operational suite. Han et al. [25] successfully forecasted drought based on remote sensing data using ARIMA model. Chattopadhyay and Chattopadhyay [26] compared ARIMA and ARNN models using univariate modeling of summer-monsoon rainfall time series. Anctil et al. [27] studied the impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. The results showed that the best performance about evenly for 3- and 5-year training sets, but multiple-layer perceptrons (MLPs) performed better whenever the training set was dominated by wet weather. The MLPs continued to improve for input vectors of 9 years and more, which was not the case of the conceptual model. Jia and Culver [28] using bootstrapped ANNs suggested that even a small set of periodic instantaneous observations of stage from a staff gauge, which can easily be collected by volunteers, can be a useful data set for effective hydrological modeling. M. Baareh et al. [29] applied the ANN and AR models to the river flow forecasting problem. A comparative study of both ANN and the AR conventional model networks indicated that the ANNs performed better than the AR model. They showed that ANN models can be used to train and forecast the daily flows of the Black Water River near Dendron in Virginia and the Gila River near Clifton in Arizona. Xiong and O’Connor [30] used four different error-forecast updating models—AR, AR-threshold (AR-TS), fuzzy AR-threshold (FU-AR-TS), and an ANN—for real-time river flow forecasting. They found that all of these four updating models are very successful in improving the flow forecast accuracy. Chenoweth et al. [31] estimated the ARMA model parameters using neural networks. Their results showed that the ability of neural networks to accurately identify the order of an ARMA model was much lower than reported by previous researchers, and is especially low for time series with fewer than 100 observations. Using forecasting of hydrologic time series with ridge regression in feature space, Yu and Liong [32] showed that the training speed in the data mining method was much faster than the ARIMA model. See and Abrahart [33] used data fusion for hydrological forecasting. Their results showed that, using data fusion methodologies for ANN, fuzzy logic, and ARMA models, accuracy of forecasting increased. Using hybrid approaches, Srinivas and Srinivasan [34] improved the accuracy of AR model parameters for annual streamflows. Using Fourier coefficients, Ludlow and Enders [35] estimated the ARMA model parameters with relatively good accuracy. Chenoweth et al. [36] estimated the ARMA model parameters using Hilbert coefficients. Their results showed that Hilbert coefficients are a useful tool for estimating ARMA model parameters. Balaguer et al. [37] used the time delay neural network (TDNN) and ARMA model in support centers for crisis management. The obtained correlation results for TDNN model and ARMA were 0.88 and 0.97, respectively. This study confirmed the superiority of the ARMA model to the TDNN. Toth et al. [38] used the ANN and ARMA models to forecast rainfall. The results show the success of both short-term rainfall-forecasting models for forecasting floods in real time. Mohammadi et al. [39] forecasted Karaj reservoir inflow using data of melting snow and ANN and ARMA methods, as well as regression analysis. Sixty percent of inflow in dams occurs between April and June, so forecasting the inflow in this season is very important for a dam’s performance. The highest inflows were in the spring due to the snow melt caused by draining in threshold winter. The results showed that an ANN, compared with other methods, has lower significant errors. Mohammadi et al. [40] in another study estimated the parameters of an ARMA model for river flow forecasting using goal programming. Their results showed that the goal programming is a precise and effective method for estimating ARMA model parameters for forecasting inflow. Other researchers [41,42,43,44,45,46,47,48] estimated the parameters of the ARMA and ARIMA models and compared their ability for inflow forecasting. By comparing root mean square errors of the model, it was determined that the ARIMA model can forecast inflow to the Dez reservoir from 12 months with a lower error than can the ARMA model.

Therefore, considering the above-mentioned research, the efficacy of time series models forecasting field and hydrologic sampling can be determined. The effect of recorded data in ANN forecasting has been previously studied. However, concurrent use of time series models to determine the number of required observation data has not been performed. This study aims to forecast monthly rainfall using time series models and determine appropriate observation data according to different climate conditions.

2. Material and Methods

In this study, to investigate the effect of climate conditions on the amount of appropriate observation data, four synoptic stations with different climate conditions in Iran, including temperate, humid, arid, and semi-arid were selected.

Table 1. Information of synoptic stations used in this research.

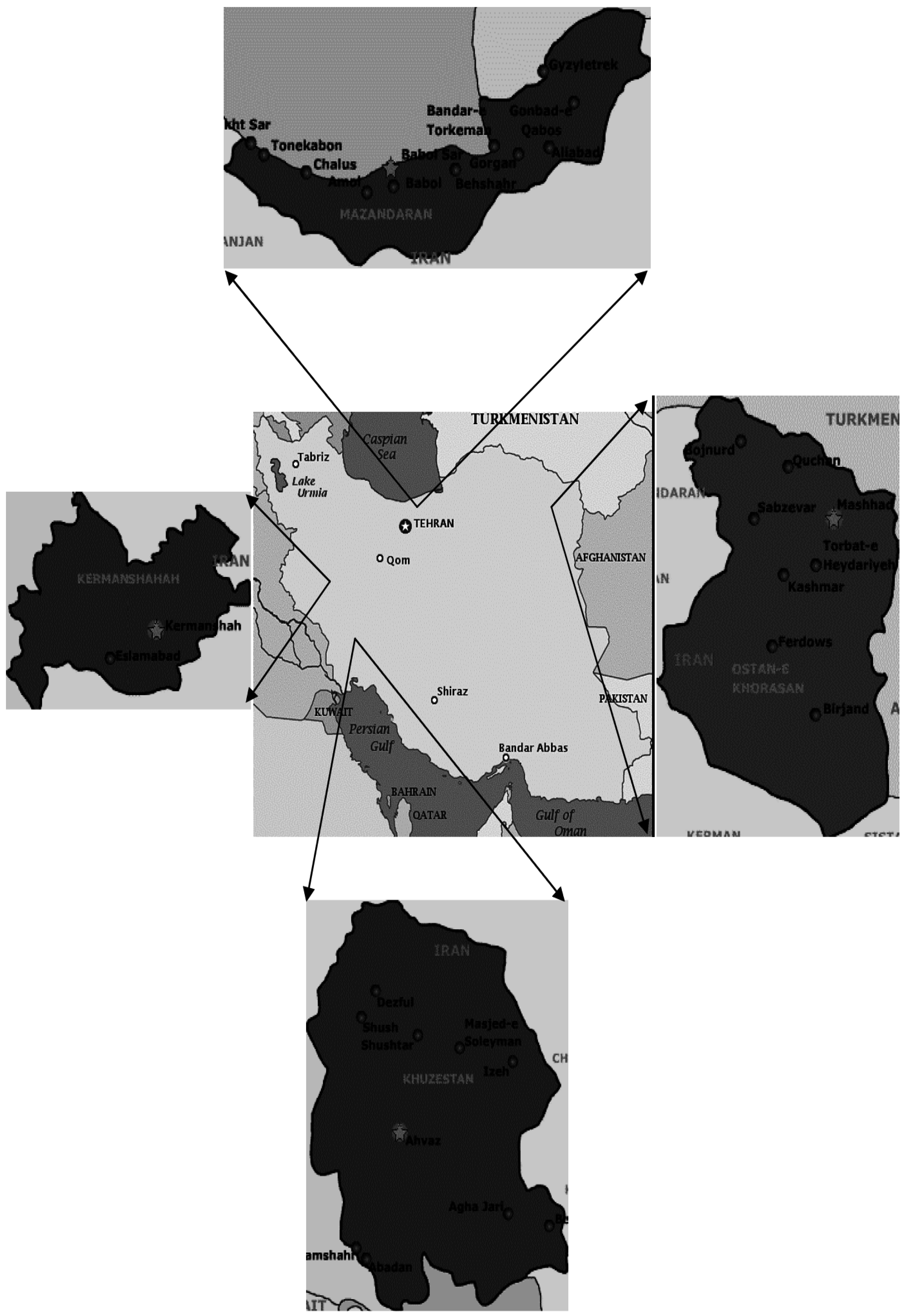
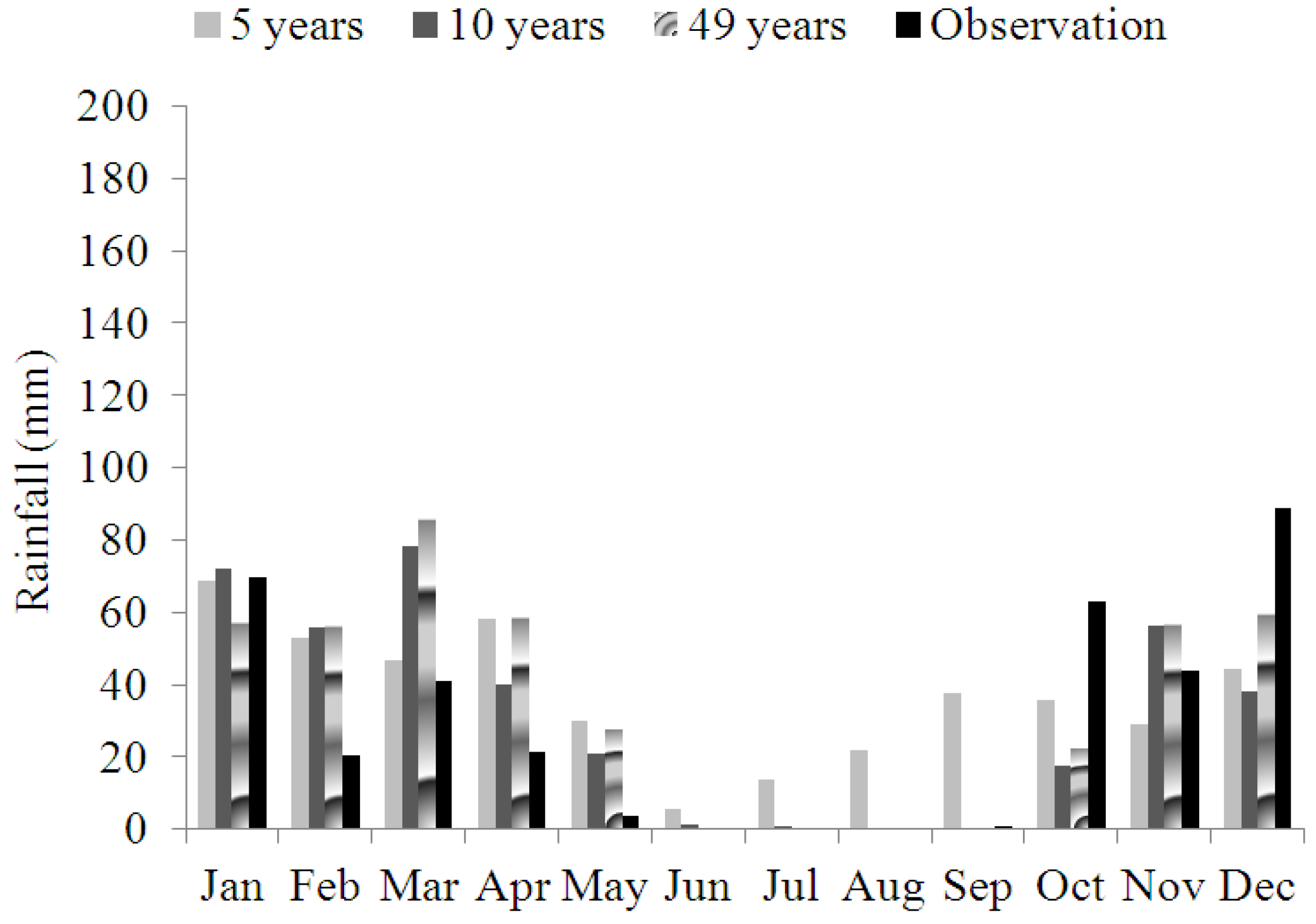
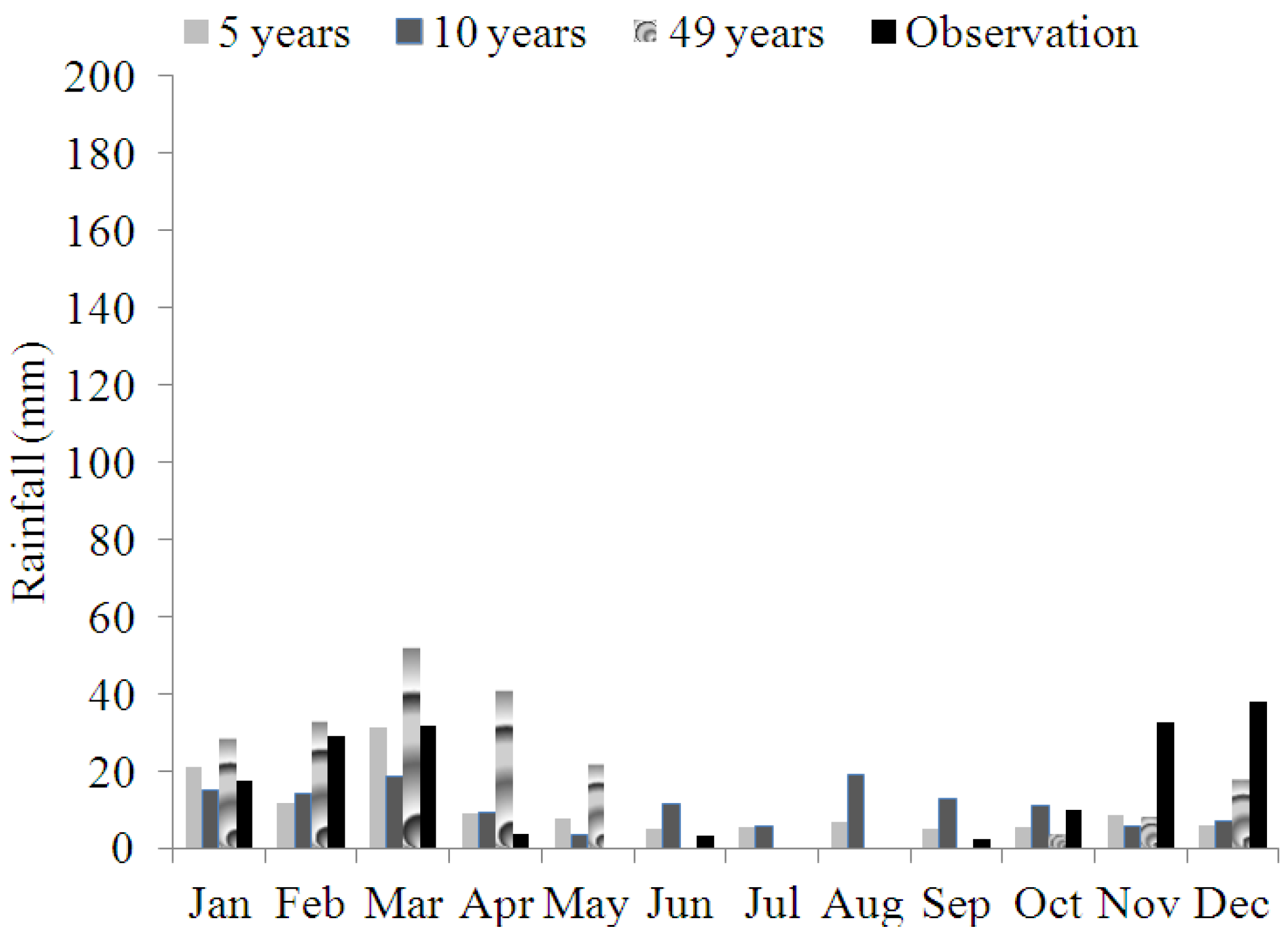
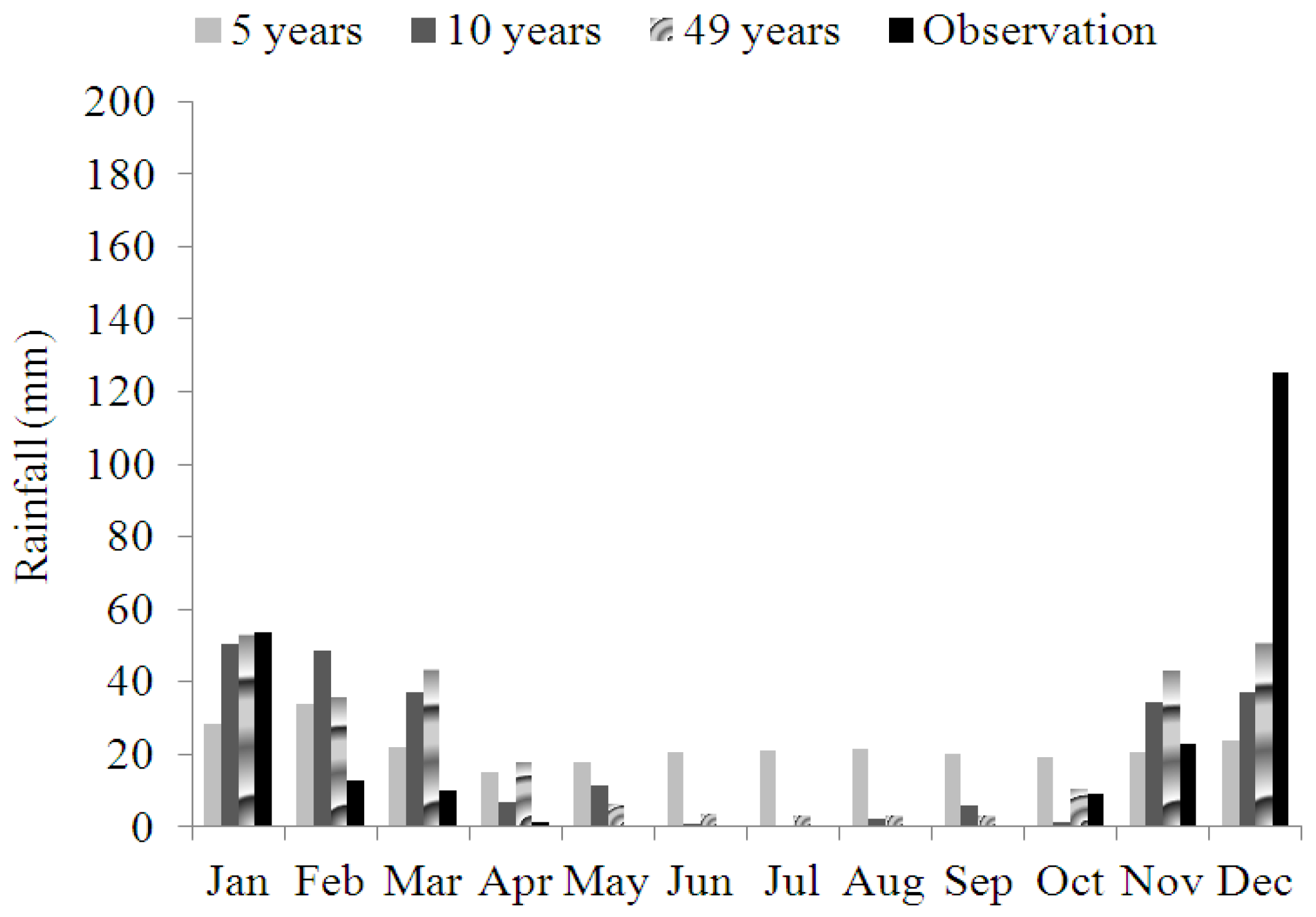
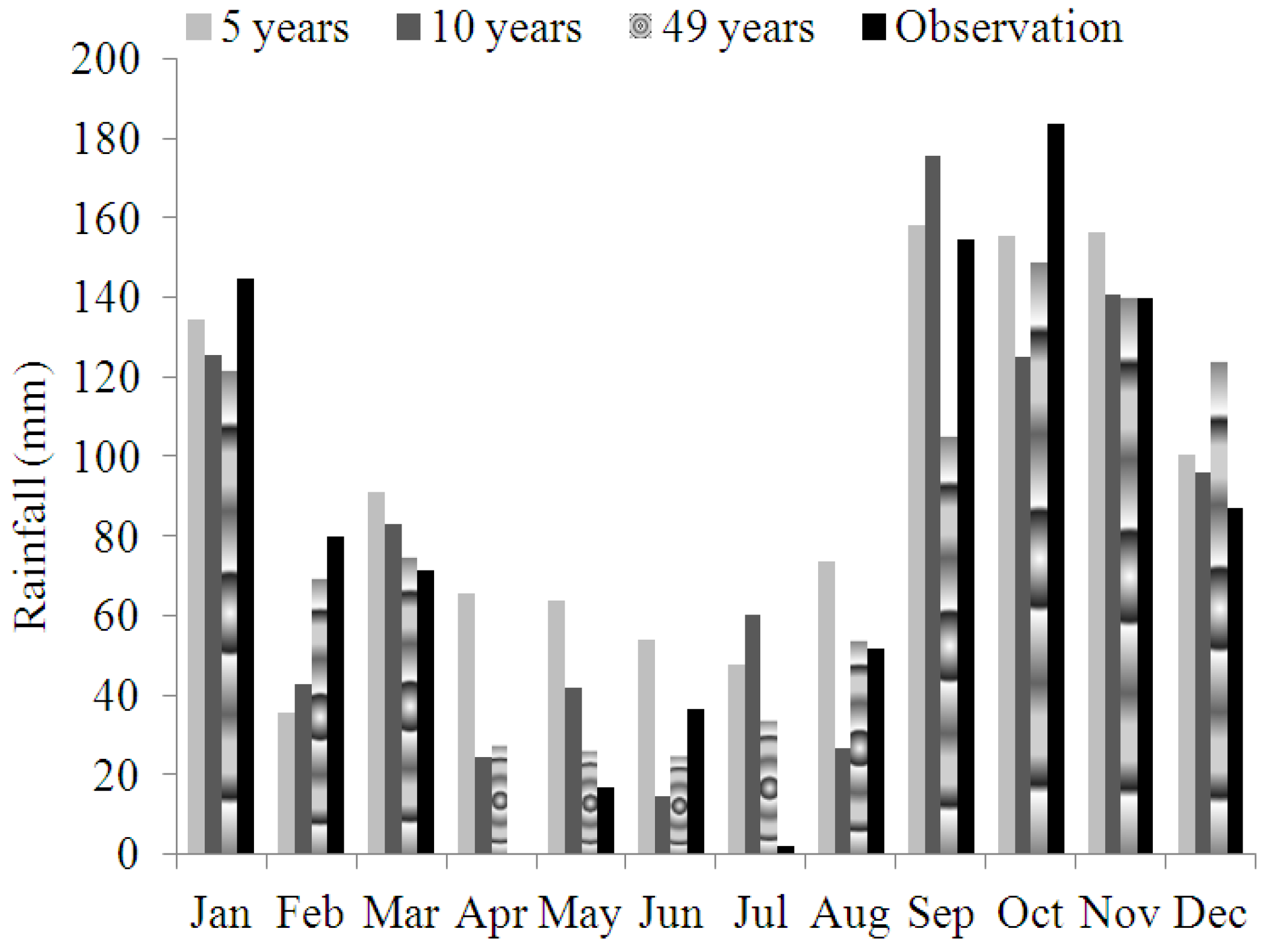
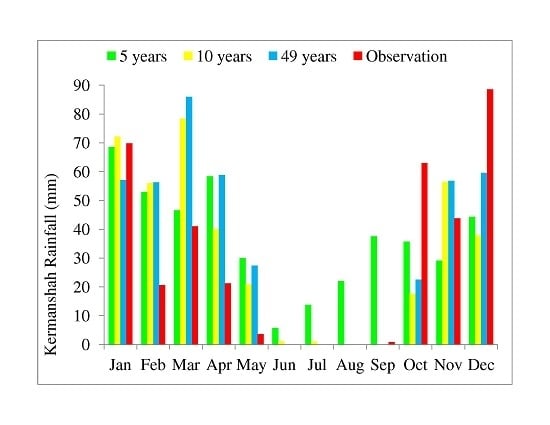
Station	Climate	Elevation Related to Sea Level (m)	Longitude	Altitude
Kermanshah	Temperate	999.2	59°38′ E	36°16′ N
Mashhad	Semi-arid	1322.0	47°7′ E	34°17′ N
Ahvaz	Arid	22.5	48°40′ E	31°20′ N
Babolsar	Humid	−21.0	52°39′ E	36°43′ N

displays information on the synoptic stations used in this study. In order to forecast rainfall on a monthly basis, the rainfall data period from 1951 to 2000 was gathered. In fact, the used data involved 2400 data (all stations) that began in January 1951 and ended in December 2000. Figure 1 shows the locations of the synoptic stations. In this study, time series models were used to forecast monthly rainfall. These models include ARIMA, ARMA, AR, and MA. For this purpose, MINITAB software was used to run all time series models. Finally, via three methods, the ability of time series models to forecast monthly rainfall was surveyed. In the first method, 60 data (1995–1999) regarding the amount of rainfall forecasted for the year 2000 was used. In the second method, 10 years of monthly rainfall data (1990–1999) regarding the amount of rainfall forecasted for the year 2000 was used. In the third method, 588 data (1951–1999) regarding the amount of rainfall forecasted for the year 2000 was used.

3. Results and Discussion

Table 2. Obtained R² for four different stations according to the amount of observation data.

Station	5 Years (60 Data)	10 Years (120 Data)	49 Years (588 Data)
Kermanshah	0.81	0.81	0.81
Mashhad	0.96	0.96	0.96
Ahvaz	0.77	0.83	0.87
Babolsar	0.70	0.73	0.82

shows the obtained R² for four different stations according to the amount of observation data. Figure 2, Figure 3, Figure 4 and Figure 5 show the amount of forecasted rainfall for Kermanshah, Mashhad, Ahvaz, and Babolsar synoptic stations, respectively.

According to the obtained results for R² in Table 2, in a temperate climate (Kermanshah), due to low changes of monthly rainfall over the long term, 60 observation data was sufficient for forecasting. In this station, the R² was 0.81, and an increase in observation data is not recommend.

In a semi-arid climate (Mashhad), due to the low monthly rainfall relative to the Kermanshah and Babolsar stations and the lack of torrent precipitation in arid climates (for example, December in Figure 4), the highest R² was obtained.

In the Mashhad station, data from 5 years prior was sufficient for forecasting, and this is a good result for deficit data situations. However, according to Table 2 and Figure 4 and Figure 5, with 60 observation data, the accuracy of forecasted rainfall was not ideal.

The Ahvaz station, with an arid climate due to drought periods and torrent precipitation, needs at least 588 data for accurate forecasting (R² = 0.87 rather than R² = 0.77).

The Babolsar station, with a humid climate due to flood periods in some years, depends on an increase in observation data if rainfall forecasting is to improve in accuracy. A difference in R² from 49 years of observation data accrued in the Babolsar synoptic station, compared with only 5 years of observation data (R² = 0.82 rather than R² = 0.70) was observed.

4. Conclusions

This paper reports the study of the effect of the length of the recorded data for monthly rainfall forecasting. Monthly rainfall data for three periods of 5, 10, and 49 years were collected from Kermanshah, Mashhad, Ahvaz, and Babolsar stations and used for calibration time series models. Then, the accuracy of forecasting models was investigated with the following year’s data. The following was concluded:

• In temperate and semi-arid climates, 60 observation data is sufficient for the following year’s rainfall forecasting.
• The accuracy of the time series models increased with increasing amounts of observation data of arid and humid climates.
• Time series models are appropriate tools for forecasting monthly rainfall forecasting in semi-arid climates.
• Determining the most critical rainfall month in each climate condition for agriculture schedules is a recommended aim for future studies.