Integrating Multiple-Try DREAM(ZS) to Model-Based Bayesian Geoacoustic Inversion Applied to Seabed Backscattering Strength Measurements
Abstract
:1. Introduction
2. Methodology
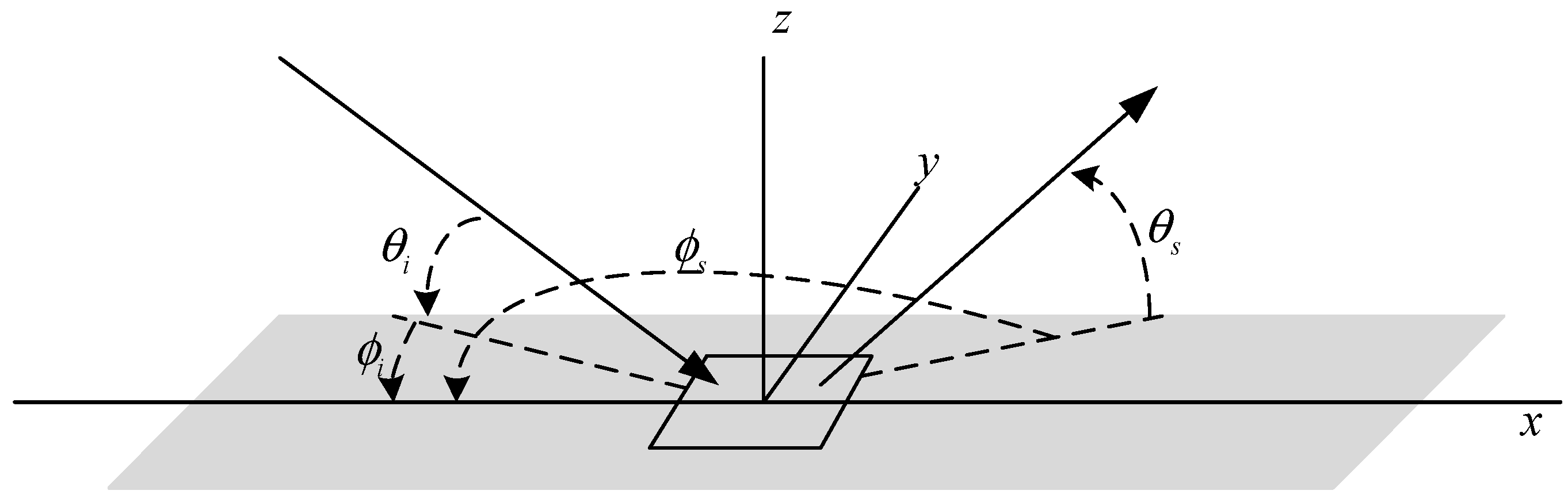
2.1. Acoustic Scattering Model Based on Effective Density Fluid Approximation
2.2. Model-Based Bayesian Inversion
2.3. PPDs Exploration Using Multiple-Try DREAM(ZS)
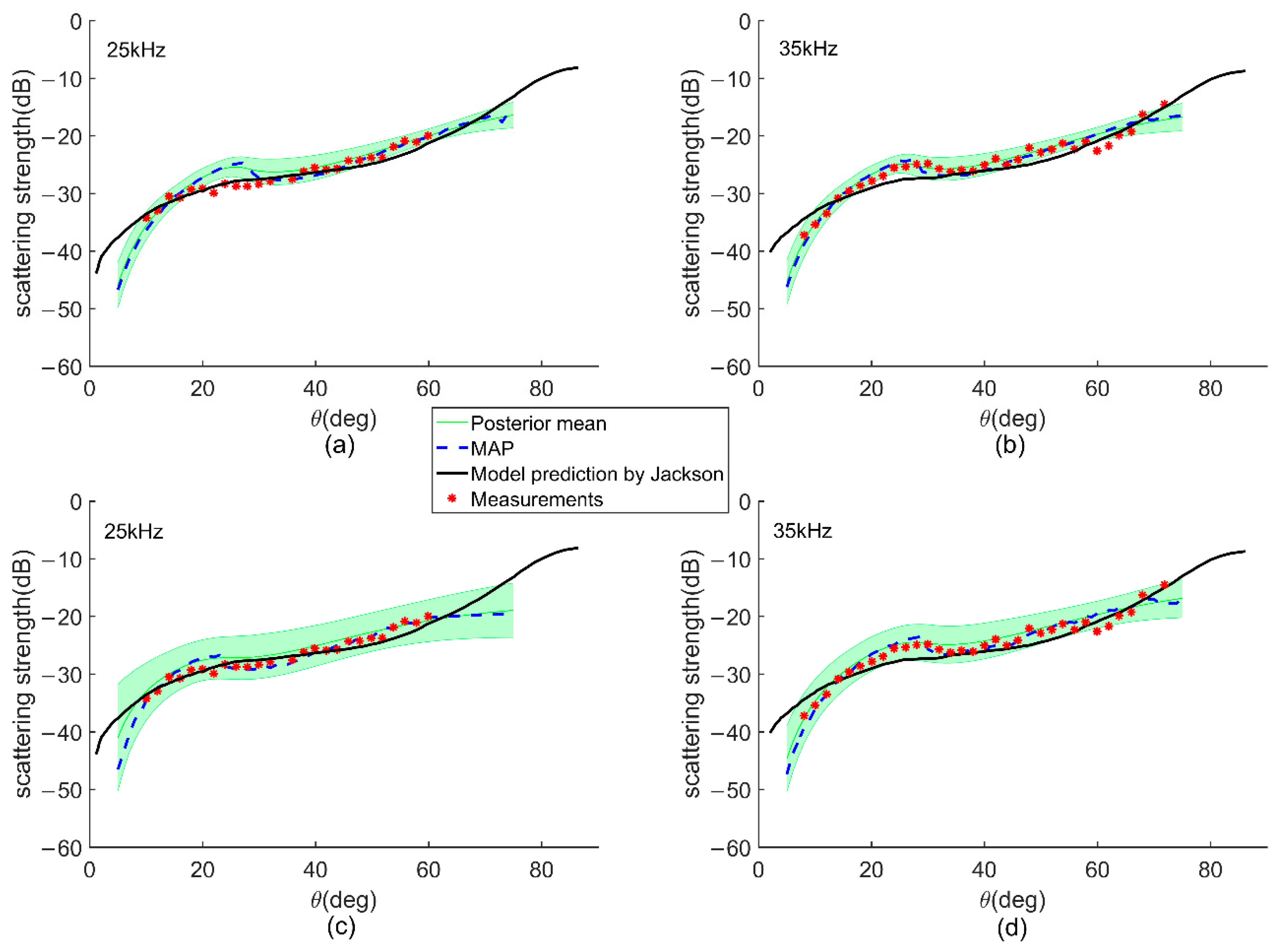
3. Experiment, Results, and Discussion
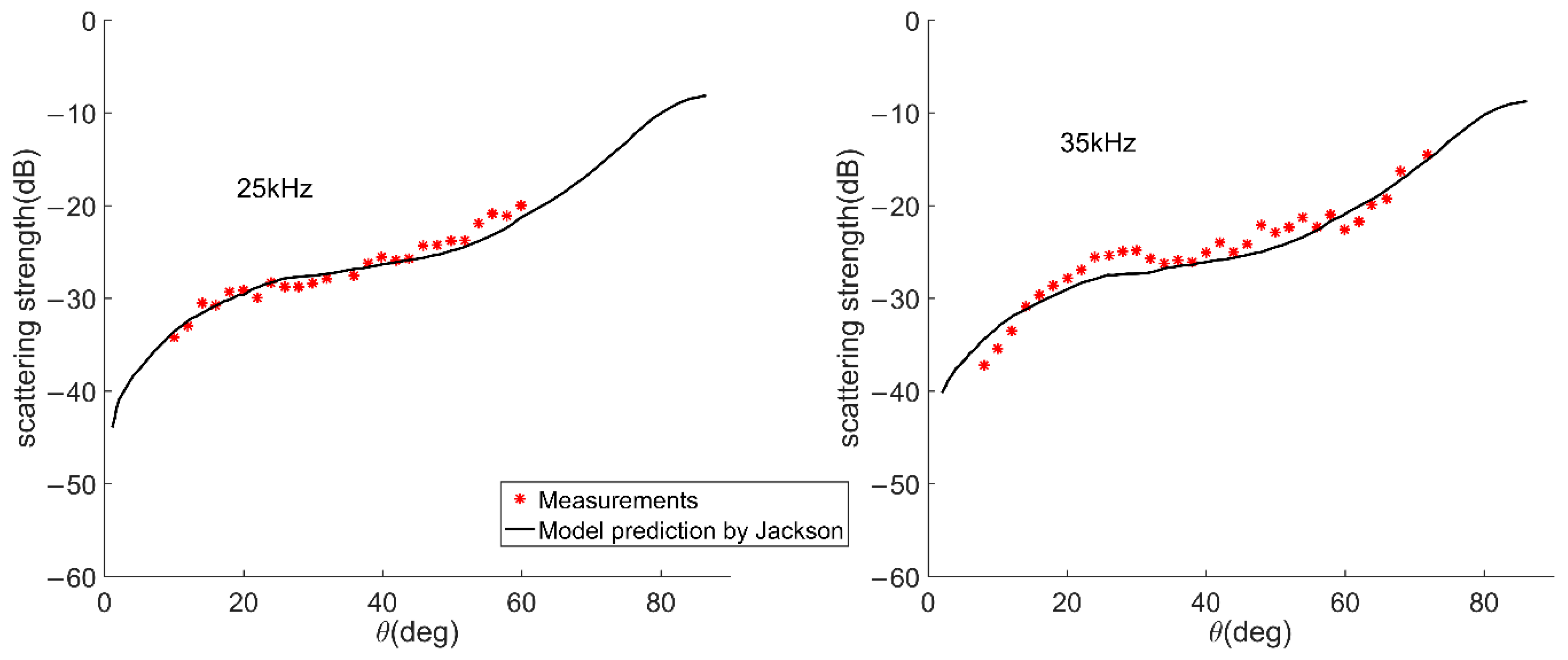
3.1. Geoacouctic and Backscattering Measurements at the Quinault Site
3.2. Geoacoustic Inversion
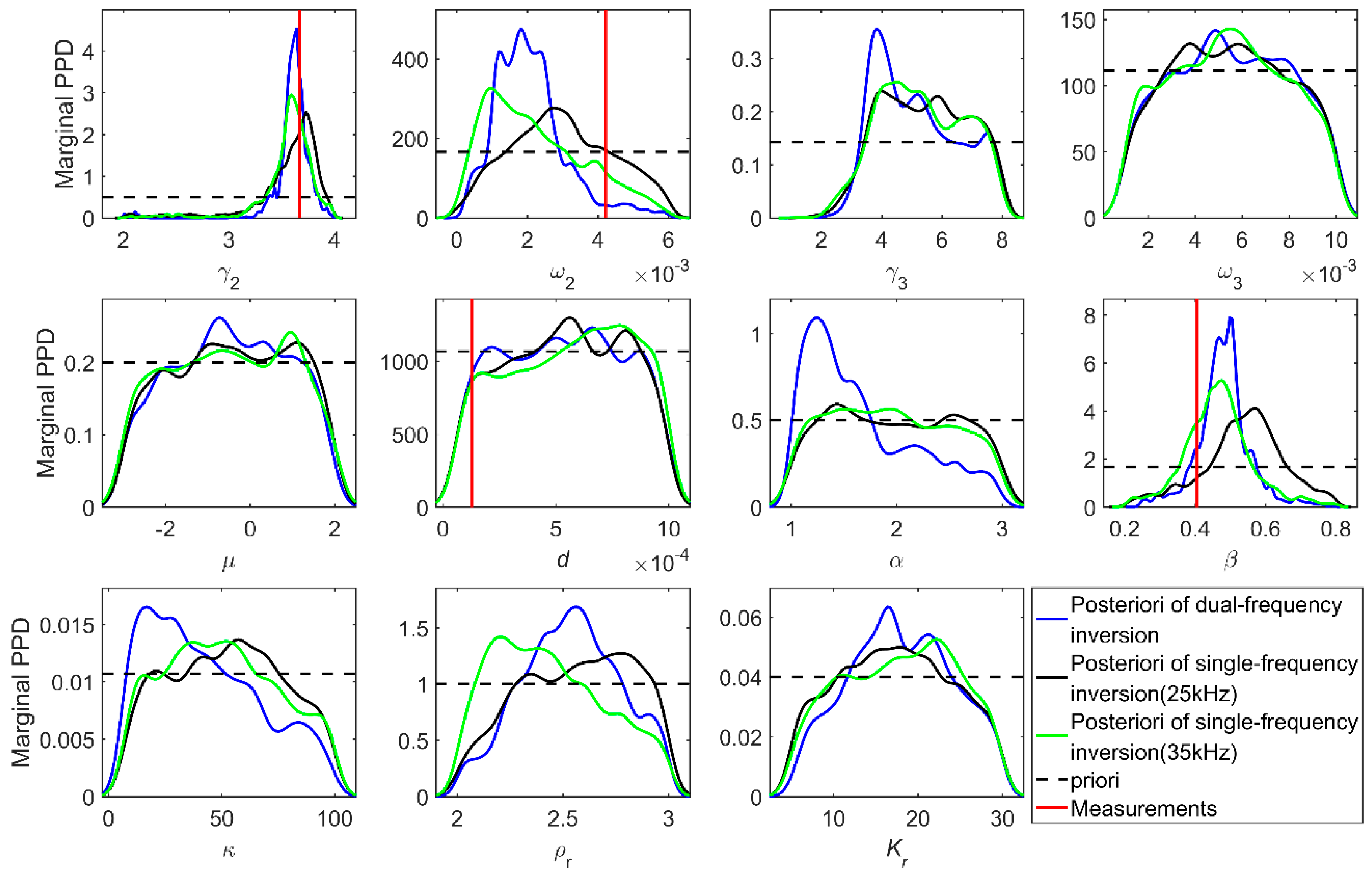
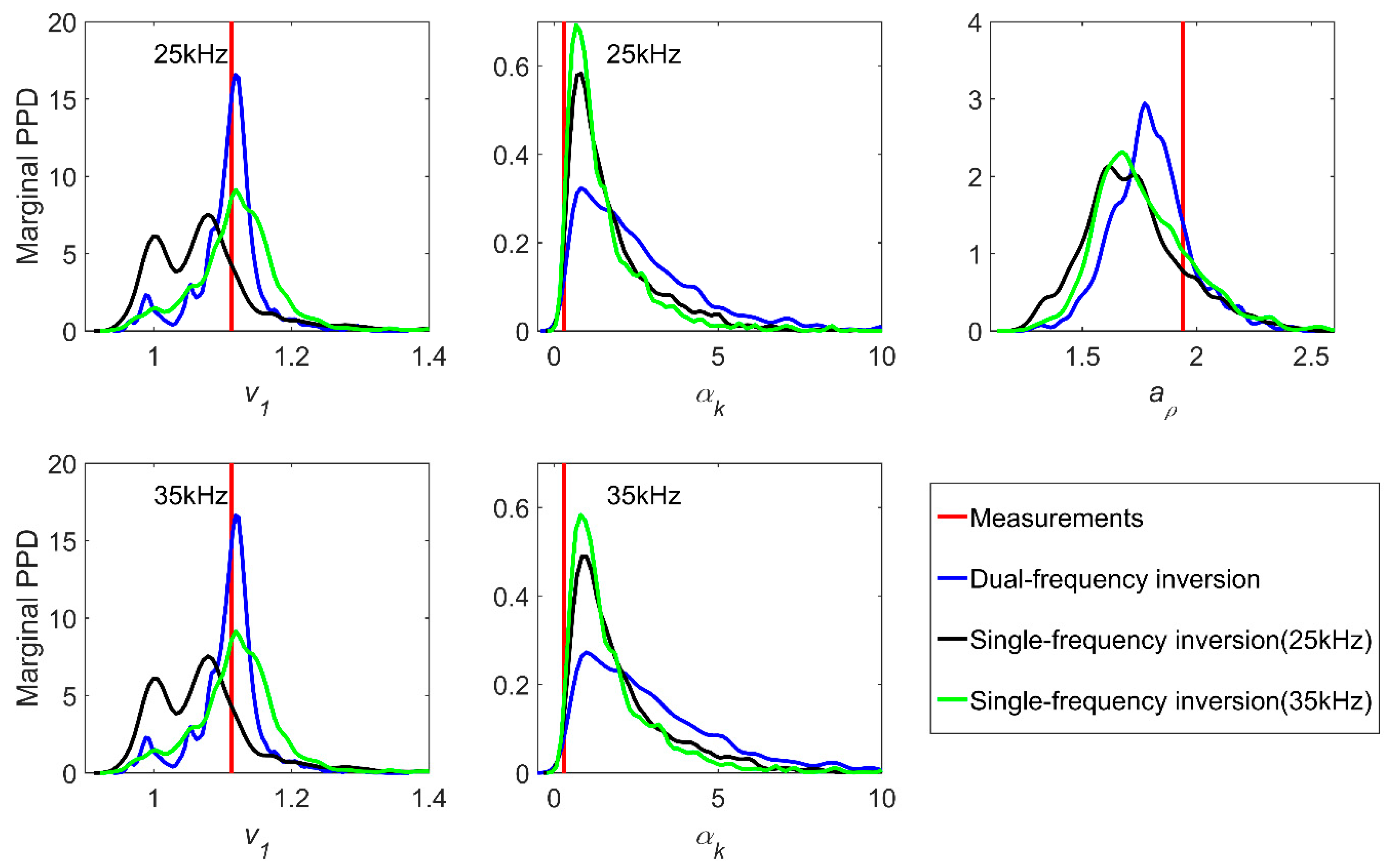
3.2.1. Parameter Uncertainty Analysis
3.2.2. Model Prediction Uncertainty Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Anderson, J.T.; Van Holliday, D.; Kloser, R.; Reid, D.G.; Simard, Y. Acoustic seabed classification: Current practice and future directions. ICES J. Mar. Sci. 2008, 65, 1004–1011. [Google Scholar] [CrossRef]
- Zhou, T.; Li, H.S.; Zhu, J.J.; Wei, Y.K. A geoacoustic estimation scheme based on bottom backscatter signals from multiple angles. Acta Phys. Sin.-Chin. Ed. 2014, 63. [Google Scholar] [CrossRef]
- Yang, K.D.; Ma, Y.L. A geoacoustic inversion method based on bottom reflection signals. Acta Phys. Sin.-Chin. Ed. 2009, 58, 1798–1805. [Google Scholar]
- Siemes, K.; Snellen, M.; Amiri-Simkooei, A.R.; Simons, D.G.; Hermand, J.-P. Predicting Spatial Variability of Sediment Properties from Hydrographic Data for Geoacoustic Inversion. IEEE J. Ocean. Eng. 2010, 35, 766–778. [Google Scholar] [CrossRef]
- Haris, K.; Chakraborty, B.; De, C.; Prabhudesai, R.G.; Fernandes, W. Model-based seafloor characterization employing multi-beam angular backscatter data—A comparative study with dual-frequency single beam. J. Acoust. Soc. Am. 2011, 130, 3623–3632. [Google Scholar] [CrossRef] [PubMed]
- Thorsos, E.I.; Jackson, D.R. Thirty Years of Progress in Theory and Modeling of Sea Surface and Seabed Scattering. Aip. Conf. Proc. 2012, 1495, 127–149. [Google Scholar]
- Williams, K.L.; Thorsos, E.I.; Jackson, D.R.; Hefner, B.T. Thirty years of sand acoustics: A perspective on experiments, models and data/model comparisons. Aip. Conf. Proc. 2012, 1495, 166–192. [Google Scholar]
- Jackson, D.R.; Briggs, K.B. High-frequency bottom backscattering: Roughness versus sediment volume scattering. J. Acoust. Soc. Am. 1992, 92, 962–977. [Google Scholar] [CrossRef]
- Jackson, D.R.; Briggs, K.B.; Williams, K.L.; Richardson, M.D. Tests of models for high-frequency seafloor backscatter. IEEE J. Ocean. Eng. 1996, 21, 458–470. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R. Bistatic bottom scattering: Model, experiments, and model/data comparison. J. Acoust. Soc. Am. 1998, 103, 169–181. [Google Scholar] [CrossRef]
- Stoll, R.D. Sediment Acoustics. Lecture Notes in Earth Sciences; Springer: Berlin, Germany, 1989; pp. 1–101. [Google Scholar]
- Williams, K.L.; Grochocinski, J.M.; Jackson, D.R. Interface scattering by poroelastic seafloors: First-order theory. J. Acoust. Soc. Am. 2001, 110, 2956–2963. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R.; Thorsos, E.I.; Tang, D.J.; Briggs, K.B. Acoustic backscattering experiments in a well characterized sand sediment: Data/model comparisons using sediment fluid and Biot models. IEEE J. Ocean. Eng. 2002, 27, 376–387. [Google Scholar] [CrossRef]
- Chotiros, N.P. Acoustics of the Seabed as a Poroelastic Medium; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Williams, K.L. An effective density fluid model for acoustic propagation in sediments derived from Biot theory. J. Acoust. Soc. Am. 2001, 110, 2276–2281. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.L.; Jackson, D.R.; Thorsos, E.I.; Dajun, T.; Schock, S.G. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media. IEEE J. Ocean. Eng. 2002, 27, 413–428. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R.; Dajun, T.; Briggs, K.B.; Thorsos, E.I. Acoustic Backscattering from a Sand and a Sand/Mud Environment: Experiments and Data/Model Comparisons. IEEE J. Ocean. Eng. 2009, 34, 388–398. [Google Scholar] [CrossRef]
- Williams, K.L. Adding thermal and granularity effects to the effective density fluid model. J. Acoust. Soc. Am. 2013, 133, EL431–EL437. [Google Scholar] [CrossRef] [Green Version]
- De, C.C.; Chakraborty, B. Model-Based Acoustic Remote Sensing of Seafloor Characteristics. IEEE Trans. Geosci. Remote 2011, 49, 3868–3877. [Google Scholar] [CrossRef]
- Dosso, S.E.; Nielsen, P.L.; Harrison, C.H. Bayesian inversion of reverberation and propagation data for geoacoustic and scattering parameters. J. Acoust. Soc. Am. 2009, 125, 2867–2880. [Google Scholar] [CrossRef]
- Dosso, S.E.; Dettmer, J. Bayesian matched-field geoacoustic inversion. Inverse Probl. 2011, 27, 55009. [Google Scholar] [CrossRef]
- Chapman, N.R. Perspectives on Geoacoustic Inversion of Ocean Bottom Reflectivity Data. J. Mar. Sci. Eng. 2016, 4, 61. [Google Scholar] [CrossRef]
- Yang, K.D.; Xiao, P.; Duan, R.; Ma, Y.L. Bayesian Inversion for Geoacoustic Parameters from Ocean Bottom Reflection Loss. J. Comput. Acoust. 2017, 25. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. Adaptive proposal distribution for random walk Metropolis algorithm. Comput. Stat. 1999, 14, 375–395. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 113–117. [Google Scholar] [CrossRef]
- Braak, C.J.F.T. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Braak, C.J.F.T.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef] [Green Version]
- Laloy, E.; Vrugt, J.A. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM((ZS)) and high-performance computing. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Dosso, S.E. Quantifying uncertainty in geoacoustic inversion. I. A fast Gibbs sampler approach. J. Acoust. Soc. Am. 2002, 111, 129–142. [Google Scholar] [CrossRef] [PubMed]
- Dosso, S.E.; Nielsen, P.L. Quantifying uncertainty in geoacoustic inversion. II. Application to broadband, shallow-water data. J. Acoust. Soc. Am. 2002, 111, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Bonomo, A.L.; Isakson, M.J. A comparison of three geoacoustic models using Bayesian inversion and selection techniques applied to wave speed and attenuation measurements. J. Acoust. Soc. Am. 2018, 143, 2501. [Google Scholar] [CrossRef]
- Zou, B.; Zhai, J.; Xu, J.; Li, Z.; Gao, S. A Method for Estimating Dominant Acoustic Backscatter Mechanism of Water-Seabed Interface via Relative Entropy Estimation. Math. Probl. Eng. 2018, 2018, 10. [Google Scholar] [CrossRef]
- Zou, B.; Zhai, J.; Qi, Z.; Li, Z. A Comparison of Three Sediment Acoustic Models Using Bayesian Inversion and Model Selection Techniques. Remote Sens. 2019, 11, 562. [Google Scholar] [CrossRef]
- Jackson, D.R.; Richardson, M.D. High-Frequency Seafloor Acoustics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Mourad, P.D.; Jackson, D.R. In High Frequency Sonar Equation Models for Bottom Backscatter and Forward Loss. In Proceedings of the OCEANS, Seattle, WA, USA, 18–21 September 1989. [Google Scholar]
- Pouliquen, E.; Lyons, A.P.; Pace, N.G. Penetration of acoustic waves into rippled sandy seafloors. J. Acoust. Soc. Am. 2000, 108 Pt 1, 2071–2081. [Google Scholar] [CrossRef]
- Zou, D.P.; Williams, K.L.; Thorsos, E.I. Influence of Temperature on Acoustic Sound Speed and Attenuation of Seafloor Sand Sediment. IEEE J. Ocean. Eng. 2015, 40, 969–980. [Google Scholar]
- Dettmer, J.; Dosso, S.E.; Holland, C.W. Model selection and Bayesian inference for high-resolution seabed reflection inversion. J. Acoust. Soc. Am. 2009, 125, 706–716. [Google Scholar] [CrossRef]
- Dettmer, J.; Holland, C.W.; Dosso, S.E. Analyzing lateral seabed variability with Bayesian inference of seabed reflection data. J. Acoust. Soc. Am. 2009, 126, 56–69. [Google Scholar] [CrossRef]
- Jiang, Y.M.; Chapman, N.R. The impact of ocean sound speed variability on the uncertainty of geoacoustic parameter estimates. J. Acoust. Soc. Am. 2009, 125, 2881–2895. [Google Scholar] [CrossRef] [PubMed]
- Lucka, F. Fast Gibbs sampling for high-dimensional Bayesian inversion. Inverse Probl. 2016, 32, 115019. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.-L.; Yang, K.-D.; Ma, Y.-L. Geoacoustic Inversion for Bottom Parameters via Bayesian Theory in Deep Ocean. Chin. Phys. Lett. 2017, 34, 034301. [Google Scholar] [CrossRef]
- Laloy, E.; Fasbender, D.; Bielders, C.L. Parameter optimization and uncertainty analysis for plot-scale continuous modeling of runoff using a formal Bayesian approach. J. Hydrol. 2010, 380, 82–93. [Google Scholar] [CrossRef]
- Laloy, E.; Weynants, M.; Bielders, C.L.; Vanclooster, M.; Javaux, M. How efficient are one-dimensional models to reproduce the hydrodynamic behavior of structured soils subjected to multi-step outflow experiments? J. Hydrol. 2010, 393, 37–52. [Google Scholar] [CrossRef]
- Scharnagl, B.; Vrugt, J.A.; Vereecken, H.; Herbst, M. Information content of incubation experiments for inverse estimation of pools in the Rothamsted carbon model: A Bayesian perspective. Biogeosciences 2010, 7, 763–776. [Google Scholar] [CrossRef]
- Liu, J.S.; Liang, F.; Wong, W.H. The Multiple-Try Method and Local Optimization in Metropolis Sampling. J. Am. Stat. Assoc. 2000, 95, 121–134. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Boehme, H.; Chotiros, N.P. Acoustic backscattering at low grazing angles from the ocean bottom. J. Acoust. Soc. Am. 1988, 84, 1018–1029. [Google Scholar] [CrossRef]
- Hefner, B.T.; Williams, K.L. Sound speed and attenuation measurements in unconsolidated glass-bead sediments saturated with viscous pore fluids. J. Acoust. Soc. Am. 2006, 120, 2538–2549. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, E.L. Compressional-Wave Attenuation in Marine Sediments. Geophysics 1972, 37, 620–646. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Porosity | 0.405 | dimensionless | |
| Grain size | phi | 2.97 | |
| Ratio of sound velocity of sediment to water | 1.113 | dimensionless | |
| Ratio of mass density of sediment to water | 1.94 | dimensionless | |
| Attenuation | 0.30 | dB/m/kHz | |
| Roughness spectral exponent (across) | 3.67 | dimensionless | |
| Roughness spectral strength (across) | 0.00422 |
| Parameter | Symbol | Value | Lower Bound | Upper Bound | Unit |
|---|---|---|---|---|---|
| Roughness spectral exponent | - | 2 | 4 | dimensionless | |
| Roughness spectral strength | - | 0.00001 | 0.006 | ||
| Density fluctuation spectral exponent | - | 1 | 8 | dimensionless | |
| Density fluctuation spectral strength | - | 0.001 | 0.01 | ||
| Ratio of compressibility to density fluctuation | - | −3 | 2 | dimensionless | |
| Mean grain diameter | - | 62.5 × 10−6 | 1 × 10−3 | m | |
| Tortuosity | - | 1 | 3 | dimensionless | |
| Porosity | - | 0.2 | 0.8 | dimensionless | |
| Permeability | - | 6.5 | 100 | ||
| Ratio of mass density of grains to water | - | 2 | 3 | dimensionless | |
| Ratio of bulk modulus of grains to water | - | 5 | 30 | dimensionless | |
| Mass density of pore fluid | 1023 | - | - | ||
| Bulk modulus of pore fluid | 2.395 × 10−9 | - | - | Pa | |
| Dynamic viscosity | 0.00105 | - | - | ||
| Compressional sound speed in water | 1530 | - | - |
| Inversion Type | RMSE Type | 25kHz | 35kHz |
|---|---|---|---|
| Dual-frequency | MAP and measurements | 1.6 | 1.2 |
| Posterior mean and measurements | 1.6 | 1.1 | |
| Jackson’s model | prediction and measurements | 1.0 | 1.6 |
| Single-frequency | MAP and measurements | 1.0 | 1.3 |
| Posterior mean and measurements | 1.3 | 1.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, B.; Qi, Z.; Hou, G.; Li, Z.; Yu, X.; Zhai, J. Integrating Multiple-Try DREAM(ZS) to Model-Based Bayesian Geoacoustic Inversion Applied to Seabed Backscattering Strength Measurements. J. Mar. Sci. Eng. 2019, 7, 372. https://doi.org/10.3390/jmse7100372
Zou B, Qi Z, Hou G, Li Z, Yu X, Zhai J. Integrating Multiple-Try DREAM(ZS) to Model-Based Bayesian Geoacoustic Inversion Applied to Seabed Backscattering Strength Measurements. Journal of Marine Science and Engineering. 2019; 7(10):372. https://doi.org/10.3390/jmse7100372
Chicago/Turabian StyleZou, Bo, Zhanfeng Qi, Guangchao Hou, Zhaoxing Li, Xiaochen Yu, and Jingsheng Zhai. 2019. "Integrating Multiple-Try DREAM(ZS) to Model-Based Bayesian Geoacoustic Inversion Applied to Seabed Backscattering Strength Measurements" Journal of Marine Science and Engineering 7, no. 10: 372. https://doi.org/10.3390/jmse7100372






