Prediction of Unsteady Developed Tip Vortex Cavitation and Its Effect on the Induced Hull Pressures
Abstract
:1. Introduction
- For the effective wake prediction, BEM/Reynolds-Averaged Navier–Stokes (RANS) interactive scheme (PC2NS) is used. PC2NS is the interface that couples the BEM with RANS solver in an iterative manner for the prediction of the effective wake on the propeller plane [16].
- Hydrodynamic BEM is applied to open propellers subject to the periodic non-axisymmetric inflow. The unsteady wake alignment scheme is employed to allow the physical variation of the trailing wake in space and time.
- BEM models tip vortex cavitation at the tip of fully aligned wake. Trajectory of the tip vortex cavitation is assumed to be following the wake panels from wetted runs. This assumption is valid only for the limited amount of blade sheet cavity as large cavity volume affects the overall blade loading.
- The unsteady cavity problem, including both the sheet cavitation on the blade and developed tip vortex cavitation, is solved for the singularities (discrete vortex and source strength) on the wetted propeller surfaces and on the surfaces beneath the cavity.
- The induced potentials on a flat barge or ship hull due to the propeller, its wake, sheet cavity, and developed tip vortex cavity are determined by solving Green’s 3rd identity in the acoustic BEM solver.
- Finally, the pressure BEM solver is implemented to predict the diffraction potentials which will lead to the solid boundary factor to estimate the fluctuating hull pressures.
2. Methodology
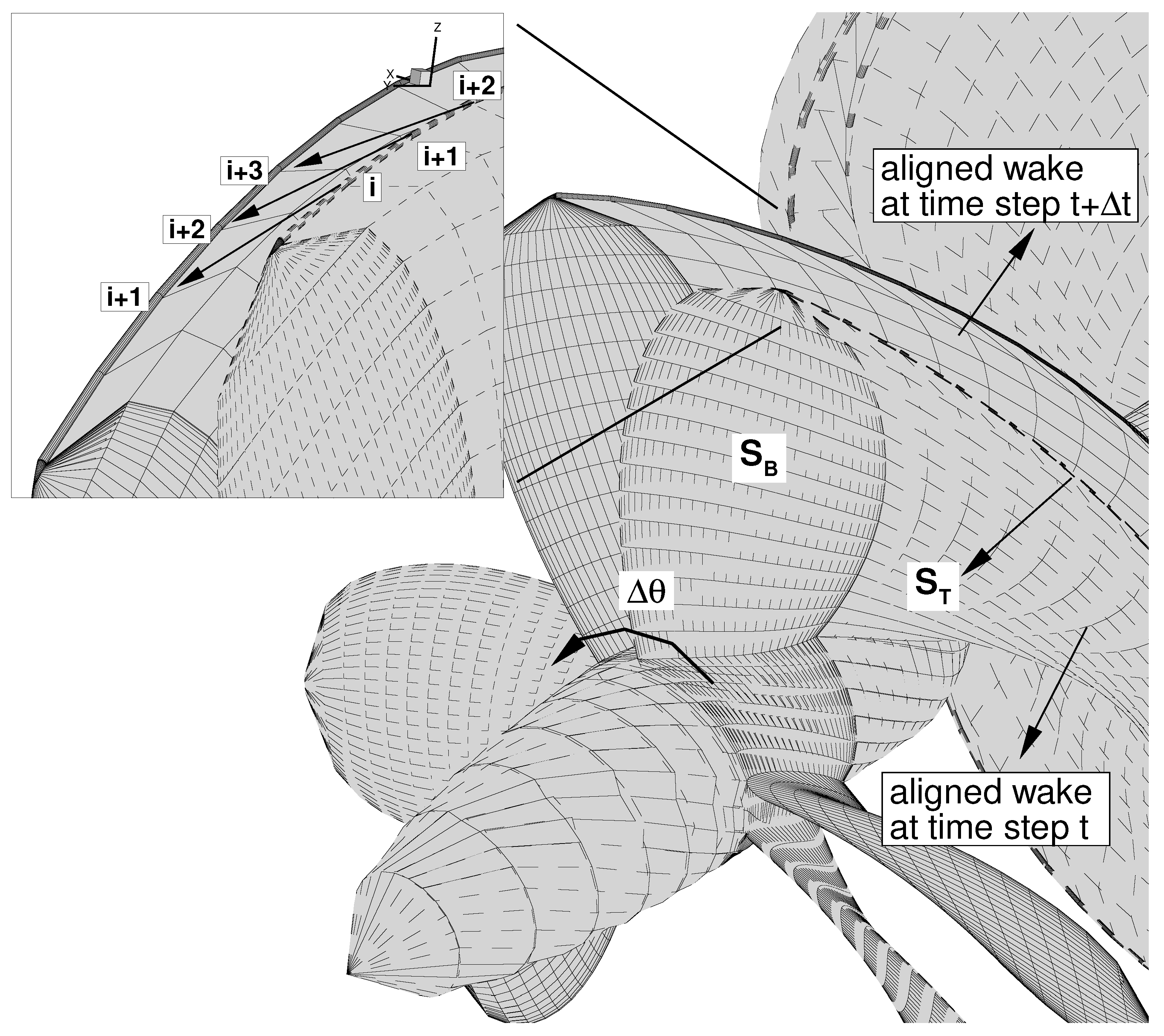
2.1. The Unsteady Wake Alignment Scheme
2.1.1. Steady Regime ()
2.1.2. Unsteady Regime ()
2.1.3. Fully Unsteady Regime (Last Two Revolutions)
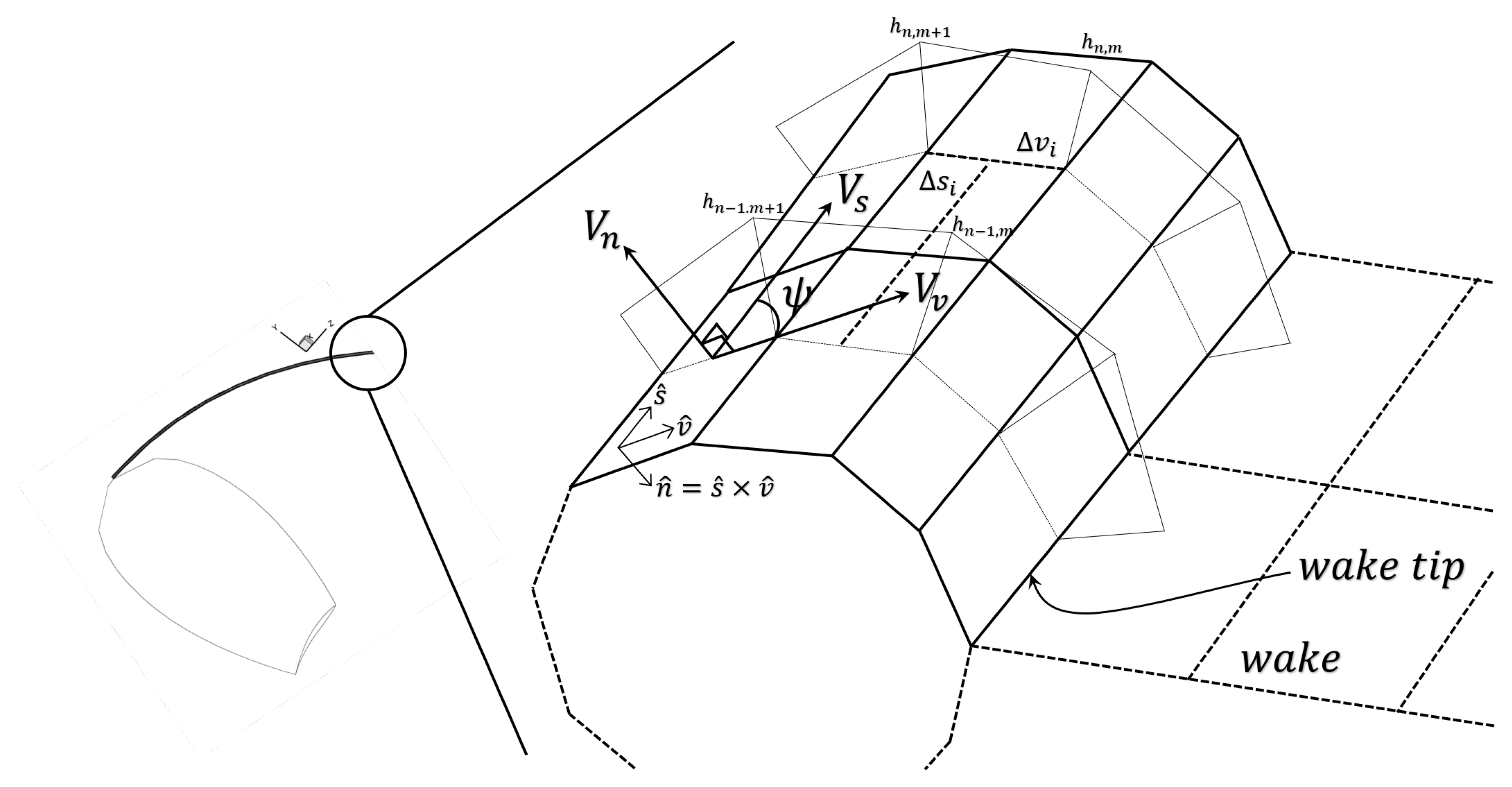
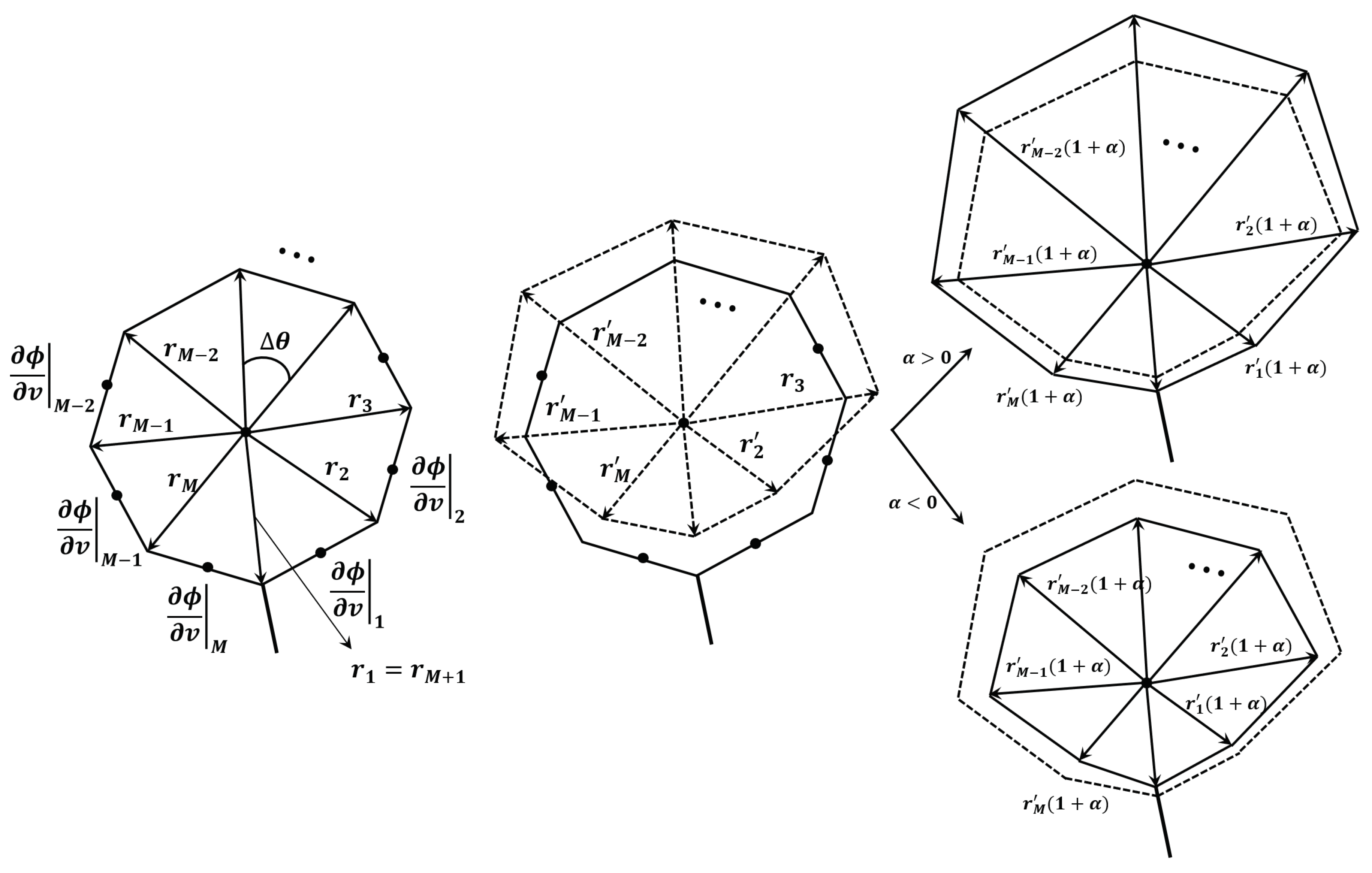
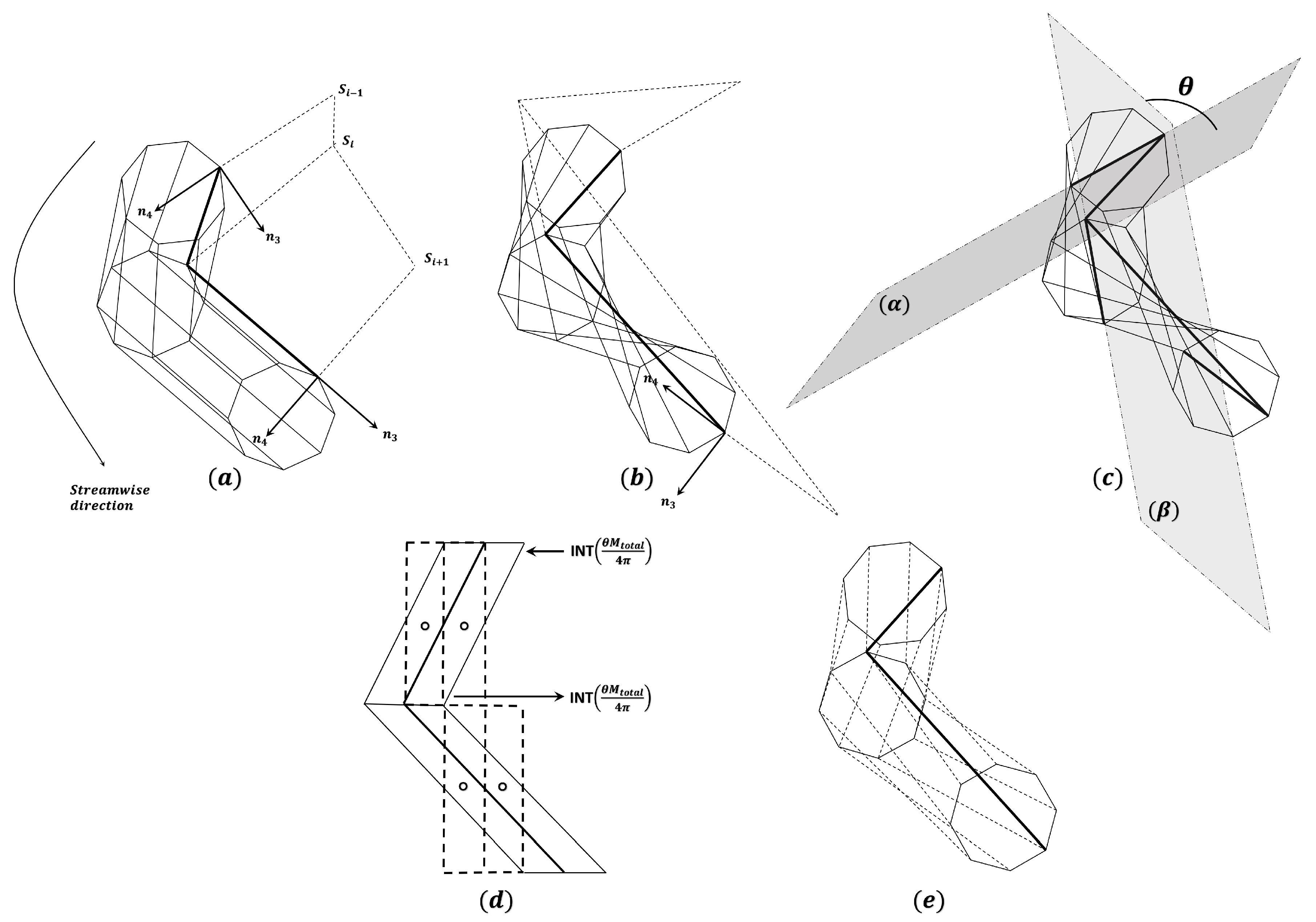
2.2. Tip Vortex Cavitation Modeling
2.2.1. Modeling Developed Tip Vortex Cavitation Using Jacobian Method
2.2.2. Modeling Developed Tip Vortex via Direct Method
2.2.3. Treatments for the Tip Vortex Collapse and Panel Distortion
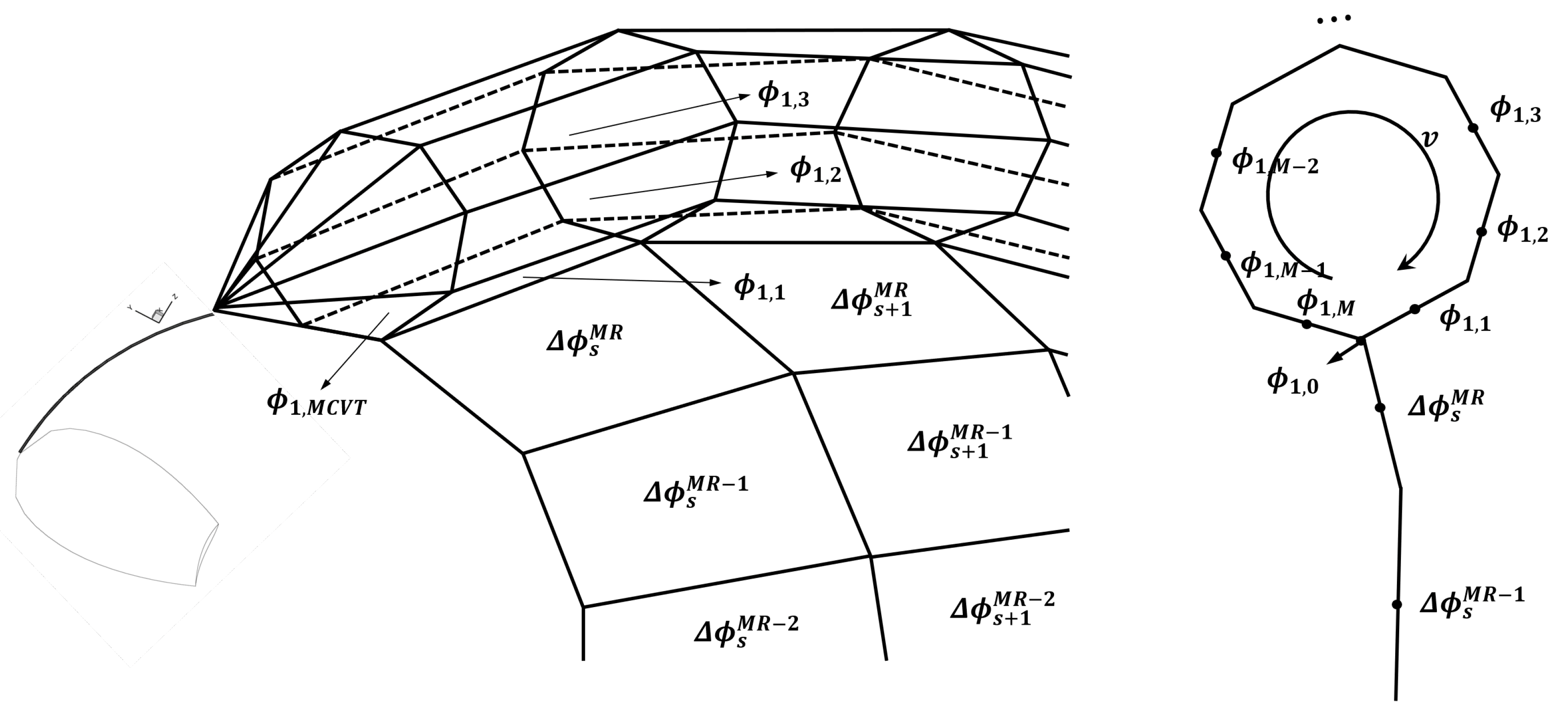
2.2.4. Discretized Green’s Formula
- known source strengths, which are equal to on .
- unknown dipole strengths on .
- known dipole strengths, which are evaluated by Equation (24) on .
- unknown source strengths on .
2.3. Acoustic Boundary Element Method: Solver for the Oscillating Hull Pressure
3. Numerical Results and Comparisons with Other Measurements
- BEM/RANS interactive method for the effective wake predictions.
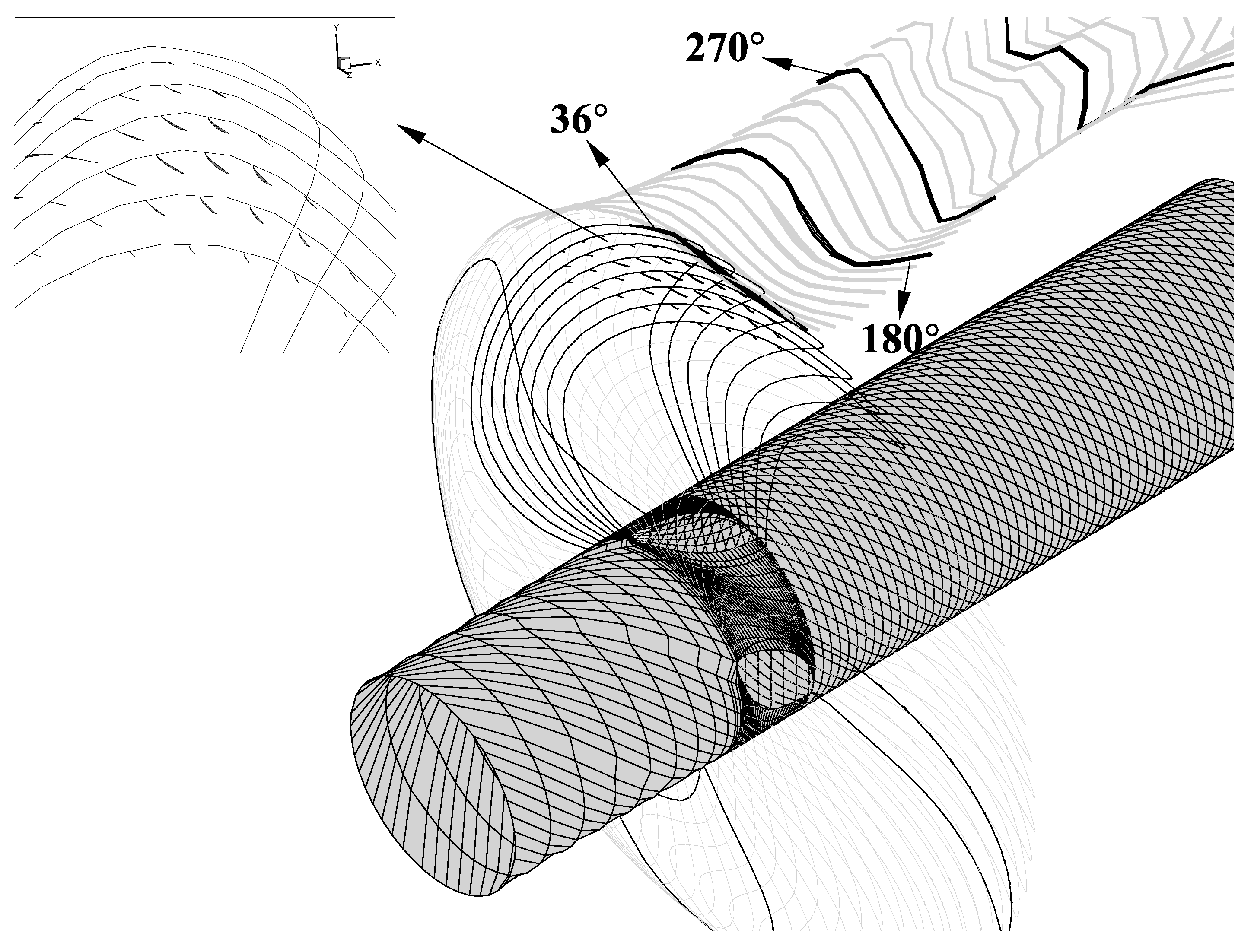
- Application of the unsteady wake alignment (UWA) scheme in the inclined-shaft flow for an open propeller.
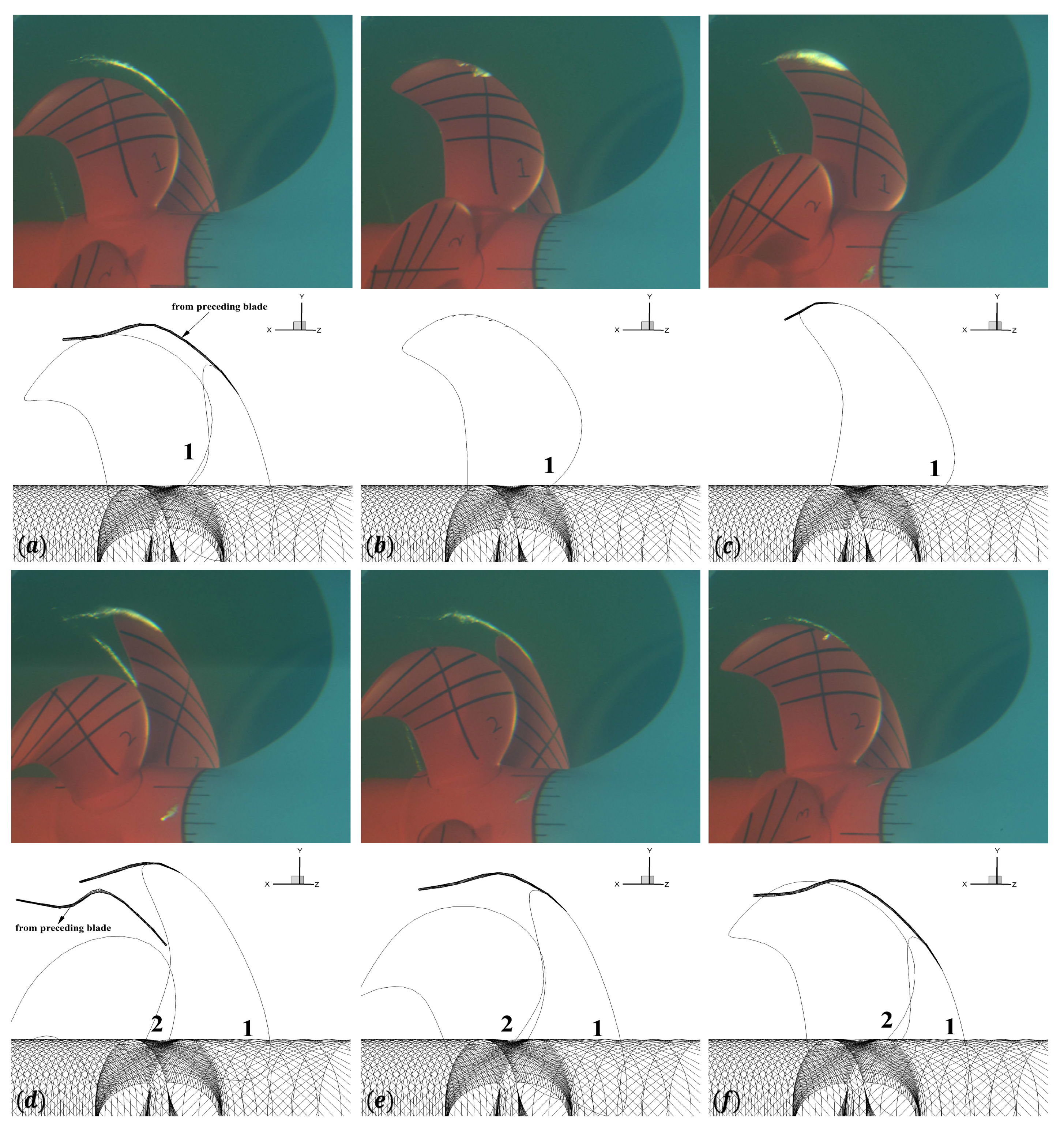
- Predictions of the developed tip vortex cavitation in the effective wake for an open propeller.
- Finally, predictions of the propeller-induced hull pressures in fully-wetted or cavitating conditions, considering hull/propeller/rudder interactions.
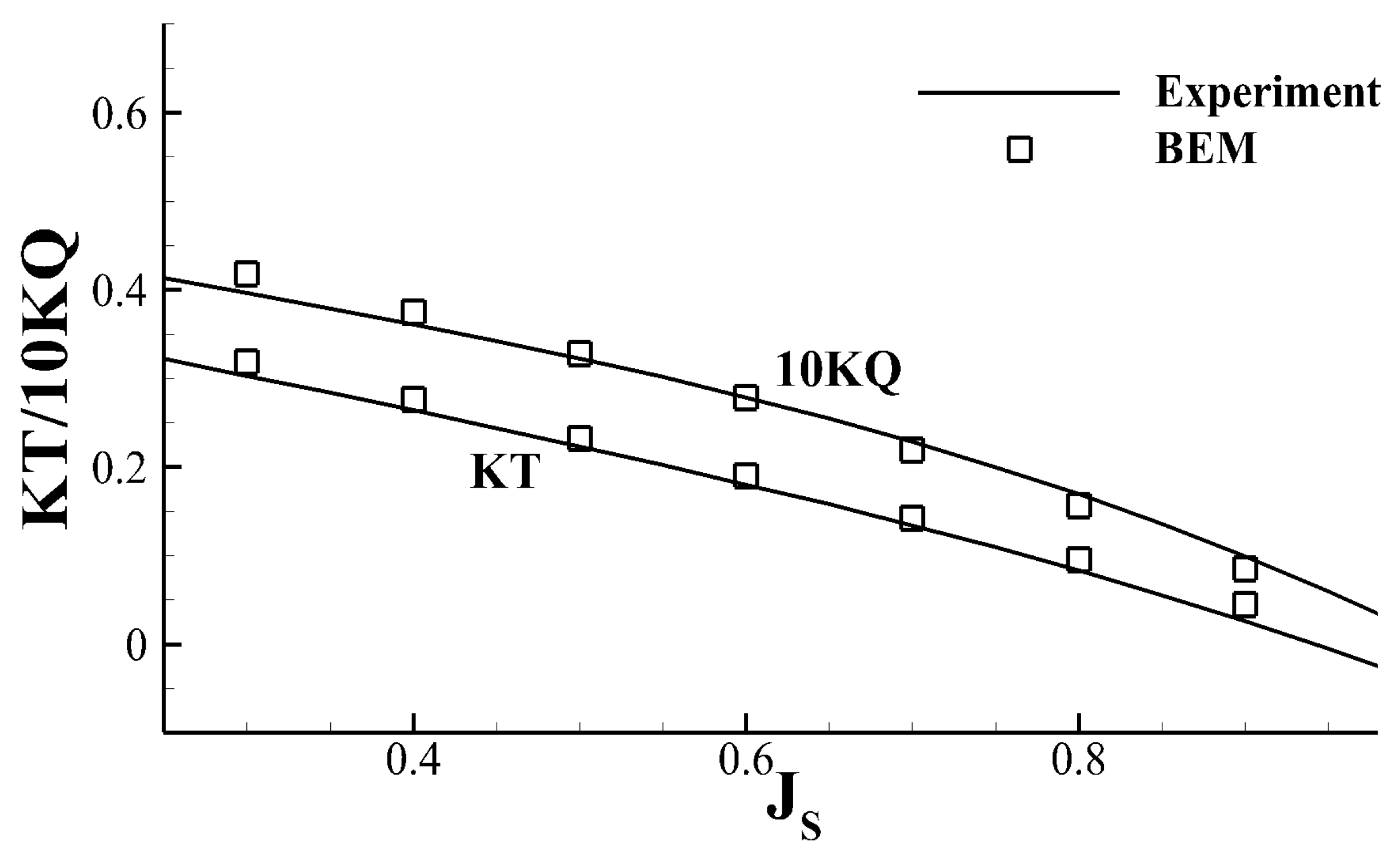
3.1. Unsteady Wake Alignment in Inclined Shaft Flow
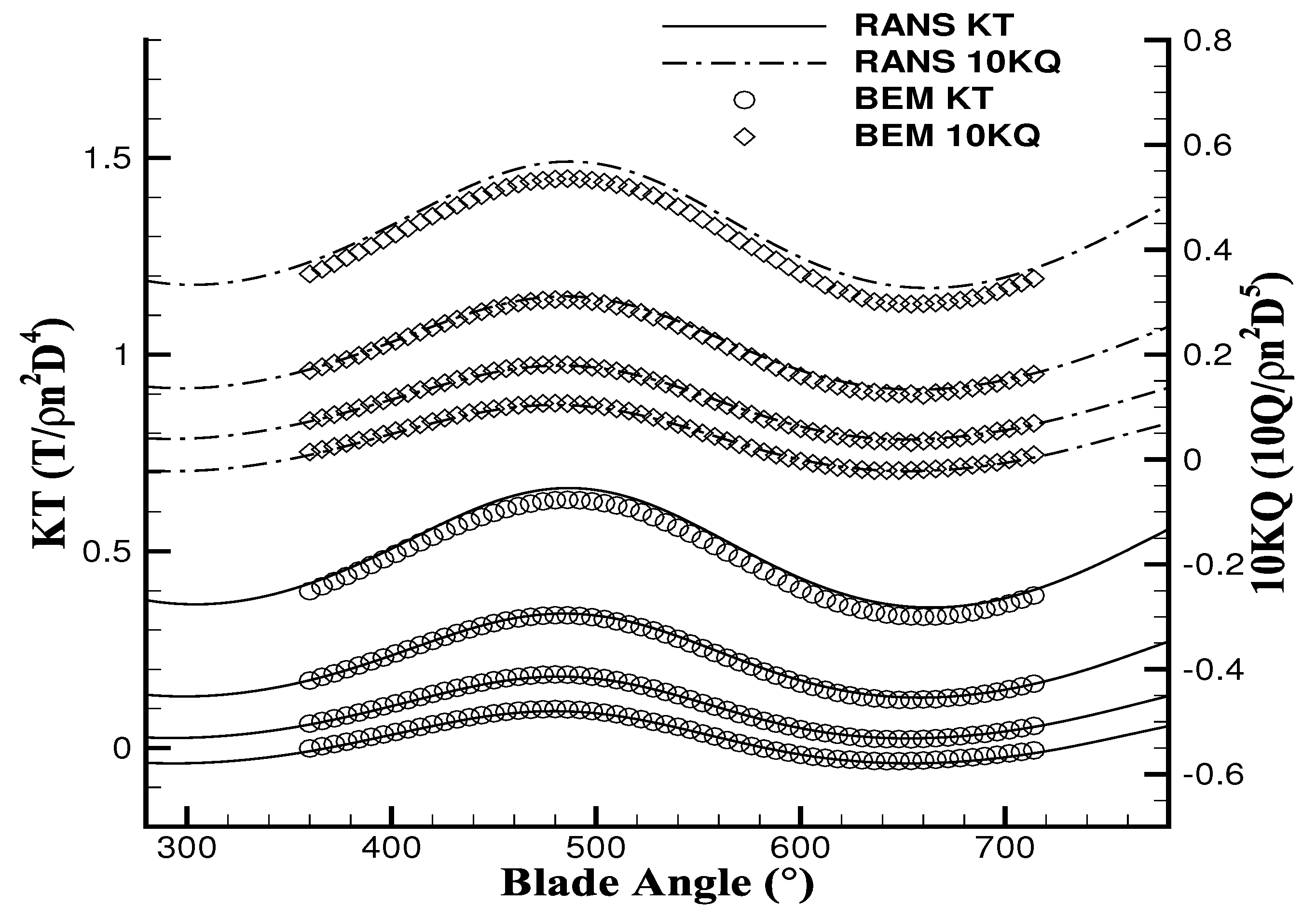
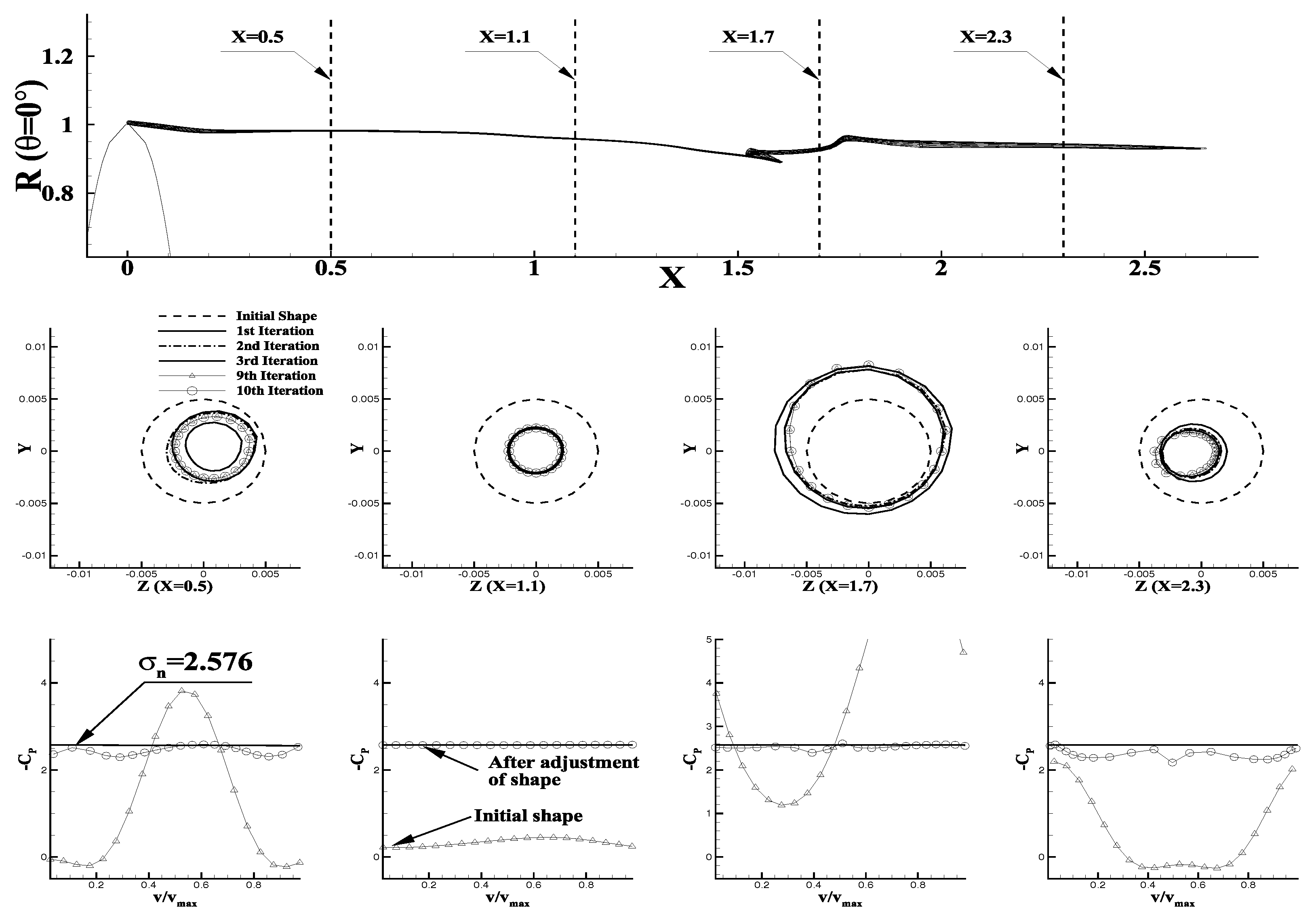
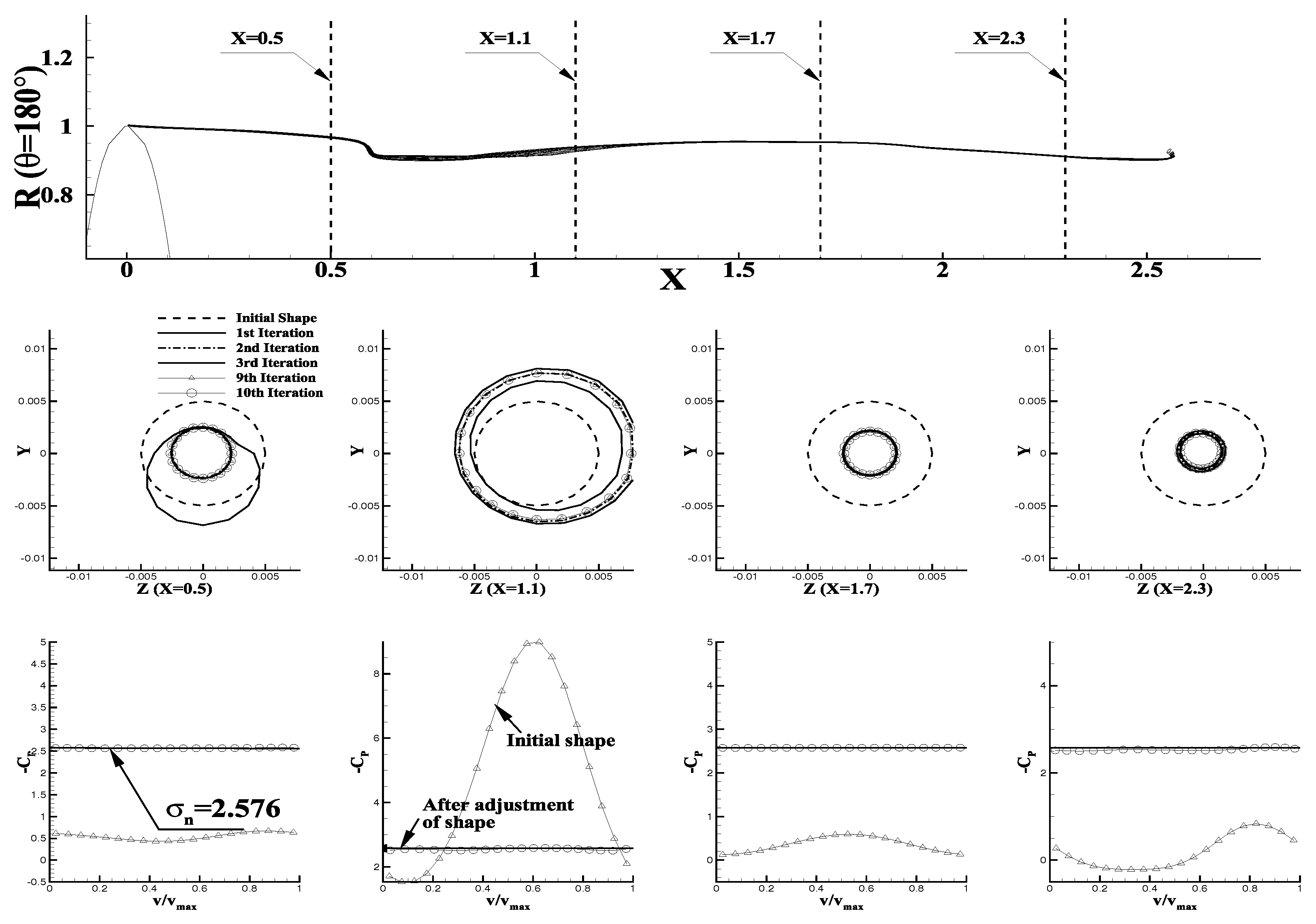
3.2. Partially Cavitating Propeller (DTMB N4148) in the Effective Wake
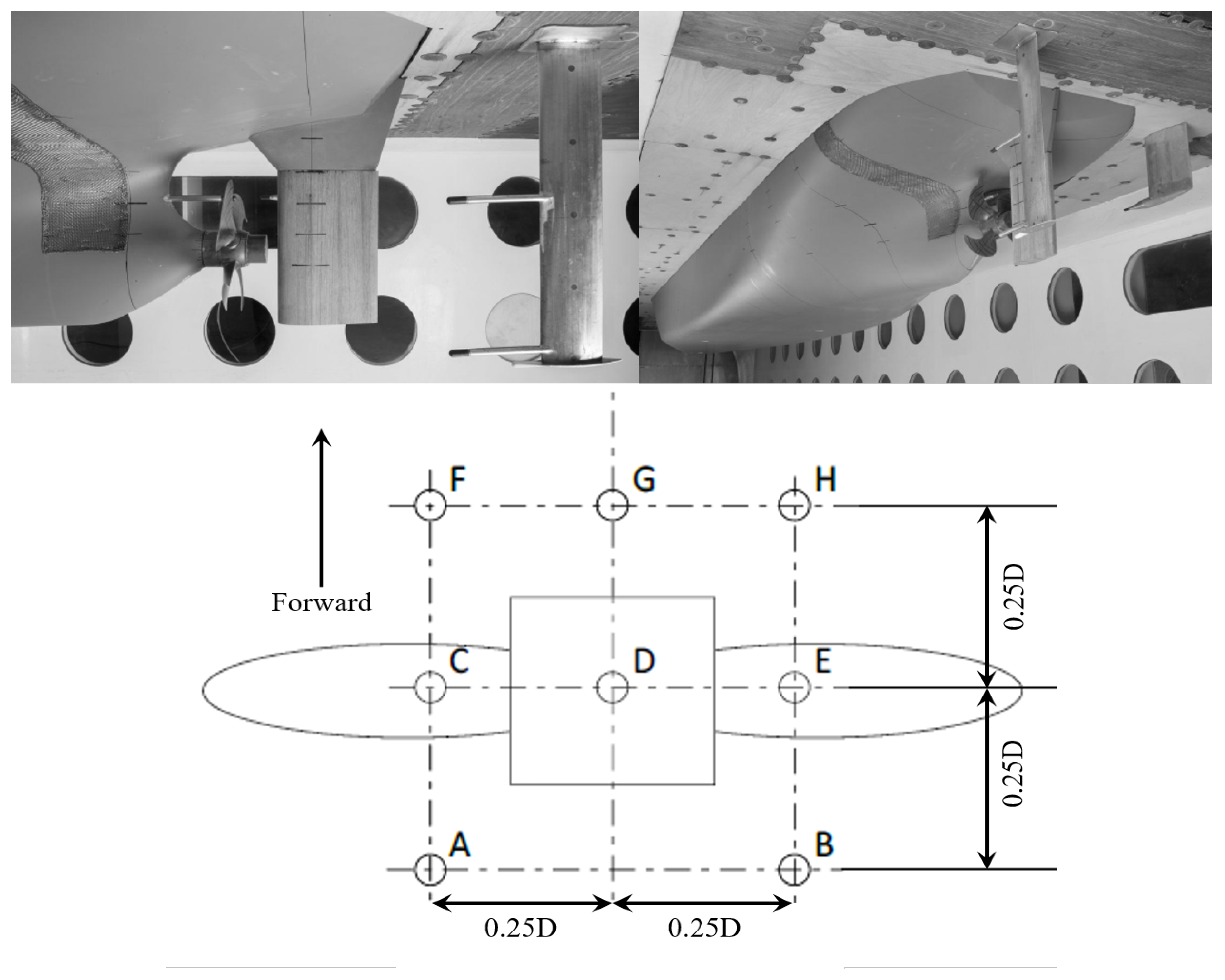
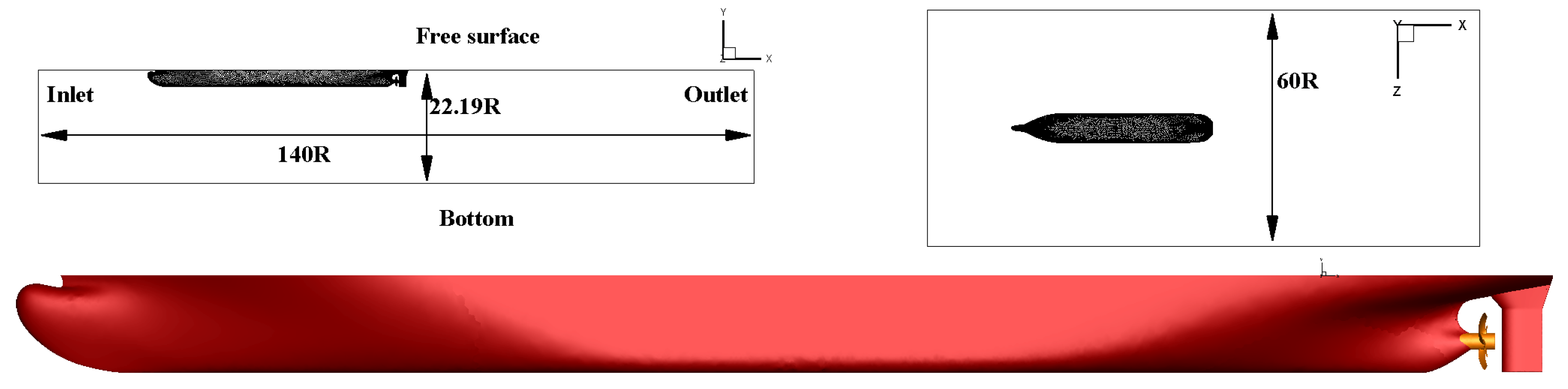
3.3. SSPA P2772 Propeller in Effective Wake Field and Hull Excitation
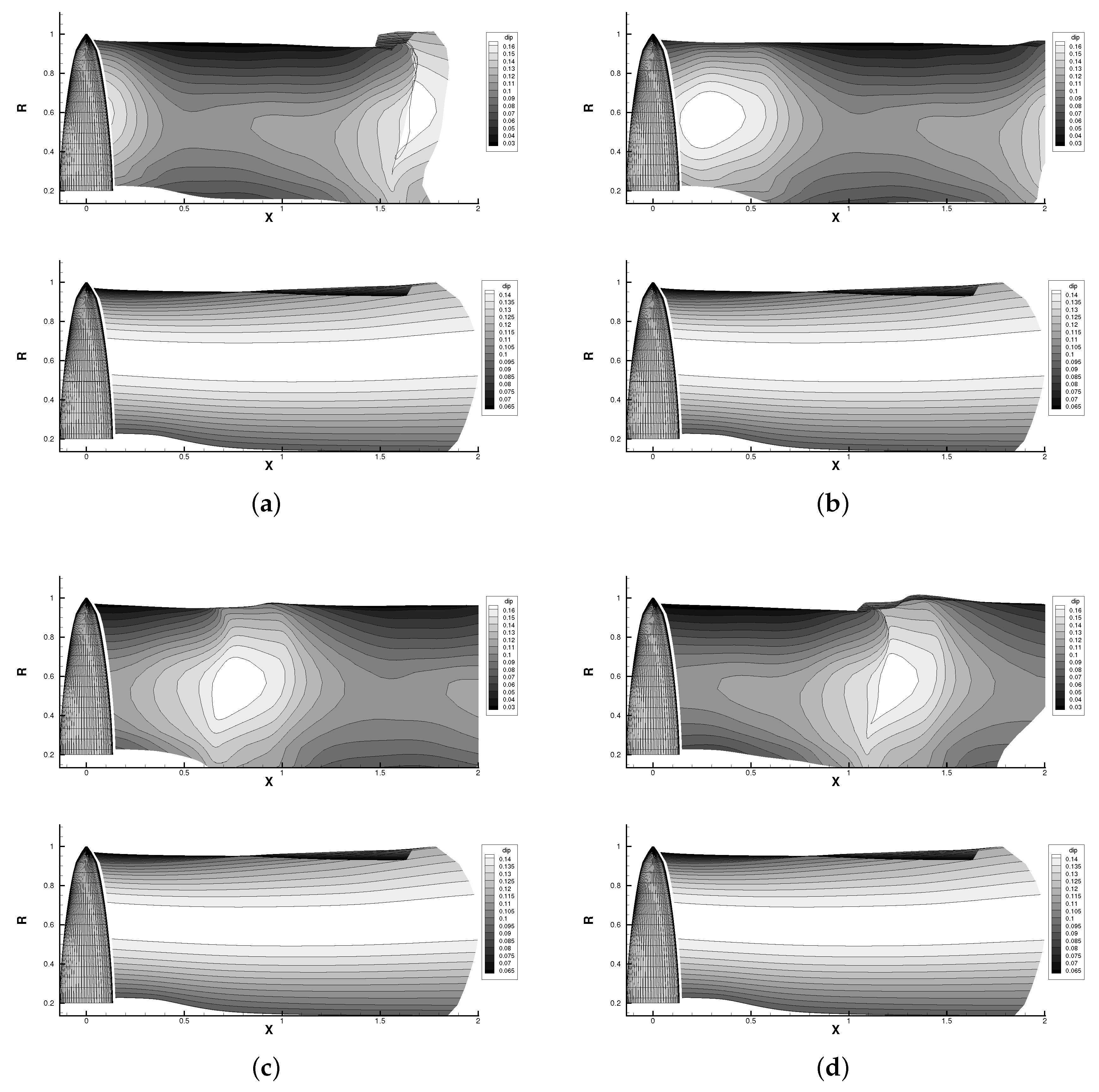
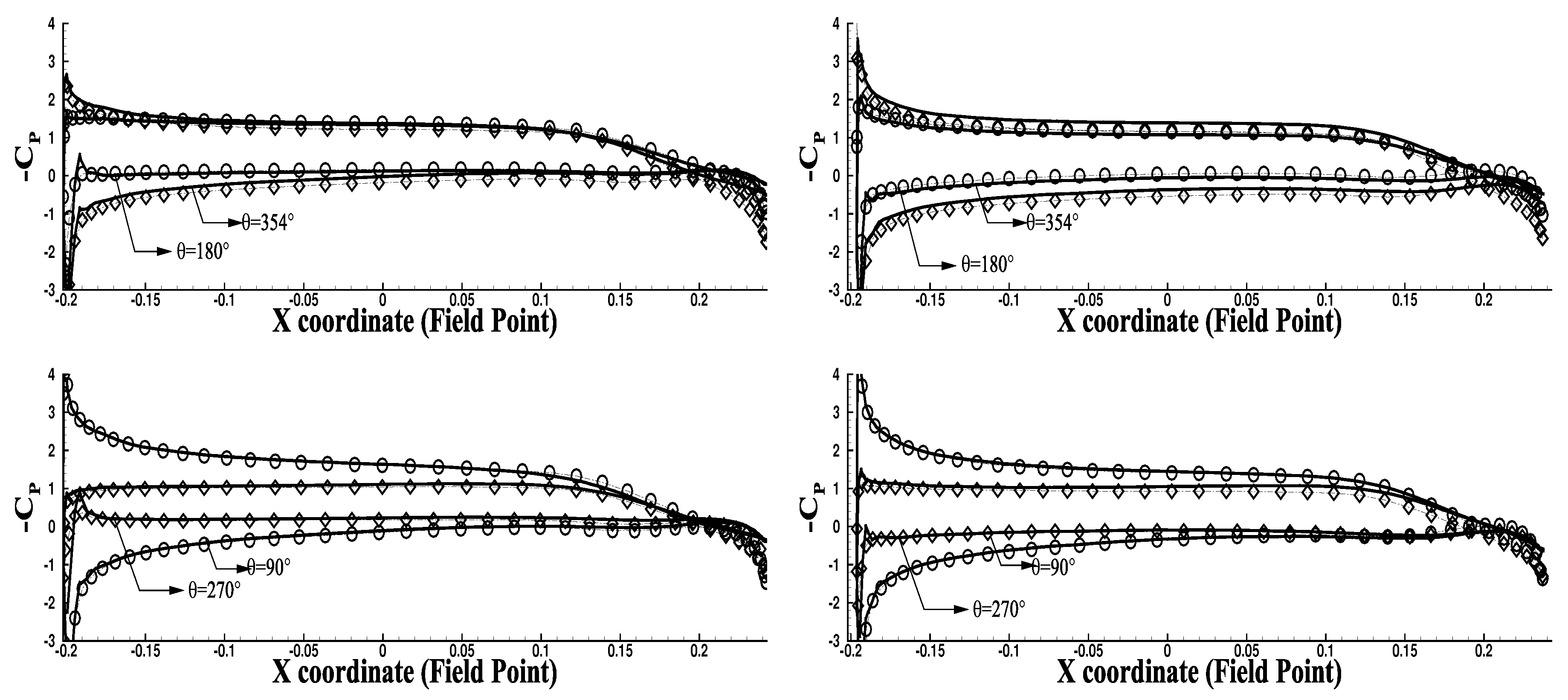
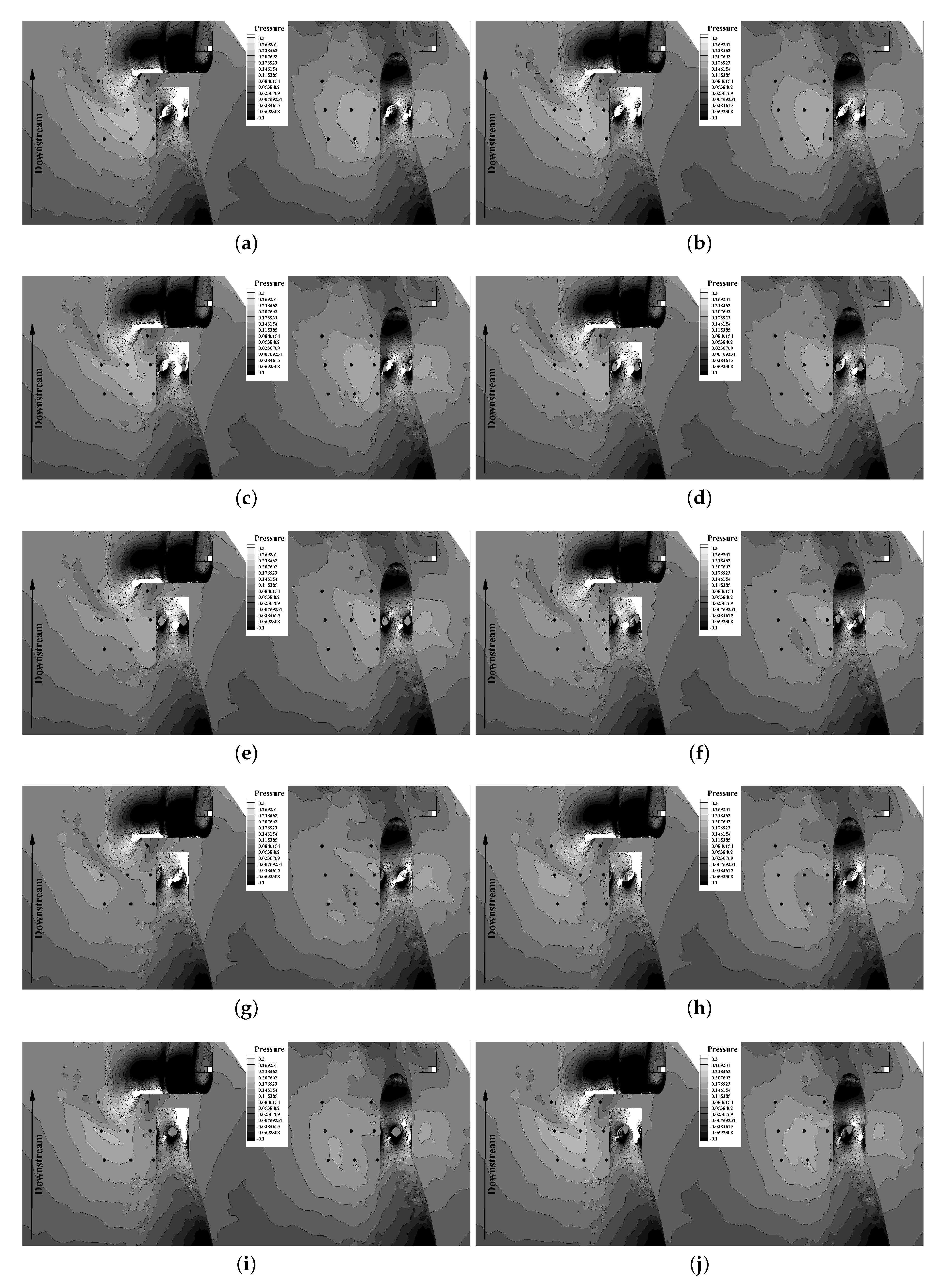
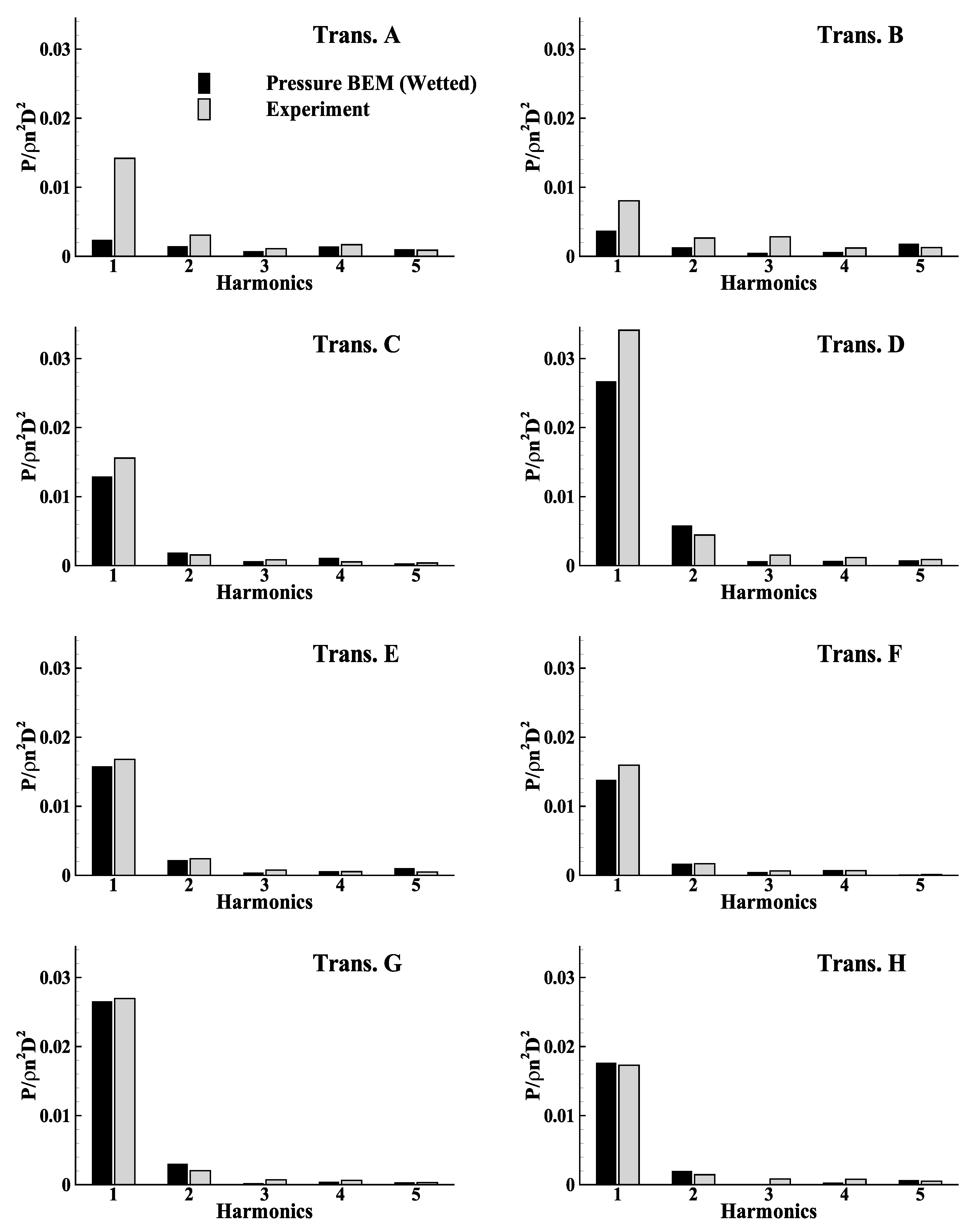
3.3.1. Fully-Wetted Condition: Effects of Rudder on the Hull Pressures
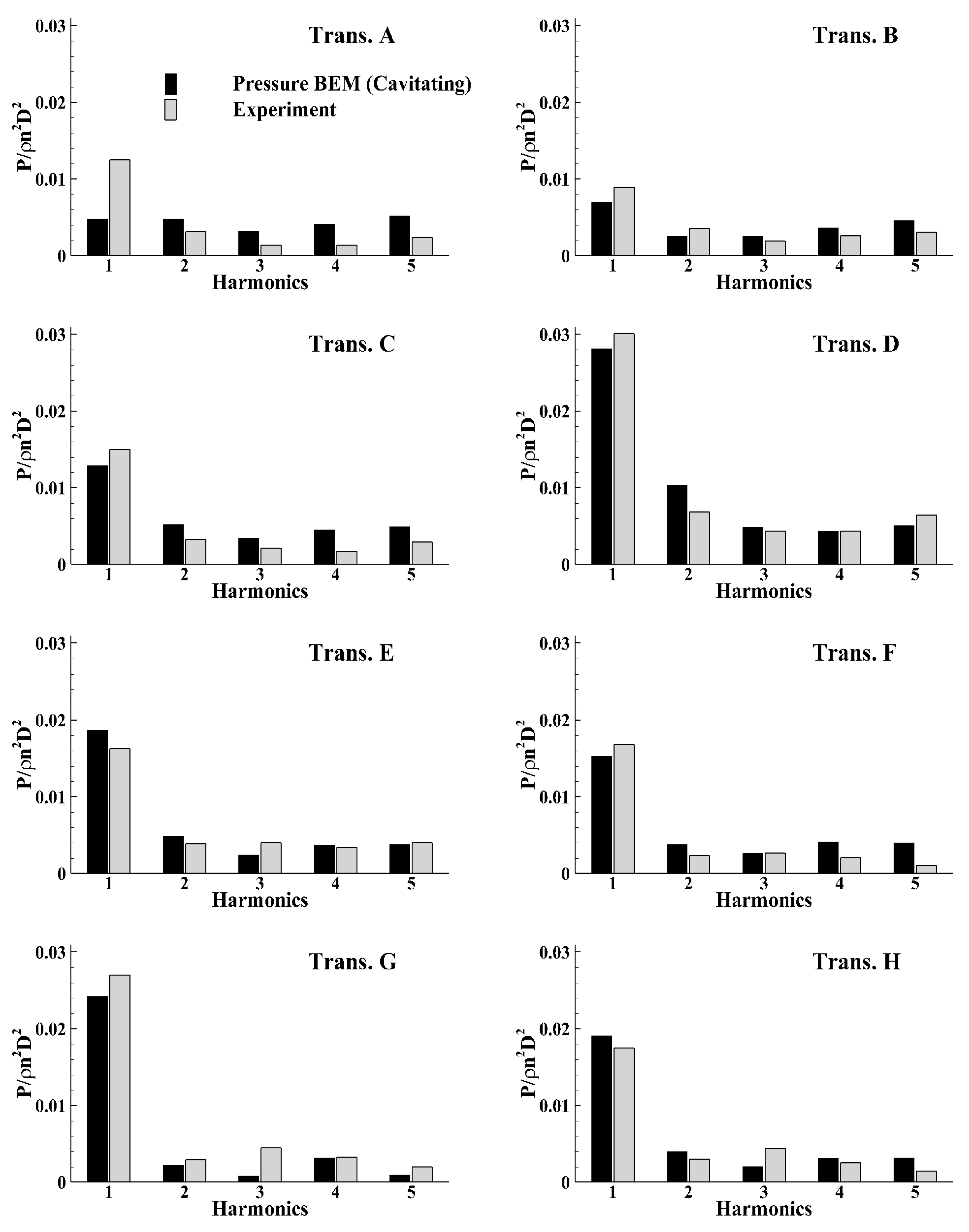
3.3.2. Cavitating Condition: Effects of Tip Vortex Cavitation on the Hull Pressures
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Breslin, J.P.; van Houten, R.J.; Kerwin, J.E.; Johnsson, C.A. Theoretical and Experimental Propeller Induced Hull Pressures Arising from Intermittent Blade Cavitation, Loading, and Thickness. Trans. Soc. Nav. Archit. Mar. Eng. 1982, 99, 111–151. [Google Scholar]
- Hallander, J.; Gustafsson, L. Aquo Model Test for M/t Olympus; Technical Report RE40116086-01-00-A; SSPA Sweden AB: Göteborg, Sweden, 2013. [Google Scholar]
- Hwang, Y.; Sun, H.; Kinnas, S.A. Prediction of Hull Pressure Fluctuations Induced by Single and Twin Propellers. In Proceedings of the Propellers/Shafting ’06 Symposium, The Society of Naval Architects & Marine Engineers (SNAME), Williamsburg, VA, USA, 12–13 September 2006. [Google Scholar]
- Bosschers, J. Propeller Tip-Vortex Cavitation and its Broadband Noise. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2018. [Google Scholar]
- Bosschers, J. A Semi-empirical Prediction Method for Broadband Hull Pressure Fluctuations and Underwater Radiated Noise by Propeller Tip Vortex Cavitation. J. Mar. Sci. Eng. 2018, 6, 49. [Google Scholar] [CrossRef] [Green Version]
- Göttsche, U.; Lampe, T.; Scharf, M.; Abdel-Maksoud, M. Evaluation of Underwater Sound Propagation of a Catamaran with Cavitating Propellers. In Proceedings of the 6th International Symposium on Marine Propulsors (SMP’19), Rome, Italy, 26–30 May 2019. [Google Scholar]
- Tani, G.; Viviani, M.; Felli, M.; Lafeber, F.H.; Lloyd, T.; Aktas, B.; Atlar, M.; Seol, H.; Hallander, J.; Sakamoto, N.; et al. Round Robin Test on Radiated Noise of a Cavitating Propeller. In Proceedings of the 6th International Symposium on Marine Propulsors (SMP’19), Rome, Italy, 26–30 May 2019. [Google Scholar]
- Gosda, R.; Berger, S.; Abdel-Maksoud, M. Investigation of Reynolds Number Scale Effects on Propeller Tip Vortex Cavitation and Propeller-Induced Hull Pressure Fluctuations. In Proceedings of the 10th International Symposium on Cavitation (CAV2018), Baltimore, MD, USA, 14–16 May 2018. [Google Scholar]
- Su, Y.; Kim, S.; Du, W.; Kinnas, S.A.; Grekula, M.; Hallander, J.; Li, Q. Prediction of the Propeller-induced Hull Pressure Fluctuation via a Potential-based Method: Study of the Rudder Effect and the Effect from Different Wake Alignment Methods. In Proceedings of the 5th International Symposium on Marine Propulsors (SMP’17), Espoo, Finland, 12–15 June 2017. [Google Scholar]
- Kim, S.; Su, Y.; Kinnas, S.A. Prediction of the Propeller-induced Hull Pressure Fluctuation via a Potential-based Method: Study of the Influence of Cavitation and Different Wake Alignment Schemes. In Proceedings of the 10th International Symposium on Cavitation (CAV2018), Baltimore, MD, USA, 14–16 May 2018. [Google Scholar]
- Kim, S.; Du, W.; Kinnas, S.A. PROPCAV (Version R2019) User’s Manual; Ocean Engineering Report 18-2; Ocean Engineering Group, UT Austin: Austin, TX, USA, 2019. [Google Scholar]
- Kim, S.; Kinnas, S.A. Prediction of Unsteady Developed Tip Vortex Cavitation and its Effect on the Induced Hull Pressures. In Proceedings of the 6th International Symposium on Marine Propulsors (SMP’19), Rome, Italy, 26–30 May 2019. [Google Scholar]
- Kim, S. An Improved Full Wake Alignment Scheme for the Prediction of Open/ducted Propeller Performance in steady and Unsteady Flow. Master’s Thesis, Ocean Engineering Group, The University of Texas at Austin, Austin, TX, USA, 2017. [Google Scholar]
- Greely, D.S.; Kerwin, J.E. Numerical Methods for Propeller Design and Analysis in Steady flow. Trans. Soc. Nav. Archit. Mar. Eng. 1982, 90, 415–453. [Google Scholar]
- Kinnas, S.A.; Fan, H.; Tian, Y. A Panel Method with a Full Wake Alignment Model for the Prediction of the Performance of Ducted Propellers. J. Ship Res. 2015, 59, 246–257. [Google Scholar] [CrossRef]
- Su, Y.; Kinnas, S.A. A Time-Accurate BEM/RANS Interactive Method for Predicting Propeller Performance Considering Unsteady Hull/Propeller/Rudder Interaction. In Proceedings of the 32nd Symposium on Naval Hydrodynamics, Hamburg, Germany, 5–10 August 2018. [Google Scholar]
- Lee, H.; Kinnas, S.A. Application of BEM in the Prediction of Unsteady Blade Sheet and Developed Tip Vortex Cavitation on Marine Propellers. J. Ship Res. 2004, 48, 15–30. [Google Scholar]
- Su, Y.; Kim, S.; Kinnas, S.A. Prediction of Propeller-induced Hull Pressure Fluctuations via a Potential-based Method: Study of the Effect of Different Wake Alignment Methods and of the Rudder. J. Mar. Sci. Eng. 2018, 6, 52. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Kinnas, S.A. A Wake Model for the Prediction of Propeller Performance at Low Advance Ratio. Int. J. Rotating Mach. 2012, 2012, 372364. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Kinnas, S.A.; Du, W. Panel Method for Ducted Propellers with Sharp Trailing Edge Duct with Fully Aligned Wake on Blade and Duct. J. Mar. Sci. Eng. 2018, 6, 89. [Google Scholar] [CrossRef] [Green Version]
- Lee, H. Modeling of Unsteady Wake Alignment and Developed Tip Vortex Cavitation. Ph.D. Thesis, Ocean Engineering Group, The University of Texas at Austin, Austin, TX, USA, 2002. [Google Scholar]
- Kinnas, S.A.; Fine, N.E. A Numerical Nonlinear Analysis of the Flow Around 2-D and 3-D Partially Cavitating Hydrofoils. J. Fluid Mech. 1993, 254, 151–181. [Google Scholar] [CrossRef]
- Kinnas, S.A. A Note on the Bernoulli Equation for Propeller Flows: The Effective Pressure. J. Ship Res. 2006, 54, 355–359. [Google Scholar]
- Arndt, R.; Arakeri, V.; Higuchi, H. Some Observations of Tip-vortex Cavitation. J. Fluid Mech. 1991, 229, 269–289. [Google Scholar] [CrossRef]
- Choi, J.; Kinnas, S.A. An Unsteady Three-dimensional Euler Solver Coupled with a Cavitating Propeller Analysis Method. In Proceedings of the 23rd Symposium on Naval Hydrodynamics, Val de Reuil, France, 17–22 September 2000. [Google Scholar]
- Boswell, R.; Jessup, S.; Kim, K.; Dahmer, D. Single Blade Loads on Propellers in Inclined and Axial Flows; Technical Report DTNSRDC-84/084; David W. Taylor Naval Ship Research and Development Center: Bethesda, MD, USA, 1984.
- Kerwin, J.E.; Lee, C. Prediction of Steady and Unsteady Marine Propeller Performance by Numerical Lifting-Surface Theory. Trans. Soc. Nav. Archit. Mar. Eng. 1978, 86, 218–256. [Google Scholar]
- Mishima, S.; Kinnnas, S.A.; Egnor, D. The CAvitating PRopeller EXperiment (CAPREX), Phases I & II; Technical Report; Department of Ocean Engineering, MIT: Cambridge, MA, USA, 1995. [Google Scholar]
- Choi, J.; Kinnas, S.A. A 3-D Euler Solver and Its Application on the Analysis of Cavitating Propellers. In Proceedings of the 25th ATTC American Towing Tank Conference, Iowa City, IA, USA, 24–25 September 1998. [Google Scholar]
- He, L.; Kinnas, S.A. Numerical Simulation of Unsteady Propeller/rudder Interaction. Int. J. Nav. Archit. Mar. Eng. 2017, 9, 677–692. [Google Scholar]
- Kim, S.; Kinnas, S.A. Prediction of Performance of Tip Loaded Propeller and Its Induced Pressures on the Hull (under review). In Proceedings of the ASME 39th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Fort Lauderdale, FL, USA, 28 June–3 July 2020. [Google Scholar]
| 1. | Note that this criterion, due to its simplicity, might allow the tip vortex cavity radius to become less than , but not smaller than . |



















| Subsection | Propeller Geometry | Wake Field | UWA | Tip Vortex Cavitation Model | Pressure-BEM |
|---|---|---|---|---|---|
| Section 3.1 | DTMB 1 4661 | 10° inclined uniform flow | ◯ | × | × |
| Section 3.2 | DTMB N4148 | effective wake from [25] | ◯ | ◯ | × |
| Section 3.3 | SSPA P2772 [2] | effective wake from BEM/RANS coupling method | ◯ | ◯ | ◯ |
| Advance Ratio | Propeller Diameter D | Water Density (kg/m3) | Ship Speed (m/s) |
|---|---|---|---|
| 0.7758 | 2.0 | 1.0 | 1.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Kinnas, S.A. Prediction of Unsteady Developed Tip Vortex Cavitation and Its Effect on the Induced Hull Pressures. J. Mar. Sci. Eng. 2020, 8, 114. https://doi.org/10.3390/jmse8020114
Kim S, Kinnas SA. Prediction of Unsteady Developed Tip Vortex Cavitation and Its Effect on the Induced Hull Pressures. Journal of Marine Science and Engineering. 2020; 8(2):114. https://doi.org/10.3390/jmse8020114
Chicago/Turabian StyleKim, Seungnam, and Spyros A. Kinnas. 2020. "Prediction of Unsteady Developed Tip Vortex Cavitation and Its Effect on the Induced Hull Pressures" Journal of Marine Science and Engineering 8, no. 2: 114. https://doi.org/10.3390/jmse8020114






