Fröhlich Condensate: Emergence of Synergetic Dissipative Structures in Information Processing Biological and Condensed Matter Systems
Abstract
:1. Introduction
“... under appropriate conditions a phenomenon quite similar to a Bose condensation may occur in substances which possess longitudinal electric modes. If energy is fed into these modes and thence transferred to other degrees of freedom of the substance, then a stationary state will be reached in which the energy content of the electric modes is larger than in the thermal equilibrium. This excess energy is found to be channelled into a single mode—exactly as in Bose condensation—provided the energy supply exceeds a critical value. Under these circumstances a random supply of energy is thus not completely thermalized but partly used in maintaining a coherent electric wave in the substance." [1]
2. Biology, Physics and Fröhlich Condensate
3. Complex Behaviour in Open Boson Systems
- A first case was evidenced by Herbert Fröhlich who considered, as already noticed, the many boson system consisting of polar vibration (LO-phonons) in bio-polymers under dark excitation (metabolic energy pumping) and embedded in a surrounding fluid [1,2,3,4,7,46]. From a Science, Technology and Innovation (STI) point of view, it was considered to have implications in medical diagnosis [9]. More recently it has been considered to be related to brain functioning and artificial intelligence [47]
- A third one is that of excitons (electron-hole pairs in semiconductors) interacting with the lattice vibrations and under the action of RF-electromagnetic fields; on an STI aspect, the phenomenon has been considered for allowing a possible exciton-laser in the THz frequency range called “Excitoner” [18,19];
- A fourth one is the case of magnons [50,51], where the thermal bath is constituted by the phonon system, with which a nonlinear interaction exists, and the magnons are driven arbitrarily out of equilibrium by a source of electromagnetic radio frequency [52]. Technological applications are related to the construction of sources of coherent microwave radiation [53,54].
- 5. A fifth one consists in a system of longitudinal acoustic phonons driven away from equilibrium by means of drifting electron excitation (presence of an electric field producing an electron current), which has been related to the creation of the so-called Saser, an acoustic laser device, with applications in computing and imaging [45,55];
4. Non-Equilibrium Thermodynamic Theory of Fröhlich Condensate
 (say 300 K). A source continuously pumps energy on the polar modes driving them out of equilibrium.
(say 300 K). A source continuously pumps energy on the polar modes driving them out of equilibrium.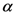 -helix structure in a protein and a rough description of the proposed mechanical model (reproduced from [7]).
-helix structure in a protein and a rough description of the proposed mechanical model (reproduced from [7]).
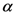 -helix structure in a protein and a rough description of the proposed mechanical model (reproduced from [7]).
-helix structure in a protein and a rough description of the proposed mechanical model (reproduced from [7]). 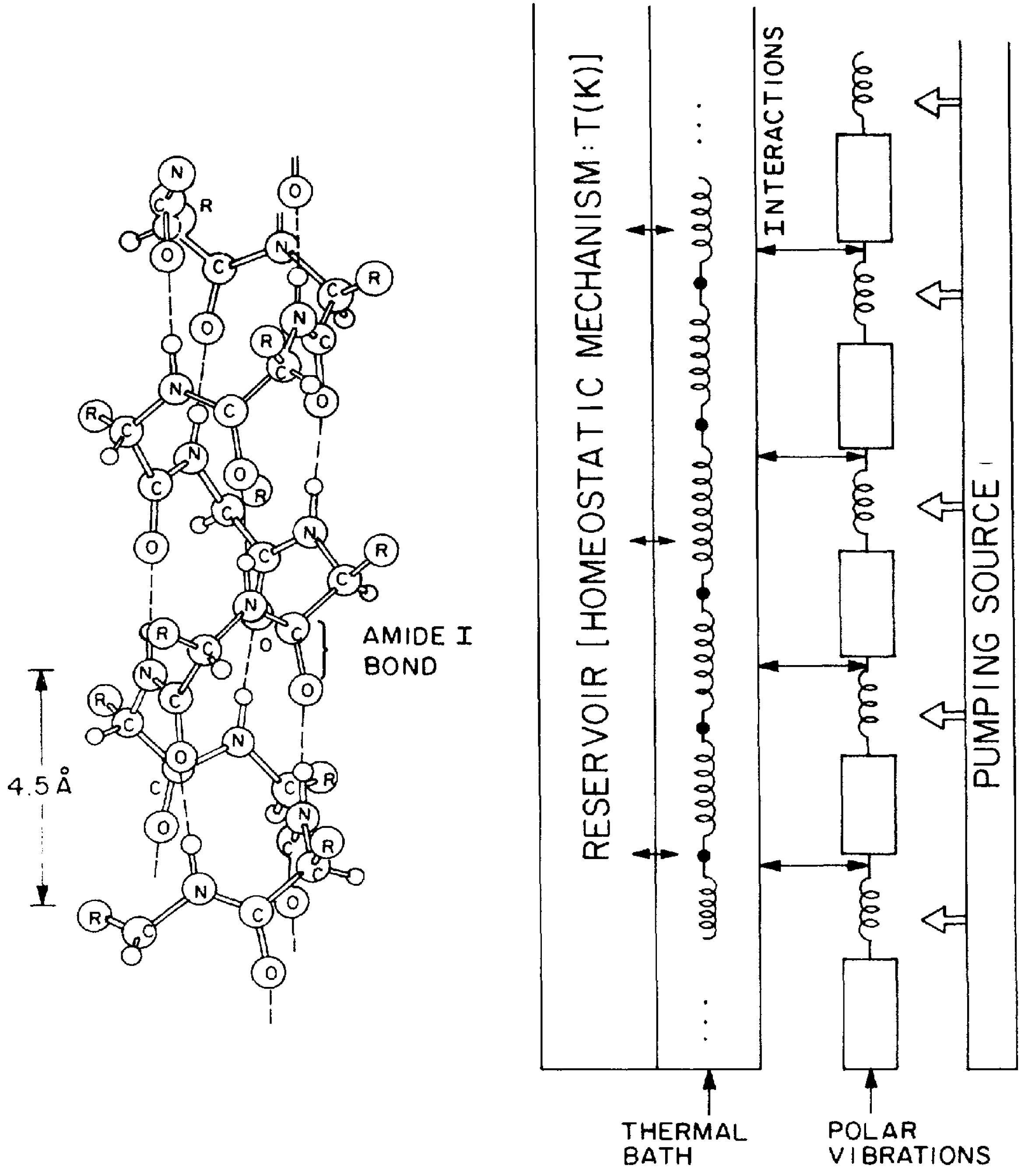
 being their frequency dispersion relation (
being their frequency dispersion relation (  is a wave-vector running over the reciprocal-space Brillouin zone), and that of the thermal bath composed by oscillations with frequency dispersion relation
is a wave-vector running over the reciprocal-space Brillouin zone), and that of the thermal bath composed by oscillations with frequency dispersion relation  , with a Debye cut-off frequency
, with a Debye cut-off frequency  . The system of polar vibrations is in interaction with an external source (that pumps energy on the system) and an anharmonic interaction is present between both systems. The latter is composed of several contributions associated with quasi-particle (phonons) collisions involving the system and the thermal bath.
. The system of polar vibrations is in interaction with an external source (that pumps energy on the system) and an anharmonic interaction is present between both systems. The latter is composed of several contributions associated with quasi-particle (phonons) collisions involving the system and the thermal bath.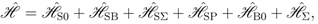

 (
(  and
and 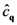 are annihilation and creation operators in that states);
are annihilation and creation operators in that states);

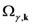 ,
,  and
and 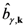 , where
, where 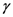 labels an eventual branch and
labels an eventual branch and 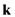 the mode);
the mode);

 stands for the interaction potential of the quasi-particles with the pumping source, which drives them out of equilibrium.
stands for the interaction potential of the quasi-particles with the pumping source, which drives them out of equilibrium. stands for the Hamiltonian of all the other degrees of freedom of the sample, and
stands for the Hamiltonian of all the other degrees of freedom of the sample, and  for the interaction potential of the system of quasi-particles and these other degrees of freedom.
for the interaction potential of the system of quasi-particles and these other degrees of freedom.
 . Here,
. Here,  is called the population operator and
is called the population operator and 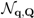 (
(  ) is the Fourier transform of the spatial change in the populations.
) is the Fourier transform of the spatial change in the populations.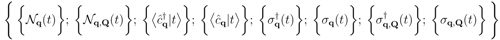

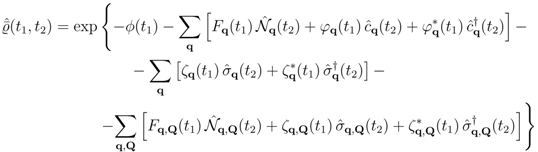
 indicating the time evolution of the non-equilibrium thermodynamic variables
indicating the time evolution of the non-equilibrium thermodynamic variables
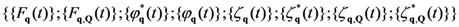
 , and
, and 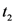 that of the microdynamical variables,
that of the microdynamical variables,  ), etc. Moreover,
), etc. Moreover, 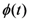 ensures the normalization of the statistical distribution, playing the role of a logarithm of a non-equilibrium partition function, say
ensures the normalization of the statistical distribution, playing the role of a logarithm of a non-equilibrium partition function, say  . The second term in the exponential in Equation (7) accounts for historicity and irreversibility, where
. The second term in the exponential in Equation (7) accounts for historicity and irreversibility, where  is a positive infinitesimal that goes to
is a positive infinitesimal that goes to  after the trace operation in the calculation of averages has been performed (introducing a Bogoliubov quasi-average that breaks the time reversal symmetry in Liouville equation [82,83] in a way according to Krylov’s “jolting” proposal for irreversibility [84,85]).
after the trace operation in the calculation of averages has been performed (introducing a Bogoliubov quasi-average that breaks the time reversal symmetry in Liouville equation [82,83] in a way according to Krylov’s “jolting” proposal for irreversibility [84,85]).
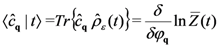
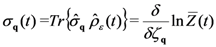
 . From now on we disregard the contributions of the coherent states and of the states of pairs—that is, we set
. From now on we disregard the contributions of the coherent states and of the states of pairs—that is, we set 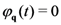 and
and 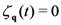 in Equation (8)—and, since we shall be dealing with experiments without resolution in space, the contributions accounting for local effects,
in Equation (8)—and, since we shall be dealing with experiments without resolution in space, the contributions accounting for local effects,  , are also discarded. We retain only
, are also discarded. We retain only  for which the state equation is verified, i.e., its relation to the associated non-equilibrium thermodynamic variable
for which the state equation is verified, i.e., its relation to the associated non-equilibrium thermodynamic variable  ,
,

 can be redefined as
can be redefined as

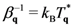 as done in semiconductor physics for “hot” carriers and phonons [86,87], and in other contexts (see for example [88,89]) as done by Casimir, Uhlenbeck and others (see [65,75,76,77]). On the other hand, it can be written
as done in semiconductor physics for “hot” carriers and phonons [86,87], and in other contexts (see for example [88,89]) as done by Casimir, Uhlenbeck and others (see [65,75,76,77]). On the other hand, it can be written
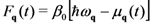
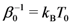 .
. shall show the “condensation” of the quasi-particles (excitations) in the states lowest in energy, thus characterizing the non-equilibrium Bose-Einstein condensation. We proceed to the derivation of its evolution equation. This is done in terms of NESEF-based nonlinear quantum kinetic theory [62,63,64,65,66,67,68], in the approximation that retains the contributions up to the second order in the interaction strengths (binary collisions with memory and vertex renormalization being discarded) [64,66,68]. We recall that the evolution equations consist of the quantum mechanical Heisenberg equations of motion of the corresponding microvariables, here
shall show the “condensation” of the quasi-particles (excitations) in the states lowest in energy, thus characterizing the non-equilibrium Bose-Einstein condensation. We proceed to the derivation of its evolution equation. This is done in terms of NESEF-based nonlinear quantum kinetic theory [62,63,64,65,66,67,68], in the approximation that retains the contributions up to the second order in the interaction strengths (binary collisions with memory and vertex renormalization being discarded) [64,66,68]. We recall that the evolution equations consist of the quantum mechanical Heisenberg equations of motion of the corresponding microvariables, here  , averaged over the non-equilibrium ensemble.
, averaged over the non-equilibrium ensemble.
standing for the rate of population enhancement due to the action of the pumping source, which involves a positive feedback process that largely improves the efficiency of the pumping source;
is the contribution arising out of the first term on the right of the interaction of the quasi-particles and the bath in Equation (4);
is the rate of change arising out of the second term in
of Equation (4), the Livshits contribution;
is the rate of change due to the third term in
of Equation (4), the Fröhlich one, which contains linear and bi-linear contributions in the quasi-particle populations (for simplicity we have omitted to make explicit the dependence on
in the populations
on the right):
wherebeingthe population (
branch,
mode) of the bosons of the thermal bath and
indicating the intensity of the interaction of the quasi-particles with the thermal bath.
 behaves like a “pumping source” for the modes
behaves like a “pumping source” for the modes  for which
for which  , populating the states of lower frequency (energy) at the expenses of those higher in frequency. On the other hand, for those modes
, populating the states of lower frequency (energy) at the expenses of those higher in frequency. On the other hand, for those modes  with
with  , the Fröhlich contribution transfer the excess energy of the states higher in frequency received from the external source to those lower in frequency. Moreover,
, the Fröhlich contribution transfer the excess energy of the states higher in frequency received from the external source to those lower in frequency. Moreover,  accounts for the rate of change associated to radiative decay (emission of photons from excited states).
accounts for the rate of change associated to radiative decay (emission of photons from excited states). , i.e., above the threshold for the onset of Fröhlich’s effect as described in [7], and also in [46]. For comparison, we have drawn the case (diamond-line) when the nonlinear coupling is switched off and a normal behaviour of similar increase is clearly observed in all the populations.
, i.e., above the threshold for the onset of Fröhlich’s effect as described in [7], and also in [46]. For comparison, we have drawn the case (diamond-line) when the nonlinear coupling is switched off and a normal behaviour of similar increase is clearly observed in all the populations. , compared with the case of absence of nonlinear interactions.
, compared with the case of absence of nonlinear interactions.  when nonlinear interaction of Equation (15) is present and
when nonlinear interaction of Equation (15) is present and  when neglected (reproduced from [7]).
when neglected (reproduced from [7]).
 , compared with the case of absence of nonlinear interactions.
, compared with the case of absence of nonlinear interactions.  when nonlinear interaction of Equation (15) is present and
when nonlinear interaction of Equation (15) is present and  when neglected (reproduced from [7]).
when neglected (reproduced from [7]). 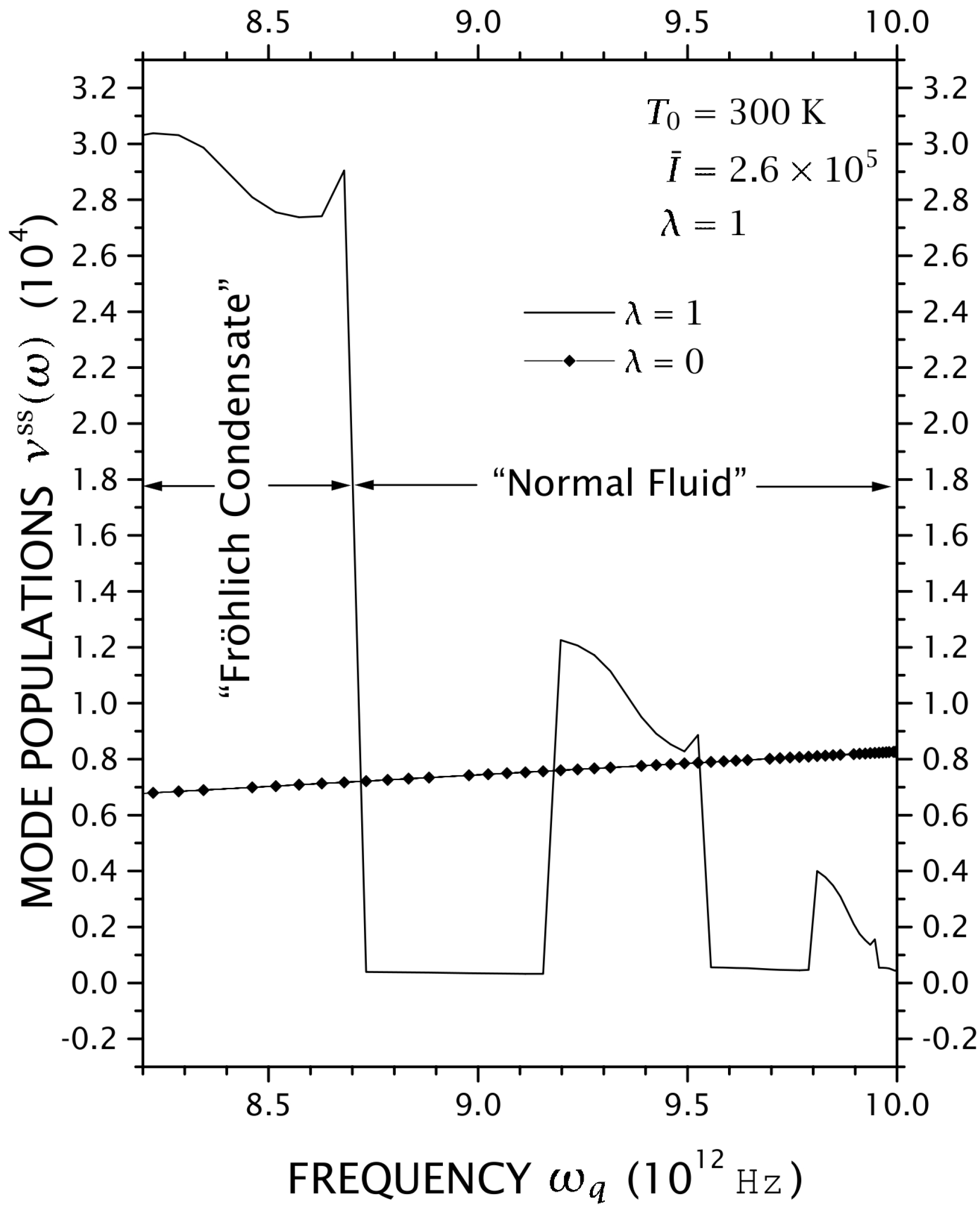
5. Concluding Remarks
References
- Fröhlich, H. Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 1968, 2, 641–649. [Google Scholar] [CrossRef]
- Fröhlich, H. Quantum mechanical concepts in biology. In From Theoretical Physics to Biology; Marois, M., Ed.; North-Holland: Amsterdam, the Netherlands, 1969; pp. 13–22. [Google Scholar]
- Fröhlich, H. Long range coherence and the action of enzymes. Nature 1970. [Google Scholar]
- Fröhlich, H. The biological effects of microwaves and related questions. In Advances in Electronics and Electron Physics; Academic Press: New York, NY, USA, 1980; Volume 17. [Google Scholar]
- Prigogine, I. Structure, dissipation, and life. In From Theoretical Physics to Biology; Marois, M., Ed.; North Holland: Amsterdam, the Netherlands, 1969. [Google Scholar]
- Fröhlich, F. Notes and articles in honor of Herbert Fröhlich. In Cooperative Phenomena; Haken, H., Wagner, M., Eds.; Springer: Berlin, Germany, 1973. [Google Scholar]
- Mesquita, M.V.; Vasconcellos, A.R.; Luzzi, R. Selective amplification of coherent polar vibrations in biopolymers. Phys. Rev. E 1993, 48, 4049–4059. [Google Scholar] [CrossRef]
- Mascarenhas, S. Bioelectrets: Electrets in biomaterials and biopolymers. In Electrets; Sessler, G.M., Ed.; Springer: Berlin, Germany, 1987. [Google Scholar]
- Hyland, G.J. Coherent GHz and THz excitations in active biosystems, and their implications. In The Future of Medical Diagnostics? Proceeding of Matra Marconi UK, Directorate of Science, Internal Report, Portsmouth, UK, 25 June 1998; pp. 14–27.
- Miller, P.F.; Gebbie, H.A. Laboratory millimeter wave measurements of atmospheric aerosols. Int. J. Infrared Milli. 1996, 17, 1573–1591. [Google Scholar] [CrossRef]
- Davydov, A.S. Biology and Quantum Mechanics; Pergamon: Oxford, UK, 1982. [Google Scholar]
- Scott, A.C. Davydov’s soliton. Phys. Rep. 1992, 217, 1–67. [Google Scholar] [CrossRef]
- Vasconcellos, A.R.; Luzzi, R. Vanishing thermal damping of Davydov’s solitons. Phys. Rev. E 1993, 48, 2246–2249. [Google Scholar] [CrossRef]
- Lu, J.; Greenleaf, J.F. Nondiffracting X-waves. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 1992, 39, 19–31. [Google Scholar] [CrossRef]
- Lu, J.; Greenleaf, J.F. Experimental verification of nondiffracting X waves. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 1992, 39, 441–446. [Google Scholar]
- Mesquita, M.V.; Vasconcellos, A.R.; Luzzi, R. Solitons in highly excited matter: Dissipative-thermodynamic and supersonic effects. Phys. Rev. E 1998, 58, 7913–7923. [Google Scholar] [CrossRef]
- Snoke, D. Coherent exciton waves. Science 1996, 273, 1351–1352. [Google Scholar] [CrossRef]
- Mysyrowicz, A.; Benson, E.; Fortin, E. Directed beams of excitons produced by stimulated scattering. Phys. Rev. Lett. 1996, 77, 896–899. [Google Scholar] [CrossRef]
- Vasconcellos, A.R.; Mesquita, M.V.; Luzzi, R. "Excitoner”: Stimulated amplification and propagation of excitons beams. Europhys. Lett. 2000, 49, 637–634. [Google Scholar] [CrossRef]
- Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell; Cambridge University: London, UK, 1944. [Google Scholar]
- Mascarenhas, S. What is biophysics? In MacMillan Encyclopaedia of Physics; Rigden, J.S., Ed.; Simon & Schuster Macmillan: New York, NY, USA, 1996. [Google Scholar]
- Glanz, J. Physicists advance into biology. Science 1996, 272, 646–648. [Google Scholar] [CrossRef]
- Heisenberg, W. The end of physics? In Across the Frontiers; Anshen, R.N., Ed.; Harper and Row: New York, NY, USA, 1975. [Google Scholar]
- Prigogine, I.; Stengers, I. Order out of Chaos: Man’s New Dialogue with Nature; Bantam: New York, NY, USA, 1984. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in non-Equilibrium Systems; Wiley-Interscience: New York, NY, USA, 1977. [Google Scholar]
- Davies, P. The New Physics: A synthesis. In the New Physics; Davies, P., Ed.; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Anderson, P.W. More is different: Broken symmetry and nature of hierarchical structure of science. Science 1972, 177, 393–396. [Google Scholar]
- von Bertalanffy, L. General Systems Theory, 3rd ed; Braziller: New York, NY, USA, 1968. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability, and Fluctuations; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Fröhlich, H. The connection between macro- and micro-physics. Rivista del Nuovo Cimento 1973, 3, 490–534. [Google Scholar] [CrossRef]
- Haken, H. Synergetics; Springer: Berlin, Germany, 1978. [Google Scholar]
- Kauffman, S. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Kapitza, P. Viscosity of liquid helium below the λ-point. Nature 1938, 141, 74. [Google Scholar] [CrossRef]
- London, F. The λ-phenomenon of liquid helium and the Bose-Einstein degeneracy. Nature 1938, 141, 643–644. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Snoke, D.; Littlewood, P. Polariton condensates. Phys. Today 2010, 63, 42. [Google Scholar]
- Kasprzak, J.; Richard, M.; Kundermann, S.; Baas, A.; Jeambrun, P.; Keeling, J.M.J.; Marchetti, F.M.; Szymanska, M.H.; Andre, R.; Staehli, J.L.; Savona, V.; Littlewood, P.B.; Deveaud, B.; Dang, L.S. Bose-Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. [Google Scholar]
- Lagoudakis, K.G.; Ostatnický, T.; Kavokin, A.V.; Rubo, Y.G.; André, R.; Deveaud-Plédra, B. Observation of half-quantum vortices in an exciton-polariton condensate. Science 2009, 326, 974–976. [Google Scholar] [CrossRef]
- Rubo, Y.G. Half vortices in exciton polariton condensates. Phys. Rev. Lett. 2007, 99, 106401:1–106401:4. [Google Scholar]
- Baumberg, J.J.; Kavokin, A.V.; Christopoulos, S.; Grundy, A.J.D.; Butté, R.; Christmann, G.; Solnyshkov, D.D.; Malpuech, G.; Baldassarri Höger von Högersthal, G.; Feltin, E.; Carlin, J.F.; Grandjean, N. Spontaneous polarization buildup in a room-temperature polariton laser. Phys. Rev. Lett. 2008, 101, 136409:1–136409:4. [Google Scholar]
- Love, A.P.D.; Krizhanovskii, D.N.; Whittaker, D.M.; Bouchekioua, R.; Sanvitto, D.; Rizeiqi, S.A.; Bradley, R.; Skolnick, M.S.; Eastham, P.R.; André, R.; Dang, L.S. Intrinsic decoherence mechanisms in the microcavity polariton condensate. Phys. Rev. Lett. 2008, 101, 067404:1–067404:4. [Google Scholar]
- Baas, A.; Lagoudakis, K.G.; Richard, M.; André, R.; Dang, L.S.; Deveaud-Plédran, B. Synchronized and desynchronized phases of exciton-polariton condensates in the presence of disorder. Phys. Rev. Lett. 2008, 100, 170401:1–170401:4. [Google Scholar]
- Amo, A.; Sanvitto, D.; Laussy, F.P.; Ballarini, D.; Valle, E.D.; Martin, M.D.; Lemaitre, A.; Bloch, J.; Krizhanovskii, D.N.; Skolnick, M.S.; Tejedor, C.; Vina, L. Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 2009, 457, 291–295. [Google Scholar]
- Snoke, D. Condensed-matter physics: Coherent questions. Nature 2006, 443, 403–404. [Google Scholar] [CrossRef]
- Kent, A.J.; Kini, R.N.; Stanton, N.M.; Henini, M.; Glavin, B.A.; Kochelap, V.A.; Linnik, T.L. Acoustic phonon emission from a weakly coupled superlattice under vertical electron transport: Observation of phonon resonance. Phys. Rev. Lett. 2006, 96, 215504:1–215504:4. [Google Scholar]
- Fonseca, A.F.; Mesquita, M.V.; Vasconcellos, A.R.; Luzzi, R. Informational-statistical thermodynamics of a complex system. J. Chem. Phys. 2000, 112, 3967–3979. [Google Scholar]
- Penrose, R. Shadows of the Mind: A Search for the Missing Science of Consciousness; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Lu, J.; Hehong, Z.; Greenleaf, J.F. Biomedical ultrasound beam forming. Ultrasound Med. Biol. 1994, 20, 403–428. [Google Scholar] [CrossRef]
- Mesquita, M.V.; Vasconcellos, A.R.; Luzzi, R. Considerations on Fröhlich’s non-equilibrium Bose-Einstein-like condensation. Phys. Lett. A 1998, 238, 206–211. [Google Scholar] [CrossRef]
- Demokritov, S.O.; Demidov, V.E.; Dzyapko, O.; Melkov, G.A.; Serga, A.A.; Hillebrands, B.; Slavin, A.N. Bose-Einstein condensation of quasi-equilibrium magnons at room temperature under pumping. Nature 2006, 443, 430–433. [Google Scholar]
- Demidov, V.E.; Dzyapko, O.; Demokritov, S.O.; Melkov, G.A.; Slavin, A.N. Observation of spontaneous coherence in Bose-Einstein condensate of magnons. Phys. Rev. Lett. 2008, 100, 047205:1–047205:4. [Google Scholar]
- Vannucchi, F.S.; Vasconcellos, A.R.; Luzzi, R. Nonequilibrium Bose-Einstein condensation of hot magnons. Phys. Rev. B 2009, 82, 140404:1–140404:4. [Google Scholar]
- Dzyapko, O.; Demidov, V.E.; Demokritov, S.O.; Melkov, G.A.; Safonov, V.L. Monochromatic microwave radiation from the system of strongly excited magnons. Appl. Phys. Lett. 2008, 92, 162510:1–162510:3. [Google Scholar]
- Ma, F.S.; Lim, H.S.; Wang, Z.K.; Piramanayagam, S.N.; Ng, S.C.; Kuok, M.H. Micromagnetic study of spin wave propagation in bicomponent magnonic component crystal waveguides. Appl. Phys. Lett. 2011, 98, 153107:1–153107:3. [Google Scholar]
- Rodrigues, C.G.; Vasconcellos, A.R.; Luzzi, R. Drifting electron excitation of acoustic phonons. J. Appl. Phys. 2012. Submitted for publication. [Google Scholar]
- Rodrigues, C.G.; Vasconcellos, A.R.; Luzzi, R. Evolution kinetics of nonequilibrium longitudinal-optical phonons generated by drifting electrons in III-nitrides: longitudinal-optical-phonon resonance. J. Appl. Phys. 2010, 108, 033716:1–033716:14. [Google Scholar]
- Komirenko, S.M.; Kim, K.W.; Demidenko, A.A.; Kochelapand, V.A.; Stroscio, M.A. Cerenkov generation of high-frequency confined acoustic phonons in quantum wells. Appl. Phys. Lett. 2000, 76, 126195:1–126195:3. [Google Scholar]
- Bandyopathyay, A. Ultrafast microtubule growth through radio-frequency-induced resonant excitation of tubulin and small molecule drugs. Private communication, 2012. [Google Scholar]
- Zubarev, D.N. Non-equilibrium Statistical Thermodynamics; Consultants Bureau: New York, NY, USA, 1974. [Google Scholar]
- Zubarev, D.N.; Morozov, V.; Röpke, G. Statistical Mechanics of non-Equilibrium Processes: Basic Concepts, Kinetic Theory; Akademie Verlag-Wiley VCH: Berlin, Germany, 1996; Volume 1. [Google Scholar]
- Kuzemsky, A.L. Statistical mechanics and the physics of many-particle model systems. Phys. Part. Nucl. 2009, 40, 949–997. [Google Scholar] [CrossRef]
- Akhiezer, A.; Peletminskii, S. Methods of Statistical Physics; Pergamon: Oxford, UK, 1981. [Google Scholar]
- McLennan, J.A. Statistical theory of transport processes. In Advances in Chemical Physics; Academic Press: New York, NY, USA, 1963; Volume 5, pp. 261–317. [Google Scholar]
- Vannucchi, F.S.; Vasconcellos, A.R.; Luzzi, R. Thermo-statistical theory of kinetic and relaxation processes. Int. J. Mod. Phys. B 2009, 23, 5283–5305. [Google Scholar] [CrossRef]
- Luzzi, R.; Vasconcellos, A.R.; Ramos, J.G. Predictive Statistical Mechanics: A non-Equilibrium Ensemble Formalism; Kluwer Academic: Dordrecht, the Netherlands, 2002. [Google Scholar]
- Lauck, L.; Vasconcellos, A.R.; Luzzi, R. A non-linear quantum transport theory. Physica A 1990, 168, 789–819. [Google Scholar] [CrossRef]
- Kuzemsky, A.L. Theory of transport processes and the method of the nonequilibrium statistical operator. Int. J. Mod. Phys. B 2007, 21, 1–129. [Google Scholar] [CrossRef]
- Madureira, J.R.; Vasconcellos, A.R.; Luzzi, R.; Lauck, L. Markovian kinetic equations in a nonequilibrium statistical ensemble formalism. Phys. Rev. E 1998, 57, 3637–3640. [Google Scholar] [CrossRef]
- Livshits, A. Participation of coherent phonons in biological processes. Biofizika 1972, 17, 694–695. [Google Scholar]
- Kalos, M.H.; Whitlock, P.A. Monte Carlo Methods; Wiley-Interscience: New York, NY, USA, 2007. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Adler, B.J.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Hobson, A. Irreversibility and information in mechanical systems. J. Chem. Phys. 1966, 45, 1352–1357. [Google Scholar] [CrossRef]
- Hobson, A. Irreversibility in simple systems. Am. J. Phys. 1966, 34, 411–416. [Google Scholar]
- Luzzi, R.; Vasconcellos, A.R.; Ramos, J.G. A non-equilibrium statistical ensemble formalism. MaxEnt-NESOM: Basic concepts, construction, application, open questions and criticism. Int. J. Mod. Phys. B 2000, 14, 3189–3264. [Google Scholar] [CrossRef]
- Luzzi, R.; Vasconcellos, A.R.; Ramos, J.G. Irreversible thermodynamics in a non-equilibrium statistical ensemble formalism. La Rivista del Nuovo Cimento 2001, 24, 1–70. [Google Scholar]
- Luzzi, R.; Vasconcellos, A.R.; Ramos, J.G. Statistical Foundations of Irreversible Thermodynamics; Teubner-BertelsmannSpringer: Stuttgart, Germany, 2000. [Google Scholar]
- Bogoliubov, N.N. Problems of a dynamical theory in statistical physics. In Studies in Statistical Mechanics I; de Boer, J., Uhlenbeck, G.E., Eds.; North Holland: Amsterdam, the Netherlands, 1962. [Google Scholar]
- Fano, U. Description of states in quantum mechanics by density matrix and operator techniques. Rev. Mod. Phys. 1957, 29, 74–93. [Google Scholar] [CrossRef]
- Balescu, R. Equilibrium and non-Equilibrium Statistical Mechanics; Wiley-Interscience: New York, NY, USA, 1975. [Google Scholar]
- Feynman, R. Statistical Mechanics; Benjamin: Reading, MA, USA, 1972. [Google Scholar]
- Bogoliubov, N.N. Lectures in Quantum Statistics; Gordon and Breach: New York, NY, USA, 1967; Volume 1. [Google Scholar]
- Bogoliubov, N.N. Lectures in Quantum Statistics; Gordon and Breach: New York, NY, USA, 1970; Volume 2. [Google Scholar]
- Krylov, N.S. Works on the Foundations of Statistical Mechanics; Princeton University Press: Princeton, NJ, USA, 1979. [Google Scholar]
- Sklar, L. Physics and Chance: Philosophical Issues in the Foundations of Statistical Mechanics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Algarte, A.C.; Vasconcellos, A.R.; Luzzi, R. Kinetic of hot elementary excitations in photoexcited polar semiconductors. Phys. Stat. Sol. 1992, 173, 487–514. [Google Scholar] [CrossRef]
- Kim, D.; Yu, P.Y. Phonon temperature overshoot in GaAs excited by picosecond laser pulses. Phys. Rev. Lett. 1990, 64, 946–949. [Google Scholar] [CrossRef]
- Casas-Vazquez, J.; Jou, D. Temperature in non-equilibrium steady-sates: A critical review of open problems and proposals. Rep. Prog. Phys. 2003, 66, 1937–2023. [Google Scholar] [CrossRef]
- Luzzi, R.; Vasconcellos, A.R. The basic principles of irreversible thermodynamics in the context of an informational-statistical approach. Physica A 1997, 241, 677–703. [Google Scholar] [CrossRef]
- Landsberg, P.T. Photons at non-zero chemical potential. J. Phys. C 1981. [Google Scholar]
- Davies, P.C. The Fifth Miracle: The Search for the Origin and Meaning of Life; Simon & Schuster: New York, NY, USA, 1999. [Google Scholar]
- Boltzmann, L. Populare Schriften; Johann Ambrosius Barth Verlag: Leipzig, Germany, 1905. [Google Scholar]
- Mainzer, K. Thinking Complexity; Springer: Berlin, Germany, 1994. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vasconcellos, Á.R.; Vannucchi, F.S.; Mascarenhas, S.; Luzzi, R. Fröhlich Condensate: Emergence of Synergetic Dissipative Structures in Information Processing Biological and Condensed Matter Systems. Information 2012, 3, 601-620. https://doi.org/10.3390/info3040601
Vasconcellos ÁR, Vannucchi FS, Mascarenhas S, Luzzi R. Fröhlich Condensate: Emergence of Synergetic Dissipative Structures in Information Processing Biological and Condensed Matter Systems. Information. 2012; 3(4):601-620. https://doi.org/10.3390/info3040601
Chicago/Turabian StyleVasconcellos, Áurea R., Fabio Stucchi Vannucchi, Sérgio Mascarenhas, and Roberto Luzzi. 2012. "Fröhlich Condensate: Emergence of Synergetic Dissipative Structures in Information Processing Biological and Condensed Matter Systems" Information 3, no. 4: 601-620. https://doi.org/10.3390/info3040601
APA StyleVasconcellos, Á. R., Vannucchi, F. S., Mascarenhas, S., & Luzzi, R. (2012). Fröhlich Condensate: Emergence of Synergetic Dissipative Structures in Information Processing Biological and Condensed Matter Systems. Information, 3(4), 601-620. https://doi.org/10.3390/info3040601














