Hybrid Destination-Based Jamming and Opportunistic Scheduling with Optimal Power Allocation to Secure Multiuser Untrusted Relay Networks

Abstract

In this paper, we investigate secure communication for a dual-hop multiuser relay network, where a source communication with N ($N\ge 1$) destinations via an untrusted variable gains relay. To exploit multiuser diversity while protecting source’s confidential message, we first propose a joint destination-based jamming and opportunistic scheduling (DJOS) scheme. Then, we derive closed-form approximated and asymptotic expressions of the secrecy outage probability (SOP) for the considered system with DJOS. Furthermore, we determine an asymptotical optimal power allocation (OPA), which minimizes the asymptotic SOP, to further improve the secrecy performance. Our analytical results show that the achievable secrecy diversity order in terms of SOP with fixed power allocation is $min(1,\frac{N}{2})$, whereas, with OPA, the achievable secrecy diversity order can be improved up to $min(1,\frac{2N}{N+2})$. This interesting result reveals that OPA can improve the secrecy diversity order of the single-user network. This is intuitive since full diversity order of 1 cannot be achieved when $N=1$, thus leaving some space for OPA to improve the diversity order. Nevertheless, for $N\ge 2$, the effect of OPA is to increase the secrecy array gain rather than the secrecy diversity order since full diversity order 1 has been achieved by the OS scheme. Finally, simulation results are presented to validate our analysis.

1. Introduction

1.1. Background

Recently, the applications of physical layer security (PLS) techniques in cooperative relaying networks have gained considerable attention. In particular, there are extensive works aimed at enhancing the secrecy performance of cooperative relaying networks by exploiting various PLS approaches, such as diversity techniques and/or cooperative jamming. Specifically, diversity techniques, such as multiple-input multiple-output (MIMO) [1], cooperative diversity (i.e., cooperative relaying) [2], and multiuser diversity [3,4], aim at increasing the capacity of the main channel while degrading that of the wiretap channel. As such, the system security can be significantly improved. On the other hand, cooperative jamming (CJ) [5,6,7,8,9,10], which exploits artificial noise to confuse external eavesdroppers, can reduce the leakage rate to the eavesdroppers to improve the system security. In particular, in CJ, artificial noise can be sent from a friendly jammer [5], the source [6,10], the relay [7], or the destination [8,9,10]. Furthermore, more recent works have been devoted to further enhance the PLS by combining diversity strategies and/or CJ scheme [11]. Besides, power allocation technique was also investigated in [12,13] to further improve the secrecy performance.

1.2. Related Works

Common to the aforementioned works is that all relays are assumed to be trusted, and the eavesdroppers are external nodes. Another feasible scenario is that relay(s) might belong to a heterogeneous network with a different security clearance. In this context, the relay(s) can be untrusted, and it is desirable to keep confidential messages from the untrusted relay(s), despite the help of the relay(s)’ [14,15,16]. The research on untrusted relay networks was pioneered by He and Yener [16]. A destination-based jamming (DJ) scheme was proposed in [16] to realize positive secrecy rate in dual-hop relay networks with an untrusted amplify-and-forward (AF) relay. Due to its excellent performance, several works focused on analyzing the performance of DJ in various untrusted relay channels, including the ergodic secrecy capacity (SEC) [17,18,19,20,21], and the secrecy outage probability (SOP) [22,23,24,25,26]. Although these works have proven that secure transmission is feasible in untrusted AF relay networks with DJ, it is worth noting that the existence of untrusted relay(s) brings fundamental changes to the system (secure) capacity and outage performance, as compared to the conventional AF channels with trusted relay(s). More specifically, in [17,18], the authors proved that the SEC of multi-untrusted AF networks degrades as the number of untrusted relay increases, which is in contrast with conventional AF networks with multiple trusted relays. On the other hand, as an alternative secrecy criterion, the SOP of AF networks with DJ was recently investigated for the single-untrusted-relay case [22] and the multi-untrusted-relay case [26]. Their analysis showed that the existence of relay’s eavesdropping resulted in a smaller (secrecy) diversity order in terms of SOP. In particular, in [26], the asymptotic SOP expression of multi-untrusted-relay networks with variable gain relaying (VGR) was derived, from which the secrecy diversity order in terms of SOP was shown to be limited to one, rather than the relay number M achieved in conventional trusted AF networks. However, this conclusion only holds for “moderate” number of relays scenario as presented by Theorems 3 and 4 in [26]. This can be attributed to the key approximation based on the law of large numbers (i.e., larger value of M) in [26]. Moreover, Figure 8 in [26] showed that the slop of the simulated SOP curve for $M=3$ is actually smaller than that of the asymptotic SOP whose diversity order is 1. Therefore, both the derivation method and the conclusion in [26] cannot be directly extended to the case of small number of relays, especially for the typical single-relay case $M=1$. In [22], the SOP of fixed-gain relaying (FGR) for the typical $M=1$ case was obtained in an integral form. However, we cannot directly obtain the secrecy diversity order from the integral form of SOP in [22] (a diversity order of $1/2$ in terms of SOP can be conjectured from the simulation in Figure 1 in [22] for the single-relay case). Motivated by this key observation, recent work [24] explicitly proved that obtained secrecy diversity order in the single-user and single-untrusted-relay scenario with FGR was limited to 1/2.

To alleviate the impact of untrusted relay, optimal power allocation (OPA) can be used to improve the secrecy performance [21,27,28,29]. For DJ-based untrusted AF relay networks, where the source and destinations were equipped with large-scale antennas while the untrusted relay was equipped with a single antenna, an OPA scheme was proposed to maximize the instantaneous secure rate (ISR) [27]. Similarly, OPA was investigated in [28] for maximizing the ISR of large-scale antenna system with single-antenna untrusted relay. The authors in [21] considered a DJ-based MIMO untrusted relay system and proposed an iterative power allocation algorithm to jointly design the source, relay, and destination precoding for maximizing the achievable ISR. Very recently, an OPA scheme was proposed in [29] to maximize the ISR in energy harvesting relay network. Noting that all these works focused on maximizing the ISR with OPaA.

1.3. Motivation and Contributions

A major limitation of the aforementioned works [17,18,19,20,21,22,23,25,26,27,28,29] is that most were limited to single user scenario, and, thus, the impact of multiuser diversity (MUD) on system secrecy performance has not been considered. In fact, very little work on the secure communication in multiuser relay networks has been reported. In [30], the authors investigated the secure issue in multiuser relay networks, where the undesired users who were not selected for data reception was treated as potential eavesdroppers. An optimal user selection scheme was proposed for the considered system, which was optimal in the sense of maximizing the secrecy rate. Still, the relay in [30] was assumed to be trusted. In recent work [24], the authors focused on the multiuser untrusted relay networks with FGR and proposed a novel joint destination-based jamming and opportunistic scheduling scheme to improve the system SOP. In particular, the results in [24] explicitly revealed that the proposed scheme can improve the secrecy diversity order from 1/2 in single-user networks up to full secrecy diversity order of 1 in multiuser relay networks. However, OPA between the source and the destination still has not been considered. To the best of our knowledge, no work has yet analyzed the utilization of OPA strategy to minimize the SOP of DJ-based multiuser untrusted relay networks.

In this paper, we aim to enhance the security of a multiuser untrusted AF relay network without expending additional resources. Based on the joint destination-based jamming and opportunistic scheduling (DJOS) scheme in [24], we optimize the power allocation between the source and the destination between source and destination under a total power constraint to further improve the secrecy outage performance. Unlike the previous work in [24], where FGR protocol is employed at the relay, we consider VGR protocol in this paper because VGR achieves better performance than FGR in general. Note that the main channel (source-relay-destination) and the wiretap channel (source-relay) in untrusted relay networks are intuitively correlated with each other, which makes the analysis for deriving the closed-form SOP expression difficult by mathematical treatment. Moreover, compared to the FGR scheme as in [24], the SOP of multiuser untrusted relay networks with VGR scheme is more difficult to analyze. In this regard, it is not easily tractable to get the exact closed-form SOP expressions of VGR scheme, even for the single-user untrusted relay scenario. To tackle this problem, on the premise of large signal-to-noise ratio (SNR), we resort to a number of approximations to obtain the SOP expressions in closed-form.

Compared to closely previous related works [24] and [26], our main contributions are summarized as follows:

• To harvest the MUD while satisfying the security constraint, we propose to apply the DJOS scheme in the considered multiuser untrusted AF relay networks with VGR. Under Rayleigh fading channels, we first derive a new closed-form approximated SOP expression for the considered system with DJOS. Note that an analytical SOP expression for multiple untrusted relay networks with VGR scheme has already derived in [26]. However, as we explained before, both the derivation method and the conclusion in [26] cannot be directly extended to the single-user and single-untrusted-relay case which has been included and studied in this paper.
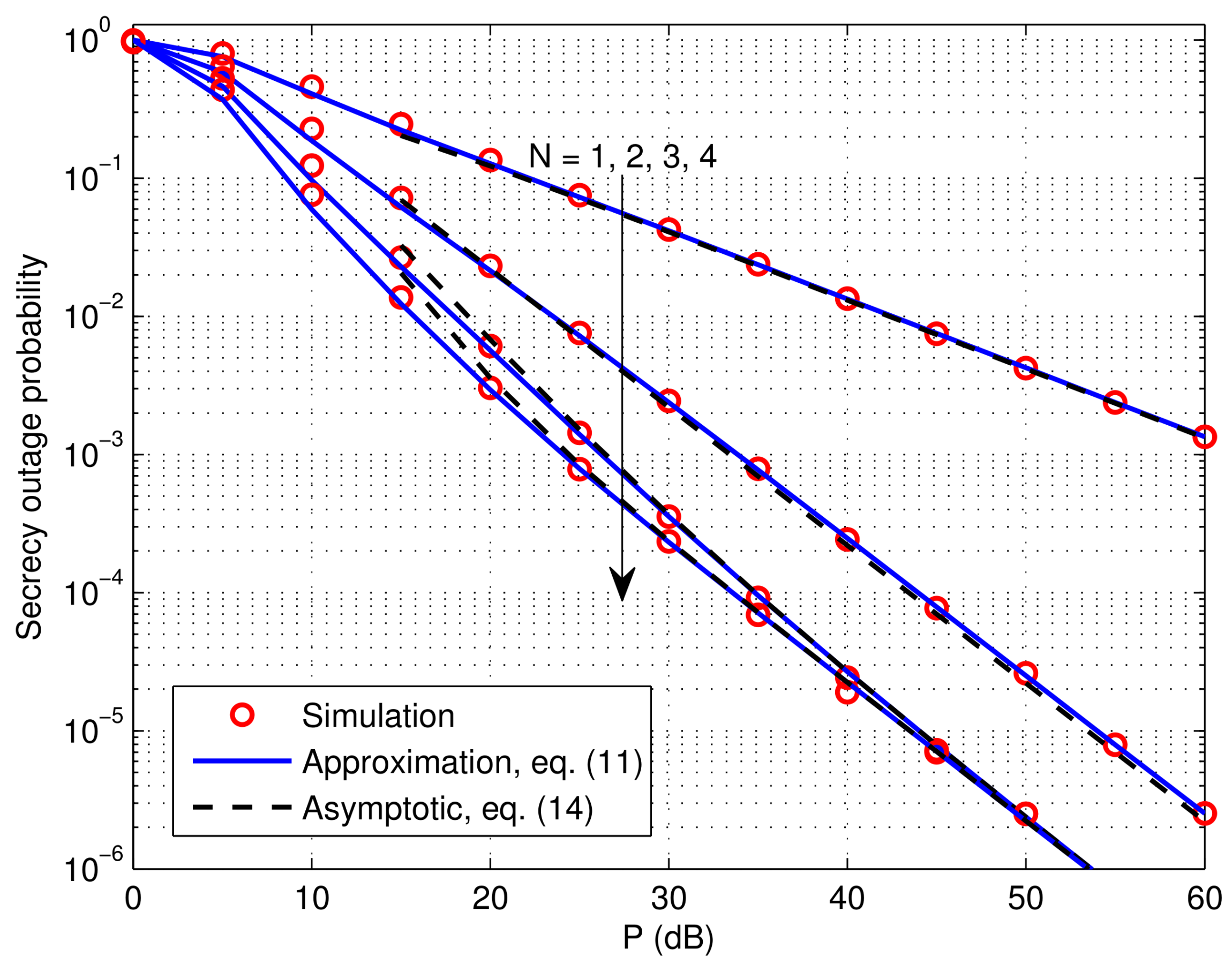
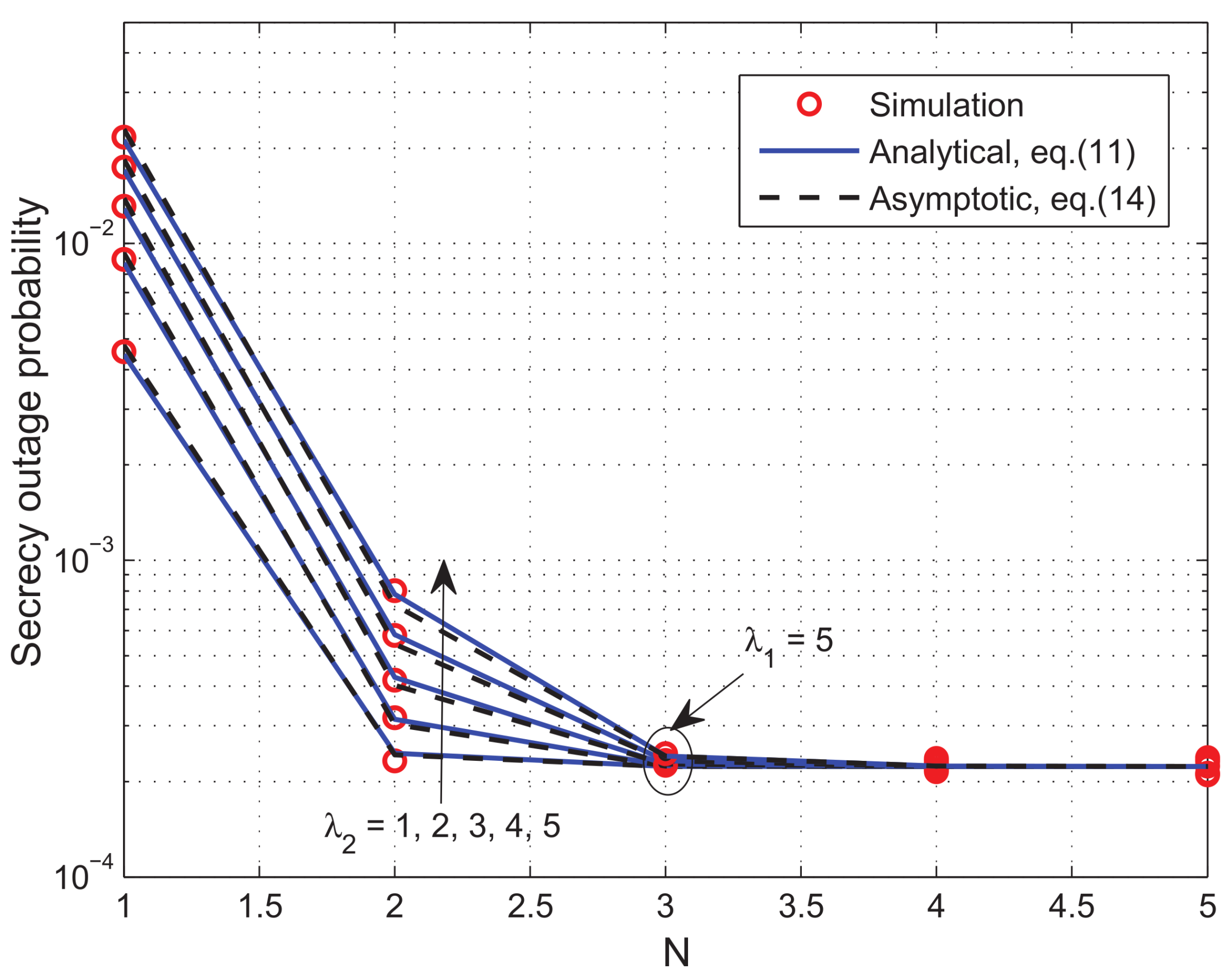
• To gain further insights, we then present the asymptotic SOP expression and prove that the achievable secrecy order is $min(1,N/2)$, where N denotes the number of destinations (users) (In this paper, the diversity order only mathematically indicates the curve slope of the outage performance metric studied at high SNRs. Prior works [8,20,24,26] have confirmed that the (secrecy) diversity order behavior in terms of SOP in cooperative relaying networks with security requirement is very different from the diversity order behavior in terms of connection outage probability (COP) in scenarios without security requirement). That is, for the single-user network ($N=1$), the achievable secrecy diversity order in terms of SOP is 1/2, while with DJOS, the secrecy diversity order in multiuser networks ($N\ge 2$) can be improved from 1/2 up to full secrecy diversity order of 1. Thus, MUD has been harvested by the OS strategy. It is worth noting that our rigorous mathematical analyses explicitly show that the obtained secrecy diversity order for the the typical single-untrusted-relay network with VGR is actually 1/2, rather than 1 as revealed in the multi-untrusted-relay case [26]. Therefore, our theoretical analysis on the single-untrusted-relay network supplements and complements the results in [26].
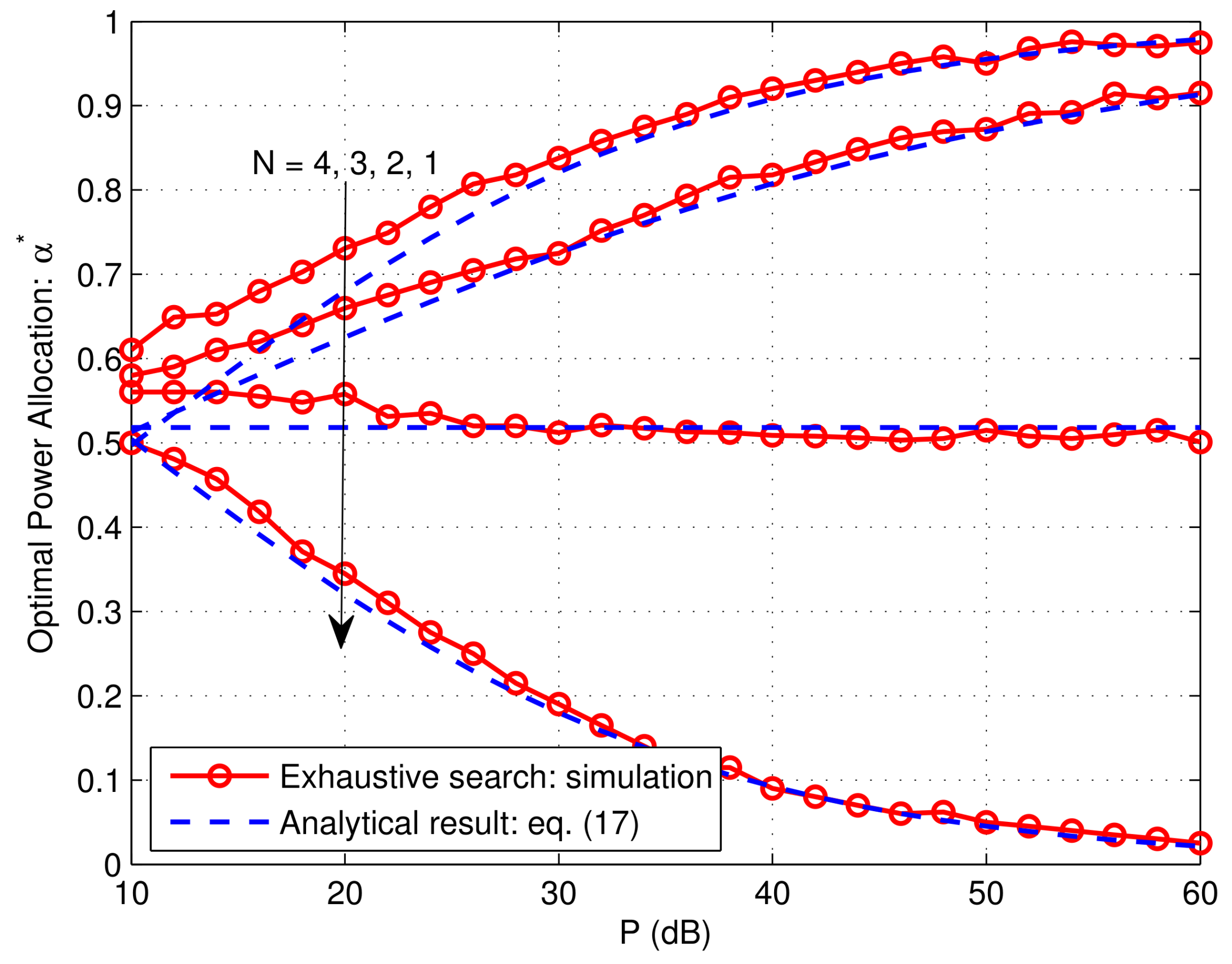
• Finally, we propose an asymptotically OPA scheme to minimize the asymptotic SOP. Interestingly, with the proposed OPA scheme, we find that the system secrecy diversity order can be improved from $min(1,\frac{N}{2})$ (without OPA) to $min(1,\frac{2N}{N+2})$. This conclusion provides some new findings that allow us to understand the impact of power allocation on the SOP performance. Specifically, for the $N=1$ case, our OPA scheme can help to improve the secrecy diversity order from 1/2 up to 2/3. It is well-known that the application of OPA in conventional trusted relay networks can only help to improve the array gain rather than the diversity gain/order [31]. This is because full diversity order of 1 is already obtained there even without OPA. However, our work explicitly show that, in the untrusted relay case, the effect of OPA is to increase the secrecy diversity order. It is intuitive that the diversity order deterioration due to eavesdropping has left some space for OPA to improve the diversity order. Moreover, when $N\ge 2$, we prove that OPA does not affect the secrecy diversity order. This is because full secrecy diversity order of 1 is already obtained by the OS scheme even without OPA. However, as we will show in Section 5, the effect of OPA is to increase the secrecy array gain and hence significantly reduces the SOP.

The rest of this paper is organized as follows. Section 2 presents the system model and the DJOS scheme. Section 3 analyzes the tight approximated secrecy outage probability, as well as the high-SNR asymptotic secrecy outage probability. Section 4 studies the optimal power allocation, which minimizes the secrecy outage probability. Section 5 presents numerical and simulation results to verify our theoretical analysis. Finally, Section 6 concludes the paper.

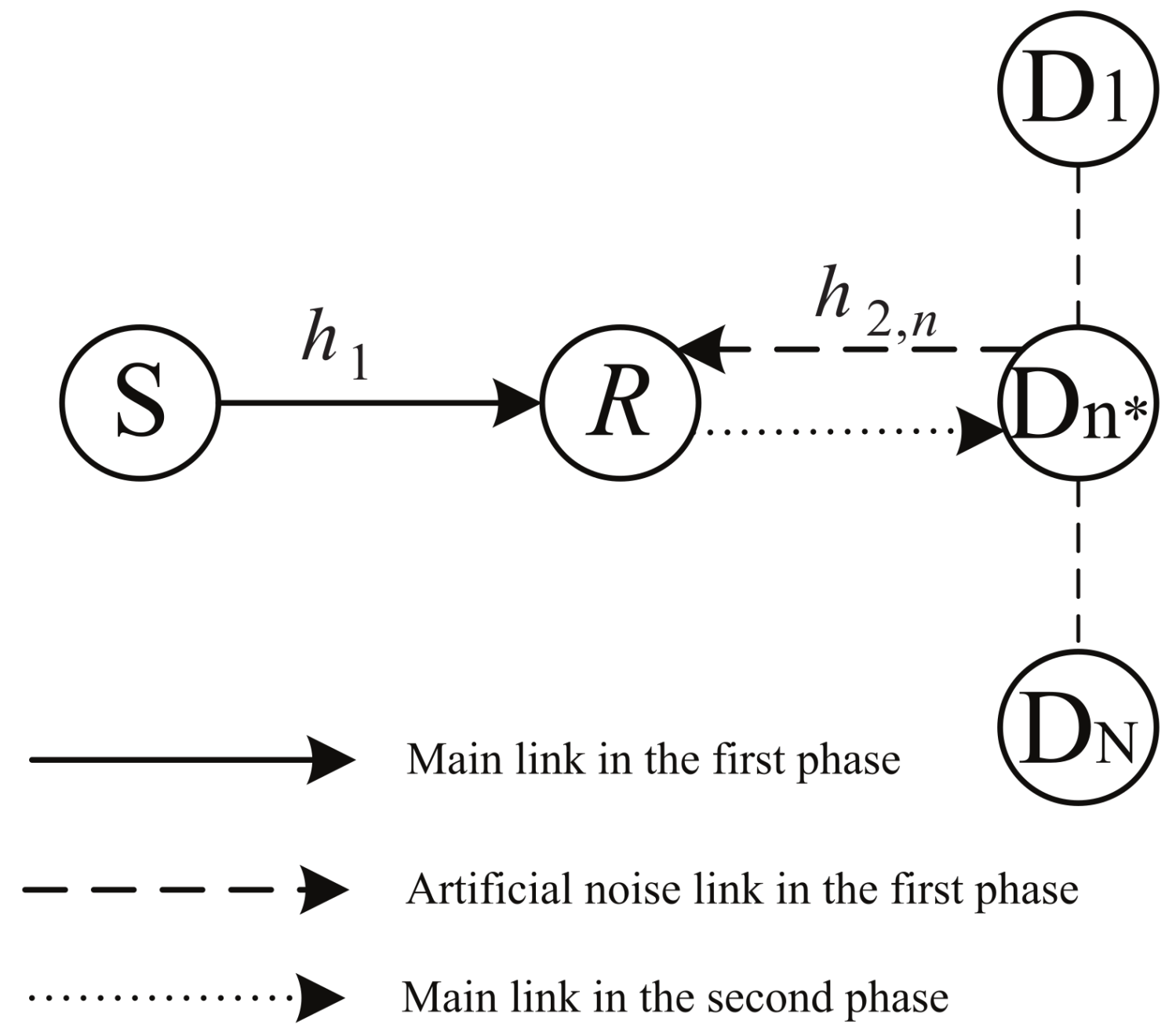
2. System Model

As shown in Figure 1, we consider a downlink cooperative cellular network where one source S communicates with N destination users $D_n$ $(n=1,\dots ,N)$ via the help of an untrusted AF relay R. Each node is equipped with a single antenna and operates in a time-division half-duplex mode. It is assumed that all channels are reciprocal and quasi-static over each transmission. Moreover, no direct links exists between the source and the destinations, due to the long distance or significant obstacle [17,18,20,22,26]. In this setting, although S has to rely on R to transmit its information, it does not trust R and would like to keep its confidential information secret from R. This model can find application in many practical scenarios such as renting a satellite relay from a third party to forward source’s confidential information [20].

To achieve both the benefits of MUD and DJ schemes, we apply the DJOS scheme in [24] for the considered multiuser untrusted relay network. Specifically, before each data transmission, only the “best” destination out of the N candidates is selected to access the channel, using a specific security optimal opportunistic scheduling (OS) strategy whose details will be given later. As will be demonstrated later, MUD can be obtained by the proposed user scheduling strategy. After this, a two-phase transmission starts. In particular, the DJ approach is adopted in Phase 1 to prevent eavesdropping at the untrusted relay R. Note that this DJ-based two-phase transmission is similar to the physical layer network coding (PNC) or analog network coding (ANC) as illustrated in [32,33], respectively. (It is well-known that both PNC and ANC can achieve full diversity order of 1 in terms of COP [34]. In this context, the (secrecy) diversity order deterioration in single-user AF network with DJ, as demonstrated in Section 4, is not due to the application of DJ in untrusted AF networks.) The data transmission process is detailed as follows.

In Phase 1, S transmits $x_s$ with power $\alpha P$ and at the same time, the nth destination (i.e., $D_n$) transmits a Gaussian interference signal $x_{d,n}$ with power $(1-\alpha )P$ to the relay. Here, P denotes a fixed total transmission power budget (P also denotes the system SNR herein) and $\alpha \in (0,1)$ is the power allocation ratio [17]. Hence, the superimposed signal received at R is given by

$$y_R=\sqrt{\alpha P}{h}_1{x}_s+\sqrt{(1-\alpha )P}{h}_{2,n}{x}_{d,n}+n_R,$$

(1)

where $h_1\sim \mathcal{CN}(0,{\lambda }_1^{-1})$ and $h_{2,n}\sim \mathcal{CN}(0,{\lambda }_{2,n}^{-1})$ denote the instantaneous channel coefficient of $S\to R$ and $R\to D_n$ links, respectively, and $n_R\sim \mathcal{CN}(0,1)$ is additive white Gaussian noise (AWGN) at the relay. Then, under Rayleigh fading channels, ${\left|h_1\right|}^2$ and ${\left|h_{2,n}\right|}^2$ are independent exponential random variables with parameters ${\lambda }_1$ and ${\lambda }_{2,n}$, respectively. Moreover, we assume that all the users are located in close proximity to each other with ${\lambda }_{2,n}={\lambda }_2$ for simplicity. Based on Equation (1), the received signal-to-interference-plus-noise ratio (SINR) at the relay R is given by

$${\gamma }_R=\frac{\alpha P|h_1{|}^2}{(1-\alpha )P|h_{2,n}{|}^2+1}.$$

(2)

In Phase 2, R simply amplifies the received signal $y_R$ with a scaling gain applied, denoted by $\mathcal{G}$, and then retransmits it to $D_n$. The received signal at $D_n$ is written as

$$y_{D_n}=h_{2,n}\mathcal{G}(\sqrt{\alpha P}{h}_1{x}_s+\sqrt{(1-\alpha )P}{h}_{2,n}{x}_{d,n}+n_R)+n_{D_n},$$

(3)

where $n_{D_n}\sim \mathcal{CN}(0,1)$ is AWGN at $D_n$. Since $x_{d,n}$ is the transmitted signal of $D_n$ in the first phase, $D_n$ can subtract the term $h_{2,n}\mathcal{G}\sqrt{(1-\alpha )P}{h}_{2,n}{x}_{d,n}$ from $y_{D_n}$ and decodes the source message based on the remainder signal $\widetilde{y_{D_n}}$, which is given by

$$\widetilde{y_{D_n}}=h_{2,n}\mathcal{G}(\sqrt{\alpha P}{h}_1{x}_s+n_R)+n_{D_n}.$$

(4)

When a variable gain relay is employed, the variable-gain relaying factor is selected as $\mathcal{G}=\sqrt{\frac{P}{\alpha P|h_1{|}^2+(1-\alpha )P|h_{2,n}{|}^2+1}}$. Plugging the expression of $\mathcal{G}$ into $\widetilde{y_{D_n}}$ and after some algebraic manipulations, we can express the SINR at $D_n$ as

$${\gamma }_{D_n}=\frac{\alpha P|h_1{|}^2\times P|h_{2,n}{|}^2}{\alpha P|h_1{|}^2+(2-\alpha )P|h_{2,n}{|}^2+1}$$

(5)

According to Equations (2) and (5), the achievable instantaneous secrecy rate at the nth destination $D_n$ is calculated by [26]

$$\begin{array}{cc}\hfill C_{S,n}& ={\left[\frac{1}{2}log(1+{\gamma }_{D_n})-\frac{1}{2}log(1+{\gamma }_R)\right]}^{+}\hfill \\ & ={\left[\frac{1}{2}log\left(\frac{1+\frac{\alpha P|h_1{|}^2·P|h_{2,n}{|}^2}{\alpha P|h_1{|}^2+(2-\alpha )P|h_{2,n}{|}^2+1}}{1+\frac{\alpha P|h_1{|}^2}{(1-\alpha )P|h_{2,n}{|}^2+1}}\right)\right]}^{+},\hfill \end{array}$$

(6)

where ${[x]}^{+}=max\{0,x\}$.

3. Opportunistic Scheduling Scheme

We now describe the opportunistic scheduling scheme, which aims at exploiting the multiuser diversity inherent in the considered multiuser relay networks as well as guaranteeing the system to achieve the optimal secrecy performance. In this regard, the user scheduling criterion is to select such a destination/user $D_{n^{*}}$ that satisfies

$$n^{*}=arg\underset{1\le n\le N}{max}{C}_{S,n}.$$

(7)

In this criterion, at a time, only the destination with the highest instantaneous secrecy rate out of N destinations is scheduled for transmitting jamming signal in Phase 1 and receiving the relay’s signal in Phase 2. Furthermore, it is not difficult to verify that the instantaneous secrecy rata $C_{S,n}$ in Equation (6) is an increasing function of $|h_{2,n}{|}^2$, so a user maximizing the instantaneous secrecy rate is identical to a user with the largest instantaneous channel gain of the second hop. Thus, the scheduling policy in Equation (7) can be formulated equivalently as

$$h_M=\underset{1\le n\le N}{max}|h_{2,n}{|}^2,$$

(8)

where $h_M$ denotes the instantaneous channel gain of the scheduled destination $D_n^{*}$.

It should be noted that Equation (8) reveals that the opportunistic scheduling strategy in conventional multiuser relay networks without security requirement [35] can be applied directly in the multiuser untrusted relay networks. Specifically, the scheduling scheme presented in Equation (8) is implemented at the relay, which is assumed to have perfect knowledge of the relay-destination links of all the N destinations (This is a common assumption in multiuser relay networks [35,36,37]. In practice, the channel state informations (CSIs) of the links can be estimated at the relay by employing reciprocity to estimate forward channels from the reverse channels. Generally speaking, the CSI estimation could be very accurate if the training period is sufficiently long [36]). At the beginning of each scheduling period, the relay broadcasts a destination synchronization message, which contains the synchronization information and the pilot signaling transmission order. Then, the relay identifies and selects the strongest user. Finally, the relay feeds back the index of the strongest user to the source.

The relay has perfect channel state information (CSI) of each link.

4. Secrecy Outage Performance Analysis

In this section, we will derive an analytical expression for the SOP with large transmit power first. Then, we provide an high-SNR asymptotic SOP expression to characterize the asymptotic secrecy outage performance of the system, i.e., secrecy diversity order and secrecy array gain. Finally, based on the asymptotic SOP expression, we determine an asymptotic power allocation to further boost the system secrecy performance.

4.1. Approximated Secrecy Outage Probability

SOP is defined as the probability that the instantaneous secrecy rate is less than a given target secrecy rate $R_s>0$ [26]. Mathematically, according to Equations (6) and (8), the SOP can be formulated as

$$\begin{array}{cc}\hfill P_{sop}& =Pr\left\{C_{S,M}<R_S\right\}\hfill \\ & =Pr\left\{\frac{1+\frac{\alpha P|h_1{|}^2·P|h_M{|}^2}{\alpha P|h_1{|}^2+(2-\alpha )P|h_M{|}^2+1}}{1+\frac{\alpha P|h_1{|}^2}{(1-\alpha )P|h_M{|}^2+1}}<2^{2R_S}\right\}.\hfill \end{array}$$

(9)

Unfortunately, it is not easily tractable to get exact closed-form expression of Equation (9). To tackle this, we resort to some approximations to facilitate our analysis. First, we apply the well-known and widely used inequality $\frac{xy}{1+x+y}<\frac{xy}{x+y}\le min(x,y)$ to tightly upper bound ${\gamma }_D$ as ${\gamma }_D<Pmin\left\{\frac{\alpha }{2-\alpha }|h_1{|}^2,|h_M{|}^2\right\}$. Moreover, to guarantee the secure transmission, we consider the worst-case, where the noise at the relay is zero. Note that this assumption is reasonable when SNR is high and it further facilitates the analysis, which is also taken into considered in [27]. That is, we have ${\gamma }_R^{}\approx \frac{\alpha |h_1{|}^2}{(1-\alpha )|h_M{|}^2}$ in high SNR regime. Then, the system SOP with selected destination $D_n^{*}$ in Equation (9) can be approximated as follows

$$P_{sop}\approx Pr\left\{\frac{1+Pmin\left\{\frac{\alpha }{2-\alpha }|h_1{|}^2,|h_M{|}^2\right\}}{1+\frac{\alpha |h_1{|}^2}{(1-\alpha )|h_M{|}^2}}<2^{2R_S}\right\}.$$

(10)

In the following theorem, we provide an analytical expression for $P_{sop}$ in Equation (10).

Theorem 1.

The secrecy outage probability of the multiuser untrusted relay networks with DJOS can be approximately expressed by:

$$P_{sop}\approx 1-J_1+J_2,$$

(11)

where $J_1$ and $J_2$ are, respectively, given by

$$\begin{array}{cc}\hfill J_1& =\sum _{n=1}^N\left(\genfrac{}{}{0pt}{}{N}{n}\right){(-1)}^{n-1}\frac{{\lambda }_{2}n}{P}{e}^{-\frac{{\lambda }_1{\theta }_1+{\lambda }_2{\theta }_{0}n}{P}}\sum _{j=0}^{\infty }\frac{{(-1)}^j{Q}^{\prime }}{j!}{\left(\frac{{\lambda }_1{\theta }_0{\theta }_1}{Q^{\prime }P}\right)}^j{\mathrm{E}}_{\mathrm{j}}\left(\frac{Q^{\prime }{\lambda }_{2}n}{P}\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill J_2& =\sum _{n=1}^N\left(\genfrac{}{}{0pt}{}{N}{n}\right){(-1)}^{n-1}{\lambda }_{2}n\sqrt{\frac{{\theta }_2\pi }{4{\lambda }_{1}P}}{e}^{\frac{{\theta }_2}{4{\lambda }_{1}P}{\left({\lambda }_{2}n-\frac{{\lambda }_1{Q}^{\prime }}{{\theta }_2}\right)}^2}\mathrm{erfc}\left(\left({\lambda }_{2}n-\frac{{\lambda }_1{Q}^{\prime }}{{\theta }_2}\right)\sqrt{\frac{{\theta }_2}{4{\lambda }_{1}P}}+\frac{Q^{\prime }+{\theta }_0}{\sqrt{{\theta }_{2}P/{\lambda }_1}}\right),\hfill \end{array}$$

(13)

with $Q=2^{2R_S}$, $Q^{\prime }=Q-1$, ${\theta }_0=\frac{Q(2-\alpha )}{1-\alpha }$, ${\theta }_1=\frac{(Q-1)(2-\alpha )}{\alpha }$, and ${\theta }_2=\frac{\alpha Q}{1-\alpha }$. Moreover, ${\mathrm{E}}_n(x)={\int }_1^{\infty }\frac{e^{-xt}}{t^n}\mathrm{d}t$ in Equation (12) is the exponential integral function and $\mathrm{erfc}(·)$ in Equation (13) is the complementary error function [38].

Proof of Theorem 1.

Please see Appendix A for the proof. ☐

4.2. Asymptotic Secrecy Outage Probability

In the following, we introduce simple expression for the asymptotic SOP in the high SNR regimes, which is useful in demonstrating the system secrecy diversity order and secrecy array gain.

Theorem 2.

The asymptotic high-SNR SOP of the considered system is given by

$$P_{sop}\approx \left\{\begin{array}{cc}\frac{\varpi }{P}+\frac{Au}{B\sqrt{P}}-\frac{A^2{u}^2}{2BP}(1+\omega )& ,N=1\hfill \\ {\displaystyle \sum _{n=1}^{⌊\frac{N}{2}⌋}}\frac{{(-1)}^{n+1}}{n!}{\left(\frac{{\lambda }_1{\theta }_1}{P}\right)}^n+\frac{\Theta (N)u^N}{P^{\frac{N}{2}}}& ,N\ge 2,\hfill \end{array}\right.$$

(14)

where $A=1.98$, $B=1.135$, $u={\lambda }_2\sqrt{\frac{{\theta }_2}{4{\lambda }_1}}$, $\omega =\frac{{\lambda }_1(Q^{\prime }+2{\theta }_0)}{{\lambda }_2{\theta }_2}$, and $\varpi ={\lambda }_1{\theta }_1+{\lambda }_2{\theta }_0+{\lambda }_2{Q}^{\prime }$. In (14), when N is an odd number, $\Theta (N)=\frac{AN!}{B\left(\frac{N}{2}-\frac{1}{2}\right)!}$, while when N is an even number, $\Theta (N)=\frac{A^{2}N!}{2B\left(\frac{N}{2}-1\right)!}$. Besides, $⌊·⌋$ in Equation (14) represents the rounding-down operation.

Proof of Theorem 2.

Please see Appendix B for the proof. ☐

Equation (14) implies that the achievable secrecy diversity order and the secrecy array gain of the considered system, for a fixed power allocation (FPA) factor α, can be respectively written as

$$G_d^{FPA}=min\left(1,\frac{N}{2}\right)=\left\{\begin{array}{cc}1/2& ,N=1\hfill \\ 1& ,N\ge 2\hfill \end{array}\right.$$

(15)

$$G_c^{FPA}=\left\{\begin{array}{cc}{(\frac{A{\lambda }_2\sqrt{{\theta }_2}}{2B})}^{-2}& ,N=1\hfill \\ {({\lambda }_1{\theta }_1+\frac{A^2{\lambda }_2^2{\theta }_2}{4B{\lambda }_1})}^{-1}& ,N=2\hfill \\ {({\lambda }_1{\theta }_1)}^{-1}& ,N\ge 3\hfill \end{array}\right.$$

(16)

Remark 1.

Recall that, when the relay is trusted, full diversity of 1 can be achieved for the single-user scenario ($N=1$) and the diversity order for multiuser scenario (N≥ 2) is unaffected by opportunistic scheduling (OS) [35]. However, when the relay is untrusted, those observations no longer exist.

First, when $N=1$, as it is revealed in Equation (15), the AF system with untrusted variable gain relay achieves a secrecy diversity order of $\frac{1}{2}$ in terms of SOP, which is in contrast to full diversity order of 1 in terms of connection outage probability (COP) achieved in trusted AF systems [35]. This result reveals that the existence of relay’s eavesdropping will cause some loss of the diversity order (as clarified in Section 2, it is not the application of DJ in untrusted AF networks that results in such a diversity order loss). Intuitively, the diversity order difference between COP and SOP lies in discrepancy between their definitions. Specifically, the concept of SOP jointly characterizes the security and reliability performance, while the COP only evaluate the reliability performance. When the relay is untrusted, the diversity loss becomes the price to satisfy the system secrecy requirement, i.e., avoiding source information intercepted by the untrusted relay. Mathematically, according to Equation (A9) in Appendix A, the external condition $X>\frac{P}{{\theta }_2}{\mathrm{Y}}^2-\frac{Q^{\prime }}{{\theta }_2}\mathrm{Y}$ in $J_2$ of Equation (A9) will result in a diversity order of $1/2$, presenting the probability of not achieving perfect secrecy ( i.e., there is some information leakage to untrusted relay R ) in single untrusted VGR system.

Furthermore, for the multiuser AF networks (i.e., $N\ge 2$) with OS, the diversity order has been improved from $1/2$ up to 1, which implies that the loss of diversity order can be compensated by the OS approach. In particular, the results in Equations (15) and (16) demonstrate the performance gains of employing OS in multiuser untrusted AF relay networks, which is harvested in form of security outage performance improvement, i.e., increased secrecy diversity gain as well as secrecy array gain.

Remark 2.

Besides, we can see from Equation (16), although the effect of OS is to increase the array gain as the number of destinations N increases, the array gain becomes saturated, when N increases to a certain extent (i.e., N ≥ 3). This is because, as N increases, the link quality between the relay and the scheduled user becomes much better than that of the source-relay link. In such case, the secrecy performance will be primarily limited by the quality of the source-relay link. Moreover, while it is generally known that further increasing N leads to array gain saturation (noting that this array gain saturated phenomenon is ubiquitous in conventional trusted multiuser relaying networks when N ≥ 2 (see [35,39] and references therein)) [35,39] when N = 2 in no secrecy constraint scenario, our results in Equation (16) demonstrate that the array gain enhancement in secrecy constraint scenario is marginal when N ≥ 3.

4.3. Asymptotic Optimal Power Allocation

We investigate the optimum power allocation in this subsection. For analytical tractability, we choose the asymptotic SOP in Equation (14) as a target function, and, hence, the optimum power allocation aims to minimize the asymptotic SOP by optimally allocating power between the source and the scheduled destination under a total power constraint of P. The asymptotic optimal power ratio ${\alpha }^{*}$ is presented in the following lemma.

Theorem 3.

For sufficiently large SNR (i.e., $P\to \infty$), the asymptotic optimal power allocation factor ${\alpha }^{*}$ that minimizes SOP is given by:

$${\alpha }^{*}\approx \frac{1}{1+{\Xi (N)}^2{P}^{\frac{2-N}{2+N}}},$$

(17)

where $\Xi (N)={\left(\frac{N\Theta (N){\beta }_2^N}{2{\beta }_1}\right)}^{\frac{1}{N+2}}$ with ${\beta }_1=2{\lambda }_1{Q}^{\prime }$ and ${\beta }_2=\frac{{\lambda }_2}{2}\sqrt{\frac{Q}{{\lambda }_1}}$.

With the asymptotical OPA derived in Equation (17), the corresponding minimum SOP is given by

$$P_{sop}({\alpha }^{*})\approx \frac{{\beta }_1}{2P}+\left({\beta }_1\Xi {(N)}^2+\Theta (N){\left(\frac{{\beta }_2}{\Xi (N)}\right)}^N\right)\frac{1}{P^{\frac{2N}{N+2}}}.$$

(18)

As can be observed by Equation (18), the secrecy diversity and array gains of the system with OPA are, respectively, given by

$$G_d^{OPA}=min\left(1,\frac{2N}{N+2}\right)=\left\{\begin{array}{cc}2/3& ,N=1\hfill \\ 1& ,N\ge 2\hfill \end{array}\right.$$

(19)

and

$$G_c^{OPA}=\left\{\begin{array}{cc}{\left(\frac{{\beta }_2\Theta (1)}{\Xi (1)}\right)}^{-\frac{3}{2}}& ,N=1\hfill \\ {\left(\frac{{\beta }_1}{2}+{\beta }_1\Xi {(2)}^2+\Theta (2){\left(\frac{{\beta }_2}{\Xi (2)}\right)}^2\right)}^{-1}& ,N=2\hfill \\ {\left(\frac{{\beta }_1}{2}\right)}^{-1}& ,N\ge 3.\hfill \end{array}\right.$$

(20)

Proof of Theorem 3.

Please see Appendix C. ☐

Remark 3.

Note that, in trusted relay systems, OPA scheme does not affect the diversity order, rather it increase only the array gain [31]. Nevertheless, as revealed in Equation (19), the OPA scheme has an impact on the diversity gain of single-user (N = 1) untrusted relay systems. Specifically, by using our proposed OPA scheme, the obtained diversity order can be improved from 1/2 up to 2/3. Thus, significantly secrecy performance improvement can be achieved, as shown in Section 5. Moreover, for multiuser scenario (N ≥ 2), the result in Equation (20) confirms that OPA has no impact on the diversity gain due to bottleneck of the source-relay link. Nevertheless, by inspecting Equation (20), we observe that the effect of OPA is to increase the secrecy array gain.

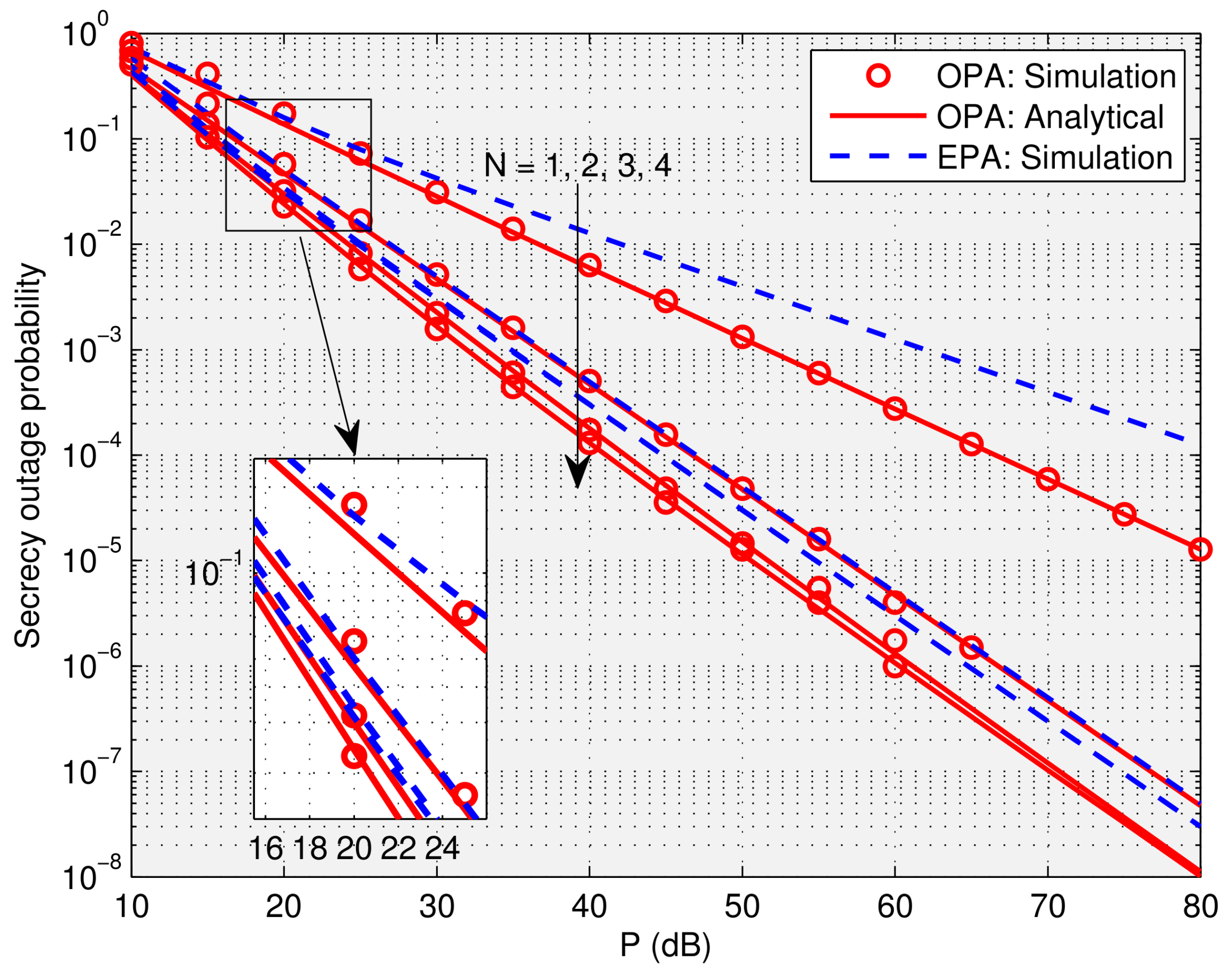
5. Numerical Results and Discussions

In this section, we present some numerical and simulation results to verify our previous theoretical analysis. The simulation results are obtained by performing $5\times {10}^6$ random channel realizations. Moreover, the analytical curves obtained by Equation (12) is truncated by the first five terms.

Figure 2 shows the system SOP versus P for different values of N. The curves are plotted for $\alpha =0.5$, ${\lambda }_1=0.5$ and ${\lambda }_2=1$. We can see that the analytical approximate SOP results are very close to the simulation results even at low SNR regions, and the asymptotic values match well with the simulations at high SNR regimes. In Figure 2, the achievable secure diversity order of the considered system can be verified to be equal to $min(1,N/2)$. As a result, we can see that the MUD gain is harvested in the form of decreased SOP and increased secrecy diversity order, as N increases from 1 to 2. Furthermore, we observe that increasing N from 2 to 3 leads to a moderate performance enhancement. This is because, when $N\ge 2$, opportunistic scheduling has no effect on the secrecy diversity order but improves the secrecy array gain. However, as revealed in Equation (16), increasing N beyond 3 does not provide an additional array gain. Thus, we can that the curves for $N=3,4$ ($N\ge 3$) overlap each other at sufficiently high SNR. This observation is also demonstrated in Figure 3, from which we can see that the secrecy outage behavior in high SNR regime is stabilized over N or ${\lambda }_2$ when $N\ge 3$, while it is only dependent on ${\lambda }_1$, thus validating the result in Equation (16). However, for $N=1,2$, we can see in Figure 3 that the secrecy outage performance is determined by both hops, as revealed in Equation (16).

Assuming that ${\lambda }_1={\lambda }_2=1$, Figure 4 provides comparisons between the optimal power allocation factor ${\alpha }^{*}$ via exhaustive search (minimizing the simulation results of the SOP) and ${\alpha }^{*}$ provided by the closed-form expression in Equation (17).

It is clear that the optimal power allocations obtained via exhaustive search match well with those via analytical results, especially in the high SNR region. Moreover, as predicted in Equation (17), we observe that ${\alpha }^{*}$ is monotonically decreasing and increasing in P for $N=1$ and $N\ge 3$, respectively, while ${\alpha }^{*}$ tends to be a constant (i.e., ${\alpha }^{*}\approx 0.5$ for the considered setting) regardless of P for $N=2$.

With the ${\alpha }^{*}$ obtain in Figure 4, we proceed to compare our proposed OPA scheme with the traditional equal PA (EPA) scheme, i.e., $\alpha =0.5$, as shown in Figure 5. This figure confirms that the OPA scheme has an obvious SNR advantage over the EPA scheme. For instance, when $N=1$ and $P_{out}={10}^{-3}$, OPA provides a significant performance gain as high as 12 dB compared to EPA. This is because the secrecy diversity order is improved from 1/2 (with EPA) to 2/3 (wit OPA). When $N\ge 2$, OPA brings marginal benefits to the array gain. This is because, due to the bottleneck of the first hop, both OPA and EPA schemes achieve the same secrecy diversity order of 1. In particular, the advantage of OPA over EPA in the secrecy outage performance diminishes when $N\ge 3$, as explicitly indicated by the array gain expression in Equation (20).

6. Conclusions

In this paper, we study the secrecy outage probability (SOP) of multiuser relay networks with an untrusted variable-gain relay. The joint destination-based jamming and opportunistic scheduling (DJOS) scheme is employed to harvest multiuser diversity and satisfying security requirement. The performance of the system is evaluated by deriving the SOP approximation as well as its asymptotic expression in closed-form. Analysis of the secrecy diversity order and the impact of number of users provides valuable insights into practical system designs. In particular, we demonstrate that the diversity order loss in single-user untrusted AF networks can be fully compensated by the opportunistic scheduling strategy. Moreover, optimal power allocation (OPA) that minimizes the asymptotic SOP is studied. We prove that OPA can result in a significant performance improvement compared to the conventional equal power allocation scheme without expending external resources.