Modeling Confined Cell Migration Mediated by Cytoskeleton Dynamics
Abstract
:1. Introduction
2. Materials and Methods
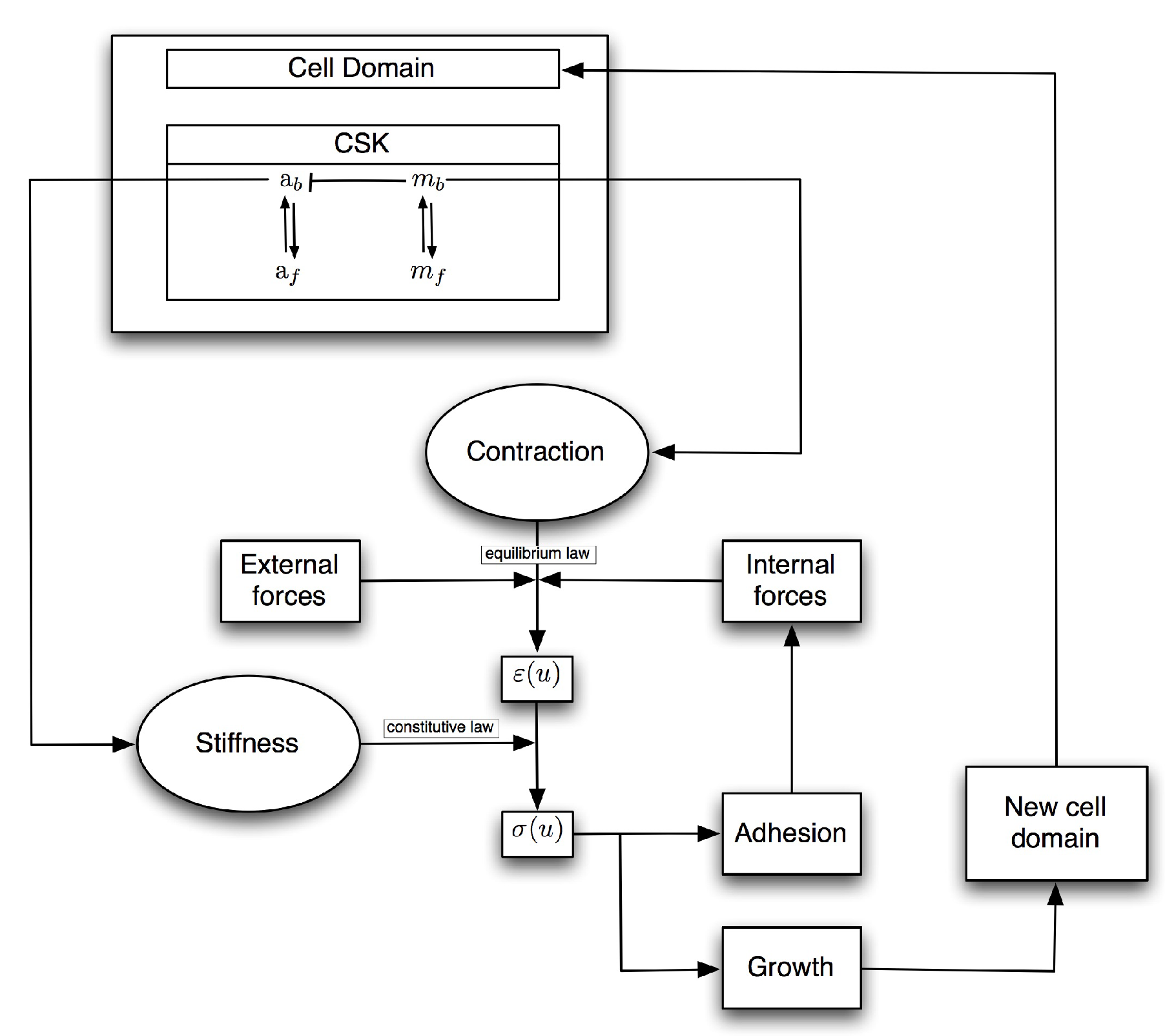
2.1. Mathematical Model
2.1.1. Mechanical Equilibrium
2.1.2. Constitutive Law
2.1.3. Reaction–Diffusion Equations
2.1.4. External Forces
2.1.5. Cell Domain Growth
2.1.6. Adhesion Process
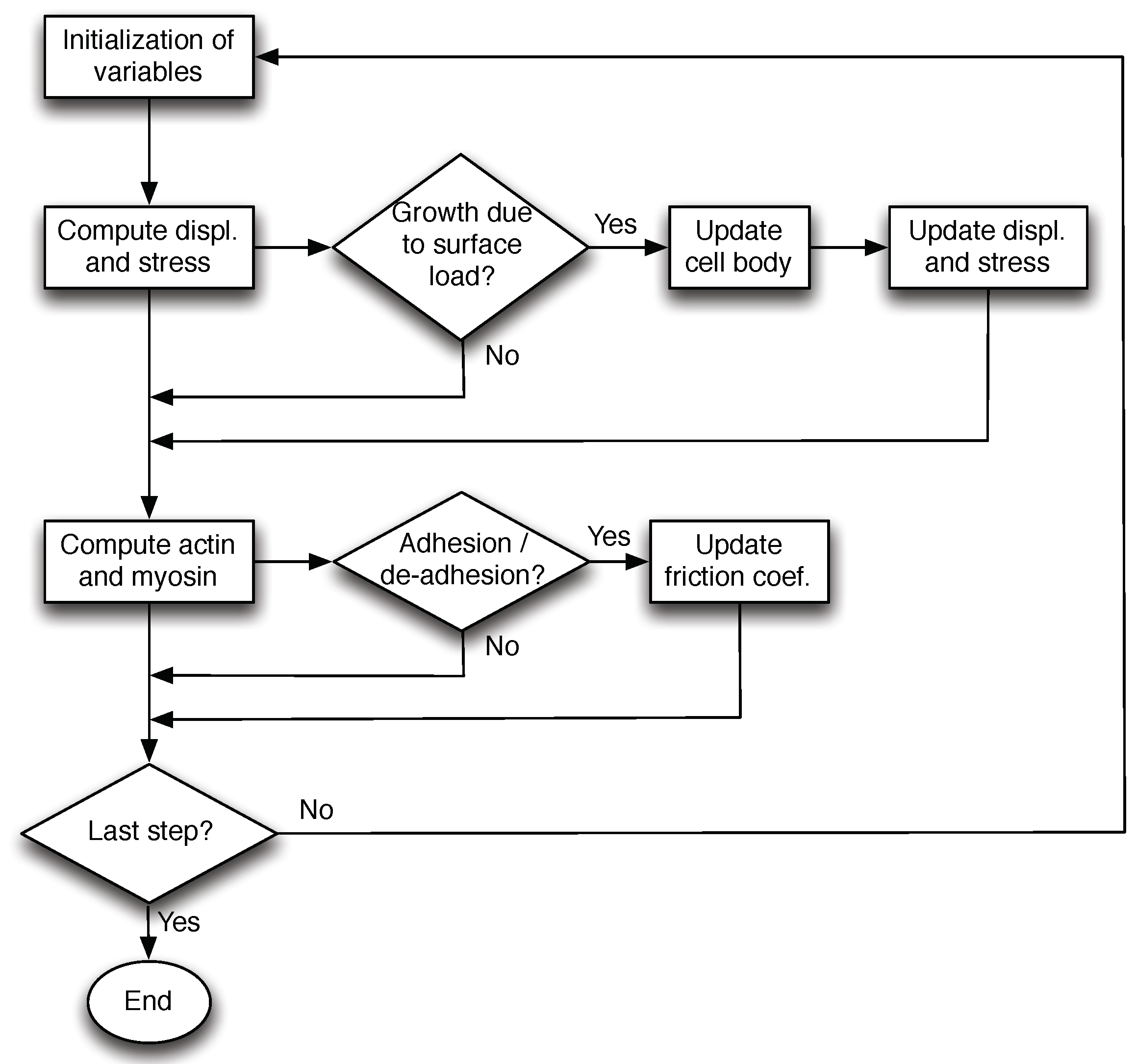
2.2. Numerical Method
- Firstly, we use the stable Crank–Nicholson scheme to compute the displacement u, and consequently the stress tensor at each time step through the corresponding constitutive law.
- Secondly, we update the actin and myosin concentrations (bound and free) using a similar scheme.
- If an external stress is applied, the cell is deformed mechanically. If the growth stress threshold is reached, the membrane is detached from the actin creating new space and Equations (16) and (17) are solved.
- Finally, after updating the variables, we check if the compression stress threshold is reached in order to update the friction coefficient with the substrate .
3. Results
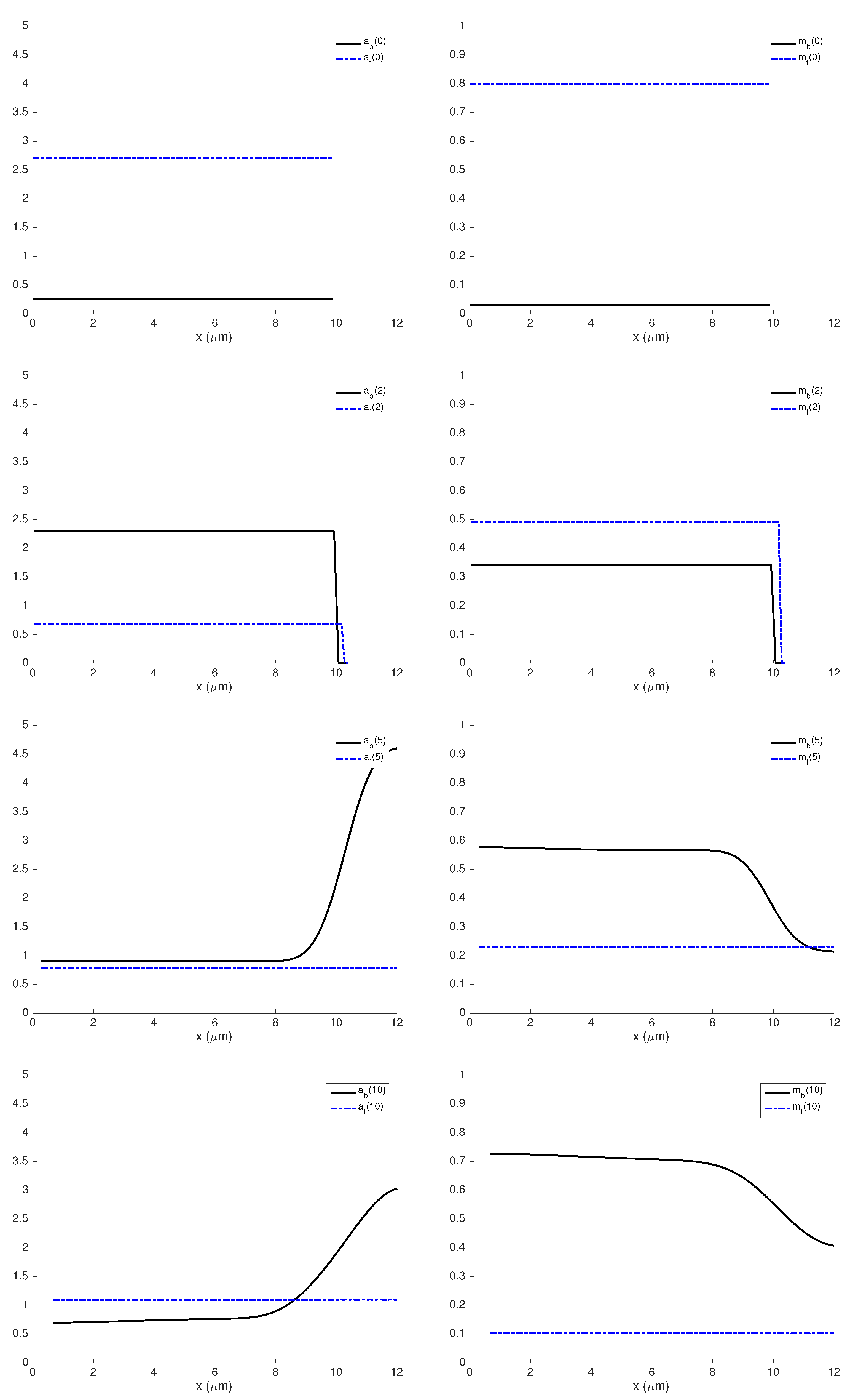
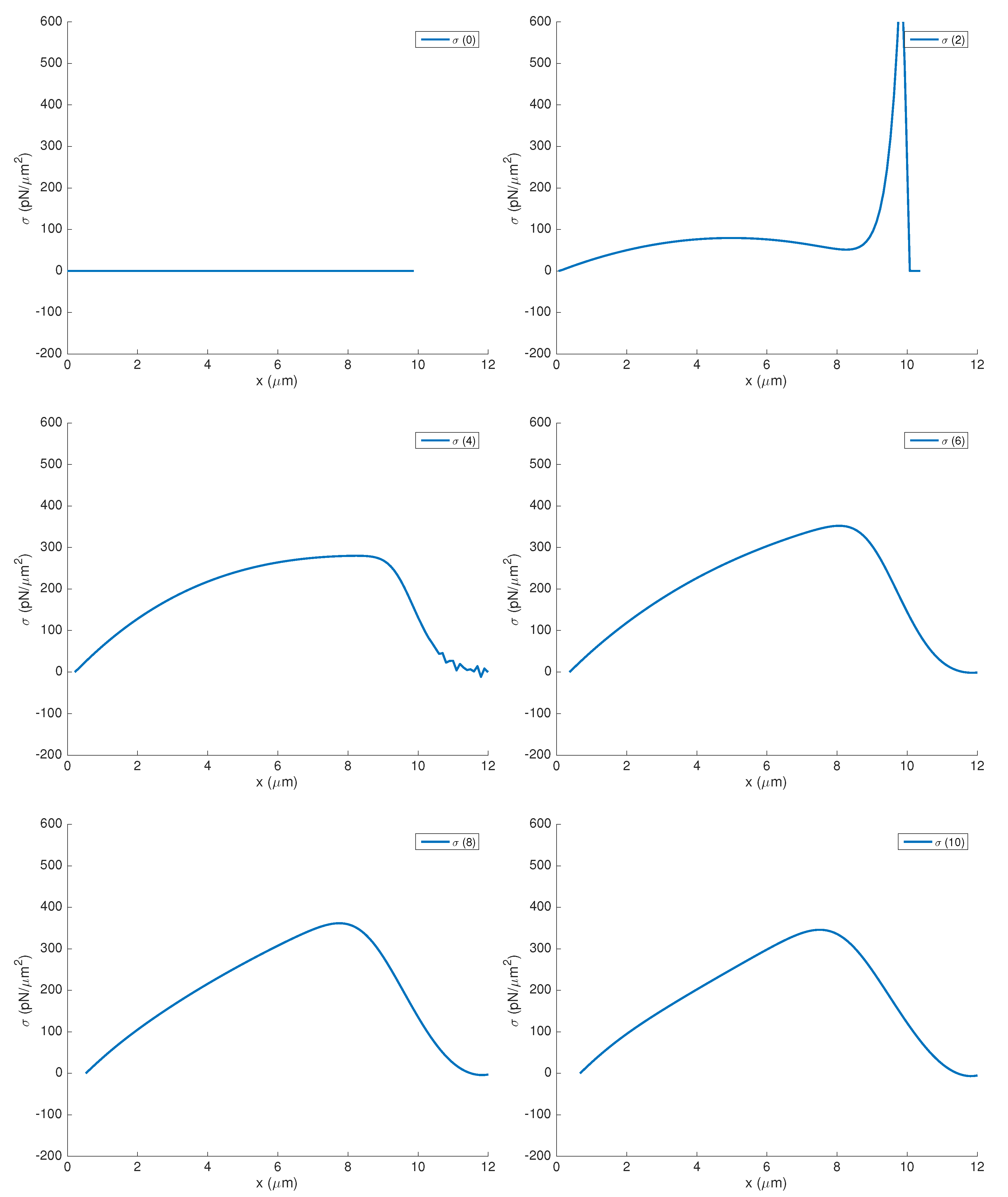
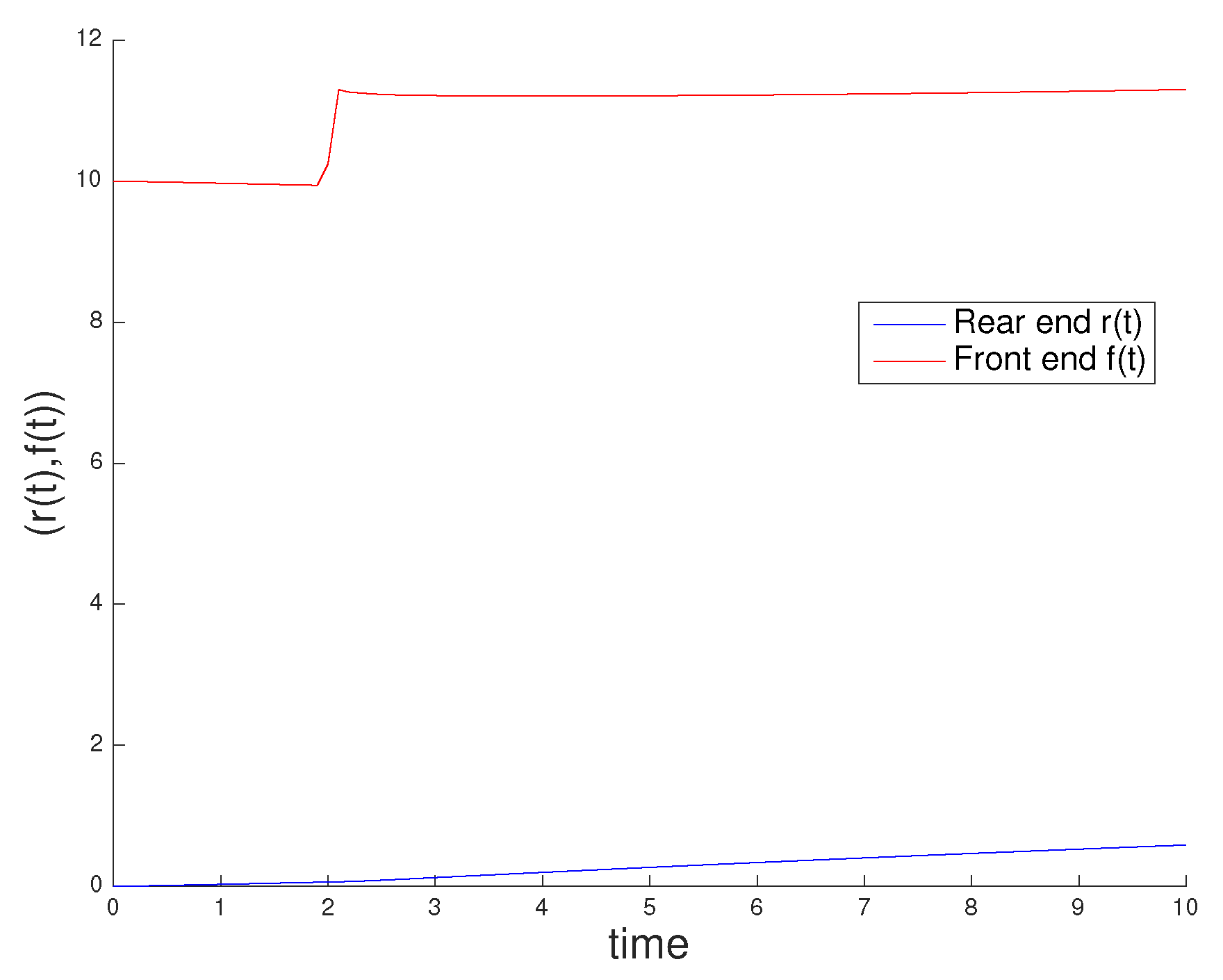
3.1. Influence of Actin and Myosin Densities on Cell Mechanics
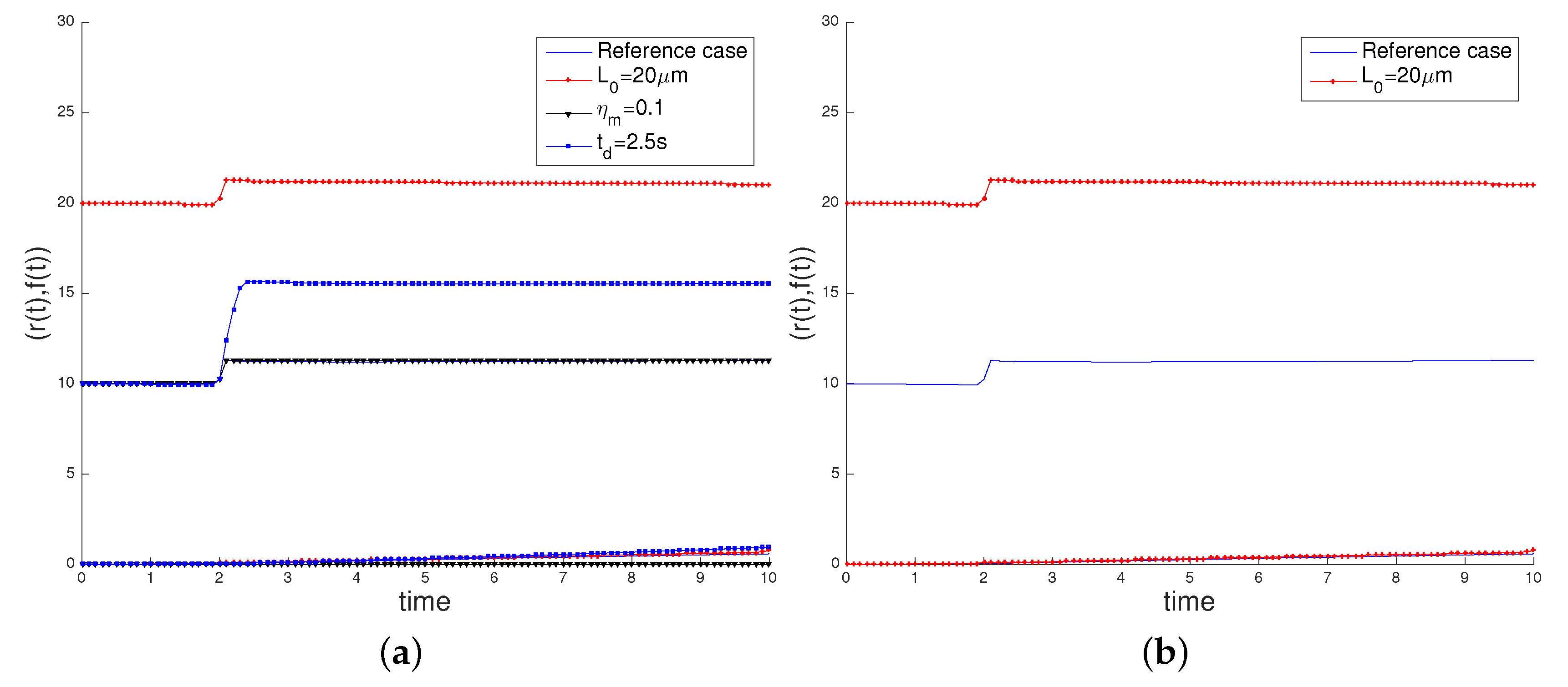
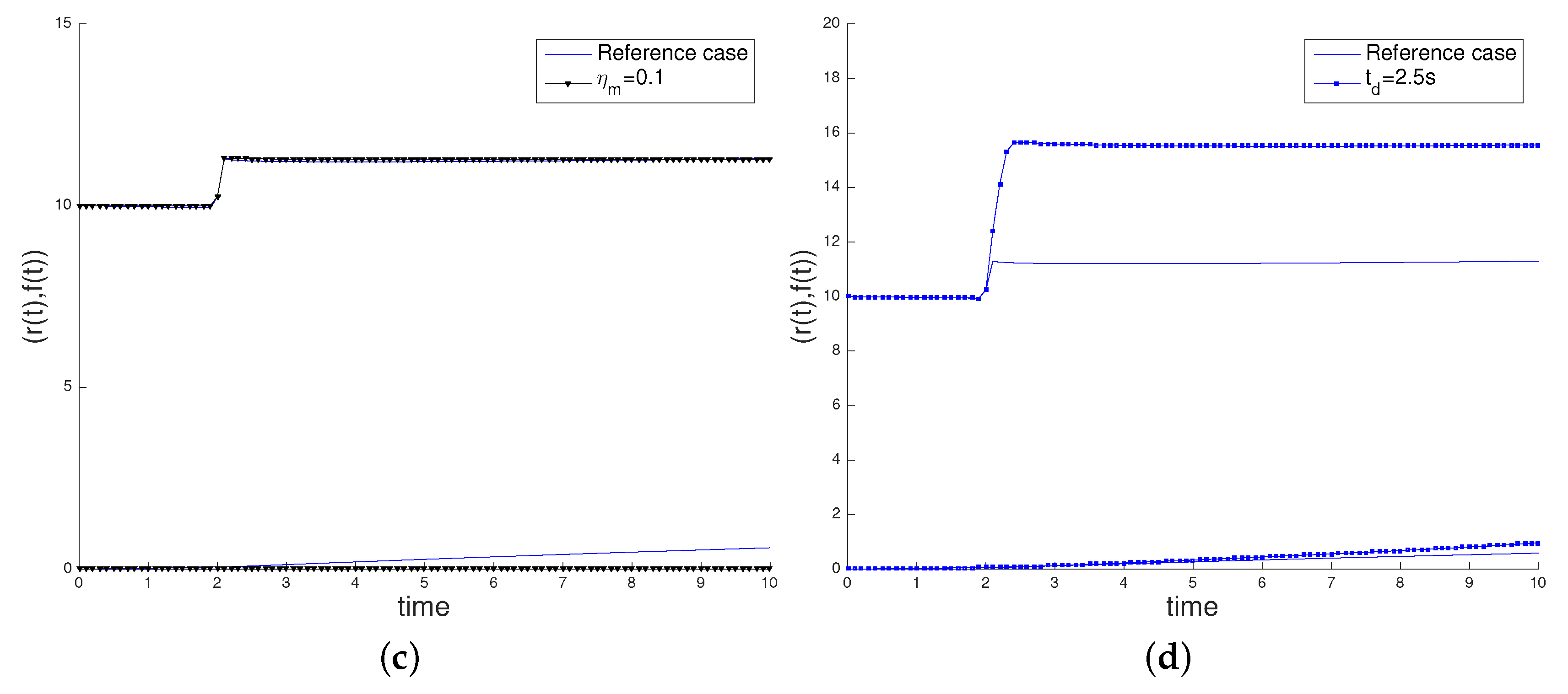
3.2. Sensitivity Analysis
- the initial cell length , increasing its value to 20 µm,
- the characteristic myosin stress , decreasing its value to 0.1 pN/µm2, in order to study the influence of the cell contractility in its movement,
- the time interval of application of the surface load, deactivating the load at = 2.5 s.
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ananthakrishnan, R.; Ehrlicher, A. The Forces Behind Cell Movement. Int. J. Biol. Sci. 2007, 3, 303–317. [Google Scholar] [CrossRef] [PubMed]
- Wilson, K.; Lewalle, A.; Fritzsche, M.; Thorogate, R.; Duke, T.; Charras, G. Mechanisms of leading edge protrusion in interstitial migration. Nat. Commun. 2013, 4, 2896. [Google Scholar] [CrossRef] [PubMed]
- Pravincumar, P.; Bader, D.L.; Knight, M.M. Viscoelastic Cell Mechanics and Actin Remodelling Are Dependent on the Rate of Applied Pressure. PLoS ONE 2012, 7, e43938. [Google Scholar] [CrossRef] [PubMed]
- Larripa, K.; Mogilner, A. Transport of a 1D viscoelastic actinmyosin strip of gel as a model of a crawling cell. Physica A 2006, 372, 113–123. [Google Scholar] [CrossRef] [PubMed]
- Zheltukhin, S.; Lui, R. One-dimensional viscoelastic cell motility models. Math. Biosci. 2011, 229, 30–40. [Google Scholar] [CrossRef] [PubMed]
- Mogilner, A. Mathematics of cell motility: Have we got its number? J. Math. Biol. 2009, 58, 105–134. [Google Scholar] [CrossRef] [PubMed]
- Holmes, W.R.; Edelstein-Keshet, L. A Comparison of Computational Models for Eukaryotic Cell Shape and Motility. PLoS Comput. Biol. 2012, 8, e1002793. [Google Scholar] [CrossRef] [PubMed]
- Gracheva, M.E.; Othmer, H.G. A continuum model of motility in ameboid cells. Bull. Math. Biol. 2004, 66, 167–193. [Google Scholar] [CrossRef] [PubMed]
- George, U.Z.; Stéphanou, A.; Madzvamuse, A. Mathematical modelling and numerical simulations of actin dynamics in the eukaryotic cell. J. Math. Biol. 2013, 66, 547–593. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, B.; Jacobson, K.; Mogilner, A. Multiscale two-dimensional modeling of a motile simple-shaped cell. Multiscale Model. Simul. 2005, 3, 413–439. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, B.; Fournier, M.F.; Jacobson, K.; Verkhovsky, A.B.; Mogilner, A. Actin-Myosin Viscoelastic Flow in the Keratocyte Lamellipod. Biophys. J. 2009, 97, 1853–1863. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, A.E. Mechanisms of cell propulsion by active stresses. New J. Phys. 2011, 13, 073009. [Google Scholar] [CrossRef] [PubMed]
- Kuusela, E.; Alt, W. Continuum model of cell adhesion and migration. J. Math. Biol. 2009, 58, 135–161. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, Y.; Prudhomme, S.; Zaman, M.H. Modeling of adhesion, protrusion, and contraction coordination for cell migration simulations. J. Math. Biol. 2014, 68, 267–302. [Google Scholar] [CrossRef] [PubMed]
- Allena, R.; Aubry, D. ‘Run-and-tumble’ or ‘look-and-run’? A mechanical model to explore the behavior of a migrating amoeboid cell. J. Theor. Biol. 2012, 306, 15–31. [Google Scholar] [CrossRef] [PubMed]
- Mak, M.; Reinhart-King, C.A.; Erickson, D. Microfabricated Physical Spatial Gradients for Investigating Cell Migration and Invasion Dynamics. PLoS ONE 2011, 6, e20825. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.J.; Piel, M.; Faure-Andre, G.; Lennon-Dumenil, A.M.; Joanny, J.F.; Prost, J.; Voituriez, R. Pushing off the Walls: A Mechanism of Cell Motility in Confinement. Phys. Rev. Lett. 2009, 102, 058103. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.J.; Voituriez, R. Mechanisms of Cell Motion in Confined Geometries. Math. Model. Nat. Phenom. 2010, 5, 84–105. [Google Scholar] [CrossRef]
- Aubry, D.; Thiam, H.; Piel, M.; Allena, R. A computational mechanics approach to assess the link between cell morphology and forces during confined migration. Biomech. Model. Mechanobiol. 2015, 14, 143–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stroka, K.M.; Gu, Z.; Sun, S.X.; Konstantopoulos, K. Bioengineering paradigms for cell migration in confined microenvironments. Curr. Opin. Cell Biol. 2014, 30, 41–50. [Google Scholar] [CrossRef] [PubMed]
- Shao, D.; Levine, H.; Rappel, W. Coupling actin flow, adhesion, and morphology in a computational cell motility model. Phys. Rev. Lett. 2013, 109, 6851–6856. [Google Scholar] [CrossRef] [PubMed]
- Walther, G.R.; Marée, A.F.M.; Edelstein-Keshet, L.; Grieneisen, V.A. Deterministic Versus Stochastic Cell Polarisation through Wave-Pinning. Bull. Math. Biol. 2012, 74, 2570–2599. [Google Scholar] [CrossRef] [PubMed]
- Stroka, K.M.; Jiang, H.; Chen, S.H.; Tong, Z.; Wirtz, D.; Sun, S.X.; Konstantopoulos, K. Water permeation drives tumor cell migration in confined microenvironments. Cell 2014, 157, 611–623. [Google Scholar] [CrossRef] [PubMed]
- Scianna, M.; Preziosi, L. Modeling the influence of nucleus elasticity on cell invasion in fiber networks and microchannels. J. Theor. Biol. 2013, 317, 394–406. [Google Scholar] [CrossRef] [PubMed]
- Giverso, C.; Grillo, A.; Preziosi, L. Influence of nucleus deformability on cell entry into cylindrical structures. Biomech. Model. Mechan. 2014, 13, 481–502. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.J.; Le Berre, M.; Lautenschlaeger, F.; Maiuri, P.; Callan-Jones, A.; Heuzé, M.; Takaki, T.; Voituriez, R.; Piel, M. Confinement and Low Adhesion Induce Fast Amoeboid Migration of Slow Mesenchymal Cells. Cell 2015, 160, 659–672. [Google Scholar] [CrossRef] [PubMed]
- Lautscham, L.A.; Kämmerer, C.; Lange, J.R.; Kolb, T.; Mark, C.; Schilling, A.; Strissel, P.L.; Strick, R.; Gluth, C.; Rowat, A.C.; et al. Migration in Confined 3D Environments Is Determined by a Combination of Adhesiveness, Nuclear Volume, Contractility, and Cell Stiffness. Biophys. J. 2015, 109, 900–913. [Google Scholar] [CrossRef] [PubMed]
- Bergert, M.; Erzberger, A.; Desai, R.A.; Aspalter, I.M.; Oates, A.C.; Charras, G.; Salbreux, G.; Paluch, E.K. Force transmission during adhesion-independent migration. Nat. Cell Biol. 2015, 17, 524–529. [Google Scholar] [CrossRef] [PubMed]
- Chabaud, M.; Heuzé, M.; Bretou, M.; Vargas, P.; Maiuri, P.; Solanes, P.; Maurin, M.; Terriac, E.; Le Berre, M.; Lankar, D.; et al. Cell migration and antigen capture are antagonistic processes coupled by myosin II in dendritic cells. Nat. Commun. 2015, 6, 7526. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Symbol | Value | Source |
|---|---|---|---|
| Substrate friction | 103 pNs/µm3 | [4] | |
| Reduced substrate friction | 10−3 pNs/µm3 | Estimated | |
| Initial Young modulus | 104 pNs/µm2 | [4] | |
| Myosin stress | 103 pNs/µm2 | [4] | |
| Bound actin and myosin diffusion coefficient | 0.1 µm2/s | [4] | |
| Free actin and myosin diffusion coefficient | 104 µm2/s | Estimated | |
| Activation rate for bound actin | 0.067 s−1 | [22] | |
| Inactivation rate for bound actin | 0.9 s−1 | [22] | |
| Bound actin maximal rate | 1 s−1 | [22] | |
| Bound actin saturation parameter | K | 1 µM | [22] |
| Activation rate for bound myosin | 0.25 s−1 | Estimated | |
| Depolymerization rate for bound myosin | 0.02 s−1 | Estimated |
| Parameter | Symbol | Value |
|---|---|---|
| Initial length of the cell body | 10 µm | |
| Simulation spatial step | 0.1 µm | |
| Total time of the simulation | T | 10 s |
| Simulation time step | 0.01 s | |
| Stress threshold for growth | 500 pN | |
| Stress threshold for contraction | 750 pN | |
| Activation time | 2 s | |
| Activation stress | 25,000 pN | |
| Deactivation time | 2.1 s | |
| Deactivation stress | 500 pN |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez, M.T.; García-Aznar, J.M. Modeling Confined Cell Migration Mediated by Cytoskeleton Dynamics. Computation 2018, 6, 33. https://doi.org/10.3390/computation6020033
Sánchez MT, García-Aznar JM. Modeling Confined Cell Migration Mediated by Cytoskeleton Dynamics. Computation. 2018; 6(2):33. https://doi.org/10.3390/computation6020033
Chicago/Turabian StyleSánchez, María Teresa, and José Manuel García-Aznar. 2018. "Modeling Confined Cell Migration Mediated by Cytoskeleton Dynamics" Computation 6, no. 2: 33. https://doi.org/10.3390/computation6020033
APA StyleSánchez, M. T., & García-Aznar, J. M. (2018). Modeling Confined Cell Migration Mediated by Cytoskeleton Dynamics. Computation, 6(2), 33. https://doi.org/10.3390/computation6020033






