Wear of Functionally Graded Coatings under Frictional Heating Conditions
Abstract
:1. Introduction
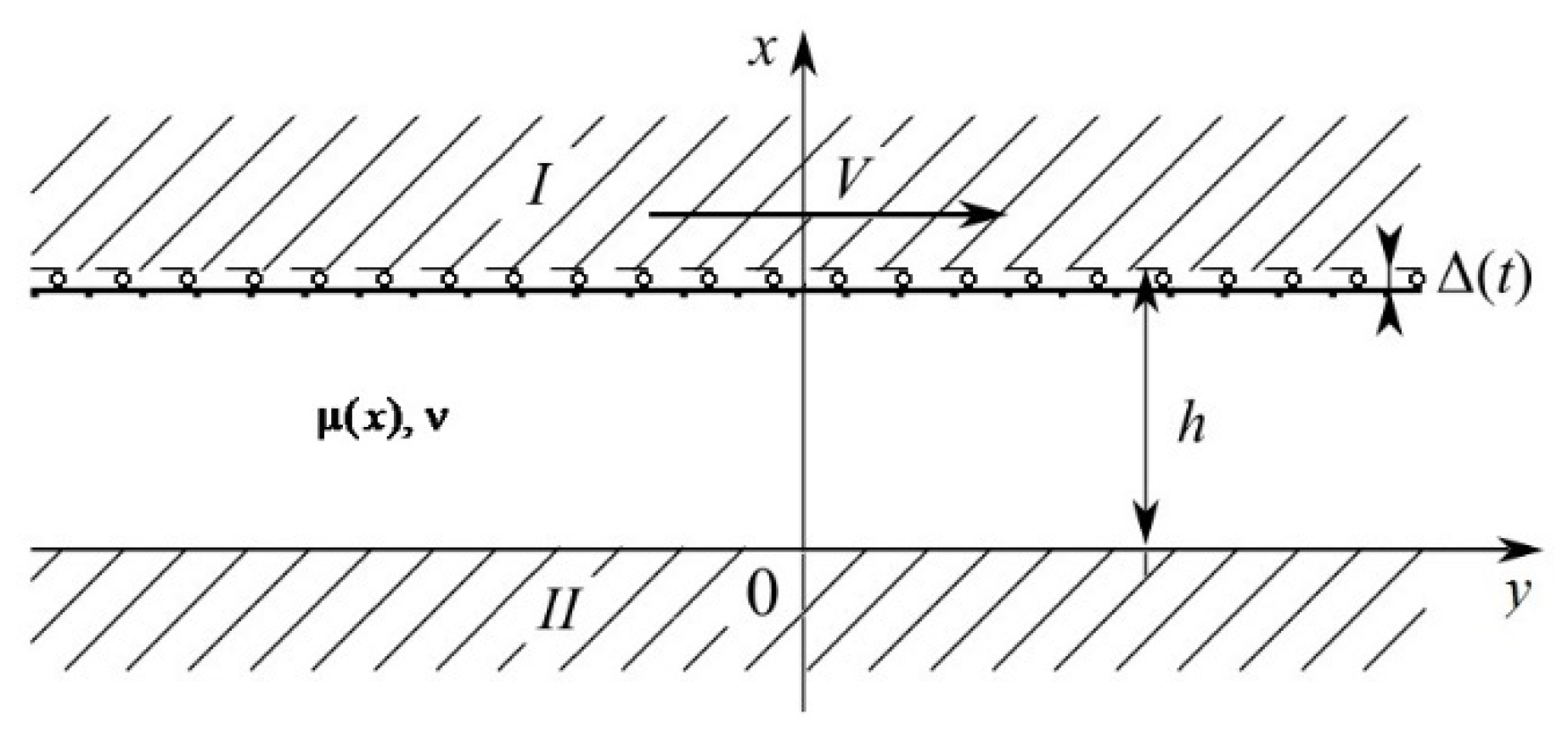
2. Problem Statement
3. Exact Solution for Arbitrary µ(x)
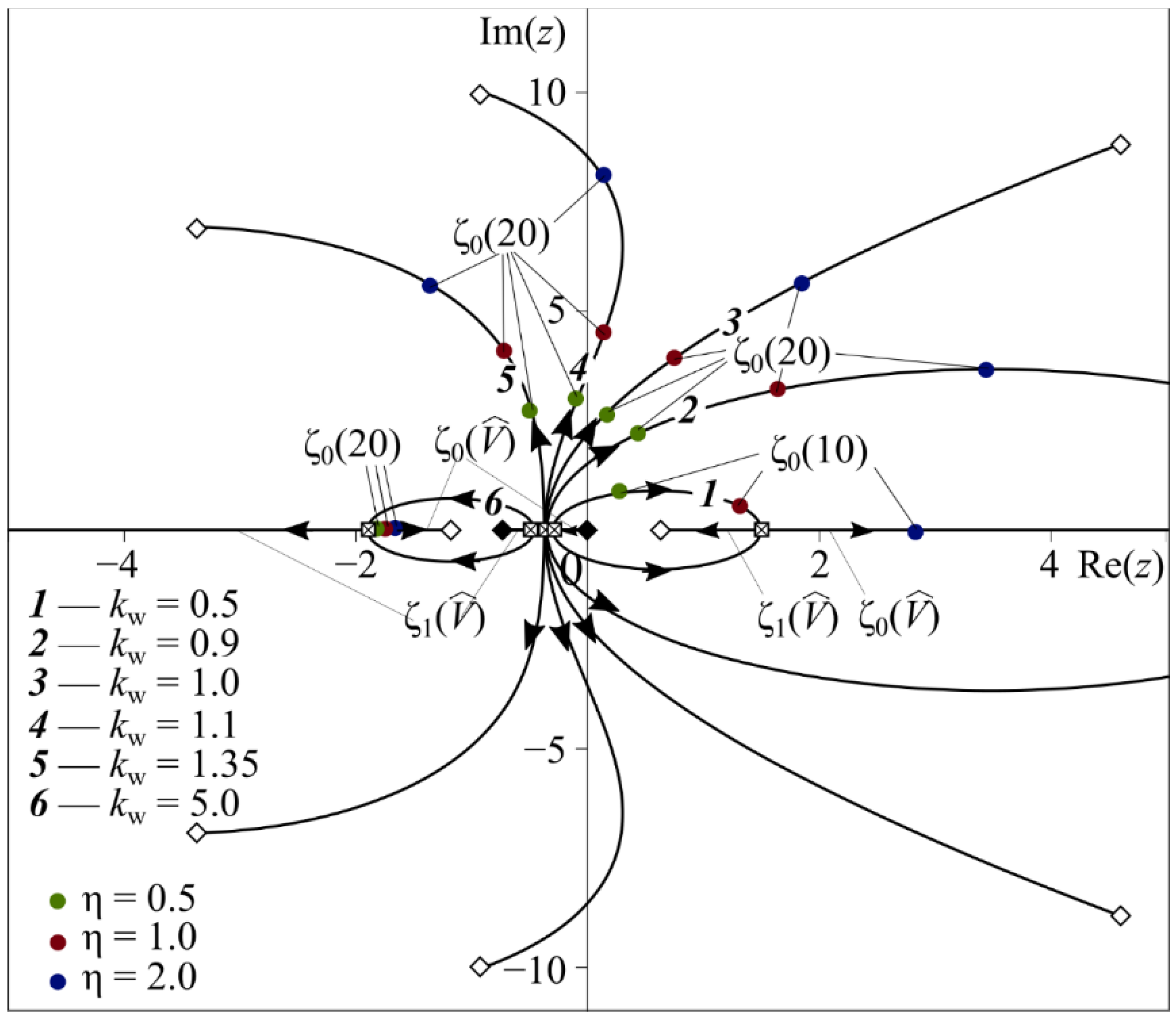
4. Poles of the Integrands
5. Formulas for Exact Solution
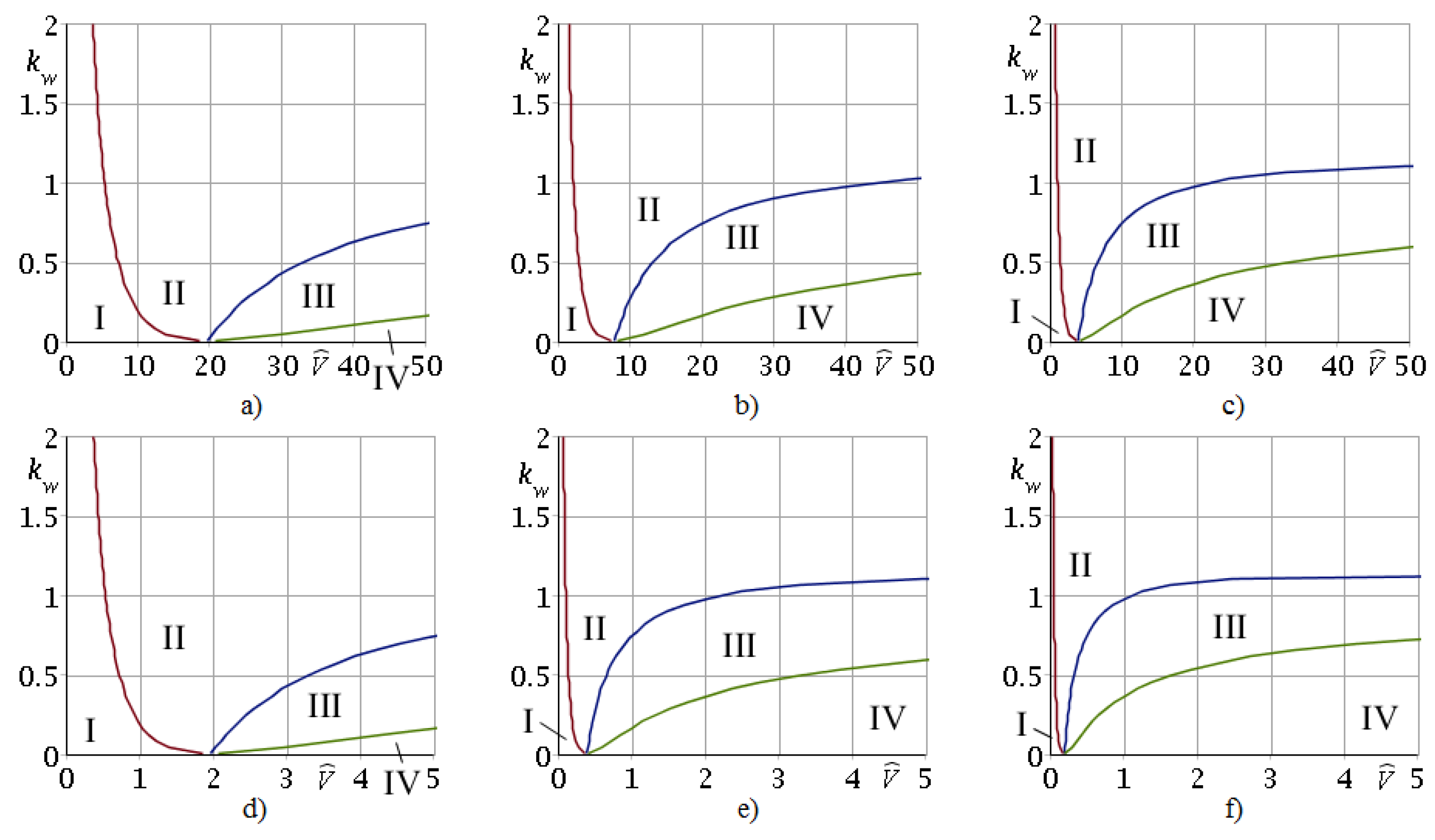
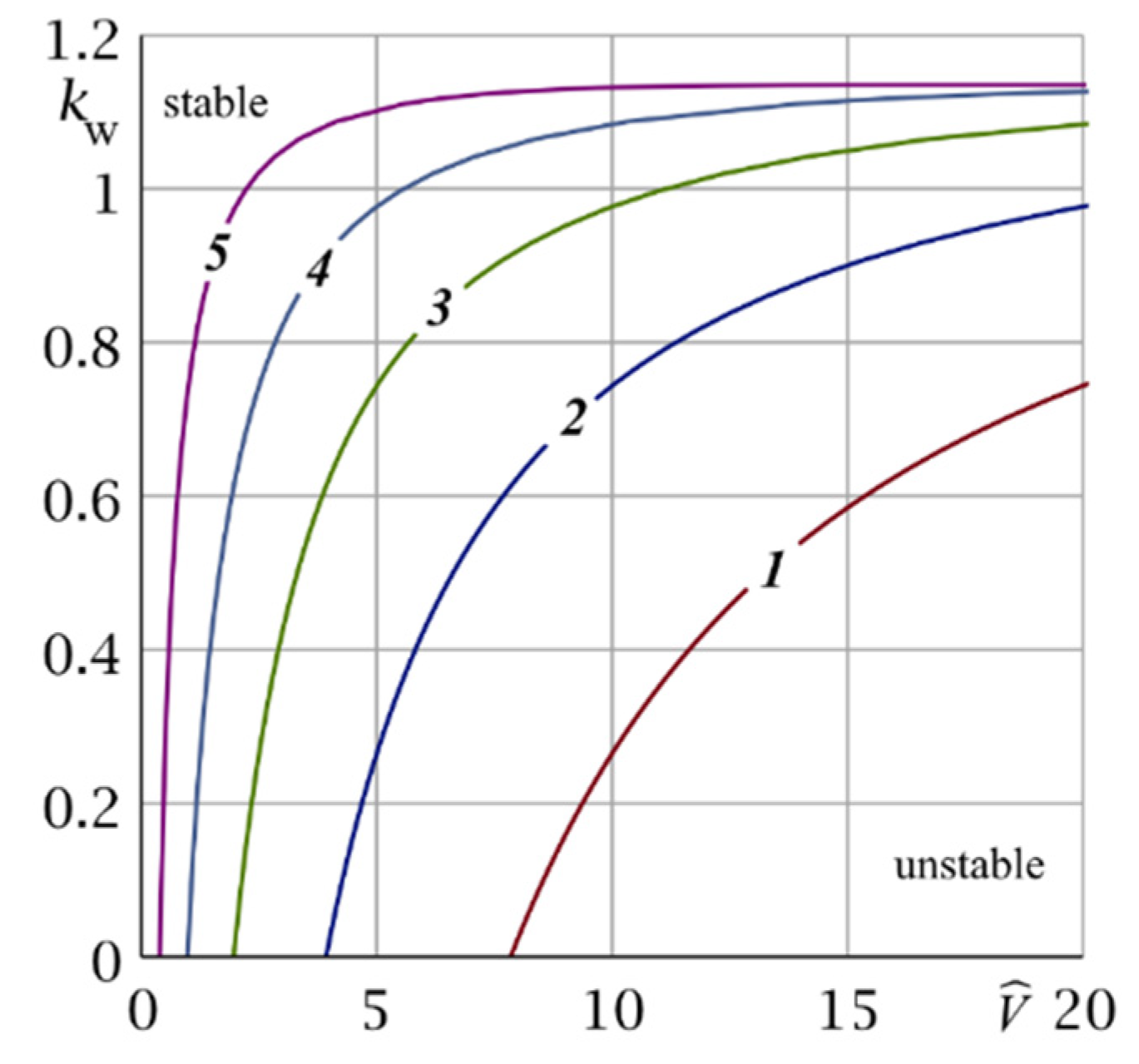
6. Domains of Stability and Instability
7. Features of Wear of FGM Coating
8. Discussion
9. Conclusions
- −
- A dimensionless parameter of the FGIM of the coating, which characterizes the FGM of the coating and its presence in all formulas of the main parameters of the contact with friction;
- −
- Boundaries of the regions of thermoelastic instability in the space of dimensionless parameters of the problem: , , , ;
- −
- Features of the kinematic scheme of wear, which consists in setting an arbitrary law of upsetting of a hard abrasive on the surface of a strip made of FGM and leading to an uncontrolled increase in temperature and contact stresses;
- −
- A special grinding scheme, consisting in the development of such a law of displacement of a hard abrasive into the surface of a strip made of FGM, with the help of which the growth of both the temperature at the contact and the contact stresses is limited.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| horizontal component of displacements in the coating | |
| normal component of stresses in the coating | |
| shear component of stresses in the coating | |
| the coating temperature | |
| thickness of the coating | |
| sliding velocity of the abrasive (half-plane I) | |
| shear modulus of the coating material | |
| Poisson’s ratio of the coating material | |
| coefficient of linear heat expansion of the coating material | |
| the thermal diffusivity of the coating material | |
| the coefficient of friction | |
| the proportionality coefficient between the work of friction forces and the volume of removed material | |
| the thermal conductivity of the coating material | |
| the heat transfer coefficient through the coating–substrate interface | |
| coating wear | |
| the amount of frictional heat originated at the contact interface | |
| the law of indentation of a hard abrasive (half-plane I) into the coating |
References
- Watanabe, Y.; Nakamura, T. Microstructures and wear resistances of hybrid Al–(Al3Ti+Al3Ni) FGMs fabricated by a centrifugal method. Intermetallics 2001, 9, 33–43. [Google Scholar] [CrossRef]
- El-Hadad, S.; Sato, H.; Watanabe, Y. Wear of Al/Al3Zr functionally graded materials fabricated by centrifugal solid-particle method. J. Mater. Process. Technol. 2010, 210, 2245–2251. [Google Scholar] [CrossRef]
- Melgarejo, Z.H.; Suárez, O.M.; Sridharan, K. Wear resistance of a functionally-graded aluminum matrix composite. Scr. Mater. 2006, 55, 95–98. [Google Scholar] [CrossRef]
- Gomes, J.R.; Ribeiro, A.R.; Vieira, A.C.; Miranda, A.S.; Rocha, L.A. Wear mechanisms in functionally graded aluminium matrix composites: Effect of the presence of an aqueous solution. Mater. Sci. Forum. 2005, 492–493, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Sato, H.; Murase, T.; Fujii, T.; Onaka, S.; Watanabe, Y.; Kato, M. Formation of a wear-induced layer with nanocrystalline structure in Al–Al3Ti functionally graded material. Acta Mater. 2008, 56, 4549–4558. [Google Scholar] [CrossRef]
- Vieira, A.C.; Sequeira, P.D.; Gomes, J.R.; Rocha, L.A. Dry sliding wear of Al alloy/SiCp functionally graded composites: Influence of processing conditions. Wear 2009, 267, 585–592. [Google Scholar] [CrossRef]
- Radhika, N.; Raghu, R. The mechanical properties and abrasive wear behavior of functionally graded aluminum/AlB2 composites produced by centrifugal casting. Part. Sci. Technol. 2017, 35, 575–582. [Google Scholar] [CrossRef]
- Hu, F.Y.; Cui, A.Y.; Hu, B.; Fu, P.F.; Zhao, P.Z.; Lu, C.L. Microstructure and wear behavior of Ti-matrix functional gradient layer. Adv. Mater. Res. 2011, 311–313, 2093–2098. [Google Scholar] [CrossRef]
- Miyoshi, K.; Pohlchuck, B.; Street, K.; Zabinski, J.; Sanders, J.H.; Voevodin, A.; Wu, R. Sliding wear and fretting wear of diamondlike carbon-based, functionally graded nanocomposite coatings. Wear 1999, 225–229, 65–73. [Google Scholar] [CrossRef]
- Cetinel, H.; Uyulgan, B.; Tekmen, C.; Ozdemir, I.; Celık, E. Wear properties of functionally gradient layers on stainless steel substrates for high temperature applications. Surf. Coat. Technol. 2003, 174–175, 1089–1094. [Google Scholar] [CrossRef]
- Prchlik, L.; Sampath, S.; Gutleber, J.; Bancke, G.; Ruff, A.W. Friction and wear properties of WC-Co and Mo-Mo2C based functionally graded materials. Wear 2001, 249, 1103–1115. [Google Scholar] [CrossRef]
- Askari, E.; Mehrali, M.; Metselaar, I.H.S.C.; Kadri, N.A.; Rahman, M.M. Fabrication and mechanical properties of Al2O3/SiC/ZrO2 functionally graded material by electrophoretic deposition. J. Mech. Behav. Biomed. Mater. 2012, 12, 144–150. [Google Scholar] [CrossRef]
- Siahpoosh, H.; Abbasi, A.; Aliofkhazraei, M.; Khajavi, B.; Majidi, H. Effect of pulse frequency on tribological behaviour of functionally graded Ni/Al2O3 nanocomposite coatings. Procedia Mater. Sci. 2015, 11, 498–502. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Han, Y.; Huang, J. Formation of Al2O3–ZrO2 composite coating on zirconium by micro-arc oxidation. Scr. Mater. 2008, 59, 203–206. [Google Scholar] [CrossRef]
- Nai, S.M.L.; Gupta, M.; Lim, C.Y.H. Synthesis and wear characterization of Al based, free standing functionally graded materials: Effects of different matrix compositions. Compos. Sci. Technol. 2003, 63, 1895–1909. [Google Scholar] [CrossRef]
- Guler, M.A.; Erdogan, F. The frictional sliding contact problems of rigid parabolic and cylindrical stamps on graded coatings. Int. J. Mech. Sci. 2007, 49, 161–182. [Google Scholar] [CrossRef]
- Altenbach, H.; Eremeyev, V.A. Eigen-vibrations of plates made of functionally graded material. Comput. Mater. Contin. 2009, 9, 153–177. [Google Scholar]
- Selvadurai, A.P.S.; Katebi, A. Mindlin’s problem for an incompressible elastic half-space with an exponential variation in the linear elastic shear modulus. Int. J. Eng. Sci. 2013, 65, 9–21. [Google Scholar] [CrossRef]
- Tokovyy, Y.; Ma, C.-C. An analytical solution to the three-dimensional problem on elastic equilibrium of an exponentially-inhomogeneous layer. J. Mech. 2015, 31, 545–555. [Google Scholar] [CrossRef]
- Aizikovich, S.M.; Vasil’ev, A.S.; Volkov, S.S. The axisymmetric contact problem of the indentation of a conical punch into a half-space with a coating inhomogeneous in depth. J. Appl. Math. Mech. 2015, 79, 500–505. [Google Scholar] [CrossRef]
- Alinia, Y.; Beheshti, A.; Guler, M.A.; El-Borgi, S.; Polycarpou, A.A. Sliding contact analysis of functionally graded coating/substrate system. Mech. Mater. 2016, 94, 142–155. [Google Scholar] [CrossRef]
- Ma, J.; El-Borgi, S.; Ke, L.L.; Wang, Y.S. Frictional contact problem between a functionally graded magnetoelectroelastic layer and a rigid conducting flat punch with frictional heat generation. J. Therm. Stress. 2016, 39, 245–277. [Google Scholar] [CrossRef]
- Volkov, S.S.; Vasiliev, A.S.; Aizikovich, S.M.; Seleznev, N.M.; Leontieva, A.V. Stress-strain state of an elastic soft functionally-graded coating subjected to indentation by a spherical punch. PNRPU Mech. Bull. 2016, 4, 20–34. [Google Scholar]
- Selvadurai, A.P.S.; Katebi, A. The Boussinesq–Mindlin problem for a non-homogeneous elastic halfspace. Z. Angew. Math. Phys. 2016, 67, 68. [Google Scholar] [CrossRef]
- Kudish, I.I.; Volkov, S.S.; Vasiliev, A.S.; Aizikovich, S.M. Lubricated point heavily loaded contacts of functionally graded materials. Part 1. Drycontacts. Math. Mech. Solids 2018, 201823, 1061–1080. [Google Scholar] [CrossRef]
- Vasiliev, A.S.; Volkov, S.S.; Aizikovich, S.M. Approximated analytical solution of a problem on indentation of an electro-elastic half-space with inhomogeneous coating by a conductive punch. Dokl. Phys. 2018, 63, 18–22. [Google Scholar] [CrossRef]
- Singh, S.; Singh, R. Wear modelling of Al-Al2O3 functionally graded material prepared by FDM assisted investment castings using dimensionless analysis. J. Manuf. Process. 2015, 20, 507–514. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Dow, T.A.; Burton, R.A. The role of wear in the initiation of thermoelastic instabilities of rubbing contact. J. Lubr. Technol. 1973, 95, 71–75. [Google Scholar] [CrossRef]
- Alexandrov, V.M.; Annakulova, G.K. A contact problem of thermo-elasticity with wear and heat release caused by friction. Trenie i Iznos 1990, 11, 24–28. [Google Scholar]
- Alexandrov, V.M.; Annakulova, G.K. Interaction between coatings of a body with deformation, wear, and heat release due to friction. Trenie i Iznos 1992, 13, 154–160. [Google Scholar]
- Zmitrowicz, A. A thermodynamical model of contact, friction and wear: I governing equations. Wear 1987, 114, 135–168. [Google Scholar] [CrossRef]
- Zmitrowicz, A. A thermodynamical model of contact, friction and wear: II constitutive equations for materials and linearized theories. Wear 1987, 114, 169–197. [Google Scholar] [CrossRef]
- Strömberg, N.; Johansson, L.; Klarbring, A. Derivation and analysis of a generalized standard model for contact, friction and wear. Int. J. Solids Struct. 1996, 33, 1817–1836. [Google Scholar] [CrossRef]
- Andrews, K.T.; Shillor, M.; Wright, S.; Klarbring, A. A dynamic thermoviscoelastic contact problem with friction and wear. Int. J. Eng. Sci. 1997, 35, 1291–1309. [Google Scholar] [CrossRef]
- Strömberg, N. Finite element treatment of two-dimensional thermoelastic wear problem. Comput. Methods Appl. Mech. Eng. 1999, 177, 441–455. [Google Scholar] [CrossRef] [Green Version]
- Evtushenko, A.A.; Pyr’ev, Y.A. Influence of wear on the development of thermoelastic instability of a frictional contact. Izv. Ross. Akad. Nauk Mekhanika Tverd. Tela 1997, 1, 114–121. [Google Scholar]
- Pyr’ev, Y.A.; Grilitsky, D.V. The non-stationary problem of the frictional contact for a cylinder taking into account heat release and wear. Appl. Math. Tech. Phys. 1996, 37, 99–104. [Google Scholar]
- Awrejcewicz, J.; Pyryev, Y. Thermoelastic contact of a rotating shaft with a rigid bush in conditions of bush wear and stick-slip movements. Int. J. Eng. Sci. 2002, 40, 1113–1130. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Mitrin, B.I.; Lubyagin, I.A. Effect of wear on frictional heating and thermoelastic instability of sliding contact. Comput. Contin. Mech. 2016, 9, 430–442. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Mitrin, B.I.; Lubyagin, I.A. Wear resistance of coating materials under the frictional heating conditions. J. Frict. Wear 2017, 38, 265–271. [Google Scholar] [CrossRef]
- Belyakov, N.S.; Nosko, A.P. Thermoelastic problem of friction of plane-parallel layers with allowance for nonstationarity of thermal processes. J. Frict. Wear 2010, 31, 317–325. [Google Scholar] [CrossRef]
- Gu, R.J.; Kuttler, K.L.; Shillor, M. Frictional wear of a thermoelastic beam. J. Math. Anal. Appl. 2000, 242, 212–236. [Google Scholar] [CrossRef] [Green Version]
- Papangelo, A.; Ciavarella, M. The effect of wear on ThermoElastic Instabilities (TEI) in bimaterial interfaces. Tribol. Int. 2020, 142, 105977. [Google Scholar] [CrossRef]
- Papangelo, A.; Ciavarella, M. Can wear completely suppress thermoelastic instabilities? J. Tribol. 2020, 142, 051501. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Mitrin, B.I.; Lubyagin, I.A.; Kudish, I.I. Diagnostics of wear thermoelastic instability based on sliding contact parameter monitoring. IMA J. Appl. Math. 2019, 84, 345–365. [Google Scholar] [CrossRef]
- Kovalenko, A.D. Thermoelasticity: Basic Theory and Applications; Wolters-Noordhoff: Groningen, The Netherlands, 1970. [Google Scholar]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Oxford University Press: London, UK, 1950. [Google Scholar]
- Ditkin, V.A.; Prudnikov, A.P. Operational Calculus; Vishaya Shkola: Moscow, Russia, 1975. (In Russian) [Google Scholar]
- Brychkov, Y.A.; Prudnikov, A.P. Integral Transformations of Generalized Functions; Gordon & Breach Science Publishers, CRC-Press: New York, NY, USA, 1989. [Google Scholar]
- Hurwitz, A.; Courant, R. Theory of Functions; Nauka Publishers: Moscow, Russia, 1968. (In Russian) [Google Scholar]
- Zelentsov, V.B.; Mitrin, B.I.; Aizikovich, S.M.; Ke, L.L. Instability of solution of the dynamic sliding frictional contact problem of coupled thermoelasticity. Mater. Phys. Mech. 2015, 23, 14–19. [Google Scholar]
- Zelentsov, V.B.; Mitrin, B.I.; Aizikovich, S.M. Dynamic and quasi-static instability of sliding thermoelastic frictional contact. J. Frict. Wear 2016, 37, 213–220. [Google Scholar] [CrossRef]
- Zelentsov, V.B.; Mitrin, B.I. Thermoelastic instability in the quasi-static coupled thermoelasticity problem dealt with the sliding contact with frictional heating. Mech. Solids 2019, 54, 58–69. [Google Scholar] [CrossRef]

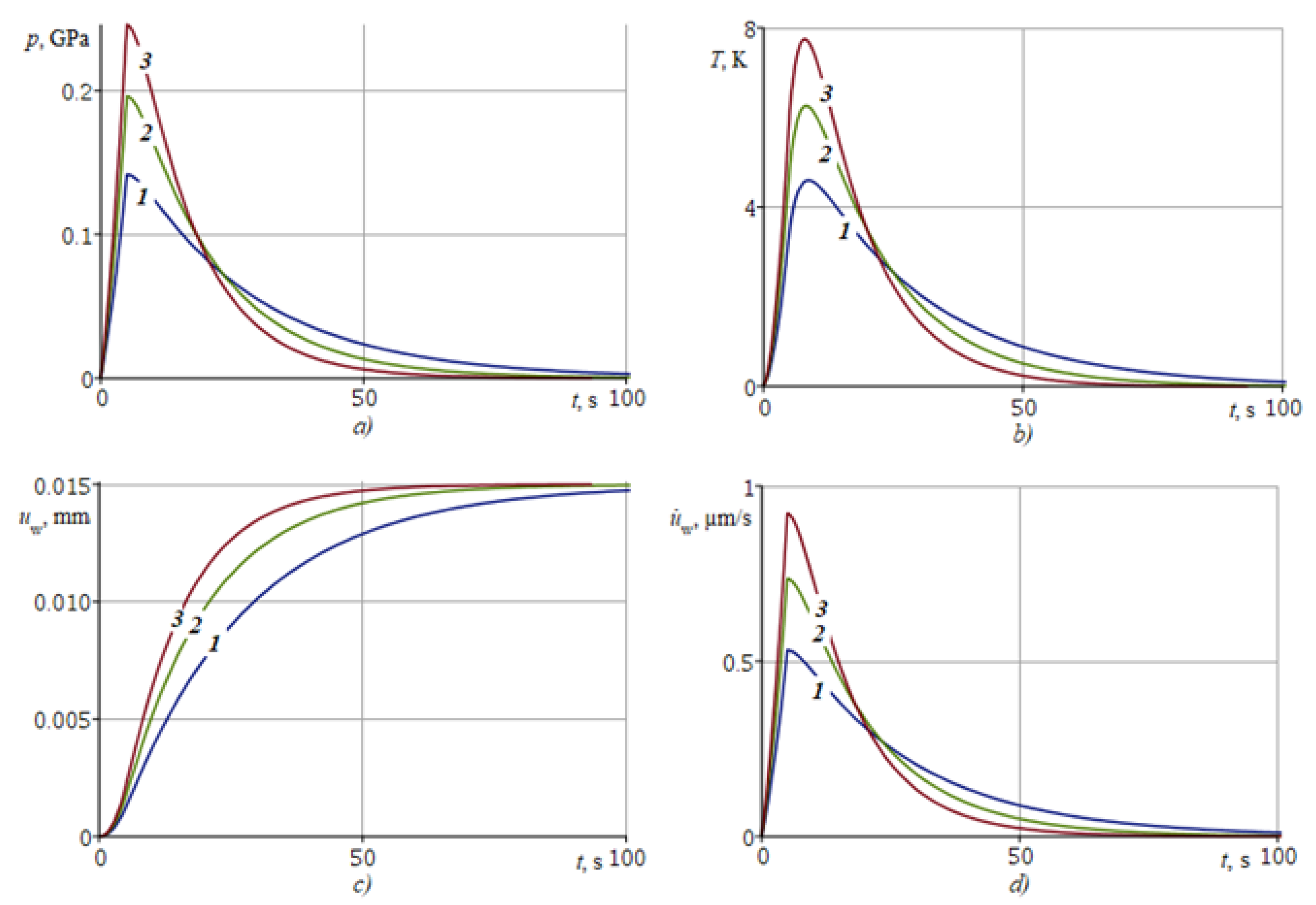
| Curve No. | η | |
|---|---|---|
| 1 | 50 | 0.361287 |
| 2 | 75 | 0.497067 |
| 3 | 100 | 0.619564 |
| tw, s | ||||||
|---|---|---|---|---|---|---|
| V = 2.5 mm/s | V = 5.0 mm/s | V = 2.5 mm/s | V = 5.0 mm/s | V = 2.5 mm/s | V = 5.0 mm/s | |
| 50 | 192.3 | 124.6 | 0.142 | 0.144 | 4.600 | 8.996 |
| 75 | 128.9 | 30.2 | 0.196 | 0.201 | 6.292 | 12.279 |
| 100 | 93.3 | 18.6 | 0.246 | 0.253 | 7.749 | 15.153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zelentsov, V.B.; Lapina, P.A.; Mitrin, B.I. Wear of Functionally Graded Coatings under Frictional Heating Conditions. Nanomaterials 2022, 12, 142. https://doi.org/10.3390/nano12010142
Zelentsov VB, Lapina PA, Mitrin BI. Wear of Functionally Graded Coatings under Frictional Heating Conditions. Nanomaterials. 2022; 12(1):142. https://doi.org/10.3390/nano12010142
Chicago/Turabian StyleZelentsov, Vladimir B., Polina A. Lapina, and Boris I. Mitrin. 2022. "Wear of Functionally Graded Coatings under Frictional Heating Conditions" Nanomaterials 12, no. 1: 142. https://doi.org/10.3390/nano12010142






