Heat Transport during Colloidal Mixture of Water with Al2O3-SiO2 Nanoparticles within Porous Medium: Semi-Analytical Solutions
Abstract
:1. Introduction
Novelty of This Study
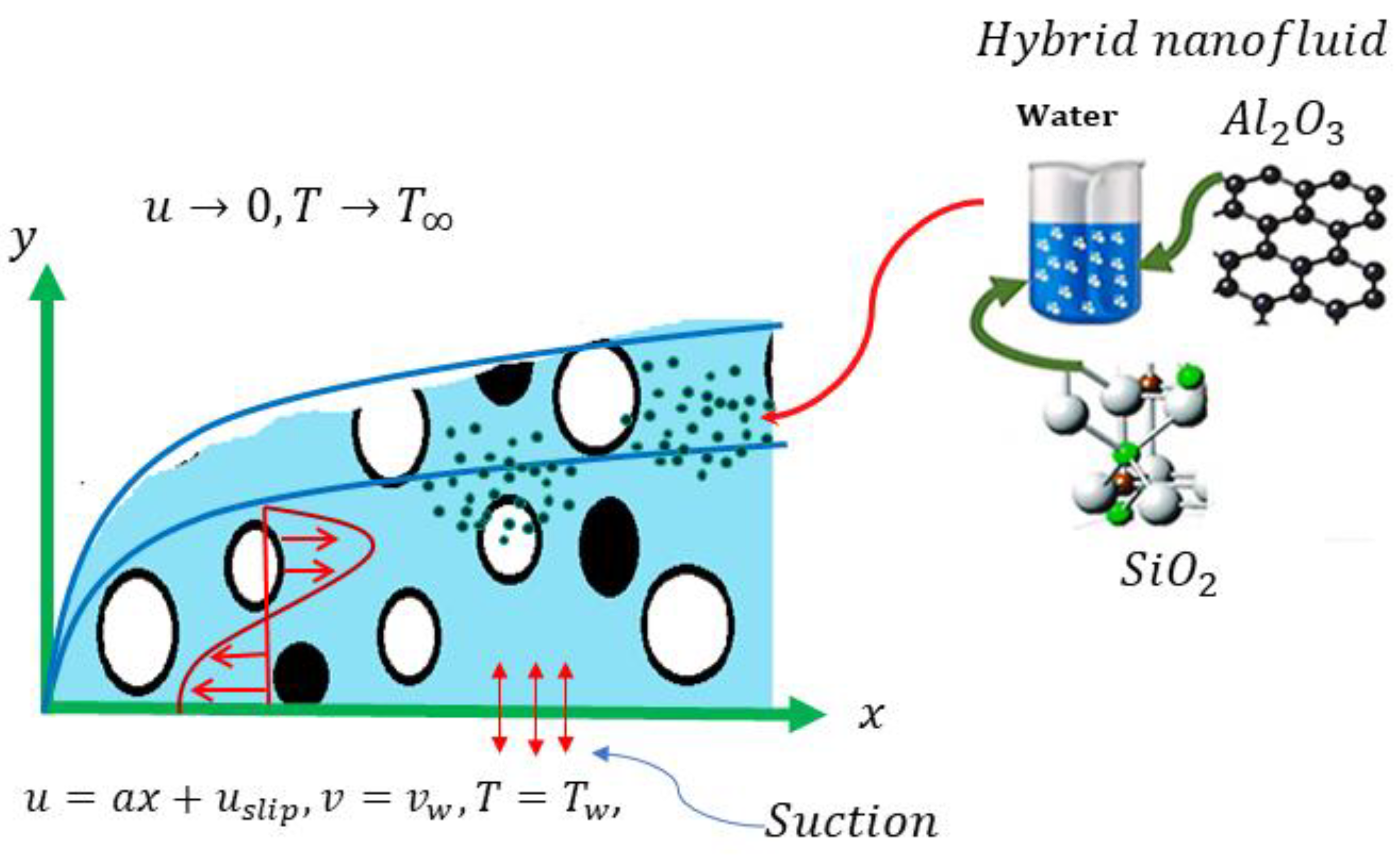
2. Problem Description and Governing Equations
3. Closed-Form Solution for Velocity Field
4. Skin-Friction Coefficient
5. Numerical Solution for Temperature Field
6. Physical Outcomes and Discussion
6.1. Validation
6.2. Solution Domain
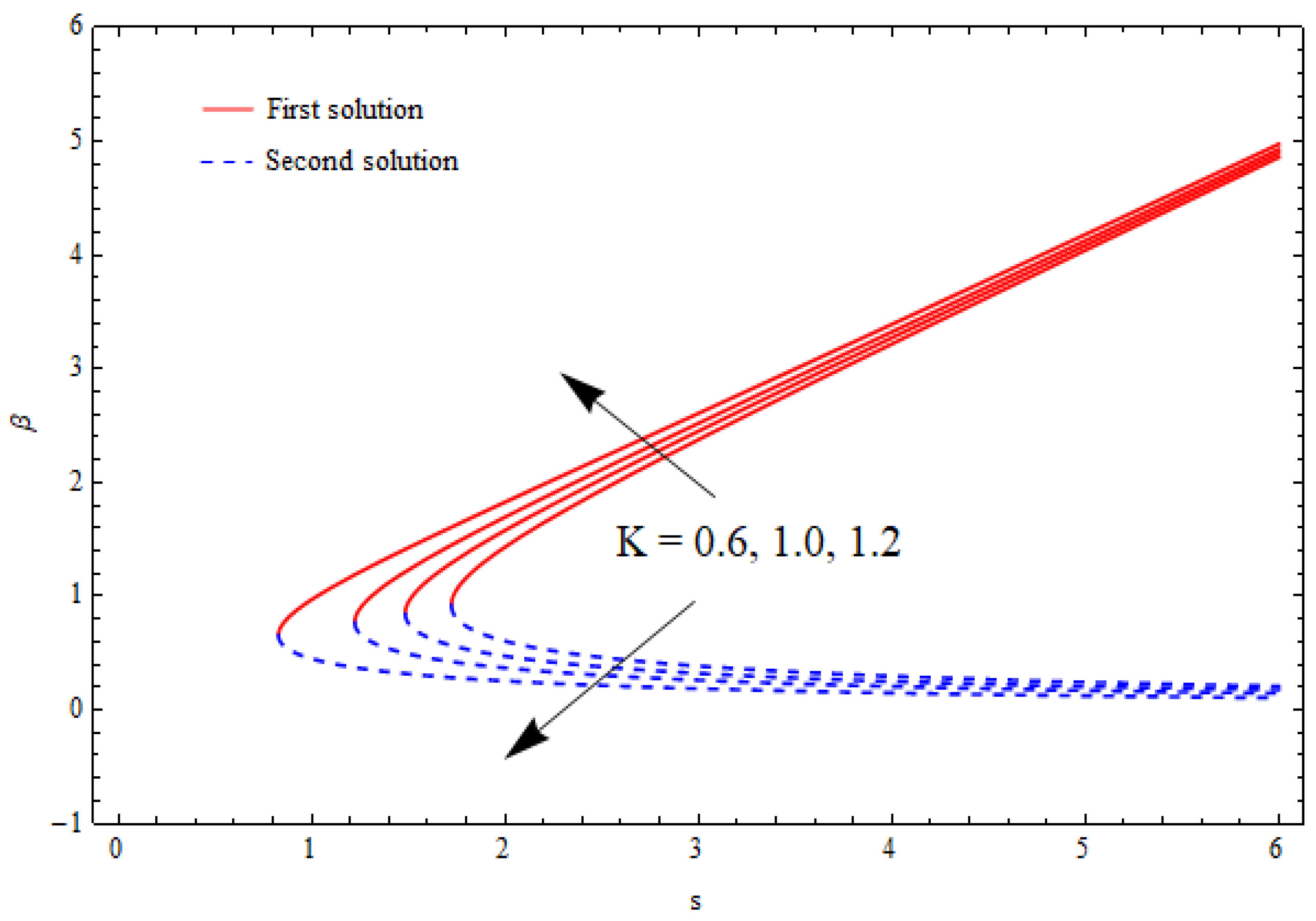
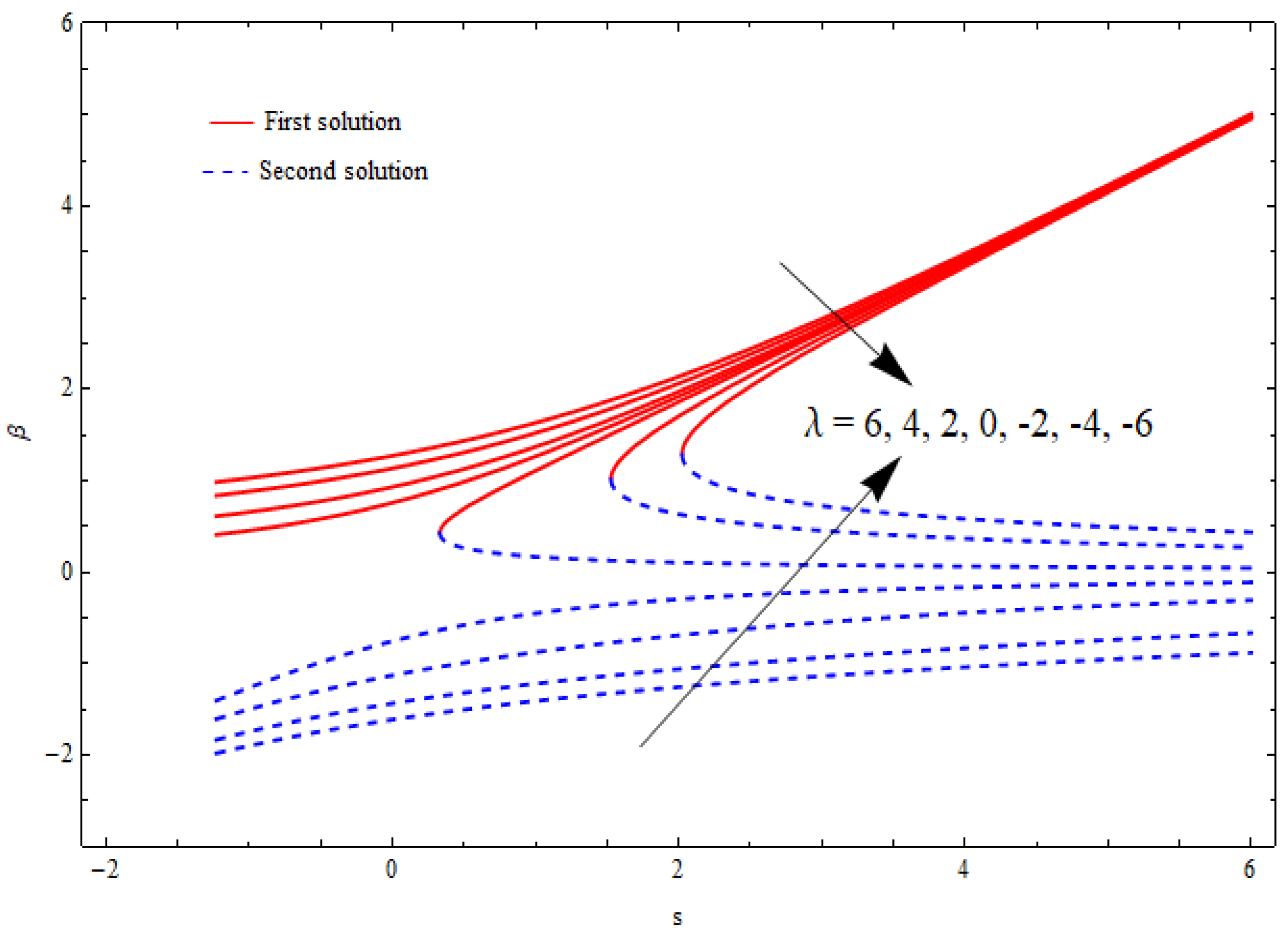
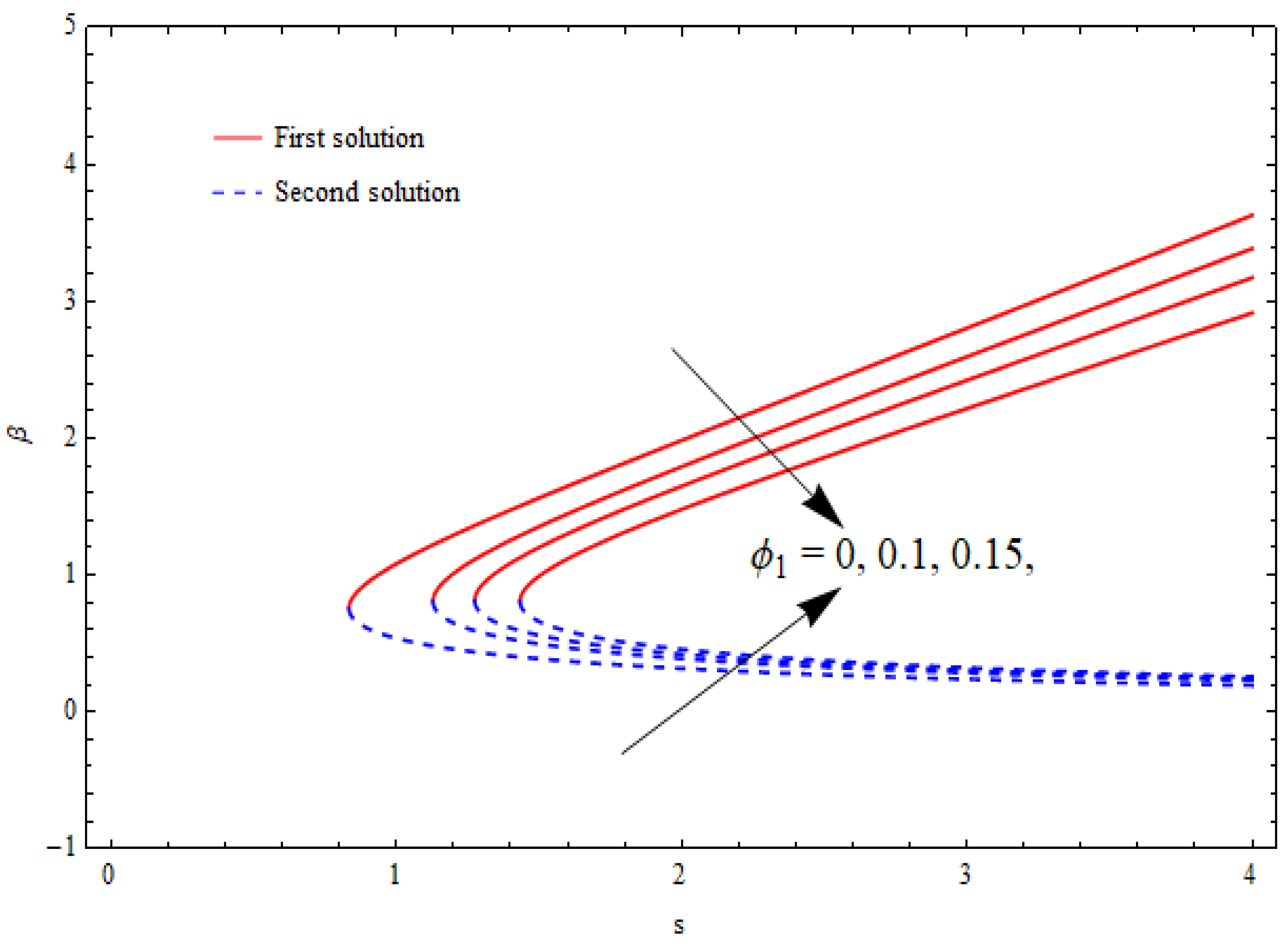
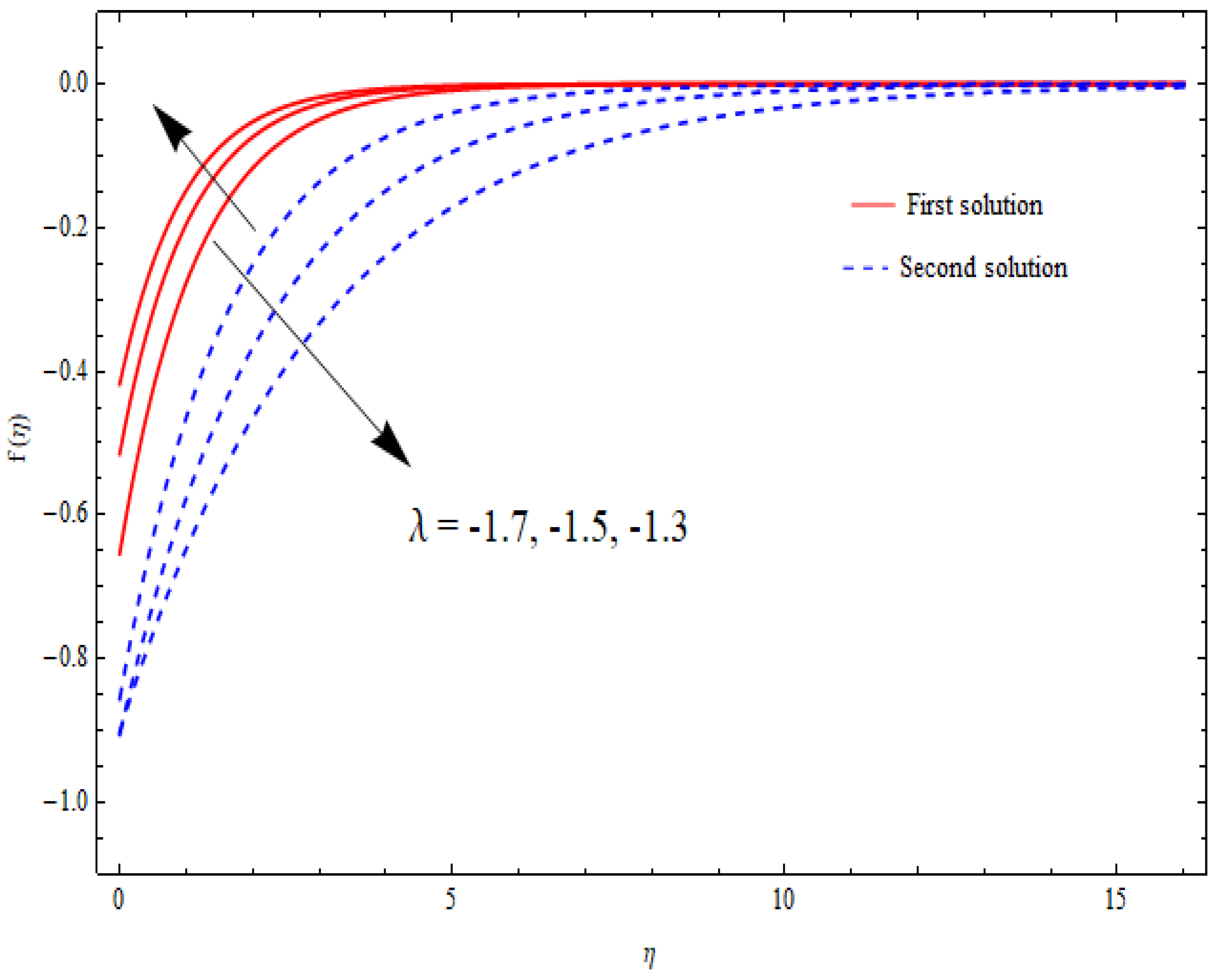
6.3. Flow Analysis
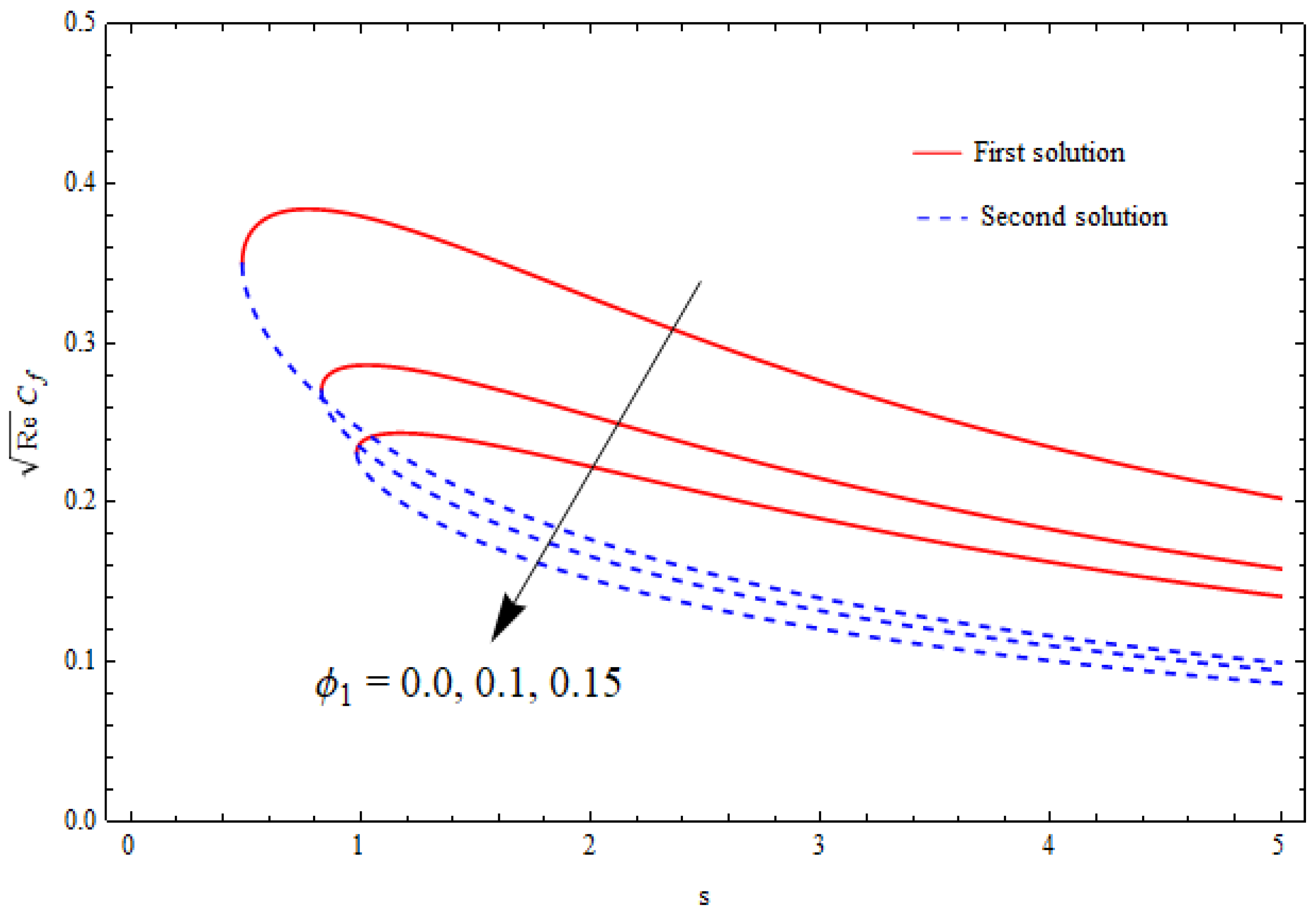
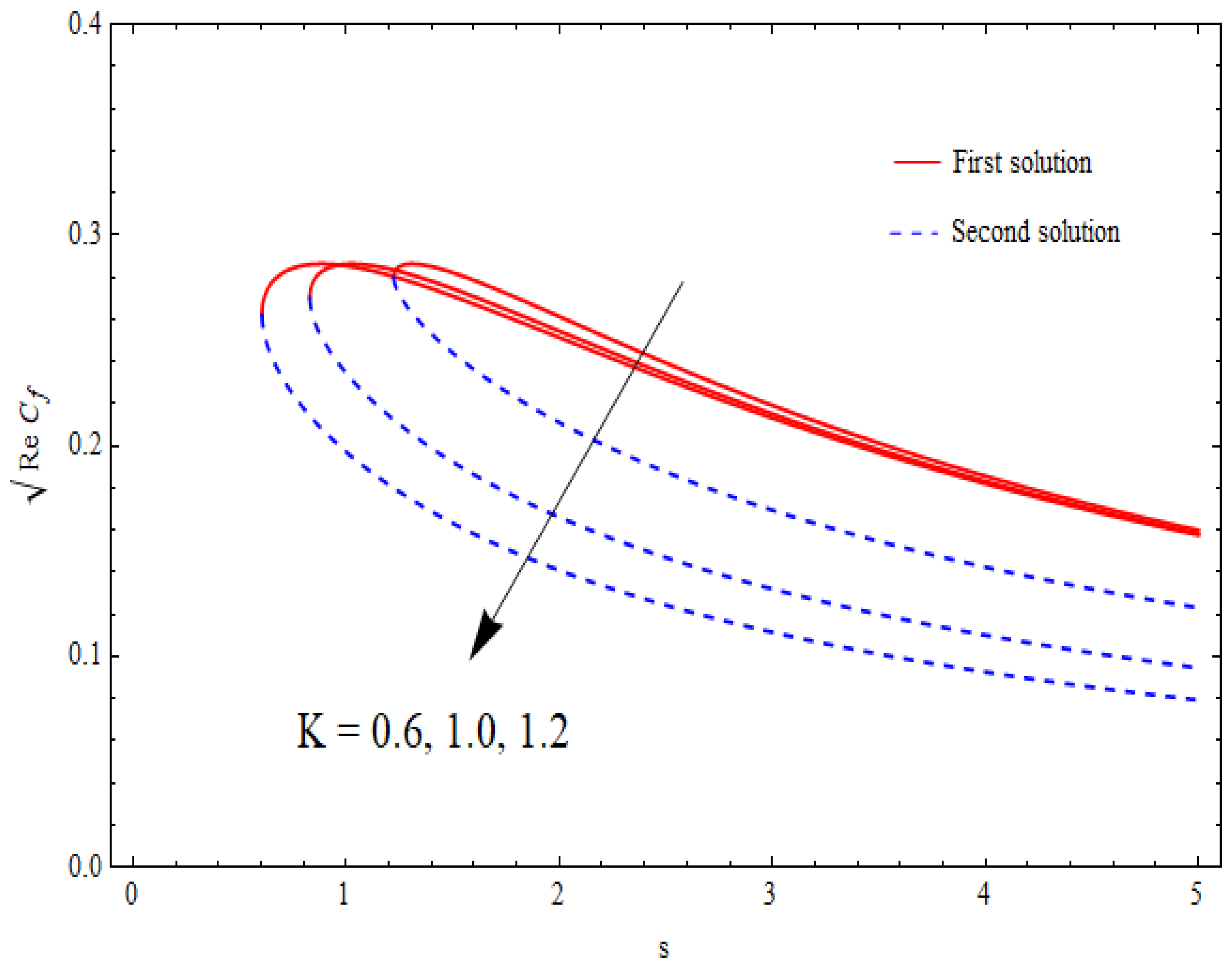
6.4. Skin-Friction Coefficient
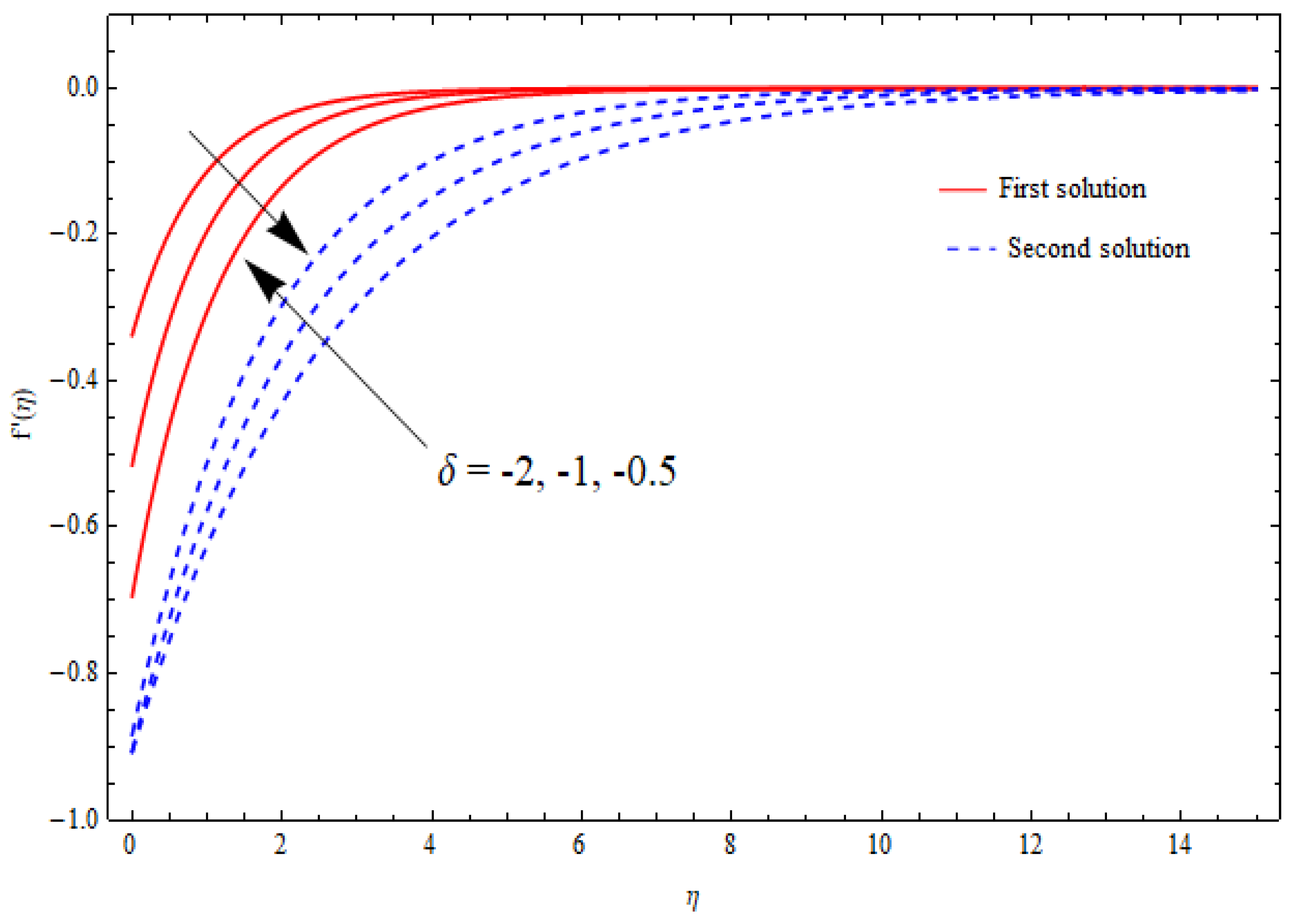
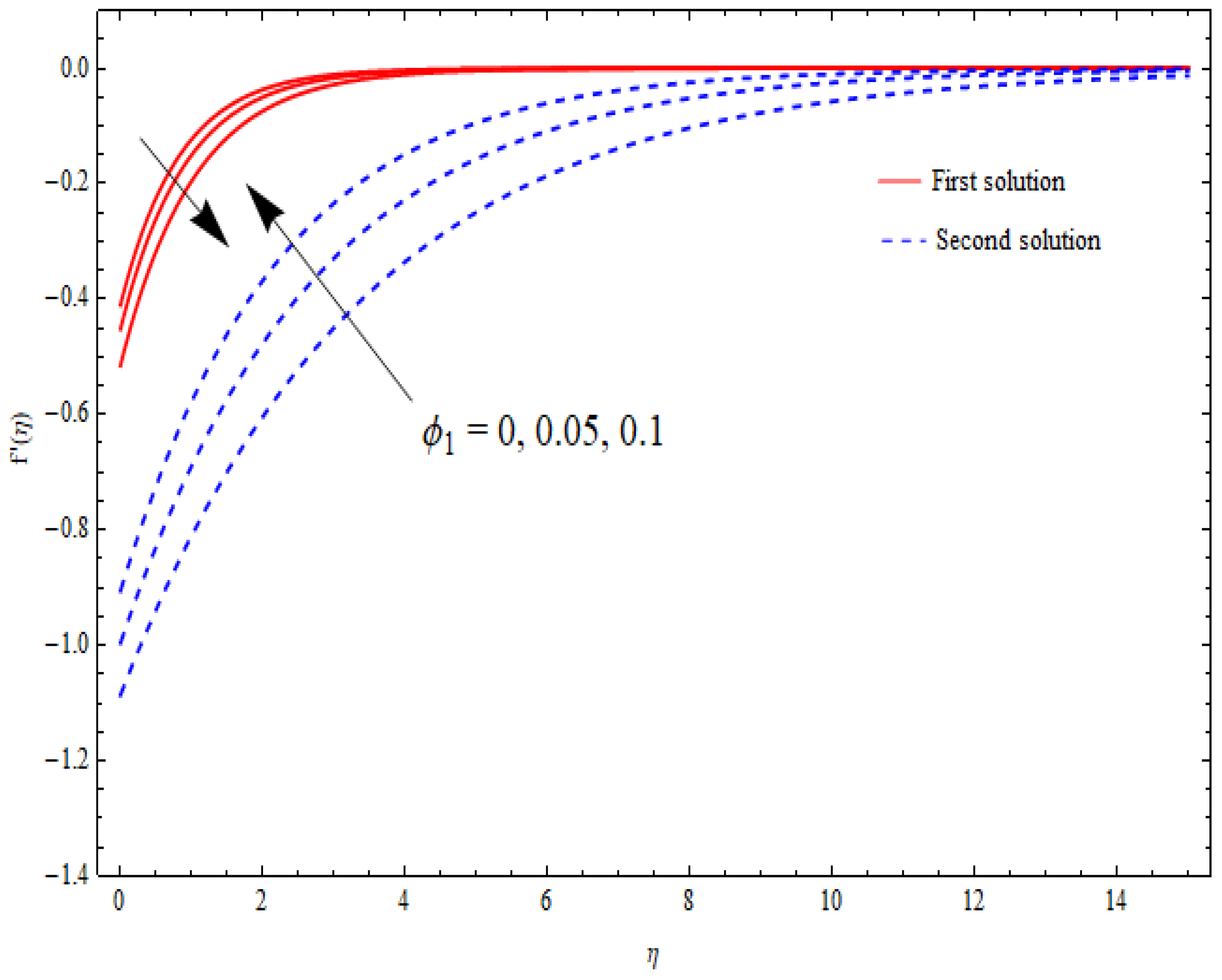
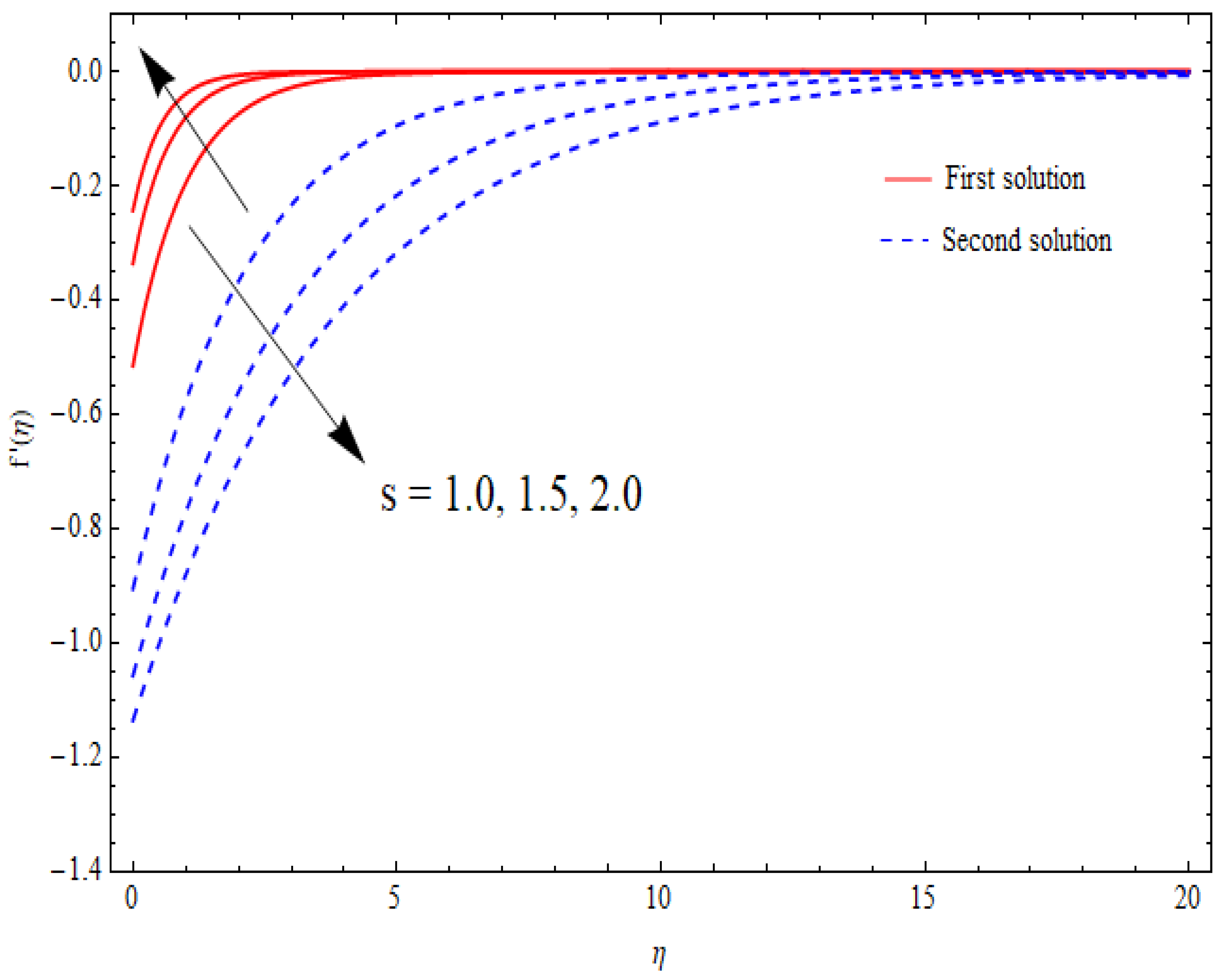
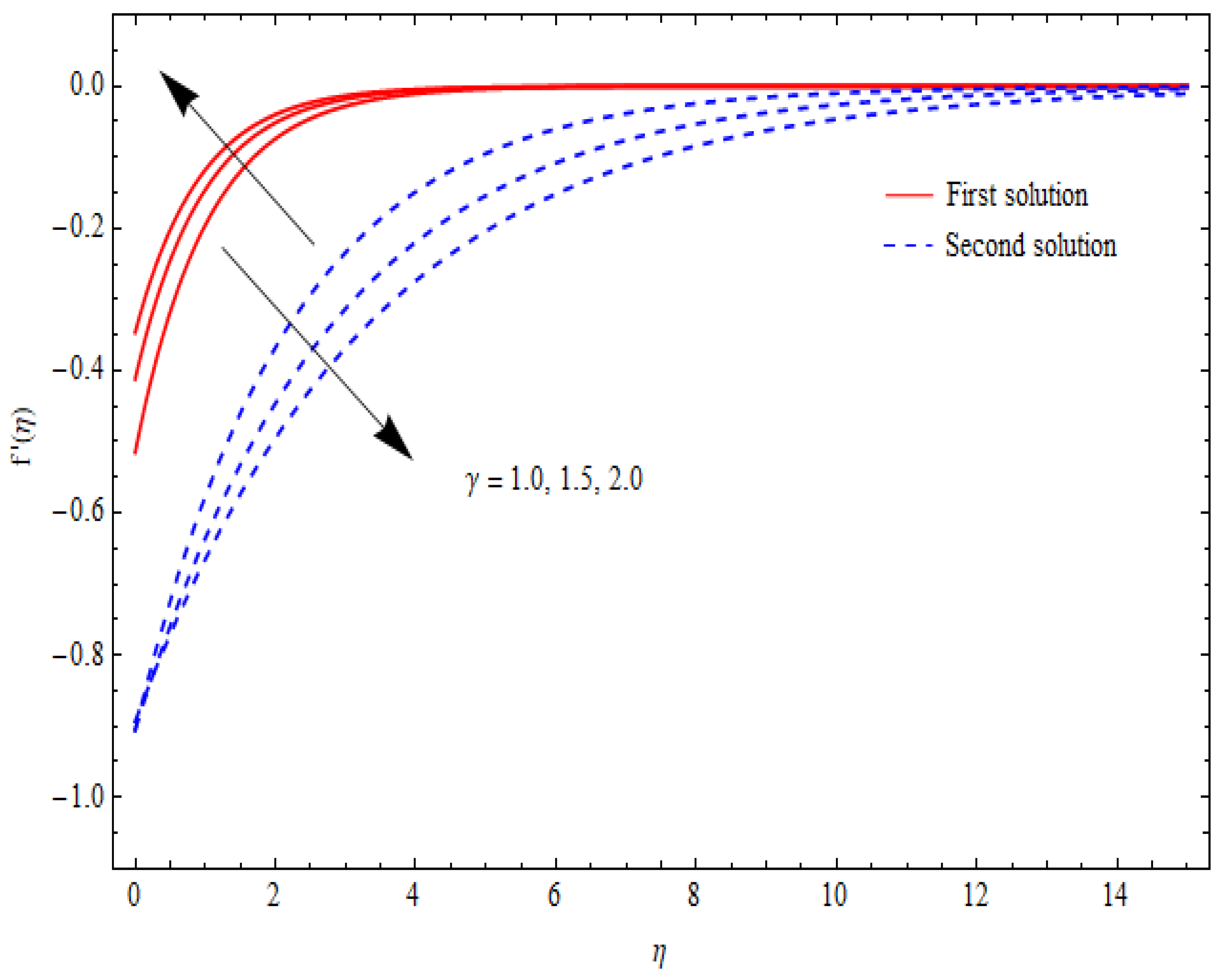
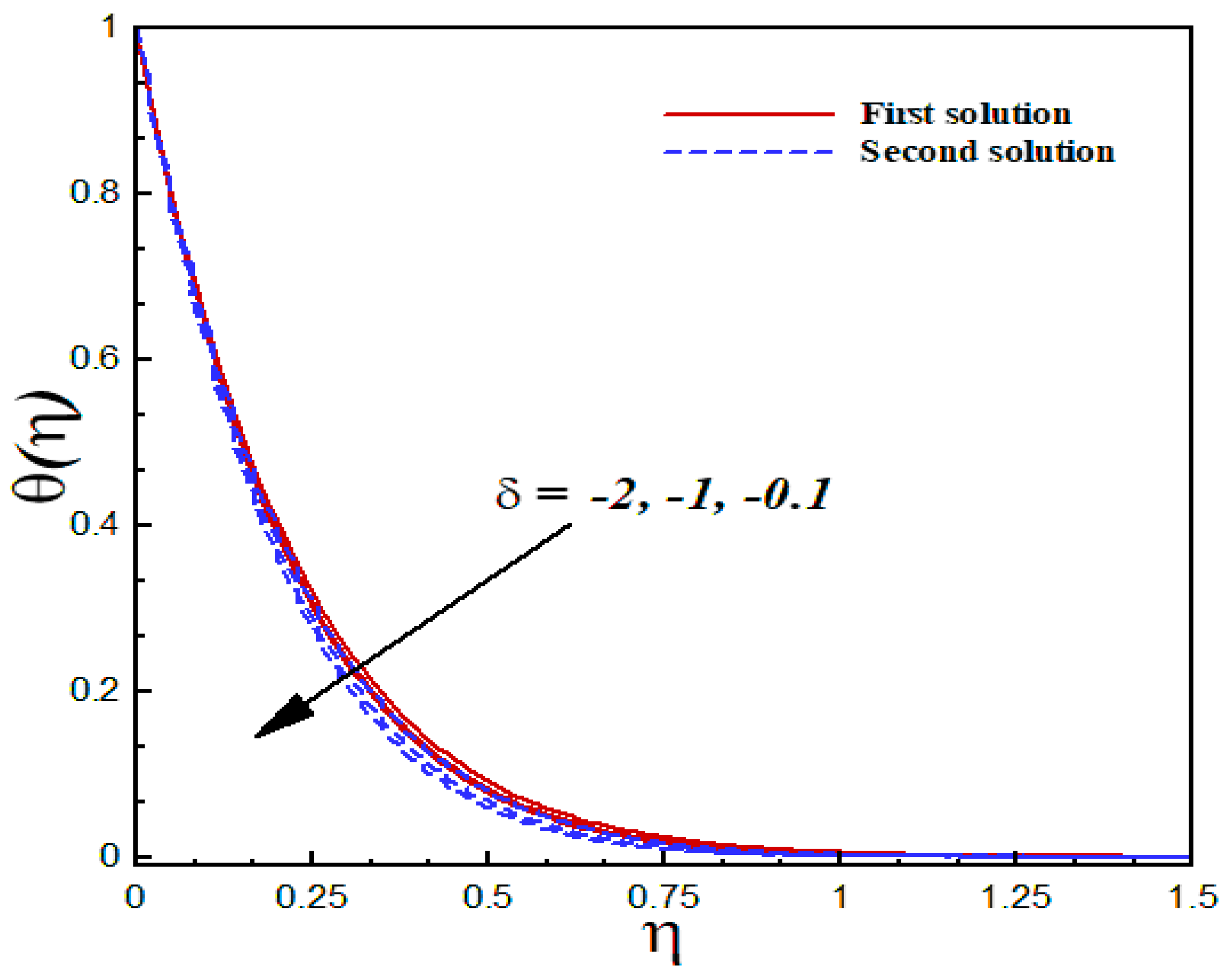
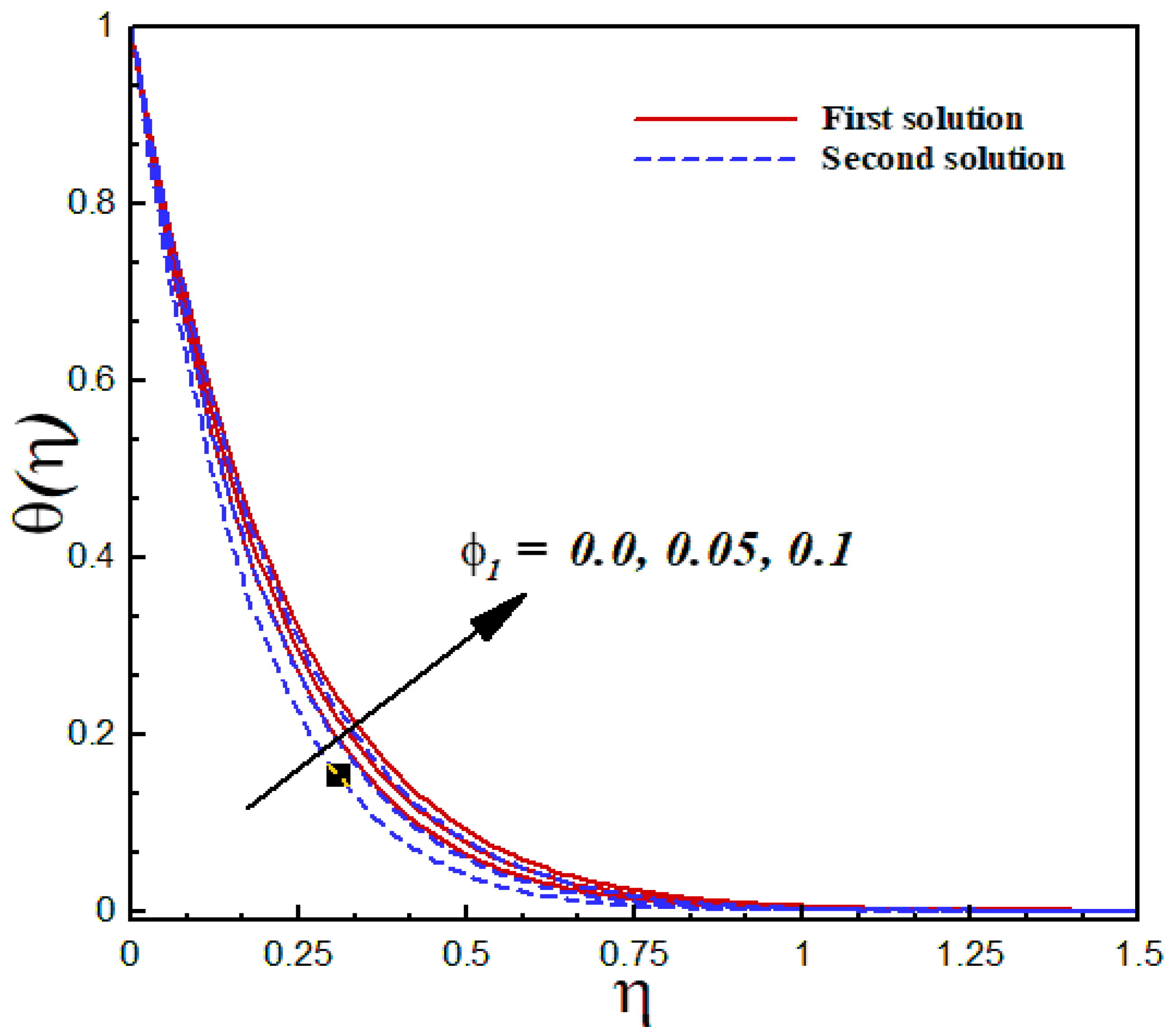
6.5. Thermal Analysis
7. Conclusions
- The velocity distributions displayed different behaviors for the increasing porosity parameter.
- Dual solutions (upper-branch solution and lower-branch solution) existed for shrinking flow within a specific range of the suction parameter.
- A significant reduction in friction at the wall was noticed for a higher porosity parameter.
- The solution range was significantly increased with increasing values of the porosity parameter.
- A decrement in the velocity profiles for upper branch solution was noted against the nanoparticle volume fraction.
- The skin-friction coefficient showed a substantial enhancement with a higher nanoparticle volume fraction for both the solutions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Numerical investigation of three-dimensional hybrid Cu-Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Nigerian Mathem. Soc. 2017, 36, 419–433. [Google Scholar]
- Yousefi, R.M.; Dinarvand, S.; Yazdi, M.E.; Pop, I. Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylinder. Int. J. Numer. Method Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S.; Khan, A.U. Rotating flow of Ag-CuO/H2O hybrid nanofluid with radiation and partial slip boundary effects. Eur. Phys. J. E 2018, 41, 75. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Zubair, T.; Haq, R.U.; Wang, W. Cu-Al2O3/Water hybrid nanofluid through a permeable surface in the presence of nonlinear radiation and variable thermal conductivity via LSM. Int. J. Heat Mass Transf. 2018, 42, 1347–1356. [Google Scholar] [CrossRef]
- Hashim; Khan, M.; Sharjeel; Khan, U. Stability analysis in the transient flow of Carreau fluid with non-linear radiative heat transfer and nanomaterials: Critical points. J. Mol. Liq. 2018, 272, 787–800. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer of a hybrid nanofluid past a permeable moving surface. Chin. J. Phys. 2020, 66, 606–619. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Selimefendigil, F.; Oztop, H.F. Effects of a rotating cone on the mixed convection in a double lid-driven 3D porous trapezoidal nanofluid filled cavity under the impact of magnetic field. Nanomaterials 2020, 10, 449. [Google Scholar] [CrossRef] [Green Version]
- Saif, R.S.; Hashim; Zaman, M.; Ayaz, M. Thermally stratified flow of hybrid nanofluids with radiative heat transport and slip mechanism: Multiple solutions. Commun. Theor. Phys. 2021, 74, 015801. [Google Scholar] [CrossRef]
- Ali, B.; Khan, S.A.; Hussein, A.K.; Thumma, T.; Hussain, S. Hybrid nanofluids: Significance of gravity modulation, heat source/sink, and magnetohydrodynamic on dynamics of micropolar fluid over an inclined surface via finite element simulation. Appl. Math. Comput. 2022, 419, 126878. [Google Scholar] [CrossRef]
- Ali, B.; Ali, M.; Saman, I.; Hussain, S.; Yahya, A.U.; Hussain, I. Tangent hyperbolic nanofluid: Significance of Lorentz and buoyancy forces on dynamics of bioconvection flow of rotating sphere via finite element simulation. Chin. J. Phys. 2022, 77, 658–671. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Für Angew. Math. Und Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Wang, C.Y. The three-dimensional flow due to a stretching flat surface. Phys. Fluids 1984, 27, 1915–1917. [Google Scholar] [CrossRef]
- Andersson, H.I. MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech. 1992, 95, 227–230. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transf. 2002, 38, 517–521. [Google Scholar] [CrossRef]
- Hamid, A.; Khan, M. Heat and mass transport phenomena of nanoparticles on time-dependent flow of Williamson fluid towards heated surface. Neural Computing and Applications 2020, 32, 3253–3263. [Google Scholar]
- Goldstein, S. On backward boundary layers and flow in converging passages. J. Fluid Mech. 2006, 21, 33–45. [Google Scholar] [CrossRef]
- Miklavcic, M.; Wang, C.Y. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 64, 283–290. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J. Thermal boundary layers over a shrinking sheet: An analytical solution. Acta Mech. 2010, 209, 325–343. [Google Scholar] [CrossRef]
- Merkin, J.H.; Kumaran, V. The unsteady MHD boundary-layer flow on a shrinking sheet. Eur. J. Mech. B/Fluids 2010, 29, 357–363. [Google Scholar] [CrossRef]
- Fang, T.; Yao, S.; Zhang, J.; Aziz, A. Viscous flow over a shrinking sheet with a second order slip flow model. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1831–1842. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Heat and mass transfer of MHD second order slip flow. Comput. Fluids 2013, 71, 426–434. [Google Scholar] [CrossRef]
- Naganthran, K.; Nazar, R.; Pop, I. Stability analysis of impinging oblique stagnation-point flow over a permeable shrinking surface in a viscoelastic fluid. Int. J. Mech. Sci. 2017, 131–132, 663–671. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Sidui, S. Unsteady heat transfer in non-axisymmetric Homann stagnation-point flows towards a stretching/shrinking sheet. Eur. J. Mech. B/Fluids 2019, 75, 199–208. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flows with slip: Exact solutions of the Navier-Stokes Equations. Z. f¨Ur Angew. Math. Und Phys. 2003, 54, 184–189. [Google Scholar] [CrossRef]
- Wang, C.Y. Analysis of viscous flow due to a stretching sheet with surface slip and suction. Nonlinear Anal. Real World Appl. 2009, 10, 375–380. [Google Scholar] [CrossRef]
- Fang, T.; Aziz, A. Viscous Flow with Second-Order Slip Velocity over a Stretching Sheet. Z. Für Nat. A 2010, 65, 1087–1092. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Multiple Solutions of Hydromagnetic Permeable Flow and Heat for Viscoelastic Fluid. J. Thermophys. Heat Transf. 2011, 25, 595–605. [Google Scholar] [CrossRef]
- Aly, E.H.; Vajravelu, K. Exact and numerical solutions of MHD nano boundary-layer flows over stretching surfaces in a porous medium. Appl. Math. Comput. 2014, 232, 191–204. [Google Scholar] [CrossRef]
- Nandy, S.K.; Pop, I. Effects of magnetic field and thermal radiation on stagnation flow and heat transfer of nanofluid over a shrinking surface. Int. Commun. Heat Mass Transf. 2014, 53, 50–55. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Aly, E.H.; Pop, I. Semi-analytical solution for the flow of a nanofluid over a permeable stretching/shrinking sheet with velocity slip using Buongiorno’s mathematical model. Eur. J. Mech. B/Fluids 2016, 58, 39–49. [Google Scholar] [CrossRef]
- Aladdin, N.A.L.; Bachok, N. Boundary Layer Flow and Heat Transfer of Al2O3-TiO2/Water Hybrid Nanofluid over a Permeable Moving Plate. Symmetry 2020, 12, 1064. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Dogonchi, A.S.; Ganji, D.D. Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv. 2019, 9, 025103. [Google Scholar] [CrossRef] [Green Version]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Alawi, O.A.; Sidik, N.A.C.; Xian, H.W.; Kean, T.H.; Kazi, S.N. Thermal conductivity and viscosity models of metallic oxides nanofluids. Int. J. Heat Mass Transf. 2018, 116, 1314–1325. [Google Scholar] [CrossRef]
- Wu, L. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef]





| Physical Properties | Base Liquid | Nanoparticles | |
|---|---|---|---|
| 997.1 | 3970 | 2200 | |
| 4179 | 765 | 703 | |
| 0.613 | 40 | 1.2 | |
| s | γ | Upper Branch | Lower Branch | ||
|---|---|---|---|---|---|
| Turkyilmazoglu [27] | Present Study | Turkyilmazoglu [27] | Present Study | ||
| 2 | 0 | 1.8832035 | 1.883203505 | 0.53101006 | 0.531010056 |
| - | 1 | 1.9212896 | 1.921289609 | 0.40052899 | 0.400528985 |
| - | 3 | 1.9519690 | 1.951968975 | 0.29676823 | 0.296768226 |
| - | 10 | 1.9795599 | 1.979559862 | 0.18882968 | 0.188829678 |
| 3 | 0 | 2.9655726 | 2.965572633 | 0.33720300 | 0.337203003 |
| - | 1 | 2.9737635 | 2.9737634890 | 0.27228263 | 0.272282625 |
| - | 3 | 2.9822017 | 2.982201678 | 0.21301670 | 0.213016696 |
| - | 10 | 2.9916152 | 2.991615203 | 0.14289554 | 0.142895541 |
| 5 | 0 | 4.9922728 | 4.992272838 | 0.20030956 | 0.200309564 |
| - | 1 | 4.9935252 | 4.993525154 | 0.17232557 | 0.172325571 |
| - | 3 | 4.9951096 | 4.995109595 | 0.14226228 | 0.142262284 |
| - | 10 | 4.9973652 | 4.997365206 | 0.10102758 | 0.101027578 |
| γ | δ | Turkyilmazoglu [27] | Present Study |
|---|---|---|---|
| 0 | 0 | 2.41421356 | 2.414213547 |
| - | −1 | 0.38942826 | 0.389428256 |
| - | −3 | 0.15150097 | 0.151500971 |
| - | −5 | 0.09425550 | 0.094255503 |
| 1 | 0 | 0.68232780 | 0.682327801 |
| - | −1 | 0.28168830 | 0.281688300 |
| - | −3 | 0.13178867 | 0.131788669 |
| - | −5 | 0.08620469 | 0.086204692 |
| 3 | 0 | 0.28704681 | 0.287046812 |
| - | −1 | 0.18074365 | 0.180743647 |
| - | −3 | 0.10449187 | 0.104491866 |
| - | −5 | 0.07360578 | 0.073605784 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashim; Hafeez, M.; Khedher, N.B.; Tag-EIDin, S.M.; Oreijah, M. Heat Transport during Colloidal Mixture of Water with Al2O3-SiO2 Nanoparticles within Porous Medium: Semi-Analytical Solutions. Nanomaterials 2022, 12, 3688. https://doi.org/10.3390/nano12203688
Hashim, Hafeez M, Khedher NB, Tag-EIDin SM, Oreijah M. Heat Transport during Colloidal Mixture of Water with Al2O3-SiO2 Nanoparticles within Porous Medium: Semi-Analytical Solutions. Nanomaterials. 2022; 12(20):3688. https://doi.org/10.3390/nano12203688
Chicago/Turabian StyleHashim, Muhammad Hafeez, Nidhal Ben Khedher, Sayed Mohamed Tag-EIDin, and Mowffaq Oreijah. 2022. "Heat Transport during Colloidal Mixture of Water with Al2O3-SiO2 Nanoparticles within Porous Medium: Semi-Analytical Solutions" Nanomaterials 12, no. 20: 3688. https://doi.org/10.3390/nano12203688





