Analysis of Nanofluid Particles in a Duct with Thermal Radiation by Using an Efficient Metaheuristic-Driven Approach
Abstract
:1. Introduction
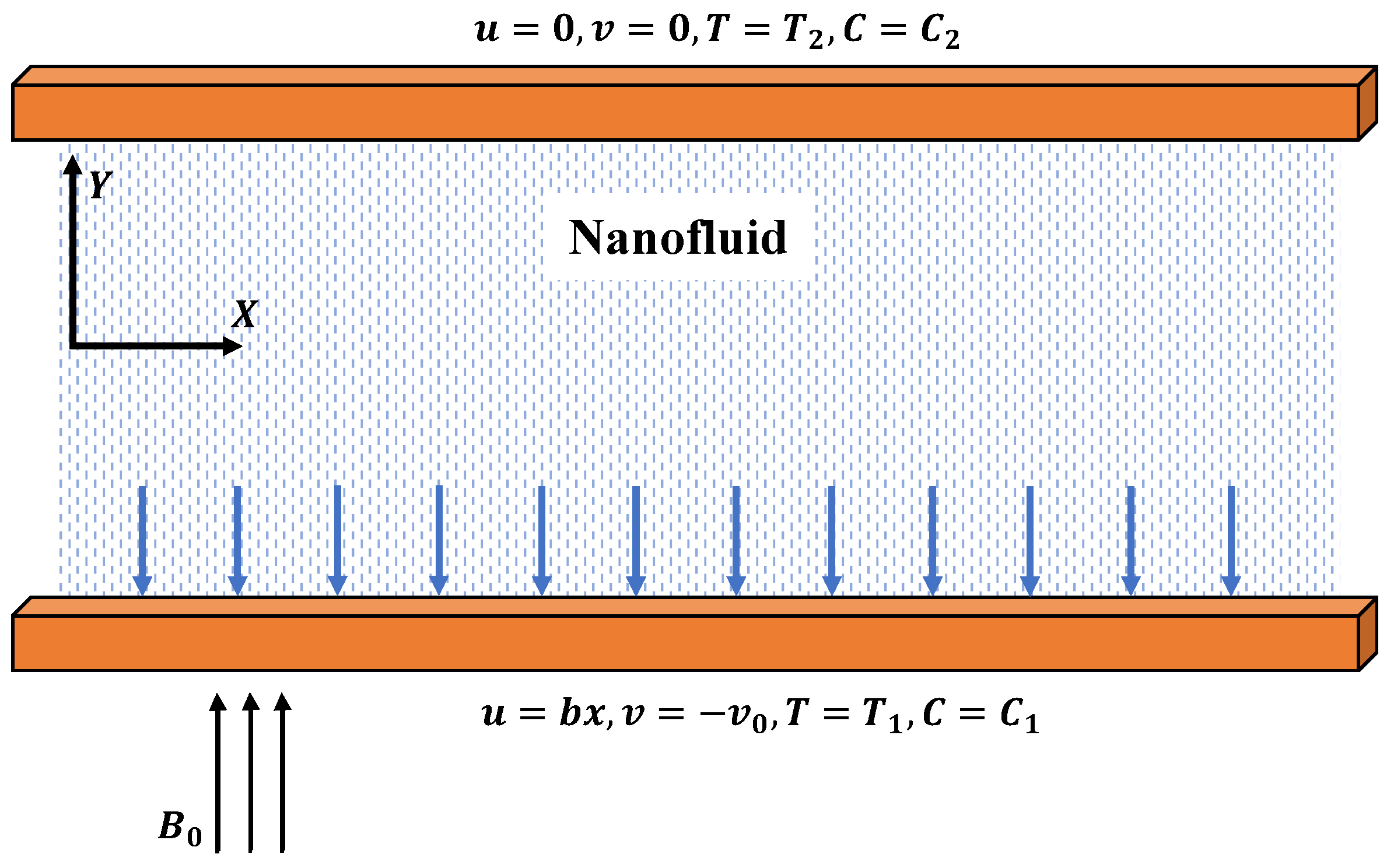
- In this study, a mathematical model of the steady two-phase flow of a nanofluid in a semipermeable duct in the presence of external forces was formulated by using the Buongiorno model and basic concepts of continuity and momentum equations. Further, the model was reduced to a system of ordinary differential equations.
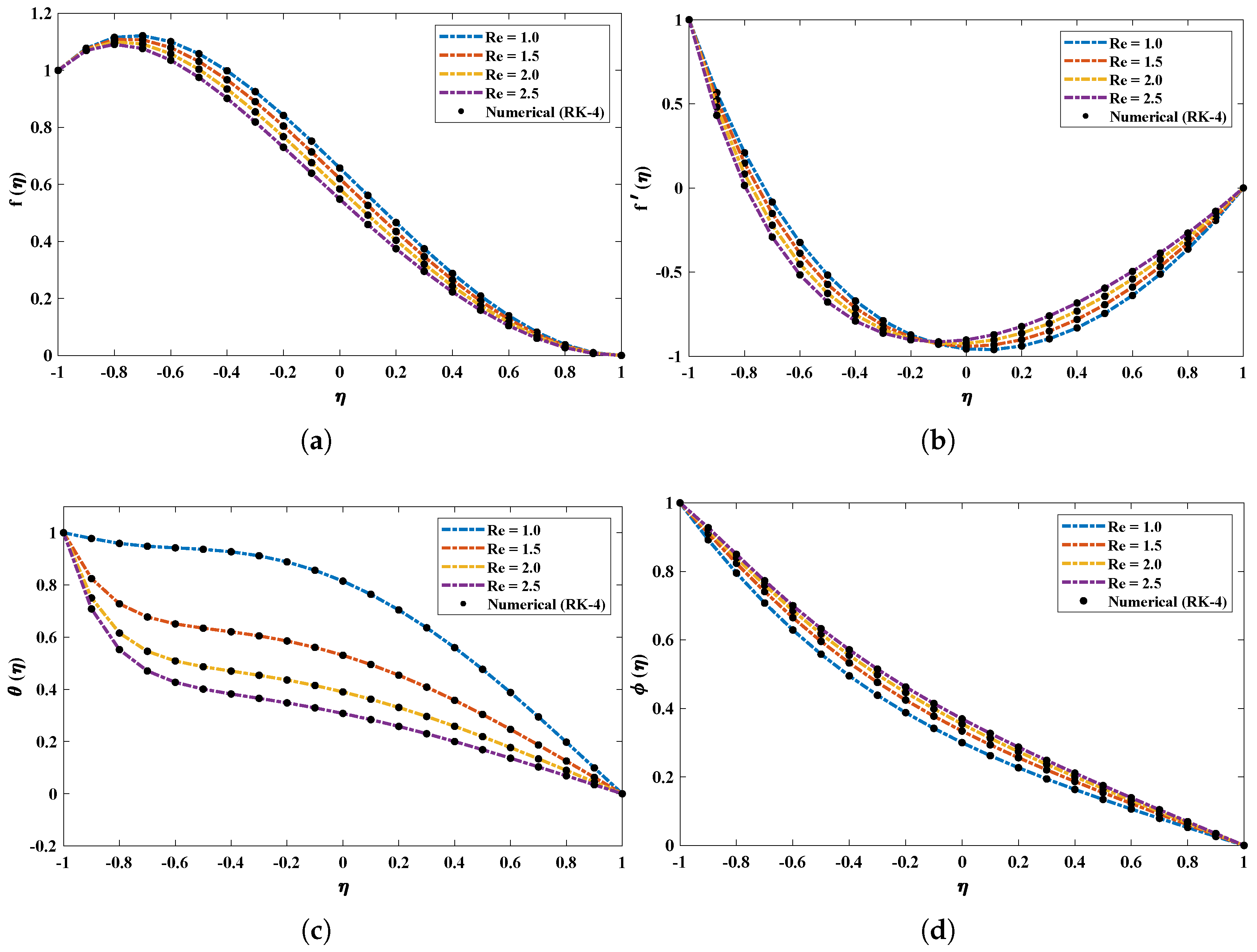
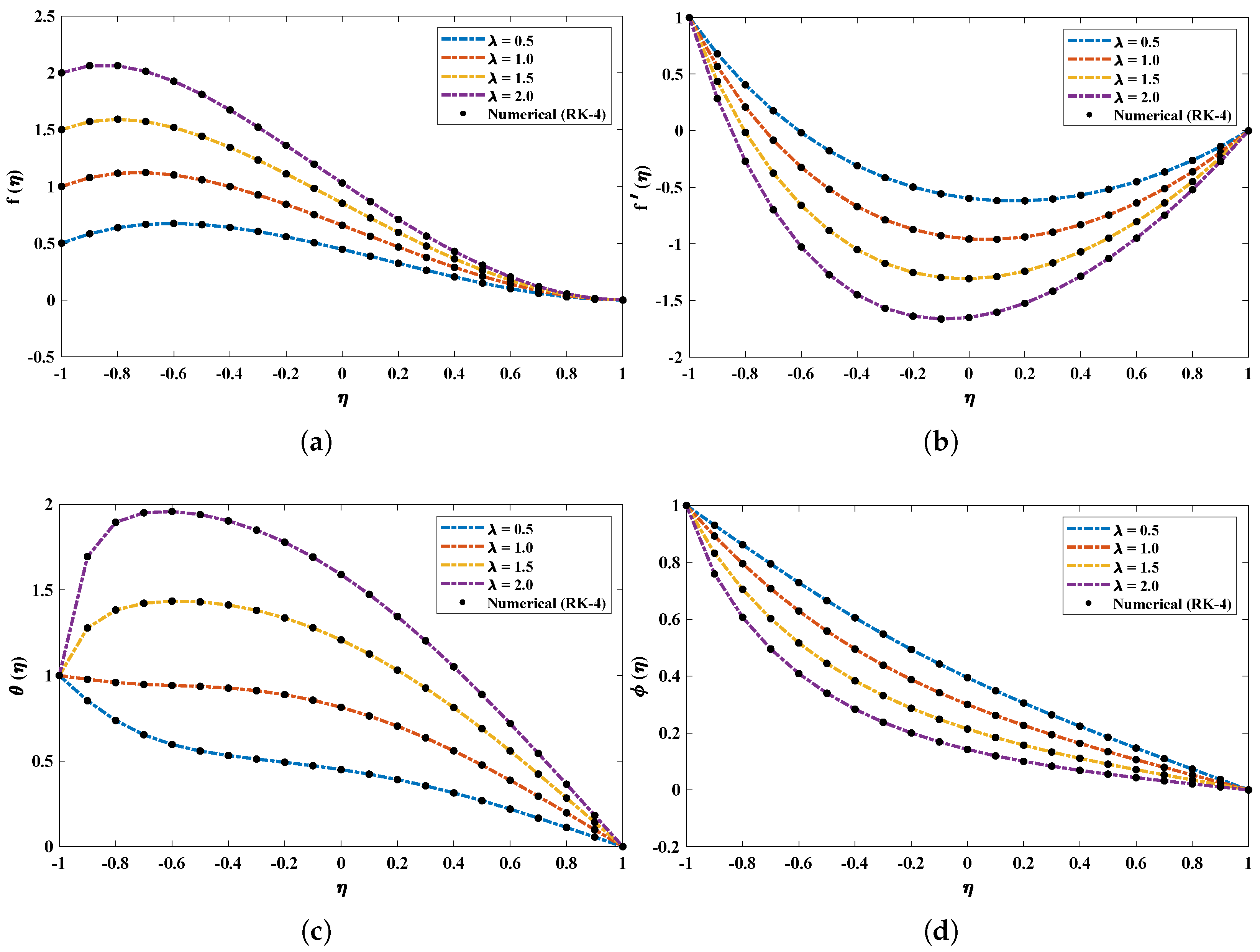
- Moreover, to study the effect of variations in certain parameters, such as the thermophoretic parameter , Hartmann number , Brownian and radiation motion parameters, Eckert number , Reynolds number and Schmidt number , on the velocity profile, thermal profile, Nusselt number and skin friction coefficient of the nanofluid, a soft computing metaheuristic technique was designed. The intelligent computational strength of artificial neural networks was utilized with a combination of unsupervised and supervised learning strategies.
- The results obtained with the proposed ANN-AOA-IPA technique were compared with the methods available in the latest literature. In addition, to study the convergence and stability of the results, the proposed algorithm was implemented for 100 independent runs.
- Extensive graphical, statistical and sensitivity analyses were conducted to study the errors in approximate solutions based on mean absolute deviations, Theil’s inequality coefficient and error in Nash–Sutcliffe efficiency.
2. Mathematical Formulation
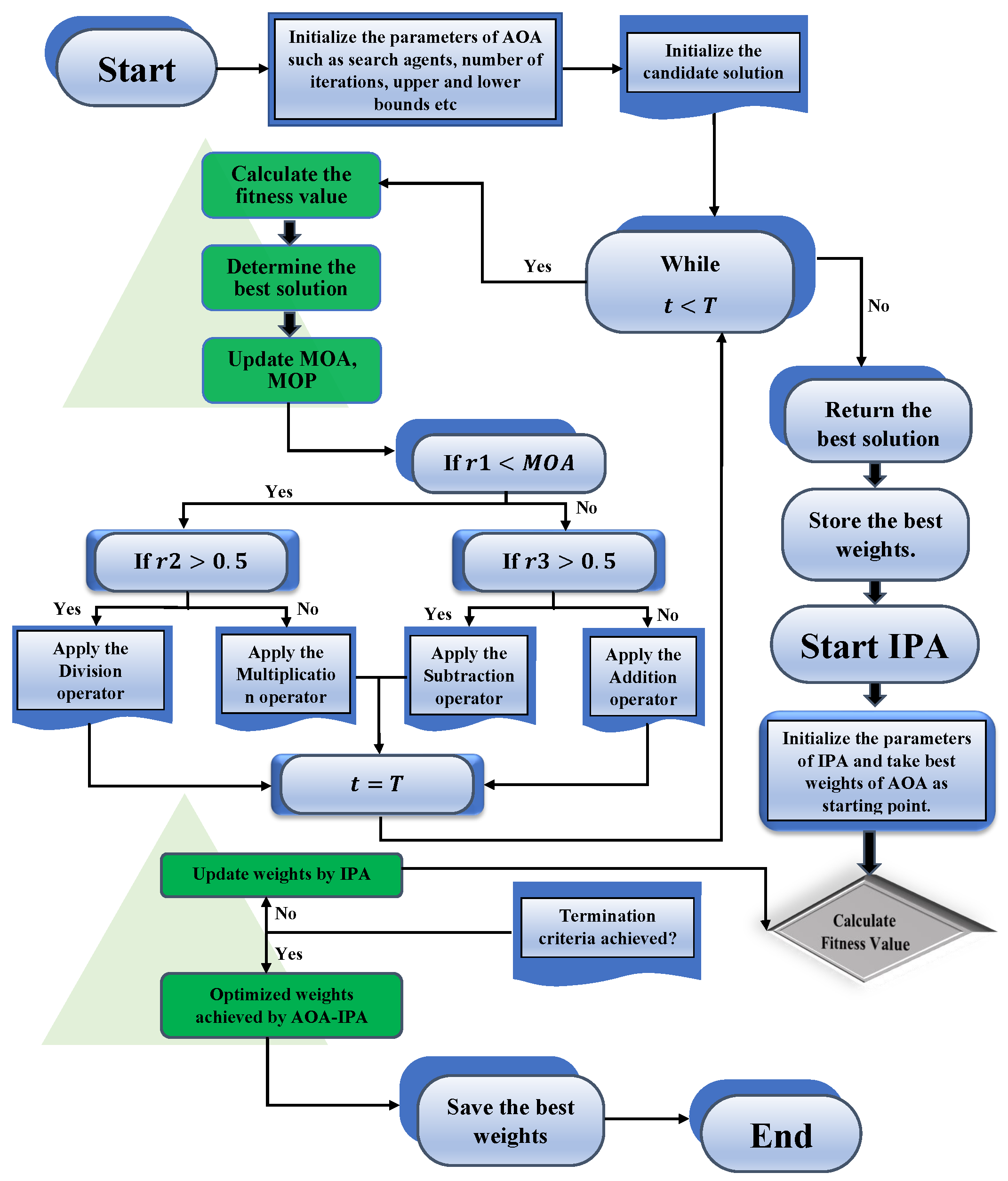
3. Methodology
3.1. Neural Network Modeling
3.2. Optimization Methods
3.2.1. Arithmetic Optimization Algorithm
3.2.2. The Proposed Hybridized Algorithm
4. Numerical Experimentation and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AOA | Arithmetic optimization algorithm |
| IPA | Interior point algorithm |
| TIC | Theil’s inequality coefficient |
| MAD | Mean absolute deviation |
| NSE | Nash–Sutcliffe efficiency |
| ENSE | Error in Nash–Sutcliffe efficiency |
| Thermophoretic parameter | |
| Hartmann number | |
| Brownian motion parameter | |
| Radiation motion parameter | |
| Reynolds number | |
| Schmidt number | |
| Suction parameter | |
| Eckert number | |
| Specific heat capacity | |
| Prandtl number | |
| Magnetic field | |
| Mean absorption coefficient | |
| Dynamic viscosity | |
| Nusselt number | |
| Electrical conductivity | |
| Skin friction coefficient | |
| Horizontal and vertical velocities | |
| Similarity-independent variable | |
| Thermal radiation | |
| Dimensionless temperature | |
| Stefan–Boltzmann constant | |
| Dimensionless concentration | |
| h | Activation function |
| Unknown neurons in ANN structure | |
| k | Number of neurons |
| Random numbers | |
| Upper and lower bounds | |
| Controlling parameter in AOA | |
| Sensitivity parameter in AOA | |
| f, p (subscripts) | Fluid phase, particulate phase |
Appendix A
References
- Bahiraei, M.; Godini, A.; Shahsavar, A. Thermal and hydraulic characteristics of a minichannel heat exchanger operated with a non-Newtonian hybrid nanofluid. J. Taiwan Inst. Chem. Eng. 2018, 84, 149–161. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab.: Lemont, IL, USA, 1995.
- Arabpour, A.; Karimipour, A.; Toghraie, D. The study of heat transfer and laminar flow of kerosene/multi-walled carbon nanotubes (MWCNTs) nanofluid in the microchannel heat sink with slip boundary condition. J. Therm. Anal. Calorim. 2018, 131, 1553–1566. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Thermal radiation and slip effects on MHD stagnation point flow of non-Newtonian nanofluid over a convective stretching surface. Neural Comput. Appl. 2019, 31, 207–217. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Comput. Methods Appl. Mech. Eng. 2019, 344, 306–318. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Finite element method for PCM solidification in existence of CuO nanoparticles. J. Mol. Liq. 2018, 265, 347–355. [Google Scholar] [CrossRef]
- Rashidi, M.; Ganesh, N.V.; Hakeem, A.A.; Ganga, B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J. Mol. Liq. 2014, 198, 234–238. [Google Scholar] [CrossRef]
- Vajravelu, K.; Kumar, B. Analytical and numerical solutions of a coupled non-linear system arising in a three-dimensional rotating flow. Int. J.-Non-Linear Mech. 2004, 39, 13–24. [Google Scholar] [CrossRef]
- Seyf, H.R.; Nikaaein, B. Analysis of Brownian motion and particle size effects on the thermal behavior and cooling performance of microchannel heat sinks. Int. J. Therm. Sci. 2012, 58, 36–44. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U. Cooling performance of a microchannel heat sink with nanofluids. Appl. Therm. Eng. 2006, 26, 2457–2463. [Google Scholar] [CrossRef]
- Rout, B.; Mishra, S.; Thumma, T. Effect of viscous dissipation on Cu-water and Cu-kerosene nanofluids of axisymmetric radiative squeezing flow. Heat Transf. Res. 2019, 48, 3039–3054. [Google Scholar] [CrossRef]
- Khodabandeh, E.; Safaei, M.R.; Akbari, S.; Akbari, O.A.; Alrashed, A.A. Application of nanofluid to improve the thermal performance of horizontal spiral coil utilized in solar ponds: Geometric study. Renew. Energy 2018, 122, 1–16. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, G.; Wang, N.; Zhang, X. Experimental Study on the Thermal Start-Up Performance of the Graphene/Water Nanofluid-Enhanced Solar Gravity Heat Pipe. Nanomaterials 2018, 8, 72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmed, N.; Khan, U.; Mohyud-Din, S.T. Unsteady radiative flow of chemically reacting fluid over a convectively heated stretchable surface with cross-diffusion gradients. Int. J. Therm. Sci. 2017, 121, 182–191. [Google Scholar] [CrossRef]
- Khan, U.; Ahmad, S.; Hayyat, A.; Khan, I.; Nisar, K.S.; Baleanu, D. On the Cattaneo–Christov Heat Flux Model and OHAM analysis for three different types of nanofluids. Appl. Sci. 2020, 10, 886. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, A.A.; Arabbeiki, M.; Ali, H.M.; Goodarzi, M.; Safaei, M.R. Configuration and Optimization of a Minichannel Using Water–Alumina Nanofluid by Non-Dominated Sorting Genetic Algorithm and Response Surface Method. Nanomaterials 2020, 10, 901. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Muhammad, T.; Alsaedi, A. Effects of homogeneous and heterogeneous reactions in flow of nanofluids over a nonlinear stretching surface with variable surface thickness. J. Mol. Liq. 2016, 221, 1121–1127. [Google Scholar] [CrossRef]
- Abdel-Wahed, M.; Elbashbeshy, E.; Emam, T. Flow and heat transfer over a moving surface with non-linear velocity and variable thickness in a nanofluids in the presence of Brownian motion. Appl. Math. Comput. 2015, 254, 49–62. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.I.M. Analytical modelling of free convection of non-Newtonian nanofluids flow in porous media with gyrotactic microorganisms using OHAM. Aip Conf. Proc. Am. Inst. Phys. 2014, 1635, 131–137. [Google Scholar]
- Xu, G.; Chen, W.; Deng, S.; Zhang, X.; Zhao, S. Performance Evaluation of a Nanofluid-Based Direct Absorption Solar Collector with Parabolic Trough Concentrator. Nanomaterials 2015, 5, 2131–2147. [Google Scholar] [CrossRef] [Green Version]
- Govindaraju, M.; Selvaraj, M. Boundary layer flow of gold–thorium water based nanofluids over a moving semi-infinite plate. Res. Eng. Struct. Mater. 2020, 6, 361. [Google Scholar]
- El-Masry, Y.; Abd Elmaboud, Y.; Abdel-Sattar, M. The impacts of varying magnetic field and free convection heat transfer on an Eyring–Powell fluid flow with peristalsis: VIM solution. J. Taibah Univ. Sci. 2020, 14, 19–30. [Google Scholar] [CrossRef] [Green Version]
- Thumma, T.; Mishra, S.; Bég, O.A. ADM solution for Cu/CuO–water viscoplastic nanofluid transient slip flow from a porous stretching sheet with entropy generation, convective wall temperature and radiative effects. J. Appl. Comput. Mech. 2021, 3, 1–15. [Google Scholar]
- Khan, N.A.; Sulaiman, M.; Aljohani, A.J.; Kumam, P.; Alrabaiah, H. Analysis of multi-phase flow through porous media for imbibition phenomena by using the LeNN-WOA-NM algorithm. IEEE Access 2020, 8, 196425–196458. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Kumam, P.; Aljohani, A.J. A new soft computing approach for studying the wire coating dynamics with Oldroyd 8-constant fluid. Phys. Fluids 2021, 33, 036117. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Laouini, G.; Alshammari, F.S. Study of Rolling Motion of Ships in Random Beam Seas with Nonlinear Restoring Moment and Damping Effects Using Neuroevolutionary Technique. Materials 2022, 15, 674. [Google Scholar] [CrossRef]
- Shoaib, M.; Zubair, G.; Raja, M.A.Z.; Nisar, K.S.; Abdel-Aty, A.H.; Yahia, I.S. Study of 3-D Prandtl Nanofluid Flow over a Convectively Heated Sheet: A Stochastic Intelligent Technique. Coatings 2022, 12, 24. [Google Scholar] [CrossRef]
- Khan, N.A.; Khalaf, O.I.; Romero, C.A.T.; Sulaiman, M.; Bakar, M.A. Application of euler neural networks with soft computing paradigm to solve nonlinear problems arising in heat transfer. Entropy 2021, 23, 1053. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Kumam, P.; Bakar, M.A. Thermal analysis of conductive-convective-radiative heat exchangers with temperature dependent thermal conductivity. IEEE Access 2021, 9, 138876–138902. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shoaib, M.; Hussain, S.; Nisar, K.S.; Islam, S. Computational intelligence of Levenberg-Marquardt backpropagation neural networks to study thermal radiation and Hall effects on boundary layer flow past a stretching sheet. Int. Commun. Heat Mass Transf. 2022, 130, 105799. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Aljohani, A.J.; Bakar, M.A. Mathematical models of CBSC over wireless channels and their analysis by using the LeNN-WOA-NM algorithm. Eng. Appl. Artif. Intell. 2022, 107, 104537. [Google Scholar] [CrossRef]
- Kandelousi, M.S. KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel. Phys. Lett. A 2014, 378, 3331–3339. [Google Scholar] [CrossRef]
- Khan, N.A.; Alshammari, F.S.; Romero, C.A.T.; Sulaiman, M.; Mirjalili, S. An Optimistic Solver for the Mathematical Model of the Flow of Johnson Segalman Fluid on the Surface of an Infinitely Long Vertical Cylinder. Materials 2021, 14, 7798. [Google Scholar] [CrossRef] [PubMed]
- Raptis, A. Radiation and free convection flow through a porous medium. Int. Commun. Heat Mass Transf. 1998, 25, 289–295. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Alarfaj, F.K. Numerical Analysis of Electrohydrodynamic Flow in a Circular Cylindrical Conduit by Using Neuro Evolutionary Technique. Energies 2021, 14, 7774. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.; Abualigah, L.; Oliva, D.; Algamal, Z.Y.; Anter, A.M.; Ali Ibrahim, R.; Ghoniem, R.M.; Abd Elaziz, M. Boosting Arithmetic Optimization Algorithm with Genetic Algorithm Operators for Feature Selection: Case Study on Cox Proportional Hazards Model. Mathematics 2021, 9, 2321. [Google Scholar] [CrossRef]
- Zheng, R.; Jia, H.; Abualigah, L.; Liu, Q.; Wang, S. An improved arithmetic optimization algorithm with forced switching mechanism for global optimization problems. Math. Biosci. Eng. 2022, 19, 473–512. [Google Scholar] [CrossRef]
- Guo, H.; Sun, Z.; Sun, H.; Ebrahimian, H. Optimal model of the combined cooling, heating, and power system by improved arithmetic optimization algorithm. Energy Sources Part Recover. Util. Environ. Eff. 2021, 1–23. [Google Scholar] [CrossRef]
- Xu, Y.P.; Tan, J.W.; Zhu, D.J.; Ouyang, P.; Taheri, B. Model identification of the Proton Exchange Membrane Fuel Cells by Extreme Learning Machine and a developed version of Arithmetic Optimization Algorithm. Energy Rep. 2021, 7, 2332–2342. [Google Scholar] [CrossRef]
- Dahl, J.; Andersen, E.D. A primal-dual interior-point algorithm for nonsymmetric exponential-cone optimization. Math. Program. 2021, 4, 1–30. [Google Scholar] [CrossRef]
- Boudjellal, N.; Roumili, H.; Benterki, D. A primal-dual interior point algorithm for convex quadratic programming based on a new parametric kernel function. Optimization 2021, 70, 1703–1724. [Google Scholar] [CrossRef]
- Bleyer, J. Advances in the simulation of viscoplastic fluid flows using interior-point methods. Comput. Methods Appl. Mech. Eng. 2018, 330, 368–394. [Google Scholar] [CrossRef] [Green Version]
- Stefanova, M.; Yakunin, S.; Petukhova, M.; Lupuleac, S.; Kokkolaras, M. An interior-point method-based solver for simulation of aircraft parts riveting. Eng. Optim. 2018, 50, 781–796. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, I.; AlSalman, H.; Islam, S.; Asif Zahoor Raja, M.; Shoaib, M.; Gumaei, A.; Fiza, M.; Ullah, K.; Rahman, M.; et al. Levenberg–Marquardt Backpropagation for Numerical Treatment of Micropolar Flow in a Porous Channel with Mass Injection. Complexity 2021, 2021. [Google Scholar] [CrossRef]
- Khan, N.A.; Alshammari, F.S.; Romero, C.A.T.; Sulaiman, M. Study of Nonlinear Models of Oscillatory Systems by Applying an Intelligent Computational Technique. Entropy 2021, 23, 1685. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Groundwater level prediction in Apulia region (Southern Italy) using NARX neural network. Environ. Res. 2020, 190, 110062. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Alarfaj, F.K. Theoretical Analysis on Absorption of Carbon Dioxide (CO2) into Solutions of Phenyl Glycidyl Ether (PGE) Using Nonlinear Autoregressive Exogenous Neural Networks. Molecules 2021, 26, 6041. [Google Scholar] [CrossRef]



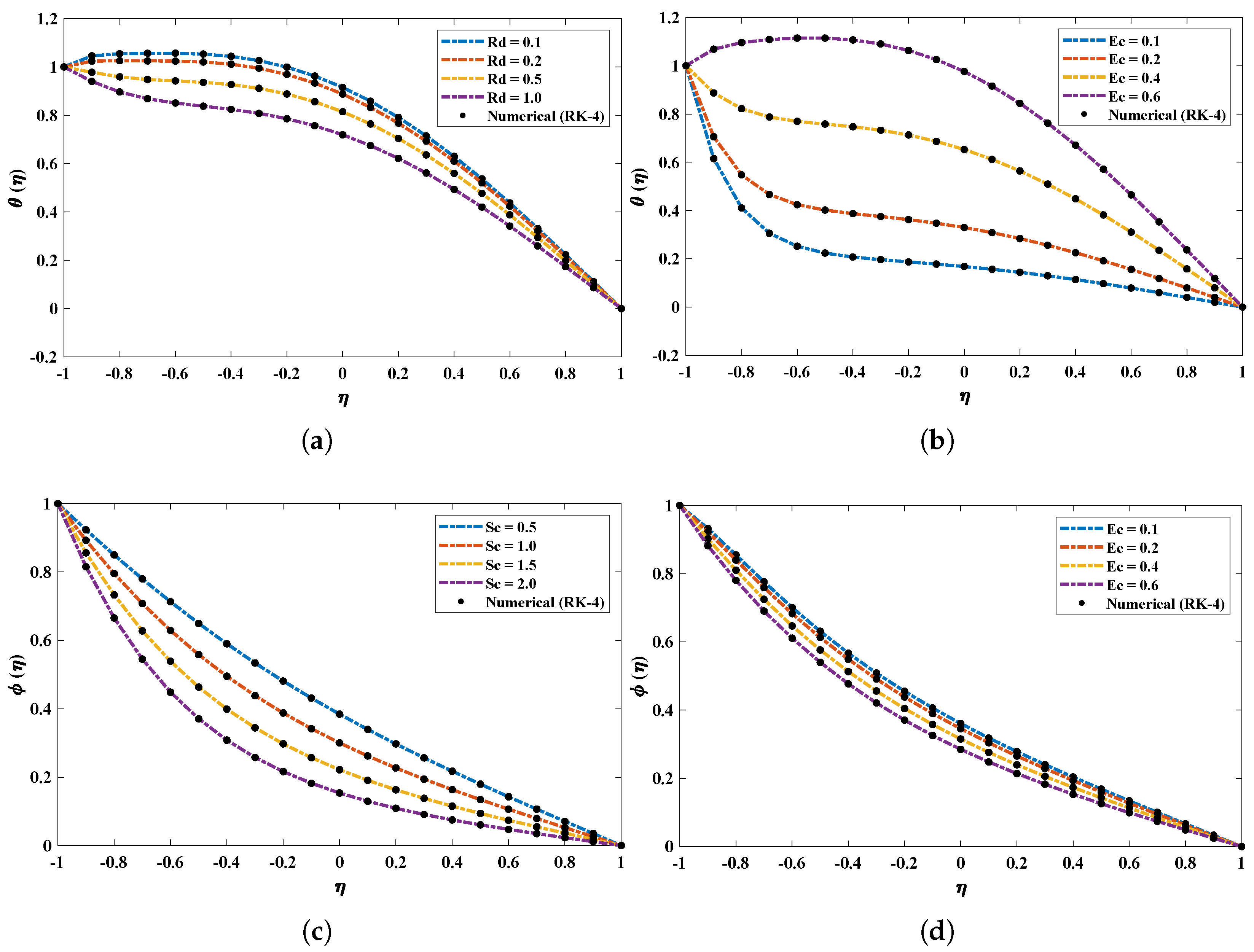
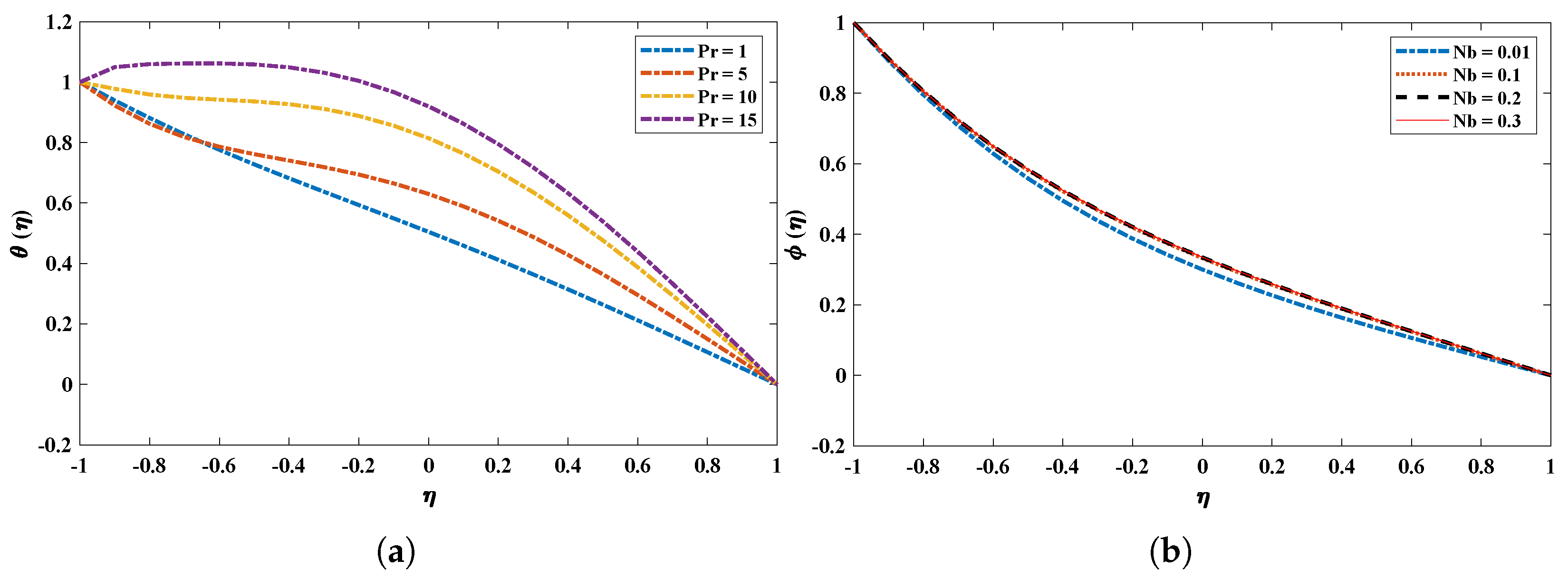
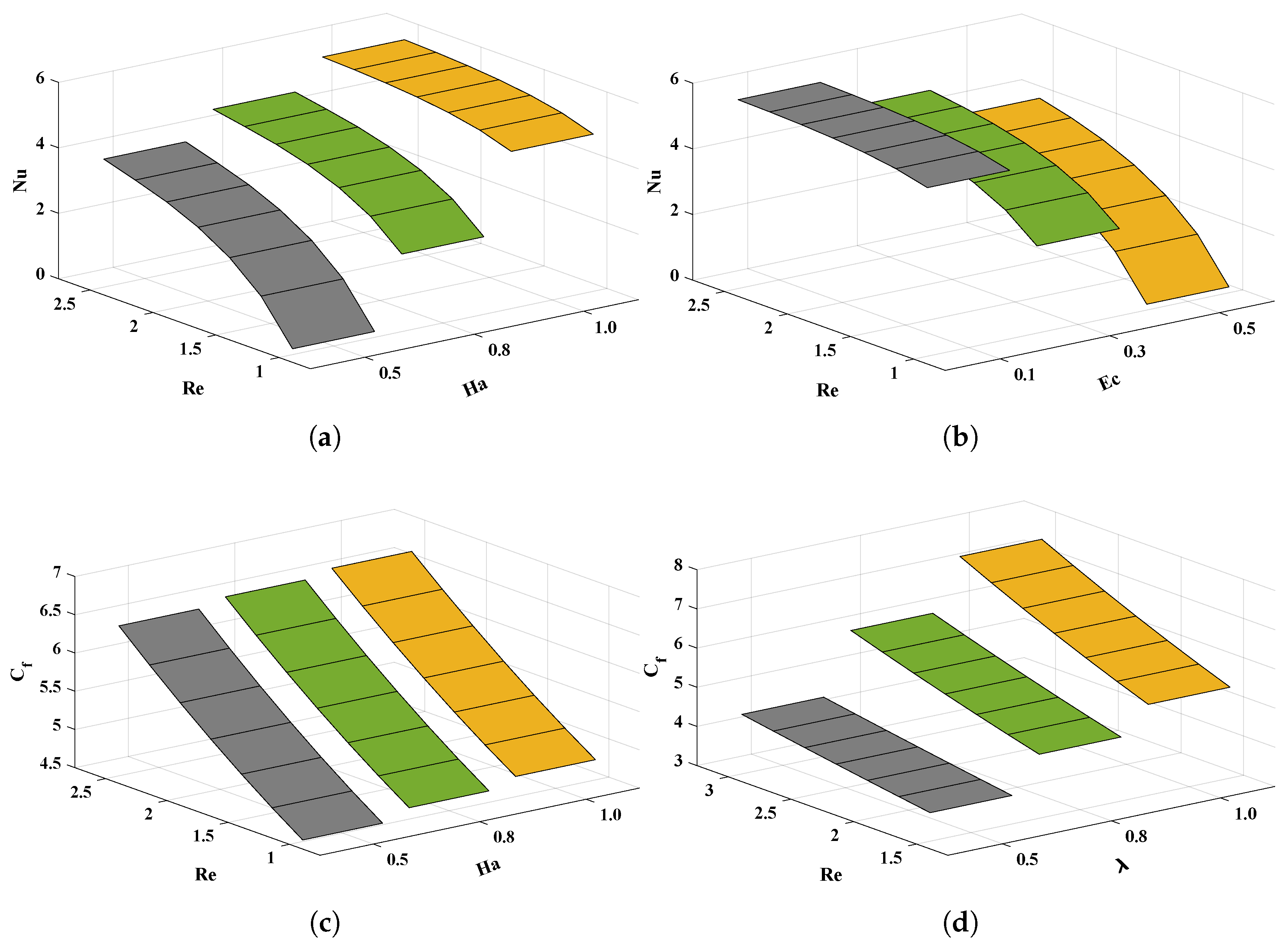

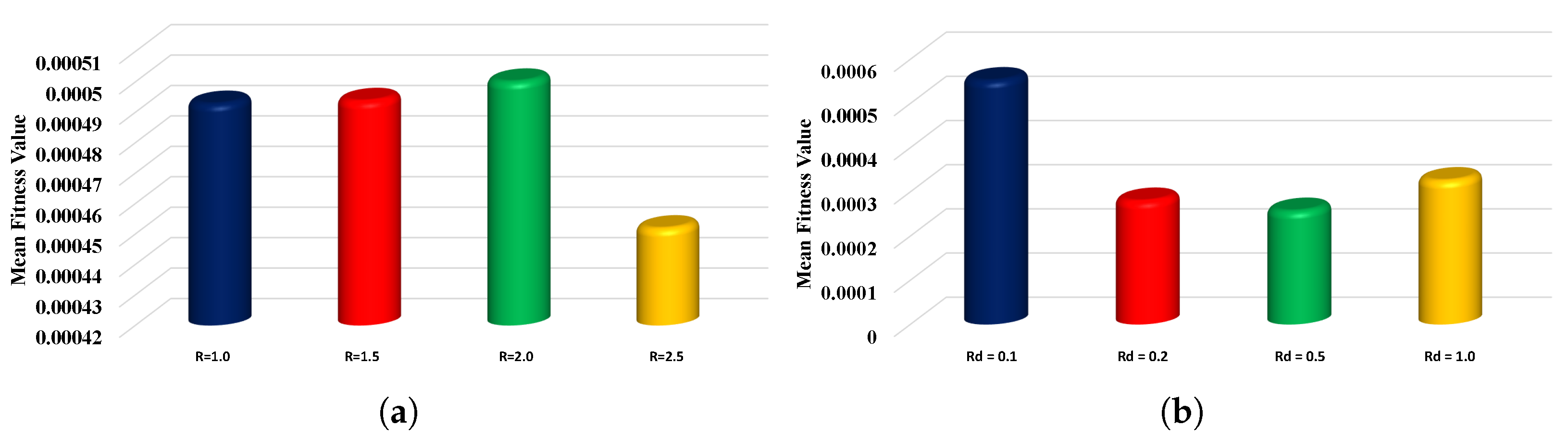
| Algorithm | Parameters | Settings | Parameter | Settings |
|---|---|---|---|---|
| Arithmetic optimization algorithm | Lower bound | −5 | Upper bound | 5 |
| Search agents | 80 | Dimensions | 90 | |
| Maximum iterations | 5000 | Fitness | ||
| Tolerance function | Tolerance constrained | |||
| Interior point algorithm | Lower bound | −5 | Upper bound | 5 |
| Maximum iterations | 1000 | Fitness | ||
| Function evaluations | 1,500,000 | Tolerance function |
| Numerical | NN-BLM [45,46] | NARX-LM [47,48] | ANN-AOA-IPA | Numerical | NN-BLM [45,46] | NARX-LM [47,48] | ANN-AOA-IPA | |
|---|---|---|---|---|---|---|---|---|
| −1 | 1.00000000 | 0.99996385 | 0.99999938 | 1.00000055 | 1.00000000 | 0.94071596 | 1.10009813 | 0.99999946 |
| −0.9 | 1.07763894 | 1.08608331 | 1.07761050 | 1.07763906 | 1.07282631 | 1.07270067 | 1.10009797 | 1.07282754 |
| −0.8 | 1.11587590 | 1.11489475 | 1.11586776 | 1.11587661 | 1.10009813 | 1.09571348 | 1.09998164 | 1.10009954 |
| −0.7 | 1.12166425 | 1.11870199 | 1.12166471 | 1.12162656 | 1.09252600 | 1.08619716 | 1.09250160 | 1.09251966 |
| −0.6 | 1.10084648 | 1.10025358 | 1.10034744 | 1.10084649 | 1.05832581 | 1.05931735 | 1.05836175 | 1.05837758 |
| −0.5 | 1.05841043 | 1.06827881 | 1.05847989 | 1.05841021 | 1.00395629 | 1.00385653 | 1.00388772 | 1.00337256 |
| −0.4 | 0.99868221 | 0.99875324 | 0.99874777 | 0.99868209 | 0.93461860 | 0.93460208 | 0.93467741 | 0.93460079 |
| −0.3 | 0.92547167 | 0.92546679 | 0.92552296 | 0.92547108 | 0.85459585 | 0.99372664 | 0.85454526 | 0.85459395 |
| −0.2 | 0.84218219 | 0.84218203 | 0.84220346 | 0.84218178 | 0.76748579 | 0.76748917 | 0.76746195 | 0.76748827 |
| −0.1 | 0.75189435 | 0.75180907 | 0.75194013 | 0.75189332 | 0.67636211 | 0.67637960 | 0.67636574 | 0.67636559 |
| 0.0 | 0.65743016 | 0.65745095 | 0.65746523 | 0.65742961 | 0.58388820 | 0.58389632 | 0.58387412 | 0.58389402 |
| 0.1 | 0.56140356 | 0.32841222 | 0.56142094 | 0.56140284 | 0.49239957 | 0.49242261 | 0.49239969 | 0.49246100 |
| 0.2 | 0.46626097 | 0.46626563 | 0.46695412 | 0.46635119 | 0.40396540 | 0.40401405 | 0.40396405 | 0.40396402 |
| 0.3 | 0.37431537 | 0.37432027 | 0.37531147 | 0.37456661 | 0.32043680 | 0.32050855 | 0.32041108 | 0.32043193 |
| 0.4 | 0.28777627 | 0.28778534 | 0.28822966 | 0.28780743 | 0.24348682 | 0.24445067 | 0.24351486 | 0.24342219 |
| 0.5 | 0.20877774 | 0.20874843 | 0.20881059 | 0.20877765 | 0.17464595 | 0.13850070 | 0.17472544 | 0.17465424 |
| 0.6 | 0.13940632 | 0.13343492 | 0.13945447 | 0.13940621 | 0.11533566 | 0.11527305 | 0.11531411 | 0.11533162 |
| 0.7 | 0.08173037 | 0.08206249 | 0.08172059 | 0.08173037 | 0.06690252 | 0.05927328 | 0.06692670 | 0.06690254 |
| 0.8 | 0.03783243 | 0.03762772 | 0.03781267 | 0.03874270 | 0.03065445 | 0.03157715 | 0.03069898 | 0.03065476 |
| 0.9 | 0.00984625 | 0.01255599 | 0.01366272 | 0.00987969 | 0.00790112 | 0.06554558 | 0.00777912 | 0.00799663 |
| 1 | 0.00000000 | 0.00342423 | 0.00361723 | 0.00000143 | 0.00000006 | 0.03495787 | 0.00046412 | −0.00002026 |
| NN-BLM | NARX-LM | ANN-AOA-IPA | NN-BLM | NARX-LM | ANN-AOA-IPA | |
|---|---|---|---|---|---|---|
| −1 | ||||||
| −0.9 | ||||||
| −0.8 | ||||||
| −0.7 | ||||||
| −0.6 | ||||||
| −0.5 | ||||||
| −0.4 | ||||||
| −0.3 | ||||||
| −0.2 | ||||||
| −0.1 | ||||||
| 0.0 | ||||||
| 0.1 | ||||||
| 0.2 | ||||||
| 0.3 | ||||||
| 0.4 | ||||||
| 0.5 | ||||||
| 0.6 | ||||||
| 0.7 | ||||||
| 0.8 | ||||||
| 0.9 | ||||||
| 1 | ||||||
| Population Space | Number of Neurons | |||||
|---|---|---|---|---|---|---|
| Pop = 40 | Pop = 60 | Pop = 80 | k = 10 | k = 20 | k = 30 | |
| −1 | ||||||
| −0.9 | ||||||
| −0.8 | ||||||
| −0.7 | ||||||
| −0.6 | ||||||
| −0.5 | ||||||
| −0.4 | ||||||
| −0.3 | ||||||
| −0.2 | ||||||
| −0.1 | ||||||
| 0 | ||||||
| 0.1 | ||||||
| 0.2 | ||||||
| 0.3 | ||||||
| 0.4 | ||||||
| 0.5 | ||||||
| 0.6 | ||||||
| 0.7 | ||||||
| 0.8 | ||||||
| 0.9 | ||||||
| 1 | ||||||
| Mean Absolute Deviations | Theil’s Inequality Coefficient | Error in Nash–Sutcliffe Efficiency | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | Mean | Standard Deviation | Minimum | Mean | Standard Deviation | Minimum | Mean | Standard Deviation | ||
| Mean Absolute Deviations | Theil’s Inequality Coefficient | Error in Nash–Sutcliffe Efficiency | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | Mean | Standard Deviation | Minimum | Mean | Standard Deviation | Minimum | Mean | Standard Deviation | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Alshammari, F.S. Analysis of Nanofluid Particles in a Duct with Thermal Radiation by Using an Efficient Metaheuristic-Driven Approach. Nanomaterials 2022, 12, 637. https://doi.org/10.3390/nano12040637
Khan NA, Sulaiman M, Tavera Romero CA, Alshammari FS. Analysis of Nanofluid Particles in a Duct with Thermal Radiation by Using an Efficient Metaheuristic-Driven Approach. Nanomaterials. 2022; 12(4):637. https://doi.org/10.3390/nano12040637
Chicago/Turabian StyleKhan, Naveed Ahmad, Muhammad Sulaiman, Carlos Andrés Tavera Romero, and Fahad Sameer Alshammari. 2022. "Analysis of Nanofluid Particles in a Duct with Thermal Radiation by Using an Efficient Metaheuristic-Driven Approach" Nanomaterials 12, no. 4: 637. https://doi.org/10.3390/nano12040637







