Coexistence of Bloch and Parametric Mechanisms of High-Frequency Gain in Doped Superlattices
Abstract
:1. Introduction
2. Main Equations and Explanations
3. Results and Discussion
3.1. Overview of the Small-Signal Results and Introduction to the Large-Signal Effects
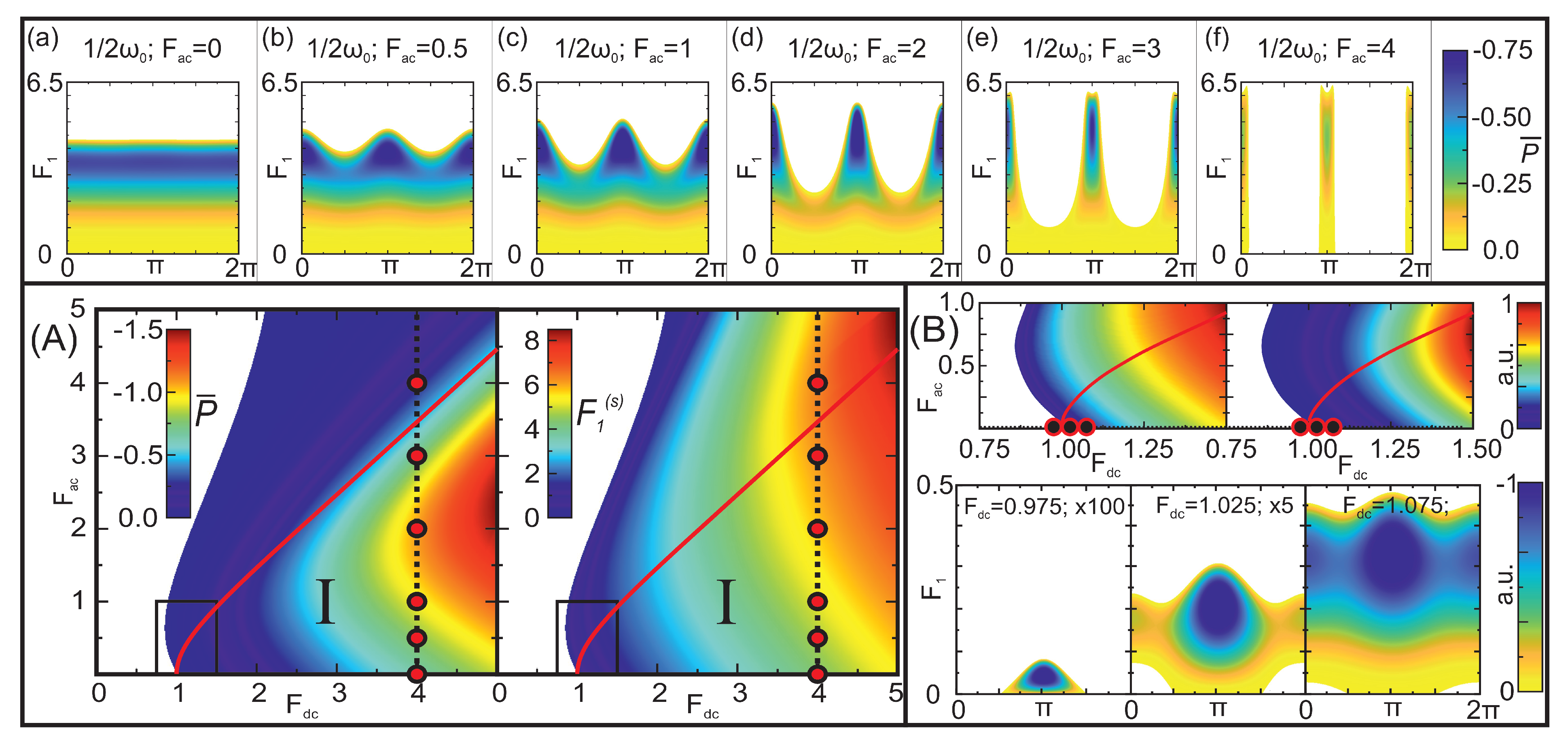
3.2. Pure Parametric Gain
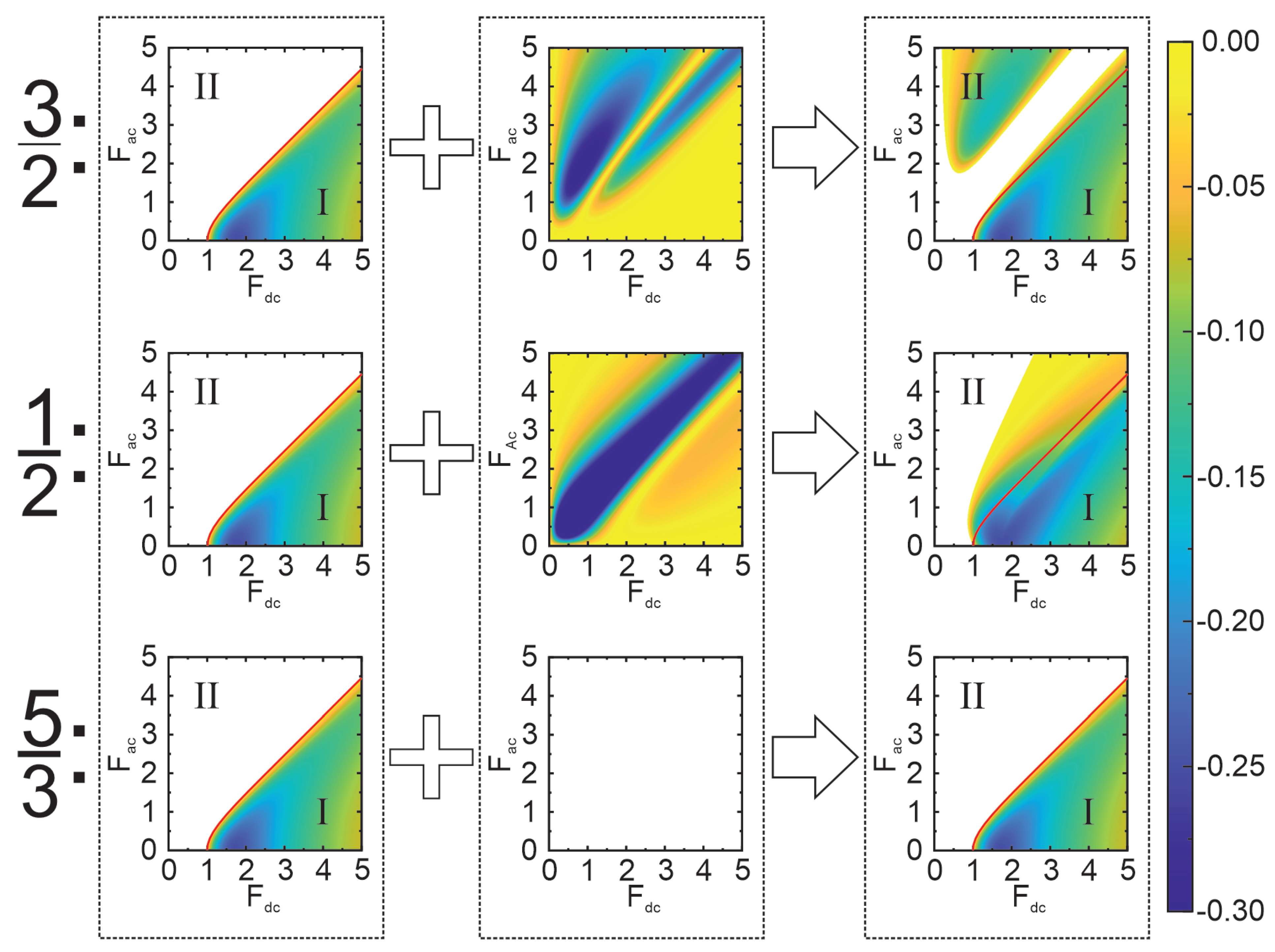
3.3. Coexistence of Bloch and Parametric Gain
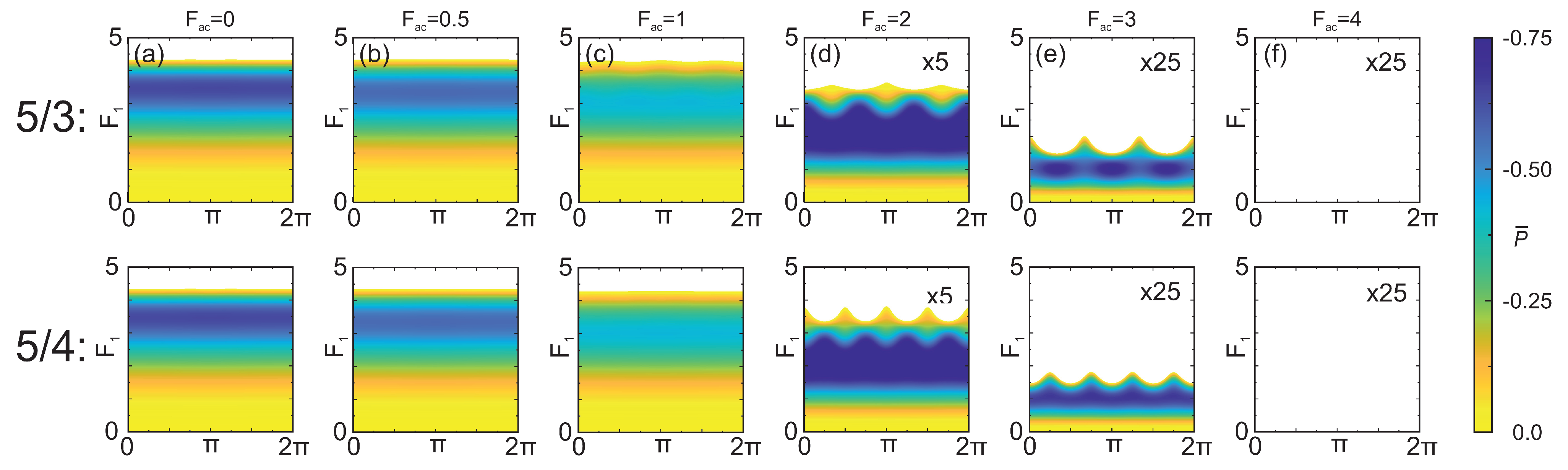
3.4. Pure Parametric Fractional Frequency Generation via Ignition
4. Concluding Remarks and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Esaki, L.; Tsu, R. Superlattice and Negative Differential Conductivity in Semiconductors. IBM J. Res. Dev. 1970, 14, 61–65. [Google Scholar] [CrossRef]
- Leo, K. High-Field Transport in Semiconductor Superlattices; Springer: Berlin/Heidelberg, Germany, 2003; p. 242. [Google Scholar] [CrossRef]
- Feldmann, J.; Leo, K.; Shah, J.; Miller, D.A.B.; Cunningham, J.E.; Meier, T.; von Plessen, G.; Schulze, A.; Thomas, P.; Schmitt-Rink, S. Optical Investigation of Bloch Oscillations in a Semiconductor Superlattice. Phys. Rev. B 1992, 46, 7252–7255. [Google Scholar] [CrossRef]
- Waschke, C.; Roskos, H.G.; Schwedler, R.; Leo, K.; Kurz, H.; Köhler, K. Coherent Submillimeter-Wave Emission from Bloch Oscillations in a Semiconductor Superlattice. Phys. Rev. Lett. 1993, 70, 3319–3322. [Google Scholar] [CrossRef] [PubMed]
- Lyssenko, V.G.; Valušis, G.; Löser, F.; Hasche, T.K.; Leo, K.; Dignam, M.M.; Köhler, R. Direct Measurement of the Spatial Displacement of Bloch-Oscillating Electrons in Semiconductor Superlattices. Phys. Rev. Lett. 1997, 79, 301–304. [Google Scholar] [CrossRef]
- Romanova, J.Y.; Demidov, E.V.; Mourokh, L.G.; Romanov, Y.A. Zener Tunneling in Semiconductor Superlattices. J. Phys. Condens. Matter 2011, 23, 305801. [Google Scholar] [CrossRef]
- Bauer, T.; Kolb, J.; Hummel, A.B.; Roskos, H.G.; Köhler, K. Coherent Hall Effect in a Semiconductor Superlattice. Phys. Rev. Lett. 2002, 88, 086801. [Google Scholar] [CrossRef] [Green Version]
- Apostolakis, A.; Balanov, A.G.; Kusmartsev, F.V.; Alekseev, K.N. Beyond the Ordinary Acoustoelectric Effect: Superluminal Phenomena in the Acoustic Realm and Phonon-mediated Bloch Gain. Phys. Rev. B 2022, 106, 014312. [Google Scholar] [CrossRef]
- McGilly, L.J.; Kerelsky, A.; Finney, N.R.; Shapovalov, K.; Shih, E.M.; Ghiotto, A.; Zeng, Y.; Moore, S.L.; Wu, W.; Bai, Y.; et al. Visualization of Moiré Superlattices. Nat. Nanotechnol. 2020, 15, 580–584. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional Superconductivity in Magic-angle Graphene Superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Sunku, S.S.; Ni, G.X.; Jiang, B.Y.; Yoo, H.; Sternbach, A.; McLeod, A.S.; Stauber, T.; Xiong, L.; Taniguchi, T.; Watanabe, K.; et al. Photonic Crystals for Nano-light in Moiré Graphene Superlattices. Science 2018, 362, 1153–1156. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated Insulator Behaviour at Half-Filling in Magic-Angle Graphene Superlattices. Nature 2018, 556, 80–84. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Kahn, S.; Leconte, N.; Taniguchi, T.; Watanabe, K.; Crommie, M.; Jung, J.; Zettl, A. High-Order Fractal Quantum Oscillations in Graphene / BN Superlattices in the Extreme Doping Limit. Phys. Rev. Lett. 2023, 130, 186204. [Google Scholar] [CrossRef]
- Belkin, M.A.; Capasso, F. New Frontiers in Quantum Cascade Lasers: High Performance Room Temperature Terahertz Sources. Phys. Scr. 2015, 90, 118002. [Google Scholar] [CrossRef]
- Ktitorov, S.; Simin, G.; Sindalovskii, V. Bragg Reflections and the High-Frequency Conductivity of an Electronic Solid-State Plasma. Sov. Phys. Solid State 1972, 13, 1872. [Google Scholar]
- Terazzi, R.; Gresch, T.; Giovannini, M.; Hoyler, N.; Sekine, N.; Faist, J. Bloch Gain in Quantum Cascade Lasers. Nat. Phys. 2007, 3, 329–333. [Google Scholar] [CrossRef] [Green Version]
- Wacker, A. Coexistence of Gain and Absorption. Nat. Phys. 2007, 3, 298–299. [Google Scholar] [CrossRef]
- Renk, K.F.; Stahl, B.I.; Rogl, A.; Janzen, T.; Ustinov, V.; Zhukov, A. Subterahertz Superlattice Parametric Oscillator. Phys. Rev. Lett. 2005, 95, 126801. [Google Scholar] [CrossRef] [Green Version]
- Renk, K.; Rogl, A.; Stahl, B. Semiconductor-Superlattice Parametric Oscillator for Generation of Sub-terahertz and Terahertz Waves. J. Lumin. 2007, 125, 252–258. [Google Scholar] [CrossRef]
- Leitenstorfer, A.; Moskalenko, A.S.; Kampfrath, T.; Kono, J.; Castro-Camus, E.; Peng, K.; Qureshi, N.; Turchinovich, D.; Tanaka, K.; Markelz, A.G.; et al. The 2023 Terahertz Science and Technology Roadmap. J. Phys. D Appl. Phys. 2023, 56, 223001. [Google Scholar] [CrossRef]
- Endres, C.P.; Lewen, F.; Giesen, T.F.; Schlemmer, S.; Paveliev, D.G.; Koschurinov, Y.I.; Ustinov, V.M.; Zhucov, A.E. Application of Superlattice Multipliers for High-Resolution Terahertz Spectroscopy. Rev. Sci. Instrum. 2007, 78, 043106. [Google Scholar] [CrossRef] [Green Version]
- Pereira, M.F.; Zubelli, J.P.; Winge, D.; Wacker, A.; Rodrigues, A.S.; Anfertev, V.; Vaks, V. Theory and Measurements of Harmonic Generation in Semiconductor Superlattices with Applications in the 100 GHz to 1 THz Range. Phys. Rev. B 2017, 96, 045306. [Google Scholar] [CrossRef] [Green Version]
- Apostolakis, A.; Pereira, M.F. Superlattice Nonlinearities for Gigahertz-Terahertz Generation in Harmonic Multipliers. Nanophotonics 2020, 9, 3941–3952. [Google Scholar] [CrossRef]
- Pavelyev, D.G.; Vasilev, A.P.; Kozlov, V.A.; Obolenskaya, E.S.; Obolensky, S.V.; Ustinov, V.M. Increase of Self-Oscillation and Transformation Frequencies in THz Diodes. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 231–236. [Google Scholar] [CrossRef]
- Goto, H. Quantum Computation Based on Quantum Adiabatic Bifurcations of Kerr-Nonlinear Parametric Oscillators. J. Phys. Soc. Jpn. 2019, 88, 061015. [Google Scholar] [CrossRef] [Green Version]
- Aumentado, J. Superconducting Parametric Amplifiers: The State of the Art in Josephson Parametric Amplifiers. IEEE Microw. Mag. 2020, 21, 45–59. [Google Scholar] [CrossRef]
- Kruk, S.; Wang, L.; Sain, B.; Dong, Z.; Yang, J.; Zentgraf, T.; Kivshar, Y. Asymmetric Parametric Generation of Images with Nonlinear Dielectric Metasurfaces. Nat. Photonics 2022, 16, 561–565. [Google Scholar] [CrossRef]
- Čižas, V.; Subačius, L.; Alexeeva, N.V.; Seliuta, D.; Hyart, T.; Köhler, K.; Alekseev, K.N.; Valušis, G. Dissipative Parametric Gain in a GaAs/AlGaAs Superlattice. Phys. Rev. Lett. 2022, 128, 236802. [Google Scholar] [CrossRef]
- Kroemer, H. Theory of the Gunn Effect. Proc. IEEE 1964, 52, 1736. [Google Scholar] [CrossRef] [Green Version]
- Ignatov, A.; Piskarev, V.; Shashkin, V. Instability (Domainization) of an Electric Field in Multilayer Quantum Structures. Sov. Phys. Semiconducors 1985, 19, 1345. [Google Scholar]
- Hyart, T.; Shorokhov, A.V.; Alekseev, K.N. Theory of Parametric Amplification in Superlattices. Phys. Rev. Lett. 2007, 98, 220404. [Google Scholar] [CrossRef] [Green Version]
- Romanov, Y.; Romanova, Y. Self-Oscillations in Semiconductor Superlattices. J. Exp. Theor. Phys. 2000, 91, 1033. [Google Scholar] [CrossRef]
- Romanov, Y.A.; Romanova, J.Y.; Mourokh, L.G. Semiconductor Superlattice in a Biharmonic Field: Absolute Negative Conductivity and Static Electric-Field Generation. J. Appl. Phys. 2006, 99, 013707. [Google Scholar] [CrossRef]
- Shorokhov, A.V.; Alekseev, K.N. Theoretical Backgrounds of Nonlinear THz Spectroscopy of Semiconductor Superlattices. Int. J. Mod. Phys. B 2009, 23, 4448–4458. [Google Scholar] [CrossRef] [Green Version]
- Hyart, T.; Alekseev, K.N. Nondegenerate Parametric Amplification in Superlattices and the Limits of Strong and Weak Dissipation. Int. J. Mod. Phys. B 2009, 23, 4403–4413. [Google Scholar] [CrossRef] [Green Version]
- Romanova, Y. Parametric Generation of High-Frequency Harmonics in Semiconductor Superlattices. Semiconductors 2012, 46, 1451. [Google Scholar] [CrossRef]
- Hyart, T.; Alexeeva, N.V.; Leppänen, A.; Alekseev, K.N. Terahertz Parametric Gain in Semiconductor Superlattices in the Absence of Electric Domains. Appl. Phys. Lett. 2006, 89, 132105. [Google Scholar] [CrossRef] [Green Version]
- Hyart, T.; Alekseev, K.N.; Thuneberg, E.V. Bloch Gain in Dc-Ac-Driven Semiconductor Superlattices in the Absence of Electric Domains. Phys. Rev. B 2008, 77, 165330. [Google Scholar] [CrossRef] [Green Version]
- Romanov, Y.A.; Bovin, V.P.; Orlov, L.K. Nonlinear Amplification of Electromagnetic Oscillations in Semiconductors with Superlattices. Sov. Phys. Semiconductors 1978, 12, 987. [Google Scholar]
- Ignatov, A.A.; Renk, K.F.; Dodin, E.P. Esaki-Tsu Superlattice Oscillator: Josephson-Like Dynamics of Carriers. Phys. Rev. Lett. 1993, 70, 1996–1999. [Google Scholar] [CrossRef]
- Wacker, A. Semiconductor Superlattices: A Model System for Nonlinear Transport. Phys. Rep. 2002, 357, 1–111. [Google Scholar] [CrossRef] [Green Version]
- Pereira, M.F.; Apostolakis, A. Combined Structural and Voltage Control of Giant Nonlinearities in Semiconductor Superlattices. Nanomaterials 2021, 11, 1287. [Google Scholar] [CrossRef] [PubMed]
- Pereira, M.F. Harmonic Generation in Biased Semiconductor Superlattices. Nanomaterials 2022, 12, 1504. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Wei, S.; Zheng, Y.; Wang, C.; Cao, J. Theoretical Analysis of Terahertz Frequency Multiplier Based on Semiconductor Superlattices. Nanomaterials 2022, 12, 1114. [Google Scholar] [CrossRef] [PubMed]
- Winnerl, S.; Schomburg, E.; Grenzer, J.; Regl, H.J.; Ignatov, A.A.; Semenov, A.D.; Renk, K.F.; Pavel’ev, D.G.; Koschurinov, Y.; Melzer, B.; et al. Quasistatic and Dynamic Interaction of High-Frequency Fields with Miniband Electrons in Semiconductor Superlattices. Phys. Rev. B 1997, 56, 10303–10307. [Google Scholar] [CrossRef]
- Savvidis, P.G.; Kolasa, B.; Lee, G.; Allen, S.J. Resonant Crossover of Terahertz Loss to the Gain of a Bloch Oscillating InAs/AlSb Superlattice. Phys. Rev. Lett. 2004, 92, 196802. [Google Scholar] [CrossRef] [Green Version]
- Haddad, G.; Trew, R. Microwave Solid-State Active Devices. IEEE Trans. Microw. Theory Tech. 2002, 50, 760–779. [Google Scholar] [CrossRef]
- Torrey, C.; Whitmer, C. Crystal Rectifiers; McGraw-Hill Book Company Inc.: New York, NY, USA; London, UK, 1948. [Google Scholar]
- Alekseev, K.; Gorkunov, M.; Demarina, N.; Hyart, T.; Alexeeva, N.; Shorokhov, A. Suppressed Absolute Negative Conductance and Generation of High-Frequency Radiation in Semiconductor Superlattices. Europhys. Lett. 2006, 73, 934. [Google Scholar] [CrossRef] [Green Version]
- Copeland, J.A. LSA Oscillator-Diode Theory. J. Appl. Phys. 2004, 38, 3096–3101. [Google Scholar] [CrossRef]
- Wang, C.; Cao, J.C. Terahertz Generation by Quantum-Dot Miniband Superlattices in the Absence of Electric Field Domains. J. Appl. Phys. 2012, 111, 053711. [Google Scholar] [CrossRef]
- Kroemer, H. Large-Amplitude Oscillation Dynamics and Domain Suppression in a Superlattice Bloch Oscillator. arXiv 2000, arXiv:cond-mat/0009311. [Google Scholar]
- Winge, D.O.; Dupont, E.; Wacker, A. Ignition of Quantum Cascade Lasers in a State of Oscillating Electric Field Domains. Phys. Rev. A 2018, 98, 023834. [Google Scholar] [CrossRef] [Green Version]
- Valušis, G.; Lisauskas, A.; Yuan, H.; Knap, W.; Roskos, H.G. Roadmap of Terahertz Imaging 2021. Sensors 2021, 21, 4092. [Google Scholar] [CrossRef]
- Duan, S.; Mo, B.; Wang, X.; Chan, E.H.W.; Feng, X.; Guan, B.O.; Yao, J. Photonic-Assisted Regenerative Microwave Frequency Divider With a Tunable Division Factor. J. Light. Technol. 2020, 38, 5509–5516. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čižas, V.; Alexeeva, N.; Alekseev, K.N.; Valušis, G. Coexistence of Bloch and Parametric Mechanisms of High-Frequency Gain in Doped Superlattices. Nanomaterials 2023, 13, 1993. https://doi.org/10.3390/nano13131993
Čižas V, Alexeeva N, Alekseev KN, Valušis G. Coexistence of Bloch and Parametric Mechanisms of High-Frequency Gain in Doped Superlattices. Nanomaterials. 2023; 13(13):1993. https://doi.org/10.3390/nano13131993
Chicago/Turabian StyleČižas, Vladislovas, Natalia Alexeeva, Kirill N. Alekseev, and Gintaras Valušis. 2023. "Coexistence of Bloch and Parametric Mechanisms of High-Frequency Gain in Doped Superlattices" Nanomaterials 13, no. 13: 1993. https://doi.org/10.3390/nano13131993




