Low-Temperature Emission Dynamics of Methylammonium Lead Bromide Hybrid Perovskite Thin Films at the Sub-Micrometer Scale
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methylamonium Lead Bromide Thin Film Preparation
2.2. Low-Temperature Confocal Microscopy
2.3. Hyperspectral Microscopy
2.4. Two-Color Fluorescence Lifetime Imaging Microscopy
2.5. Fitting the Fluorescence Lifetime Imaging Experiments
3. Results
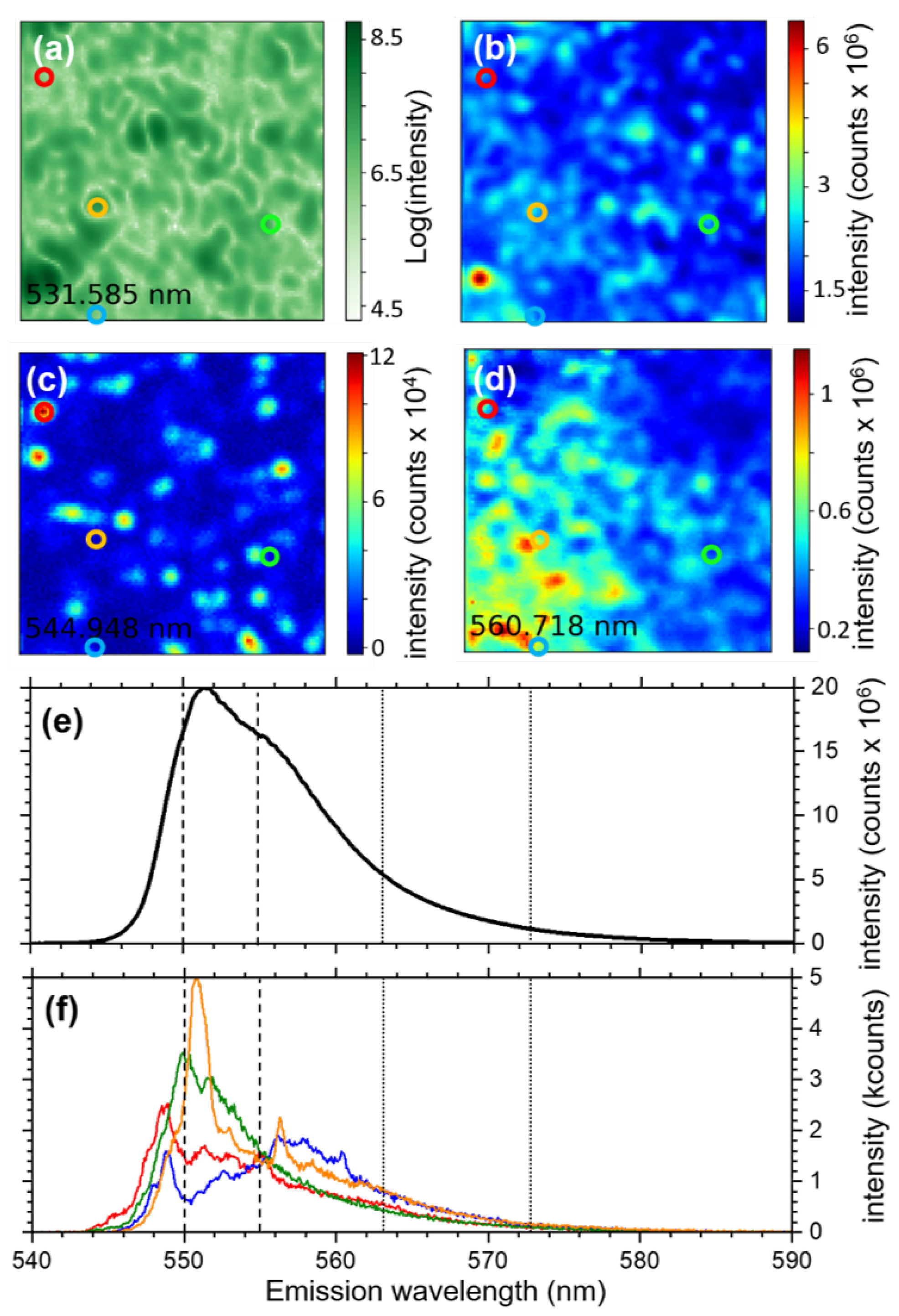
3.1. Hyperspectral Microscopy Under Continuous, Quasi-Resonant Excitation
3.1.1. Ensemble Measurements
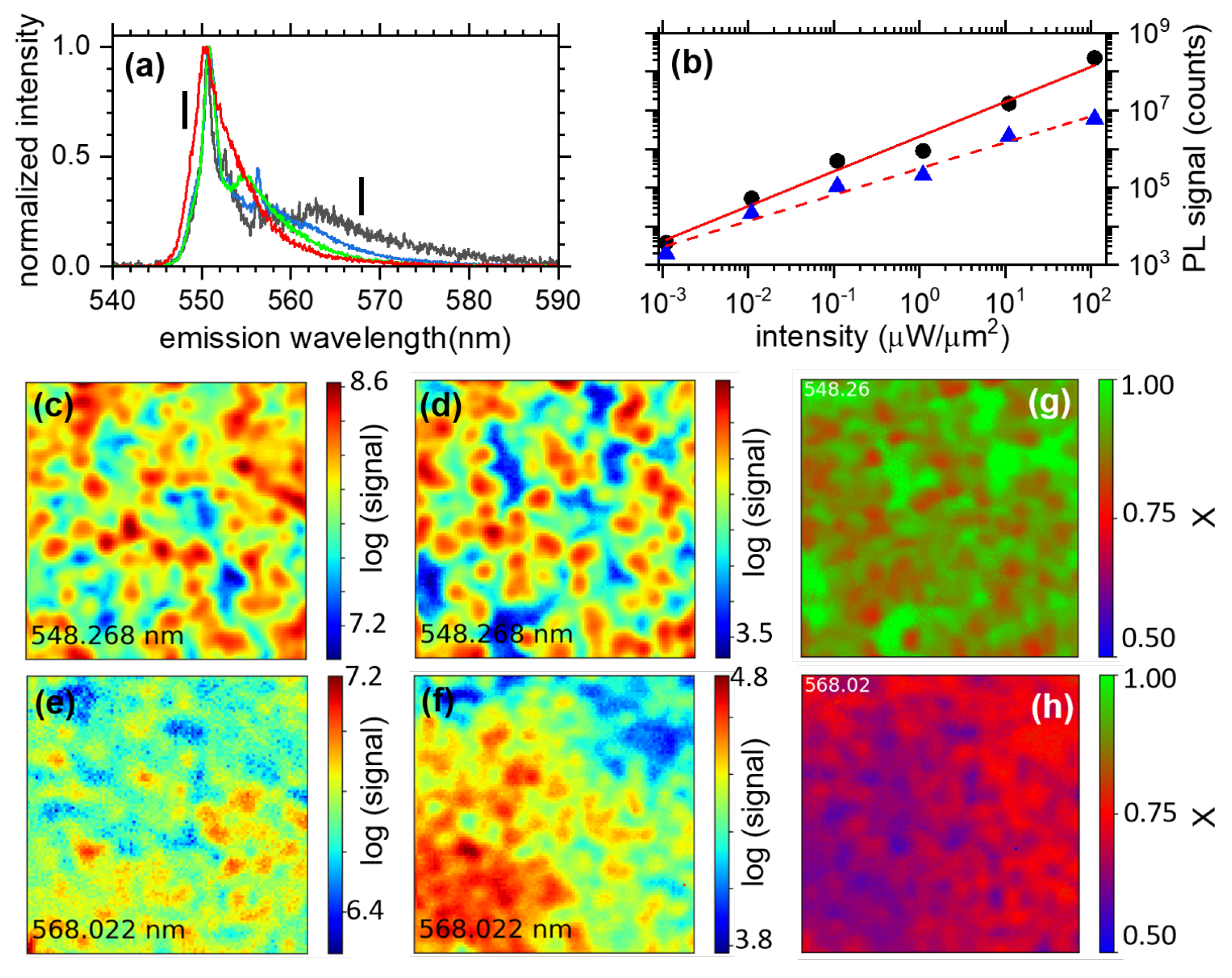
3.1.2. Hyperspectral Microscopy
3.1.3. Power Dependence
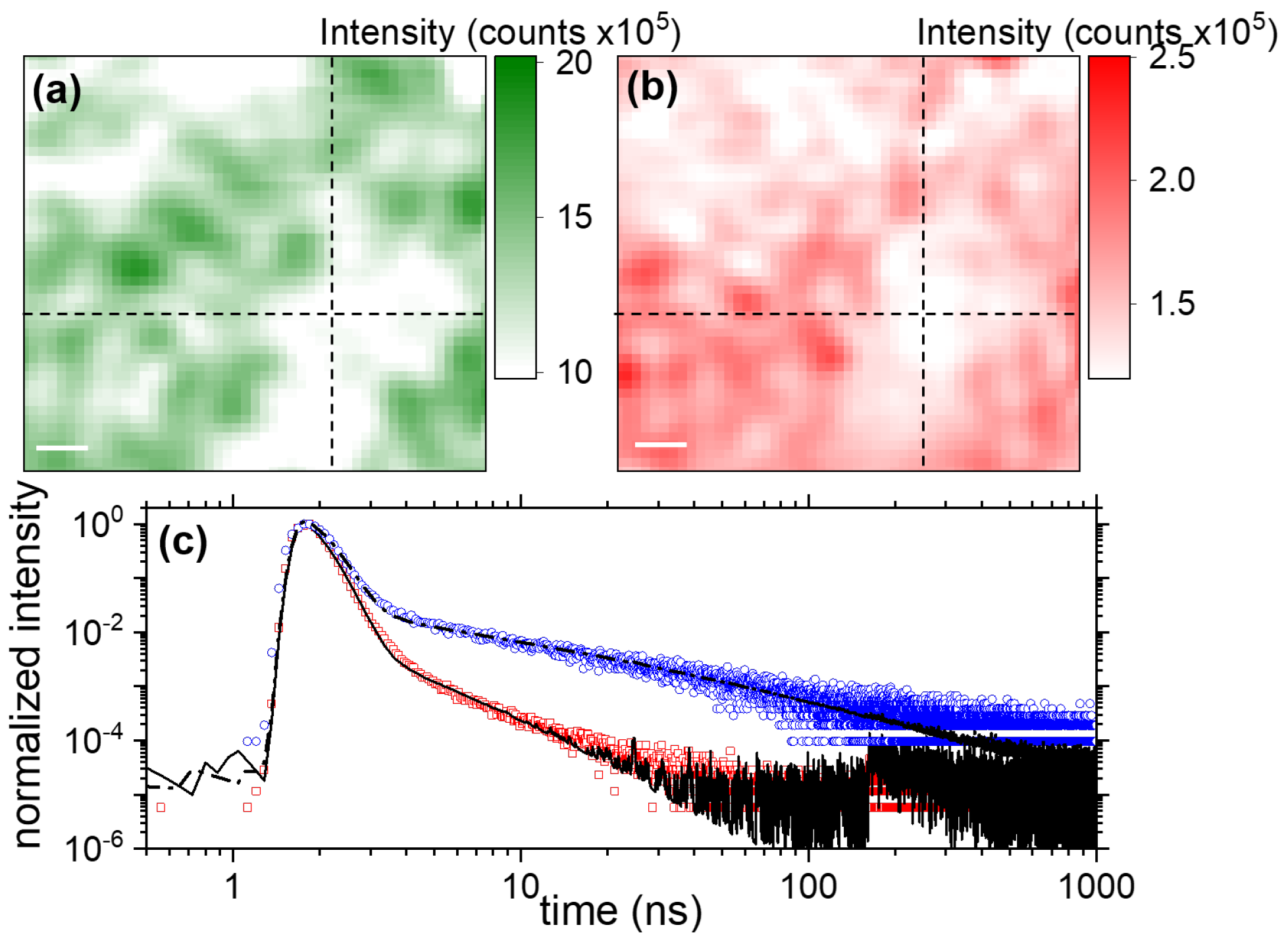
3.2. Fluorescence Lifetime Imaging Microscopy Under Pulsed, Non-Resonant Excitation
3.2.1. Exciton- and Trap-Related Emission Dynamics
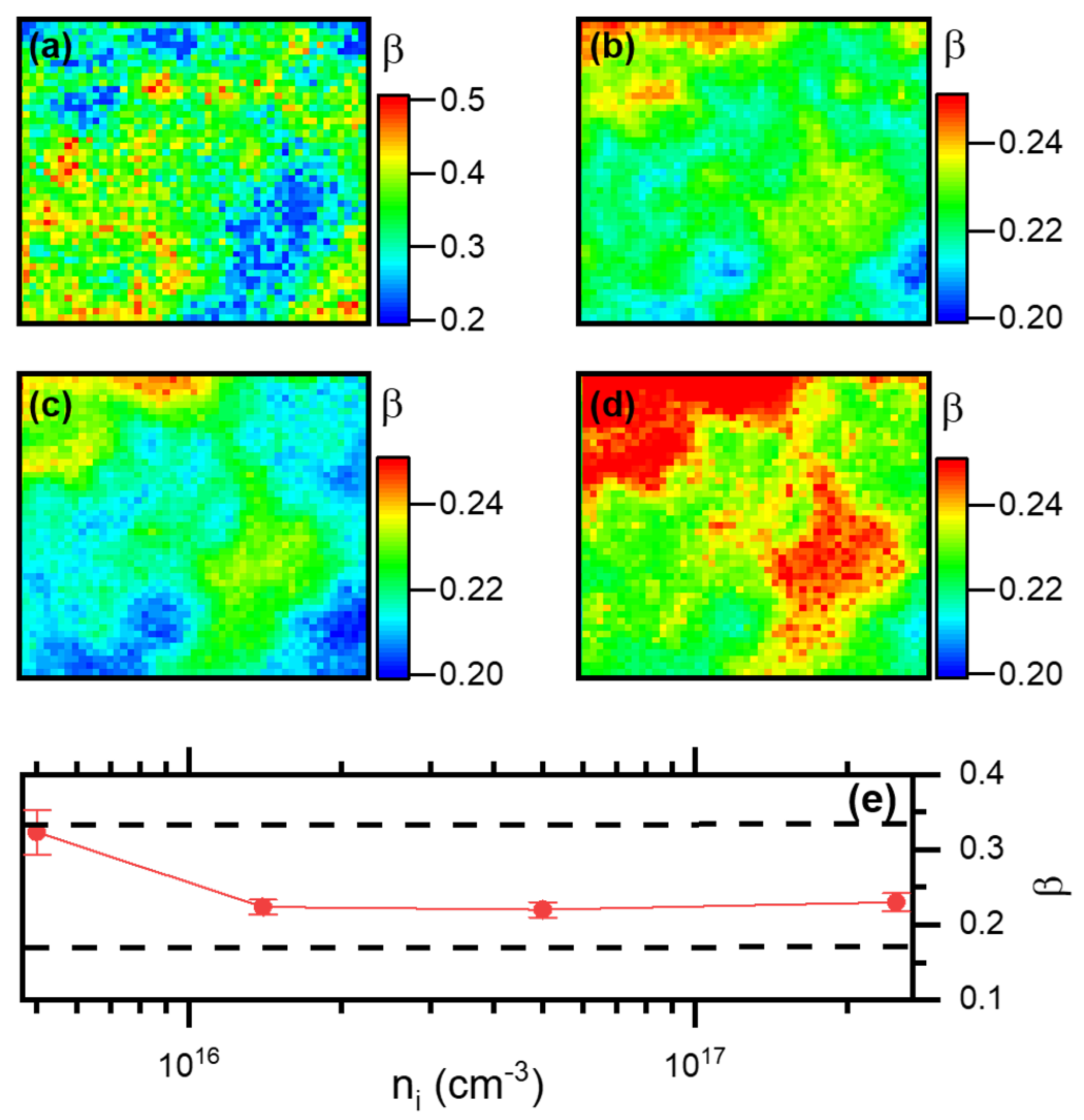
3.2.2. Evolution of the Average Lifetime
3.2.3. Determination of the Density of Traps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, H.S.; Lee, C.R.; Im, J.H.; Lee, K.B.; Moehl, T.; Marchioro, A.; Moon, S.J.; Humphry-Baker, R.; Yum, J.H.; Moser, J.E.; et al. Lead Iodide Perovskite Sensitized All-Solid-State Submicron Thin Film Mesoscopic Solar Cell with Efficiency Exceeding 9%. Sci. Rep. 2012, 2, 591. [Google Scholar] [CrossRef] [PubMed]
- Chung, I.; Lee, B.; He, J.; Chang, R.P.H.; Kanatzidis, M.G. All-solid-state dye-sensitized solar cells with high efficiency. Nature 2012, 485, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites. Science 2012, 338, 643–647. [Google Scholar] [CrossRef]
- Nayak, P.K.; Mahesh, S.; Snaith, H.J.; Cahen, D. Photovoltaic Solar Cell Technologies: Analysing the State of the Art. Nat. Rev. Mater. 2019, 4, 269–285. [Google Scholar] [CrossRef]
- Lan, Y.F.; Yao, J.S.; Yang, J.N.; Song, Y.H.; Ru, X.C.; Zhang, Q.; Feng, L.Z.; Chen, T.; Song, K.H.; Yao, H.B. Spectrally Stable and Efficient Pure Red CsPbI 3 Quantum Dot Light-Emitting Diodes Enabled by Sequential Ligand Post-Treatment Strategy. Nano Lett. 2021, 21, 8756–8763. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.Y.; Zou, C.; Mao, C.; Corp, K.L.; Yao, Y.C.; Lee, Y.J.; Schlenker, C.W.; Jen, A.K.Y.; Lin, L.Y. CsPbBr 3 Perovskite Quantum Dot Vertical Cavity Lasers with Low Threshold and High Stability. ACS Photonics 2017, 4, 2281–2289. [Google Scholar] [CrossRef]
- Fu, C.; Li, Z.Y.; Wang, J.; Zhang, X.; Liang, F.X.; Lin, D.H.; Shi, X.F.; Fang, Q.L.; Luo, L.B. A Simple-Structured Perovskite Wavelength Sensor for Full-Color Imaging Application. Nano Lett. 2023, 23, 533–540. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, H.; Ma, D.; Rosei, F. Harnessing the properties of colloidal quantum dots in luminescent solar concentrators. Chem. Soc. Rev. 2018, 47, 5866–5890. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, L.; Fang, Z.; Wang, S.; Yang, T.; Zhu, L.; Hou, X.; Wang, H.; Wang, Z.L. Piezoelectric Nanogenerator Based on In Situ Growth All-Inorganic CsPbBr3 Perovskite Nanocrystals in PVDF Fibers with Long-Term Stability. Adv. Funct. Mater. 2021, 31, 2011073. [Google Scholar] [CrossRef]
- Mykhaylyk, V.B.; Kraus, H.; Saliba, M. Bright and Fast Scintillation of Organolead Perovskite MAPbBr3 at Low Temperatures. Mater. Horizons 2019, 6, 1740–1747. [Google Scholar] [CrossRef]
- Yu, D.; Wang, P.; Cao, F.; Gu, Y.; Liu, J.; Han, Z.; Huang, B.; Zou, Y.; Xu, X.; Zeng, H. Two-dimensional halide perovskite as β-ray scintillator for nuclear radiation monitoring. Nat. Commun. 2020, 11, 3395. [Google Scholar] [CrossRef]
- Dong, Q.; Fang, Y.; Shao, Y.; Mulligan, P.; Qiu, J.; Cao, L.; Huang, J. Electron-hole diffusion lengths >175 μm in solution-grown CH3NH3PbI3 single crystals. Science 2015, 347, 967–970. [Google Scholar] [CrossRef]
- Chen, Z.; Turedi, B.; Alsalloum, A.Y.; Yang, C.; Zheng, X.; Gereige, I.; AlSaggaf, A.; Mohammed, O.F.; Bakr, O.M. Single-Crystal MAPbI3 Perovskite Solar Cells Exceeding 21% Power Conversion Efficiency. ACS Energy Lett. 2019, 4, 1258–1259. [Google Scholar] [CrossRef]
- Leyden, M.R.; Meng, L.; Jiang, Y.; Ono, L.K.; Qiu, L.; Juarez-Perez, E.J.; Qin, C.; Adachi, C.; Qi, Y. Methylammonium Lead Bromide Perovskite Light-Emitting Diodes by Chemical Vapor Deposition. J. Phys. Chem. Lett. 2017, 8, 3193–3198. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Zeng, Y.; Meng, F.; Gao, S.; Fan, S.; Liu, Y.; Zhang, Y.; Wageh, S.; Al-Ghamdi, A.A.; Xiao, J.; et al. A High-Performance Self-Powered Photodetector Based on MAPbBr3 Single Crystal Thin Film/MoS2 Vertical Van Der Waals Heterostructure. Adv. Mater. Interfaces 2022, 9, 2200912. [Google Scholar] [CrossRef]
- Wenger, B.; Nayak, P.K.; Wen, X.; Kesava, S.V.; Noel, N.K.; Snaith, H.J. Consolidation of the optoelectronic properties of CH3NH3PbBr3 perovskite single crystals. Nat. Commun. 2017, 8, 590. [Google Scholar] [CrossRef]
- Fu, J.; Jamaludin, N.F.; Wu, B.; Li, M.; Solanki, A.; Ng, Y.F.; Mhaisalkar, S.; Huan, C.H.A.; Sum, T.C. Localized Traps Limited Recombination in Lead Bromide Perovskites. Adv. Energy Mater. 2019, 9, 1803119. [Google Scholar] [CrossRef]
- Che, X.; Traore, B.; Katan, C.; Fang, H.H.; Loi, M.A.; Even, J.; Kepenekian, M. Charge Trap Formation and Passivation in Methylammonium Lead Tribromide. J. Phys. Chem. C 2019, 123, 13812–13817. [Google Scholar] [CrossRef]
- Droseros, N.; Tsokkou, D.; Banerji, N. Photophysics of Methylammonium Lead Tribromide Perovskite: Free Carriers, Excitons, and Sub-Bandgap States. Adv. Energy Mater. 2020, 10, 1903258. [Google Scholar] [CrossRef]
- Niedzwiedzki, D.M.; Kouhnavard, M.; Diao, Y.; D’Arcy, J.M.; Biswas, P. Spectroscopic investigations of electron and hole dynamics in MAPbBr3 perovskite film and carrier extraction to PEDOT hole transport layer. Phys. Chem. Chem. Phys. 2021, 23, 13011–13022. [Google Scholar] [CrossRef]
- Gerhard, M.; Louis, B.; Frantsuzov, P.A.; Li, J.; Kiligaridis, A.; Hofkens, J.; Scheblykin, I.G. Heterogeneities and Emissive Defects in MAPbI 3 Perovskite Revealed by Spectrally Resolved Luminescence Blinking. Adv. Optical Mater. 2021, 9, 2001380. [Google Scholar] [CrossRef]
- Saleh, G.; Biffi, G.; Di Stasio, F.; Martín-García, B.; Abdelhady, A.L.; Manna, L.; Krahne, R.; Artyukhin, S. Methylammonium Governs Structural and Optical Properties of Hybrid Lead Halide Perovskites through Dynamic Hydrogen Bonding. Chem. Mater. 2021, 33, 8524–8533. [Google Scholar] [CrossRef]
- Ventosinos, F.; Moeini, A.; Pérez-del Rey, D.; Bolink, H.J.; Schmidt, J.A. Density of states within the bandgap of perovskite thin films studied using the moving grating technique. J. Chem. Phys. 2022, 156, 114201. [Google Scholar] [CrossRef]
- Xue, H.; Brocks, G.; Tao, S. Intrinsic defects in primary halide perovskites: A first-principles study of the thermodynamic trends. Phys. Rev. Mater. 2022, 6, 055402. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.; Zhang, X. Low-Temperature Discrimination of Defect States by Exciton Dynamics in Thin-Film MAPbBr3 Perovskite. J. Phys. Chem. Lett. 2022, 13, 6093–6100. [Google Scholar] [CrossRef] [PubMed]
- de Quilettes, D.W.; Vorpahl, S.M.; Stranks, S.D.; Nagaoka, H.; Eperon, G.E.; Ziffer, M.E.; Snaith, H.J.; Ginger, D.S. Impact of microstructure on local carrier lifetime in perovskite solar cells. Science 2015, 348, 683–686. [Google Scholar] [CrossRef]
- Moerman, D.; Eperon, G.E.; Precht, J.T.; Ginger, D.S. Correlating Photoluminescence Heterogeneity with Local Electronic Properties in Methylammonium Lead Tribromide Perovskite Thin Films. Chem. Mater. 2017, 29, 5484–5492. [Google Scholar] [CrossRef]
- Edri, E.; Kirmayer, S.; Henning, A.; Mukhopadhyay, S.; Gartsman, K.; Rosenwaks, Y.; Hodes, G.; Cahen, D. Why Lead Methylammonium Tri-Iodide Perovskite-Based Solar Cells Require a Mesoporous Electron Transporting Scaffold (but Not Necessarily a Hole Conductor). Nano Lett. 2014, 14, 1000–1004. [Google Scholar] [CrossRef]
- Yin, W.J.; Shi, T.; Yan, Y. Unique Properties of Halide Perovskites as Possible Origins of the Superior Solar Cell Performance. Adv. Mater. 2014, 26, 4653–4658. [Google Scholar] [CrossRef]
- de Quilettes, D.W.; Jariwala, S.; Burke, S.; Ziffer, M.E.; Wang, J.T.W.; Snaith, H.J.; Ginger, D.S. Tracking Photoexcited Carriers in Hybrid Perovskite Semiconductors: Trap-Dominated Spatial Heterogeneity and Diffusion. ACS Nano 2017, 11, 11488–11496. [Google Scholar] [CrossRef]
- Phung, N.; Al-Ashouri, A.; Meloni, S.; Mattoni, A.; Albrecht, S.; Unger, E.L.; Merdasa, A.; Abate, A. The Role of Grain Boundaries on Ionic Defect Migration in Metal Halide Perovskites. Adv. Energy Mater. 2020, 10, 1903735. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, A.; Yan, J.; Li, D.; Chen, Y. Revealing the properties of defects formed by CH3NH2 molecules in organic-inorganic hybrid perovskite MAPbBr3. Appl. Phys. Lett. 2017, 110, 123903. [Google Scholar] [CrossRef]
- McGovern, L.; Koschany, I.; Grimaldi, G.; Muscarella, L.A.; Ehrler, B. Grain Size Influences Activation Energy and Migration Pathways in MAPbBr3 Perovskite Solar Cells. J. Phys. Chem. Lett. 2021, 12, 2423–2428. [Google Scholar] [CrossRef]
- Tilchin, J.; Dirin, D.N.; Maikov, G.I.; Sashchiuk, A.; Kovalenko, M.V.; Lifshitz, E. Hydrogen-like Wannier–Mott Excitons in Single Crystal of Methylammonium Lead Bromide Perovskite. ACS Nano 2016, 10, 6363–6371. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, W. Temperature and excitation wavelength-dependent photoluminescence of CH3NH3PbBr3 crystal. Opt. Lett. 2018, 43, 4923–4926. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Duim, H.; Loi, M.A. Disentangling Dual Emission Dynamics in Lead Bromide Perovskite. Adv. Opt. Mater. 2023, 11, 2202866. [Google Scholar] [CrossRef]
- Dar, M.I.; Jacopin, G.; Meloni, S.; Mattoni, A.; Arora, N.; Boziki, A.; Zakeeruddin, S.M.; Rothlisberger, U.; Grätzel, M. Origin of unusual bandgap shift and dual emission in organic-inorganic lead halide perovskites. Sci. Adv. 2016, 2, e1601156. [Google Scholar] [CrossRef]
- Sarang, S.; Ishihara, H.; Chen, Y.C.; Lin, O.; Gopinathan, A.; Tung, V.C.; Ghosh, S. Low temperature excitonic spectroscopy and dynamics as a probe of quality in hybrid perovskite thin films. Phys. Chem. Chem. Phys. 2016, 18, 28428–28433. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, H.; Niu, J.; Zhang, H.; Lou, S.; Gao, C.; Zhan, Y.; Zhang, X.; Jin, Q.; Zheng, L. Temperature-dependent photoluminescence spectra and Decay dynamics of MAPbBr3 and MAPbI3 thin films. AIP Adv. 2018, 8, 095108. [Google Scholar] [CrossRef]
- Sadhukhan, P.; Pradhan, A.; Mukherjee, S.; Sengupta, P.; Roy, A.; Bhunia, S.; Das, S. Low temperature excitonic spectroscopy study of mechano-synthesized hybrid perovskite. Appl. Phys. Lett. 2019, 114, 131102. [Google Scholar] [CrossRef]
- Shi, J.; Li, Y.; Wu, J.; Wu, H.; Luo, Y.; Li, D.; Jasieniak, J.J.; Meng, Q. Exciton Character and High-Performance Stimulated Emission of Hybrid Lead Bromide Perovskite Polycrystalline Film. Adv. Opt. Mater. 2020, 8, 1902026. [Google Scholar] [CrossRef]
- Wang, K.H.; Li, L.C.; Shellaiah, M.; Wen Sun, K. Structural and Photophysical Properties of Methylammonium Lead Tribromide (MAPbBr3) Single Crystals. Sci. Rep. 2017, 7, 13643. [Google Scholar] [CrossRef] [PubMed]
- Baronnier, J.; Houel, J.; Dujardin, C.; Kulzer, F.; Mahler, B. Doping MAPbBr3 hybrid perovskites with CdSe/CdZnS quantum dots: From emissive thin films to hybrid single-photon sources. Nanoscale 2022, 14, 5769–5781. [Google Scholar] [CrossRef]
- Shibata, H.; Sakai, M.; Yamada, A.; Matsubara, K.; Sakurai, K.; Tampo, H.; Ishizuka, S.; Kim, K.K.; Niki, S. Excitation-Power Dependence of Free Exciton Photoluminescence of Semiconductors. Jpn. J. Appl. Phys. 2005, 44, 6113. [Google Scholar] [CrossRef]
- He, H.; Yu, Q.; Li, H.; Li, J.; Si, J.; Jin, Y.; Wang, N.; Wang, J.; He, J.; Wang, X.; et al. Exciton localization in solution-processed organolead trihalide perovskites. Nat. Commun. 2016, 7, 10896. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef]
- Stranks, S.D.; Burlakov, V.M.; Leijtens, T.; Ball, J.M.; Goriely, A.; Snaith, H.J. Recombination Kinetics in Organic-Inorganic Perovskites: Excitons, Free Charge, and Subgap States. Phys. Rev. Appl. 2014, 2, 034007. [Google Scholar] [CrossRef]
- Utzat, H.; Sun, W.; Kaplan, A.E.K.; Krieg, F.; Ginterseder, M.; Spokoyny, B.; Klein, N.D.; Shulenberger, K.E.; Perkinson, C.F.; Kovalenko, M.V.; et al. Coherent single-photon emission from colloidal lead halide perovskite quantum dots. Science 2019, 363, 1068–1072. [Google Scholar] [CrossRef]
- Klafter, J.; Shlesinger, M.F. On the relationship among three theories of relaxation in disordered systems. Proc. Natl. Acad. Sci. USA 1986, 83, 848–851. [Google Scholar] [CrossRef]
- Sillen, A.; Engelborghs, Y. The Correct Use of “Average” Fluorescence Parameters. Photochem. Photobiol. 1998, 67, 475–486. [Google Scholar] [CrossRef]
- Trinh, A.L.; Esposito, A. Biochemical resolving power of fluorescence lifetime imaging: Untangling the roles of the instrument response function and photon-statistics. Biomed. Opt. Express 2021, 12, 3775. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baronnier, J.; Mahler, B.; Dujardin, C.; Houel, J. Low-Temperature Emission Dynamics of Methylammonium Lead Bromide Hybrid Perovskite Thin Films at the Sub-Micrometer Scale. Nanomaterials 2023, 13, 2376. https://doi.org/10.3390/nano13162376
Baronnier J, Mahler B, Dujardin C, Houel J. Low-Temperature Emission Dynamics of Methylammonium Lead Bromide Hybrid Perovskite Thin Films at the Sub-Micrometer Scale. Nanomaterials. 2023; 13(16):2376. https://doi.org/10.3390/nano13162376
Chicago/Turabian StyleBaronnier, Justine, Benoit Mahler, Christophe Dujardin, and Julien Houel. 2023. "Low-Temperature Emission Dynamics of Methylammonium Lead Bromide Hybrid Perovskite Thin Films at the Sub-Micrometer Scale" Nanomaterials 13, no. 16: 2376. https://doi.org/10.3390/nano13162376
APA StyleBaronnier, J., Mahler, B., Dujardin, C., & Houel, J. (2023). Low-Temperature Emission Dynamics of Methylammonium Lead Bromide Hybrid Perovskite Thin Films at the Sub-Micrometer Scale. Nanomaterials, 13(16), 2376. https://doi.org/10.3390/nano13162376





