Magnetic Bimerons in Cylindrical Nanotubes
Abstract
:1. Introduction
2. Models and Methods
3. Results and Discussion
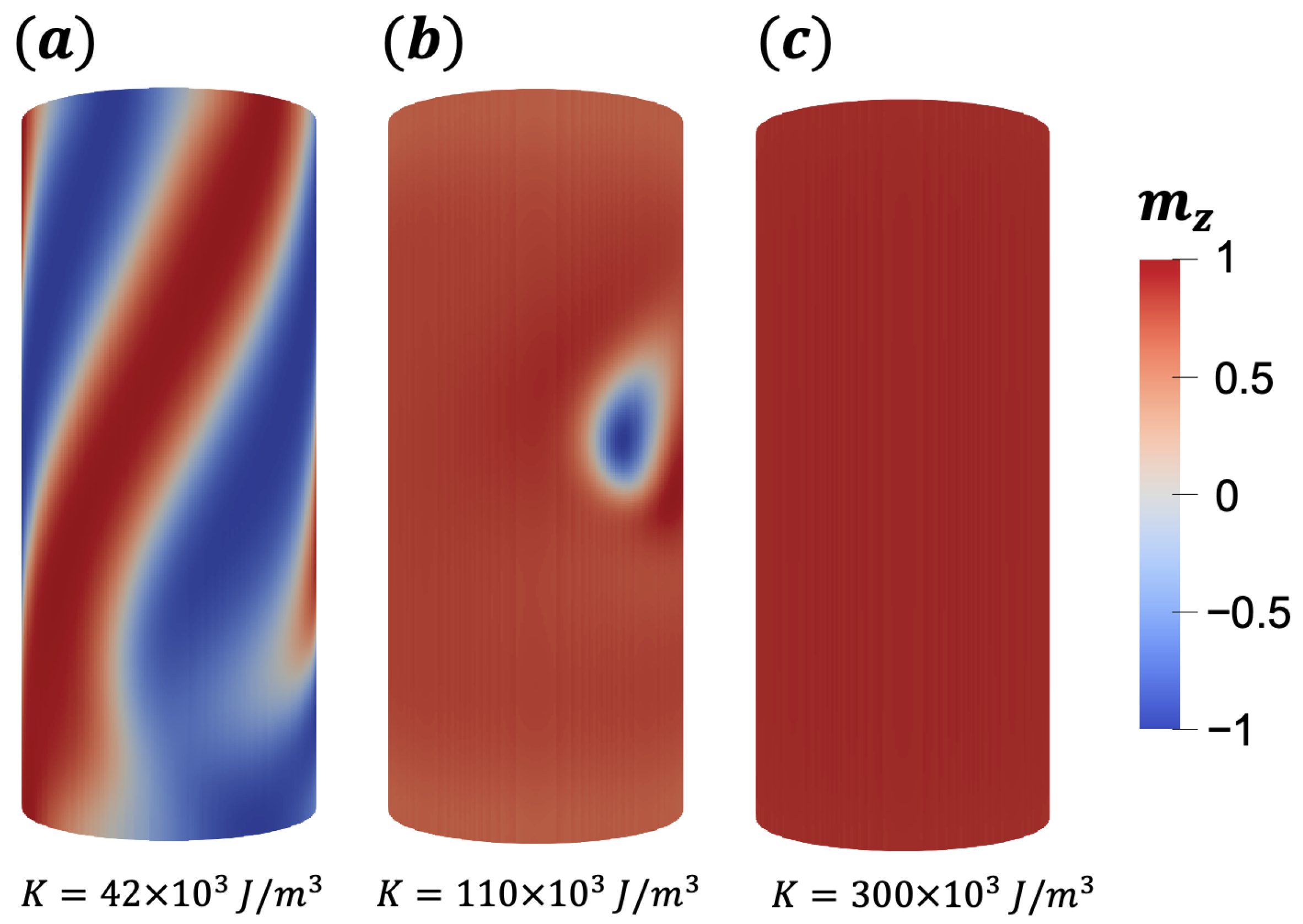
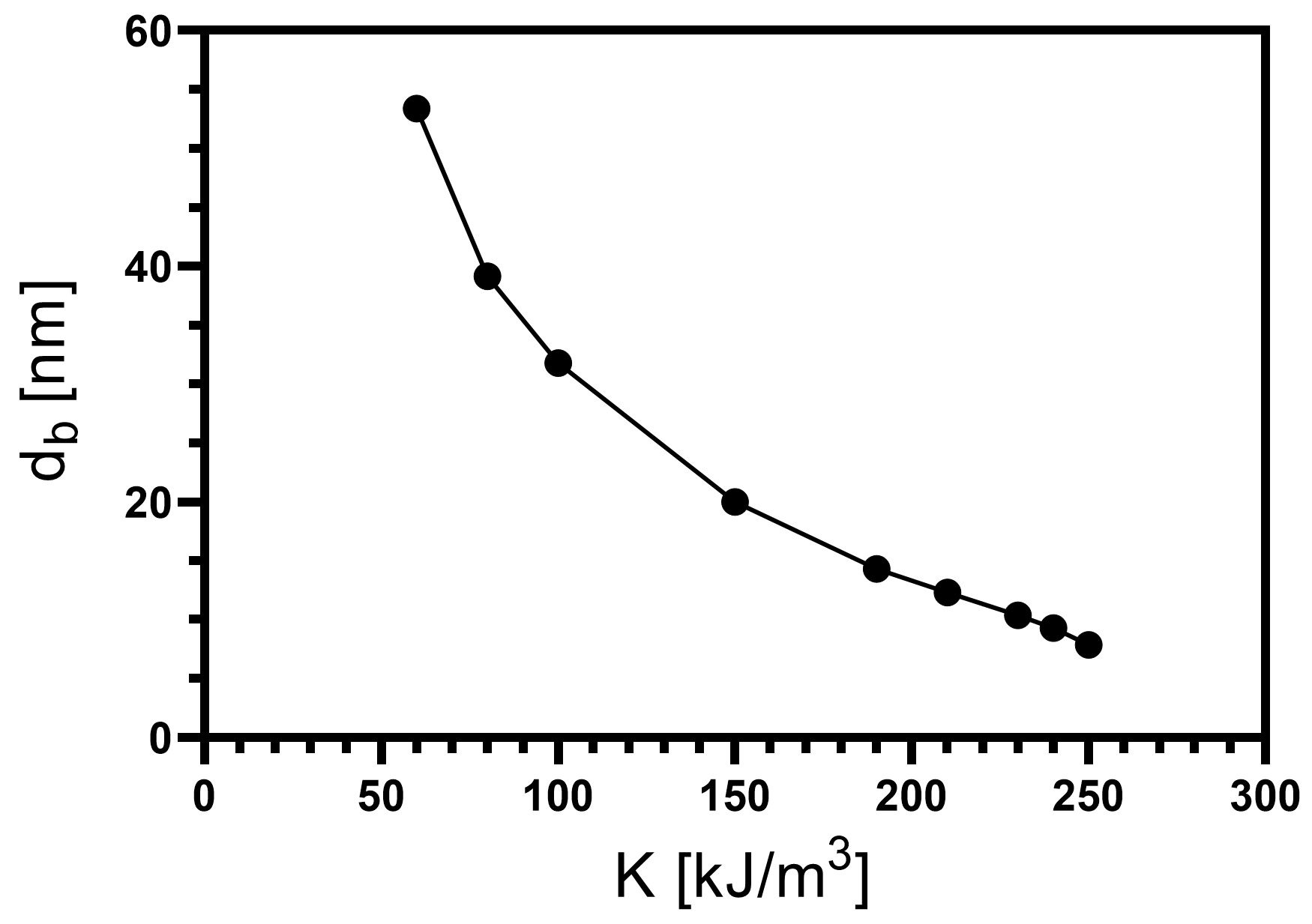
3.1. Bimeron Stabilization as a Function of the Anisotropy Strength
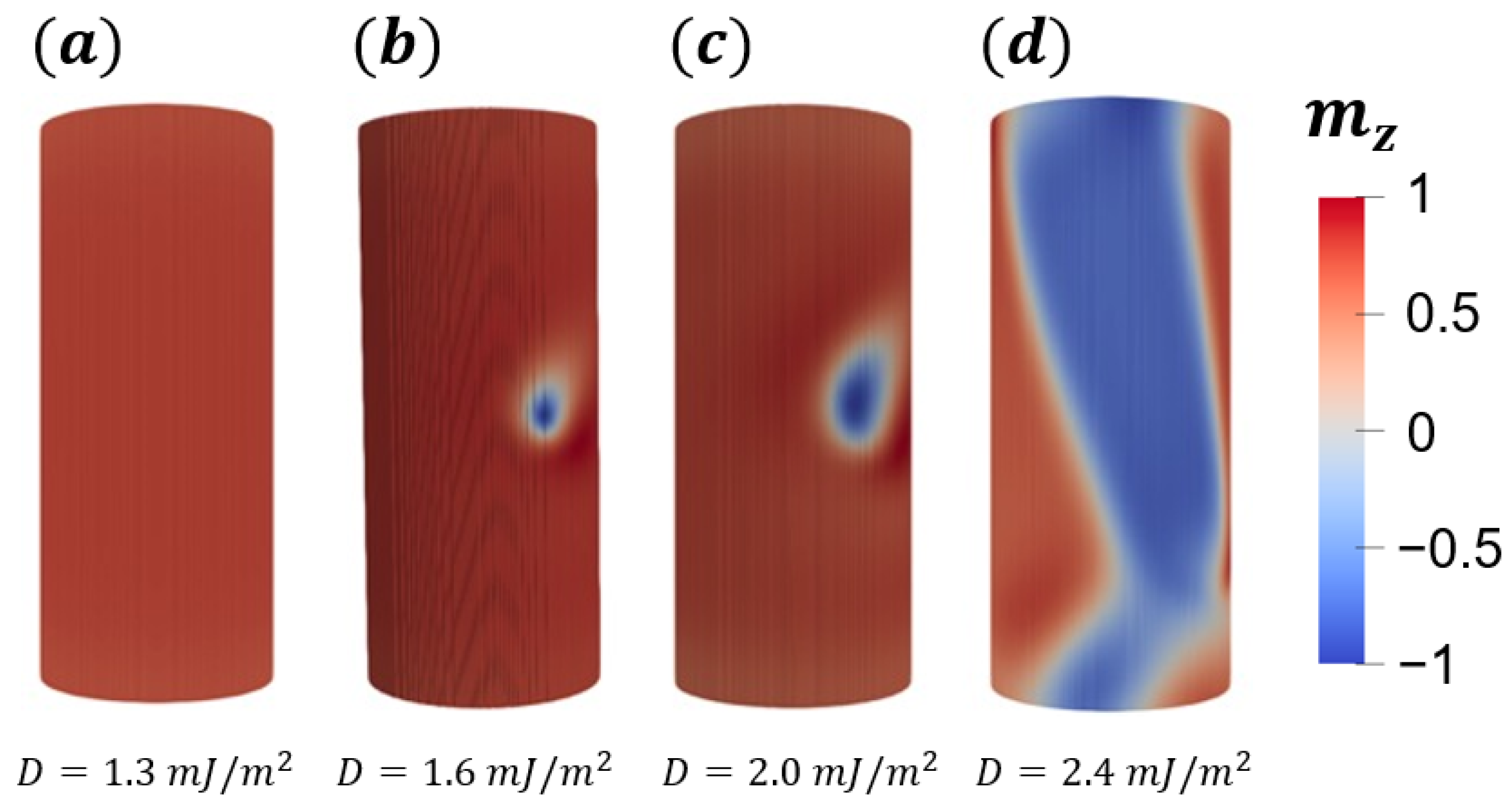
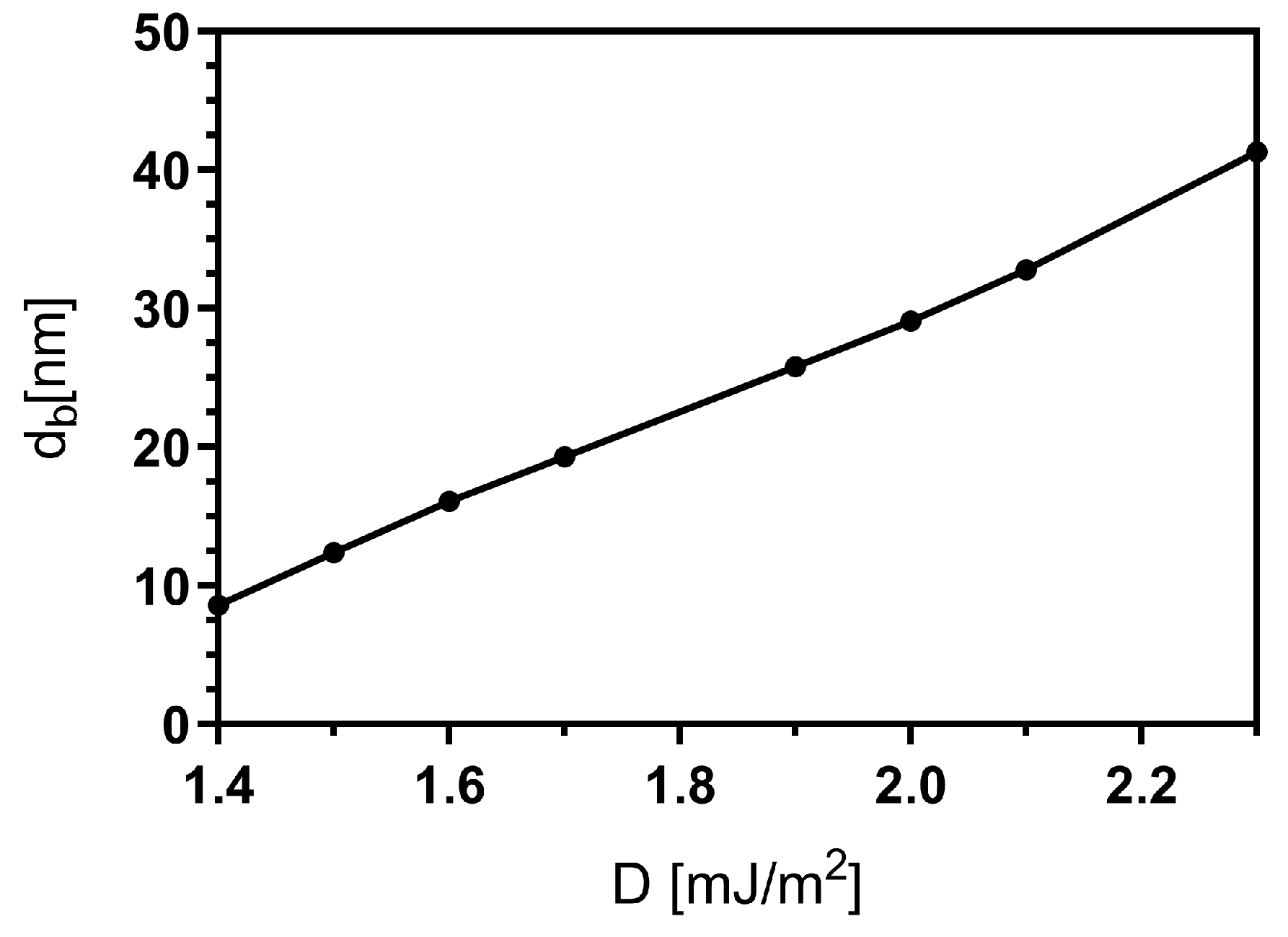
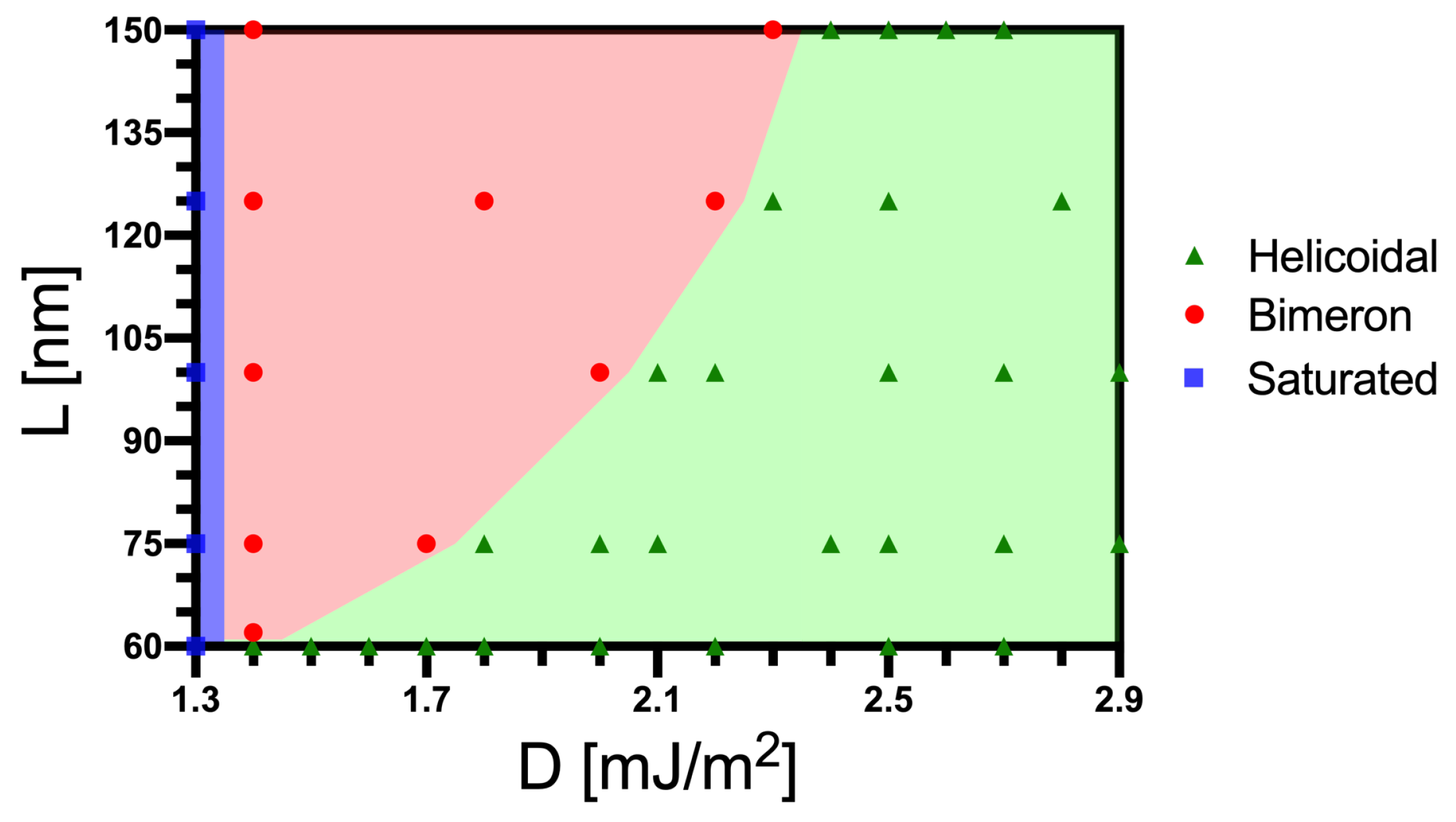
3.2. Bimeron Stabilization as a Function of the Dzyaloshinskii–Moriya Constant
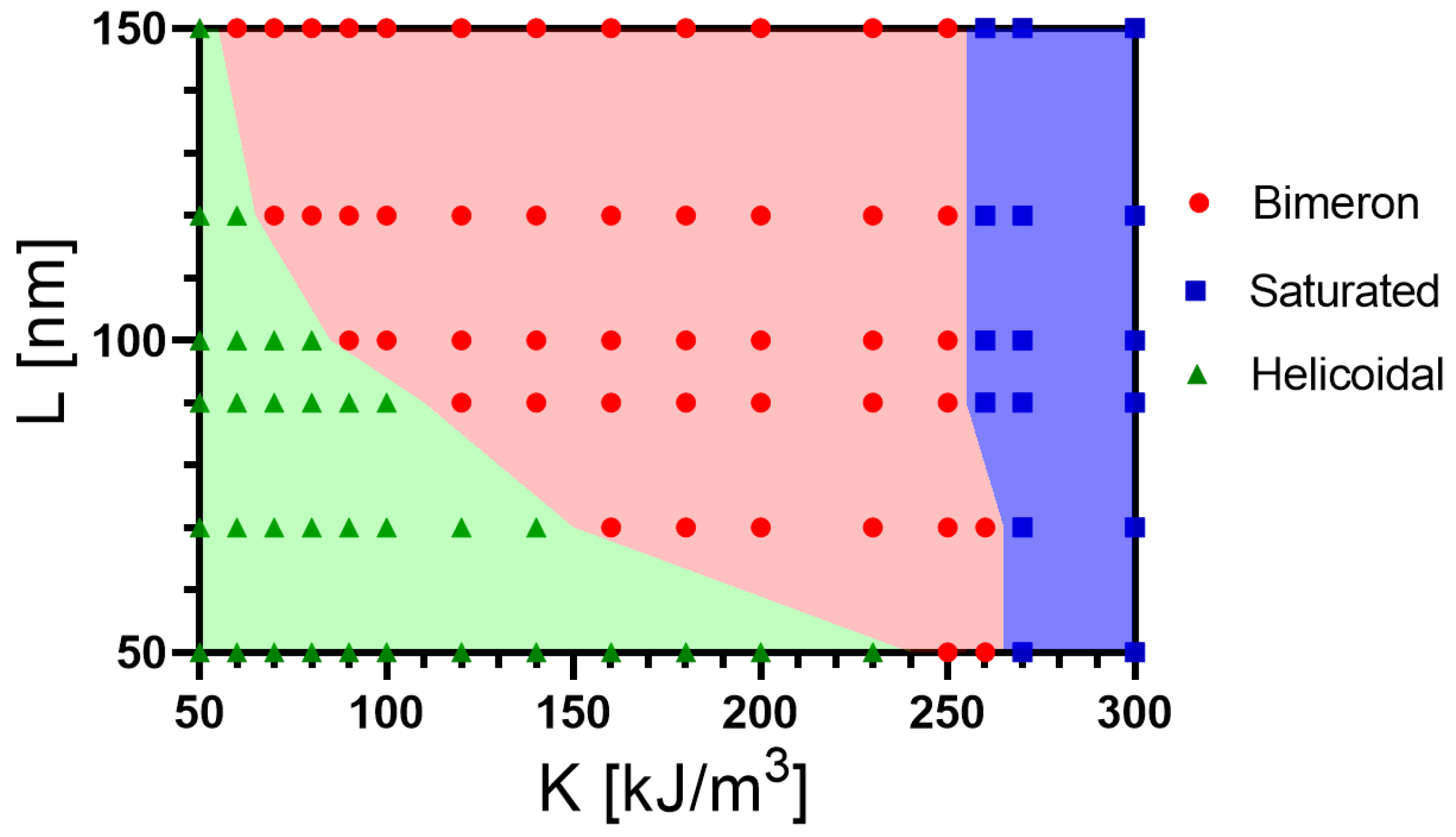
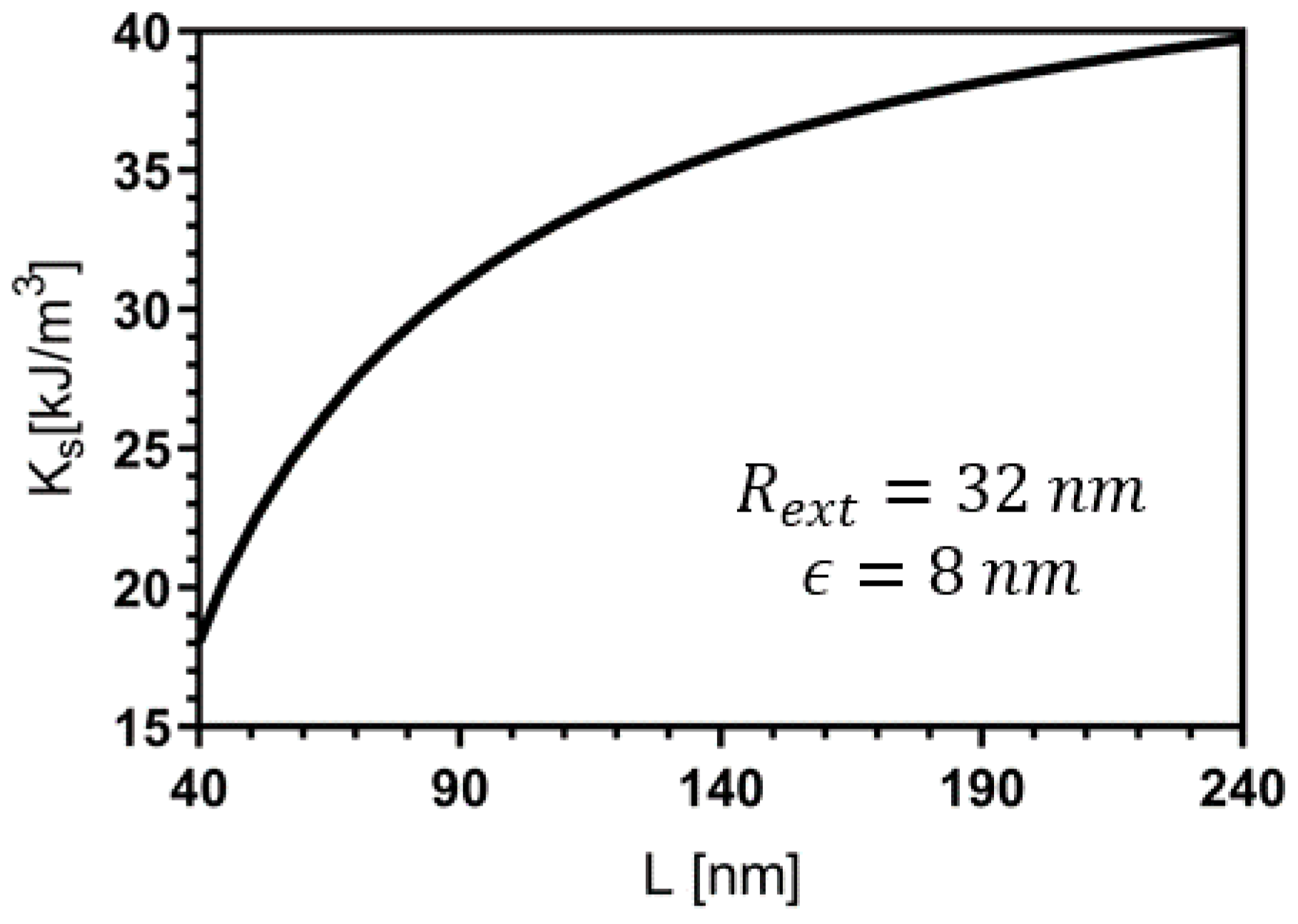
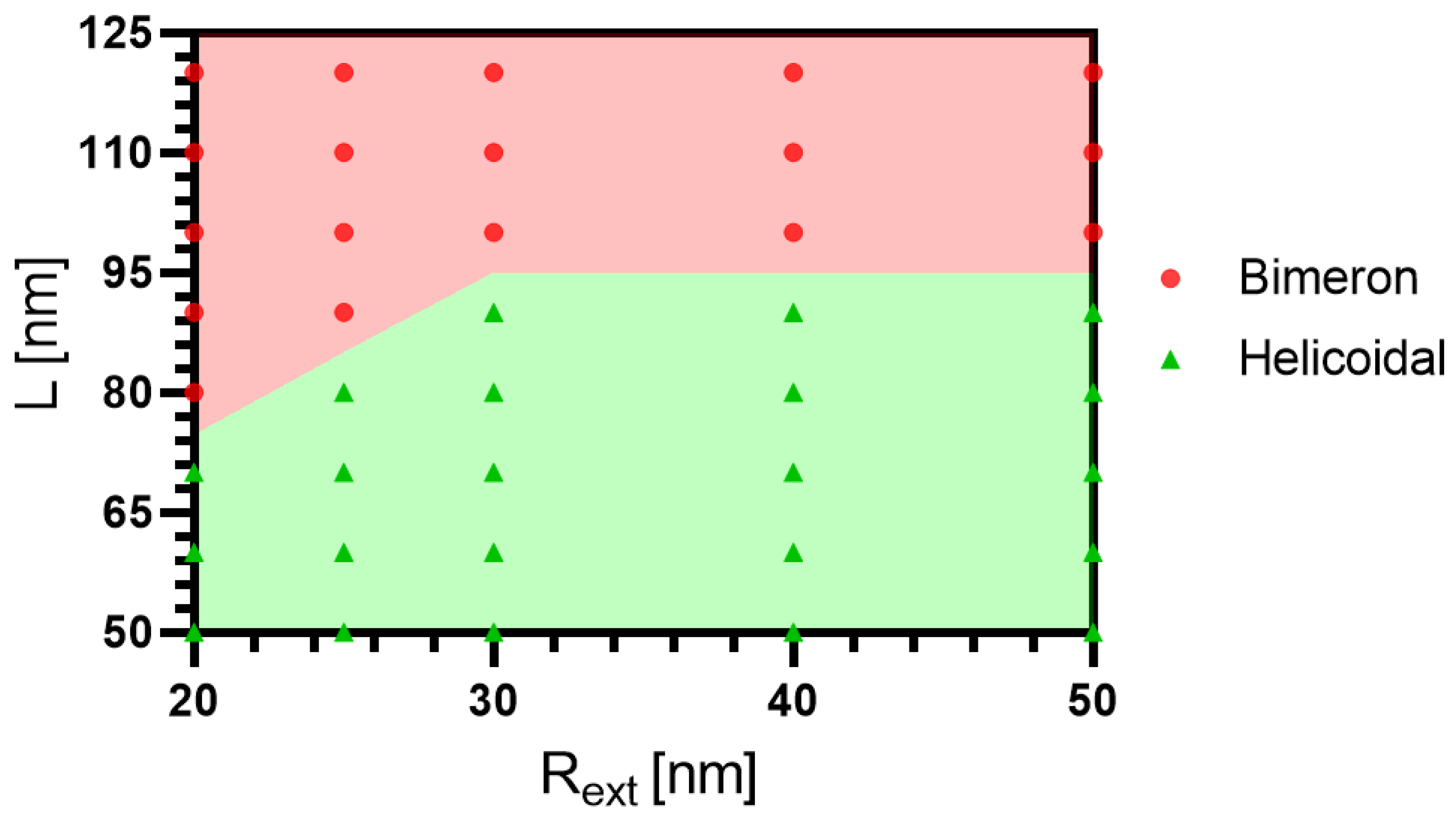
3.3. Bimeron Stabilization as a Function of the Geometric Parameters of the Nanotube
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DM | Dzyaloshinskii–Moriya |
| DMI | Dzyaloshinskii–Moriya interaction |
| LLG | Landau–Lifshitz–Gilbert |
| Bimeron’s core diameter |
References
- Nakahara, M. Geometry, Topology and Physics, 2nd ed.; Taylor and Francis Group: London, UK, 2003. [Google Scholar]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nano 2013, 8, 899. [Google Scholar]
- Parkin, S.; Yang, S.-H. Memory on the racetrack. Nat. Nanotechnol. 2015, 10, 195. [Google Scholar]
- Kiselev, N.S.; Bogdanov, A.N.; Schäfer, R.; Röβler, U.K. Identification and space-time evolution of vortex-like motion of atoms in a loaded solid. J. Phys. D Appl. 2011, 44, 39. [Google Scholar]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nano 2013, 8, 152. [Google Scholar]
- Pappas, C.; Lelièvre-Berna, E.; Falus, P.; Bentley, M.P.; Moskvin, E.; Grigoriev, S.; Fouquet, P.; Farago, B. Chiral paramagnetic skyrmion-like phase in MnSi. Phys. Rev. Lett. 2009, 102, 197202. [Google Scholar]
- Tonomura, A.; Yu, X.; Yanagisawa, K.; Matsuda, T.; Onose, Y.; Kanazawa, N.; Park, H.S.; Tokura, Y. Real-space observation of skyrmion lattice in helimagnet MnSi thin samples. Nano Lett. 2012, 12, 1673. [Google Scholar]
- Moskvin, E.; Grigoriev, S.; Dyadkin, V.; Eckerlebe, H.; Baenitz, M.; Schmidt, M.; Wilhelm, H. Complex chiral modulations in FeGe close to magnetic ordering. Phys. Rev. Lett. 2013, 110, 077207. [Google Scholar]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901. [Google Scholar]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106. [Google Scholar]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713. [Google Scholar]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636. [Google Scholar]
- Zhang, X.; Xia, J.; Shen, L.; Ezawa, M.; Tretiakov, O.A.; Zhao, G.; Liu, X.; Zhou, Y. Static and dynamic properties of bimerons in a frustrated ferromagnetic monolayer. Phys. Rev. B 2020, 101, 144435. [Google Scholar]
- Fernandes, R.L.; Lopes, R.J.C.; Pereira, A.R. Skyrmions and merons in two-dimensional antiferromagnetic systems. Sol. State Commun. 2019, 290, 55. [Google Scholar]
- Iakovlev, I.A.; Sotnikov, O.M.; Mazurenko, V.V. Bimeron nanoconfined design. Phys. Rev. B 2018, 97, 184415. [Google Scholar]
- Kolesnikov, A.G.; Stebliy, M.E.; Samardak, A.S.; Ognev, A.V. Skyrmionium–high velocity without the skyrmion Hall effect. Sci. Rep. 2018, 8, 16966. [Google Scholar]
- Col, S.D.; Jamet, S.; Rougemaille, N.; Locatelli, A.; Mentes, T.O.; Burgos, B.S.; Afid, R.; Darques, M.; Cagnon, L.; Toussaint, J.C.; et al. Observation of Bloch-point domain walls in cylindrical magnetic nanowires. Phys. Rev. B 2014, 89, 180405(R). [Google Scholar] [CrossRef]
- Donnelly, C.; Guizar-Sicairos, M.; Scagnoli, V.; Gliga, S.; Holler, M.; Raabe, J.; Heyderman, L.J. Three-dimensional magnetization structures revealed with X-ray vector nanotomography. Nature 2017, 547, 328. [Google Scholar]
- Tai, J.B.; Smalyukh, I.I. Static Hopf solitons and knotted emergent fields in solid-state noncentrosymmetric magnetic nanostructures. Phys. Rev. Lett. 2018, 121, 187201. [Google Scholar]
- Castillo-Sepúlveda, S.; Cacilhas, R.; Carvalho-Santos, V.L.; Corona, R.M.; Altbir, D. Magnetic hopfions in toroidal nanostructures driven by an Oersted magnetic field. Phys. Rev. B 2021, 104, 184406. [Google Scholar]
- Moon, K.-W.; Yoon, J.; Kim, C.; Hwang, C. Existence of in-plane magnetic skyrmion and its motion under current flow. Phys. Rev. Appl. 2019, 12, 064054. [Google Scholar]
- Amaral, M.A.; Silva, R.L.; Pereira, A.R.; Moura-Melo, W.A. Discrete double core skyrmions in magnetic thin films. J. Magn. Magn. Mater. 2009, 321, 3360. [Google Scholar]
- Araújo, A.S.; Lopes, R.J.C.; Carvalho-Santos, V.L.; Pereira, A.R.; Silva, R.L.; Silva, R.C.; Altbir, D. Typical skyrmions versus bimerons: A long-distance competition in ferromagnetic racetracks. Phys. Rev. B 2020, 102, 104409. [Google Scholar] [CrossRef]
- Gaididei, Y.; Kravchuk, V.P.; Sheka, D.D. Curvature effects in thin magnetic shells. Phys. Rev. Lett. 2014, 112, 257203. [Google Scholar] [CrossRef] [PubMed]
- Yershov, K.V.; Kravchuk, V.P.; Sheka, D.D.; Röβler, U.K. Curvature effects on phase transitions in chiral magnets. SciPost Phys. 2020, 9, 43. [Google Scholar]
- Sheka, D.D. A perspective on curvilinear magnetism. Appl. Phys. Lett. 2021, 118, 230502. [Google Scholar]
- Kravchuk, V.P.; Röβler, U.K.; Volkov, O.M.; Sheka, D.D.; Brink, J.V.; Makarov, D.; Fuchs, H.; Fangohr, H.; Gaididei, Y. Topologically stable magnetization states on a spherical shell: Curvature-stabilized skyrmions. Phys. Rev. B 2016, 94, 144402. [Google Scholar]
- Yang, J.; Abert, C.; Suess, D.; Kim, S.-K. Intrinsic DMI-free skyrmion formation and robust dynamic behaviors in magnetic hemispherical shells. Sci. Rep. 2021, 11, 3886. [Google Scholar]
- Carvalho-Santos, V.L.; Corona, R.M.; Altbir, D.; Castillo-Sepúlveda, S. Shifts in the skyrmion stabilization due to curvature effects in dome-and antidome-shaped surfaces. Phys. Rev. B 2020, 102, 024444. [Google Scholar]
- Tejo, F.; Toneto, D.; Oyarzún, S.; Hermosilla, J.; Danna, C.S.; Palma, J.L.; da Silva, R.B.; Dorneles, L.S.; Denardin, J.C. Stabilization of magnetic skyrmions on arrays of self-assembled hexagonal nanodomes for magnetic recording applications. ACS Appl. Mater. Interfaces 2020, 12, 53454. [Google Scholar]
- Yershov, K.V.; Kákay, A.; Kravchuk, V.P. Curvature-induced drift and deformation of magnetic skyrmions: Comparison of the ferromagnetic and antiferromagnetic cases. Phys. Rev. B 2022, 105, 054425. [Google Scholar]
- Carvalho-Santos, V.L.; Castro, M.A.; Salazar-Aravena, D.; Laroze, D.; Corona, R.M.; Allende, S.; Altbir, D. Skyrmion propagation along curved racetracks. Appl. Phys. Lett. 2021, 118, 172407. [Google Scholar]
- Korniienko, A.; Kákay, A.; Sheka, D.D.; Kravchuk, V.P. Effect of curvature on the eigenstates of magnetic skyrmions. Phys. Rev. B 2020, 102, 014432. [Google Scholar]
- Farias, W.S.; Santence, A.; Coura, P.Z. The influence of curved surfaces on the propagation of skyrmions in a magnetic racetrack. J. Magn. Mag. Mat. 2023, 568, 170386. [Google Scholar]
- Kechrakos, D.; Tzannetou, L.; Patsopoulos, A. Magnetic skyrmions in cylindrical ferromagnetic nanostructures with chiral interactions. Phys. Rev. B 2020, 102, 054439. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Y. Formation and annihilation of skyrmions in a bucket-shaped nanotube. Phys. Lett. A 2021, 415, 127656. [Google Scholar]
- Kim, S.K. Dynamics of bimeron skyrmions in easy-plane magnets induced by a spin supercurrent. Phis. Rev. B 2019, 99, 224406. [Google Scholar]
- Zarzuela, R.; Bharadwaj, V.K.; Kim, K.; Sinova, J.; Everschor-Sitte, K. Stability and dynamics of in-plane skyrmions in collinear ferromagnets. Phys. Rev. B 2020, 101, 054405. [Google Scholar]
- Gao, N.; Je, S.-G.; Im, M.-Y.; Choi, J.W.; Yang, M.; Li, Q.; Wang, T.Y.; Lee, S.; Han, H.-S.; Lee, K.-S.; et al. Creation and annihilation of topological meron pairs in in-plane magnetized films. Nat. Commun. 2019, 10, 5603. [Google Scholar]
- Ohara, K.; Zhang, X.; Chen, Y.; Kato, S.; Xia, J.; Ezawa, M.; Tretiakov, O.; Hou, Z.; Zhou, Y.; Zhao, G.; et al. Reversible transformation between isolated skyrmions and bimerons. Nano Lett. 2022, 22, 8559. [Google Scholar]
- Castro, M.A.; Altbir, D.; Galvez-Poblete, D.; Corona, R.M.; Oyarzún, S.; Pereira, A.R.; Allende, S.; Carvalho-Santos, V.L. Skyrmion-bimeron dynamic conversion in magnetic nanotracks. Phys. Rev. B 2023, 108, 094436. [Google Scholar]
- Yu, X.; Kanazawa, N.; Zhang, X.; Takahashi, Y.; Vlakobovskii, K.; Nakajima, K.; Tanigaki, T.; Mochizuki, M.; Tokura, Y. Spontaneous Vortex-Antivortex Pairs And Their Topological Transitions in A Chiral-Lattice Magnet. Adv. Mater. 2023, 2306441. [Google Scholar] [CrossRef] [PubMed]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Waeyenberge, B.V. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar]
- Yu, X.; Morikawa, D.; Yokouchi, T.; Shibata, K.; Kanazawa, N.; Kagawa, F.; Arima, T.-H.; Tokura, Y. Aggregation and collapse dynamics of skyrmions in a non-equilibrium state. Nat. Phys. 2018, 14, 832. [Google Scholar] [CrossRef]
- Toscano, D.; Santece, I.A.; Guedes, R.C.O.; Assis, H.S.; Miranda, A.L.S.; de Araujo, C.I.L.; Sato, F.; Coura, P.Z.; Leonel, S.A. Traps for pinning and scattering of antiferromagnetic skyrmions via magnetic properties engineering. J. Appl. Phys. 2020, 127, 193902. [Google Scholar]
- Camley, R.E.; Livesey, K.L. Consequences of the Dzyaloshinskii-Moriya Interaction. Surf. Sci. Rep. 2023, 78, 100605. [Google Scholar]
- Pathak, S.A.; Hertel, R. Geometrically constrained skyrmions. Magnetochemistry 2021, 7, 26. [Google Scholar] [CrossRef]
- Yoo, J.-W.; Lee, S.-J.; Moon, J.-H.; Lee, K.-J. Phase diagram of a single skyrmion in magnetic nanowires. IEEE Trans. Magn. 2014, 50, 1500504. [Google Scholar] [CrossRef]
- Wang, X.S.; Yuan, H.Y.; Wang, X.R. A theory on skyrmion size. Commun. Phys. 2018, 1, 31. [Google Scholar]
- Prychynenko, D.; Sitte, M.; Litzius, K.; Krüger, B.; Bourianoff, G.; Kläui, M.; Sinova, J.; Everschor-Sitte, K. Magnetic skyrmion as a nonlinear resistive element: A potential building block for reservoir computing. Phys. Rev. Appl. 2018, 9, 014034. [Google Scholar] [CrossRef]
- Salazar-Cardona, M.M.; Korber, L.; Schultheiss, H.; Lenz, K.; Thomas, A.; Nielsch, K.; Kakay, A.; Otalora, J.A. Nonreciprocity of spin waves in magnetic nanotubes with helical equilibrium magnetization. Appl. Phys. Lett. 2021, 118, 262411. [Google Scholar] [CrossRef]
- Salinas, H.D.; Restrepo, J.; Iglesias, Ò. Change in the magnetic configurations of tubular nanostructures by tuning dipolar interactions. Sci. Rep. 2018, 8, 10275. [Google Scholar] [PubMed]
- Iwasaki, J.; Mochizuki, M.; Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 2013, 8, 742. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galvez, D.; Castro, M.; Bittencourt, G.; Carvalho, V.; Allende, S. Magnetic Bimerons in Cylindrical Nanotubes. Nanomaterials 2023, 13, 2841. https://doi.org/10.3390/nano13212841
Galvez D, Castro M, Bittencourt G, Carvalho V, Allende S. Magnetic Bimerons in Cylindrical Nanotubes. Nanomaterials. 2023; 13(21):2841. https://doi.org/10.3390/nano13212841
Chicago/Turabian StyleGalvez, David, Mario Castro, Guilherme Bittencourt, Vagson Carvalho, and Sebastian Allende. 2023. "Magnetic Bimerons in Cylindrical Nanotubes" Nanomaterials 13, no. 21: 2841. https://doi.org/10.3390/nano13212841




