High-Performance On-Chip Racetrack Resonator Based on GSST-Slot for In-Memory Computing
Abstract
1. Introduction
2. Device Principle and Parameter Optimization
2.1. Device Design and Scalar Multiplication Concepts
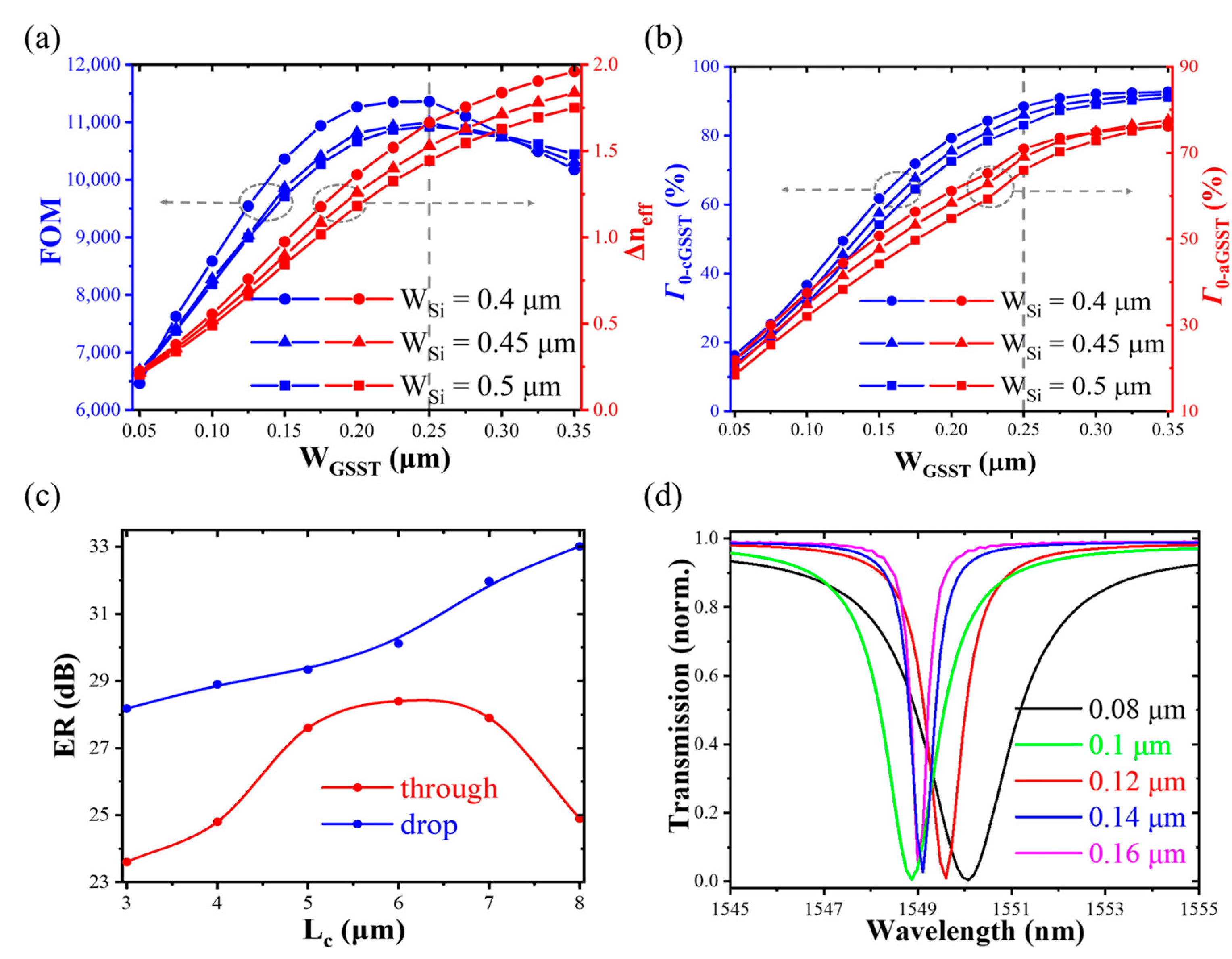
2.2. Parameter Optimization
3. Device Simulation
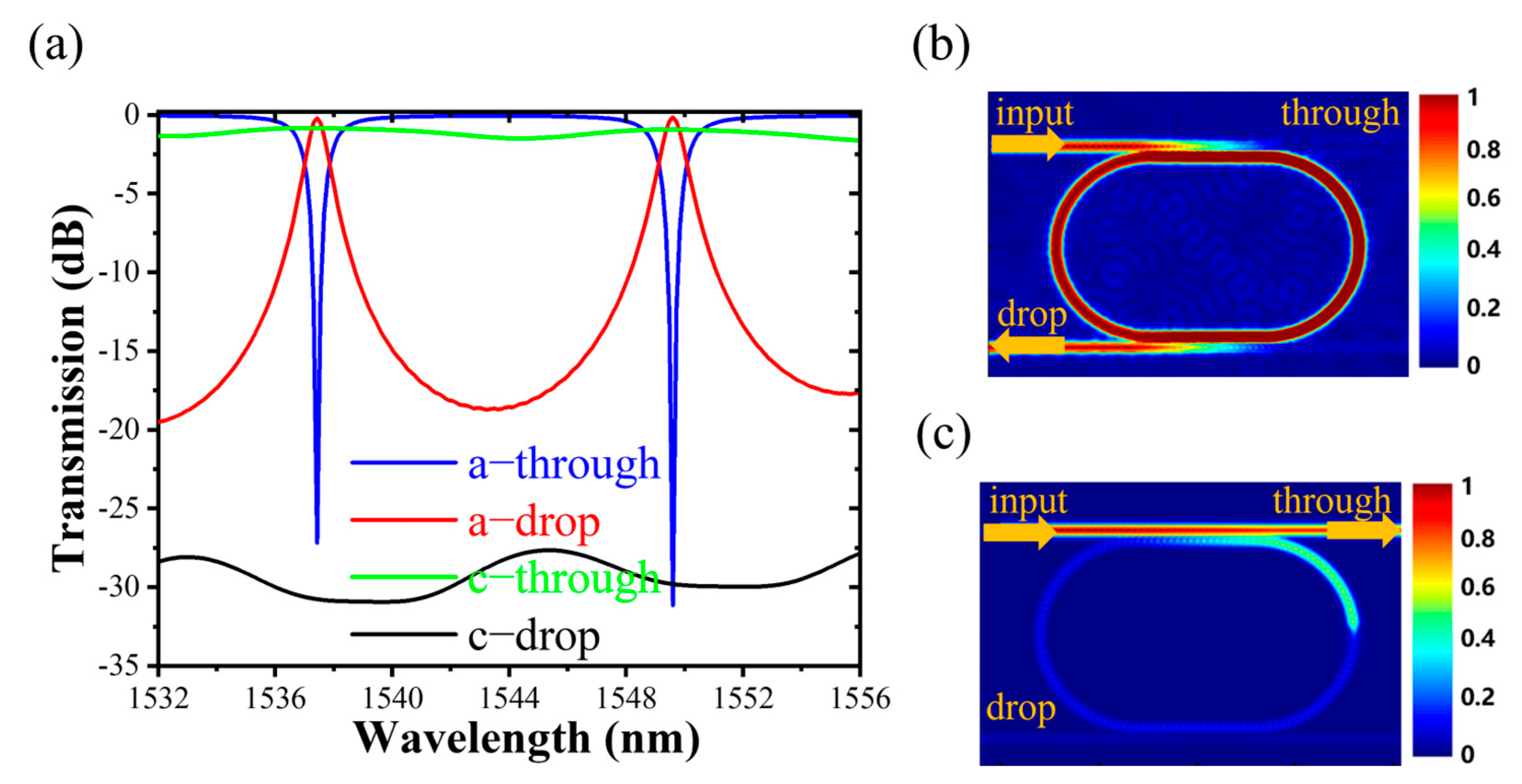
3.1. Switching Simulation
3.2. Thermal Simulation
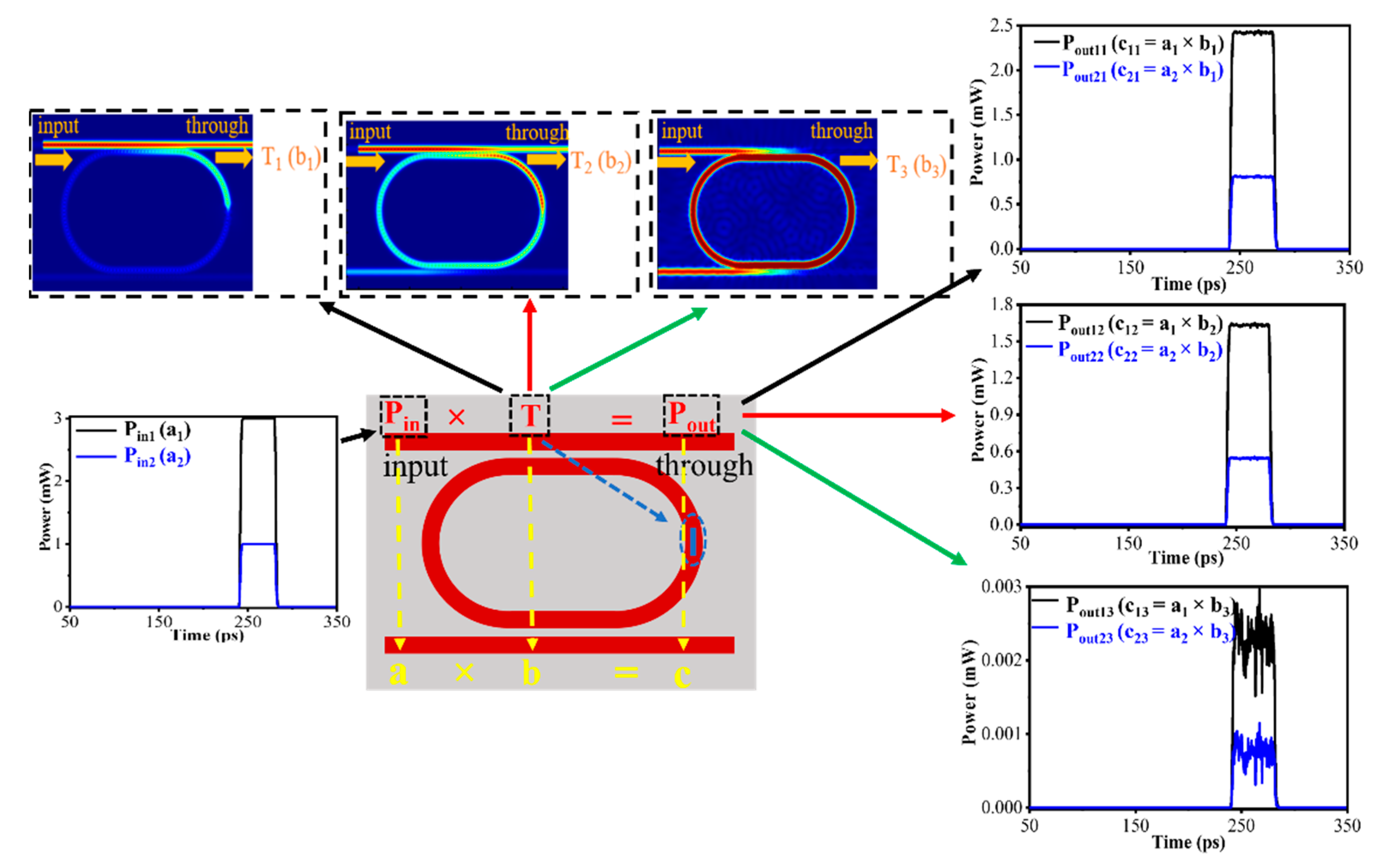
4. Scalar Multiplication
5. Recognition Test
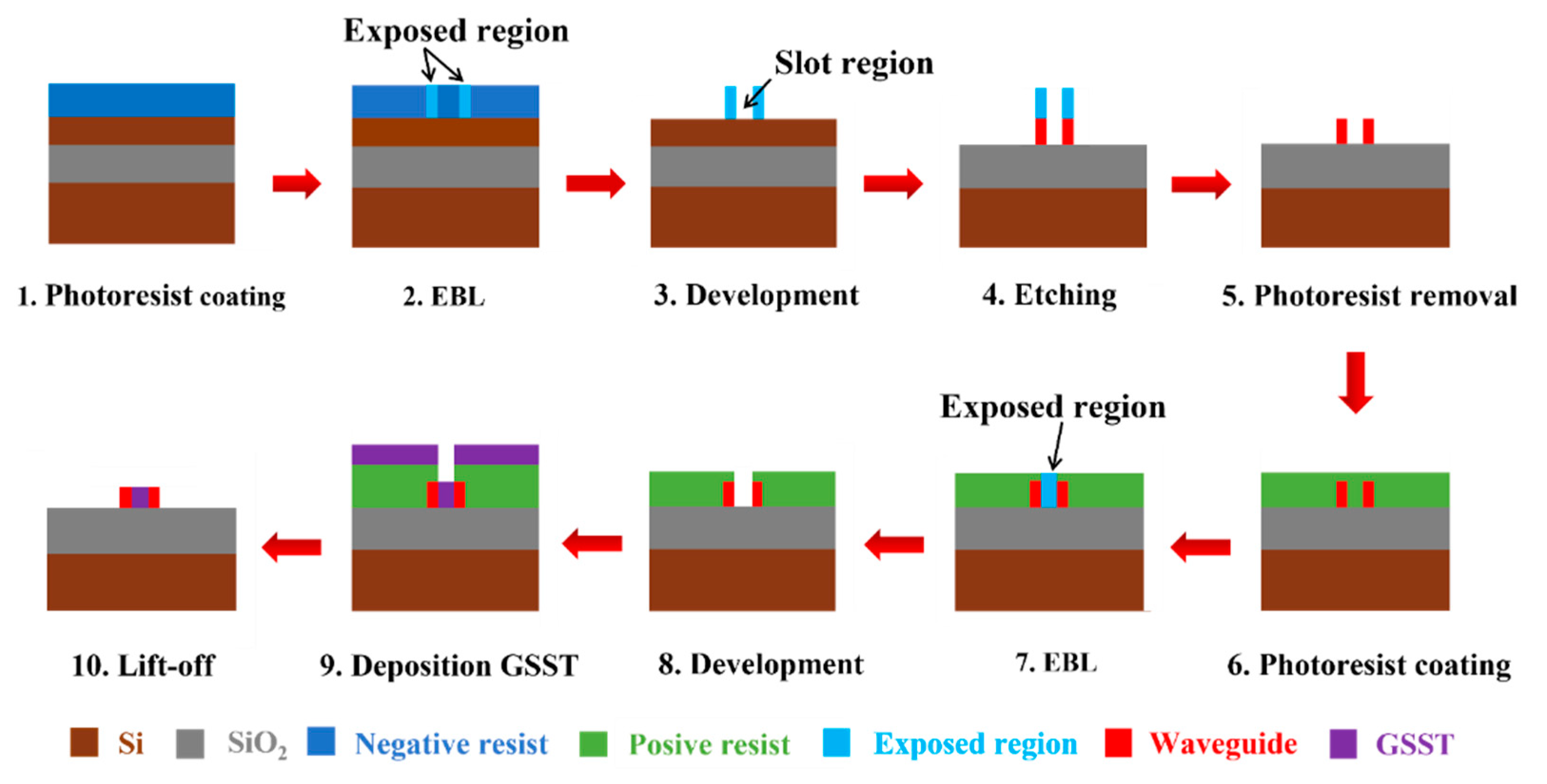
6. Fabrication Method
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ríos, C.; Stegmaier, M.; Hosseini, P.; Wang, D.; Scherer, T.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. Integrated all-photonic non-volatile multi-level memory. Nat. Photon. 2015, 9, 725–732. [Google Scholar] [CrossRef]
- Sun, C.; Wade, M.T.; Lee, Y.; Orcutt, J.S.; Alloatti, L.; Georgas, M.S.; Waterman, A.S.; Shainline, J.M.; Avizienis, R.R.; Lin, S.; et al. Single-chip microprocessor that communicates directly using light. Nature 2015, 528, 534–538. [Google Scholar] [CrossRef]
- Kielpinski, D.; Bose, R.; Pelc, J.; van Vaerenbergh, T.; Mendoza, G.; Tezak, N.; Beausoleil, R.G. Information processing with large-scale optical integrated circuits. In Proceedings of the 2016 IEEE International Conference on Rebooting Computing (ICRC), San Diego, CA, USA, 17–19 October 2016; pp. 1–4. [Google Scholar]
- Vandoorne, K.; Mechet, P.; van Vaerenbergh, T.; Fiers, M.; Morthier, G.; Verstraeten, D.; Schrauwen, B.; Dambre, J.; Bienstman, P. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 2014, 5, 3541. [Google Scholar] [CrossRef]
- Jia, S.; Li, H.; Gotoh, T.; Longeaud, C.; Zhang, B.; Lyu, J.; Lv, S.; Zhu, M.; Song, Z.; Liu, Q.; et al. Ultrahigh drive current and large selectivity in GeS selector. Nat. Commun. 2020, 11, 4636. [Google Scholar] [CrossRef]
- Zheng, J.; Fang, Z.; Wu, C.; Zhu, S.; Xu, P.; Doylend, J.K.; Deshmukh, S.; Pop, E.; Dunham, S.; Li, M.; et al. Nonvolatile Electrically Reconfigurable Integrated Photonic Switch Enabled by a Silicon PIN Diode Heater. Adv. Mater. 2020, 32, e2001218. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Jia, S.; Shi, N.; Ge, Q.; Gotoh, T.; Lv, S.; Liu, Q.; Dronskowski, R.; Elliott, S.R.; Song, Z.; et al. Elemental electrical switch enabling phase segregation–free operation. Science 2021, 374, 1390–1394. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Yu, H.; Lee, S.; Peng, R.; Takeuchi, I.; Li, M. Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network. Nat. Commun. 2021, 12, 96. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, L.; Lu, L.; Xu, J.; Wang, N.; Hu, H.; Rahman, B.M.A.; Zhou, Z.; Chen, J. Miniature Multilevel Optical Memristive Switch Using Phase Change Material. ACS Photon. 2019, 6, 2205–2212. [Google Scholar] [CrossRef]
- Ríos, C.; Youngblood, N.; Cheng, Z.; Le Gallo, M.; Pernice, W.H.P.; Wright, C.D.; Sebastian, A.; Bhaskaran, H. In-memory computing on a photonic platform. Sci. Adv. 2019, 5, eaau5759. [Google Scholar] [CrossRef]
- Feldmann, J.; Stegmaier, M.; Gruhler, N.; Ríos, C.; Bhaskaran, H.; Wright, C.D.; Pernice, W.H.P. Calculating with light using a chip-scale all-optical abacus. Nat. Commun. 2017, 8, 1256. [Google Scholar] [CrossRef]
- Chakraborty, I.; Saha, G.; Roy, K. Photonic In-Memory Computing Primitive for Spiking Neural Networks Using Phase-Change Materials. Phys. Rev. Appl. 2019, 11, 014063. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M.; Xie, Y.; Shi, Y.; Kumar, R.; Panepucci, R.R.; Dai, D. Wavelength-selective 2 × 2 optical switch based on a Ge2Sb2Te5-assisted microring. Photon. Res. 2020, 8, 1171–1176. [Google Scholar] [CrossRef]
- Ali, N.; Panepucci, R.R.; Xie, Y.; Dai, D.; Kumar, R. Electrically controlled 1 x 2 tunable switch using a phase change material embedded silicon microring. Appl. Opt. 2021, 60, 3559–3568. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Liu, S.; Liu, T.; Gao, Y.; Yin, Y.; Sun, X.; Zhang, D. Optical Switch Based on Ge2Sb2Se4Te1-Assisted Racetrack Microring. Photonics 2022, 9, 117. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, J.; Xu, P.; Wang, Y.; Majumdar, A. Ultra-low-power nonvolatile integrated photonic switches and modulators based on nanogap-enhanced phase-change waveguides. Opt. Express 2020, 28, 37265–37275. [Google Scholar] [CrossRef]
- Afshari-Bavil, M.; Dong, M.-L.; Li, C.; Feng, S.; Zhu, L. Thermally Controllable High-Efficiency Unidirectional Coupling in a Double-Slit Structure Filled with Phase Change Material. IEEE Photon. J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Song, J.; Ghosh, S.; Zhang, H.; Zhou, L.; Rahman, B.M.A. Design, optimization, and performance evaluation of GSST clad low-loss non-volatile switches. Appl. Opt. 2019, 58, 8687–8694. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhang, Y.; Li, J.; Soref, R.; Gu, T.; Hu, J. Broadband nonvolatile photonic switching based on optical phase change materials: Beyond the classical figure-of-merit. Opt. Lett. 2017, 43, 94–97. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, X.; Lu, L.; Chen, J.; Rahman, B.M.A.; Zhou, L. Comparison of the phase change process in a GST-loaded silicon waveguide and MMI. Opt. Express 2021, 29, 3503–3514. [Google Scholar] [CrossRef]
- Yin, Y.-X.; Yin, X.-J.; Zhang, X.-P.; Yan, G.-W.; Wang, Y.; Wu, Y.-D.; An, J.-M.; Wang, L.-L.; Zhang, D.-M. High-Q-Factor Silica-Based Racetrack Microring Resonators. Photonics 2021, 8, 43. [Google Scholar] [CrossRef]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, C.; Luo, Y.; Yang, Z.; Zhang, W.; Li, L.; Xu, P.; Zhang, P.; Xu, T. High Q-factor, ultrasensitivity slot microring resonator sensor based on chalcogenide glasses. Opt. Express 2022, 30, 3866. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Xu, L.; Chen, J.; Zhou, L.; Rahman, B.M.A.; Wu, X.; Lu, L.; Xu, Y.; Xu, J.; Song, J.; et al. Ultracompact Si-GST Hybrid Waveguides for Nonvolatile Light Wave Manipulation. IEEE Photon. J. 2018, 10, 1–10. [Google Scholar] [CrossRef]
- Finite Difference Time Domain (FDTD) Solver Introduction. Available online: https://optics.ansys.com/hc/en-us/articles/360034914633 (accessed on 1 March 2022).
- Soltani, M.; Yegnanarayanan, S.; Li, Q.; Adibi, A. Systematic Engineering of Waveguide-Resonator Coupling for Silicon Microring/Microdisk/Racetrack Resonators: Theory and Experiment. IEEE J. Quantum Electron. 2010, 46, 1158–1169. [Google Scholar] [CrossRef]
- Jiang, W.; Rahman, B.M.A. Compact and Nonvolatile Mode-Selective Switch with Nano-Heater. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–10. [Google Scholar] [CrossRef]
- Wu, C.; Yu, H.; Li, H.; Zhang, X.; Takeuchi, I.; Li, M. Low-Loss Integrated Photonic Switch Using Subwavelength Patterned Phase Change Material. ACS Photon. 2018, 6, 87–92. [Google Scholar] [CrossRef]
- Rudé, M.; Pello, J.; Simpson, R.E.; Osmond, J.; Roelkens, G.; van der Tol, J.J.; Pruneri, V. Optical switching at 1.55 μm in silicon racetrack resonators using phase change materials. Appl. Phys. Lett. 2013, 103, 141119. [Google Scholar] [CrossRef]
- Voshchinnikov, N.V.; Videen, G.; Henning, T. Effective medium theories for irregular fluffy structures: Aggregation of small particles. Appl. Opt. 2007, 46, 4065–4072. [Google Scholar] [CrossRef]
- Aspnes, D.E. Local-field effects and effective—Medium theory: A microscopic perspective. Am. J. Phys. 1982, 50, 704–709. [Google Scholar] [CrossRef]
- Chen, Y.G.; Kao, T.S.; Ng, B.; Li, X.; Luo, X.G.; Luk’Yanchuk, B.; Maier, S.; Hong, M.H. Hybrid phase-change plasmonic crystals for active tuning of lattice resonances. Opt. Express 2013, 21, 13691–13698. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, B.; Zhang, Z.; Cheng, C.; Zhang, Z.; Zhang, H.; Chen, R.; Chen, H. On-Chip Photonic Synapses Based on Slot-Ridge Waveguides with PCMs For In-Memory Computing. IEEE Photon. J. 2021, 13, 1–13. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C.J.C. The MNIST Database of Handwritten Digits. 1998. Available online: http://yann.lecun.com/exdb/mnist (accessed on 3 June 2022).
- Chen, J.; Lin, C.Y.; Li, Y.; Qin, C.; Lu, K.; Wang, J.M.; Chen, C.K.; He, Y.H.; Chang, T.C.; Sze, S.M.; et al. LiSiOX-Based Analog Memristive Synapse for Neuromorphic Computing. IEEE Electron Device Lett. 2019, 40, 542–545. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, D.; Liu, Y.; Fang, C.; Wang, S.; Wang, G.; Huang, Y.; Yu, X.; Han, G.; Hao, Y. All-Optical Synapse with Directional Coupler Structure Based on Phase Change Material. IEEE Photon. J. 2021, 13, 1–6. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Boybat, I.; Di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.C.P.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Ohno, S.; Tang, R.; Toprasertpong, K.; Takagi, S.; Takenaka, M. Si Microring Resonator Crossbar Array for On-Chip Inference and Training of the Optical Neural Network. ACS Photon. 2022, 9, 2614–2622. [Google Scholar] [CrossRef]




| Material | Cp (J/kgK) | K (W/mK) | ρ (kg/m3) |
|---|---|---|---|
| aGSST [27] | 213 | 0.19 | 5870 |
| cGSST [27] | 199 | 0.57 | 6270 |
| Si [20] | 720 | 149 | 2330 |
| SiO2 [20] | 740 | 1.38 | 2200 |
| Device Type | PCM Size (μm3) | Resonator Circumference (μm) | ER-Through/ ER-Drop (dB) | IL-Through/ IL-Drop (dB) | RW Shift (nm) | Ewrite/ Eerase (pJ) |
|---|---|---|---|---|---|---|
| GST disk/ Si3N4-microing [28] | 0.25 × 0.785 × 0.01 | - | 13.64/ 21.25 | 0.46/ 0.75 | ~1 | 200/- |
| GST pad/ Si-racetrack [29] | 3 × 1.5 × 0.02 | 37.4 | 12.36/- | 2.5/- | 0.2 | 3600/ 900 |
| GST embed/ Si-microing [14] | 1 × 0.48 × 0.02 | 31.4 | 25.57/ 18.75 | 1.95/ 5.04 | 4.63 | 1063/ 181 |
| GSST pad/ Si-racetrack [15] | 15 × 0.3 × 0.045 | 92.8 | 18/- | 0.19/- | ~0 | - |
| GSST slot/ Si-racetrack (this study) | 1 × 0.25 × 0.22 | 43.4 | 30.22/ 29.64 | 0.93/ 0.16 | 7.13 | 500/ 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Lu, Y.; Cai, L. High-Performance On-Chip Racetrack Resonator Based on GSST-Slot for In-Memory Computing. Nanomaterials 2023, 13, 837. https://doi.org/10.3390/nano13050837
Zhu H, Lu Y, Cai L. High-Performance On-Chip Racetrack Resonator Based on GSST-Slot for In-Memory Computing. Nanomaterials. 2023; 13(5):837. https://doi.org/10.3390/nano13050837
Chicago/Turabian StyleZhu, Honghui, Yegang Lu, and Linying Cai. 2023. "High-Performance On-Chip Racetrack Resonator Based on GSST-Slot for In-Memory Computing" Nanomaterials 13, no. 5: 837. https://doi.org/10.3390/nano13050837
APA StyleZhu, H., Lu, Y., & Cai, L. (2023). High-Performance On-Chip Racetrack Resonator Based on GSST-Slot for In-Memory Computing. Nanomaterials, 13(5), 837. https://doi.org/10.3390/nano13050837







