Crystalline Defects Induced during MPCVD Lateral Homoepitaxial Diamond Growth
Abstract
:1. Introduction
2. Materials and Methods
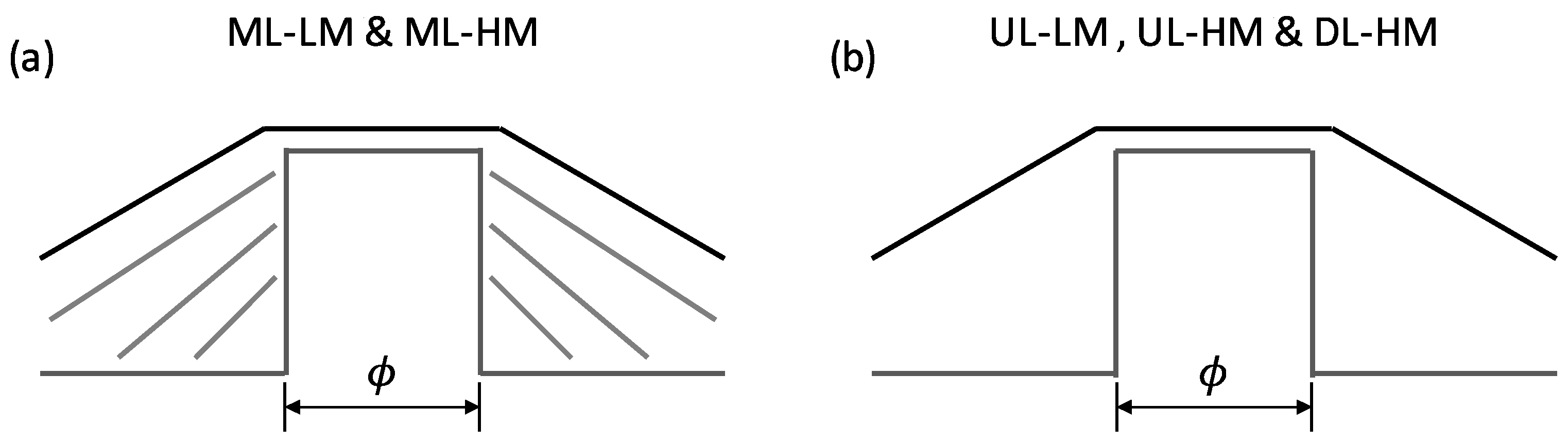
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Siegert, K.S.; Lange, F.R.L.; Sittner, E.R.; Volker, H.; Scholockermann, C.E.; Siegrist, T.; Wuttig, M. Impact of vacancy ordering on thermal transport in crystalline phase-change materials. Rep. Prog. Phys. 2015, 478, 013001. [Google Scholar] [CrossRef] [PubMed]
- Lloret, F.; Araujo, D.; Alegre, M.P.; Gonzalez-Leal, J.M.; Villar, M.P.; Eon, D.; Bustarret, E. TEM study of defects versus growth orientations in heavily boron-doped diamond. Phys. Stat. Sol. A 2015, 212, 2468–2473. [Google Scholar] [CrossRef] [Green Version]
- Alegre, M.P.; Araujo, D.; Fiori, A.; Pinero, J.C.; Lloret, F.; Villar, M.P.; Achatz, P.; Chicot, G.; Bustarret, E.; Jomard, F. Critical boron-doping levels for generation of dislocations in synthetic diamond. Appl. Phys. Lett. 2014, 105, 173103. [Google Scholar] [CrossRef] [Green Version]
- Araújo, D.; Achatz, P.; El Bouayadi, R.; García, A.J.; Alegre, M.P.; Villar, M.P.; Jomard, F.; Bustarret, E. Local boron doping quantification in homoepitaxial diamond structrures. Diam. Relat. Mater. 2010, 19, 972–975. [Google Scholar] [CrossRef]
- Prokhorov, I.A.; Ralchenko, V.G.; Bolshakov, A.P.; Polskiy, A.V.; Vlasov, A.V.; Subbotin, I.A.; Podurets, K.M.; Pashaev, E.M.; Sozontov, E.A. Analysis of syntetic diamond single cristal by X-ray topography and double-cristal diffractometry. Crystallogr. Rep. 2013, 58, 1010–1016. [Google Scholar] [CrossRef]
- Alvarez, J.; Boutchich, M.; Kleider, J.P.; Teraji, T.; Koide, Y. Direct observation of the leakage current in epitaxial diamond Schottky barrier devices by conductive-probe atomic force microscopy and Raman imaging. J. Phys. D Appl. Phys. 2014, 47, 55102. [Google Scholar] [CrossRef]
- Liang, Q.; Yan, C.-S.; Lai, J.; Meng, Y.-F.; Krasnicki, S.; Shu, H.; Mao, H.-K.; Hemley, R. Large área single-crystal dimamond synthesis by 915 MHz microwave plasma-assisted chemical vapor deposition. Cryst. Growth Des. 2014, 14, 3234–3238. [Google Scholar] [CrossRef]
- Lodes, M.A.; Kachold, F.S.; Rosiwal, S.M. Mechanical properties of micro- and nanocrystalline diamond foils. Philos. Trans. R. Soc. A 2015, 373, 20140136. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.Q.; Bai, J.; Zhou, Y.S.; Gao, Y.; Park, K.; Guillemet, T.; Jiang, L.; Zeng, X.C.; Lu, Y.F. Control of crystallographic orientation in diamond synthesis through laser resonant vibrational excitation of precursor molecules. Sci. Rep. 2014, 4, 4581. [Google Scholar] [CrossRef]
- Chicot, G.; Thi, T.N.T.; Fiori, A.; Jomard, F.; Gheeraert, E.; Bustarret, E.; Pernot, J. Hole transport in boron delta-doped diamond structures. Appl. Phys. Lett. 2012, 101, 162101. [Google Scholar] [CrossRef] [Green Version]
- Bousquet, J.; Chicot, G.; Eon, D.; Bustarret, E. Spectroscopic ellipsometry of homoepitaxial diamond multilayers and delta-doped structures. Appl. Phys. Lett. 2014, 104, 021905. [Google Scholar] [CrossRef] [Green Version]
- Chicot, G.; Fiori, A.; Volpe, P.N.; Tran-Thi, T.N.; Gerbedoen, J.C.; Bousquet, J.; Alegre, M.P.; Piñero, J.C.; Araújo, D.; Jomard, F.; et al. Electronic and physico-chemical properties of nanometric boron delta-doped diamond structures. J. Appl. Phys. 2014, 116, 083702. [Google Scholar] [CrossRef]
- Makino, T.; Oyama, K.; Kato, H.; Takeuchi, D.; Ogura, M.; Okushi, H.; Yamasaki, S. Diamond electronic devices fabricated using heavily doped hopping p+ and n+ layer. Jap. J. Appl. Phys. 2014, 53, 05FA12. [Google Scholar] [CrossRef]
- Traore, A.; Muret, P.; Fiori, A.; Eon, D.; Gheeraert, E.; Pernot, J. Zr/Oxidized diamond interface for high power Schottky diodes. Appl. Phys. Lett. 2014, 104, 052105. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, D.; Makino, T.; Kato, H.; Ogura, M.; Tokuda, N.; Matsumoto, T.; Kuwabara, D.; Okushi, H.; Yamasaki, S. Free exciton luminescence from a diamond p-i-n diode grown on a substrate produced by heteroepitaxy. Phys. Status Solidi A 2014, 211, 2251–2256. [Google Scholar] [CrossRef]
- Muret, P.; Traoré, A.; Maréchal, A.; Eon, D.; Pernot, J.; Piñero, J.C.; Villar, M.P.; Araujo, D. Potential barrier heights at metal on oxygen-terminated diamond interfaces. J. Appl. Phys. 2015, 118, 204505. [Google Scholar] [CrossRef] [Green Version]
- Jiang, D.; Mu, W.; Chen, S.; Fu, Y.; Jeppson, K.; Liu, J. Vertically stackted carbon nanotubes based interconnects for through silicon via application. IEEE Trans. Electron Dev. 2015, 36, 499–501. [Google Scholar] [CrossRef]
- Sato, K.; Iwasaki, T.; Hoshino, Y.; Kato, H.; Makino, T.; Ogura, M.; Yamasaki, S.; Nakamura, S.; Ichikawa, K.; Sawabe, A.; et al. Analysis of selective growth of n-type diamond in lateral p-n junction diodes by cross-sectional transmission electron microscopy. Jpn. J. Appl. Phys. 2014, 53, 05FP01. [Google Scholar] [CrossRef]
- Tokuda, N.; Umezawa, H.; Yamabe, K.; Okushi, H.; Yamasaki, S. Growth of atomically step-free surface on diamond {111} mesas. Diam. Relat. Mater. 2010, 19, 288–290. [Google Scholar] [CrossRef]
- Tokuda, N.; Makino, T.; Inokuma, T.; Yamasaki, S. Formation of step-free surfaces on diamond (111) mesas by homoepitaxial lateral growth. Jpn. J. Appl. Phys. 2012, 51, 090107. [Google Scholar] [CrossRef]
- Steeds, J.W.; Gilmore, A.; Wilson, J.A.; Butler, J.E. On the nature of extended defects in CVD diamond and the origin of compressive stresses. Diam. Relat. Mater. 1998, 7, 1437–1450. [Google Scholar] [CrossRef]
- Lloret, F.; Fiori, A.; Araujo, D.; Eon, D.; Villar, M.P.; Bustarret, E. Stratigraphic of a diamond epitaxial three-dimensional overgrowth using doping superlattices. Appl. Phys. Lett. 2016, 108, 181901. [Google Scholar] [CrossRef] [Green Version]
- Sugiyama, M.; Sigesato, G. A review of focused ion beam techbnology and its applications in transmission electron microscopy. J. Electron Microsc. 2004, 53, 527–536. [Google Scholar] [CrossRef]
- Wild, C.; Kohl, R.; Herres, N.; Müller-Sebert, W.; Koidl, P. Oriented CVD diamond films—Twin formation, structure and morphology. Diam. Relat. Mater. 1994, 3, 373–381. [Google Scholar] [CrossRef]
- Tamor, M.A.; Emerson, M.P. On the role of penetration twins in the morphological development of vapor-grown diamond films. J. Mater. Res. 1994, 9, 1839–1849. [Google Scholar] [CrossRef]
- Bogatskiy, A.; Butler, J.E. A geometric model of growth for cubic crystals: Diamond. Diam. Relat. Mater. 2015, 53, 58–65. [Google Scholar] [CrossRef]
- Tallaire, A.; Ouisse, T.; Lantreibecq, A.; Cours, R.; Legros, M.; Bensalah, H.; Barjon, J.; Mille, V.; Brinza, O.; Achard, J. Identification of dislocations in synthetic chemically vapor deposited diamond single crystals. Cryst. Growth Des. 2016, 16, 2741–2746. [Google Scholar] [CrossRef]
- Lloret, F.; Araujo, D.; Eon, D.; Villar, M.P.; Gonzalez-Leal, J.M.; Bustarret, E. Influence of methane concentration on MPCVD overgrowth of 100-oriented etched diamond substrates. Phys. Status Solidi A 2016, 213, 2570–2574. [Google Scholar] [CrossRef]
- Lloret, F.; Eon, D.; Bustarret, E.; Fiori, A.; Araujo, D. Boron-doping proximity effects on dislocations generation during non-planar MPCVD homepitaxial diamond growth. Nanomaterials 2018, 8, 480. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ichinose, H.; Nakanose, M.; Ito, K.; Ishida, Y. Structure modelling of Sigma 3 and Sigma 9 coincident boundaries in CVD diamond thin films. J. Electron Microsc. 1999, 48, 245–251. [Google Scholar] [CrossRef]




| Sample | Layer | CH4/H2 | O2/H2 | B2H6/CH4 | Time (min) | Group |
|---|---|---|---|---|---|---|
| #A | Doped | 0.25% | - | 10,700 | 2 × 13 | ML-LM |
| Undoped | 0.1% | - | - | 60 × 13 | ||
| #B | Undoped | 0.1% | - | - | 840 × 1 | UL-LM |
| #C | Doped | 0.5% | - | 9600 | 1 × 13 | ML-HM |
| Undoped | 0.75% | 0.32% | - | 10 × 13 | ||
| #D | Undoped | 0.75% | 0.32% | - | 140 × 1 | UL-HM |
| #E | Doped | 0.5% | - | 14,000 | 11 × 10 | ML-HM |
| Undoped | 0.75% | 0.32% | - | 11 × 10 | ||
| #F | Undoped | 0.75% | 0.25% | - | 30 × 1 | UL-HM |
| #G | Doped | 0.5% | - | 6000 | 10 × 1 | DL-HM |
| Sample | Layer | Burgers Vector |
|---|---|---|
| #A | Low Doping-Low Methane | No |
| Undoped-Low Methane | ||
| #B | Undoped-Low Methane | No |
| #C | Low Doping-High Methane | |
| Undoped-High Methane | ||
| #D | Undoped-High Methane | |
| #E | High Doping-High Methane | |
| Undoped-High Methane | ||
| #F | Undoped-High Methane | |
| #G | High Doping-High Methane |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lloret, F.; Eon, D.; Bustarret, E.; Araujo, D. Crystalline Defects Induced during MPCVD Lateral Homoepitaxial Diamond Growth. Nanomaterials 2018, 8, 814. https://doi.org/10.3390/nano8100814
Lloret F, Eon D, Bustarret E, Araujo D. Crystalline Defects Induced during MPCVD Lateral Homoepitaxial Diamond Growth. Nanomaterials. 2018; 8(10):814. https://doi.org/10.3390/nano8100814
Chicago/Turabian StyleLloret, Fernando, David Eon, Etienne Bustarret, and Daniel Araujo. 2018. "Crystalline Defects Induced during MPCVD Lateral Homoepitaxial Diamond Growth" Nanomaterials 8, no. 10: 814. https://doi.org/10.3390/nano8100814
APA StyleLloret, F., Eon, D., Bustarret, E., & Araujo, D. (2018). Crystalline Defects Induced during MPCVD Lateral Homoepitaxial Diamond Growth. Nanomaterials, 8(10), 814. https://doi.org/10.3390/nano8100814






