Quantum Characteristics of a Nanomechanical Resonator Coupled to a Superconducting LC Resonator in Quantum Computing Systems
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Hamiltonian and the Unitary Transformation
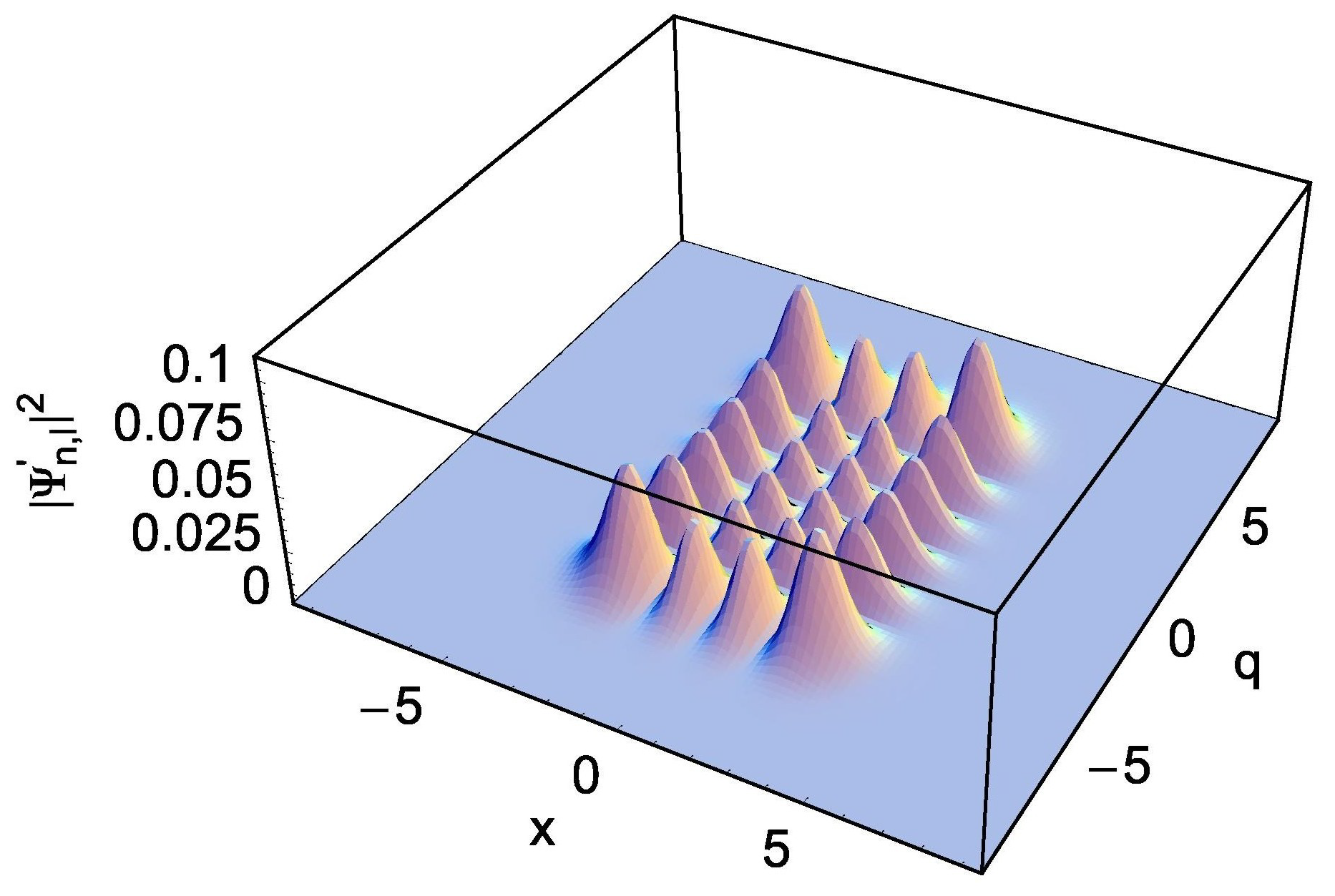
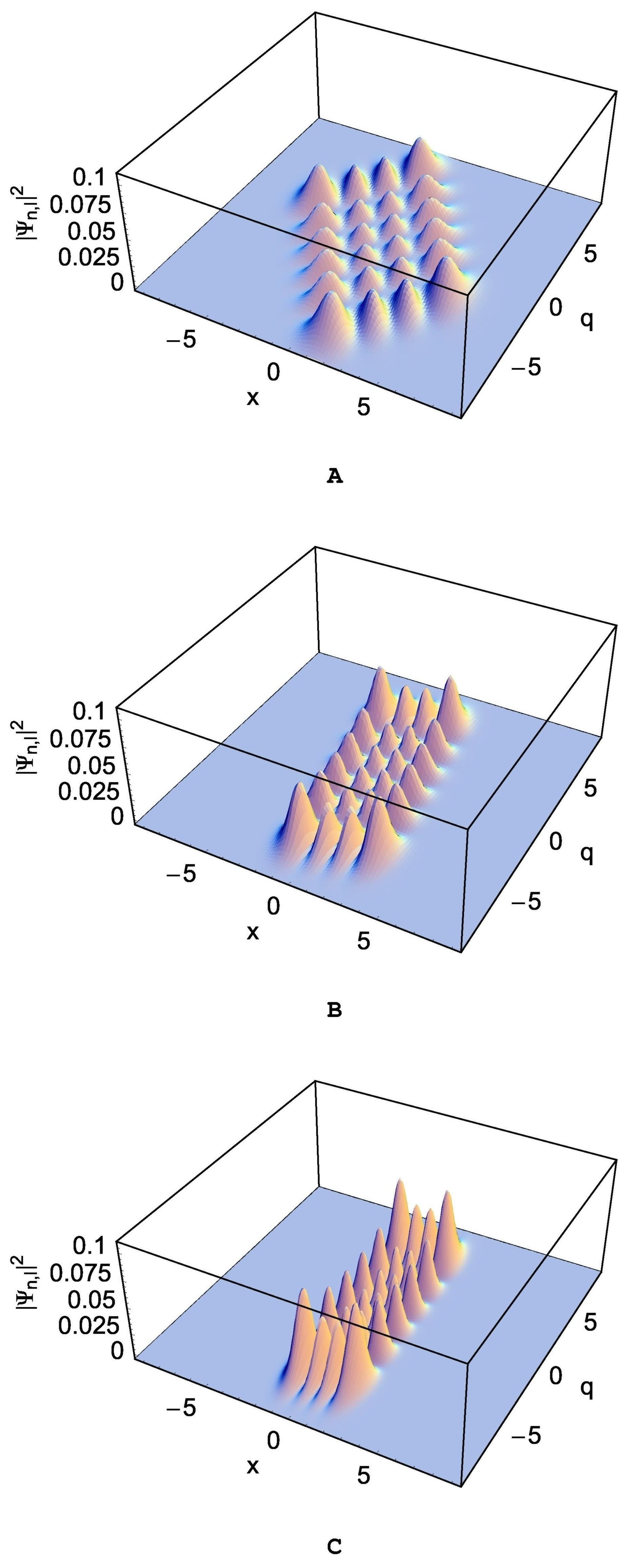
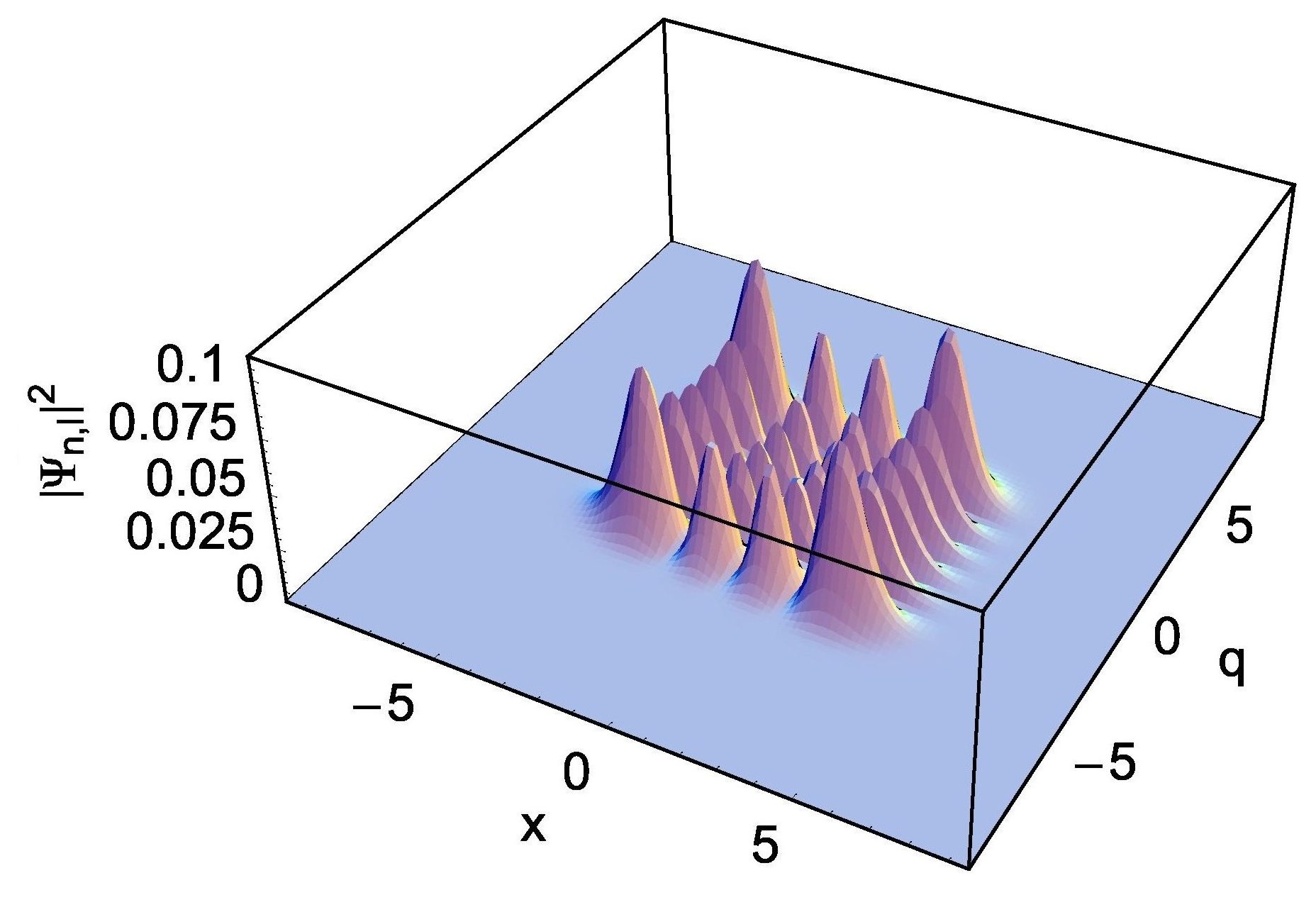
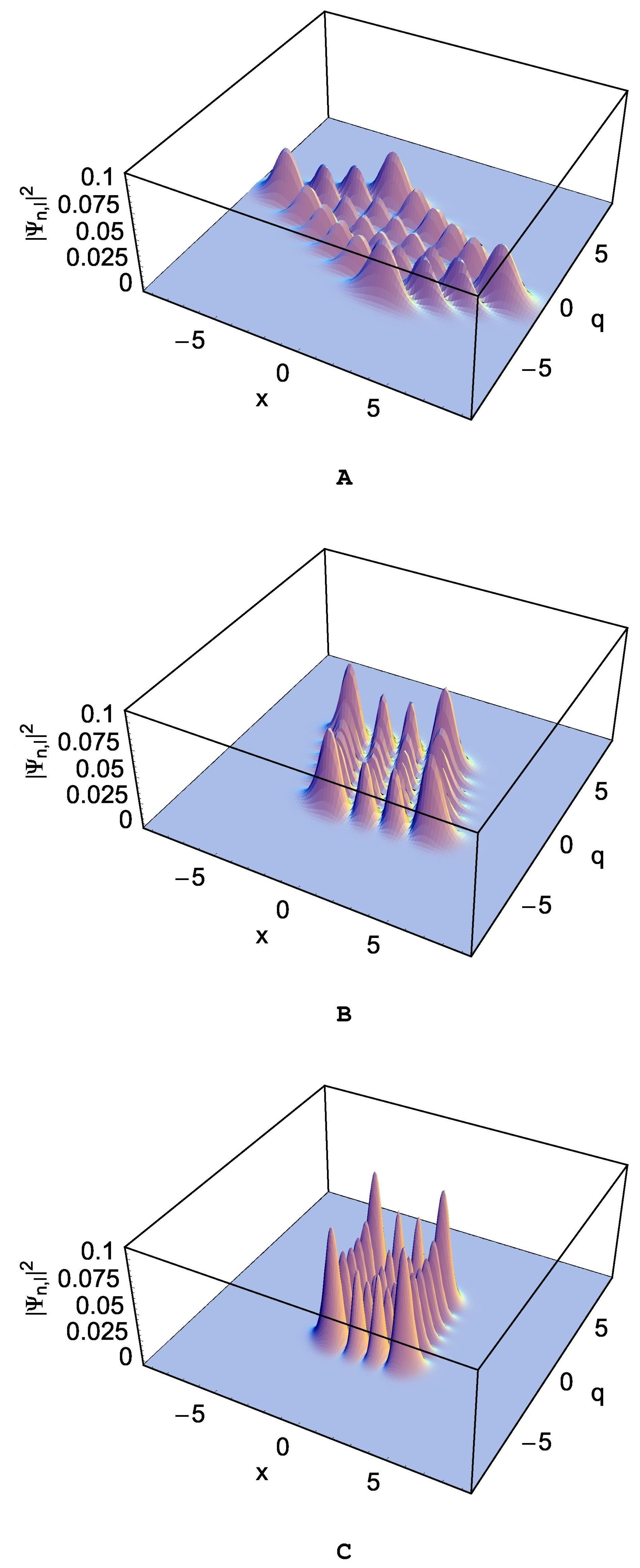
3.2. Quantum Wave Solutions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Favero, I.; Marquardt, F. Focus on optomechanics. New J. Phys. 2014, 16, 085006. [Google Scholar] [CrossRef] [Green Version]
- Rabl, P.; Kolkowitz, S.J.; Koppens, F.H.L.; Harris, J.G.E.; Zoller, P.; Lukin, M.D. A quantum spin transducer based on nanoelectromechanical resonator arrays. Nat. Phys. 2010, 6, 602–608. [Google Scholar] [CrossRef] [Green Version]
- Tetard, L.; Passian, A.; Venmar, K.T.; Lynch, R.M.; Voy, B.H.; Shekhawat, G.; Dravid, V.P.; Thundat, T. Imaging nanoparticles in cells by nanomechanical holography. Nat. Nanotechnol. 2008, 3, 501–505. [Google Scholar] [CrossRef] [PubMed]
- Sawadsky, A.; Kaufer, H.; Nia, R.M.; Tarabrin, S.P.; Khalili, F.Y.; Hammerer, K.; Schnabel, R. Observation of generalized optomechanical coupling and cooling on cavity resonance. Phys. Rev. Lett. 2015, 114, 043601. [Google Scholar] [CrossRef] [PubMed]
- LaHaye, M.D.; Buu, O.; Camarota, B.; Schwab, K.C. Approaching the quantum limit of a nanomechanical resonator. Science 2004, 304, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Woolley, M.J.; Milburn, G.J.; Caves, C.M. Nonlinear quantum metrology using coupled nanomechanical resonators. New J. Phys. 2008, 10, 125018. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.-Q.; Law, C.K.; Kuang, L.-M.; Nori, F. Enhancement of mechanical effects of single photons in modulated two-mode optomechanics. Phys. Rev. A 2015, 92, 013822. [Google Scholar] [CrossRef]
- Wang, D.-Y.; Bai, C.-H.; Liu, S.; Zhang, S.; Wang, H.-F. Optomechanical cooling beyond the quantum backaction limit with frequency modulation. Phys. Rev. A 2018, 98, 023816. [Google Scholar] [CrossRef]
- Choi, J.R. Hamiltonian dynamics and adiabatic invariants for time-dependent superconducting qubit-oscillators and resonators in quantum computing systems. Adv. Math. Phys. 2015, 2015, 120573. [Google Scholar] [CrossRef]
- Tian, L. Ground state cooling of a nanomechanical resonator via parametric linear coupling. Phys. Rev. B 2009, 79, 193407. [Google Scholar] [CrossRef]
- Jacobs, K.; Nurdin, H.I.; Strauch, F.W.; James, M. Frequency conversion: Side-band cooling, state-swapping, and coherent control of mechanical resonators. arXiv, 2010; arXiv:1003.2653v3. [Google Scholar]
- Cleland, A.N.; Geller, M.R. Mechanical quantum resonators. AIP Conf. Proc. 2005, 786, 396–400. [Google Scholar]
- Pechal, M.; Arrangoiz-Arriola, P.; Safavi-Naeini, A.H. Superconducting circuit quantum computing with nanomechanical resonators as storage. Quantum Sci. Technol. 2018, 4, 015006. [Google Scholar] [CrossRef]
- Armour, A.D.; Blencowe, M.P. Probing the quantum coherence of a nanomechanical resonator using a superconducting qubit: I. Echo scheme. New J. Phys. 2008, 10, 095004. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef] [Green Version]
- Safavi-Naeini, A.H.; Chan, J.; Hill, J.T.; Alegre, T.P.M.; Krause, A.; Painter, O. Observation of quantum motion of a nanomechanical resonator. Phys. Rev. Lett. 2012, 108, 033602. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, K.; Nurdin, H.I.; Strauch, F.W.; James, M. Comparing resolved-sideband cooling and measurement-based feedback cooling on an equal footing: Analytical results in the regime of ground-state cooling. Phys. Rev. A 2015, 91, 043812. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.R. Exact solution of a quantized LC circuit coupled to a power source. Phys. Scr. 2006, 73, 587–595. [Google Scholar] [CrossRef]
- Xiang, Z.-L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623–653. [Google Scholar] [CrossRef] [Green Version]
- Peropadre, B.; Zueco, D.; Wulschner, F.; Deppe, F.; Marx, A.; Gross, R.; García-Ripoll, J.J. Tunable coupling engineering between superconducting resonators: From sidebands to effective gauge fields. Phys. Rev. B 2013, 87, 134504. [Google Scholar] [CrossRef] [Green Version]
- Fedortchenko, S.; Felicetti, S.; Marković, D.; Jezouin, S.; Keller, A.; Coudreau, T.; Huard, B.; Milman, P. Quantum simulation of ultrastrongly coupled bosonic modes using superconducting circuits. Phys. Rev. A 2017, 95, 042313. [Google Scholar] [CrossRef]
- Lakehal, H.; Maamache, M.; Choi, J.R. Novel quantum description for nonadiabatic evolution of light wave propagation in time-dependent linear media. Sci. Rep. 2016, 6, 19860. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khandekar, D.C.; Lawande, S.V. Exact propagator for a time-dependent harmonic oscillator with and without a singular perturbation. J. Math. Phys. 1975, 16, 384–388. [Google Scholar] [CrossRef]
- Terraneo, M.; Georgeot, B.; Shepelyansky, D.L. Quantum computation and analysis of Wigner and Husimi functions: Toward a quantum image treatment. Phys. Rev. E 2005, 71, 066215. [Google Scholar] [CrossRef] [PubMed]
- Xue, F.; Wang, Y.D.; Sun, C.P.; Okamoto, H.; Yamaguchi, H.; Semba, K. Controllable coupling between flux qubit and nanomechanical resonator by magnetic field. New J. Phys. 2007, 9, 35. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Liao, J.-Q.; Tian, L.; Nori, F. Steady-state mechanical squeezing in an optomechanical system via Duffing nonlinearity. Phys. Rev. A 2015, 91, 013834. [Google Scholar] [CrossRef]
- Malka, D.; Cohen, M.; Turkiewicz, J.; Zalevsky, Z. Optical micro-multi-racetrack resonator filter based on SOI waveguides. Photonics Nanostruct. Fundam. Appl. 2015, 16, 16–23. [Google Scholar] [CrossRef]
- McGehee, W.R.; Michels, T.; Aksyuk, V.; McClelland, J.J. Two-dimensional imaging and modification of nanophotonic resonator modes using a focused ion beam. Optica 2017, 4, 1444–1450. [Google Scholar] [CrossRef]
- Cohen, E.; Malka, D.; Shemer, A.; Shahmoon, A.; Zalevsky, Z.; London, M. Neural networks within multi-core optic fibers. Sci. Rep. 2016, 6, 29080. [Google Scholar] [CrossRef] [Green Version]
- Shabairou, N.; Cohen, E.; Wagner, O.; Malka, D.; Zalevsky, Z. Color image identification and reconstruction using artificial neural networks on multimode fiber images: Towards an all-optical design. Opt. Lett. 2018, 43, 5603–5606. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Cao, X.-Z.; Su, Q.-P.; Xiong, S.-J.; Yang, C.-P. Multi-target-qubit unconventional geometric phase gate in a multi-cavity system. Sci. Rep. 2016, 6, 21562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tavrov, A.V.; Miyamoto, Y.; Kawabata, T.; Takeda, M.; Andreev, V.A. Interferometric microimaging based on geometrical spin-redirection phase. Opt. Lett. 2000, 25, 460–462. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-H.; Tan, G.; Zhan, T.; Weng, Y.; Liu, G.; Gou, F.; Peng, F.; Tabiryan, N.V.; Gauza, S.; Wu, S.-T. Recent progress in Pancharatnam-Berry phase optical elements and the applications for virtual/augmented realities. Opt. Data Process. Storage 2017, 3, 79–88. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.R.; Ju, S. Quantum Characteristics of a Nanomechanical Resonator Coupled to a Superconducting LC Resonator in Quantum Computing Systems. Nanomaterials 2019, 9, 20. https://doi.org/10.3390/nano9010020
Choi JR, Ju S. Quantum Characteristics of a Nanomechanical Resonator Coupled to a Superconducting LC Resonator in Quantum Computing Systems. Nanomaterials. 2019; 9(1):20. https://doi.org/10.3390/nano9010020
Chicago/Turabian StyleChoi, Jeong Ryeol, and Sanghyun Ju. 2019. "Quantum Characteristics of a Nanomechanical Resonator Coupled to a Superconducting LC Resonator in Quantum Computing Systems" Nanomaterials 9, no. 1: 20. https://doi.org/10.3390/nano9010020



