Thermal Transport in a 2D Nanophononic Solid: Role of bi-Phasic Materials Properties on Acoustic Attenuation and Thermal Diffusivity
Abstract
:1. Introduction
2. Numerical Tools
3. Vibrational Properties
3.1. Equilibrium Vibrational Properties
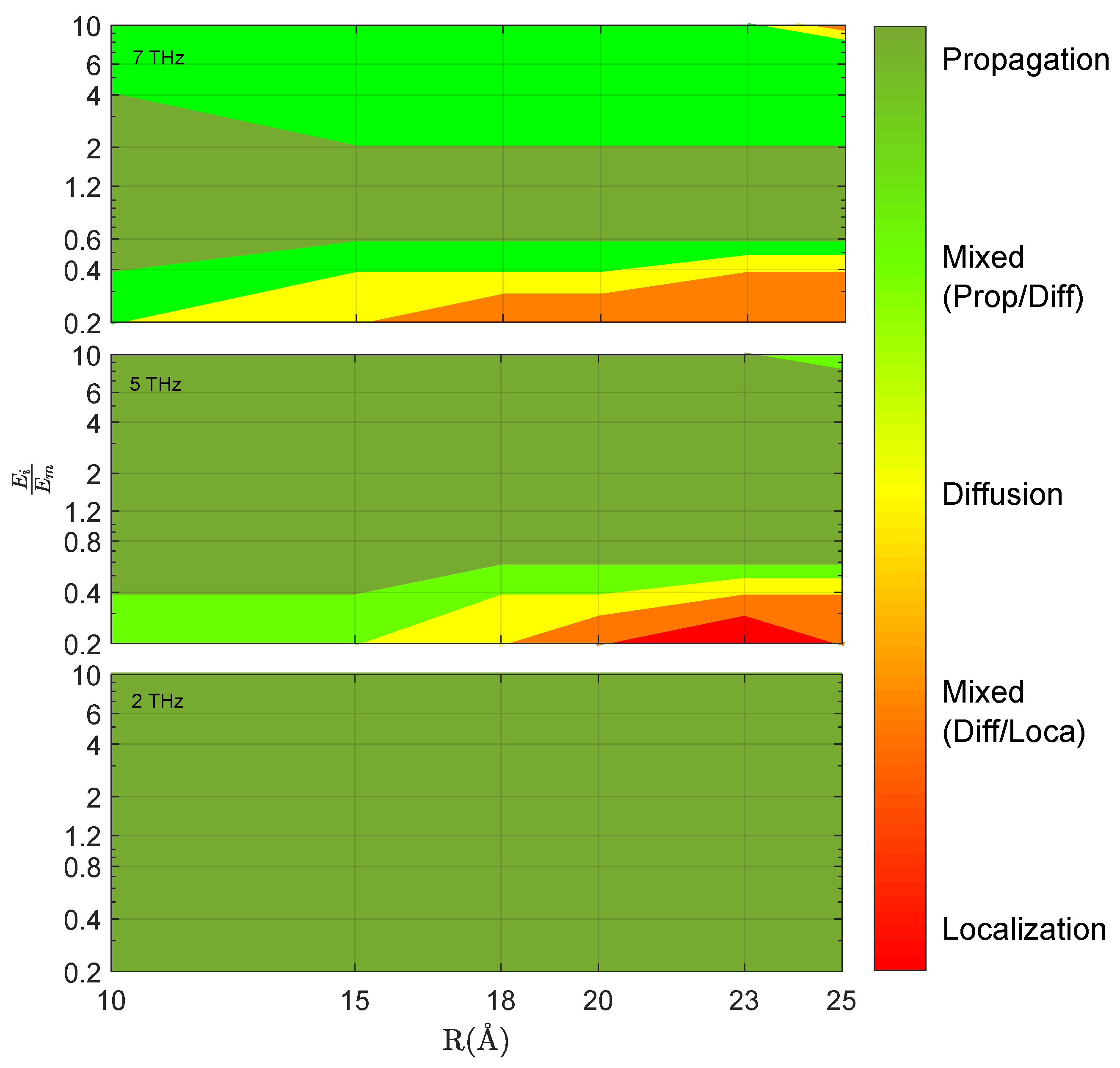
3.2. Wave-Packet Propagation: Different Regimes
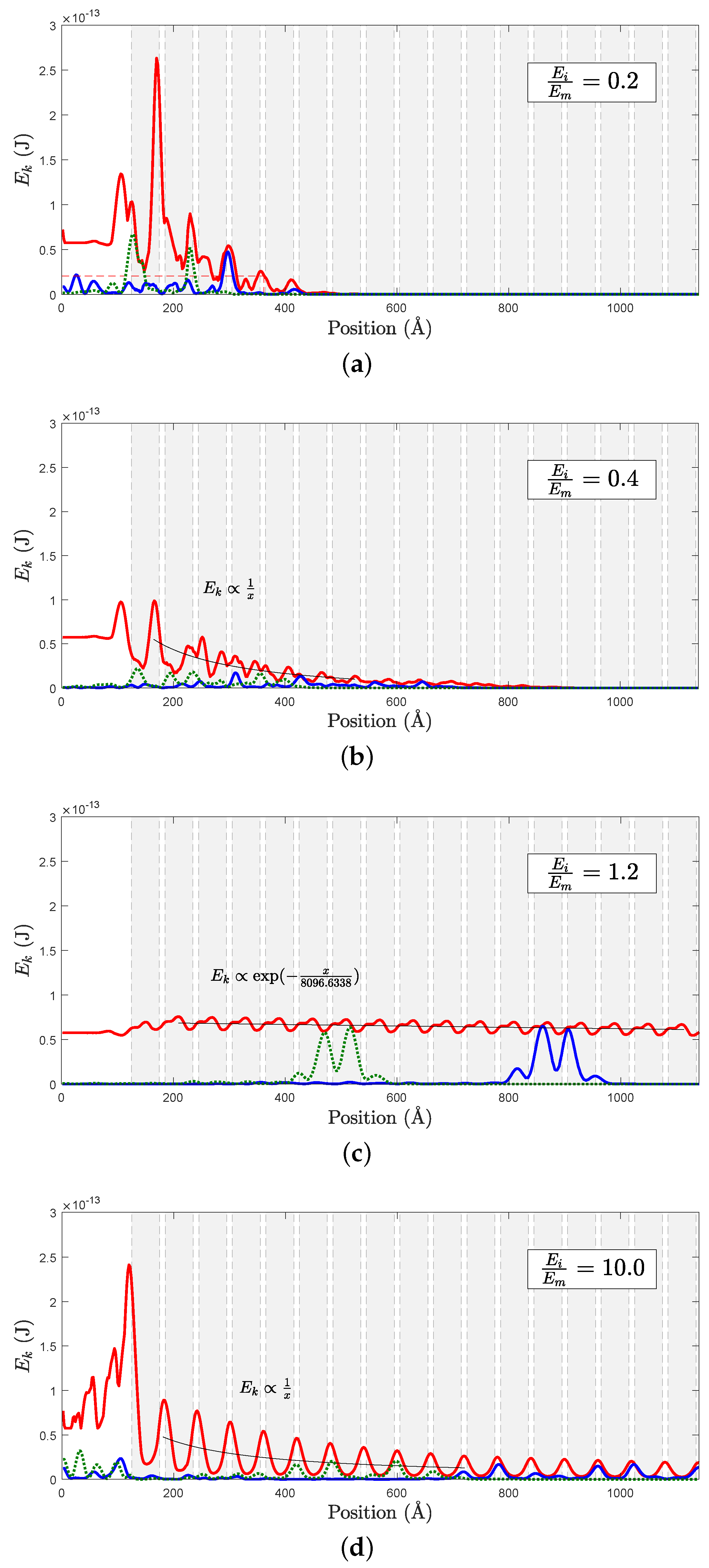
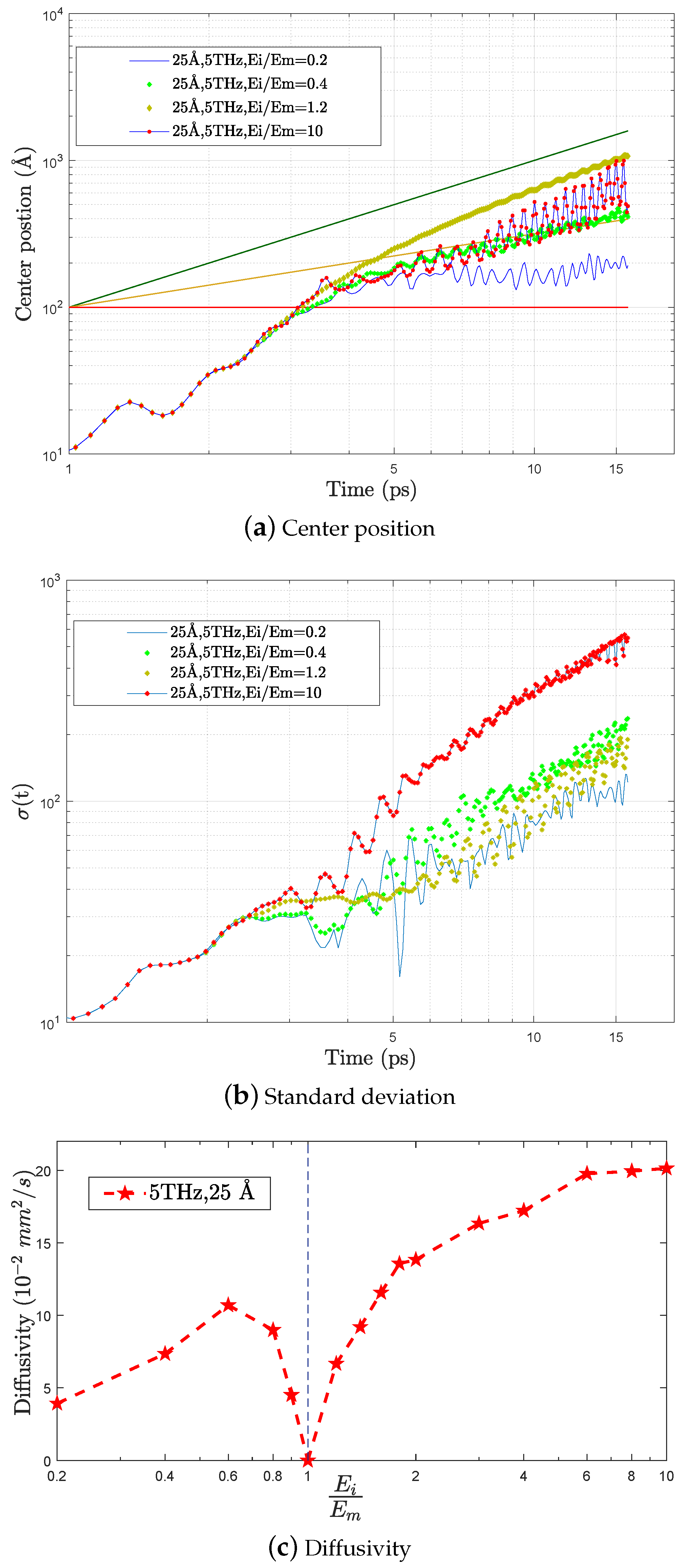
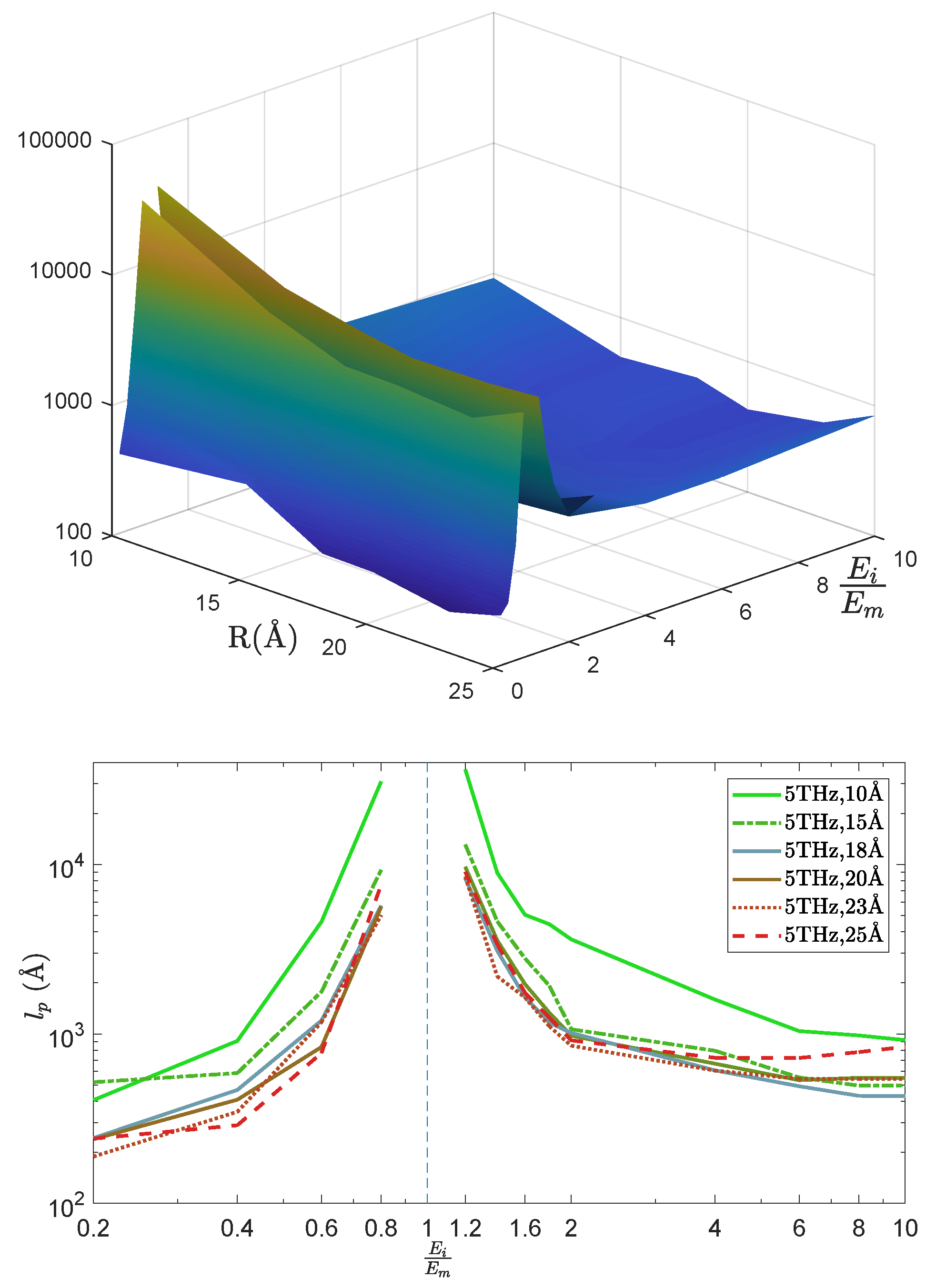
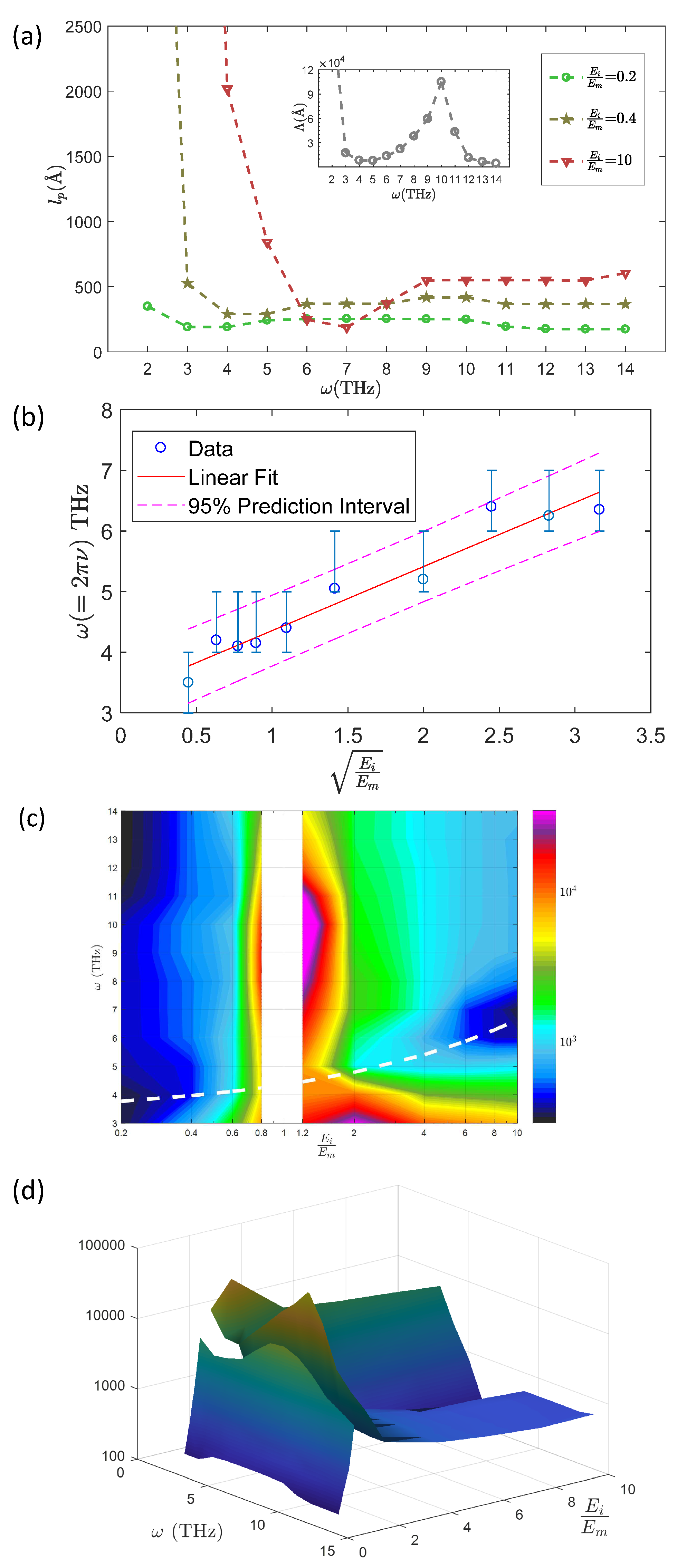
4. Mean Free Path vs. Penetration Length
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Finite Elements Simulations
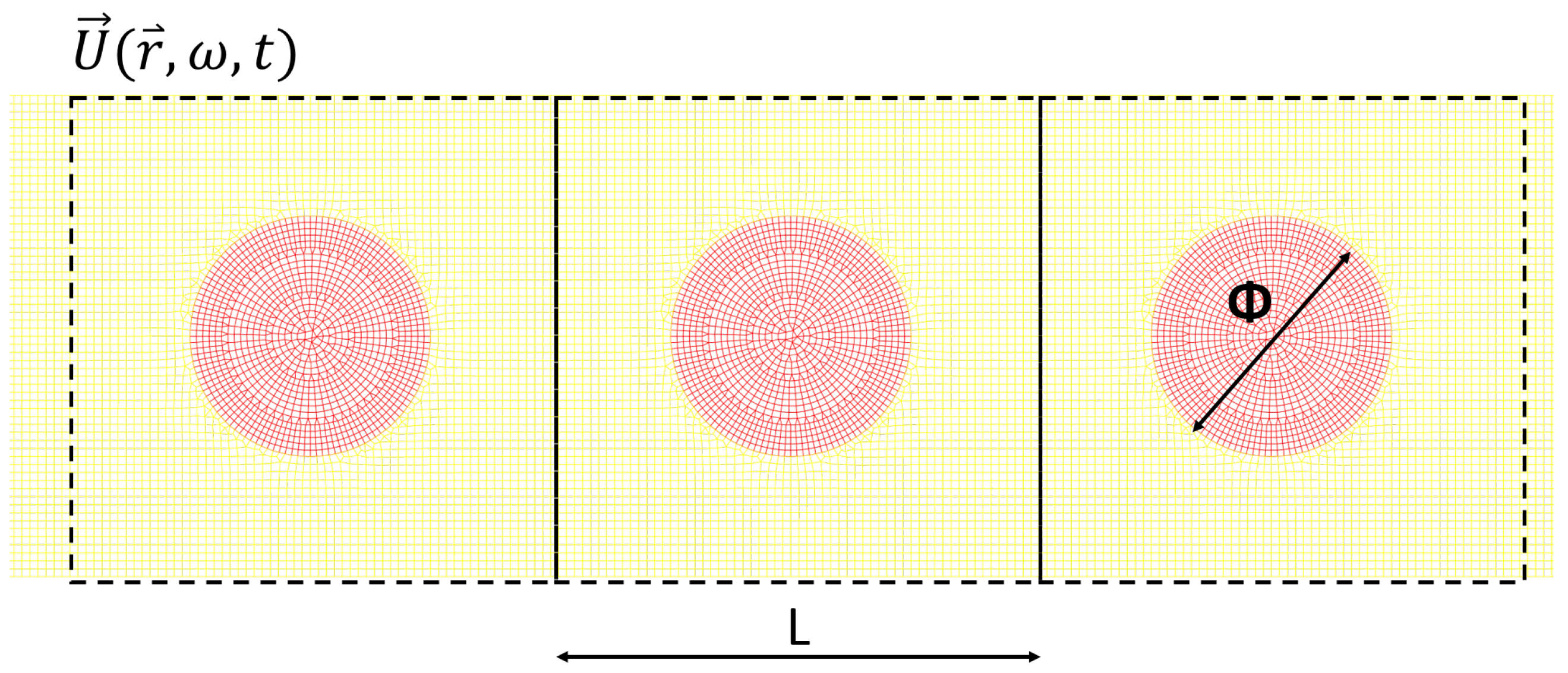
Appendix A.1. Wave Packet
Appendix A.2. Boundary Conditions
Appendix A.3. Time Integration
Appendix A.4. Algorithm
References
- Waldrop, M.M. The chips are down for Moore’s law. Nat. News 2016, 530, 144. [Google Scholar] [CrossRef] [PubMed]
- Prasher, R.S.; Hu, X.J.; Chalopin, Y.; Mingo, N.; Lofgreen, K.; Volz, S.; Cleri, F.; Keblinski, P. Turning Carbon Nanotubes from Exceptional Heat Conductors into Insulators. Phys. Rev. Lett. 2009, 102, 105901. [Google Scholar] [CrossRef] [PubMed]
- Termentzidis, K.; Chantrenne, P.; Keblinski, P. Nonequilibrium molecular dynamics simulation of the in-plane thermal conductivity of superlattices with rough interfaces. Phys. Rev. B 2009, 79, 214307. [Google Scholar] [CrossRef] [Green Version]
- Merabia, S.; Termentzidis, K. Thermal conductance at the interface between crystals using equilibrium and nonequilibrium molecular dynamics. Phys. Rev. B 2012, 86, 094303. [Google Scholar] [CrossRef] [Green Version]
- Zen, N.; Puurtinen, T.A.; Isotalo, T.J.; Chaudhuri, S.; Maasilta, I.J. Engineering thermal conductance using a two-dimensional phononic crystal. Nat. Commun. 2014, 5, 3435. [Google Scholar] [CrossRef]
- France-Lanord, A.; Merabia, S.; Albaret, T.; Lacroix, D.; Termentzidis, K. Thermal properties of amorphous/crystalline silicon superlattices. J. Phys. Condens. Matter 2014, 26, 355801. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.; Minnich, A.J. Sub-amorphous thermal conductivity in amorphous heterogeneous nanocomposites. RSC Adv. 2016, 6, 105154–105160. [Google Scholar] [CrossRef] [Green Version]
- Anufriev, R.; Nomura, M. Reduction of thermal conductance by coherent phonon scattering in two-dimensional phononic crystals of different lattice types. Phys. Rev. B 2016, 93, 045410. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Minnich, A.J. Thermal transport in nanocrystalline Si and SiGe by ab initio based Monte Carlo simulation. Sci. Rep. 2017, 7, 44254. [Google Scholar] [CrossRef]
- Verdier, M.; Lacroix, D.; Didenko, S.; Robillard, J.F.; Lampin, E.; Bah, T.M.; Termentzidis, K. Influence of amorphous layers on the thermal conductivity of phononic crystals. Phys. Rev. B 2018, 97, 115435. [Google Scholar] [CrossRef] [Green Version]
- Vandersande, J.W.; Wood, C. The thermal conductivity of insulators and semiconductors. Contemp. Phys. 1986, 27, 117–144. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Larkin, J.M.; McGaughey, A.J.H. Thermal conductivity accumulation in amorphous silica and amorphous silicon. Phys. Rev. B 2014, 89, 144303. [Google Scholar] [CrossRef]
- Allen, P.B.; Feldman, J.L. Thermal Conductivity of Glasses: Theory and Application to Amorphous Si. Phys. Rev. Lett. 1990, 64, 2466. [Google Scholar] [CrossRef]
- Allen, P.B.; Feldman, J.L.; Fabian, J.; Wooten, F. Diffusons, locons and propagons: Character of atomie yibrations in amorphous Si. Philos. Mag. B 1999, 79, 1715–1731. [Google Scholar] [CrossRef]
- Economou, E.N.; Zdetsis, A. Classical wave propagation in periodic structures. Phys. Rev. B 1989, 40, 1334–1337. [Google Scholar] [CrossRef]
- Maslov, K.; Kinra, V.K. Acoustic response of a periodic layer of nearly rigid spherical inclusions in an elastic solid. J. Acoust. Soc. Am. 1999, 106, 3081–3088. [Google Scholar] [CrossRef]
- Elford, D.P. Band Gap Formation in Acoustically Resonant Phononic Crystals. Ph.D. Thesis, Loughborough University, London, UK, 2010. [Google Scholar]
- Tanaka, Y.; Tomoyasu, Y.; ichiro Tamura, S. Band structure of acoustic waves in phononic lattices: Two-dimensional composites with large acoustic mismatch. Phys. Rev. B 2000, 62, 7387–7392. [Google Scholar] [CrossRef] [Green Version]
- Damart, T.; Giordano, V.M.; Tanguy, A. Nanocrystalline inclusions as a low-pass filter for thermal transport ina-Si. Phys. Rev. B 2015, 92, 94201. [Google Scholar] [CrossRef] [Green Version]
- Anufriev, R.; Ramiere, A.; Maire, J.; Nomura, M. Heat guiding and focusing using ballistic phonon transport in phononic nanostructures. Nat. Commun. 2017, 8, 15505. [Google Scholar] [CrossRef]
- Meyer, R. Vibrational band structure of nanoscale phononic crystals. Phys. Status Solidi A 2016, 213, 2927–2935. [Google Scholar] [CrossRef] [Green Version]
- Sheng, P. Introduction to Wave Scattering, Localization and Mesoscopic Phenomena; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 88. [Google Scholar]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity Of Fluids with Nanoparticles; Technical Report; Argonne National Laboratory: Lemont, IL, USA, 1995. [Google Scholar]
- Wang, N.; Chen, H.; He, H.; Norimatsu, W.; Kusunoki, M.; Koumoto, K. Enhanced thermoelectric performance of Nb-doped SrTiO 3 by nano-inclusion with low thermal conductivity. Sci. Rep. 2013, 3, 3449. [Google Scholar] [CrossRef] [PubMed]
- Schlichting, K.; Padture, N.; Klemens, P. Thermal conductivity of dense and porous yttria-stabilized zirconia. J. Mater. Sci. 2001, 36, 3003–3010. [Google Scholar] [CrossRef]
- Tlili, A.; Pailhès, S.; Debord, R.; Ruta, B.; Gravier, S.; Blandin, J.J.; Blanchard, N.; Gomès, S.; Assy, A.; Tanguy, A.; et al. Thermal transport properties in amorphous/nanocrystalline metallic composites: A microscopic insight. Acta Mater. 2017, 136, 425–435. [Google Scholar] [CrossRef]
- Morthomas, J.; Gonçalves, W.; Perez, M.; Foray, G.; Martin, C.L.; Chantrenne, P. A novel method to predict the thermal conductivity of nanoporous materials from atomistic simulations. J. Non-Cryst. Solids 2019, 516, 89–98. [Google Scholar] [CrossRef]
- Tlili, A. The Effect of A Partial Nanocrystallization on the Transport Properties of Amorphous/Crystalline Composites. Ph.D. Thesis, Université de Lyon, Lyon, France, 2017. [Google Scholar]
- Tlili, A.; Giordano, V.M.; Beltukov, Y.M.; Desmarchelier, P.; Merabia, S.; Tanguy, A. Enhancement and anticipation of the Ioffe-Regel crossover in amorphous/nanocrystalline composites. Nanoscale 2019, unpublished. [Google Scholar] [CrossRef]
- Tanguy, A.; Wittmer, J.; Leonforte, F.; Barrat, J.L. Continuum limit of amorphous elastic bodies: A finite-size study of low-frequency harmonic vibrations. Phys. Rev. B 2002, 66, 174205. [Google Scholar] [CrossRef] [Green Version]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Phonon wave-packet dynamics at semiconductor interfaces by molecular-dynamics simulation. Appl. Phys. Lett. 2002, 80, 2484–2486. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar]
- Bettess, P. Infinite elements. Int. J. Numer. Methods Eng. 1977, 11, 53–64. [Google Scholar] [CrossRef]
- Kim, H.S. A Study on the Performance of Absorbing Boundaries Using Dashpot. Engineering 2014, 6, 593–600. [Google Scholar] [CrossRef] [Green Version]
- Bonnet, M.; Frangi, A.; Rey, C. The Finite Element Method in Solid Mechanics; McGraw Hill Education: New York, NY, USA, 2014; p. 365. [Google Scholar]
- Li, S.; Brun, M.; Djeran-Maigre, I.; Kuznetsov, S. Hybrid asynchronous absorbing layers based on Kosloff damping for seismic wave propagation in unbounded domains. Comput. Geotech. 2019, 109, 69–81. [Google Scholar] [CrossRef]
- Beltukov, Y.; Parshin, D.; Giordano, V.; Tanguy, A. Propagative and diffusive regimes of acoustic damping in bulk amorphous material. Phys. Rev. E 2018, 98, 023005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fusco, C.; Albaret, T.; Tanguy, A. Role of local order in the small-scale plasticity of model amorphous materials. Phys. Rev. E 2010, 82, 066116. [Google Scholar] [CrossRef] [PubMed]
- Beltukov, Y.M.; Fusco, C.; Parshin, D.A.; Tanguy, A. Boson peak and Ioffe-Regel criterion in amorphous siliconlike materials: The effect of bond directionality. Phys. Rev. E 2016, 93, 023006. [Google Scholar] [CrossRef] [Green Version]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Swinehart, D.F. The Beer-Lambert Law. J. Chem. Educ. 1962, 39, 333. [Google Scholar] [CrossRef]
- Chen, X.; Parker, D.; Singh, D.J. Acoustic impedance and interface phonon scattering in Bi2Te3 and other semiconducting materials. Phys. Rev. B 2013, 87, 045317. [Google Scholar] [CrossRef]
- Schirmacher, W.; Ruocco, G.; Mazzone, V. Theory of heterogeneous viscoelasticity. Philos. Mag. 2015, 96, 620–635. [Google Scholar] [CrossRef] [Green Version]
- Luo, H. Continuum constitutive laws to describe acoustic attenuation at a molecular scale. 2020. in preparation. [Google Scholar]
- Lu, Y.; Blal, N.; Gravouil, A. Datadriven HOPGD based computational vademecum for welding parameter identification. Comput. Mech. 2018, 64, 47–62. [Google Scholar] [CrossRef]
- Lu, Y.; Blal, N.; Gravouil, A. Multi-parametric space-time computational vademecum for parametric studies: Application to real time welding simulations. Finite Elem. Anal. Des. 2018, 139, 62–72. [Google Scholar] [CrossRef]
- Stasio, J.D.; Dureisseix, D.; Gravouil, A.; Georges, G.; Homolle, T. Benchmark cases for robust explicit time integrators in non-smooth transient dynamics. Adv. Model. Simul. Eng. Sci. 2019, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Geradin, D.J.R. Mechanical Vibrations: Theory and Application to Structural Dynamics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
Sample Availability: The input files used in CasT3M code, and the numerical data are available from the authors. |






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Gravouil, A.; Giordano, V.; Tanguy, A. Thermal Transport in a 2D Nanophononic Solid: Role of bi-Phasic Materials Properties on Acoustic Attenuation and Thermal Diffusivity. Nanomaterials 2019, 9, 1471. https://doi.org/10.3390/nano9101471
Luo H, Gravouil A, Giordano V, Tanguy A. Thermal Transport in a 2D Nanophononic Solid: Role of bi-Phasic Materials Properties on Acoustic Attenuation and Thermal Diffusivity. Nanomaterials. 2019; 9(10):1471. https://doi.org/10.3390/nano9101471
Chicago/Turabian StyleLuo, Haoming, Anthony Gravouil, Valentina Giordano, and Anne Tanguy. 2019. "Thermal Transport in a 2D Nanophononic Solid: Role of bi-Phasic Materials Properties on Acoustic Attenuation and Thermal Diffusivity" Nanomaterials 9, no. 10: 1471. https://doi.org/10.3390/nano9101471