Effects of Joule Heating and Viscous Dissipation on Magnetohydrodynamic Boundary Layer Flow of Jeffrey Nanofluid over a Vertically Stretching Cylinder

Abstract

This article investigates unsteady magnetohydrodynamic (MHD) mixed convective and thermally radiative Jeffrey nanofluid flow in view of a vertical stretchable cylinder with radiation absorption and heat; the reservoir was addressed. The mathematical formulation of Jeffrey nanofluid is established based on the theory of boundary layer approximations pioneered by Prandtl. The governing model expressions in partial differential equations (PDEs) form was transformed into dimensionless form via similarity transformation technique. The set of nonlinear nondimensional partial differential equations are solved with the help of the homotopic analysis method. For the purpose of accuracy, the optimizing system parameters, convergence, and stability analysis of the analytical algorithm (CSA) were performed graphically. The velocity, temperature, and concentration flow are studied and shown graphically with the effect of system parameters such as Grashof number, Hartman number, Prandtl number, thermal radiation, Schmidt number, Eckert number, Deborah number, Brownian parameter, heat source parameter, thermophoresis parameter, and stretching parameter. Moreover, the consequence of system parameters on skin friction coefficient, Nusselt number, and Sherwood number is also examined graphically and discussed.

1. Introduction

Nanotechnology has gained potential consideration of researchers and scientists in recent times because of its fruitful engineering and industrials usages in various manufacturing units. Such applications contain magnetic cell division, vehicle cooling, fusion control, cryopreservation, silicone mirror, electronics cooling, delivery of drugs, and many more of its utilization. The nanofluid is a particular class of fluids suspended by small metallic particles whose size is up to. Furthermore, nanoparticles have a higher thermal conductivity to controlled significant enhancement due to the rate of heat transfer. In the last few years, Jeffrey fluid model is one of the subclasses of fluids that has increased wide attraction to the researchers [1,2,3,4,5,6,7,8,9,10]. Piswas et al. [11,12] have investigated mixed convective Jeffrey nanofluid flow in view of stretchable sheet surface with magnetic field effect and thermal radiation effects numerically by utilizing explicit finite difference method. Zin et al. [13] highlighted the effect of heat transfer features for unsteady hydromagnetic convective rotating Jeffrey fluids over a porous sheet. Further, the heat transfer analysis of a Jeffrey nanofluid was investigated by Zin et al. [14]. Ramzan et al. [15] evaluated Jeffrey nanofluid flow and the impacts of solutal stratification over an inclined flat stretching cylindrical surface together with heat absorption/generation/mechanism. A time-dependent Jeffrey convective fluid flow between two revolving cylinders was analyzed by Shifang et al. [16]. Dalir et al. [17] elucidated outcomes of entropy generation in magnetohydrodynamics Jeffrey non-Newtonian nanofluid past a permeable plane sheet analyzed and discussed. Moreover, the heat flow characteristics on Jeffrey fluid have been studied. Evaluations of the hydromagnetic and radiative nature of Jeffrey fluids over a stretching plane surface enclosure by a surface slip and melting heat were disclosed by Das et al. [18]. Srinivasa and Eswara [19] studied the consequence of heat generation or absorption on the free convection flow of an incompressible, electrically conducting fluid about an isothermal truncated cone in the presence of a transverse magnetic field. A numerical model is developed to investigates the influence of magnetohydrodynamics and heat mass transference effects of a Jeffrey fluid past by a stretching surface with chemical reaction, and thermal radiation analysis was analyzed by Narayana et al. [20]. Hayat et al. [21] discussed the influence of double stratified convective Jeffrey fluid flow due to inclined cylinder along with heat generation/absorption. Ijaz and Ayub [22] explored mixed convective Jeffrey fluid flow near axisymmetric stagnation point flow in view of a permeable angular cylinder with homogeneous-heterogeneous reactions are considered. Hayat et al. [23] studied boundary layer flow and heat transference effects in Jeffrey nanofluid flow with thermal conductivity, and radiation influence is taken to be temperature-dependent. Farooq et al. [24] analyzed the mutual effects of Joule heating and Newtonian heating in hydrodynamic Jeffrey fluid past by a stretching cylinder with a heat reservoir. Ghaffar et al. [25] have addressed a computational investigation of non-Newtonian viscoelastic incompressible fluid over a vertical flat surface with melting heat effects. Nanofluids are a new class of heat transfer liquids; the term nanofluid was invented by Choi [26] that contains a base fluid and nanosized material particles whose diameter less than 1–100 nm or fibers suspended in the ordinary base liquids. The nanoparticles are made of various materials. Buongiorno [27] proposed a nanofluid model to analyzed thermal conductivity and heat transfer features. Tiwari and Das [28] studied the effects of nanofluids numerically inside a two-sided lid-driven differentially heated square cavity to gain insight into convective recirculation and flow processes induced by a nanofluid. Babu et al. [29] analyzed multivariate Jeffrey fluid in view of a vertical permeable plate with hall current and evenly distributed magnetic effect. Moreover, the chemical reaction and generation of thermal radiation were evaluated. Selvi and Muthuraj [30] investigated MHD oscillatory Jeffrey convective flow in a vertical permeable channel with Joule heating and viscous dissipation. Turkyilmazoglu [31] pointed out the salient features of heat mass transmission effects on unsteady natural convection flow of nanofluids over a vertical plan surface with magnetic and radiation effects are disclosed. The effects of nanoparticles on the annular condensation flow of argon–copper nanofluids passing inside a microchannel were examined by ta molecular dynamic method by Ghahremanian et al. [32]. A numerical investigation was carried out to examine the Joule heating effect on magneto hydromagnetic flow and heat transfer effects on a Jeffrey fluid in view of a permeable stretching sheet with power-law heat flux and heat source by Babu and Narayana [33]. Khan et al. [34] examine the nanomaterials for the development of heat transfer and thermal conductivity features of non-Newtonian fluids. Muhammad et al. [35] examine magnetized Carreau nanofluid conveying microorganisms over a moving wedge with velocity slip and thermal radiation features. Khan et al. [36,37] investigate single- and double-layer wire coating analysis using Phan-Thien-Tanner (PTT) viscoelastic fluid as a coating material. Hayat et al. [38] investigated the consequences of the radiative nature of Jeffrey fluid past through an inclined heated stretching cylindrical sheet.

2. Problem Description

The present flow problem deal with the steady-state flow of non-Newtonian Jeffrey nanofluid owing to the heated vertical cylinder subjected to radiations effect, enclosure by a magnetic field of magnitude $B_0$. The cylinder has a radius $r_0$, whereas stretching velocity is defined as $U\left(x^{*}\right)=c_0{x}^{*}$. This flow is governed by the cylindrical coordinate $\left(x^{*},r^{*}\right)$ system. Herein, the impact of Joule heating is taken into account. Further, heat generation/absorption is also considered in the formulation of the flow problem. Flow configuration is shown in Figure 1.

Basic flow equations for considered flow problem defined as:

$$\frac{\partial u^{*}}{\partial x^{*}}+\frac{\partial v^{*}}{\partial r^{*}}=0$$

(1)

$$\begin{array}{l}\frac{\partial u^{*}}{\partial t^{*}}+u^{*}\left(\frac{\partial u^{*}}{\partial x^{*}}\right)+v^{*}\left(\frac{\partial u^{*}}{\partial r^{*}}\right)={\mathsf{\beta }}_T\mathrm{g}(T^{*}-T_{\infty }^{*})-u^{*}\left(\frac{\mathsf{\sigma }{B}_0^2}{\mathsf{\rho }}\right)+\\ \frac{\mathsf{\upsilon }}{1+\mathsf{\lambda }}\left(\frac{{\partial }^2{u}^{*}}{\partial r^{*}{}^2}+{\mathsf{\lambda }}^{*}\left(\frac{{\partial }^3{u}^{*}}{\partial r^{*}{}^2\partial t^{*}}+\frac{\partial v^{*}}{\partial r^{*}}\frac{{\partial }^2{u}^{*}}{\partial r^{*}{}^2}+v^{*}\frac{{\partial }^3{u}^{*}}{\partial r^{*}{}^3}+\frac{\partial u^{*}}{\partial r^{*}}\frac{{\partial }^2{u}^{*}}{\partial x^{*}\partial r^{*}}+u^{*}\frac{{\partial }^3{u}^{*}}{\partial x^{*}\partial r^{*}{}^2}\right)\right)\end{array},$$

(2)

$$\begin{array}{l}\frac{\partial T^{*}}{\partial t^{*}}+u^{*}\left(\frac{\partial T^{*}}{\partial x^{*}}\right)+v^{*}\left(\frac{\partial T^{*}}{\partial r^{*}}\right)=\alpha \left(\frac{{\partial }^2{T}^{*}}{\partial r^{*}{}^2}\right)+\left(\frac{16{\mathsf{\sigma }}^{*}{T}_0^{*3}}{3k^{*}\mathsf{\rho }{c}_p}\right)\frac{{\partial }^2{T}^{*}}{\partial r^{*}{}^2}+\frac{\mathsf{\sigma }{B}_0^2}{\mathsf{\rho }{c}_p}{u}^{*}{}^2+\\ \mathsf{\tau }\left(D_B\left(\frac{\partial T^{*}}{\partial r^{*}}\right)\left(\frac{\partial C^{*}}{\partial r^{*}}\right)+\frac{D_T}{T_0^{*}}{\left(\frac{\partial T^{*}}{\partial r^{*}}\right)}^2\right)+\left(\frac{Q_0}{\mathsf{\rho }{c}_p}\right)(T^{*}-T_{\infty }^{*})\end{array},$$

(3)

$$\frac{\partial C^{*}}{\partial t^{*}}+U^{*}\frac{\partial C^{*}}{\partial x^{*}}+V^{*}\frac{\partial C^{*}}{\partial r^{*}}=D_B\left(\frac{{\partial }^2{C}^{*}}{\partial r^{*2}}\right)+\frac{D_T}{T_{\infty }}\left(\frac{{\partial }^2{T}^{*}}{\partial r^{*2}}\right),$$

(4)

The signified conditions for the given problem as:

$$\left\{\begin{array}{l}{u}^{*}\left(0,x^{*},r^{*}\right)=0,v^{*}\left(0,x^{*},r^{*}\right)=0,T^{*}\left(0,x^{*},r^{*}\right)=T_{\infty }^{*},C^{*}\left(0,x^{*},r^{*}\right)=C_{\infty }^{*},\\ u^{*}\left(t^{*},0,r^{*}\right)=0,v^{*}\left(t^{*},0,r^{*}\right)=0,T^{*}\left(t^{*},0,r^{*}\right)=T_{\infty }^{*},C^{*}\left(t^{*},0,r^{*}\right)=C_{\infty }^{*},\\ u^{*}\left(t^{*},x^{*},r_0\right)=U\left(x^{*}\right)=c_0{x}^{*},v^{*}\left(t^{*},x^{*},r_0\right)=0,T^{*}\left(t^{*},x^{*},r_0\right)=T_{\infty }^{*},\\ C^{*}\left(t^{*},x^{*},r_0\right)=C_{\infty }^{*},\\ u^{*}\left(t^{*},x^{*},r^{*}\right)\to 0,\frac{\partial u^{*}}{\partial r^{*}}\to 0,v^{*}\left(t^{*},x^{*},r^{*}\right)\to 0,\\ T^{*}\left(t^{*},x^{*},r^{*}\right)\to T_{\infty }^{*},C^{*}\left(t^{*},x^{*},r^{*}\right)\to C_{\infty }^{*}for{r}^{*}\to \infty \end{array}\right\}.$$

(5)

Herein $\left(u^{*},v^{*}\right)$ are shown velocity components in $x^{*}\mathrm{and}{r}^{*}$ directions, respectively.

$\left(\mathsf{\rho }\right)$, fluid density, $\left({\mathsf{\beta }}_T\right)$, represent thermal expansion, $\left(\mathrm{g}\right)$, acceleration due gravity, $\left(\alpha =\frac{k}{\mathsf{\rho }{c}_p}\right)$, thermal diffusibility, $\left(D_T\right)$, coefficient of thermophoretic diffusion, $\left(\mathsf{\sigma }\right)$, denote the fluid conducting nature, $\left(c_p\right)$, denote fluid specific heat, $\left(T_{\infty }^{*}\right)$, ambient temperature, $\left({\mathsf{\sigma }}^{*}\right)$, Stefan–Boltzmann constant, $\left(T_w^{*}\right)$, surface temperature, (μ), viscosity, $\left(\mathsf{\lambda }\right)$, relaxation and retardation times ratio, $\left(k\right)$, denote thermal conductivity, $\left({\mathsf{\lambda }}^{*}\right)$, retardation time, $\left(B_0\right)$, magnetic field, $\left(k^{*}\right)$, coefficient of mean absorption, $\left(T^{*}\right)$, temperature, (τ), the ratio of heat capacities, $\left(D_B\right)$, Brownian diffusion and $\left(Q_0\right)$, heat absorption/generation coefficient, (ν),Transformation variable, (d), Positive constant number.

By incorporating the following similarity variables given in Equation (6):

$$x=\frac{x^{*}}{r_0},r=\frac{r^{*}}{r_0},U=\frac{u^{*}{r}_0}{\upsilon },V=\frac{v^{*}{r}_0}{\upsilon },t=\frac{t^{*}\upsilon }{r_0^2},T=\frac{T^{*}-T_{\infty }^{*}}{T_w^{*}-T_{\infty }^{*}},C=\frac{C^{*}-C_{\infty }^{*}}{C_w^{*}-C_{\infty }^{*}}.$$

(6)

After utilizing the transformation variables in Equations (1)–(5), we get the dimensionless form as given below:

Dimensionless continuity, momentum, energy and concentration equations defined in Equations (7)–(10):

$$\frac{\partial U}{\partial x}+\frac{\partial V}{\partial r}=0,$$

(7)

$$\begin{array}{l}\frac{\partial U}{\partial t}+U\left(\frac{\partial U}{\partial x}\right)+V\left(\frac{\partial U}{\partial r}\right)=T\mathrm{Gr}-{\left(\mathrm{Ha}\right)}^2+\\ \frac{1}{\left(1+\mathsf{\lambda }\right)}\left(\frac{{\partial }^{2}U}{\partial r^2}+\mathsf{\beta }\left(\frac{{\partial }^{3}U}{\partial r^2\partial t}+\frac{\partial V}{\partial r}\frac{{\partial }^{2}U}{\partial r^2}+V\frac{{\partial }^{3}U}{\partial r^3}+\frac{\partial U}{\partial r}\frac{{\partial }^{2}U}{\partial x\partial r}+U\frac{{\partial }^{3}U}{\partial x\partial r^2}\right)\right)\end{array},$$

(8)

$$\frac{\partial T}{\partial t}+U\frac{\partial T}{\partial x}+V\frac{\partial T}{\partial r}=\mathrm{Pr}\left(\frac{{\partial }^{2}T}{\partial r^2}\right)+\left(\frac{Tr}{\mathrm{Pr}}\right)\left(\frac{{\partial }^{2}T}{\partial r^2}\right)+\mathrm{Ec}{\left(\mathrm{Ha}\right)}^{2}U+N_b\left(\frac{\partial T}{\partial r}\right)\left(\frac{\partial C}{\partial r}\right)+N_t\left(\frac{\partial T}{\partial r}\right)+{\mathsf{\beta }}_{1}T,$$

(9)

$$\frac{\partial C}{\partial t}+U\frac{\partial C}{\partial x}+V\frac{\partial C}{\partial r}=\left(\frac{1}{\mathrm{Sc}}\right)\left(\frac{{\partial }^{2}C}{\partial r^2}\right)+\left(\frac{N_t}{N_b}\right)\left(\frac{{\partial }^{2}T}{\partial r^2}\right),$$

(10)

Following are the governing variables appearing in Equations (8)–(10) are defined as follows:

$\mathrm{Gr}=\left(\frac{{\mathrm{g}\mathsf{\beta }}_T{r}_0^3\left(T_w^{*}-T_{\infty }^{*}\right)}{{\mathsf{\upsilon }}^2}\right)$, $\mathrm{Ec}=\left(\frac{{\upsilon }^2}{c_p{r}_0^2\left(T_w^{*}-T_{\infty }^{*}\right)}\right)$, $Tr=\left(\frac{16{\mathsf{\sigma }}^{*}{T}_{\infty }^{*3}}{3k^{*}k}\right)$, $\mathrm{Pr}=\left(\frac{\mathsf{\rho }{c}_p\mathsf{\upsilon }}{k}\right)$, $\mathrm{Ha}=\left(r_0{B}_0\sqrt{\frac{\mathsf{\sigma }}{\mathsf{\rho }\mathsf{\upsilon }}}\right)$, $\mathsf{\beta }=\left(\frac{{\mathsf{\lambda }}^{*}\mathsf{\upsilon }}{r_0^2}\right)$, $N_t=\left(\frac{\mathsf{\tau }{D}_T\left(T_w-T_{\infty }\right)}{T_{\infty }\mathsf{\upsilon }}\right)$, $N_b=\left(\frac{\mathsf{\tau }{D}_B\left(C_w-C_{\infty }\right)}{\mathsf{\upsilon }}\right)$, ${\mathsf{\beta }}_1=\left(\frac{r_0^2{Q}_0}{\mathsf{\upsilon }\mathsf{\rho }{c}_p}\right)$, $A_0=\left(\frac{r_0^2{c}_0}{\mathsf{\upsilon }}\right)$, $\mathrm{Sc}=\left(\frac{\upsilon }{D_B}\right)$, explains Grashof number, Eckert number, radiation factor, Prandtl number, magnetic parameter, Deborah number, thermophoresis, Brownian parameter, heat source parameter, stretching parameter and Schmidt number, respectively.

Transformed conditions are defined by:

$$\left\{\begin{array}{l}U\left(0,x,r\right)=0,V\left(0,x,r\right)=0,T\left(0,x,r\right)=0,C\left(0,x,r\right)=0,\\ U\left(t,0,r\right)=0,V\left(t,0,r\right)=0,T\left(t,0,r\right)=0,C\left(t,0,r\right)=0,\\ U\left(t,x,1\right)=A_{0}x,V\left(t,x,1\right)=0,T\left(t,x,1\right)=1,C\left(t,x,1\right)=1,\\ U\left(t,x,r\right)\to 0,\frac{\partial u\left(t,x,r\right)}{\partial r}\to 0,V\left(t,x,r\right)\to 0,\\ T\left(t,x,r\right)\to 0,C\left(t,x,r\right)\to 0\mathrm{for}r\to \infty \end{array}\right\}.$$

(11)

Expressions of physical quantities of interest are $\left(N{u}_x,S{h}_x\right)$ given in Equation (12):

$$N{u}_x=\frac{r_0{q}_w}{k\left(T_w^{*}-T_{\infty }^{*}\right)},S{h}_x=\frac{x^{*}{q}_m}{d\left(C_w^{*}-C_{\infty }^{*}\right)}.$$

(12)

Whereas wall heat $\left(q_w\right)$ and mass flux $\left(q_m\right)$ defined in Equations (13) and (14):

$$q_w=-k\left(1+\frac{16{\mathsf{\sigma }}^{*}{T}_0^{*3}}{3k^{*}k}\right){\frac{\partial T^{*}}{\partial r^{*}}|}_{\mathrm{at}{r}^{*}=r_0},$$

(13)

$$q_m=-d{\frac{\partial C^{*}}{\partial r^{*}}|}_{\mathrm{at}{r}^{*}=r_0}.$$

(14)

In light of Equations (12) and (13), we obtained as follows:

$$N{u}_x=-\left(1+Tr\right){\frac{\partial T}{\partial r}|}_{\mathrm{at}r=1},$$

(15)

$$S{h}_x=-{\frac{\partial C}{\partial r}|}_{\mathrm{at}r=1}.$$

(16)

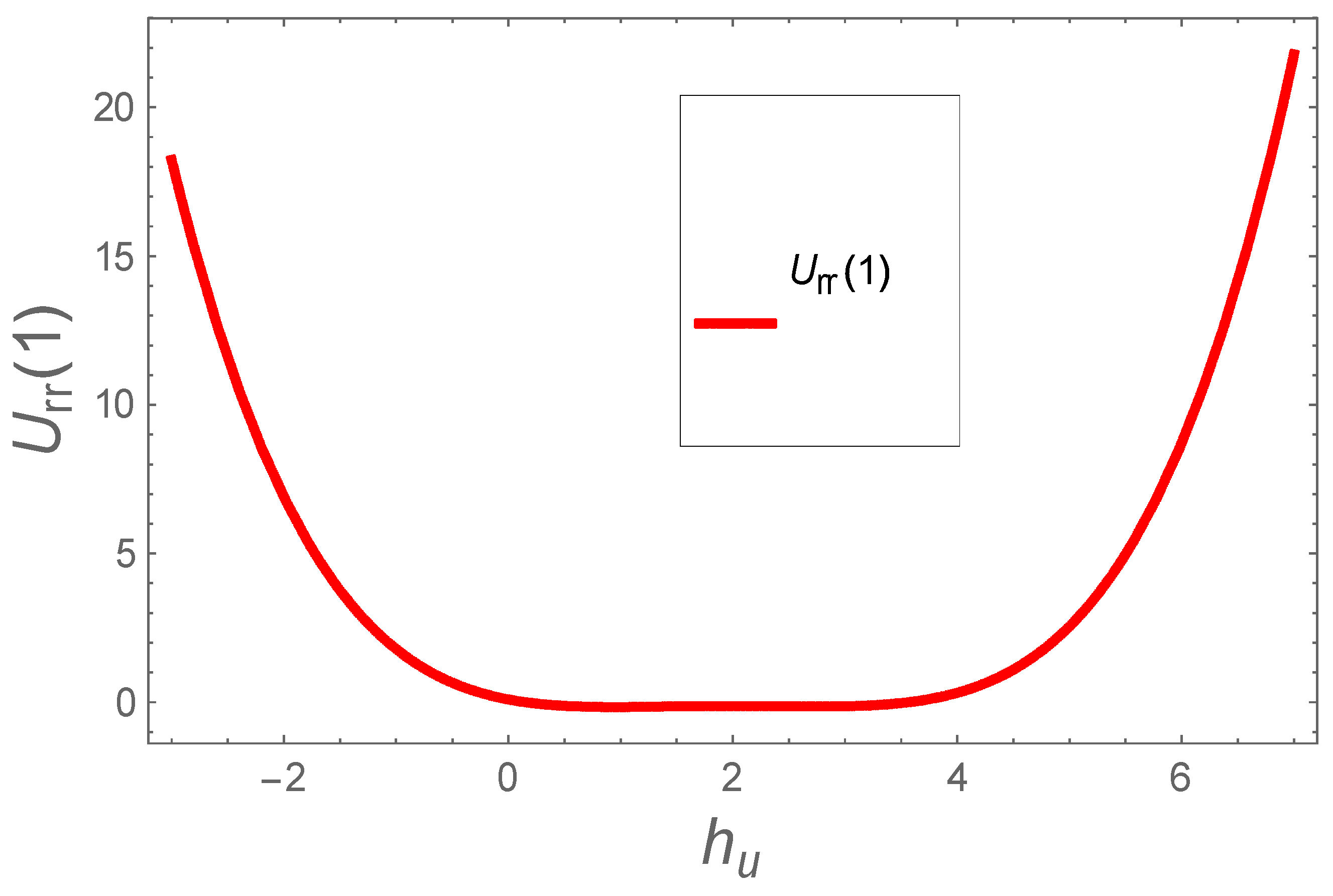
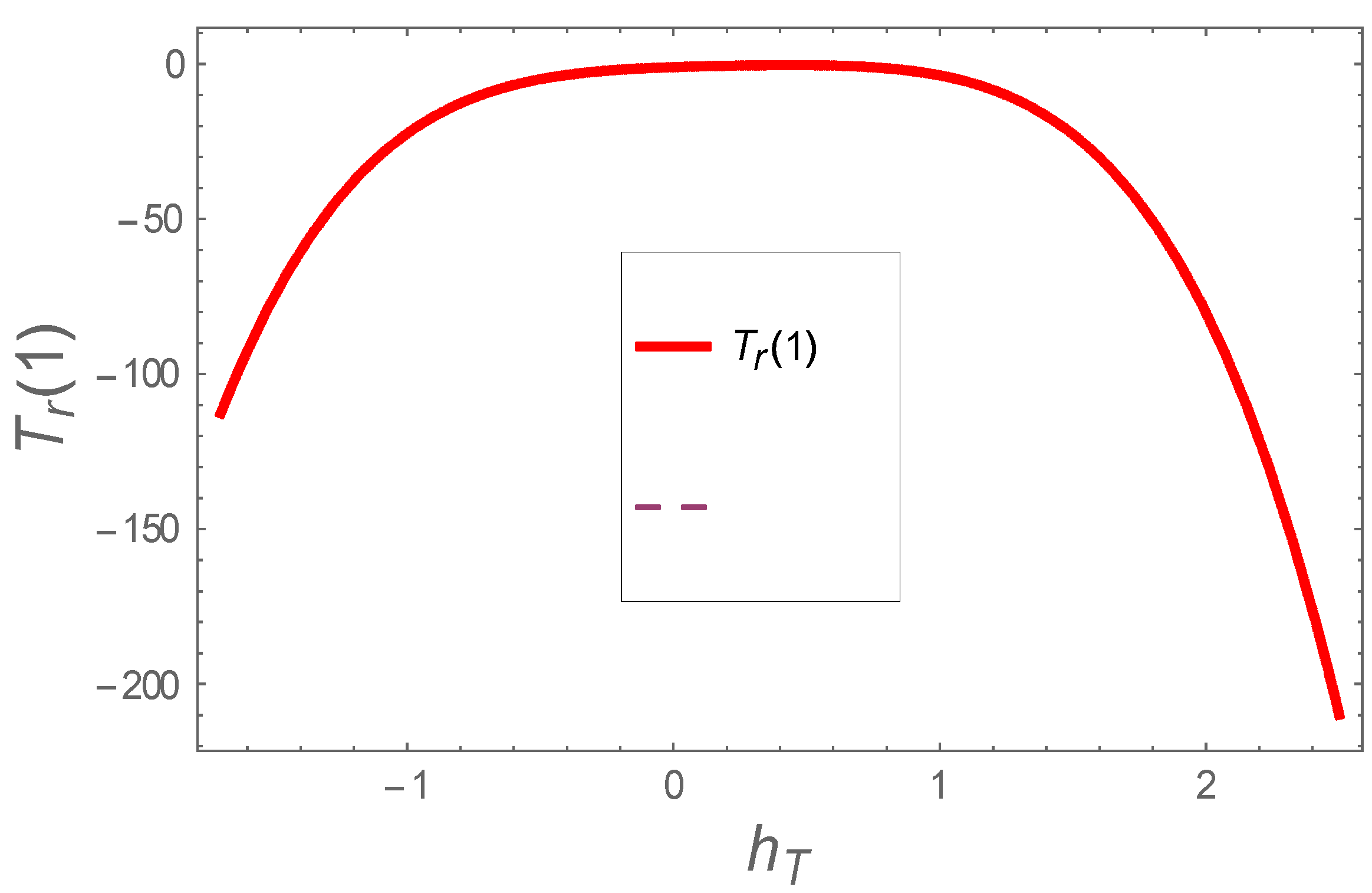
3. Simulations and Convergence Analysis

The analytical homotopic analysis method/technique is a computational algorithm mostly utilized to obtained convergence solutions of highly nonlinear ordinary/partial differential equations. For convergence solutions of Equations (8)–(10), we employed the HAM algorithm. Following are the unique distinctions of this algorithm. A detailed description can be found in [39,40,41].

• This algorithm is self-determining of any larger/smaller change;
• The convergence analysis of the established systems can be authenticated smoothly;
• Further, this algorithm delivers additional ordinary authentication to choose guess functions with linear operators.

The $\hslash —\mathrm{curves}$, in homotopic analysis method, play a vital for convergence criteria for the nonlinear flow equations given in Equations (8)–(10). For that purpose, we unveiled $\hslash —\mathrm{curves}$ in Figure 2, Figure 3 and Figure 4. The parallel parts in these figures signify the acceptable approximations of variables ${\hslash }_U$, ${\hslash }_T$ and ${\hslash }_C$. We noticed that $0.5\le {\hslash }_C\le 3.5$, $-0.5\le {\hslash }_T\le 0.5$ and $0.0\le {\hslash }_C\le 0.2$.

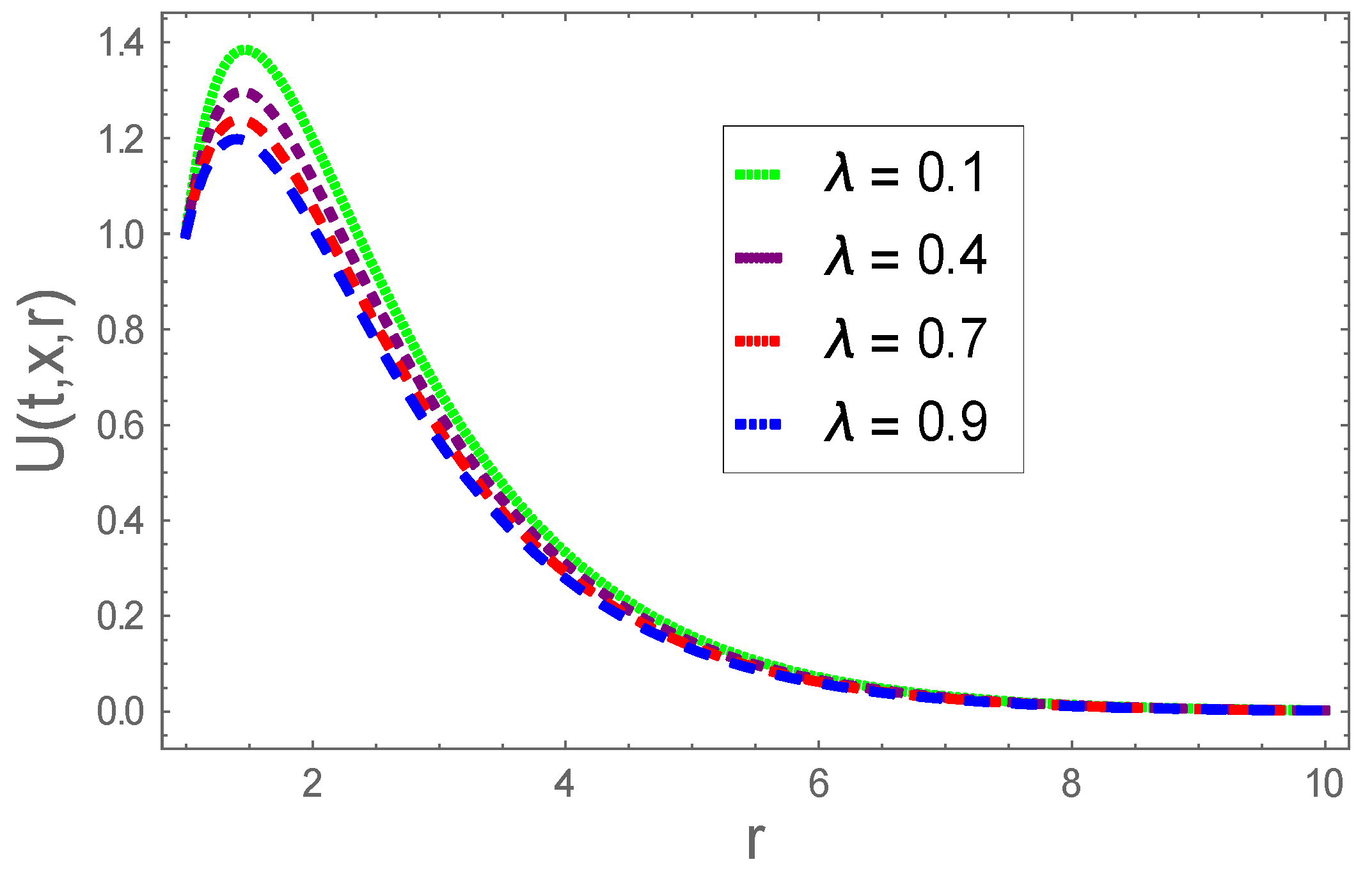
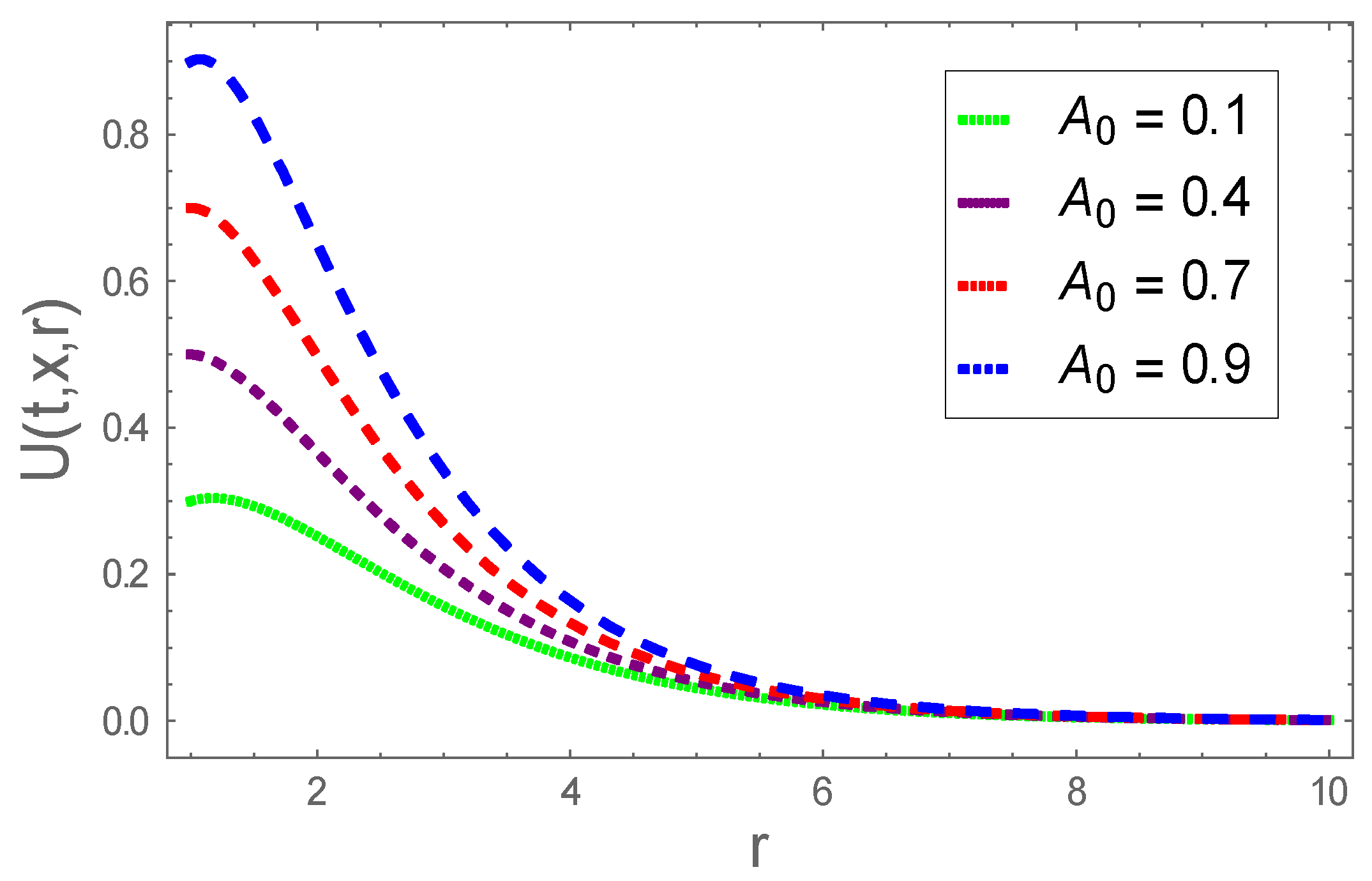
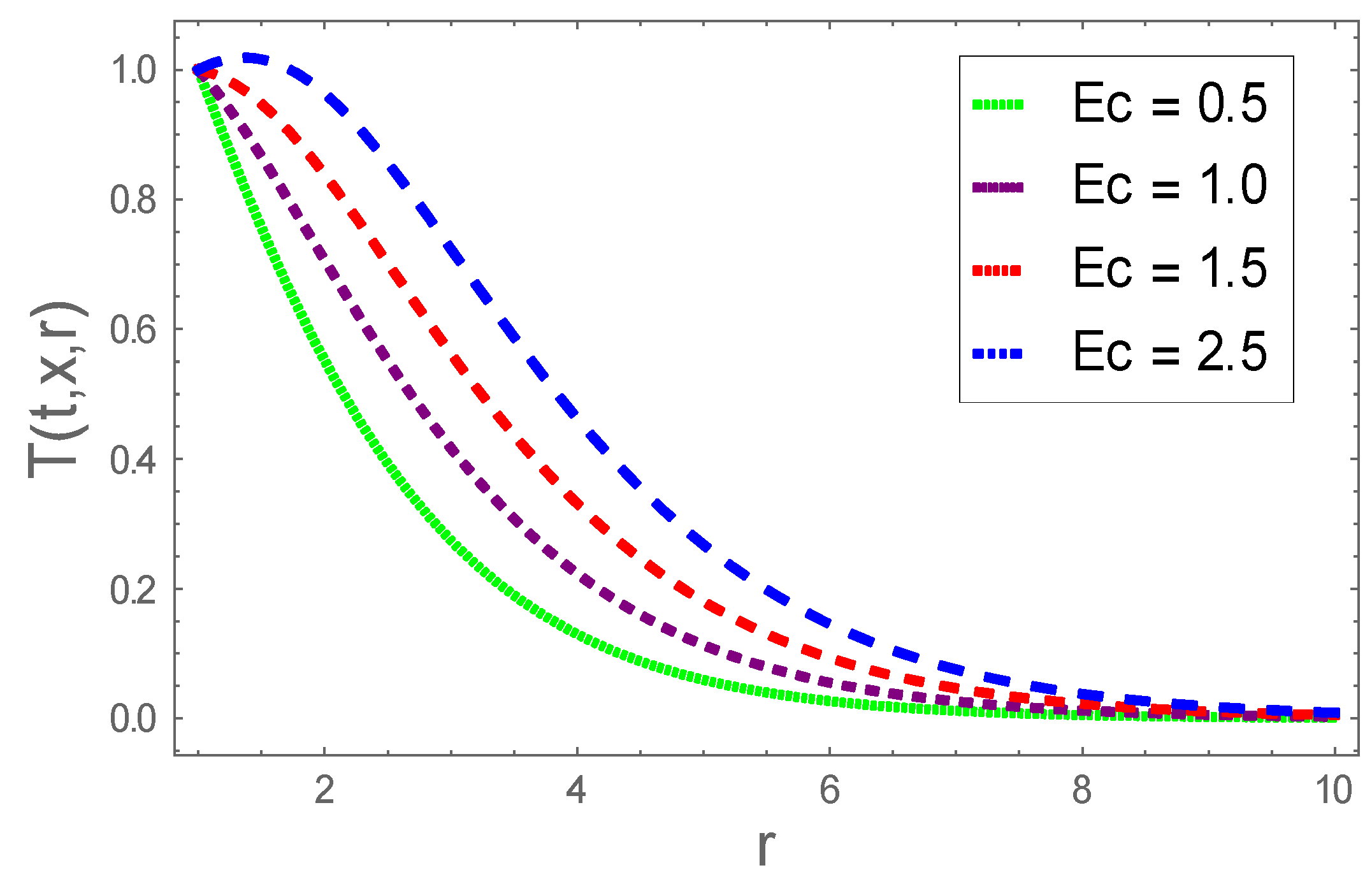
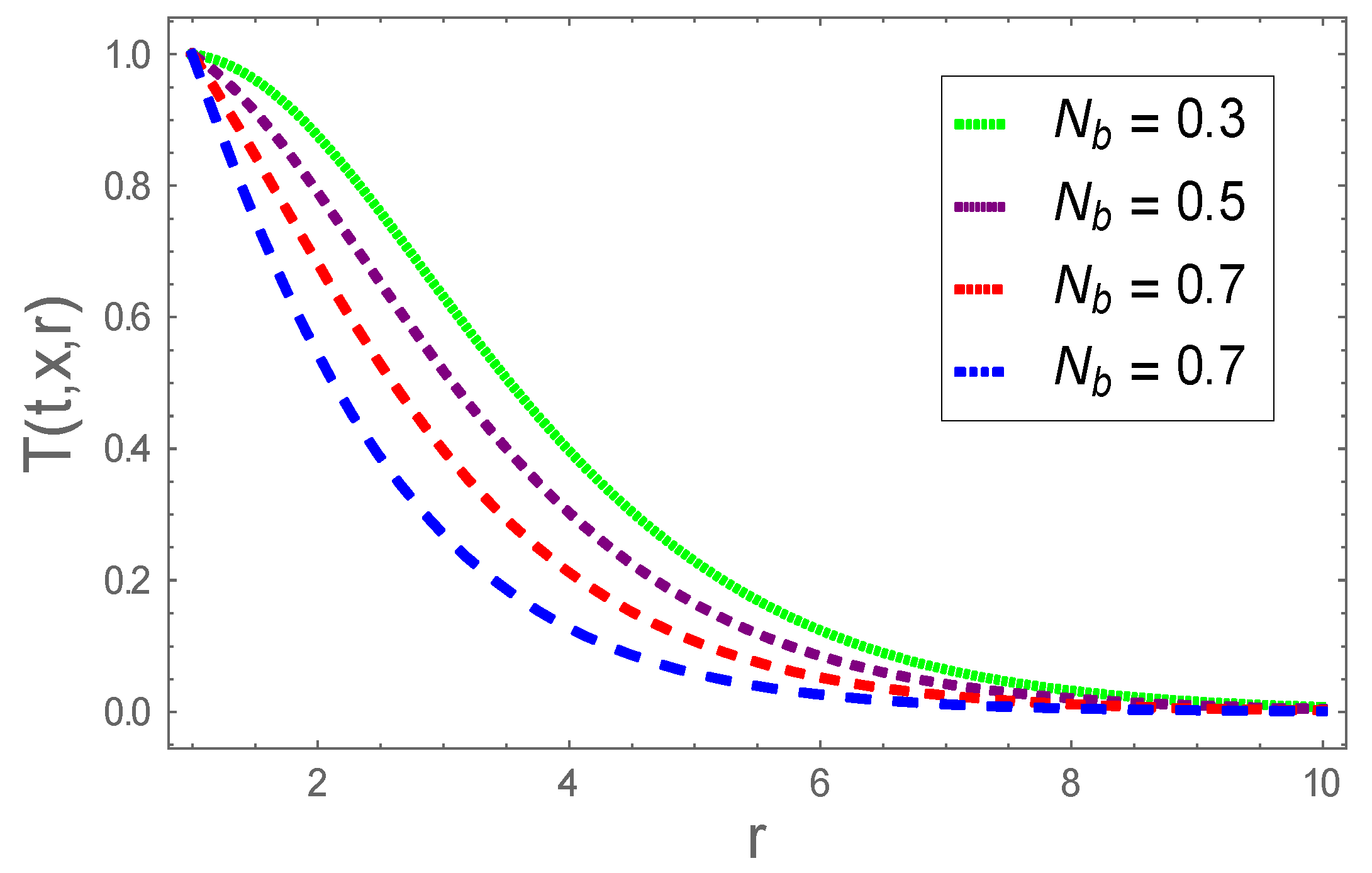
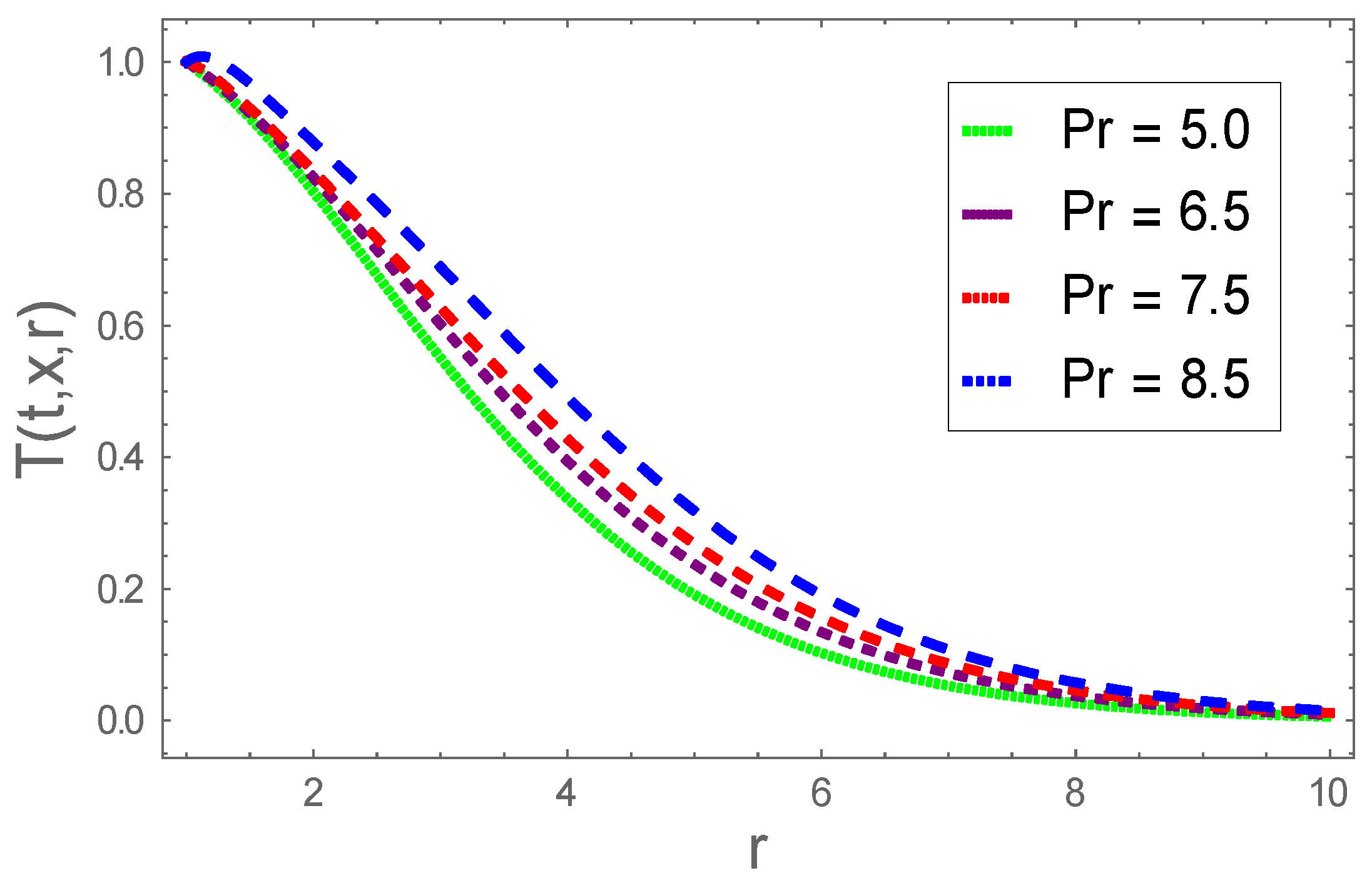
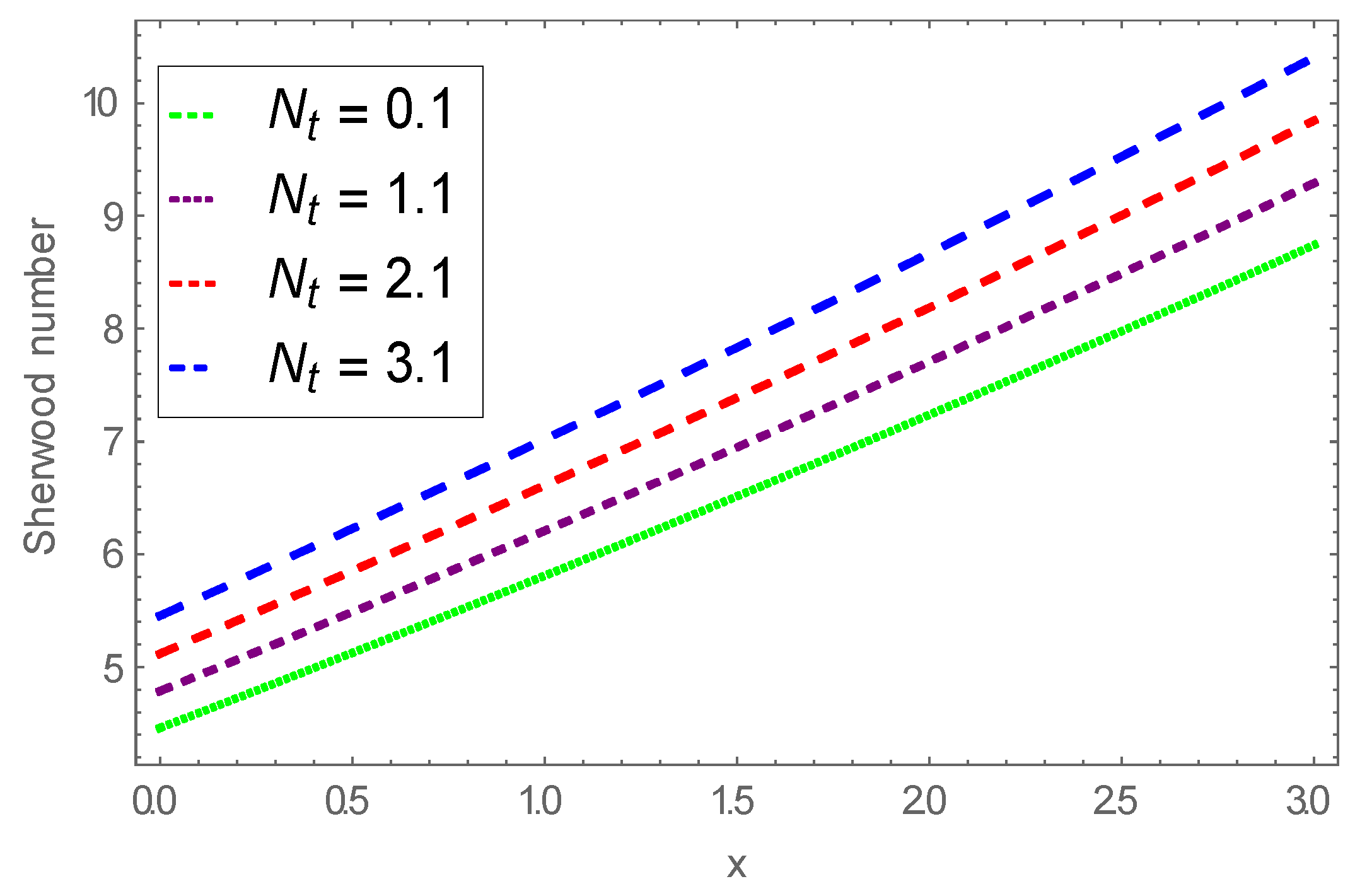
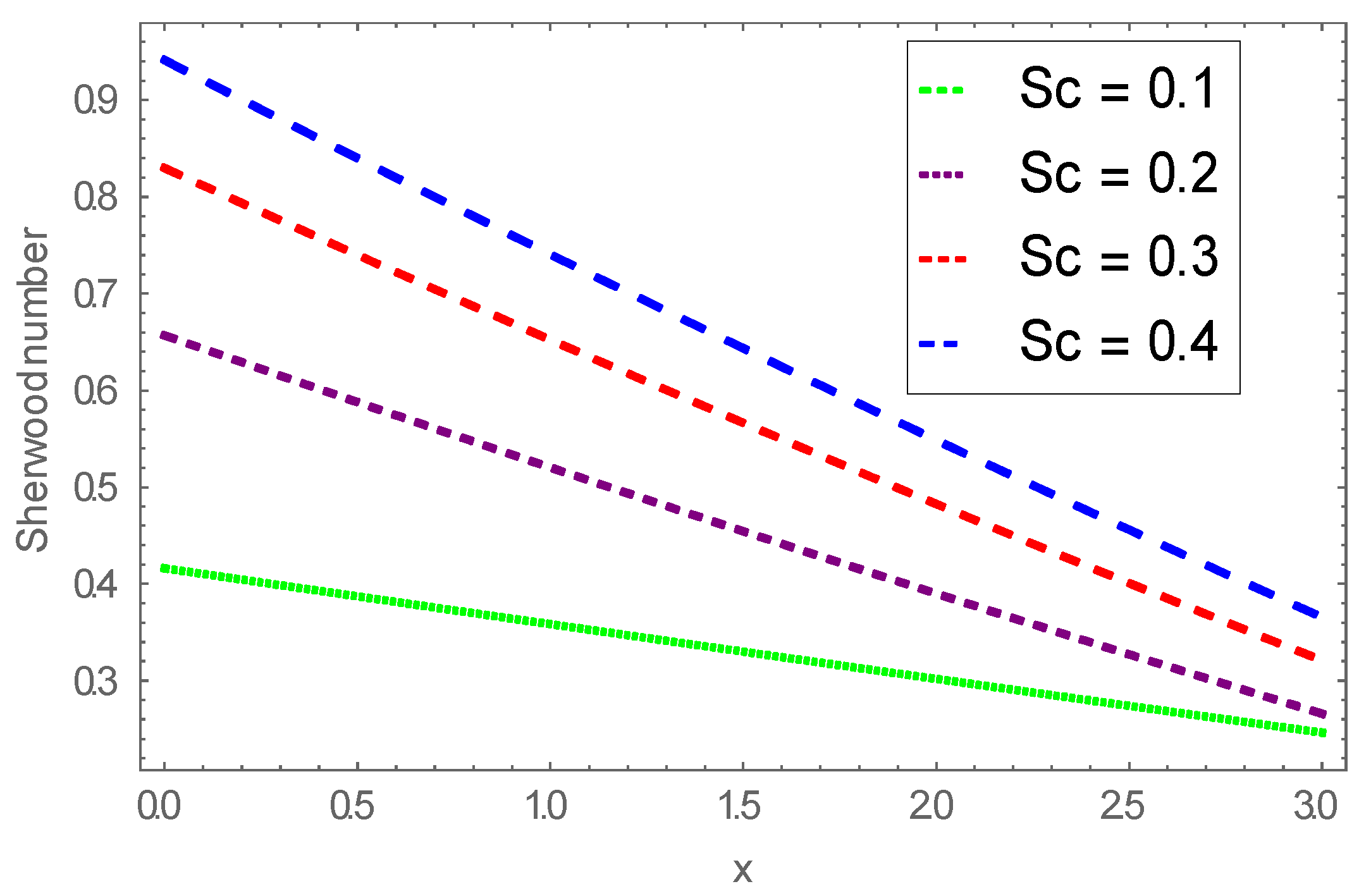
4. Graphical Results and Analysis

In this segment, we considered the set of nonlinear differential flow laws given in Equations (8)–(10) subject to boundary conditions in Equation (11) are solved by employing an analytical algorithm called homotopic analysis method (HAM). This is a multipurpose computational algorithm mostly employed for highly nonlinear problems in modern scientific analysis, which includes various problems in mass heat transfer, electrical systems, engineering and many other scientific fields. The salient features $\mathrm{Gr},\mathrm{Ha},\mathrm{Ec},{\mathsf{\beta },\mathsf{\beta }}_1,\mathsf{\lambda },N_b,\mathrm{Sc},A_0,N_t\mathrm{and}\mathrm{Pr}$ against the Nusselt number $\left(N{u}_x\right)$, velocity $U\left(t,x,r\right)$, thermal distribution $T\left(t,x,r\right)$, the Sherwood number $\left(S{h}_x\right)$ and solutal distribution $C\left(t,x,r\right)$ are explained in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23.

Figure 5 depicts variations in the velocity $U\left(t,x,r\right)$ profile subjected to Grashof number $\left(\mathrm{Gr}\right)$. This figure discloses the direct relation of $\left(\mathrm{Gr}\right)$ with the bouncy force. As the anticipated velocity $U\left(t,x,r\right)$ rises, subject to increment in $\left(\mathrm{Gr}\right)$. The attributes of $\left(\mathrm{Ha}\right)$ on $U\left(t,x,r\right)$ are disclosed in Figure 6. As clearly, reported in this graph that the Hartmann number is directly linked with the Lorentz force greater the magnitude of the $\left(\mathrm{Ha}\right)$ produces more resistance to fluid flow due to which velocity profile shown decreasing behavior. The attributes of $\left(\mathsf{\lambda }\right)$ are exposed in Figure 7. Here, we noticed that lower $U\left(t,x,r\right)$ velocity subject to increment in $\left(\mathsf{\lambda }\right)$. Figure 8 depicts variations in velocity $U\left(t,x,r\right)$ profile subjected to stretching parameter $\left(A_0\right)$. This figure discloses $U\left(t,x,r\right)$ augmentation for higher values of $\left(A_0\right)$. Figure 9 depicts variations in velocity profile $U\left(t,x,r\right)$ subjected to Deborah number $\left(\mathsf{\beta }\right)$ This figure unveils $U\left(t,x,r\right)$ augmented for higher $\left(\mathsf{\beta }\right)$. It was noticed that lower $\left(\mathsf{\beta }\right)$, material acts in a more fluid-like way, with an associated Newtonian fluid. In contrast, larger $\left(\mathsf{\beta }\right)$, material behavior as a non-Newtonian regime, gradually dominated by elasticity and demonstrating solid-like behavior. The thermal field $T\left(t,x,r\right)$ curves for the heat-source parameter $\left({\mathsf{\beta }}_1\right)$ are unveiled in Figure 10. One can observe that temperature $T\left(t,x,r\right)$ distribution is a growing function of $\left({\mathsf{\beta }}_1\right)$. Figure 11 elucidates the consequence of Eckert’s number $\left(\mathrm{Ec}\right)$ on $T\left(t,x,r\right)$ temperature distribution. As anticipated, that $T\left(t,x,r\right)$ upsurges subject to increment in $\left(\mathrm{Ec}\right)$. The input of $\left(N_b\right)$ on $T\left(t,x,r\right)$ is evaluated through Figure 12. The temperature distribution diminishes when Brownian motion $\left(N_b\right)$ upsurges. Hence, $T\left(t,x,r\right)$ dwindles. Figure 13 delineates the thermophoresis $\left(N_t\right)$ parameter effect against temperature $T\left(t,x,r\right)$. Hence, an increase in $\left(N_t\right)$ consequently $T\left(t,x,r\right)$ escalates fluid temperature. The contribution of $\left(\mathrm{Pr}\right)$ on $T\left(t,x,r\right)$ was evaluated through Figure 14. Thermal boundary layer diffusivity upsurges when $\left(\mathrm{Pr}\right)$ augmented. Hence, Prandtl number enhances the temperature $T\left(t,x,r\right)$ boundary layer. The attributes of $\left(N_b\right)$ and $\left(N_t\right)$ effects $U\left(t,x,r\right)$ are delineated in Figure 15 and Figure 16. These figures confirm that concentration $C\left(t,x,r\right)$ profile diminishes subject to large values $\left(N_b\right)$, while the reverse effect is are found in $U\left(t,x,r\right)$ profile when $\left(N_t\right)$ thermophoresis enlarged. The contributions of the Schmidt number $\left(\mathrm{Sc}\right)$ on the concentration $U\left(t,x,r\right)$ profile are analyzed in Figure 17. As (Sc) is delineated as the ratio of kinematic viscosity to mass diffusivity, it is perceived as boosting through larger (Sc). Consequently, escalates fluid viscosity, due to which decaying in $U\left(t,x,r\right)$ noticed.

Figure 18, Figure 19 and Figure 20 highlight $\left(N_b\right)$, $\left(N_t\right)$ and $\left(\mathrm{Ha}\right)$ impact on $\left(N{u}_x\right)$. Here, in Figure 18 $\left(N{u}_x\right)$ diminishes as $\left(N_b\right)$. However, it is perceived that dimensionless heat transfer rate enhances boots through larger $\left(N_t\right)$ and $\left(\mathrm{Ha}\right)$. Figure 19 and Figure 20 reports the effects of $\left(N_b\right)$ and $\left(N_t\right)$ against $\left(N{u}_x\right)$. As anticipated, $\left(N{u}_x\right)$ enhances for large $\left(N_b\right)$ and $\left(N_t\right)$. The attributes of $\left(N_b\right)$, $\left(N_t\right)$ and $\left(\mathrm{Sc}\right)$ are disclosed in Figure 21, Figure 22 and Figure 23 against $\left(S{h}_x\right)$. Clearly noticed that in Figure 21 $\left(S{h}_x\right)$ diminishes for escalating values of $\left(N_b\right)$ and reverse behavior are found for $\left(N_t\right)$ and $\left(\mathrm{Sc}\right)$ displayed in Figure 22 and Figure 23.

5. Conclusions

In this investigation, we carried out attributes of the convective flow of a Jeffrey nanofluid with the vertical stretching plane surface by incorporating magnetic influence. The frequent engineering utilizations in designing several engineering products, cooling processes and many other fields. The non-Newtonian Jeffrey nanofluid gained a serious attraction of researchers to analyzed Jeffrey fluid with different aspects and geometry. The constitutive nonlinear PDEs for mass conservation, momentum and energy are changed to dimensionless form by utilizing appropriate set transformation variables. Further, these equations are solved with an efficient and validated algorithm analytically. This investigation gives valuable scope to researchers and engineers who deal with different non-Newtonian nanofluids. Significant outcomes of this work are:

• It is pointed out that both Grashof number and heat source parameter escalating velocity profile;
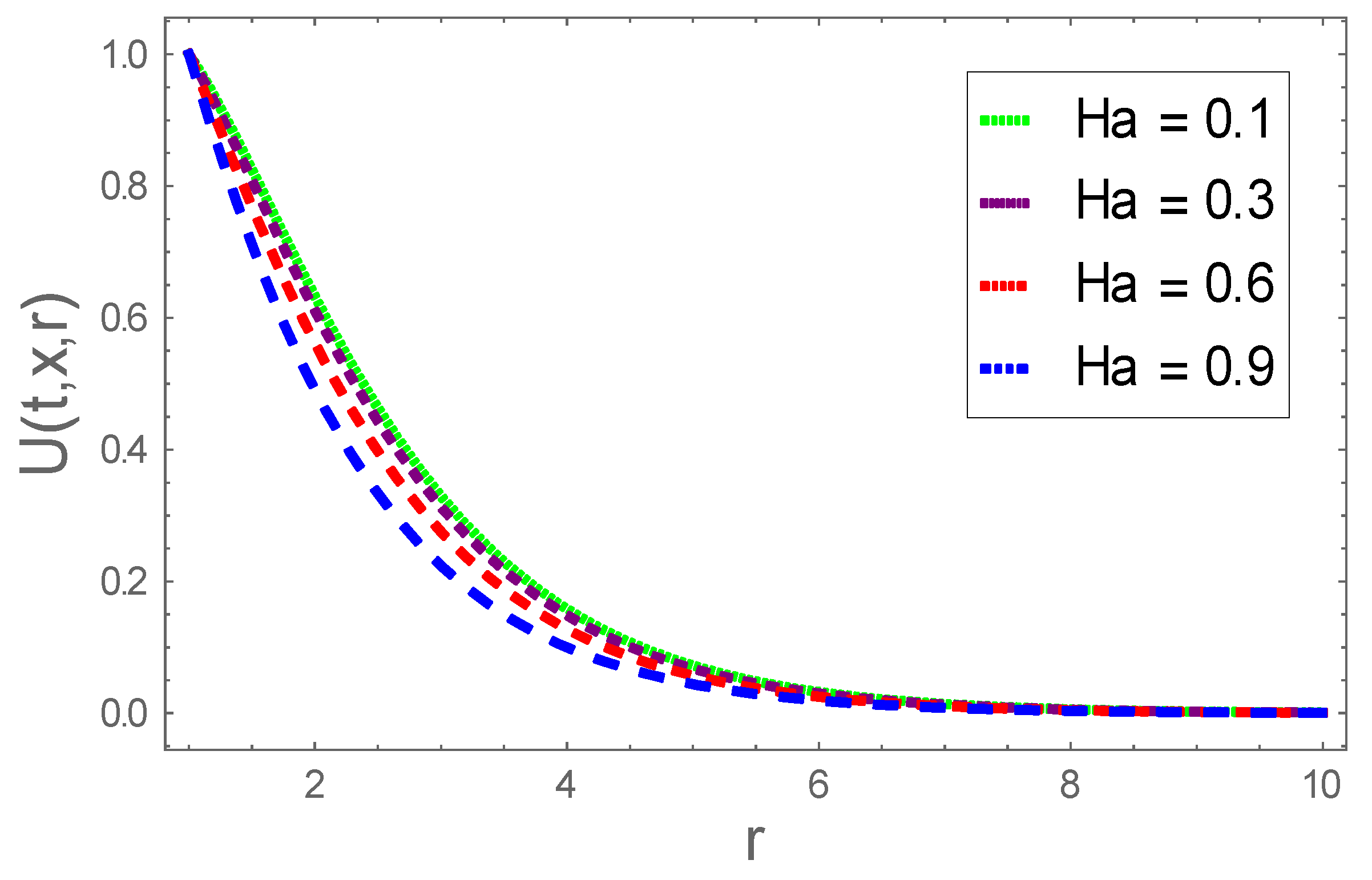
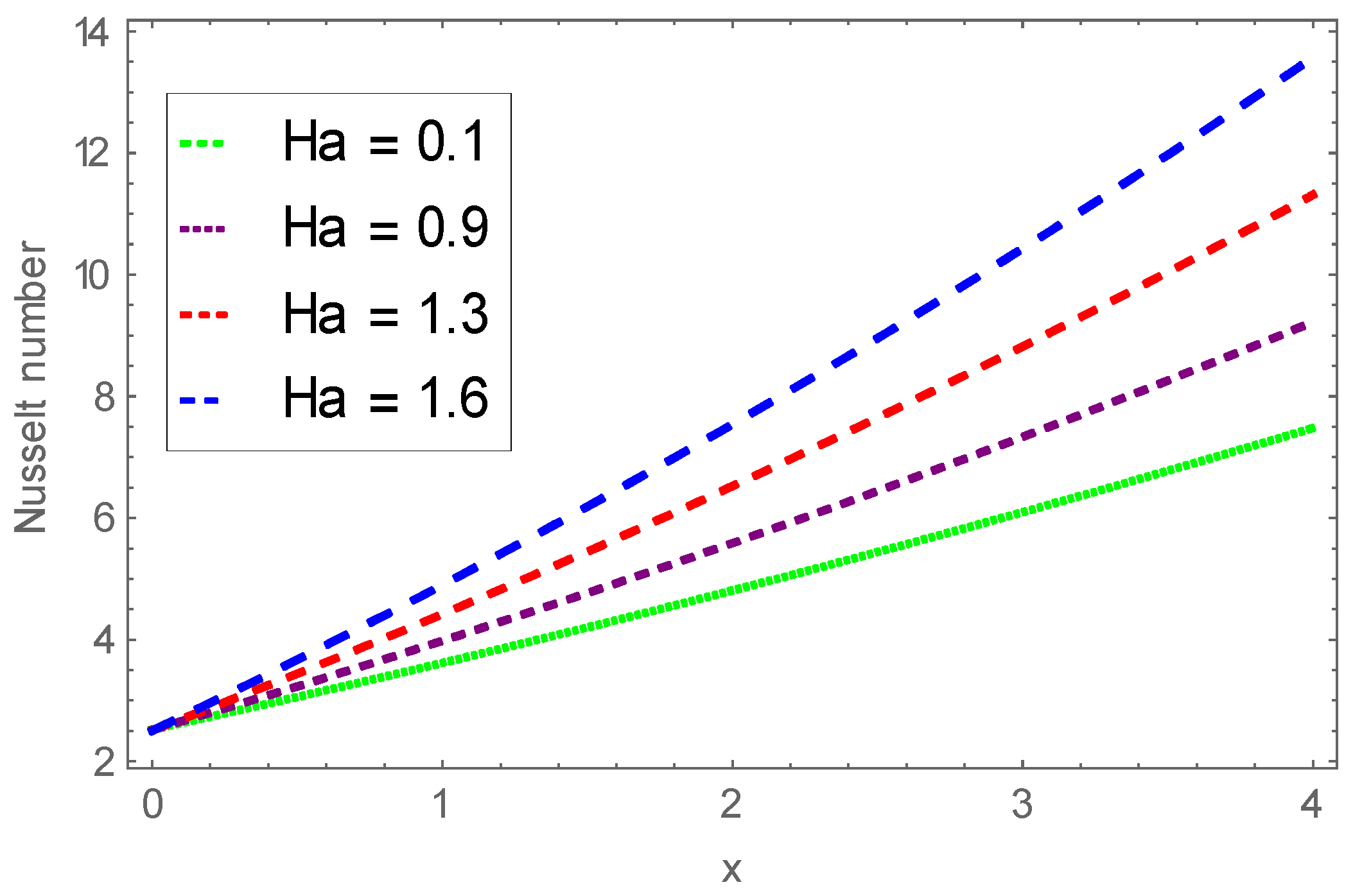
• Velocity profile diminished for larger Hartmann number;
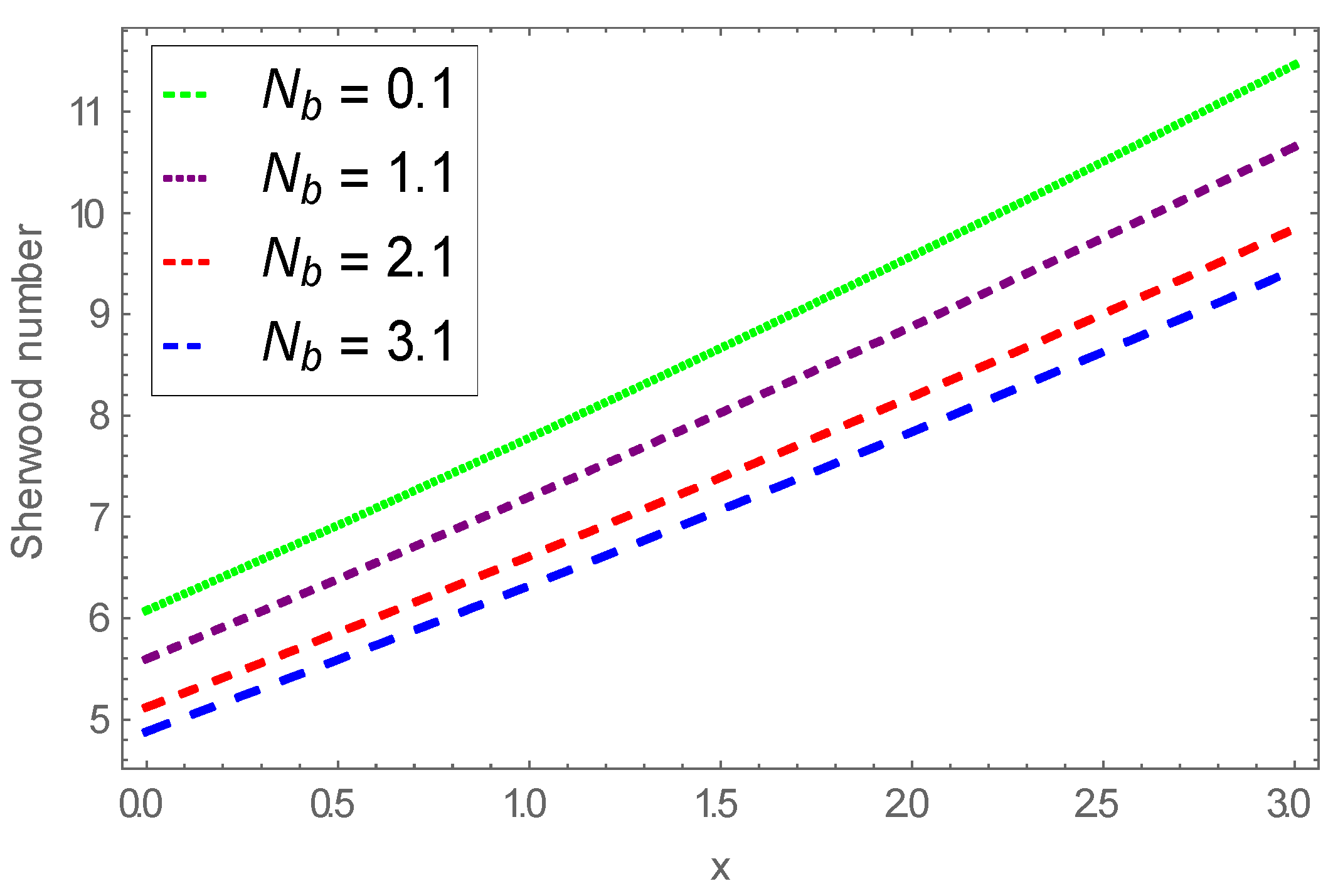
• The thermal field augmented as Eckert number and thermophoresis enhanced and diminished for larger Brownian motion parameter;
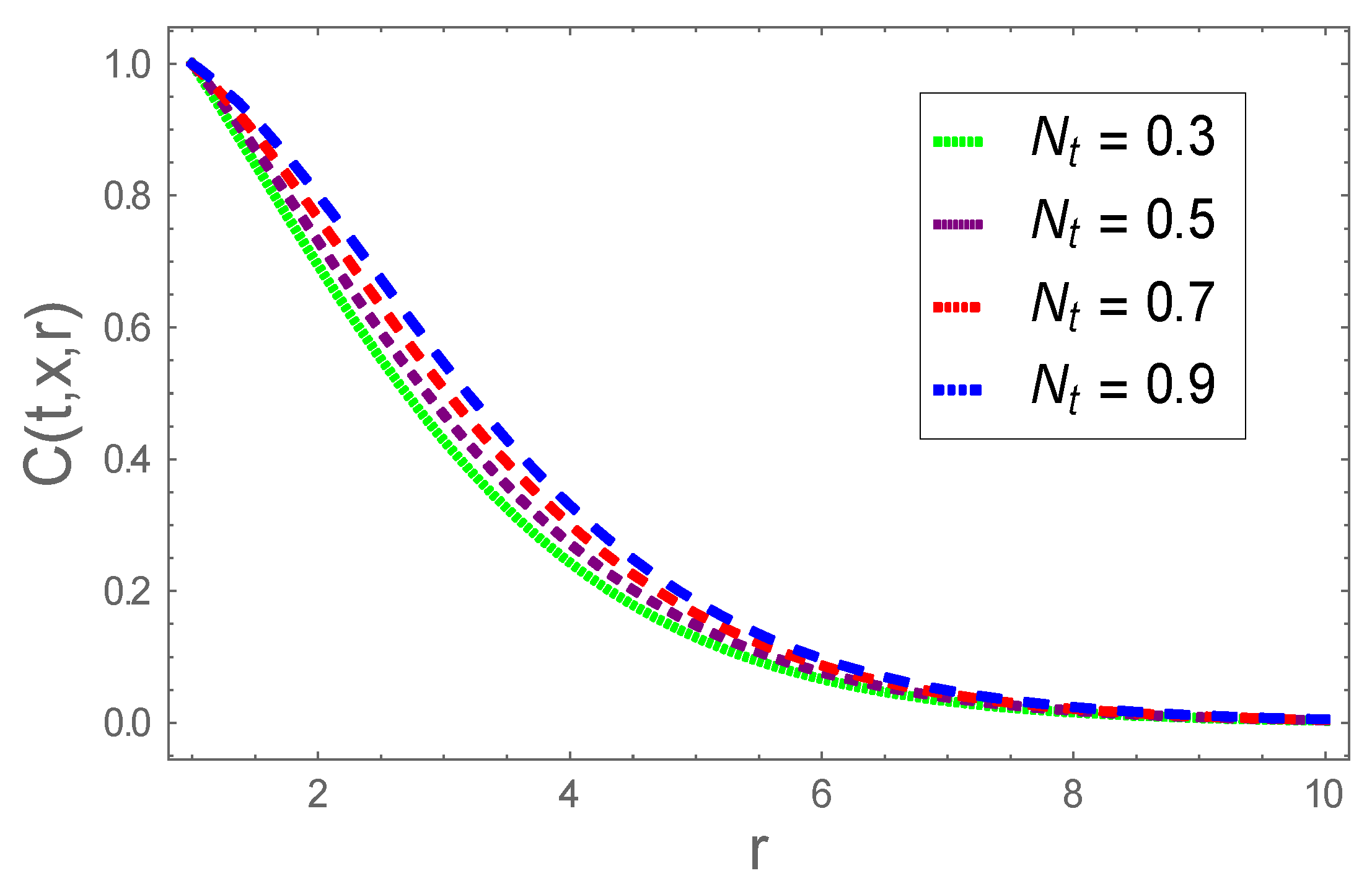
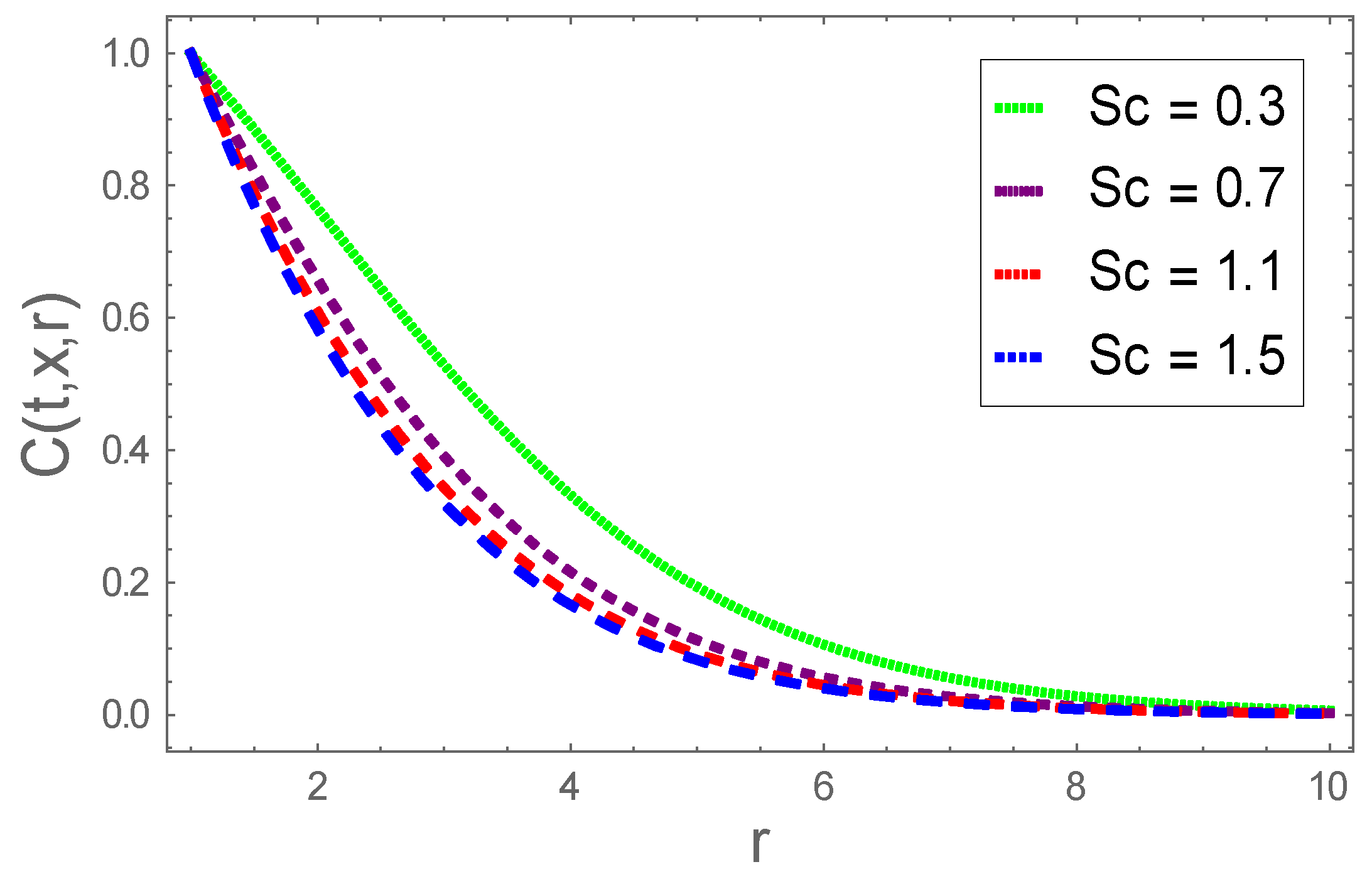
• We found a lower concentration profile subject to a larger Schmidt number; however, a reverse trend is found for the thermophoresis parameter;
• Momentum and thermal boundary layers are extensively affected by the resistive Lorentz force; therefore, this resistive force effectively controls the momentum boundary layer of Jeffrey nanofluid;
• Undergoing investigations are fruitful for designing heat exchanger equipment and metallurgical processes.