Optimal Data Processing Method for the Application of Eu3+ Photoluminescence Piezospectroscopy in Thermal Barrier Coatings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Calibration Experiments
2.3. Numerical Experiments
3. Model and Methods
3.1. The Theoretical Model of Eu3+ Photoluminescence Piezospectroscopy
3.2. Data Processing Methods
4. Results and Discussion
4.1. Results of the Numerical Experiments
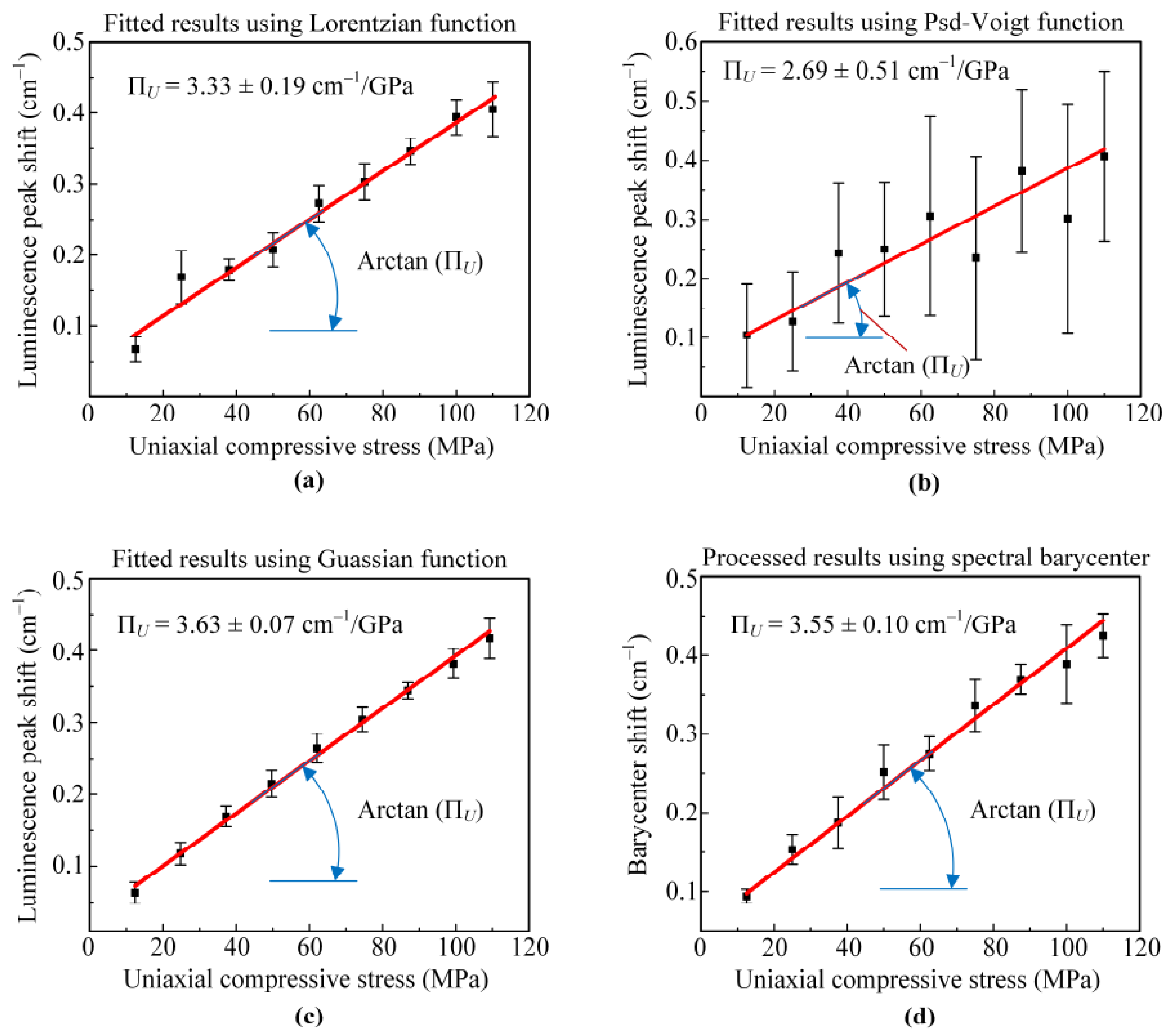
4.2. Results of the Calibration Experiments
4.3. Combined Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clarke, D.R.; Oechsner, M.; Padture, N.P. Thermal-barrier coatings for more efficient gas-turbine engines. MRS Bull. 2012, 37, 891–899. [Google Scholar] [CrossRef] [Green Version]
- Hardwicke, C.U.; Lau, Y.C. Advances in thermal spray coatings for gas turbines and energy generation: A review. J. Therm. Spray Technol. 2013, 22, 564–576. [Google Scholar] [CrossRef]
- Clarke, D.R.; Phillpot, S.R. Thermal barrier coating materials. Mater. Today 2005, 8, 22–29. [Google Scholar] [CrossRef]
- Schulz, U.; Leyens, C.; Fritscher, K.; Peters, M.; Saruhan-Brings, B.; Lavigne, O.; Dorvaux, J.M.; Poulain, M.; Mevrel, R.; Caliez, M.L. Some recent trends in research and technology of advanced thermal barrier coatings. Aerosp. Sci. Technol. 2003, 7, 73–80. [Google Scholar] [CrossRef]
- Padture, N.P. Advanced structural ceramics in aerospace propulsion. Nat. Mater. 2016, 15, 804–809. [Google Scholar] [CrossRef] [PubMed]
- Belmonte, M. Advanced ceramic materials for high temperature applications. Adv. Eng. Mater. 2006, 8, 693–703. [Google Scholar] [CrossRef] [Green Version]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef]
- Wellman, R.G.; Nicholls, J.R. Erosion, corrosion and erosion–corrosion of EB PVD thermal barrier coatings. Tribol. Int. 2008, 41, 657–662. [Google Scholar] [CrossRef] [Green Version]
- Jiang, P.; Fan, X.; Sun, Y.; Li, D.; Li, B.; Wang, T. Competition mechanism of interfacial cracks in thermal barrier coating system. Mater. Des. 2017, 132, 559–566. [Google Scholar] [CrossRef] [Green Version]
- Evans, H.E. Oxidation failure of TBC systems: An assessment of mechanisms. Surf. Coat. Technol. 2011, 206, 1512–1521. [Google Scholar] [CrossRef]
- Jiang, P.; Yang, L.; Sun, Y.; Li, D.; Wang, T. Nondestructive measurements of residual stress in air plasma-sprayed thermal barrier coatings. J. Am. Ceram. Soc. 2021, 104, 1455–1464. [Google Scholar] [CrossRef]
- Jiang, P.; Fan, X.; Sun, Y.; Li, D.; Wang, T. Bending-driven failure mechanism and modelling of double-ceramic-layer thermal barrier coating system. Int. J. Solids Struct. 2018, 130, 11–20. [Google Scholar] [CrossRef]
- Clarke, D.; Christensen, R.; Tolpygo, V. The evolution of oxidation stresses in zirconia thermal barrier coated superalloy leading to spalling failure. Surf. Coat. Technol. 1997, 94, 89–93. [Google Scholar] [CrossRef]
- Schlichting, K.; Vaidyanathan, K.; Sohn, Y.; Jordan, E.; Gell, M.; Padture, N. Application of Cr3+ photoluminescence piezo-spectroscopy to plasma-sprayed thermal barrier coatings for residual stress measurement. Mater. Sci. Eng. A 2000, 291, 68–77. [Google Scholar] [CrossRef]
- Gentleman, M.; Clarke, D. Concepts for luminescence sensing of thermal barrier coatings. Surf. Coat. Technol. 2004, 188, 93–100. [Google Scholar] [CrossRef]
- Eldridge, J.I.; Bencic, T.J. Monitoring delamination of plasma-sprayed thermal barrier coatings by reflectance-enhanced luminescence. Surf. Coat. Technol. 2006, 201, 3926–3930. [Google Scholar] [CrossRef] [Green Version]
- Eldridge, J.I.; Singh, J.; Wolfe, D.E. Erosion-indicating thermal barrier coatings using luminescent sublayers. J. Am. Ceram. Soc. 2006, 89, 3252–3254. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Y.; Zhu, L.; Gu, L.; Huang, W.; Fan, X.; Zou, B.; Wang, Y.; Cao, X. A simple non-destructive method to indicate the spallation and damage degree of the double-ceramic-layer thermal barrier coating of La2(Zr0.7Ce0.3)2O7 and 8YSZ:Eu. J. Eur. Ceram. Soc. 2013, 33, 2207–2213. [Google Scholar] [CrossRef]
- Zhao, S.; Gu, L.; Zhao, Y.; Huang, W.; Zhu, L.; Fan, X.; Zou, B.; Cao, X. Thermal cycling behavior and failure mechanism of La2(Zr0.7Ce0.3)2O7/Eu3+-doped 8YSZ thermal barrier coating prepared by atmospheric plasma spraying. J. Alloys Compd. 2013, 580, 101–107. [Google Scholar] [CrossRef]
- Li, C.; Fan, X.; Jiang, P.; Jin, X. Delamination-indicating of atmosphere-plasma-sprayed thermal barrier coating system using Eu3+ luminescence mapping. Mater. Lett. 2018, 222, 41–44. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, C.; Huang, F.; Wang, C.; Zhao, S.; Cui, Q.; Cao, X.; Li, F. Residual stress inspection by Eu3+ photoluminescence piezo-spectroscopy: An application in thermal barrier coatings. J. Appl. Phys. 2013, 114, 073502. [Google Scholar] [CrossRef]
- Manero II, A.; Selimov, A.; Fouliard, Q.; Knipe, K.; Wischek, J.; Meid, C.; Karlsson, A.M.; Bartsch, M.; Raghavan, S. Piezospectroscopic evaluation and damage identification for thermal barrier coatings subjected to simulated engine environments. Surf. Coat. Technol. 2017, 323, 30–38. [Google Scholar] [CrossRef]
- Sohn, Y.; Schlichting, K.; Vaidyanathan, K.; Gell, M.; Jordan, E. Nondestructive evaluation of residual stress for thermal barrier coated turbine blades by Cr3+ photoluminescence piezospectroscopy. Metall. Mater. Trans. A 2000, 31, 2388–2391. [Google Scholar] [CrossRef]
- Lima, C.; Dosta, S.; Guilemany, J.; Clarke, D. The application of photoluminescence piezospectroscopy for residual stresses measurement in thermally sprayed TBCs. Surf. Coat. Technol. 2017, 318, 147–156. [Google Scholar] [CrossRef]
- Hanhan, I.; Durnberg, E.; Freihofer, G.; Akin, P.; Raghavan, S. Portable piezospectroscopy system: Non-contact in-situ stress sensing through high resolution photo-luminescent mapping. J. Instrum. 2014, 9, P11005. [Google Scholar] [CrossRef]
- Ma, Q.; Clarke, D.R. Stress measurement in single-crystal and polycrystalline ceramics using their optical fluorescence. J. Am. Ceram. Soc. 1993, 76, 1433–1440. [Google Scholar] [CrossRef]
- Jiang, P.; Fan, X.; Sun, Y.; Wang, H.; Su, L.; Wang, T. Thermal-cycle dependent residual stress within the crack-susceptible zone in thermal barrier coating system. J. Am. Ceram. Soc. 2018, 101, 4256–4261. [Google Scholar] [CrossRef]
- Zhao, S.; Ren, Z.; Zhao, Y.; Xu, J.; Zou, B.; Hui, Y.; Zhu, L.; Zhou, X.; Cao, X. The application of Eu3+ photoluminescence piezo-spectroscopy in the LaMgAl11O19/8YSZ:Eu double-ceramic-layer coating system. J. Eur. Ceram. Soc. 2015, 35, 249–257. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, Z.; Yang, L.; Zhou, Y.; Wei, Y. Spallation of thermal barrier coatings with real thermally grown oxide morphology under thermal stress. Mater. Des. 2018, 146, 180–193. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Cai, H.N.; Li, C.J. Comprehensive dynamic failure mechanism of thermal barrier coatings based on a novel crack propagation and TGO growth coupling model. Ceram. Int. 2018, 44, 22556–22566. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Cai, H.N.; Meng, G.H.; Tahir, A.; Zhang, W.W. An innovative model coupling TGO growth and crack propagation for the failure assessment of lamellar structured thermal barrier coatings. Ceram. Int. 2020, 46, 1532–1544. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Cai, H.N.; Tahir, A.; Zhang, W.W.; Li, X.F.; Zhang, Y.; Huang, Y.P.; Liu, Y. Stress states in plasma-sprayed thermal barrier coatings upon temperature cycling: Combined effects of creep, plastic deformation, and TGO growth. Ceram. Int. 2019, 45, 19829–19844. [Google Scholar] [CrossRef]
- Shen, Z.; Zhong, B.; He, L.; Xu, Z.; Mu, R.; Huang, G. LaZrCeO/YSZ TBCs by EB-PVD: Microstructural evolution, residual stress and degradation behavior. Mater. Chem. Front. 2019, 3, 892–900. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Baxter, G.; Collins, S.F. Stress-and temperature-dependent wideband fluorescence of a phosphor composite for sensing applications. Exp. Mech. 2017, 57, 57–63. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, L.; Li, D.; Zhong, X.; Zhao, H.; Tao, S. Stress analysis and failure mechanisms of plasma-sprayed thermal barrier coatings. J. Therm. Spray Tech. 2017, 26, 1–12. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, H.; Zhong, X.; Ni, J.; Zhuang, Y.; Wang, L.; Tao, S. Evolution of residual stresses in PS-PVD thermal barrier coatings on thermal cycling. J. Therm. Spray Tech. 2018, 27, 914–923. [Google Scholar] [CrossRef]
- Fabisiak, K.; Łoś, S.; Paprocki, K.; Szybowicz, M.; Winiecki, J.; Dychalska, A. Orientation dependence of cathodoluminescence and photoluminescence spectroscopy of defects in chemical-vapor-deposited diamond microcrystal. Mater. 2020, 13, 5446. [Google Scholar] [CrossRef] [PubMed]
- Sonntag, J.; Li, J.; Plaud, A.; Loiseau, A.; Barjon, J.; Edgar, J.; Stampfer, C. Excellent electronic transport in heterostructures of graphene and monoisotopic boron-nitride grown at atmospheric pressure. 2D Mater. 2020, 7, 031009. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Qiu, W.; Tan, H.; Guo, J.; Kang, Y. Micro-raman spectroscopy stress measurement method for porous silicon film. Opt. Laser Eng. 2010, 48, 1119–1125. [Google Scholar] [CrossRef]
- Xu, C.; Xue, T.; Qiu, W.; Kang, Y. Size effect of the interfacial mechanical behavior of graphene on a stretchable substrate. ACS Appl. Mater. Interfaces 2016, 8, 27099–27106. [Google Scholar] [CrossRef]
- Lei, Z.K.; Kang, Y.L.; Hao, C.; Ming, H.; Yu, Q. Residual stress on surface and cross-section of porous silicon studied by micro-Raman spectroscopy. Chin. Phys. Lett. 2005, 22, 984. [Google Scholar] [CrossRef]
- Qiu, W.; Cheng, C.L.; Liang, R.R.; Zhao, C.W.; Lei, Z.K.; Zhao, Y.C.; Ma, L.L.; Xu, J.; Fang, H.J.; Kang, Y.L. Measurement of residual stress in a multi-layer semiconductor heterostructure by micro-Raman spectroscopy. Acta Mech. Sin. 2016, 32, 805–812. [Google Scholar] [CrossRef]
- Dou, W.; Xu, C.; Guo, J.; Du, H.; Qiu, W.; Xue, T.; Kang, Y.; Zhang, Q. Interfacial mechanical properties of double-layer graphene with consideration of the effect of stacking mode. ACS Appl. Mater. Interfaces 2018, 10, 44941–44949. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Ma, L.; Li, Q.; Xing, H.; Cheng, C.; Huang, G. A general metrology of stress on crystalline silicon with random crystal plane by using micro-Raman spectroscopy. Acta Mech. Sin. 2018, 34, 1095–1107. [Google Scholar] [CrossRef]
- Lu, N.; Zhang, Y.; Qiu, W. Comparison and selection of data processing methods for the application of Cr3+ photoluminescence piezospectroscopy to thermal barrier coatings. Coatings 2021, 11, 181. [Google Scholar] [CrossRef]
- Lavasani, H.Q.; Valefi, Z.; Ehsani, N.; Masoule, S.T. Studying the effect of spraying parameters on the sintering of YSZ TBC using APS method. Surf. Coat. Technol. 2019, 360, 238–246. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, S.S.; Zhang, S.L. Numerical simulation for the raman spectrum of SiC nano-rod. Chin. J. Light Scatter. 2004, 16, 299–302. [Google Scholar] [CrossRef]
- Tai, F.C.; Lee, S.C.; Chen, J.; Wei, C.; Chang, S.H. Multipeak fitting analysis of raman spectra on DLCH film. J. Raman Spectrosc. 2009, 40, 1055–1059. [Google Scholar] [CrossRef]
- Tohidi, T.; Jamshidi-Ghaleh, K. Effect of TEA on photoluminescence properties of PbS nanocrystalline thin films. Appl. Phys. A 2015, 118, 1247–1258. [Google Scholar] [CrossRef]
- Syassen, K. Ruby under pressure. High. Press. Res. 2008, 28, 75–126. [Google Scholar] [CrossRef]
- Huang, M.; Yan, H.; Chen, C.; Song, D.; Heinz, T.F.; Hone, J. Phonon softening and crystallographic orientation of strained graphene studied by Raman spectroscopy. Proc. Natl. Acad. Sci. USA 2009, 106, 7304–7308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reichert, F.; Pérez-Mas, A.M.; Barreda, D.; Blanco, C.; Santamaria, R.; Kuttner, C.; Fery, A.; Langhof, N.; Krenkel, W. Influence of the carbonization temperature on the mechanical properties of thermoplastic polymer derived C/C-SiC composites. J. Eur. Ceram. Soc. 2017, 37, 523–529. [Google Scholar] [CrossRef] [Green Version]
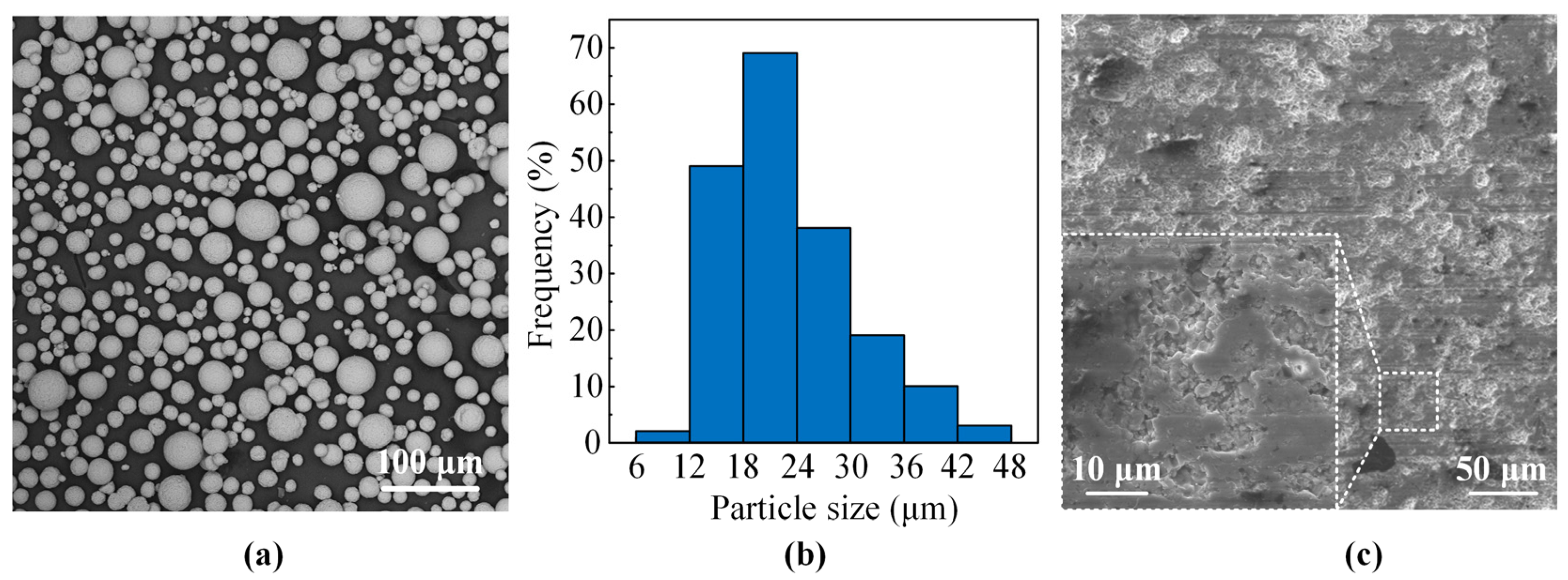

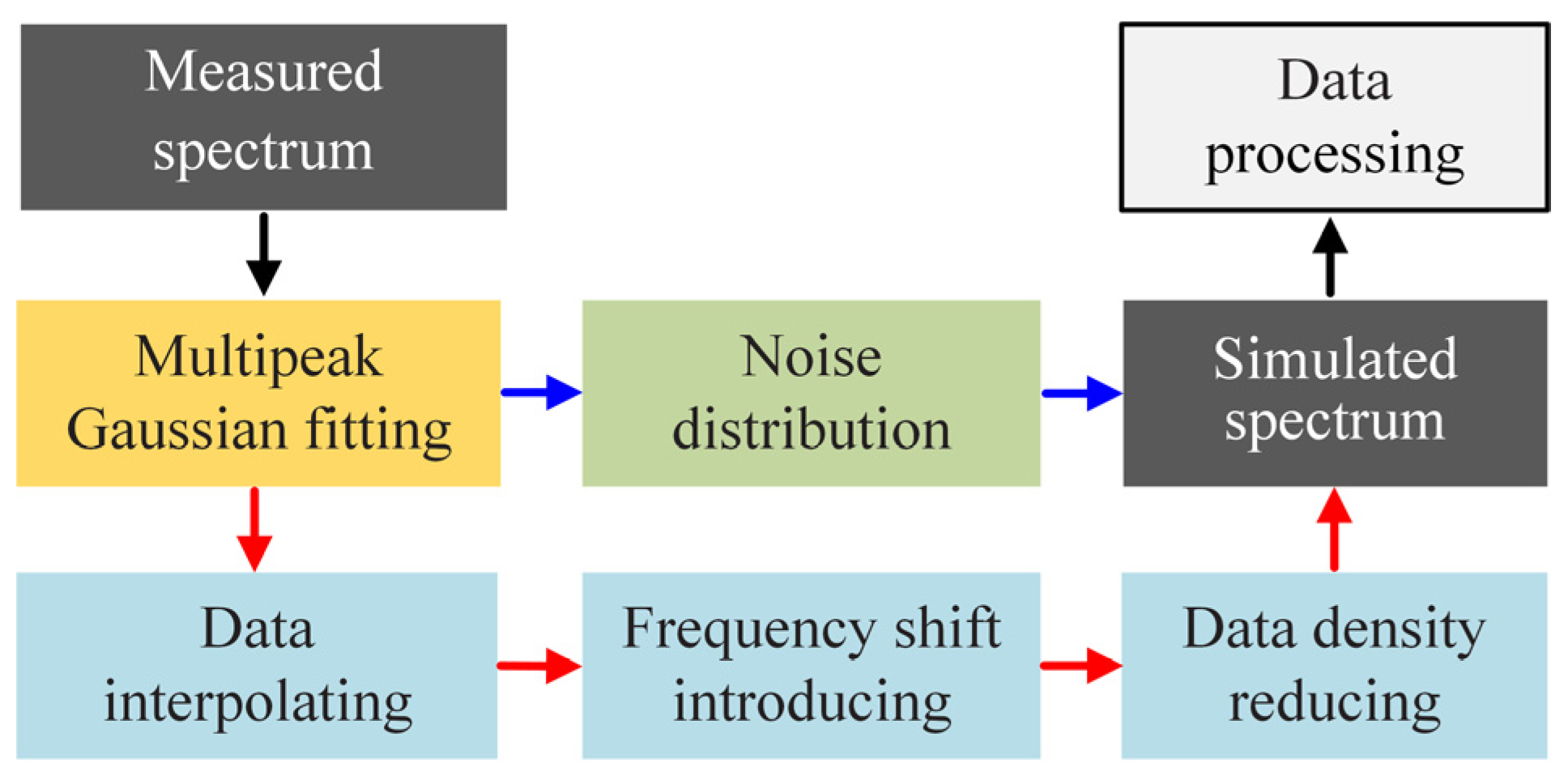

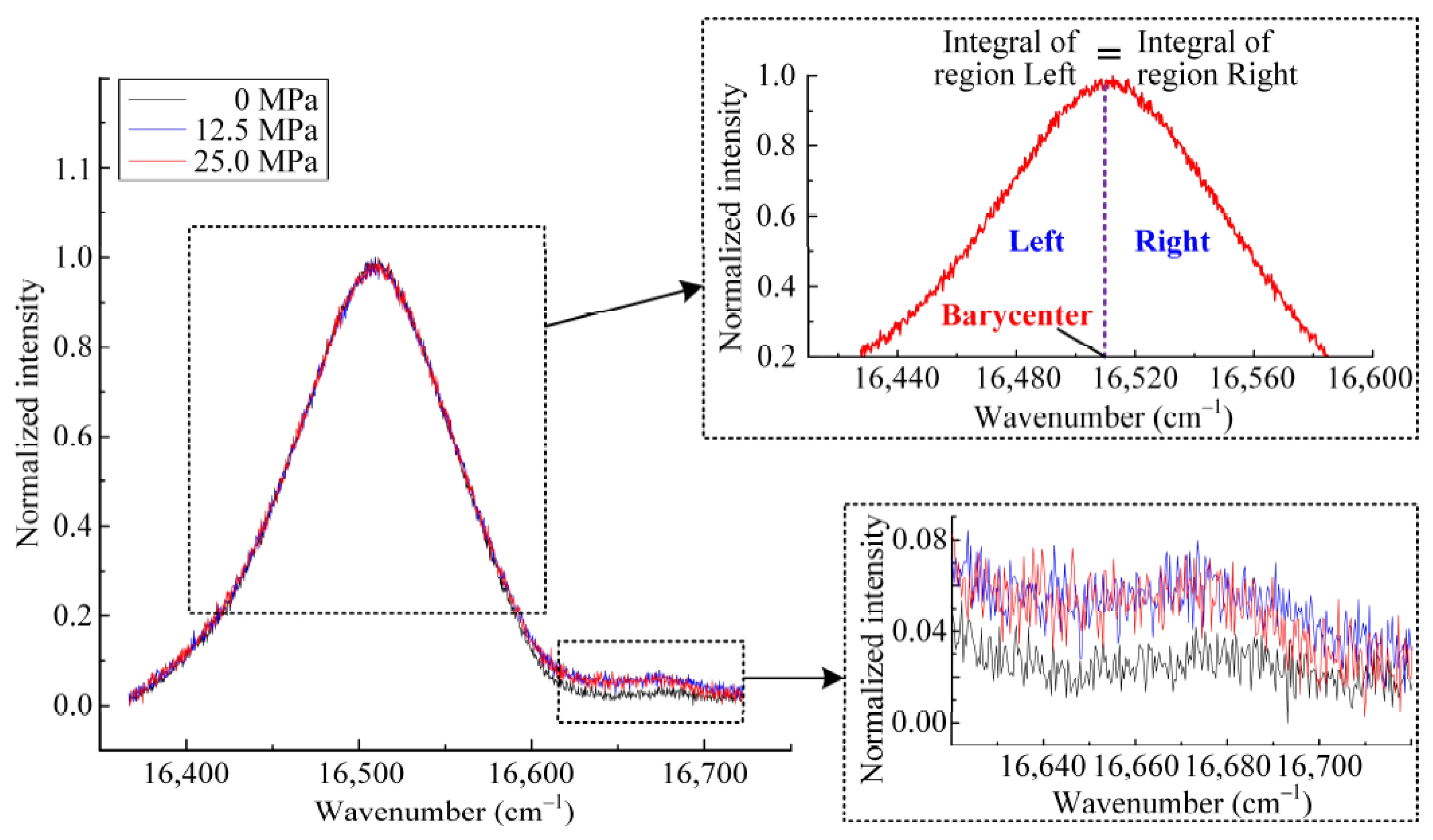
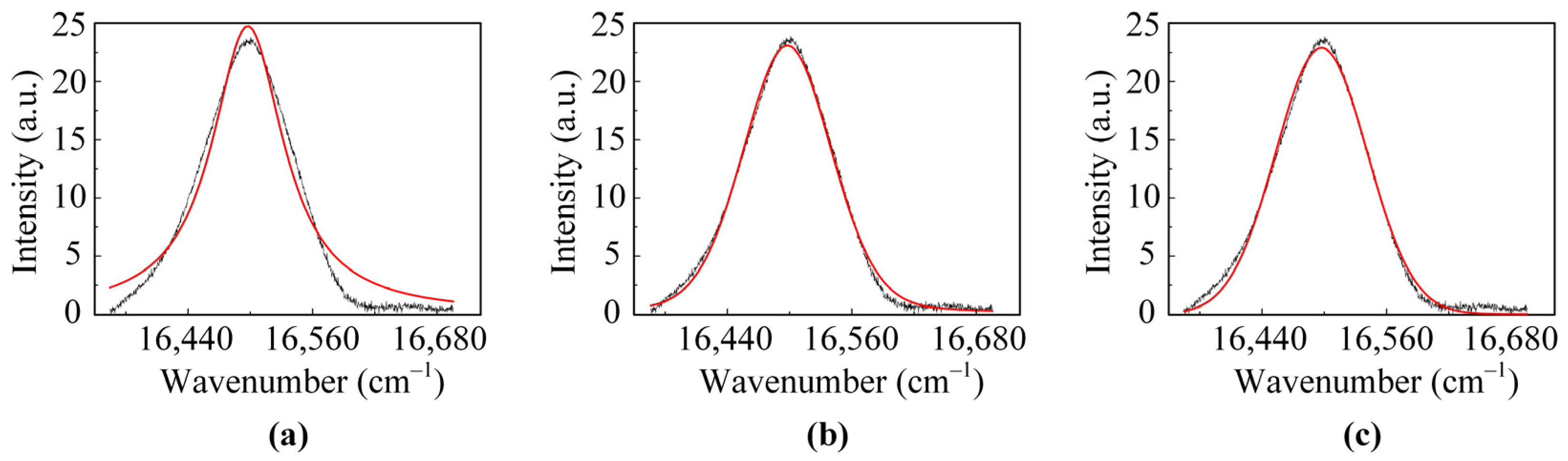

| Current (A) | Voltage (V) | Gas Flow (L/min) | Feedstock Rate (g/min) | Spraying Distance (mm) | Spraying Angle (°) |
|---|---|---|---|---|---|
| 630 | 72 | Ar: 38 H2: 60 | 30 | 100 | 90 |
| Fitting Function | Lorentzian | Psd-Voigt | Gaussian | |
|---|---|---|---|---|
| GOF | Simulated data | 0.9683 | 0.9966 | 0.9958 |
| Measured data | 0.9699 | 0.9966 | 0.9953 | |
| Processing Method | ΠU (cm−1/GPa) | R2 | Relative Error of ΠU |
|---|---|---|---|
| Pre-set value | 2.59 | - | 0 |
| Lorentzian | 2.61 ± 8.86 × 10−4 | 1 | 0.77% |
| Psd-Voigt | 3.65 ± 0.57 | 0.7141 | 35.52% |
| Gaussian | 2.58 ± 1.93 × 10−4 | 1 | 0.39% |
| Barycenter | 2.67 ± 6.76 × 10−4 | 1 | 2.62% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lu, N.; Qiu, W. Optimal Data Processing Method for the Application of Eu3+ Photoluminescence Piezospectroscopy in Thermal Barrier Coatings. Coatings 2021, 11, 678. https://doi.org/10.3390/coatings11060678
Zhang Y, Lu N, Qiu W. Optimal Data Processing Method for the Application of Eu3+ Photoluminescence Piezospectroscopy in Thermal Barrier Coatings. Coatings. 2021; 11(6):678. https://doi.org/10.3390/coatings11060678
Chicago/Turabian StyleZhang, Yanheng, Ning Lu, and Wei Qiu. 2021. "Optimal Data Processing Method for the Application of Eu3+ Photoluminescence Piezospectroscopy in Thermal Barrier Coatings" Coatings 11, no. 6: 678. https://doi.org/10.3390/coatings11060678








