Effects of Different Degrees of Hydrophobic Treatment on Soil–Water Characteristic Curves and Infiltration Coefficients of Hygroscopic Soils
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Treatment of Hydrophobic Materials
2.2.2. Preparation of Sample
2.2.3. Sample Treatment
2.2.4. Test of Matrix Suction and Fitting of Soil–Water Characteristic Curve
2.2.5. Statistics
2.2.6. Falling Head Permeability Test
3. Results and Discussion
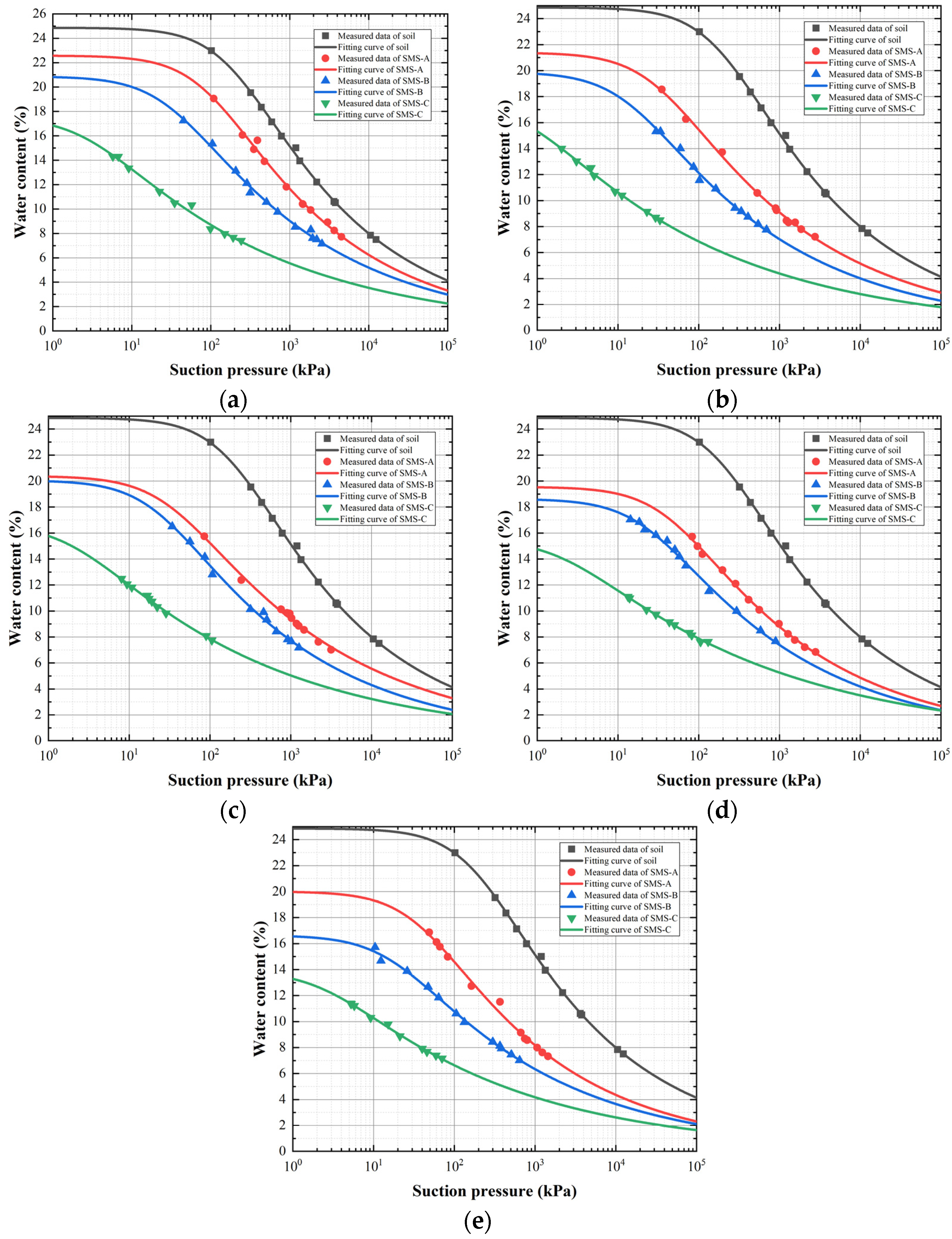
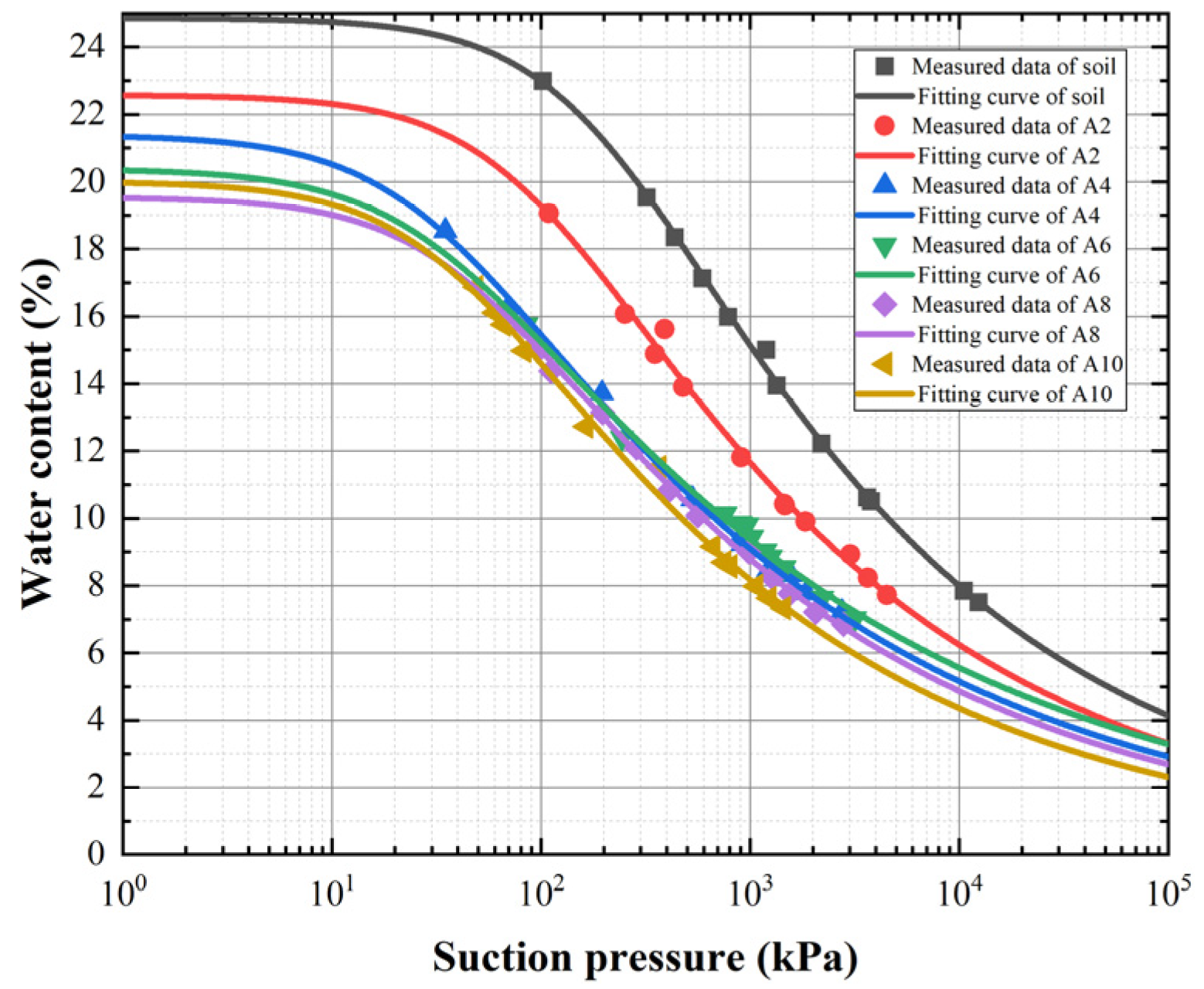
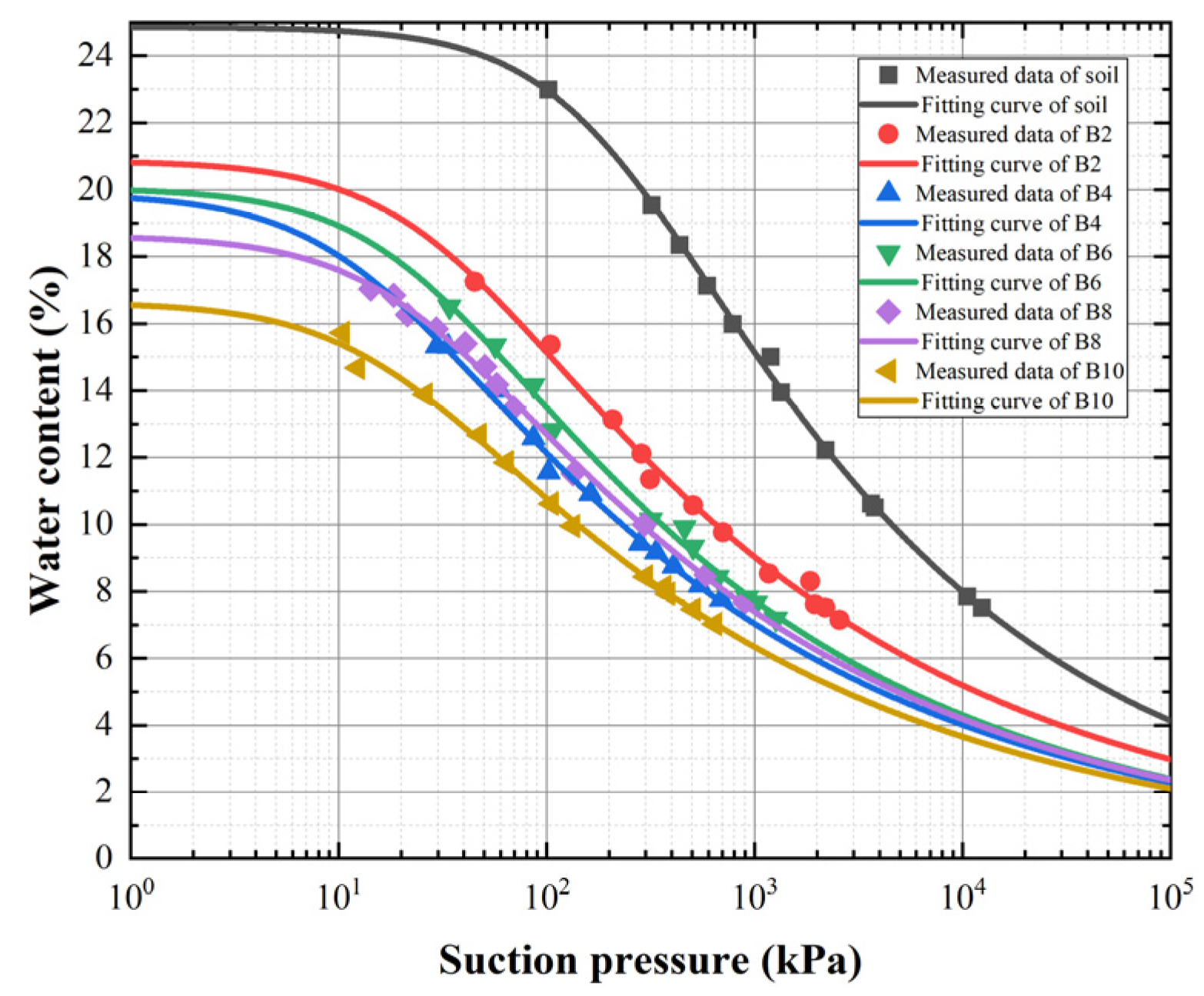
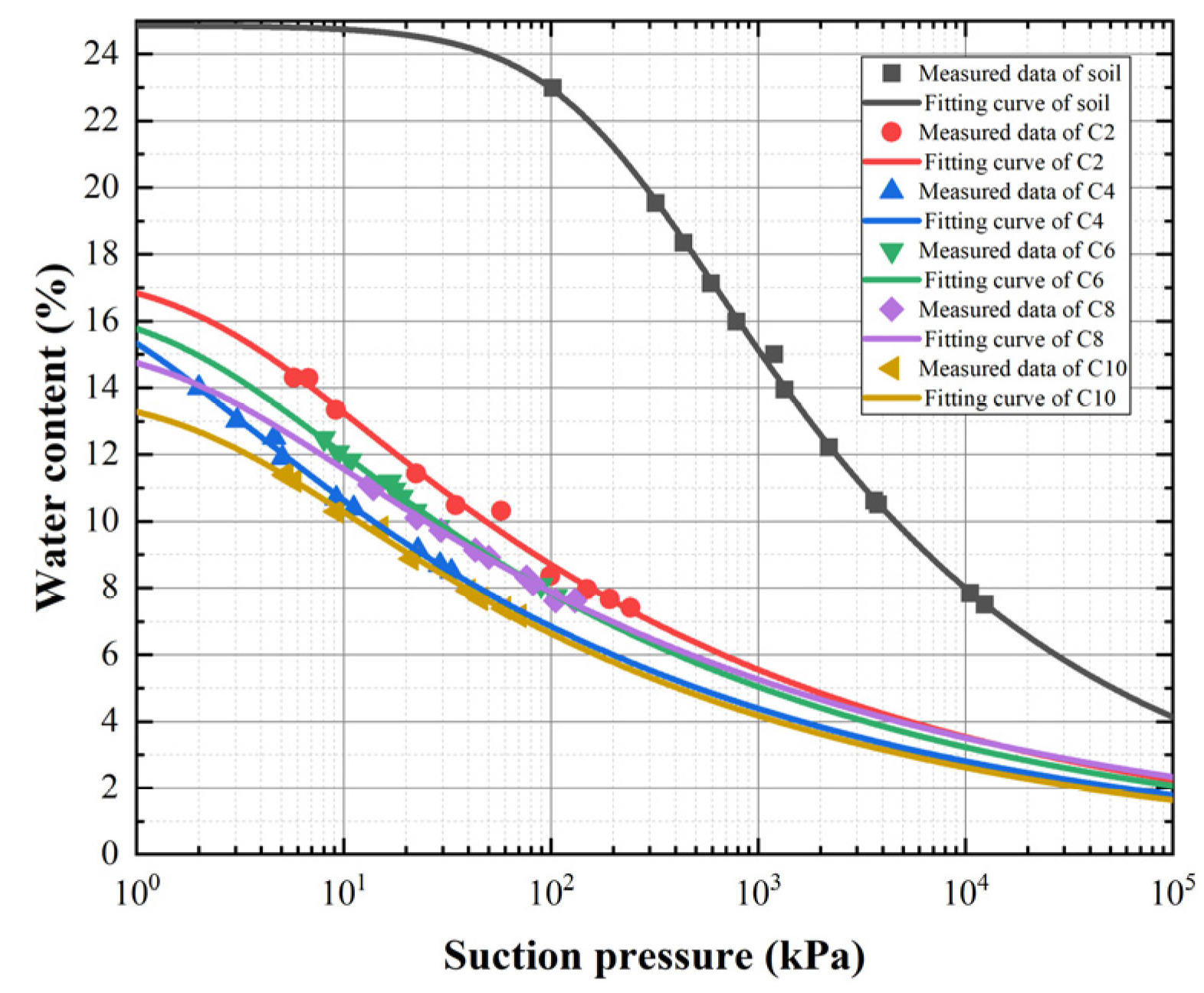
3.1. Fitting Results of Soil–Water Characteristic Curves
3.2. Effect of Hydrophobicity on SWCCs
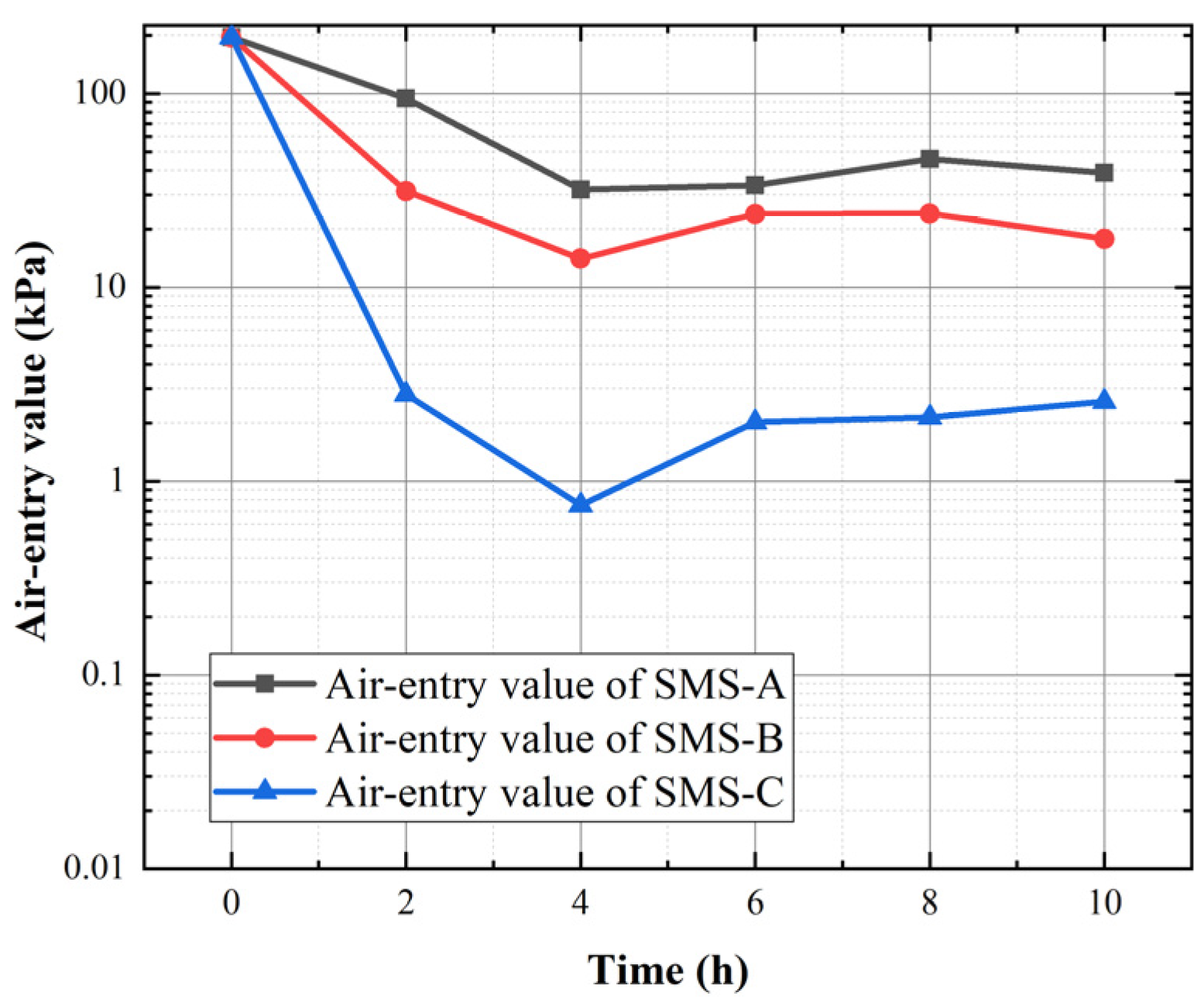
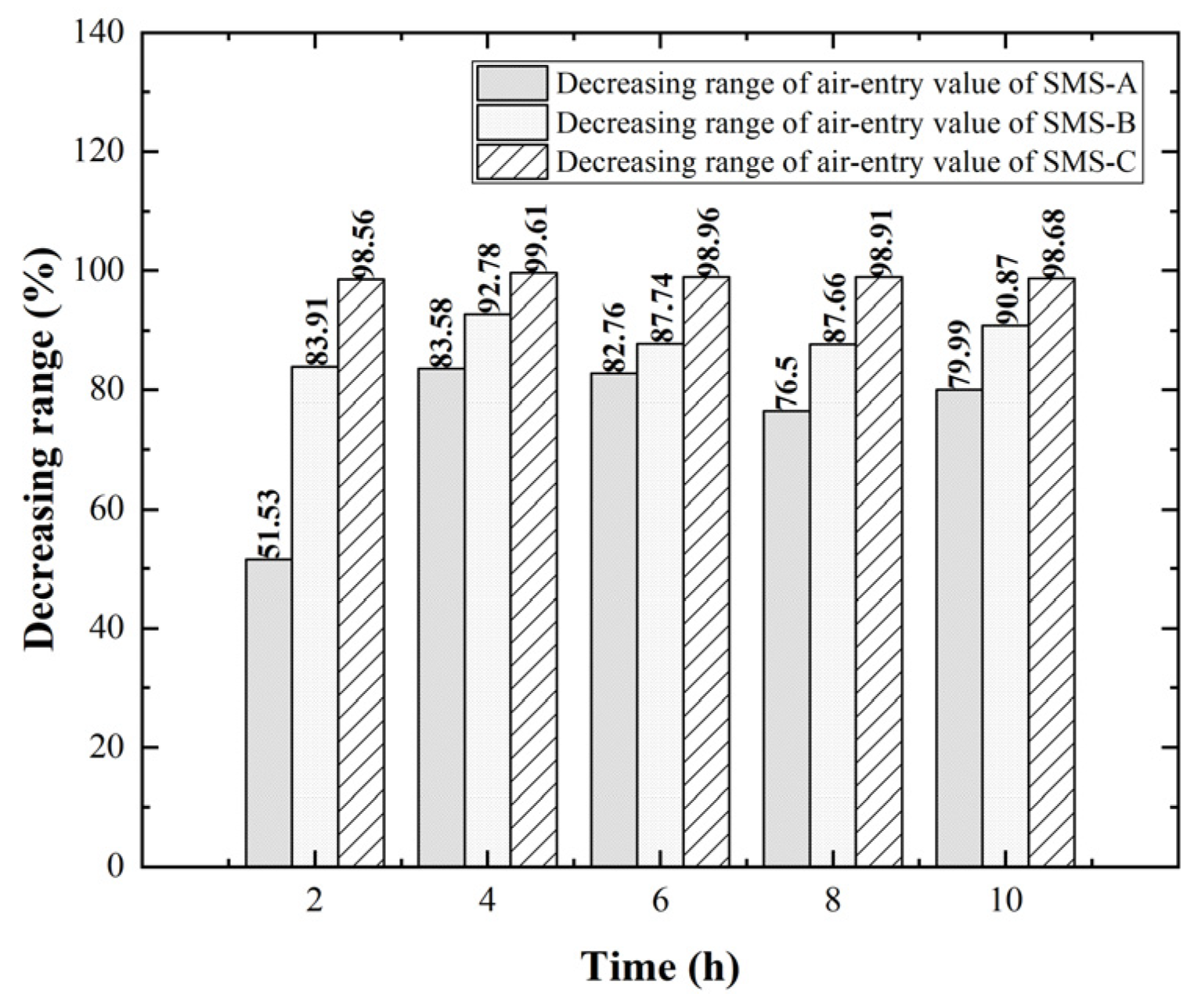
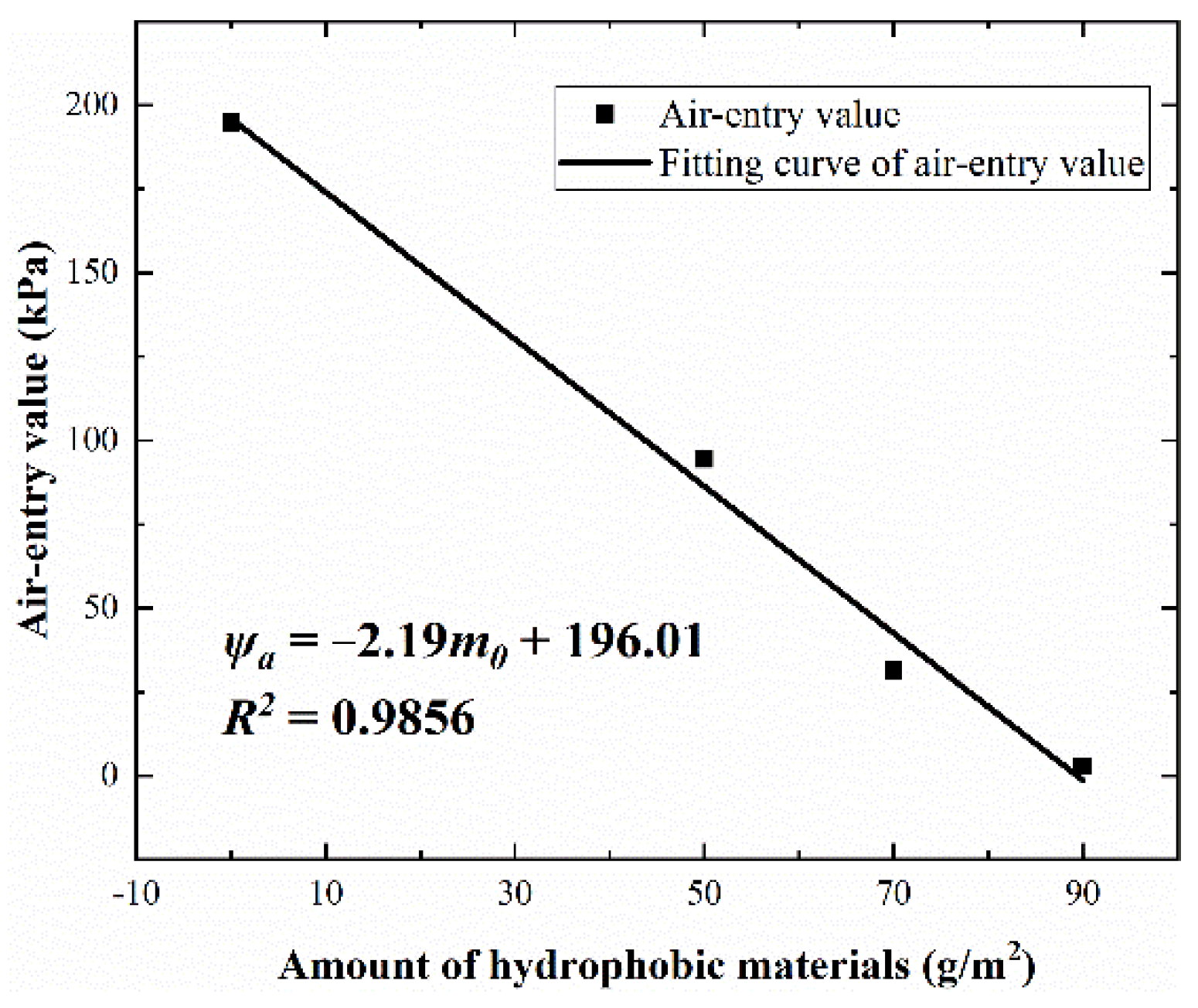
3.3. Effect of Hydrophobicity on Air-Entry Value
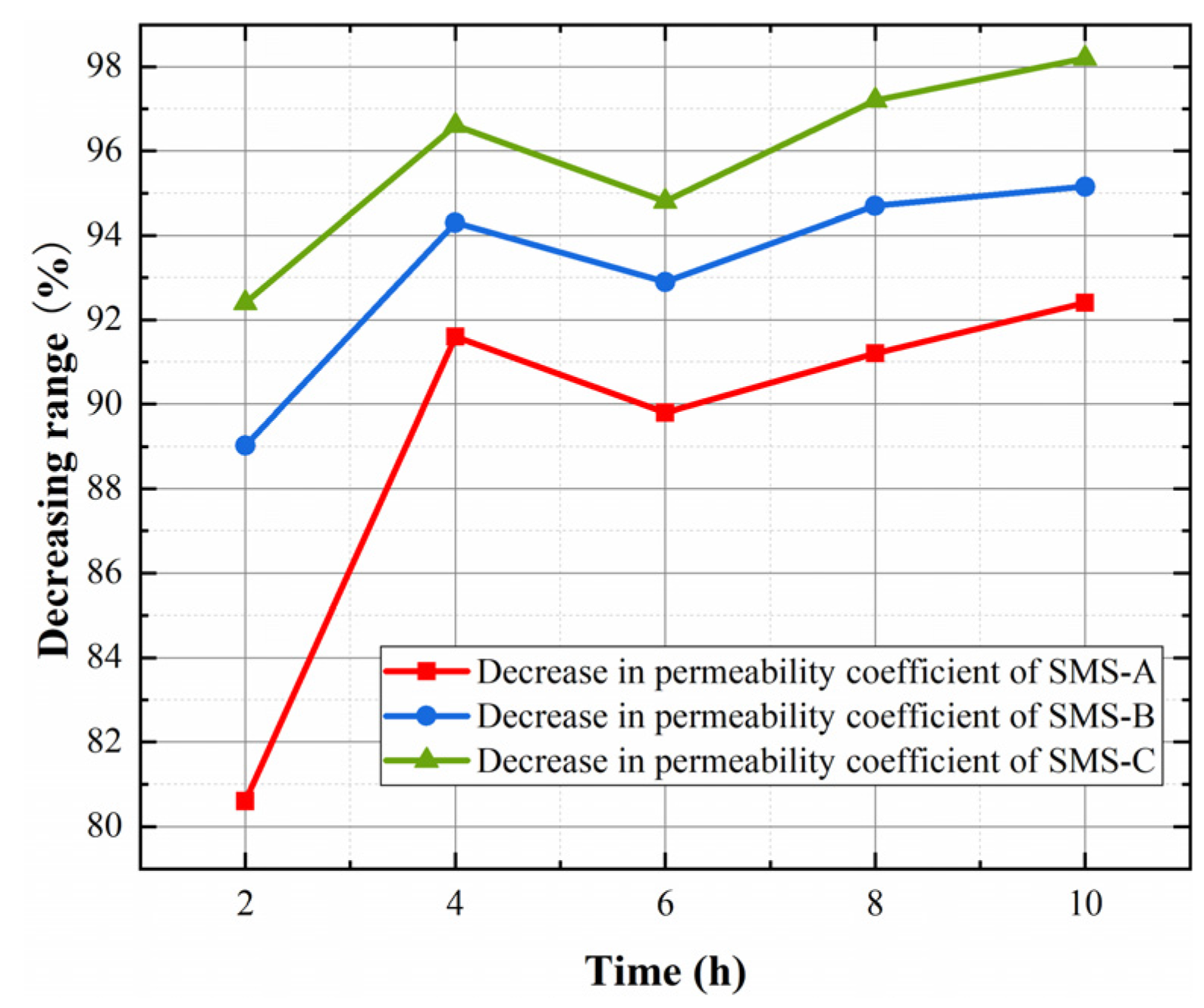
3.4. Influence of Hydrophobic Degree on Saturated Permeability Coefficient
3.5. Prediction of Unsaturated Permeability Coefficient
3.6. The Influence of Hydrophobic Materials on the Hydrophobicity of Soil
4. Conclusions
- (1)
- The soil–water characteristic curve of soil treated with silicone hydrophobic material decreased obviously. In other words, when the matrix suction was the same, the water content of the soil after hydrophobic treatment was significantly reduced, and, with the increase in the amount of silicone hydrophobic material, the decrease in water content was more obvious. When the matrix suction was 100 kPa, the water content of soil after hydrophobic treatment decreased by 24%–72% compared with that of plain soil.
- (2)
- With the increase in the amount of silicone hydrophobic material, the water holding capacity of soil particles decreased; the maximum decrease in the saturated water content and air-entry value of soil is 44% and 98.96% respectively. When the action time was 2 h, the logarithm of the air-entry value was significantly negatively correlated with the amount of silicone hydrophobic material (correlation coefficient R2 = 0.9856). When the action time was 2 h, the amount of hydrophobic material increased from 0 to 50 g/m2, 70 g/cm2, and 90 g/m2, and the saturated permeability coefficient decreased by 80.6%, 89.02%, and 92.4%.
- (3)
- When the amount of hydrophobic materials was the same and the action time was different, the changes in the soil–water characteristic curve, saturated permeability coefficient, and air-entry value were mainly affected by the water generated during the reaction of hydrophobic materials, and the inflection points appeared at 4 h and 6 h.
- (4)
- The CCG model was used to predict the unsaturated permeability coefficient of soil with different hydrophobic treatments. The results show that the unsaturated permeability coefficient and the matrix suction were significantly negatively correlated in the double-logarithmic coordinate system (correlation coefficient R2 ≥ 0.97).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weiming, L.; Zhiyong, L.; Cheng, D.; Zhuo, L. Study on Prediction Model of Dynamic Resilient Modulus of Cohesive Subgrade Soils Considering under Different Moisture. Highw. Eng. 2013, 38, 6–9, 48. [Google Scholar]
- Jin-Song, Q.; Jia-Yang, L.; Ding, Z.; Jian-Ming, L. Prediction model of resilient modulus for unsaturated clay soils considering the effect of matric suction. Rock Soil Mech. 2018, 39, 123–128. [Google Scholar] [CrossRef]
- Xin, Q.; Jin-Song, Q.; Shi-Zhou, Z. Research on prediction model of dynamic resilient modulus of subgrade soil based on matric suction. Hydrogeol. Eng. Geol. 2011, 38, 49–53, 58. [Google Scholar] [CrossRef]
- Arroyo, M.; Amaral, M.F.; Romero, E.; Fonseca, A. Isotropic yielding of unsaturated cemented silty sand. Can. Geotech. J. 2013, 50, 807–819. [Google Scholar] [CrossRef]
- Henry, K.S.; Holtz, R.D. Geocomposite capillary barriers to reduce frost heave in soils. Can. Geotech. J. 2001, 38, 678–694. [Google Scholar] [CrossRef]
- Henry, K.S.; Stormont, J.C.; Holtz, R.D. Geosynthetic capillary barriers in pavements. In Performance Confirmation of Constructed Geotechnical Facilities; University of Massachusetts: Amherst, MA, USA, 2000; pp. 350–364. [Google Scholar] [CrossRef]
- Junying, C.; Chang, L.; Lin, Z.; Youzhen, X.; Gillerman, L.; Hongyang, C. Impact of repellent levels on drainage soil water characteristic curve. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 188–193. [Google Scholar]
- Denmark, S.E.; Sweis, R.F. Cross-coupling reactions of organosilicon compounds: New concepts and recent advances. ChemInform 2003, 34, 1531–1541. [Google Scholar] [CrossRef]
- Mahedi, M.; Satvati, S.; Cetin, B.; Daniels, J.L. Chemically Induced Water Repellency and the Freeze-Thaw Durability of Soils. J. Cold Reg. Eng. 2020, 34, 04020017. [Google Scholar] [CrossRef]
- Ma, J.; Porath, L.E.; Haque, M.F.; Sett, S.; Rabbi, K.F.; Nam, S.; Miljkovic, N.; Evans, C.M. Ultra-thin self-healing vitrimer coatings for durable hydrophobicity. Nat. Commun. 2021, 12, 5210. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Kanungo, D.P.; Song, Z.; Bai, Y.; Wang, Y.; Li, D.; Qian, W. Topsoil reinforcement of sandy slope for preventing erosion using water-based polyurethane soil stabilizer. Eng. Geol. 2019, 252, 125–135. [Google Scholar] [CrossRef]
- Daniels, J.L.; Hourani, M.S. Soil improvement with organo-silane. In Advances in Ground Improvement: Research to Practice in the United States and China; American Society of Civil Engineers: Orlando, FL, USA, 2009; pp. 217–224. [Google Scholar] [CrossRef]
- Daniels, J.L.; Hourani, M.S.; Harper, L.S. Organo-silane chemistry: A water repellent technology for coal ash and soils. In Proceedings; 2009 World of Coal Ash (WOCA) Conference: Lexington, KY, USA, 2009; pp. 4–7. [Google Scholar]
- Junhua, W.; Hui, L.; Xiaoyu, Z.; Yichao, D.; Song, Y. Measurement of shear strength and its change in unsaturated soils modified by hydrophobic agent. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2019, 35, 123–129. [Google Scholar]
- Zheng, S.; Lourenço, S.D.; Cleall, P.J.; Chui, T.F.M.; Ng, A.K.; Millis, S.W. Hydrologic behavior of model slopes with synthetic water repellent soils. J. Hydrol. 2017, 554, 582–599. [Google Scholar] [CrossRef]
- Qingjie, D.; Chunpeng, H. Experimental study on capillary water rise of subgrade soil under the action of organic silicon materials. Shanxi Archit. 2021, 47, 118–120. [Google Scholar] [CrossRef]
- Romero, E.; Della Vecchia, G.; Jommi, C. An insight into the water retention properties of compacted clayey soils. Géotechnique 2011, 61, 313–328. [Google Scholar] [CrossRef]
- Fredlund, D.G. State of practice for use of the soil-water characteristic curve (SWCC) in geotechnical engineering. Can. Geotech. J. 2019, 56, 1059–1069. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Gan, J.; Fredlund, D.; Rahardjo, H. Determination of the shear strength parameters of an unsaturated soil using the direct shear test. Can. Geotech. J. 1988, 25, 500–510. [Google Scholar] [CrossRef]
- Fang-Zhi, Z.; Xiao-Ping, C. Influence of repeated drying and wetting cycles on mechanical behaviors of unsaturated soil. Chin. J. Geotech. Eng. 2010, 32, 41–46. [Google Scholar]
- Brooks, R.H. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1965; pp. 2–27. [Google Scholar]
- Li-Zhou, W. Constitutive Model and Slope Stability Evaluation and Its Application for Unsaturated Expansive Soil. Ph.D. Thesis, Chengdu University of Techology, Chengdu, China, 2006. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 1964, 7, 26–0028. [Google Scholar] [CrossRef]
- Gardner, W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- McKee, C.; Bumb, A. Flow-testing coalbed methane production wells in the presence of water and gas. SPE Form. Eval. 1987, 2, 599–608. [Google Scholar] [CrossRef]
- Xue-Dong, Z.; Cheng-Gang, Z.; Guo-Qing, C.; Yan, L. Research on influence of soil density on soil-water characteristic curve. Rock Soil Mech. 2010, 31, 1463–1468. [Google Scholar] [CrossRef]
- Wheeler, S.; Sharma, R.; Buisson, M. Coupling of hydraulic hysteresis and stress–strain behaviour in unsaturated soils. Géotechnique 2003, 53, 41–54. [Google Scholar] [CrossRef]
- Wang, H.-M.; Ni, W.-K.; Li, X.; Li, L.; Yuan, K.-Z.; Nie, Y.-P. Predicting the pore size distribution curve based on the evolution mechanism of soil–water characteristic curve. Environ. Earth Sci. 2021, 81, 23. [Google Scholar] [CrossRef]
- Bauters, T.; Steenhuis, T.; DiCarlo, D.; Nieber, J.L.; Dekker, L.; Ritsema, C.; Parlange, J.-Y.; Haverkamp, R. Physics of water repellent soils. J. Hydrol. 2000, 231, 233–243. [Google Scholar] [CrossRef]
- Bauters, T.W.; Steenhuis, T.S.; Parlange, J.Y.; DiCarlo, D.A. Preferential flow in water-repellent sands. Soil Sci. Soc. Am. J. 1998, 62, 1185–1190. [Google Scholar] [CrossRef]
- Lamparter, A.; Bachmann, J.; Deurer, M.; Woche, S. Applicability of ethanol for measuring intrinsic hydraulic properties of sand with various water repellency levels. Vadose Zone J. 2010, 9, 445–450. [Google Scholar] [CrossRef]
- Diamantopoulos, E.; Durner, W.; Reszkowska, A.; Bachmann, J. Effect of soil water repellency on soil hydraulic properties estimated under dynamic conditions. J. Hydrol. 2013, 486, 175–186. [Google Scholar] [CrossRef]
- Czachor, H.; Doerr, S.; Lichner, L. Water retention of repellent and subcritical repellent soils: New insights from model and experimental investigations. J. Hydrol. 2010, 380, 104–111. [Google Scholar] [CrossRef]
- Tao, G.; Gu, K.; Zhong, C.; Chen, Y.; Lei, D.L.K.; Li, Z.X. The test and fitting analysis of Hunan clay soil–water characteristic curve in full suction range. Arab. J. Geosci. 2021, 14, 2501. [Google Scholar] [CrossRef]
- Yan, W.L.; Birle, E.; Cudmani, R.O. A simple approach for predicting soil water characteristic curve of clayey soils using pore size distribution data. MATEC Web Conf. 2021, 337, 02012. [Google Scholar] [CrossRef]
- Yang, S.; Zheng, P.Q.; Yu, Y.T.; Zhang, J. Probabilistic analysis of soil-water characteristic curve based on machine learning algorithms. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 062030. [Google Scholar] [CrossRef]
- Zhou, J.; Ren, J.; Li, Z. An Improved Prediction Method of Soil-Water Characteristic Curve by Geometrical Derivation and Empirical Equation. Math. Probl. Eng. 2021, 2021, 9956824. [Google Scholar] [CrossRef]
- Houston, S.L.; Houston, W.N.; Wagner, A.-M. Laboratory filter paper suction measurements. Geotech. Test. J. 1994, 17, 185–194. [Google Scholar] [CrossRef]
- Gardner, R. A method of measuring the capillary tension of soil moisture over a wide moisture range. Soil Sci. 1937, 43, 277–284. [Google Scholar] [CrossRef]
- Feuerharmel, C.; Gehling, W.; Bica, A. The use of filter-paper and suction-plate methods for determining the soil-water characteristic curve of undisturbed colluvium soils. Geotech. Test. J. 2006, 29, 419–425. [Google Scholar] [CrossRef]
- Huang, W.; Zhou, C.; Liu, Z.; Sun, H.; Du, J.; Zhang, L. Improving Soil-Water Characteristics and Pore Structure of Silty Soil Using Nano-aqueous Polymer Stabilisers. KSCE J. Civ. Eng. 2021, 25, 3298–3305. [Google Scholar] [CrossRef]
- Leong, E.C.; He, L.; Rahardjo, H. Factors affecting the filter paper method for total and matric suction measurements. Geotech. Test. J. 2002, 25, 322–333. [Google Scholar] [CrossRef]
- Deka, R.; Wairiu, M.; Mtakwa, P.; Mullins, C.; Veenendaal, E.; Townend, J. Use and accuracy of the filter-paper technique for measurement of soil matric potential. Eur. J. Soil Sci. 1995, 46, 233–238. [Google Scholar] [CrossRef]
- Qiaozhen, L. Improving Rainwater Harvesting Efficiency of Loess Soil with Organic Silicon Materials. Master’s Thesis, Northwest Sci-Tech University, Yanglin, China, 2004. (In Chinese). [Google Scholar]
- Qingjie, D. Experimental Study on Water Isolation Effect of Hydrophobic Material Subgrade Waterproof Layer under Freezing and Thawing Action. Master’s Thesis, Northeast Forestry University, Harbin, China, 2021. (In Chinese). [Google Scholar]
- Jianhong, C. Experimental Study on Soil-Water Characteristic Curve of Loess Using Filter Paper Method. Master’s Thesis, Chang’an University, Xi’an, China, 2017. (In Chinese). [Google Scholar]
- McQueen, I.S.; Miller, R.F. Calibration and evaluation of a wide-range gravimetric method for measuring moisture stress. Soil Sci. 1968, 106, 225–231. [Google Scholar] [CrossRef]
- Hamblin, A. Filter-paper method for routine measurement of field water potential. J. Hydrol. 1981, 53, 355–360. [Google Scholar] [CrossRef]
- Zhi-Xiang, T.; Zheng-Zhong, W.; Jian-Rui, G.; Hao-Yuan, J.; Quan-Hong, L.; Xiao-Dong, M. Experimental study on soil-water characteristic curve and permeability curve of white sandstone and mudstone in northern Xinjiang. Chin. J. Geotech. Eng. 2020, 42, 229–233. [Google Scholar]
- Xiao-Hui, T.; Wei, Y.; Meng-Fen, S.; Na, H. Experimental study and curve fitting of soil-water characteristic curve. Rock Soil Mech. 2013, 34, 51–56. [Google Scholar] [CrossRef]
- McQueen, I.S.; Miller, R.F. Approximating soil moisture characteristics from limited data: Empirical evidence and tentative model. Water Resour. Res. 1974, 10, 521–527. [Google Scholar] [CrossRef]
- Shuang-Hong, Z.; Bo, Y.; Wei, Z.; Shuang, L.; Gang, K. Composition and properties of methyl silicate/ silicate composite coatings. J. Mater. Eng. 2021, 49, 163–170. [Google Scholar]
- Hamilton, J.; Daniel, D.E.; Olson, R.E. Measurement of hydraulic conductivity of partially saturated soils. ASTM Spec. Tech. Publ. 1981, 746, 182–196. [Google Scholar] [CrossRef]
- Aimin, L. Experimental Study on Permeability of Unsaturated Soil and Mechanism of Saturation Infiltration. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2008. (In Chinese). [Google Scholar]
- Marshall, T. A relation between permeability and size distribution of pores. J. Soil Sci. 1958, 9, 1–8. [Google Scholar] [CrossRef]
- Roy, S.; Rajesh, S. Influence of confining pressure on water retention characteristics of compacted soil. Indian Geotech. J. 2018, 48, 327–341. [Google Scholar] [CrossRef]







| Natural Water Content w (%) | Liquid Limit wL (%) | Plastic Limit wP (%) | Plasticity Index Ip (%) | Optimum Moisture Content w (%) | Maximum Dry Density ρd (g/cm3) |
|---|---|---|---|---|---|
| 24.6 (0.45) | 30.7 (0.35) | 19.0 (0.17) | 11.7 | 13.34 | 1.91 |
| Soil Type | Amount of Hydrophobic Material (g/m2) | Amount of Hydrophobic Material Solution (g) | Weight of Hydrophobic Material in Solution (g) | Action Time (h) |
|---|---|---|---|---|
| Plain soil | 0 | 0 | 0 | 0 |
| SMS-A2 | 50 | 1.5 | 0.15 | 2 |
| SMS-A4 | 4 | |||
| SMS-A6 | 6 | |||
| SMS-A8 | 8 | |||
| SMS-A10 | 10 | |||
| SMS-B2 | 70 | 0.21 | 2 | |
| SMS-B4 | 4 | |||
| SMS-B6 | 6 | |||
| SMS-B8 | 8 | |||
| SMS-B10 | 10 | |||
| SMS-C2 | 90 | 0.27 | 2 | |
| SMS-C4 | 4 | |||
| SMS-C6 | 6 | |||
| SMS-C8 | 8 | |||
| SMS-C10 | 10 |
| Soil Type | Saturated Water Content (%) | (kPa) | ||
|---|---|---|---|---|
| Plain soil | 24.86 | 194.89 | 1.2875 | 0.9983 |
| SMS-A2 | 22.58 | 94.47 | 1.2755 | 0.9916 |
| SMS-A4 | 21.39 | 32.00 | 1.2475 | 0.9970 |
| SMS-A6 | 20.39 | 33.69 | 1.2280 | 0.9892 |
| SMS-A8 | 19.55 | 45.79 | 1.2578 | 0.9971 |
| SMS-A10 | 20.01 | 39.00 | 1.2748 | 0.9921 |
| SMS-B2 | 20.87 | 31.36 | 1.2412 | 0.9925 |
| SMS-B4 | 19.89 | 14.07 | 1.2437 | 0.9918 |
| SMS-B6 | 20.06 | 23.89 | 1.2548 | 0.9922 |
| SMS-B8 | 18.63 | 24.05 | 1.2475 | 0.9957 |
| SMS-B10 | 16.64 | 17.79 | 1.2392 | 0.9950 |
| SMS-C2 | 17.56 | 2.81 | 1.1959 | 0.9874 |
| SMS-C4 | 17.67 | 0.75 | 1.1937 | 0.9946 |
| SMS-C6 | 16.71 | 2.02 | 1.1932 | 0.9946 |
| SMS-C8 | 15.53 | 2.13 | 1.1759 | 0.9947 |
| SMS-C10 | 13.92 | 2.58 | 1.2019 | 0.9951 |
| Time (h) | 2 | 4 | 6 | 8 | 10 | |
|---|---|---|---|---|---|---|
| Dosage (g/m2) | ||||||
| 0 | 32.011 | 32.011 | 32.011 | 32.011 | 32.011 | |
| 50 | 6.1931 | 2.6822 | 3.2592 | 2.8163 | 2.4425 | |
| 70 | 3.5160 | 1.8280 | 2.2714 | 1.7051 | 1.5532 | |
| 90 | 2.4291 | 1.0983 | 1.6726 | 0.8922 | 0.5681 | |
| Soil Type | a | b | R2 |
|---|---|---|---|
| Plain soil | −2.17 | −3.02 | 0.97 |
| SMS-A2 | −2.16 | −4.87 | 0.97 |
| SMS-A4 | −2.16 | −6.13 | 0.98 |
| SMS-A6 | −2.16 | −5.88 | 0.98 |
| SMS-A8 | −2.16 | −6.3 | 0.98 |
| SMS-A10 | −2.16 | −6.28 | 0.98 |
| SMS-B2 | −2.15 | −6.40 | 0.98 |
| SMS-B4 | −2.15 | −7.70 | 0.98 |
| SMS-B6 | −2.15 | −7.13 | 0.98 |
| SMS-B8 | −2.15 | −7.56 | 0.98 |
| SMS-B10 | −2.15 | −8.3 | 0.98 |
| SMS-C2 | −2.13 | −9.98 | 0.99 |
| SMS-C4 | −2.12 | −11.64 | 0.99 |
| SMS-C6 | −2.24 | −10.87 | 0.98 |
| SMS-C8 | −2.12 | −11.49 | 0.99 |
| SMS-C10 | −2.12 | −12.11 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, H.; Chen, B.; Song, X.; Liu, Z.; Zhao, J.; Yin, G.; Li, Y.; Zong, Y.; Li, Q.; et al. Effects of Different Degrees of Hydrophobic Treatment on Soil–Water Characteristic Curves and Infiltration Coefficients of Hygroscopic Soils. Coatings 2022, 12, 1424. https://doi.org/10.3390/coatings12101424
Li X, Zhou H, Chen B, Song X, Liu Z, Zhao J, Yin G, Li Y, Zong Y, Li Q, et al. Effects of Different Degrees of Hydrophobic Treatment on Soil–Water Characteristic Curves and Infiltration Coefficients of Hygroscopic Soils. Coatings. 2022; 12(10):1424. https://doi.org/10.3390/coatings12101424
Chicago/Turabian StyleLi, Xiaolong, Haiqing Zhou, Botong Chen, Xiao Song, Ziqiang Liu, Jian Zhao, Guohong Yin, Yuling Li, Yuncui Zong, Qiushi Li, and et al. 2022. "Effects of Different Degrees of Hydrophobic Treatment on Soil–Water Characteristic Curves and Infiltration Coefficients of Hygroscopic Soils" Coatings 12, no. 10: 1424. https://doi.org/10.3390/coatings12101424





