Influence of Fin Thickness on the Thermal Performance and Selection of Coating Method for a Bus Duct Conductor
Abstract
:1. Introduction
2. Materials and Methods
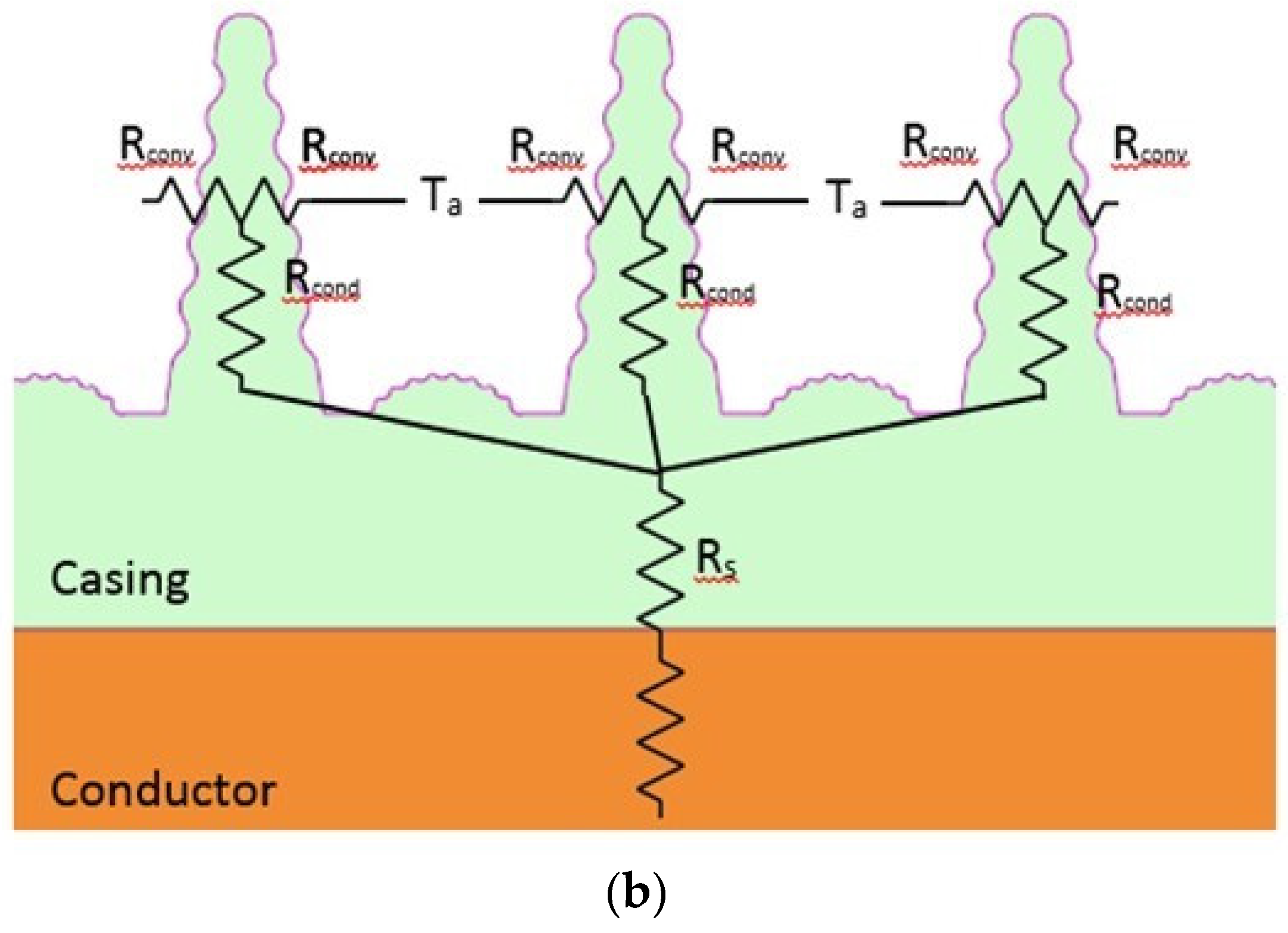
2.1. Mathematical Equations
- As = Heat transfer surface area
- h = convection heat transfer coefficient
2.2. Computational and Experimental Method
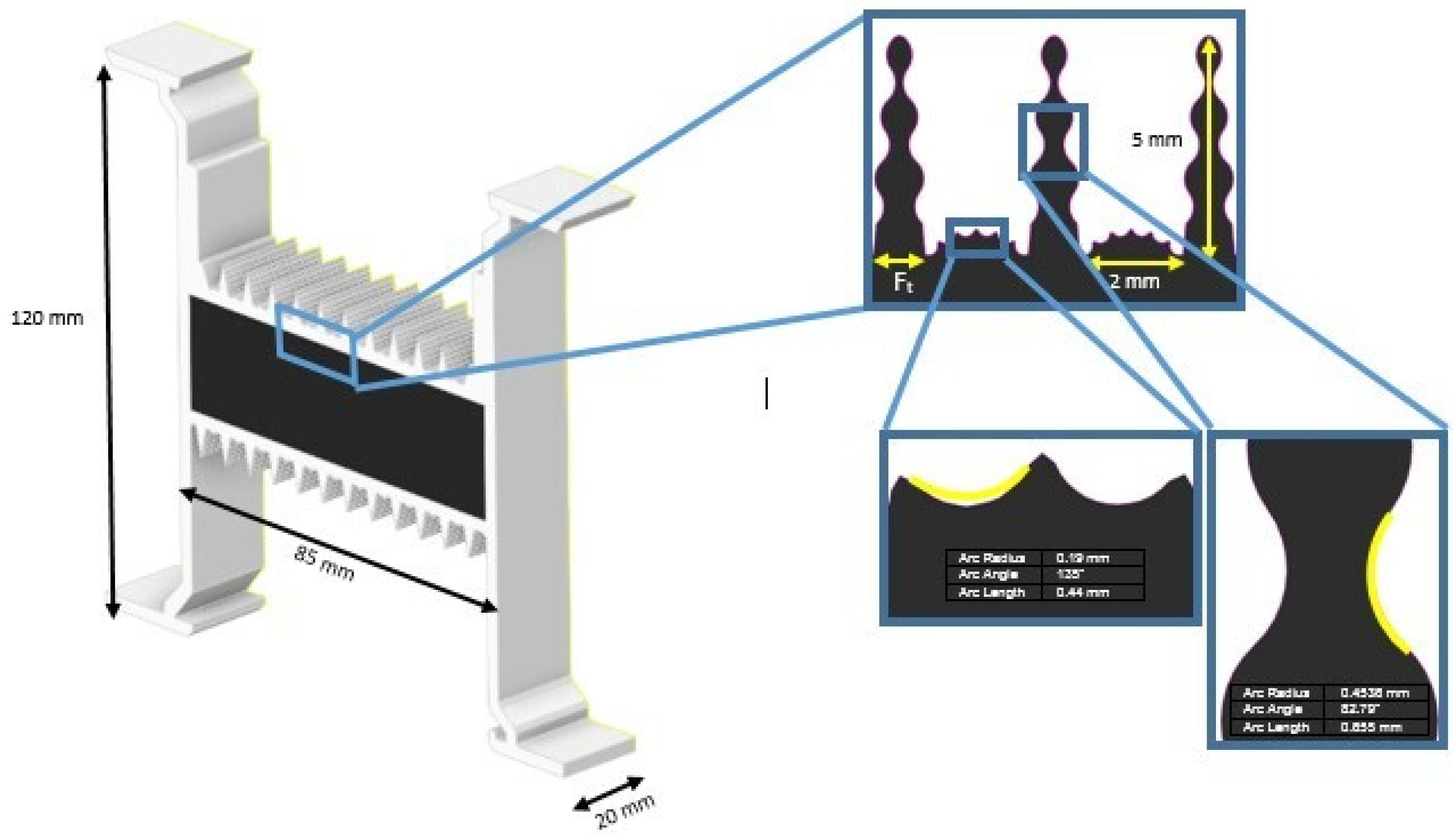
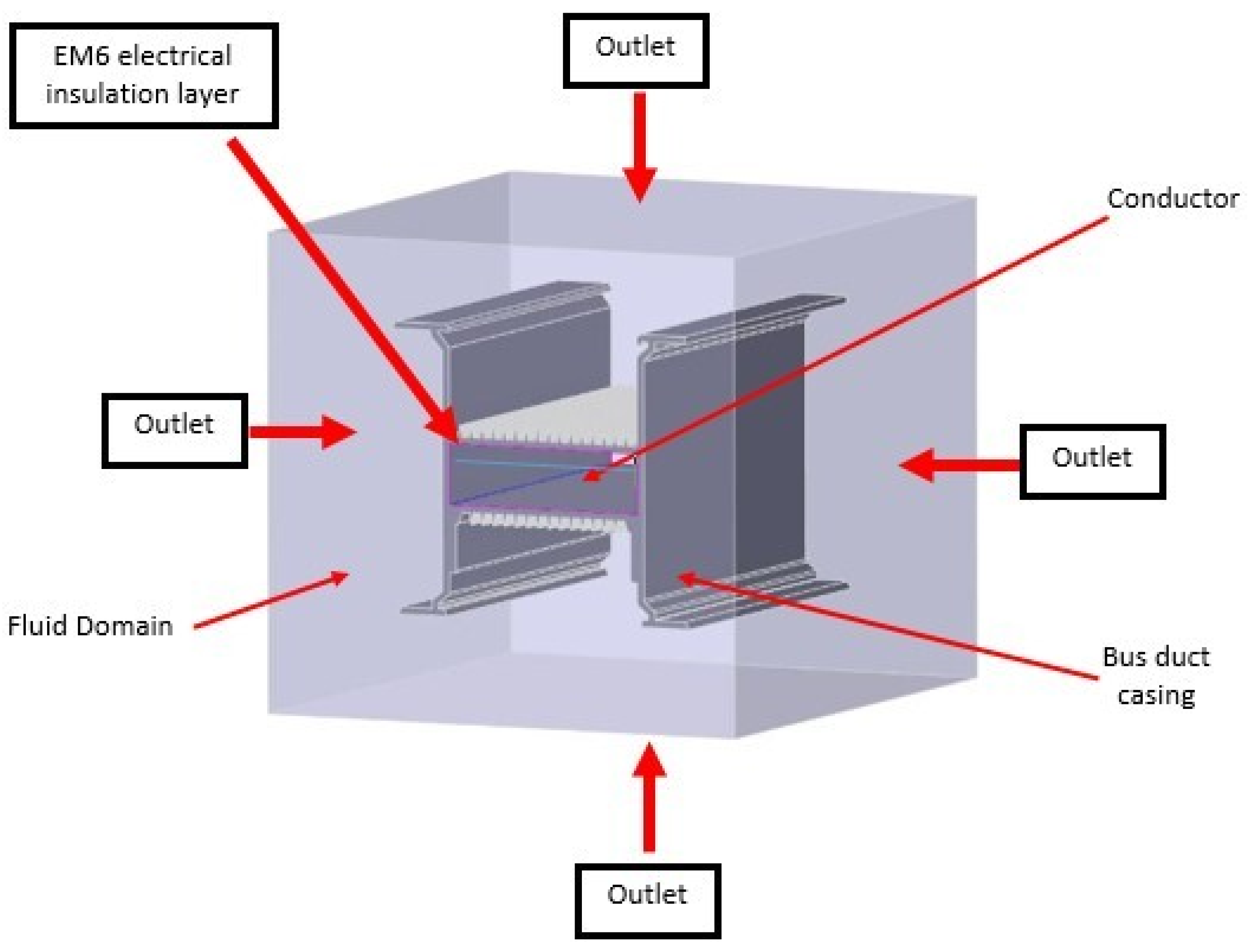
2.2.1. Geometrical Model
2.2.2. Mesh Setup
2.2.3. Grid Independence Test
2.2.4. Boundary and Initial Conditions
- Q = heat loss (W/m3)
- V = volume of geometry (m3)
- P = resistivity (kg⋅m3⋅s−3⋅A−2)
- L = length (m)
- S = cross-sectional area (m2)
- R = electrical resistance (Ω)
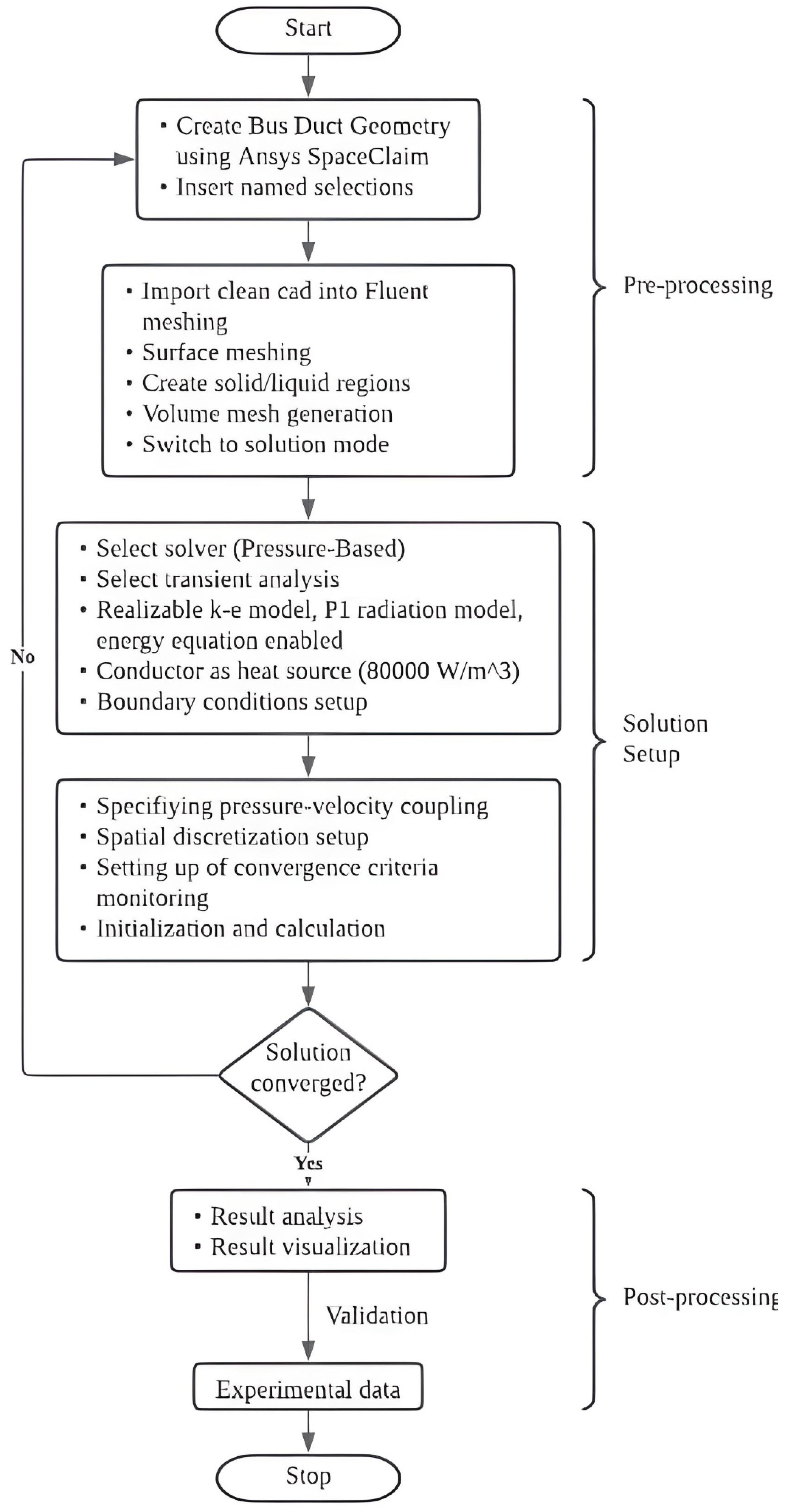
2.2.5. Simulation Setup
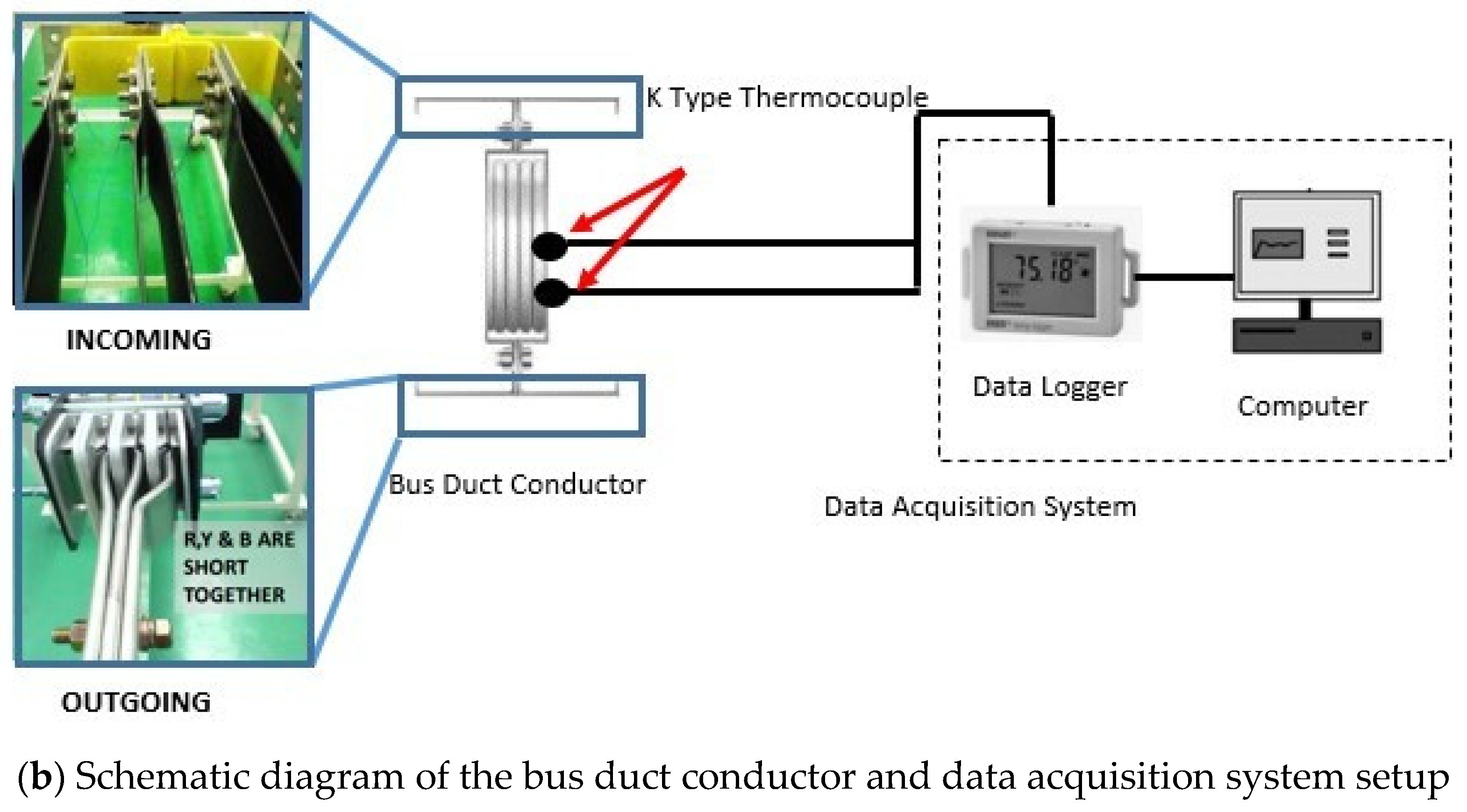
2.2.6. Experimental Setup
2.2.7. Experimental Validation
Experimental Data
Comparison between Experimental and Simulation Temperature Results
2.3. Fin Effectiveness and Fin Efficiency
2.3.1. Fin Effectiveness and Efficiency
2.3.2. Fin Effectiveness
2.3.3. Fin Efficiency
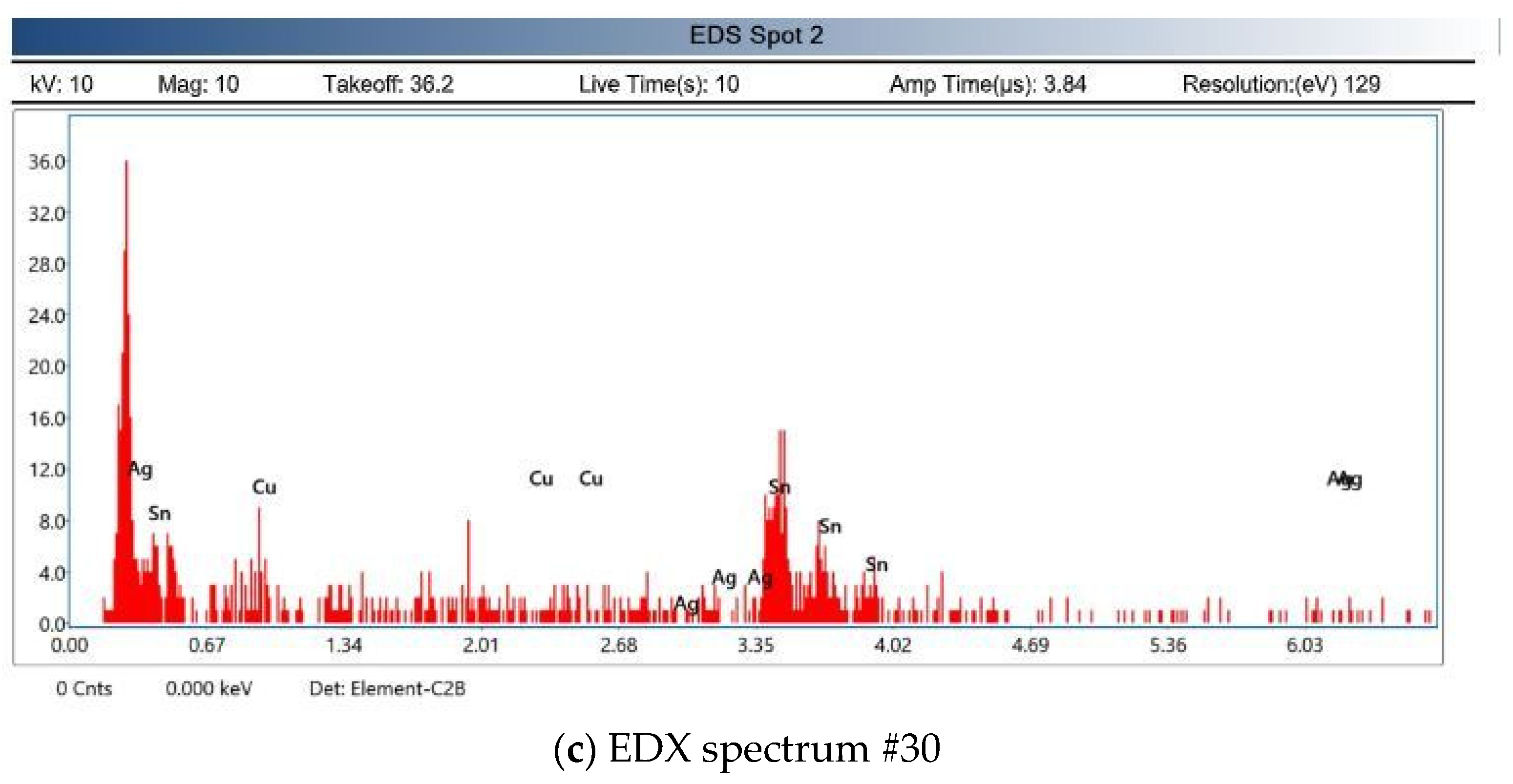
2.4. Dispersion of AgNP (Silver Nanoparticles) in Sn Plating Bath
3. Discussion
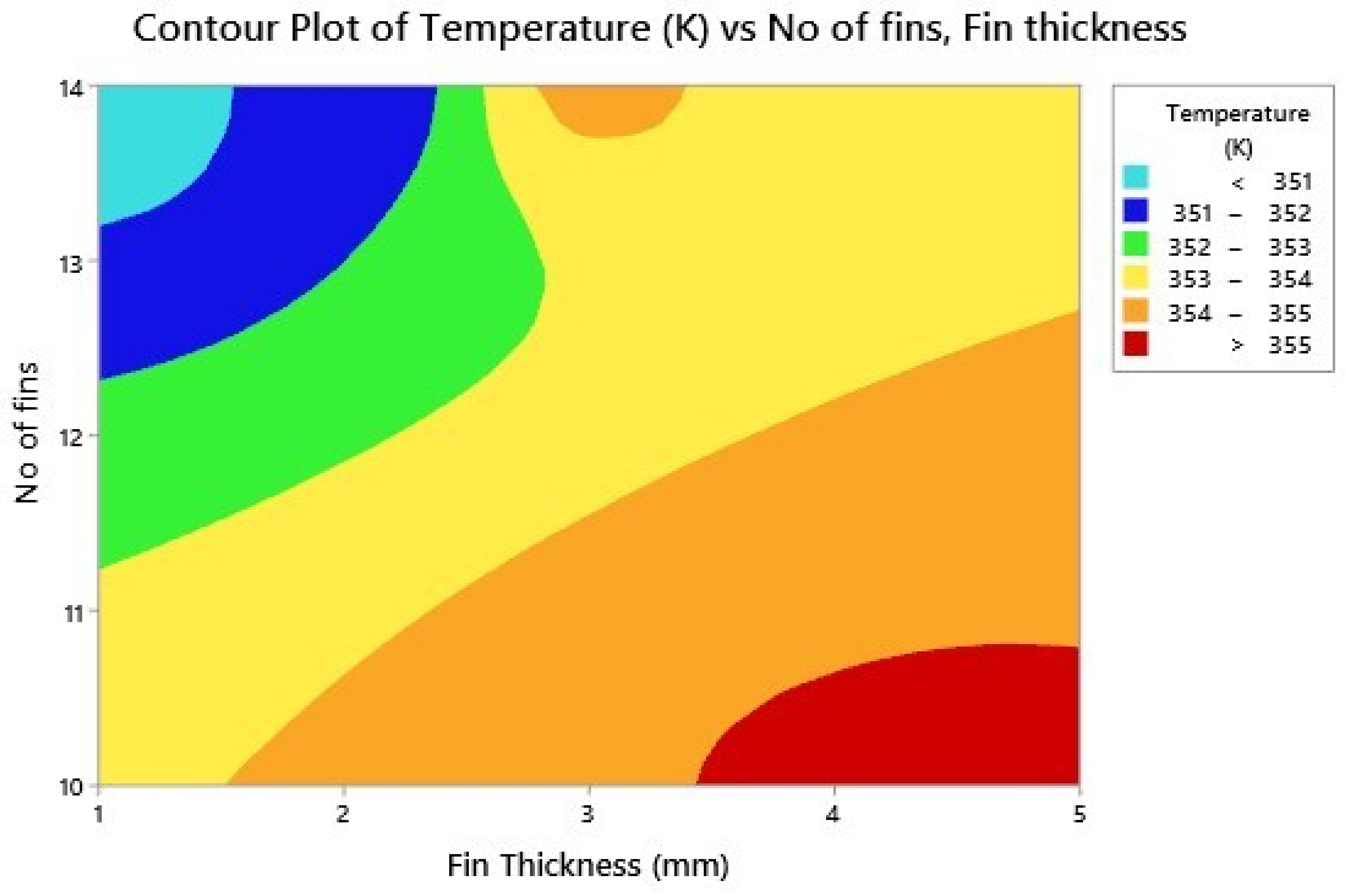
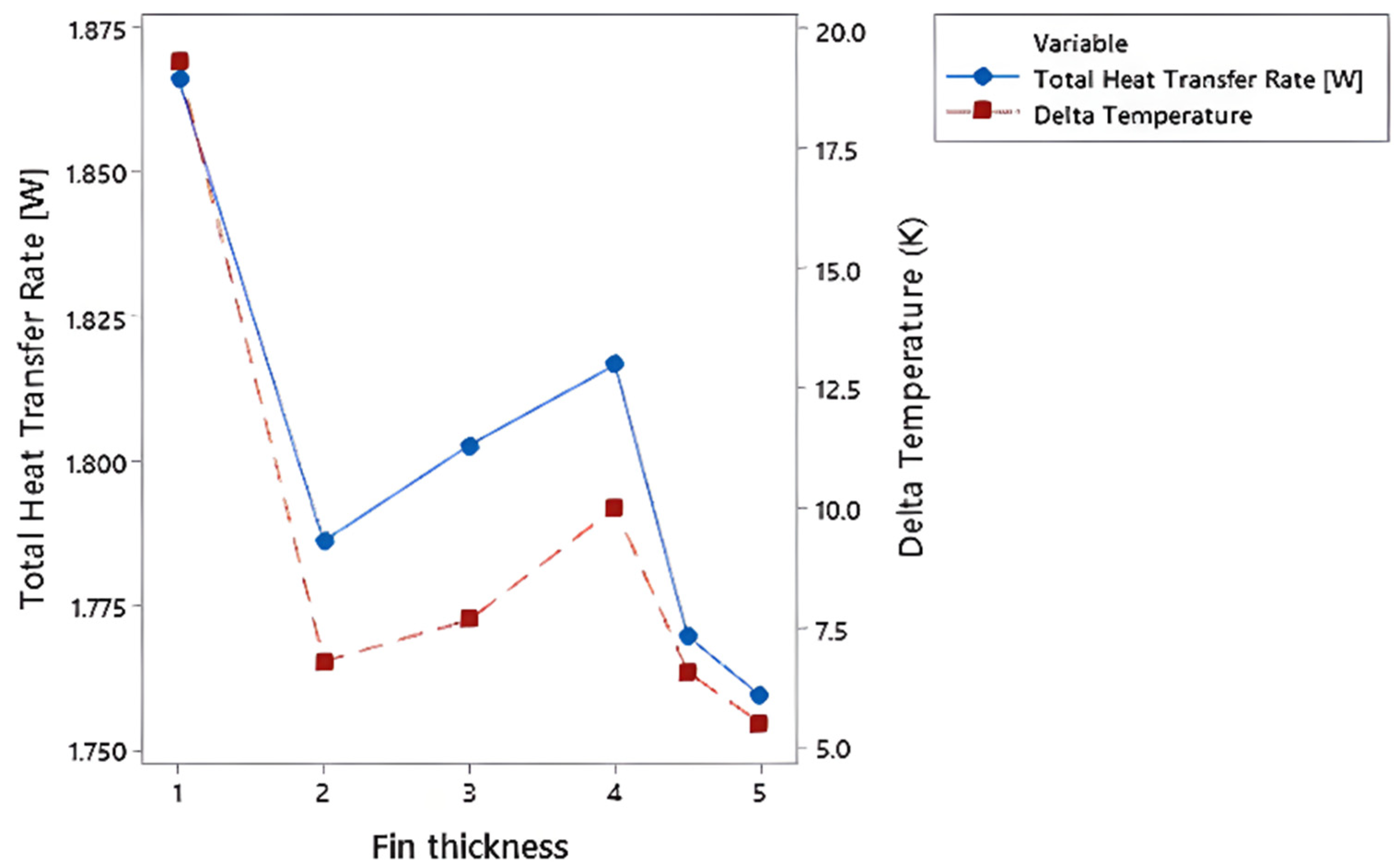
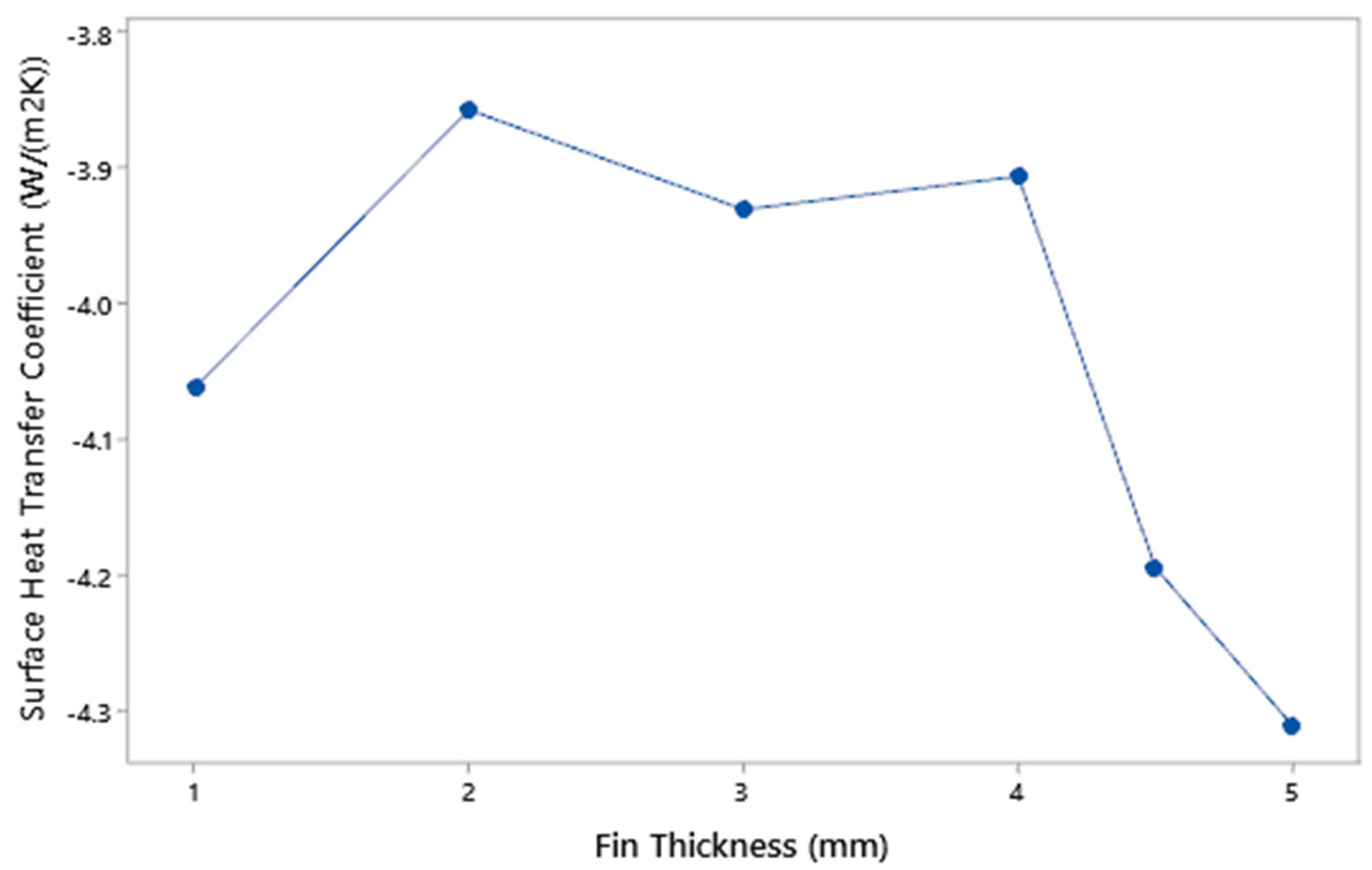
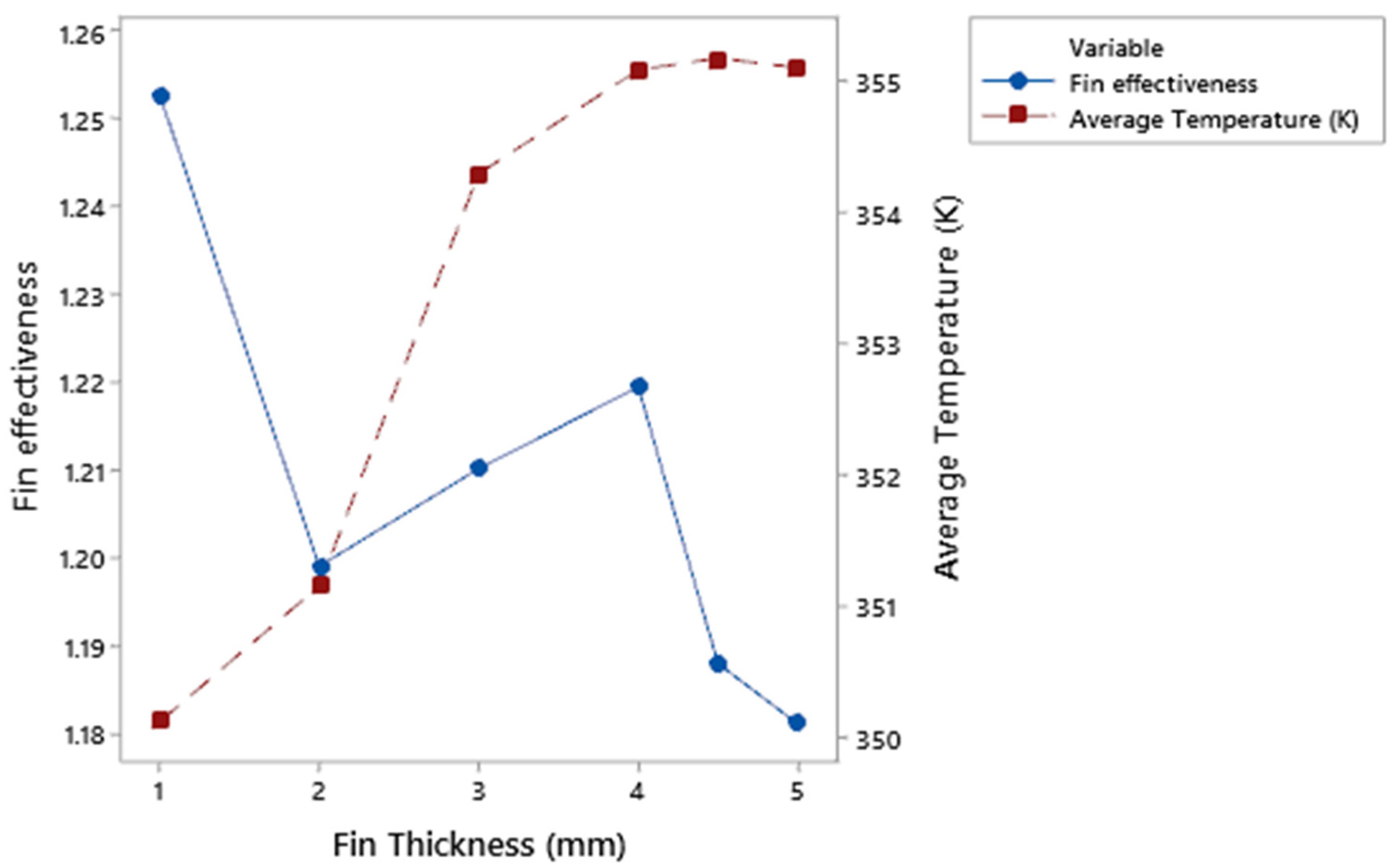
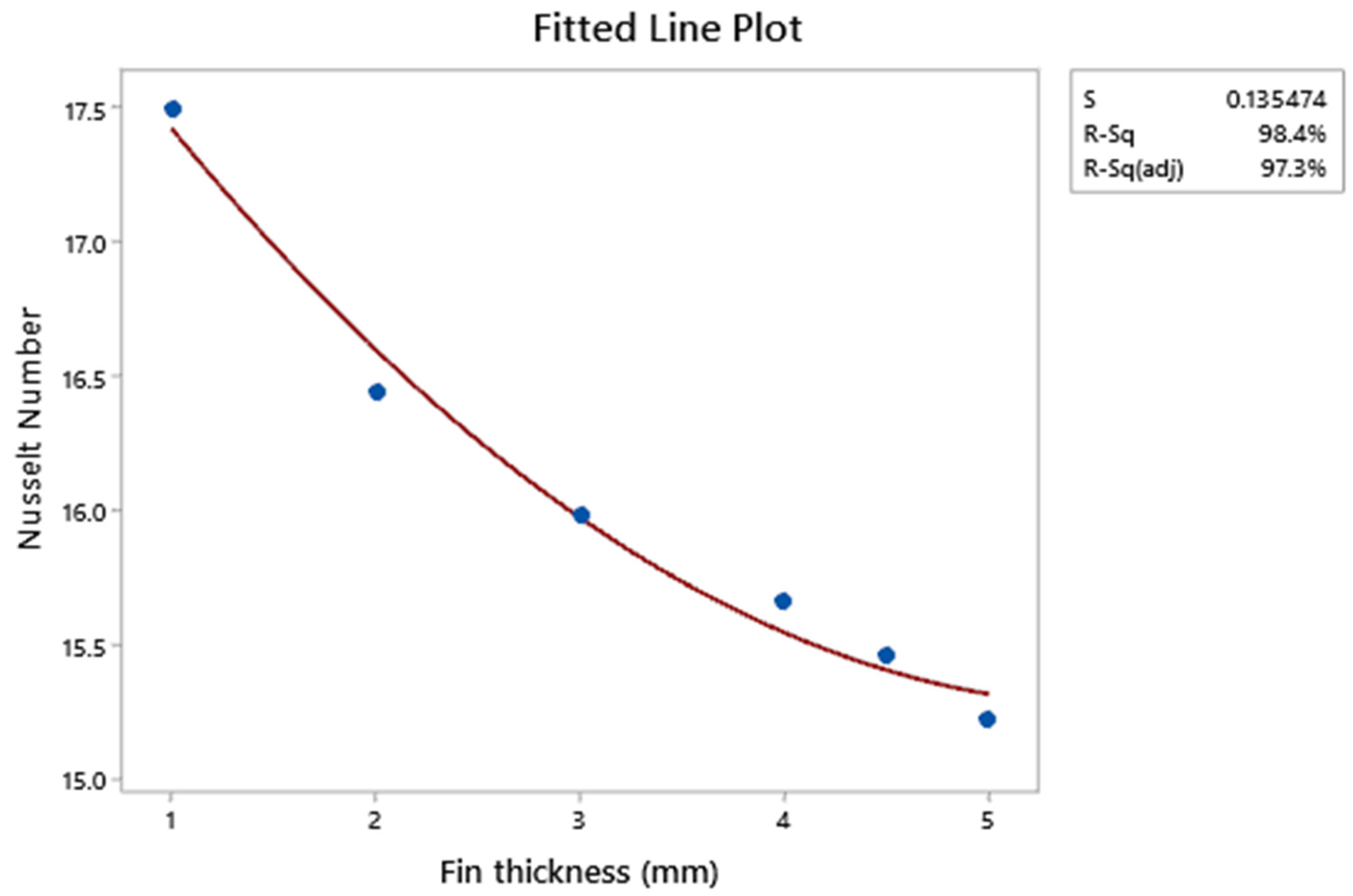
3.1. Fin Thickness (sn) Variation
- ∅q = heat flux.
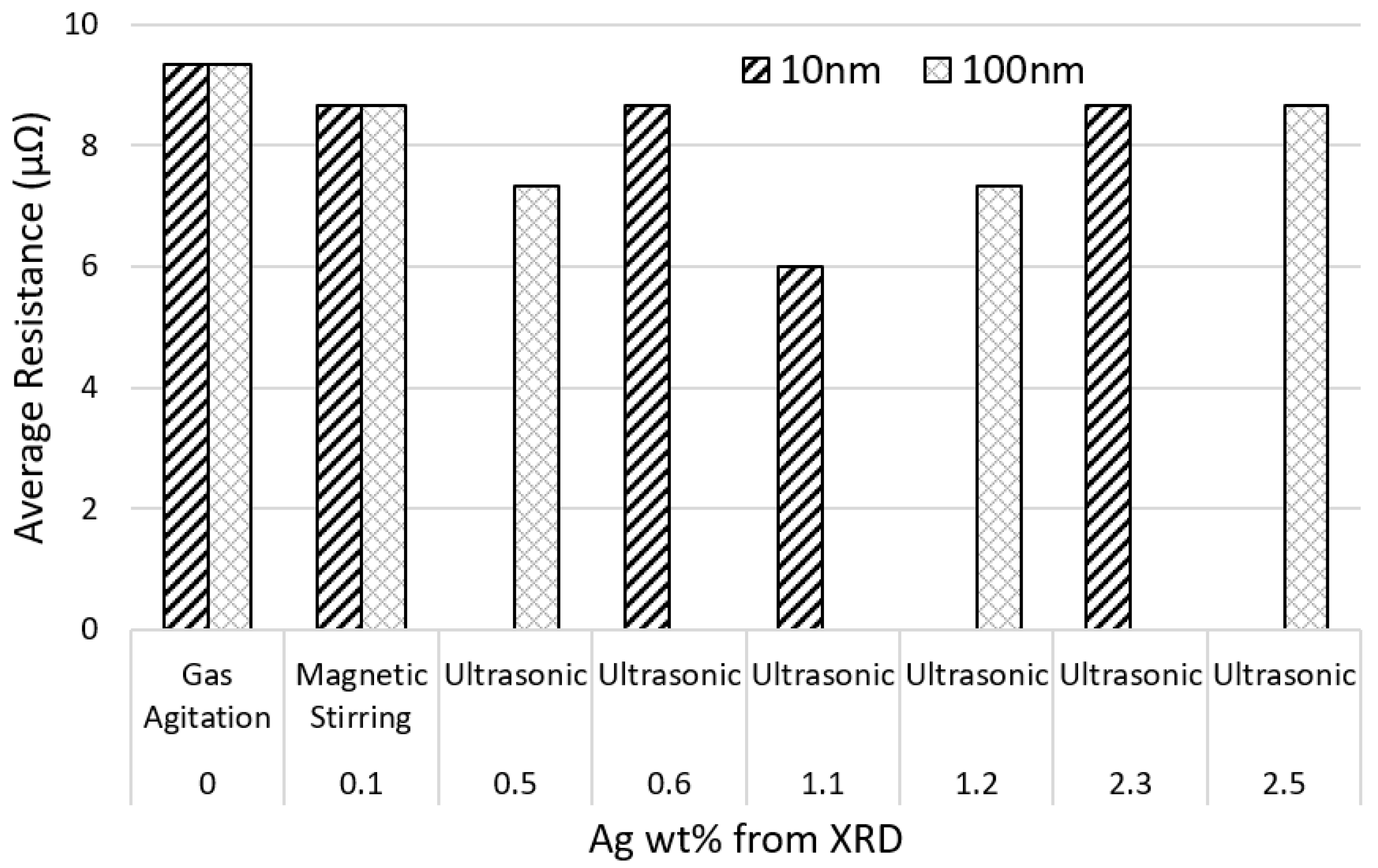
3.2. Analysis of Coated Sn-Plated Copper Substrate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thirumurugaveerakumar, S.; Sakthivel, M.; Valarmath, S. Experimental and analytical study on the bus duct system for the prediction of temperature variations due to the fluctuation of load. J. Electr. Eng. Technol. 2014, 9, 2036–2041. [Google Scholar] [CrossRef] [Green Version]
- Dhaiban, H.T.; Hussein, M.A. The optimal design of heat sinks: A review. J. Appl. Comput. Mech. 2020, 6, 1030–1043. [Google Scholar] [CrossRef]
- Hoi, S.M.; The, A.L.; Ooi, E.H.; Chew, I.M.L.; Foo, J.J. Plate-fin heat sink forced convective heat transfer augmentation with a fractal insert. Int. J. Therm. Sci. 2019, 142, 392–406. [Google Scholar] [CrossRef]
- Dake, T.J.; Majdalani, J. Improving flow circulation in heat sinks using quadrupole vortices. In Proceedings of the ASME InterPack Conference, Beijing, China, 10–13 August 2009; Volume 2, pp. 463–470. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Lin, Z.M.; Liu, S.; Su, M.; Wang, L.C.; Wang, L.B. Experimental study on the effects of fin pitches and tube diameters on the heat transfer and fluid flow characteristics of a fin punched with curved delta-winglet vortex generators. Appl. Therm. Eng. 2017, 119, 560–572. [Google Scholar] [CrossRef]
- Song, K.W.; Xi, Z.P.; Su, M.; Wang, L.C.; Wu, X.; Wang, L.B. Effect of geometric size of curved delta winglet vortex generators and tube pitch on heat transfer characteristics of fin-tube heat exchanger. Exp. Therm. Fluid Sci. 2017, 82, 8–18. [Google Scholar] [CrossRef]
- Vorayos, N.; Katkhaw, N.; Kiatsiriroat, T.; Nuntaphan, A. Heat transfer behavior of flat plate having spherical dimpled surfaces. Case Stud. Therm. Eng. 2016, 8, 370–377. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.S.; Yoon, S.Y.; Kim, B.; Lee, H.; Ha, M.Y.; Min, J.K. A topology optimization based design of a liquid-cooled heat sink with cylindrical pin fins having varying pitch. Int. J. Heat Mass Transf. 2021, 172, 121172. [Google Scholar] [CrossRef]
- Culham, J.R.; Muzychka, Y.S. Optimization of plate fin heat sinks using entropy generation minimization. IEEE Trans. Compon. Packag. Technol. 2001, 24, 159–165. [Google Scholar] [CrossRef]
- Tari, I.; Mehrtash, M. Natural convection heat transfer from horizontal and slightly inclined plate-fin heat sinks. Appl. Therm. Eng. 2013, 61, 728–736. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Vemuri, S.B. Orientation effects on natural convection/radiation heat transfer from pin-fin arrays. Int. J. Heat Mass Transf. 1986, 29, 359–368. [Google Scholar] [CrossRef]
- Jang, D.; Park, S.J.; Yook, S.J.; Lee, K.S. The orientation effect for cylindrical heat sinks with application to LED light bulbs. Int. J. Heat Mass Transf. 2014, 71, 496–502. [Google Scholar] [CrossRef]
- Effendi, N.S.; Kim, K.J. Orientation effects on natural convective performance of hybrid fin heat sinks. Appl. Therm. Eng. 2017, 123, 527–536. [Google Scholar] [CrossRef]
- Prajapati, Y.K. Influence of fin height on heat transfer and fluid flow characteristics of rectangular microchannel heat sink. Int. J. Heat Mass Transf. 2019, 137, 1041–1052. [Google Scholar] [CrossRef]
- Bhandari, P.; Prajapati, Y.K. Thermal performance of open microchannel heat sink with variable pin fin height. Int. J. Therm. Sci. 2021, 159, 106609. [Google Scholar] [CrossRef]
- Aldoori, W.H. The effect of fin height on forced convection heat transfer from rectangular fin array. Mater. Today Proc. 2021, 1–8. [Google Scholar] [CrossRef]
- Rahmani, E.; Moradi, T.; Fattahi, A.; Delpisheh, M.; Karimi, N.; Ommi, F.; Saboohi, Z. Numerical simulation of a solar air heater equipped with wavy and raccoon-shaped fins: The effect of fins’ height. Sustain. Energy Technol. Assess. 2021, 45, 101227. [Google Scholar] [CrossRef]
- Sertkaya, A.A.; Ozdemir, M.; Canli, E. Effects of pin fin height, spacing and orientation to natural convection heat transfer for inline pin fin and plate heat sinks by experimental investigation. Int. J. Heat Mass Transf. 2021, 177, 121527. [Google Scholar] [CrossRef]
- Lee, Y.J.; Kim, S.J. Thermal optimization of the pin-fin heat sink with variable fin density cooled by natural convection. Appl. Therm. Eng. 2021, 190, 116692. [Google Scholar] [CrossRef]
- Huang, X.; Shi, C.; Zhou, J.; Lu, X.; Xu, G. Performance analysis and design optimization of heat pipe sink with a variable height fin array under natural convection. Appl. Therm. Eng. 2019, 159, 113939. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Y.; Wang, J. International Journal of Thermal Sciences Theoretical and numerical investigation on the fin effectiveness and the fin efficiency of printed circuit heat exchanger with straight channels. Int. J. Therm. Sci. 2018, 132, 558–566. [Google Scholar] [CrossRef]
- Kobus, C.J.; Oshio, T. Development of a theoretical model for predicting the thermal performance characteristics of a vertical pin-fin array heat sink under combined forced and natural convection with impinging flow. Int. J. Heat Mass Transf. 2005, 48, 1053–1063. [Google Scholar] [CrossRef]
- Freegah, B.; Hussain, A.A.; Falih, A.H.; Towsyfyan, H. CFD analysis of heat transfer enhancement in plate-fin heat sinks with fillet profile: Investigation of new designs. Therm. Sci. Eng. Prog. 2020, 17, 100458. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Thermal performance and second law characteristics of two new microchannel heat sinks operated with hybrid nano fl uid containing graphene–silver nanoparticles. Energy Convers. Manag. 2018, 168, 357–370. [Google Scholar] [CrossRef]
- Hussain, A.A.; Freegah, B.; Khalaf, B.S.; Towsyfyan, H. Numerical investigation of heat transfer enhancement in plate-fin heat sinks: Effect of flow direction and fillet profile. Case Stud. Therm. Eng. 2019, 13, 100388. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y.S. Pressure drop of impingement air cooled plate fin heat sinks. J. Electron. Packag. 2007, 129, 190–194. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.C.; Indran, S. Impingement heat transfer of a plate fin heat sink with fillet profile. Int. J. Heat Mass Transf. 2013, 65, 1–9. [Google Scholar] [CrossRef]
- Li, H.Y.; Chen, K.Y. Thermal performance of plate-fin heat sinks under confined impinging jet conditions. Int. J. Heat Mass Transf. 2007, 50, 1963–1970. [Google Scholar] [CrossRef]
- Aziz, M.S.A.; Abdullah, M.Z.; Khor, C.Y.; Jalar, A.; Ani, F.C. CFD modeling of pin shape effects on capillary flow during wave soldering. Int. J. Heat Mass Transf. 2014, 72, 400–410. [Google Scholar] [CrossRef]
- Aziz, M.S.A.; Abdullah, M.Z.; Khor, C.Y.; Ani, F.C. Influence of pin offset in PCB through-hole during wave soldering process: CFD modeling approach. Int. Commun. Heat Mass Transf. 2013, 48, 116–123. [Google Scholar] [CrossRef]
- Aziz, M.S.A.; Abdullah, M.Z.; Khor, C.Y.; Jalar, A.; Ani, F.C.; Yan, N.; Cheok, C. Finite volume-based simulation of the wave soldering process: Influence of the conveyor angle on pin-through-hole capillary flow. Numer. Heat Transf. Part A Appl. 2016, 69, 295–310. [Google Scholar] [CrossRef]
- Rusdi, M.S.; Abdullah, M.Z.; Ishak, M.H.H.; Aziz, M.S.A.; Abdullah, M.K.; Rethinasamy, P. Three-dimensional CFD simulation of the stencil printing performance of solder paste. Int. J. Adv. Manuf. Technol. 2020, 108, 3351–3359. [Google Scholar] [CrossRef]
- Ishak, M.H.H.; Aziz, M.S.A.; Ismail, F.; Khor, C.Y.; Abdullah, M.Z.; Abas, M.A. Effect of filing level and fillet profile on pin-through hole solder joint. Int. J. Adv. Manuf. Technol. 2019, 102, 1467–1485. [Google Scholar] [CrossRef]
- Delgado, F.; Renedo, C.J.; Ortiz, A.; Fernández, I.; Santisteban, A. 3D thermal model and experimental validation of a low voltage three-phase busduct. Appl. Therm. Eng. 2017, 110, 1643–1652. [Google Scholar] [CrossRef] [Green Version]
- Zu, H.; Dai, W.; Li, Y.; Li, K.; Li, J. Analysis of enhanced heat transfer on a passive heat sink with high-emissivity coating. Int. J. Therm. Sci. 2021, 166, 106971. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Kim, J.; Choi, C.H.; Chung, W. Enhancement of heat dissipation of LED module with cupric-oxide composite coating on aluminum-alloy heat sink. Energy Convers. Manag. 2015, 106, 958–963. [Google Scholar] [CrossRef]
- Yildiz, O.; Lubna, M.M.; Ramesh, V.P.; Ozturk, M.; Bradford, P.D. Microporous vertically aligned CNT nanocomposites with tunable properties for use in flexible heat sinks. J. Sci. Adv. Mater. Devices 2022, 7, 100509. [Google Scholar] [CrossRef]
- Sainudeen, S.S.; Joseph, A.; Joseph, M.; Sajith, V. Heat transfer phenomena of copper-graphene nanocomposite coated aluminium heat spreaders: An interferometric study. Appl. Therm. Eng. 2022, 212, 118545. [Google Scholar] [CrossRef]
- Paramparambath, S.; Maurya, M.R.; Houkan, M.T.; Cabibihan, J.J.; Sadasivuni, K.K. Improvement of heat sink performance using paraffin/graphite/hydrogel phase change composite coating. Case Stud. Therm. Eng. 2022, 9, 102470. [Google Scholar] [CrossRef]
- Selvan, M.; Aziz, M.S.A.; Yu, K.H.; Nurulakmal, M.; Ong, H.; Khor, C. A study on the effect of fin pitch variation on the thermal performance of a bus duct conductor. Int. J. Therm. Sci. 2023, 184, 107938. [Google Scholar] [CrossRef]
- Selvan, M.; Aziz, M.S.A.; Nurulakmal, M.S.; Ong, H.P.; Khor, C.Y. Numerical study on the effect of fin length variation on the thermal performance of a bus duct conductor. Numer. Heat Transf. Part A Appl. 2022, 83, 116–133. [Google Scholar] [CrossRef]
- Standard k-ε Model. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/node58.htm (accessed on 10 October 2022).
- Zhang, Z.; Zhang, W.; Zhai, Z.J.; Chen, Q.Y. Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: Part 2—Comparison with experimental data from literature. HVAC R Res. 2007, 13, 871–886. [Google Scholar] [CrossRef]
- Yu, H.; Li, L.; Zhang, Y. Silver nanoparticle-based thermal interface materials with ultra-low thermal resistance for power electronics applications. Scr. Mater. 2012, 66, 931–934. [Google Scholar] [CrossRef]
- Coetzee, D.; Venkataraman, M.; Militky, J.; Petru, M. Influence of Nanoparticles on Thermal and Electrical Conductivity of Composites. Polymers 2020, 12, 742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Welker, R.W. Size Analysis and Identification of Particles; William Andrew Publishing: Norwich, NY, USA, 2011; pp. 179–213. [Google Scholar] [CrossRef]













| Mesh | A | B | C | D | E |
|---|---|---|---|---|---|
| Element count | 906,326 | 1,036,663 | 1,635,386 | 2,614,713 | 3,641,119 |
| Skewness level | 0.842 | 0.838 | 0.802 | 0.808 | 0.811 |
| Total heat transfer rate (W) | 3.444 | 3.461 | 3.485 | 3.486 | 3.478 |
| Deviation from case 5 (%) | 0.96 | 0.47 | 0.22 | 0.22 | 0.00 |
| Computing Time (h) | 7.1 | 8.2 | 9.4 | 10.4 | 13.1 |
| Constant | Value |
|---|---|
| C1Є | 1.44 |
| C2Є | 1.92 |
| Cµ | 0.09 |
| 1.0 | |
| 1.3 |
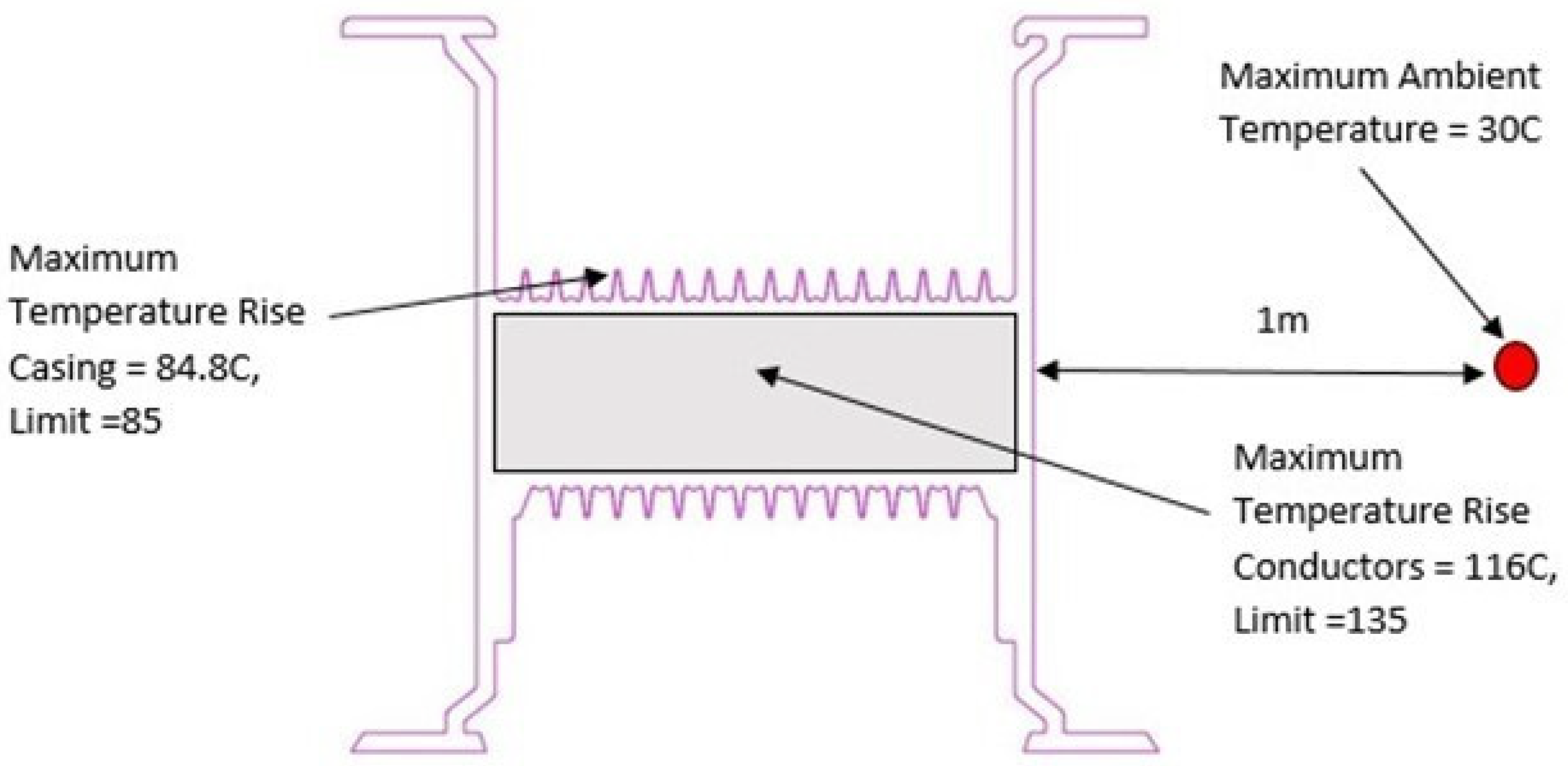
| Part Name | Temperature Rise Limit (°C) | Maximum Temperature Rise A (°C) | Ambient Temperature B (°C) | Total Absolute Temperature A + B (°C) |
|---|---|---|---|---|
| Conductor | 100.0 | 86.0 | 30.0 | 116.0 |
| Joint | 100.0 | 85.8 | 30.0 | 115.8 |
| Casing | 55.0 | 54.8 | 30.0 | 84.8 |
| Parameter | Dispersion Method | ||
|---|---|---|---|
| Ultrasonic Agitation | Magnetic Stirring | Argon Gas Agitation | |
| Current (A) | 2.0 | 2.0 | 2.0 |
| Voltage (V) | 1.0 | 1.0 | 1.5 |
| Solution (mL) | 600 | 600 | 1200 |
| Time (minute) | 3.0 | 3.0 | 5.0 |
| Specific input | U.S power: 50 Amp | Stirring speed: 200 rpm | Pressure: 2–3 Psi |
| Fin Thickness (mm) | Velocity Contour |
|---|---|
| 1.0 mm | 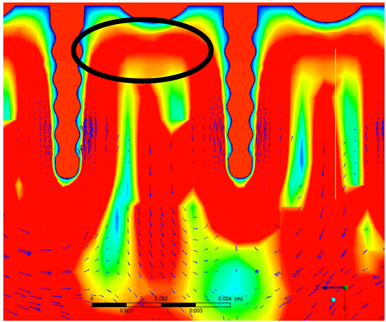 |
| 3.0 mm |  |
| 4.0 mm | 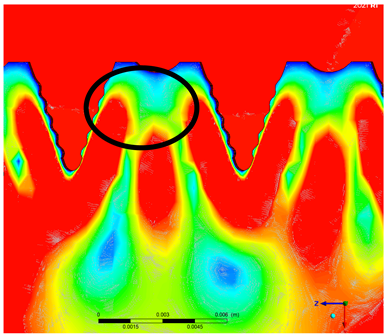 |
| 4.5 mm |  |
| 5.0 mm | 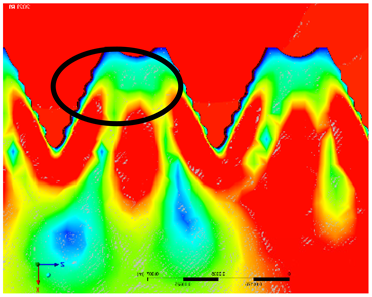 |
| No | Specimen | Dispersion Method | Ag wt% from XRD | Average Resistance (μΩ) |
|---|---|---|---|---|
| 1 | Cu Substrate | N/A | 0 | 8 |
| 2 | Sn-plated Cu substrate | Ultrasonic | 0 | 8.67 |
| 3 | 1 mL 10 nm AgNP + Sn-plated Cu substrate | Ultrasonic | 0.6 | 8.67 |
| 4 | 1 mL 100 nm AgNP + Sn-plated Cu substrate | Ultrasonic | 0.5 | 7.33 |
| 5 | 2 mL 10 nm AgNP + Sn-plated Cu substrate | Ultrasonic | 1.1 | 6.00 |
| 6 | 2 mL 100 nm AgNP + Sn-plated Cu substrate | Ultrasonic | 1.2 | 7.33 |
| 7 | 3 mL 10 nm AgNP + Sn-plated Cu substrate | Ultrasonic | 2.3 | 8.67 |
| 8 | 3 mL 100 nm AgNP + Sn-plated Cu substrate | Ultrasonic | 2.5 | 8.67 |
| 9 | 1 mL 10 nm AgNP + Sn-plated Cu substrate | Magnetic Stirring | 0.1 | 8.67 |
| 10 | 1 mL 100 nm AgNP + Sn-plated Cu substrate | Magnetic Stirring | 0.1 | 8.67 |
| 11 | 1 mL 10 nm AgNP + Sn-plated Cu substrate | Gas Agitation | 0 | 9.33 |
| 12 | 1 mL 100 nm AgNP + Sn-plated Cu substrate | Gas Agitation | 0 | 9.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvan, M.; Abdul Aziz, M.S.; Salleh, M.A.A.M.; Sharif, N.M.; Khor, C.Y.; Ong, H.P.; Zainol, M.R.R.M.A.; Vizureanu, P.; Burduhos-Nergis, D.-P.; Sandu, A.V. Influence of Fin Thickness on the Thermal Performance and Selection of Coating Method for a Bus Duct Conductor. Coatings 2023, 13, 12. https://doi.org/10.3390/coatings13010012
Selvan M, Abdul Aziz MS, Salleh MAAM, Sharif NM, Khor CY, Ong HP, Zainol MRRMA, Vizureanu P, Burduhos-Nergis D-P, Sandu AV. Influence of Fin Thickness on the Thermal Performance and Selection of Coating Method for a Bus Duct Conductor. Coatings. 2023; 13(1):12. https://doi.org/10.3390/coatings13010012
Chicago/Turabian StyleSelvan, Mark, Mohd Sharizal Abdul Aziz, Mohd Arif Anuar Mohd Salleh, Nurulakmal Mohd Sharif, Chu Yee Khor, Heng Pin Ong, Mohd Remy Rozaini Mohd Arif Zainol, Petrica Vizureanu, Diana-Petronela Burduhos-Nergis, and Andrei Victor Sandu. 2023. "Influence of Fin Thickness on the Thermal Performance and Selection of Coating Method for a Bus Duct Conductor" Coatings 13, no. 1: 12. https://doi.org/10.3390/coatings13010012
APA StyleSelvan, M., Abdul Aziz, M. S., Salleh, M. A. A. M., Sharif, N. M., Khor, C. Y., Ong, H. P., Zainol, M. R. R. M. A., Vizureanu, P., Burduhos-Nergis, D.-P., & Sandu, A. V. (2023). Influence of Fin Thickness on the Thermal Performance and Selection of Coating Method for a Bus Duct Conductor. Coatings, 13(1), 12. https://doi.org/10.3390/coatings13010012









