The Effects of Using Cements of Different Thicknesses and Amalgam Restorations with Different Young’s Modulus Values on Stress on Dental Tissue: An Investigation Using Finite Element Analysis
Abstract
:1. Background
2. Materials and Methods
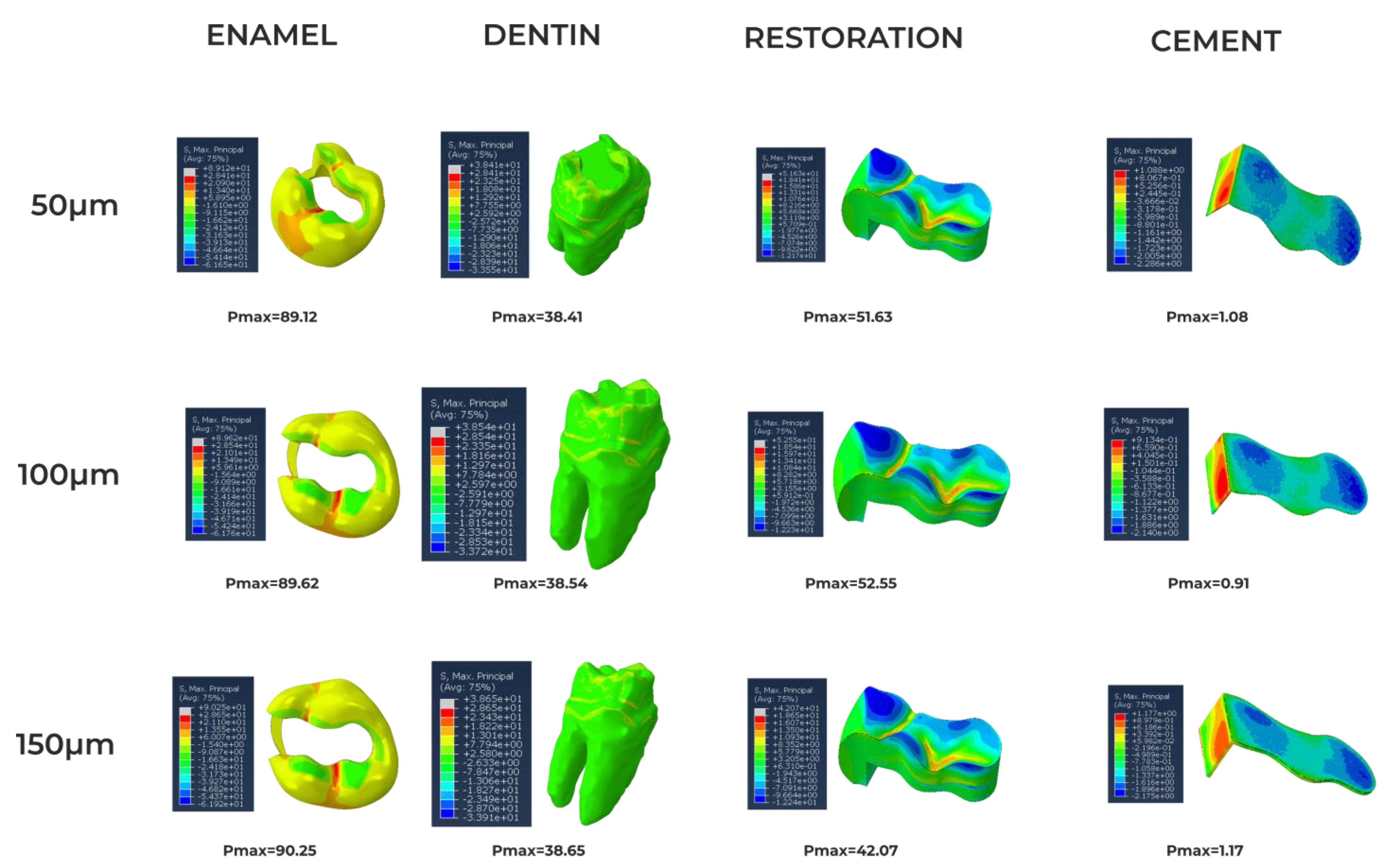
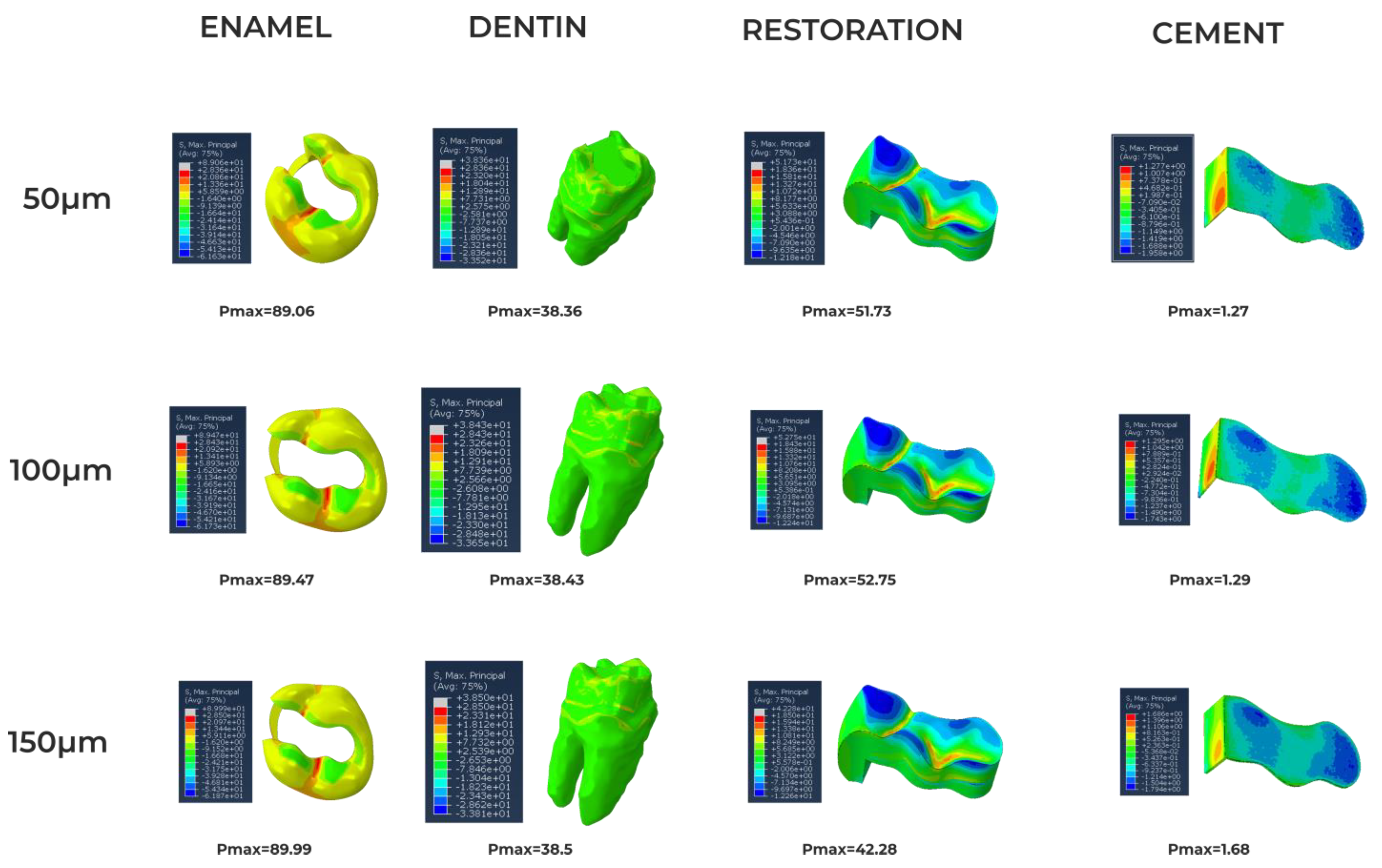
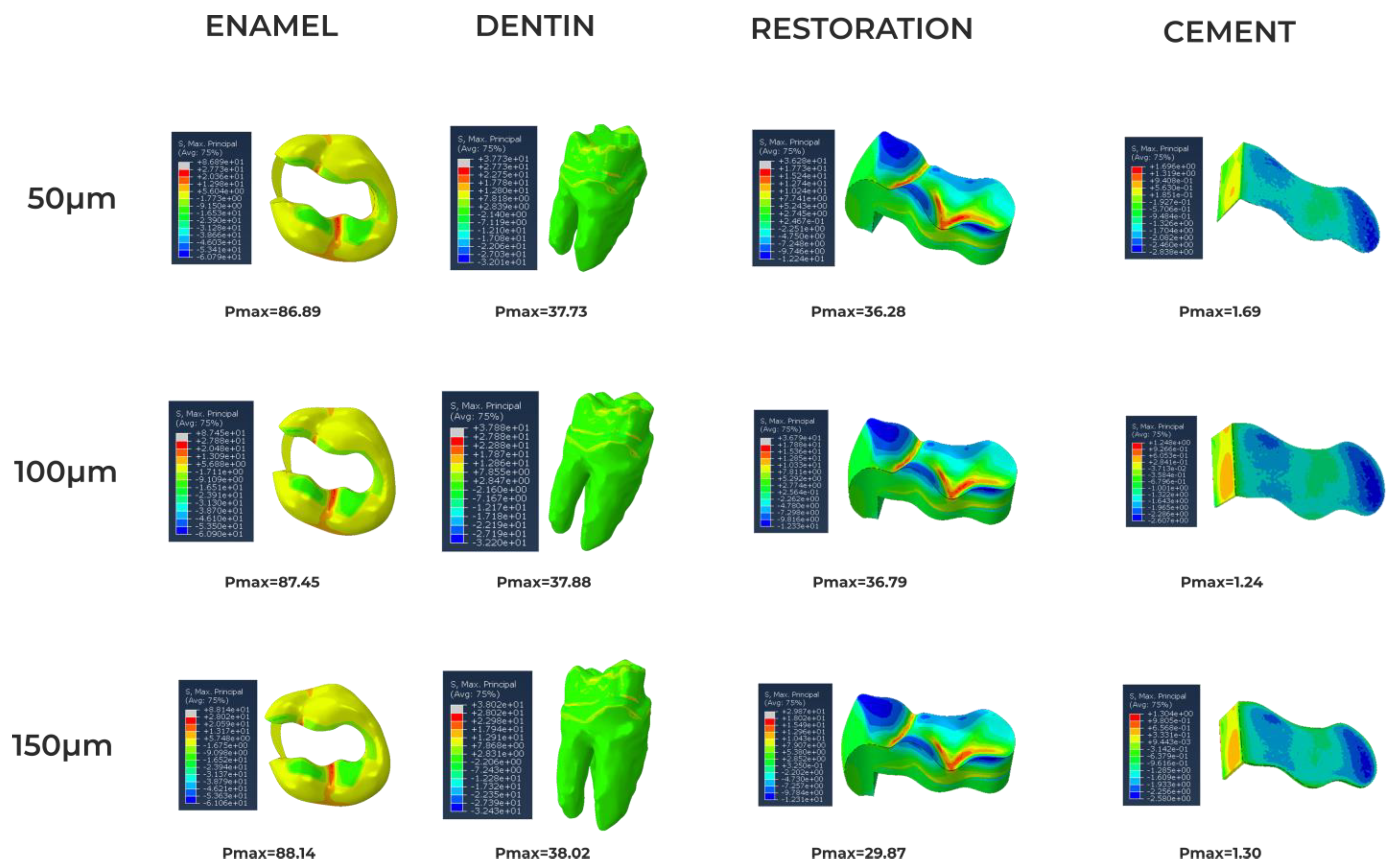
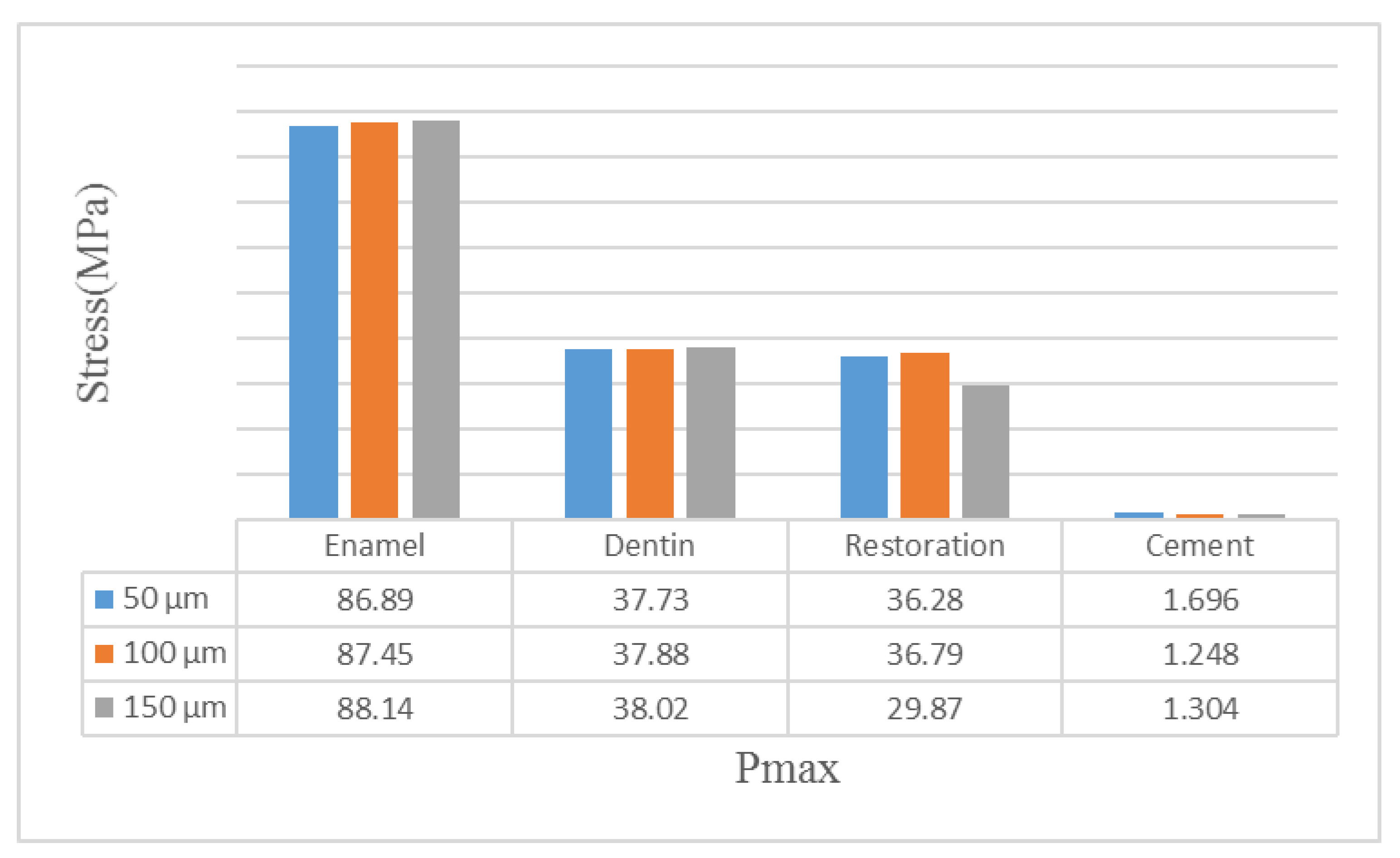
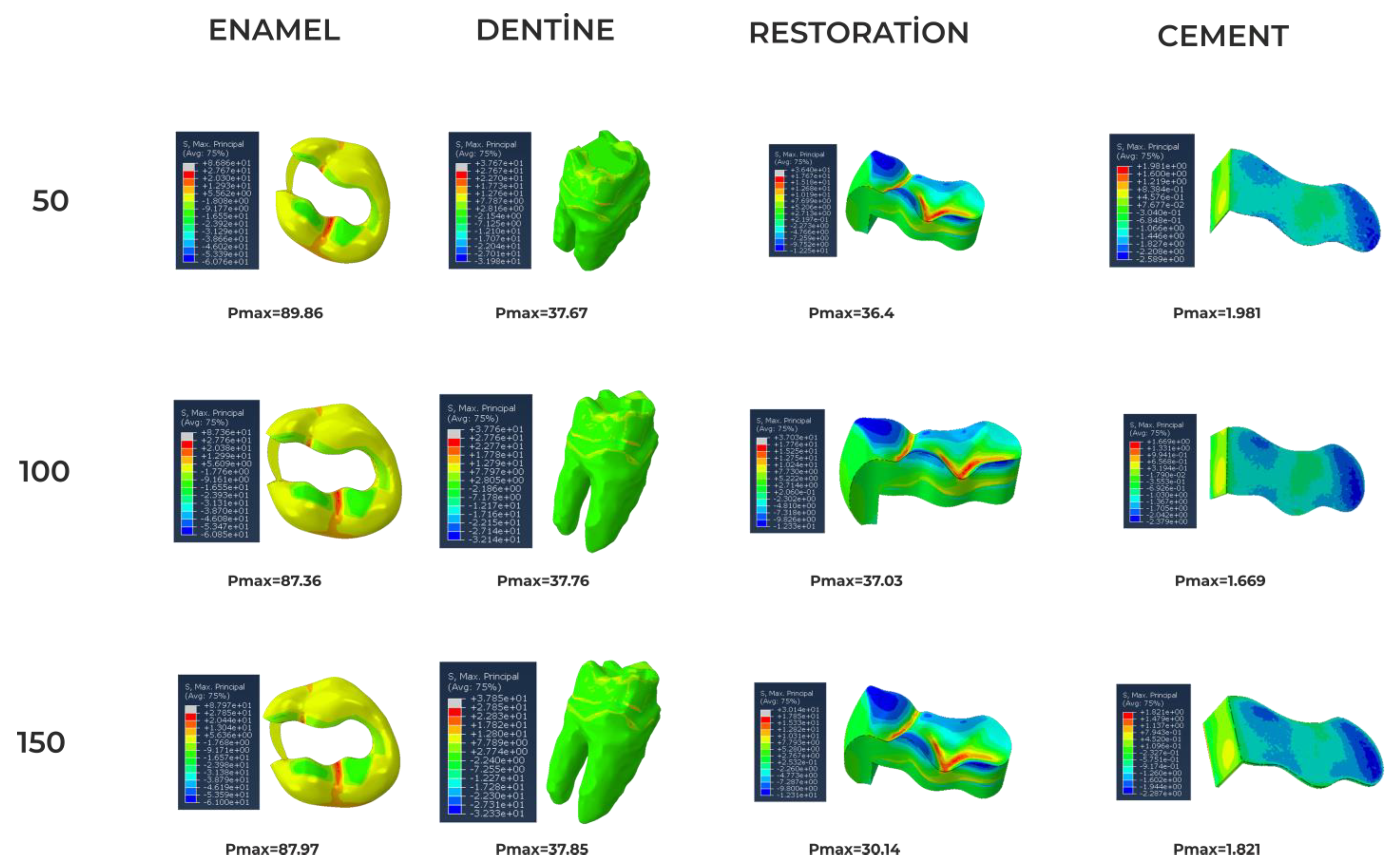
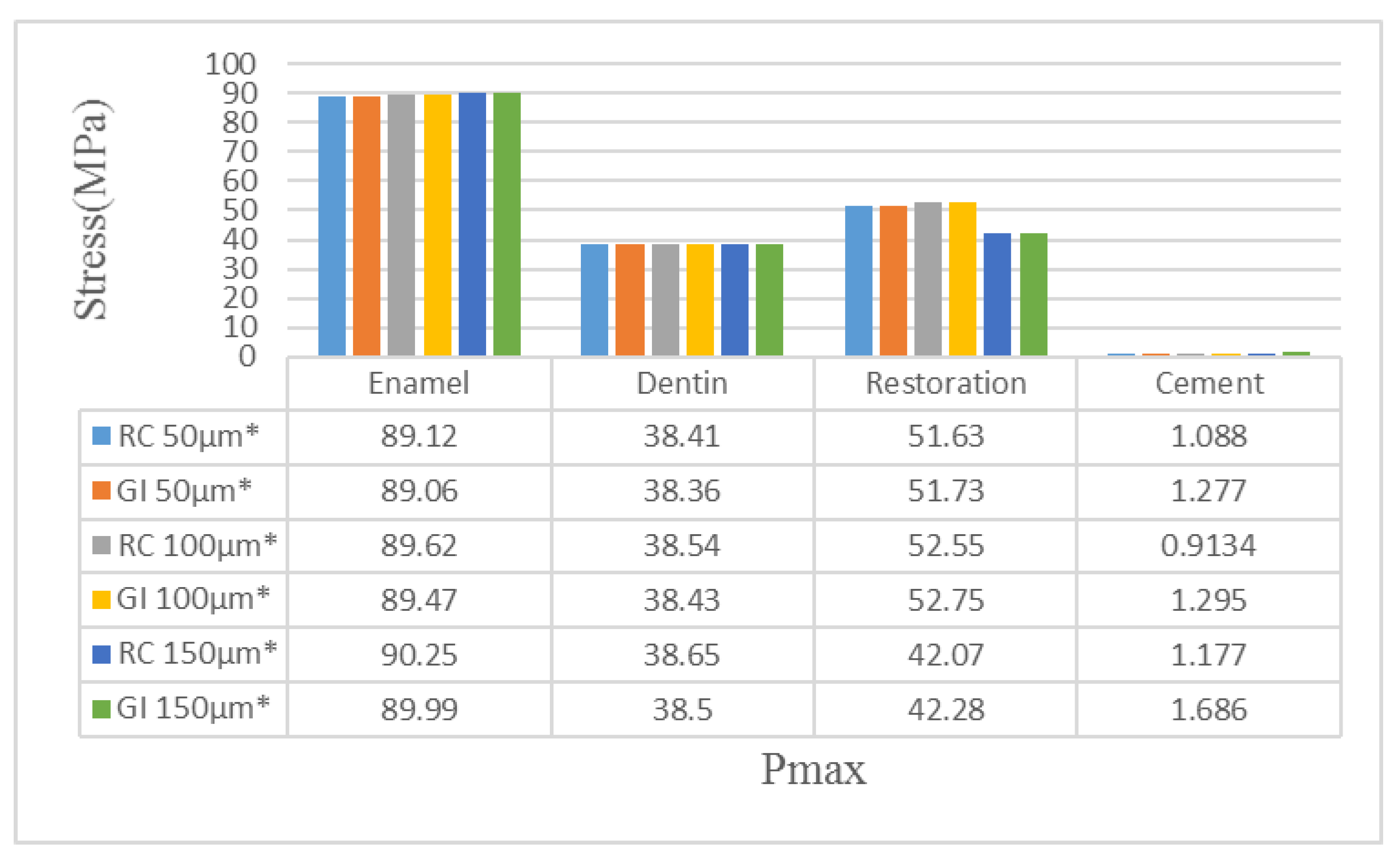
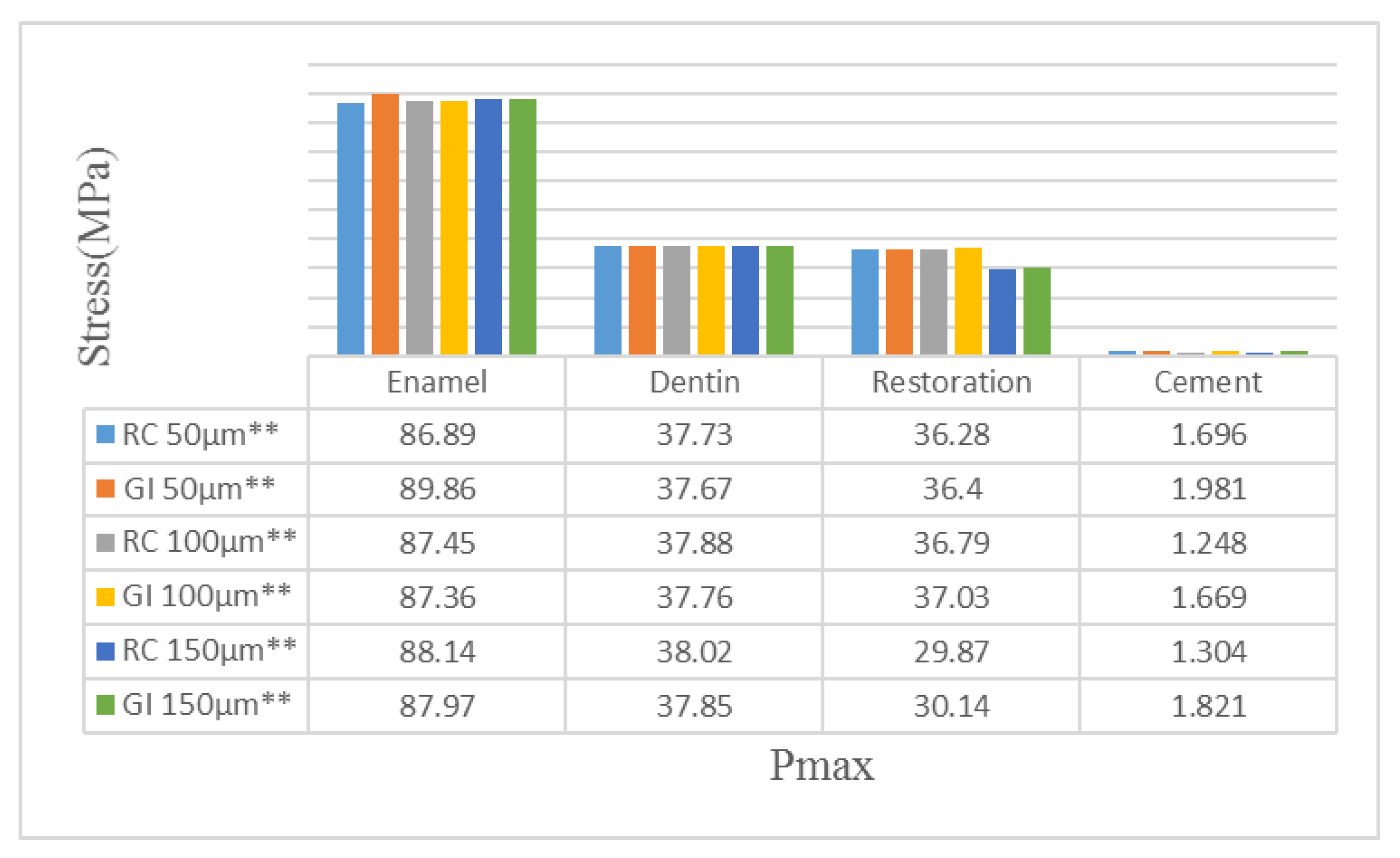
3. Results
4. Discussion
5. Conclusions
Clinical Implications
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GPa | Gigapascal |
| MPa | Megapascal |
| FEA | Finite Element Analysis |
| μ | micron |
| RC | Resin cement |
| GI | Glass ionomer cement |
| N | Newton |
References
- Williams, K.R.; Edmundson, J.T.; Rees, J.S. Finite element stress analysis of restored teeth. Dent. Mater. 1987, 3, 200–206. [Google Scholar] [CrossRef] [PubMed]
- Musani, I.; Prabhakar, A.R. Biomechanical stress analysis of mandibular first permanent molar; restored with amalgam and composite resin: A computerized finite element study. Int. J. Clin. Pediatr. Dent. 2010, 3, 5–14. [Google Scholar] [PubMed]
- Kotousov, A.; Kahler, B.; Swain, M. Analysis of interfacial fracture in dental restorations. Dent. Mater. 2011, 27, 1094–1101. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Fok, A.S.; Qualtrough, A. A two-stage shape optimization process for cavity preparation. Dent. Mater. 2008, 24, 1444–1453. [Google Scholar] [CrossRef]
- Asmussen, E.; Peutzfeldt, A. Class I and Class II restorations of resin composite: An FE analysis of the influence of modulus of elasticity on stresses generated by occlusal loading. Dent. Mater. 2008, 24, 600–605. [Google Scholar] [CrossRef]
- Srirekha, A.; Bashetty, K. Infinite to finite: An overview of finite element analysis. Indian J. Dent. Res. 2010, 21, 425–432. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
- Geng, J.P.; Tan, K.B.; Liu, G.R. Application of finite element analysis in implant dentistry: A review of the literature. J. Prosthet. Dent. 2001, 85, 585–598. [Google Scholar] [CrossRef] [Green Version]
- Parlar, Z.; Gökçek, E.; Yildirim, K.; Kahyaoglu, A. Influence of Cavity Design on Stress Distribution in Second Premolar Tooth Using Finite Element Analysis. Acta Phys. Pol. A 2017, 132, 949–953. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Du, W.; Zhou, X.D.; Yu, H.-Y. Review of research on the mechanical properties of the human tooth. Int. J. Oral Sci. 2014, 6, 61–69. [Google Scholar] [CrossRef] [Green Version]
- Shubhashini, N.; Meena, N.; Ashish Shetty, A.K.; Naveen, D.N. Finite element analysis of stress concentration in class V restorations of four groups of restorative materials in mandibular premolars. J. Cons. Dent. 2008, 11, 121–126. [Google Scholar] [CrossRef]
- Burke, F.J.; Wilson, N.H. When is caries caries, and what should we do about it? Quintessence Int. 1998, 29, 668–672. [Google Scholar] [PubMed]
- Roberson, T.M.; Heymann, H.O.; Swift, E.J. Sturdevant’s Art & Science of Operative Dentistry, 4th ed.; Mosby Company: Copenhagen, Denmark, 2002; p. 65. [Google Scholar]
- Yadav, R.K.; Verma, U.P.; Tiwari, R.; Chaurasia, A. Mercury or Mercury Free Restorations in Oral Cavity. Int. J. Public Health Sci. 2018, 7, 201–206. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, J.W. Glass-ionomers in medicine and dentistry. Proc. Inst. Mech. Eng. H 1998, 212, 121–126. [Google Scholar] [CrossRef] [PubMed]
- Francisconi, L.F.; Scaffa, P.M.; de Barros, V.R.; Coutinho, M.; Francisconi, P.A. Glass ionomer cement and their role in the restoration of non-carious cervical lesions. J. Appl. Oral Sci. 2009, 17, 364–369. [Google Scholar] [CrossRef] [PubMed]
- Pałka, K.; Bieniaś, J.; Dębski, H.; Niewczas, A. Finite element analysis of thermo-mechanical loaded teeth. Comput. Mater. Sci. 2012, 64, 289–294. [Google Scholar] [CrossRef]
- Rodrigues, M.D.; Soares, P.B.; Gomes, M.A.; Pereira, R.A.; Tantbirojn, D.; Versluis, A.; Soares, C.J. Direct resin composite restoration of endodontically-treated permanent molars in adolescents: Bite force and patient-specific finite element analysis. J. Appl. Oral Sci. 2020, 28, e20190544. [Google Scholar] [CrossRef] [PubMed]
- Babaei, B.; Shouha, P.; Birman, V.; Farrar, P.; Prentice, L.; Prusty, G. The effect of dental restoration geometry and material properties on biomechanical behaviour of a treated molar tooth: A 3D finite element analysis. J. Mech. Behav. Biomed. Mater. 2022, 125, 104892. [Google Scholar] [CrossRef] [PubMed]
- Sengul, F.; Gurbuz, T.; Sengul, S. Finite element analysis of different restorative materials in primary teeth restorations. Eur. J. Paediatr. Dent. 2014, 15, 317. [Google Scholar]
- Maghami, E.; Homaei, E.; Farhangdoost, K.; Pow, E.H.N.; Matinlinna, J.P.; Tsoi, J.K.H. Effect of preparation design for all-ceramic restoration on maxillary premolar: A 3D finite element study. J. Prosthodont. Res. 2018, 62, 436–442. [Google Scholar] [CrossRef]
- Guler, M.S.; Guler, C.; Cakici, F.; Cakici, E.B.; Sen, S. Finite element analysis of thermal stress distribution in different restorative materials used in class V cavities. Niger. J. Clin. Pract. 2016, 19, 30–34. [Google Scholar]
- Waltimo, A.; Könönen, M. A novel bite force recorder and maximal isometric bite force values for healthy young adults. Eur. J. Oral Sci. 1993, 101, 171–175. [Google Scholar] [CrossRef] [PubMed]
- Bakitian, F.; Papia, E.; Larsson, C.; von Steyern, P.V. Evaluation of stress distribution in tooth-supported fixed dental prostheses made of translucent zirconia with variations in framework designs: A three-dimensional finite element analysis. J. Prosthodont. 2020, 29, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Cornacchia, T.P.; Las Casas, E.B.; Cimini, C.A.; Peixoto, R.G. 3D finite element analysis on esthetic indirect dental restorations under thermal and mechanical loading. Med. Biol. Eng. Comput. 2010, 48, 1107–1113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zheng, K.; Li, E.; Li, W.; Li, Q.; Swain, M.V. Mechanical benefits of conservative restoration for dental fissure caries. J. Mech. Behav. Biomed. Mater. 2016, 53, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Dejak, B.; Młotkowski, A. A comparison of mvM stress of inlays, onlays and endocrowns made from various materials and their bonding with molars in a computer simulation of mastication–FEA. Dent. Mater. 2020, 36, 854–864. [Google Scholar] [CrossRef]
- Jiang, W.; Bo, H.; Yongchun, G.; LongXing, N. Stress distribution in molars restored with inlays or onlays with or without endodontic treatment: A three-dimensional finite element analysis. J. Prosthet. Dent. 2010, 103, 6–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; She, Y.; Liang, Y.; Xu, F.; Fang, C. The effect of endodontic access cavities on fracture resistance of first maxillary molar using the extended finite element method. J. Endod. 2019, 45, 316–321. [Google Scholar] [CrossRef]
- Ausiello, P.; Ciaramella, S.; Garcia-Godoy, F.; Gloria, A.; Lanzotti, A.; Maietta, S.; Martorelli, M. The effects of cavity-margin-angles and bolus stiffness on the mechanical behavior of indirect resin composite class II restorations. Dent. Mater. 2017, 33, e39–e47. [Google Scholar] [CrossRef]
- Kamposiora, P.; Papavasilious, G.; Bayne, S.C.; Felton, D.A. Finite element analysis estimates of cement microfracture under complete veneer crowns. J. Prosthet. Dent. 1994, 71, 435–441. [Google Scholar] [CrossRef]
- Soares, C.J.; Versluis, A.; Valdivia, A.D.C.M.; Bicalho, A.A.; Veríssimo, C.; de Castro Ferreira Barreto, B.; Roscoe, M.G. Finite Element Analysis in Dentistry-Improving the Quality of Oral Health Care. In Finite Element Analysis-from Biomedical Applications to Industrial Developments; Moratal, D., Ed.; InTech: London, UK, 2012; pp. 25–56. [Google Scholar]
- Bader, J.D.; Shugars, D.A.; Sturdevant, J.R. Consequences of posterior cusp fracture. Gen. Dent. 2004, 52, 128–131. [Google Scholar]
- O’Brien, J.W. Dental Materials and Their Selection; Quintessence Publishing Co., Inc.: Berlin, Germany, 2002; pp. 1–120. [Google Scholar]
- Arcís, R.W.; López-Macipe, A.; Toledano, M.; Osorio, E.; Rodrıéguez-Clemente, R.; Murtra, J.; Fanovich, M.A.; Pascual, C.D. Mechanical properties of visible light-cured resins reinforced with hydroxyapatite for dental restoration. Dent. Mater. 2002, 18, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Chun, K.J.; Lee, J.Y. Comparative study of mechanical properties of dental restorative materials and dental hard tissues in compressive loads. J. Dent. Biomech. 2014, 5, 1758736014555246. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.Y.; Kim, B.S.; Kim, H.; Cho, S.Y. Occlusal stress distribution and remaining crack propagation of a cracked tooth treated with different materials and designs: 3D finite element analysis. Dent. Mater. 2021, 37, 731–740. [Google Scholar] [CrossRef]
- Ausiello, P.P.; Ciaramella, S.; Lanzotti, A.; Ventre, M.; Borges, A.L.; Tribst, J.P.; Dal Piva, A.A.; Garcia-Godoy, F. Mechanical behavior of class I cavities restored by different material combinations under loading and polymerization shrinkage stress: A 3D-FEA study. Am. J. Dent. 2019, 32, 55–60. [Google Scholar] [PubMed]
- He, J.; Zheng, Z.; Wu, M.; Zheng, C.; Zeng, Y.; Yan, W. Influence of restorative material and cement on the stress distribution of endocrowns: 3D finite element analysis. BMC Oral Health 2021, 21, 495. [Google Scholar] [CrossRef]
- Neto, M.A.; Roseiro, L.; Messias, A.; Falacho, R.I.; Palma, P.J.; Amaro, A.M. Influence of cavity geometry on the fracture strength of dental restorations: Finite element study. Appl. Sci. 2021, 11, 4218. [Google Scholar] [CrossRef]
- Syed, A.U.Y.; Rokaya, D.; Shahrbaf, S.; Martin, N. Three-dimensional finite element analysis of stress distribution in a tooth restored with full coverage machined polymer crown. Appl. Sci. 2021, 11, 1220. [Google Scholar] [CrossRef]
- Nabih, S.M.; Ibrahim NI, M.; Elmanakhly, A.R. Mechanical and thermal stress analysis of hybrid ceramic and lithium disilicate based ceramic CAD-CAM inlays using 3-D finite element analysis. Braz. Dent. Sci. 2021, 24. [Google Scholar] [CrossRef]
- Tribst, J.P.M.; Dal Piva, A.M.D.O.; Penteado, M.M.; Borges, A.L.S.; Bottino, M.A. Influence of ceramic material, thickness of restoration and cement layer on stress distribution of occlusal veneers. Braz. Oral Res. 2018, 32, e118. [Google Scholar] [CrossRef]




| Material | Young’s Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Compressive Strength (MPa) |
|---|---|---|---|---|
| Dentin | 18.6 [17] | 0.31 [17] | 98.7 [18] | 297.0 [18] |
| Enamel | 84.1 [17] | 0.33 [17] | 10.3 [18] | 384.0 [18] |
| Amalgam | 35.0 [19] 50.0 [19] | 0.35 [19] 0.29 [19] | 3–58 [20] | 45–550 [20] |
| Resin Cement | 7.7 [21] | 0.3 [21] | 98 [21] | 262 [21] |
| Glass Ionomer | 10.8 [22] | 0.3 [22] | - | - |
| Study Group | Cement Thickness |
|---|---|
| RC | 50 µm |
| RC | 100 µm |
| RC | 150 µm |
| GI | 50 µm |
| GI | 100 µm |
| GI | 150 µm |
| Model | Total Elements | Total Nodes | Mesh Type |
|---|---|---|---|
| 50 μ | 7,428,602 | 1,347,225 | Linear tetrahedral elements of C3D4 |
| 100 μ | 7,445,941 | 1,350,049 | Linear tetrahedral elements of C3D4 |
| 150 μ | 7,457,979 | 1,352,224 | Linear tetrahedral elements of C3D4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gönder, H.Y.; Demirel, M.G.; Mohammadi, R.; Alkurt, S.; Fidancioğlu, Y.D.; Yüksel, I.B. The Effects of Using Cements of Different Thicknesses and Amalgam Restorations with Different Young’s Modulus Values on Stress on Dental Tissue: An Investigation Using Finite Element Analysis. Coatings 2023, 13, 6. https://doi.org/10.3390/coatings13010006
Gönder HY, Demirel MG, Mohammadi R, Alkurt S, Fidancioğlu YD, Yüksel IB. The Effects of Using Cements of Different Thicknesses and Amalgam Restorations with Different Young’s Modulus Values on Stress on Dental Tissue: An Investigation Using Finite Element Analysis. Coatings. 2023; 13(1):6. https://doi.org/10.3390/coatings13010006
Chicago/Turabian StyleGönder, Hakan Yasin, Mehmet Gökberkkaan Demirel, Reza Mohammadi, Sinem Alkurt, Yasemin Derya Fidancioğlu, and Ibrahim Burak Yüksel. 2023. "The Effects of Using Cements of Different Thicknesses and Amalgam Restorations with Different Young’s Modulus Values on Stress on Dental Tissue: An Investigation Using Finite Element Analysis" Coatings 13, no. 1: 6. https://doi.org/10.3390/coatings13010006






