First-Principles Investigation of Point Defects on the Thermal Conductivity and Mechanical Properties of Aluminum at Room Temperature
Abstract
:1. Introduction
2. Computational Detail
3. Result and Discussion
3.1. Defective Formation Energy
3.2. Mechanical Properties
3.3. Thermal Conductivity
4. Conclusions
- (1)
- The equilibrium lattice constant a0 of REAl is larger than that of Al, and it increases from Sc to La and linearly decreases to Lu with the increase of atomic number.
- (2)
- The defective formation energy Ef of all REAl is lower than that of VAl, and with the increase of the atomic number of RE, they increase from Sc to La at first and then decrease linearly to Lu.
- (3)
- Compared with Al, the elastic constant Cij, Cauchy pressure C12-C44, bulk modulus B, shear modulus G, Young’s modulus E, B/G, and Poisson’s ratio ν of all REAl decrease except for C44 of REAl (RE = La-Nd); With the increase of atomic number, the C11 and E of REAl decreases from Sc to La and slowly increases to Lu while C12, C44, B and G have little change.
- (4)
- The values of and B/G of defects increase Sc to Ce with the increase of atomic number, and it slightly change after Ce, while ν is unchanged. All defects containing perfect supercells present nonuniform and ductility.
- (5)
- The total TC κ is greatly reduced by the RE solute atom in the Al matrix, and it decreases Sc to La firstly and then increases linearly to Lu. The total TC κ of the Al matrix with early stage REAl (RE = La-Sm) is lower than that with VAl, while the total TC κ of the Al matrix with ScAl, YAl, and later stage REAl (RE = Gd-Lu) possesses a higher value.
- (6)
- When 1% RE atoms are added to the Al matrix, the reduction of TC by RE solute atoms is much greater than that by the formation of the L12 Al3RE second phase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wen, K.; Xiong, B.Q.; Fan, Y.Q.; Zhang, Y.A.; Li, Z.H.; Li, X.W.; Wang, F.; Liu, H.W. Transformation and dissolution of second phases during solution treatment of an Al-Zn-Mg-Cu alloy containing high zinc. Rare Met. 2018, 37, 376–380. [Google Scholar] [CrossRef]
- Seidman, D.N.; Marquis, E.A.; Dunand, D.C. Precipitation strengthening at ambient and elevated temperatures of heat-treatable Al(Sc) alloys. Acta Mater. 2002, 50, 4021–4035. [Google Scholar] [CrossRef]
- Czerwinski, F. Thermal Stability of Aluminum Alloys. Materials 2020, 13, 3441. [Google Scholar] [CrossRef] [PubMed]
- Senkov, O.N.; Shagiev, M.R.; Senkova, S.V.; Miracle, D.B. Precipitation of Al3(Sc, Zr) particles in an Al–Zn–Mg–Cu–Sc–Zr alloy during conventional solution heat treatment and its effect on tensile properties. Acta Mater. 2008, 56, 3723–3738. [Google Scholar] [CrossRef]
- Kim, C.W.; Cho, J.I.; Choi, S.W.; Kim, Y.C. The Effect of Alloying Elements on Thermal Conductivity of Aluminum Alloys in High Pressure Die Casting. Adv. Mater. Res. 2013, 813, 175–178. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, H.; Yang, Z.; Li, J.; Wang, X. Effect of copper content on the thermal conductivity and thermal expansion of Al–Cu/diamond composites. Mater. Des. 2012, 39, 87–92. [Google Scholar] [CrossRef]
- Kasprzak, W.; Sahoo, M.; Sokolowski, J.H.; Yamagata, H.; Kurita, H. The Effect of the Melt Temperature and the Cooling Rate on the Microstructure of the Al-20% Si Alloy Used for Monolithic Engine Blocks. Int. J. Metalcast. 2009, 3, 55–71. [Google Scholar] [CrossRef]
- Yu, S.; Wang, R.; Peng, C.; Cai, Z.; Wu, X.; Feng, Y.; Wang, X. Effect of minor scandium addition on the microstructure and properties of Al–50Si alloys for electronic packaging. J. Mater. Sci.-Mater. El. 2019, 30, 20770–20777. [Google Scholar] [CrossRef]
- Deng, J.; Chen, C.; Liu, X.; Li, Y.; Guo, S. A high-strength heat-resistant Al-5.7Ni eutectic alloy with spherical Al3Ni nano-particles by selective laser melting. Scripta Mater. 2021, 203, 114034. [Google Scholar] [CrossRef]
- Khaki-Davoudi, S.; Nourouzi, S.; Aval, H.J. Microstructure and mechanical properties of AA7075/Al3Ni composites produced by compocasting. Mater. Today Commun. 2021, 28, 102537. [Google Scholar] [CrossRef]
- Choi, S.W.; Cho, H.S.; Kang, C.S.; Kumai, S. Precipitation dependence of thermal properties for Al-Si-Mg-Cu-(Ti) alloy with various heat treatment. J. Alloys Compd. 2015, 647, 1091–1097. [Google Scholar] [CrossRef]
- Karamouz, M.; Azarbarmas, M.; Emamy, M.; Alipour, M. Microstructure, hardness and tensile properties of A380 aluminum alloy with and without Li additions. Mater. Sci. Eng. A 2013, 582, 409–414. [Google Scholar] [CrossRef]
- Han, Y.; Samuel, A.M.; Doty, H.W.; Valtierra, S.; Samuel, F.H. Optimizing the tensile properties of Al–Si–Cu–Mg 319-type alloys: Role of solution heat treatment. Mater. Des. 2014, 58, 426–438. [Google Scholar] [CrossRef]
- Lumley, R.N.; O’Donnell, R.G.; Gunasegaram, D.R.; Givord, M. Heat treatment of high-pressure die castings. Metall. Mater. Trans. A 2007, 38, 2564–2574. [Google Scholar] [CrossRef]
- Lumley, R.N.; Deeva, N.; Larsen, R.; Gembarovic, J.; Freeman, J. The role of alloy composition and T7 heat treatment in enhancing thermal conductivity of aluminum high pressure diecastings. Metall. Mater. Trans. A 2013, 44, 1074–1086. [Google Scholar] [CrossRef]
- Vandersluis, E.; Lombardi, A.; Ravindran, C.; Bois-Brochu, A.; Chiesa, F.; Mackay, R. Factors influencing thermal conductivity and mechanical properties in 319 Al alloy cylinder heads. Mater. Sci. Eng. A 2015, 648, 401–411. [Google Scholar] [CrossRef]
- Rauta, V.; Cingi, C.; Orkas, J. Effect of annealing and metallurgical treatments on thermal conductivity of aluminium alloys. Int. J. Metalcast. 2016, 10, 157–171. [Google Scholar] [CrossRef]
- Sheng, B.; Niu, M.; Shao, X. Conductivity and magnetic properties study on doped semiconductor material of 3C-SiC: A first-principle investigation. In Proceedings of the IEEE International Conference on Electric Information and Control Engineering 2011, Wuhan, China, 15–17 April 2011; pp. 5758–5761. [Google Scholar]
- Majid, A.; Rani, N.; Khan, U.D.; Almutairi, Z.A. First principles study of structural, electronic and magnetic properties of transition metals doped SiC monolayers for applications in spintronics. J. Magn. Magn. Mater. 2020, 503, 166648. [Google Scholar] [CrossRef]
- Cao, Z.; Jin, N.; Ye, J.; Du, X.; Liu, Y. First-principles study on the effects of N and Al doping on the mechanical properties and electronic structures of TiC. RSC Adv. 2020, 10, 36295–36302. [Google Scholar] [CrossRef]
- Li, C.C.; Ren, W.L.; Zhang, L.T.; Ito, K.; Wu, J.S. Effects of Al doping on the thermoelectric performance of CoSi single crystal. J. Appl. Phys. 2005, 98, 774. [Google Scholar] [CrossRef] [Green Version]
- Rajasekar, P.; Umarji, A.M. Effect of Al-doping on suppression of thermal conductivity in Si dispersed β-FeSi2. Intermetallics 2017, 89, 57–64. [Google Scholar] [CrossRef]
- Jia, P.-Z.; Xie, J.-P.; Chen, X.-K.; Zhang, Y.; Yu, X.; Zeng, Y.-J.; Xie, Z.-X.; Deng, Y.-X.; Zhou, W.-X. Recent progress of two-dimensional heterostructures for thermoelectric applications. J. Phys. Condens. Matter 2023, 35, 073001. [Google Scholar] [CrossRef] [PubMed]
- Weng, W.; Nagaumi, H.; Sheng, X.; Fan, W.; Chen, X.; Wang, X. Influence of Silicon Phase Particles on the Thermal Conductivity of Al-Si Alloys. In Light Metals 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 193–198. [Google Scholar]
- Cho, Y.H.; Kim, H.W.; Lee, J.M.; Kim, M.S. A new approach to the design of a low Si-added Al–Si casting alloy for optimising thermal conductivity and fluidity. J. Mater. Sci. 2015, 50, 7271–7281. [Google Scholar] [CrossRef]
- Vlach, M.; Čížek, J.; Smola, B.; Melikhova, O.; Vlček, M.; Kodetová, V.; Kudrnová, H.; Hruška, P. Heat treatment and age hardening of Al–Si–Mg–Mn commercial alloy with addition of Sc and Zr. Mater. Charact. 2017, 129, 1–8. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, J. First-principles investigations on vibrational, thermodynamic, mechanical properties and thermal conductivity of L12 Al3X (X=Sc, Er, Tm, Yb) intermetallics. Phys. Scr. 2015, 90, 1351–1354. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wang, S.Q. First-principles study of thermodynamic properties and solubility of aluminum-rare-earth intermetallics. Comput. Mater. Sci. 2014, 90, 56–60. [Google Scholar] [CrossRef]
- De Luca, A.; Shu, S.; Seidman, D. Effect of microadditions of Mn and Mo on dual L12- and α-precipitation in a dilute Al-Zr-Sc-Er-Si alloy. Mater. Charact. 2020, 169, 110585. [Google Scholar] [CrossRef]
- De Luca, A.; Seidman, D.; Dunand, D. Mn and Mo additions to a dilute Al-Zr-Sc-Er-Si-based alloy to improve creep resistance through solid-solution- and precipitation-strengthening. Acta Mater. 2020, 194, 60–67. [Google Scholar] [CrossRef]
- Farkoosh, A.; Dunand, D.; Seidman, D. Tungsten solubility in L12-ordered Al3Er and Al3Zr nanoprecipitates formed by aging in an aluminum matrix. J. Alloys Compd. 2020, 820, 153383. [Google Scholar] [CrossRef]
- Özer, T. Study of First Principles on Anisotropy and Elastic Constants of YAl3 Compound. Can. J. Phys. 2019, 98, 357–363. [Google Scholar] [CrossRef]
- Michi, R.A.; Perrin Toinin, J.; Farkoosh, A.R.; Seidman, D.N.; Dunand, D.C. Effects of Zn and Cr additions on precipitation and creep behavior of a dilute Al–Zr–Er–Si alloy. Acta Mater. 2019, 181, 249–261. [Google Scholar] [CrossRef]
- Dorin, T.; Babaniaris, S.; Jiang, L.; Cassel, A.; Robson, J.D. Stability and stoichiometry of L12 Al3(Sc,Zr) dispersoids in Al-(Si)-Sc-Zr alloys. Acta Mater. 2021, 216, 117117. [Google Scholar] [CrossRef]
- Henderson, H.B.; Hammons, J.A.; Baker, A.A.; McCall, S.K.; Li, T.T.; Perron, A.; Sims, Z.C.; Ott, R.T.; Meng, F.; Thompson, M.J.; et al. Enhanced thermal coarsening resistance in a nanostructured aluminum-cerium alloy produced by additive manufacturing. Mater. Des. 2021, 209, 109988. [Google Scholar] [CrossRef]
- Hung, C.J.; Nayak, S.K.; Sun, Y.; Fennessy, C.; Vedula, V.K.; Tulyani, S.; Lee, S.-W.; Alpay, S.P.; Hebert, R.J. Novel Al-X alloys with improved hardness. Mater. Des. 2020, 192, 108699. [Google Scholar] [CrossRef]
- Liu, S.H.; Wang, G.Q.; Min, W.A.; Gao, H.W.; Mao, L.C. Effects of rare earth elements on electrical conductivity of industrial aluminum. Chin. J. Nonferrous Met. 2000, 10, 335. [Google Scholar]
- Timpel, M.; Wanderka, N.; Murty, B.S.; Banhart, J. Three-dimensional visualization of the microstructure development of Sr-modified Al–15Si casting alloy using FIB-EsB tomography. Acta Mater. 2010, 58, 6600–6608. [Google Scholar] [CrossRef]
- Choi, S.W.; Kim, Y.M.; Lee, K.M.; Cho, H.S.; Hong, S.K.; Kim, Y.C.; Kang, C.S.; Kumai, S. The effects of cooling rate and heat treatment on mechanical and thermal characteristics of Al–Si–Cu–Mg foundry alloys. J. Alloys Compd. 2014, 617, 654–659. [Google Scholar] [CrossRef]
- García-García, G.; Espinoza-Cuadra, J.; Mancha-Molinar, H. Copper content and cooling rate effects over second phase particles behavior in industrial aluminum–silicon alloy 319—ScienceDirect. Mater. Des. 2007, 28, 428–433. [Google Scholar] [CrossRef]
- Marquis, E.A.; Seidman, D.N. Nanoscale structural evolution of Al3Sc precipitates in Al(Sc) alloys. Acta Mater. 2001, 49, 1909–1919. [Google Scholar] [CrossRef] [Green Version]
- Woodward, C.; Asta, M.; Kresse, G.; Hafner, J. Density of constitutional and thermal point defects in L12-Al3Sc. Phys. Rev. B 2001, 63, 094103. [Google Scholar] [CrossRef]
- Fu, C.L. Electronic, elastic, and fracture properties of trialuminide alloys: Al3Sc and Al3Ti. J. Mater. Res. 1990, 5, 971–979. [Google Scholar] [CrossRef]
- Clouet, E.; Nastar, M.; Sigli, C. Nucleation of Al3Zr and Al3Sc in aluminum alloys: From kinetic Monte Carlo simulations to classical theory. Phys. Rev. B 2004, 69, 064109. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Ke, J.L.; Zhang, Q.; Tang, B.Y.; Peng, L.M.; Ding, W.J. Mechanical properties of L12 type Al3X (X = Mg, Sc, Zr) from first-principles study. Phys. Status Solidi B 2012, 249, 1510–1516. [Google Scholar] [CrossRef]
- Colinet, C.; Pasturel, A.; Manh, D.N.; Pettifor, D.; Miodownik, P. Phase-stability study of the Al-Nb system. Phys. Rev. B 1997, 56, 552. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, P.; Chen, D.; Wu, Y.; Wang, M.; Ma, N.; Wang, H. First-principles investigation of thermodynamic, elastic and electronic properties of Al3V and Al3Nb intermetallics under pressures. J. Appl. Phys. 2015, 117, 085904. [Google Scholar] [CrossRef]
- Liu, T.; Ma, T.; Li, Y.; Ren, Y.; Liu, W. Stable, mechanical and thermodynamic properties of Al-RE intermetallics: A First-principles study. J. Rare Earths 2022, 40, 345–352. [Google Scholar] [CrossRef]
- Lv, C.; Yang, J.; Zhang, X.; Cai, Y.; Liu, X.; Wang, G.; Luo, S.-N. Interfacial effect on deformation and failure of Al/Cu nanolaminates under shear loading. J. Phys. D Appl. Phys. 2018, 51, 335301. [Google Scholar] [CrossRef]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
- Chowdhury, P.; Sehitoglu, H. Deformation physics of shape memory alloys–Fundamentals at atomistic frontier. Prog. Mater. Sci. 2017, 88, 49–88. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Derlet, P.M.; Froseth, A.G. Stacking fault energies and slip in nanocrystalline metals. Nat. Mater. 2004, 3, 399–403. [Google Scholar] [CrossRef]
- Fan, T.W.; Wang, Z.P.; Lin, J.J.; Chen, D.C.; Fang, Q.H.; Hu, T.; Nie, B.H.; Wang, K.; Hu, H.W.; Sun, H.B.; et al. First-principles predictions for stabilizations of multilayer nanotwins in Al alloys at finite temperatures. J. Alloys Compd. 2019, 783, 765–771. [Google Scholar] [CrossRef]
- Zhou, W.; Ren, X.; Ren, Y.; Yuan, S.; Ren, N.; Yang, X.; Adu-Gyamfi, S. Initial dislocation density effect on strain hardening in FCC aluminium alloy under laser shock peening. Philos. Mag. 2017, 97, 1–13. [Google Scholar] [CrossRef]
- Hui, J.; Zhang, X.; Liu, T.; Liu, W.; Wang, B. First-principles calculation of twin boundary energy and strength/embrittlement in hexagonal close-packed titanium. Mater. Des. 2022, 213, 110331. [Google Scholar] [CrossRef]
- Yan, H.; Guo, W.; Luan, T.; Ma, X.; Xu, G.; Leng, X.; Zhao, W.; Yan, J. Strengthening mechanism of Al/Sn interfaces: Study from experiments and first-principles calculation. Mater. Des. 2021, 212, 110292. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Liu, Y.; Ren, X. A comprehensive DFT study on the thermodynamic and mechanical properties of L12-Al3Ti/Al interface. Vacuum 2021, 183, 109858. [Google Scholar] [CrossRef]
- Jiang, D.; Xiao, W.; Liu, D.; Liu, S. Structural stability, electronic structures, mechanical properties and debye temperature of W-Re alloys: A first-principles study. Fusion Eng. Des. 2020, 162, 112081. [Google Scholar] [CrossRef]
- Maruhn, J.A.; Reinhard, P.G.; Suraud, E. Density Functional Theory; Plenum Press: New York, NY, USA, 2010. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Feynman, R.P. Forces in Molecules. Phys. Rev. 1939, 56, 340. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.; Tang, G.; Geng, W. VASPKIT: A User-friendly Interface Facilitating High-throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Madsen, G.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Northrup, J. Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion. Phys. Rev. Lett. 1991, 67, 2339. [Google Scholar] [CrossRef] [PubMed]
- Dong, T.; Zhang, X.; Yang, L.; Wang, F. An effect of structural vacancies on the lattice vibration, mechanical, electronic and thermodynamic properties of Cr5BSi3. Chin. Phys. B 2021, 31, 026101. [Google Scholar] [CrossRef]
- Qiu, R.; Lu, H.; Ao, B.; Huang, L.; Tang, T.; Chen, P. Energetics of intrinsic point defects in aluminium via orbital-free density functional theory. Philos. Mag. 2017, 97, 2164–2181. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, J.; Gupta, K.P. Low temperature lattice parameters of Al and Al-Zn alloys and Grüneisen parameter of Al. Cryogenics 1978, 18, 54–55. [Google Scholar] [CrossRef]
- Ehrhart, P. Atomic Defects in Metals; Ullmaier, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; Volume 25. [Google Scholar]
- Carling, K.; Wahnström, G.; Mattsson, T.R.; Mattsson, A.E.; Sandberg, N.; Grimvall, G. Vacancies in Metals: From First-Principles Calculations to Experimental Data. Phys. Rev. Lett. 2000, 85, 3862. [Google Scholar] [CrossRef]
- Fujikawa, S.I.; Sugaya, M.; Takei, H.; Hirano, K.I. Solid solubility and residual resistivity of scandium in aluminum. J. Less-Common Met. 1979, 63, 87–97. [Google Scholar] [CrossRef]
- Van De Walle, A.; Ceder, G. The effect of lattice vibrations on substitutional alloy thermodynamics. Rev. Mod. Phys. 2002, 74, 11. [Google Scholar] [CrossRef] [Green Version]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Page, Y.L.; Saxe, P. Symmetry-general least-squares extraction of elastic coefficients fromab initiototal energy calculations. Phys. Rev. B 2001, 63, 174103. [Google Scholar] [CrossRef]
- Sergio, G.V.; Alonso, J.A.; Gonzalo, S.; Martínez, J. Structure, stability, and optical absorption spectra of small TinCx clusters: A first-principles approach. Mon. Not. R. Astron. Soc. 2021, 508, 5074–5091. [Google Scholar]
- Wang, M.; Xie, J.; Xue, K.; Li, L. First-principles study of high-pressure structural stability and mechanical properties of Ni2B. Comput. Mater. Sci. 2021, 194, 110465. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z. First-principles study of structural, electronic, and mechanical properties of the nanolaminate compound Ti4GeC3 under pressure. J. Appl. Phys. 2010, 107, 201. [Google Scholar] [CrossRef]
- Hao, A.; Yang, X.; Wang, X.; Zhu, Y.; Liu, X.; Liu, R. First-principles investigations on electronic, elastic and optical properties of XC (X = Si, Ge, and Sn) under high pressure. J. Appl. Phys. 2010, 108, 9. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Meng, Y.; Wang, J.; Zhang, C.; Huang, H. Mechanical properties of defective L12-Al3X (X = Sc, Lu) phase: A first-principle study. J. Rare Earths 2020, 39, 217–224. [Google Scholar] [CrossRef]
- Gu, Q.; Ji, J.; Guo, F.; Chen, H.; Yang, T.; Tan, X. First Principle Study on the Electronic, Magnetic and Phase Stability of the Full-Heusler Compound Fe2CuSi. SPIN 2021, 11, 2150001. [Google Scholar] [CrossRef]
- Pu, Y.; Qiu, Z.; Lv, B.; Fang, C.; Lou, Y.; Wang, W.; Dai, Q. The first-principle study on certain structural, band-structural, elastic, optical and piezoelectric properties of the Ca, Zr and Ca/Zr-doped BaTiO3. Mod. Phys. Lett. B 2023, 37, 2350007. [Google Scholar] [CrossRef]
- Mebed, A.M.; Ali, M.A. First-principles calculations to investigate structural, elastic, electronic and thermoelectric properties of narrow-band gap half-Heusler RhVX(X = Si, Ge) compounds. Int. J. Mod. Phys. B 2023, 37, 22350163. [Google Scholar] [CrossRef]
- Meng, B.; Jing, T.; Xiao, W.Z. First-principle study on the stability, mechanical, electronic, and optical properties of two-dimensional scandium oxyhalides. Mater. Chem. Phys. 2022, 287, 126306. [Google Scholar] [CrossRef]
- Deng, Y.; Jia, O.H.; Chen, X.R.; Zhu, J. Phase transition and elastic constants of CaO from first-principle calculations. Phys. B 2007, 392, 229–232. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, L.; Liu, Y. First-principles calculations study the mechanical and thermal properties of Cr–Al–B ternary borides. Solid State Commun. 2021, 326, 114182. [Google Scholar] [CrossRef]
- Chen, C.; Fan, S.; Niu, J.; Huang, H.; Yuan, G. Alloying design strategy for biodegradable zinc alloys based on first-principles study of solid solution strengthening. Mater. Des. 2021, 204, 109676. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermodynamics of crystals. Am. J. Phys. 1972, 40, 1718–1719. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 1988, 37, 3924–3931. [Google Scholar] [CrossRef]
- Fu, H.; Zhao, Z.; Liu, W.; Peng, F.; Gao, T.; Cheng, X. Ab initio calculations of elastic constants and thermodynamic properties of γ-TiAl under high pressures. Intermetallics 2010, 18, 761–766. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Naukova Dumka: Kiev, Ukraine, 1983. [Google Scholar]
- Mallick, P.K. Materials, Design and Manufacturing for Lightweight Vehicles; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Takahashi, K.; Kuwahara, H.; Kawasaki, N.; Obata, T.; Sugawa, E. Enhancement of Thermal Contact Conductance Between Metal Surfaces in an Induction Motor. J Enhanc. Heat Transf. 2001, 8, 201–213. [Google Scholar] [CrossRef]
- Powell, R.W. Correlation of metallic thermal and electrical conductivities for both solid and liquid phases. Int. J. Heat Mass Transfer 1965, 8, 1033–1045. [Google Scholar] [CrossRef]
- Madsen, G.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Yadav, M.K.; Sanyal, B. First principles study of thermoelectric properties of Li-based half-Heusler alloys. J. Alloys Compd. 2015, 622, 388–393. [Google Scholar] [CrossRef]
- Mubashir, S.; Butt, M.K.; Yaseen, M.; Iqbal, J.; Laref, A. Pressure induced electronic, optical and thermoelectric properties of cubic BaZrO3: A first principle calculations. Opt. Int. J. Light Electron Opt. 2021, 239, 166694. [Google Scholar] [CrossRef]
- Remil, G.; Zitouni, A.; Bouadjemi, B.; Houari, M.; Bentata, S. A potential full Heusler thermoelectric material CO2ZrZ (Z = Al, Si, Ga and Sn) in low temperature: An Ab-initio investigation. Solid State Commun. 2021, 336, 114422. [Google Scholar] [CrossRef]
- Wen, B.; Feng, X. Thermal conductivity of metal from first principles calculations and its application in aluminum. J. Yanshan Univ. 2015, 39, 298–306. [Google Scholar]
- Brandt, R.; Neuer, G. Electrical Resistivity and Thermal Conductivity of Pure Aluminum and Aluminum Alloys up to and above the Melting Temperature. Int. J. Thermophys. 2007, 28, 1429–1446. [Google Scholar] [CrossRef]
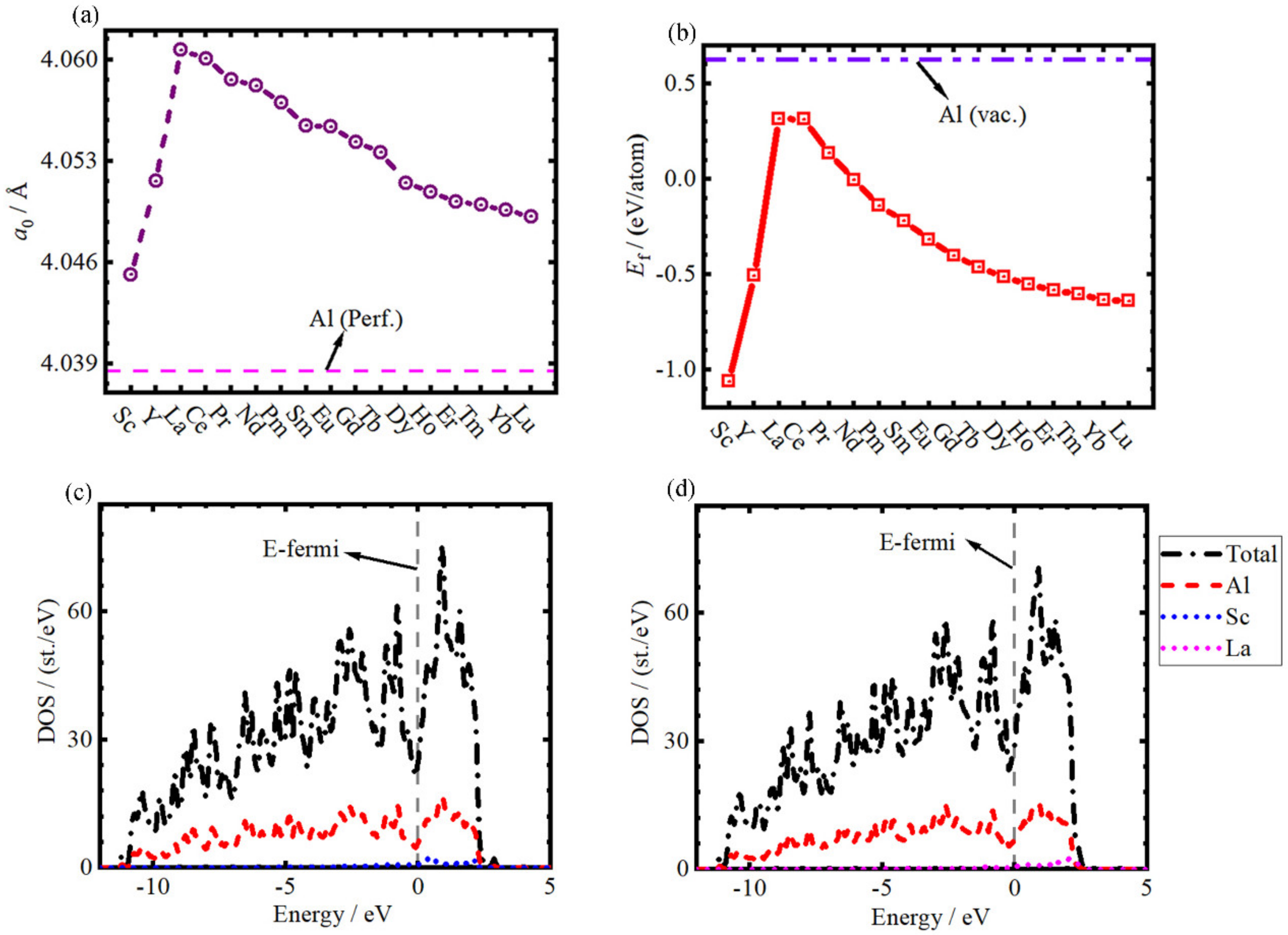

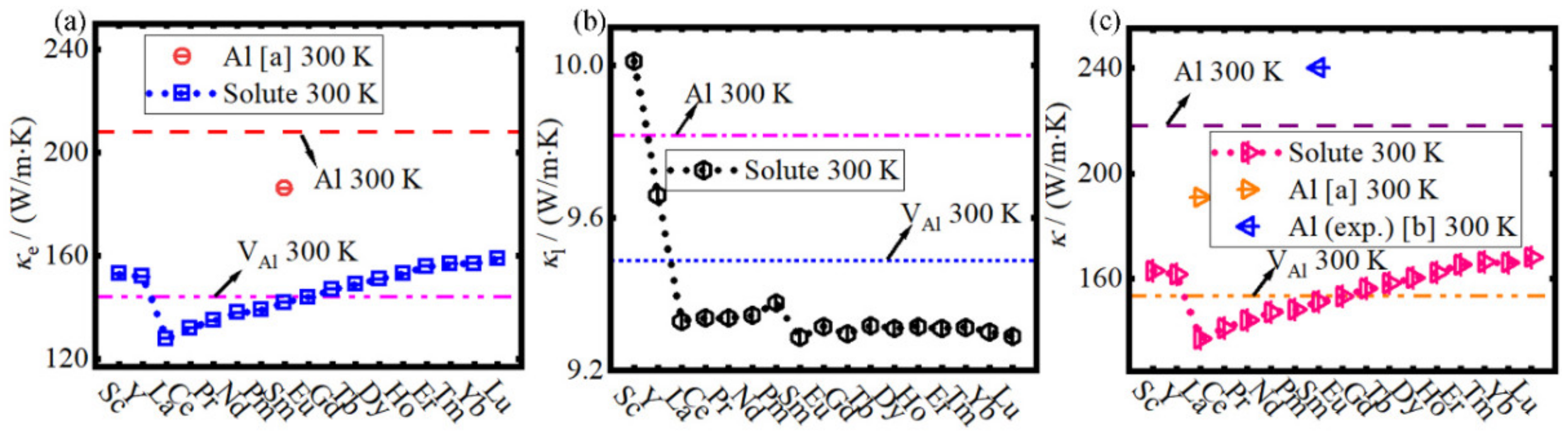
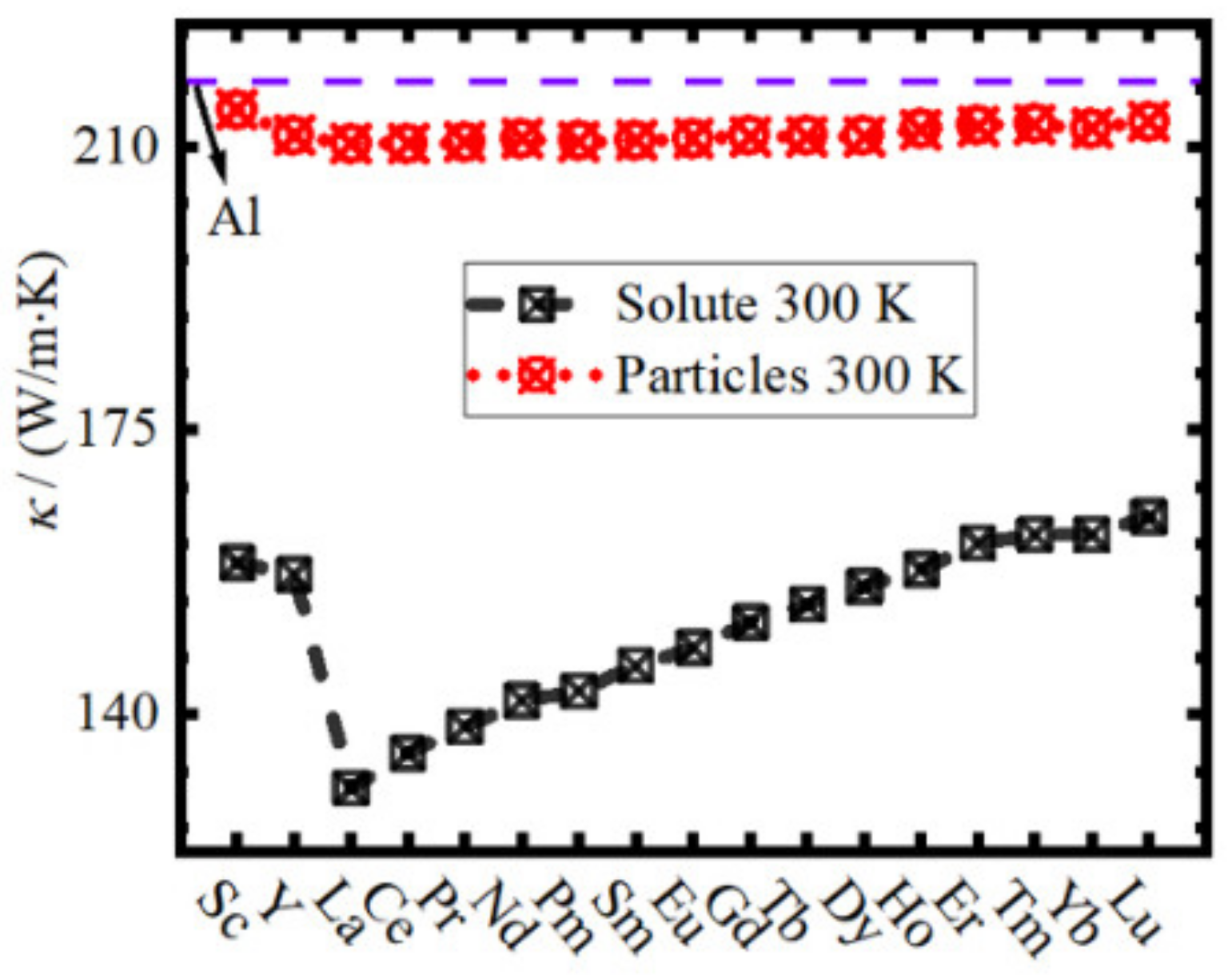
| Def. | a0 | Ef |
|---|---|---|
| Al | 4.038; 4.039 [69]; 3.983 [69]; 4.032 [70] | - |
| VAl | 4.034 | 0.626; 0.665 [69]; 0.729 [69]; 0.670 [71] 0.540 [72]; 0.700 [72] |
| ScAl | 4.045 | −1.062 |
| YAl | 4.052 | −0.507 |
| LaAl | 4.061 | 0.316 |
| CeAl | 4.060 | 0.314 |
| PrAl | 4.059 | 0.137 |
| NdAl | 4.058 | −0.004 |
| PmAl | 4.057 | −0.140 |
| SmAl | 4.055 | −0.219 |
| EuAl | 4.055 | −0.316 |
| GdAl | 4.054 | −0.402 |
| TbAl | 4.054 | −0.463 |
| DyAl | 4.051 | −0.513 |
| HoAl | 4.051 | −0.551 |
| ErAl | 4.050 | −0.584 |
| TmAl | 4.050 | −0.604 |
| YbAl | 4.050 | −0.633 |
| LuAl | 4.049 | −0.641 |
| Systems | C11 | C12 | C44 | C12–C44 | B | G | E | B/G | ν |
|---|---|---|---|---|---|---|---|---|---|
| Al Al * | 121.05 110.47 107.00 [a] 109.98 [b] | 63.64 67.33 61.00 [a] 60.11 [b] | 34.50 33.94 28.00 [a] 31.33 [b] | 29.14 33.39 28.78 [b] | 82.78 81.71 76.73 [b] | 32.05 28.30 28.59 [b] | 85.16 76.11 76.30 [b] | 2.583 2.887 2.68 [b] | 0.329 0.345 0.33 [b] |
| VAl | 93.71 | 43.19 | 35.45 | 7.74 | 60.03 | 30.95 | 79.24 | 1.939 | 0.280 |
| ScAl | 96.02 | 42.33 | 35.06 | 7.27 | 60.23 | 31.51 | 80.48 | 1.912 | 0.277 |
| YAl | 93.18 | 43.26 | 34.93 | 8.34 | 59.90 | 30.53 | 78.28 | 1.962 | 0.282 |
| LaAl | 91.05 | 43.14 | 33.98 | 9.16 | 59.11 | 29.54 | 75.96 | 2.001 | 0.286 |
| CeAl | 91.18 s | 43.29 | 33.99 | 9.31 | 59.26 | 29.54 | 75.99 | 2.006 | 0.286 |
| PrAl | 91.72 | 42.84 | 34.23 | 8.61 | 59.13 | 29.91 | 76.78 | 1.977 | 0.284 |
| NdAl | 91.45 | 43.29 | 34.25 | 9.04 | 59.34 | 29.74 | 76.45 | 1.995 | 0.285 |
| PmAl | 91.75 | 43.28 | 34.40 | 8.88 | 59.44 | 29.90 | 76.81 | 1.988 | 0.285 |
| SmAl | 92.23 | 43.30 | 34.59 | 8.71 | 59.61 | 30.11 | 77.31 | 1.980 | 0.284 |
| EuAl | 92.37 | 43.20 | 34.59 | 8.61 | 59.59 | 30.17 | 77.44 | 1.975 | 0.283 |
| GdAl | 92.01 | 43.60 | 34.68 | 8.92 | 59.74 | 30.03 | 77.15 | 1.990 | 0.285 |
| TbAl | 92.96 | 43.06 | 34.74 | 8.33 | 59.70 | 30.42 | 78.02 | 1.962 | 0.282 |
| DyAl | 93.10 | 43.37 | 34.98 | 8.39 | 59.95 | 30.51 | 78.26 | 1.965 | 0.282 |
| HoAl | 93.88 | 43.05 | 35.03 | 8.02 | 59.99 | 30.80 | 78.91 | 1.947 | 0.281 |
| ErAl | 94.14 | 42.99 | 35.08 | 7.91 | 60.04 | 30.91 | 79.14 | 1.943 | 0.280 |
| TmAl | 94.29 | 42.90 | 35.07 | 7.83 | 60.03 | 30.96 | 79.26 | 1.939 | 0.280 |
| YbAl | 94.48 | 42.80 | 35.06 | 7.74 | 60.03 | 31.03 | 79.40 | 1.935 | 0.280 |
| LuAl | 94.67 | 42.73 | 35.09 | 7.65 | 60.04 | 31.10 | 79.57 | 1.931 | 0.279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, T.; Ruan, Z.; Nie, B.; Liao, Y.; Huang, B.; Xu, Z.; Wu, Y.; Hu, T.; Chen, D. First-Principles Investigation of Point Defects on the Thermal Conductivity and Mechanical Properties of Aluminum at Room Temperature. Coatings 2023, 13, 1357. https://doi.org/10.3390/coatings13081357
Fan T, Ruan Z, Nie B, Liao Y, Huang B, Xu Z, Wu Y, Hu T, Chen D. First-Principles Investigation of Point Defects on the Thermal Conductivity and Mechanical Properties of Aluminum at Room Temperature. Coatings. 2023; 13(8):1357. https://doi.org/10.3390/coatings13081357
Chicago/Turabian StyleFan, Touwen, Zixiong Ruan, Baohua Nie, Yikai Liao, Bowen Huang, Zimeng Xu, Yuanzhi Wu, Te Hu, and Dongchu Chen. 2023. "First-Principles Investigation of Point Defects on the Thermal Conductivity and Mechanical Properties of Aluminum at Room Temperature" Coatings 13, no. 8: 1357. https://doi.org/10.3390/coatings13081357






