Improvement by Nanofibers of Load Transfer in Carbon Fiber Reinforced Composites

Abstract

This paper focuses on the load transfer improvement caused by nanofibers (NF) in carbon fiber reinforced composites. Load transfer is defined as the ability to transfer the mechanical loading between two adjacent fibers through the surrounding matrix. NF action is explored with a finite element model representing two carbon fibers separated by a layer of a NF reinforced matrix. It appears that the role of the NF network is to strengthen the matrix by increasing matrix shear rigidity, and thus to improve the load transfer between the carbon fibers. NF network morphology, defined by NF orientation, NF spatial distribution or NF diameter, governs the NF network efficiency.

1. Introduction

Extensive literature is devoted to the dispersion of nanoparticules in polymer matrices. Concerning carbon nanotubes (CNT) results are relatively disappointing compared to expectations aroused by the exceptional properties of CNTs. The main problem is the dispersion of CNTs that is poorly controlled. Meanwhile attempts are made to use CNTs at much lower concentrations allowing a controllable dispersion. The aim is then to introduce CNTs into carbon fiber reinforced composites (CFRC). Dispersion of CNTs into carbon fiber (CF) preform could be an alternative and effective solution. Several methods are proposed: CNT dispersion in the matrix prior to carbon fiber fabric impregnation, carbon fiber coating with a thin layer of CNT reinforced matrix, in situ CVD growth of CNTs onto CF surface, chemical anchoring of CNTs onto CF surface [1,2,3,4,5,6,7,8,9,10,11,12]. Various mechanical tests have been performed on CRFC reinforced by CNTs. In all cases, CNTs considerably improve CFRC mechanical properties.

It should be noted that in some cases, the exact nature of the nanoparticules used to reinforce CRFC is controversial, especially with very large nanotubes that could sometimes be referred to nanofibers. In the rest of this paper, the term nanofiber (NF) is used; it includes nanotubes and other nano-objects.

Among all the possible actions of NFs, load transfer improvement seems most relevant in the case of long NFs occupying the space between carbon fibers. Load transfer is defined as the ability to transfer the mechanical loading between two adjacent fibers through the surrounding matrix. This property is fundamental in the strength of unidirectional composites. A prematurely broken fiber leads to an overloading of adjacent fibers and thus an increase in stress level in these fibers, which can cause a cascading fracture of fibers to the ultimate composite failure. The role of the matrix is to minimize the fiber overloading intensity and to reduce in size the area of overloaded fibers. For particles with a high aspect ratio, such as fibers, the size of this area is estimated depending on the intensity of the axial stress carried by the fibers. By shearing, the matrix had to transfer the mechanical load from the intact fibers to the broken one. As one moves away from the fiber break, the broken fiber becomes active mechanically and its axial stress increases and balances with those of intact fibers.

The goal of this research study was primarily to find out information on the possible role of the NF network during load transfer. Many studies have been devoted to the modeling of load transfer. The first analytical model called “Shear-Lag” [13] was developed for a short fiber embedded into a matrix. It has been completed to take into account local failure of long fibers, the position of other neighboring fibers, the axial stiffness of the matrix and its viscoelastic behavior [14,15,16,17]. As a result of improved computer capabilities, these analytical studies have been completed by simulations based on the finite element method (FE). Recently, with a three-dimensional FE model, Blassiau have compared load transfer efficiency in the case of elastic, viscoelastic or elastoplastic matrix behaviors and with or without a crack at the fiber/matrix interface [18].

Finite element modeling perfectly meets the needs of this study because it makes it possible to vary the NF morphology and to follow load transfer variations. However, unlike previous studies using a finite element model, it is now necessary to generate a representative volume element (RVE) composed of two individual CF separated by a matrix area reinforced by a NF network. Nanofiber diameter is on the order of tens or hundreds of nanometers. Carbon fiber is about seven micrometers. Matrix area that corresponds to the fiber interspace is on the order of one micrometer, depending on fiber volume fraction. Because of the great difference in size, modeling of NF network reinforcing matrix in the fiber interspace is not trivial and requires the development of an appropriate mesh generation technique.

Two methods have been developed and are exposed in the methods section. First of all, using the homogenization numerical approach developed by Leclerc [19,20], the stiffness of matrix reinforced by NF network can be determined and introduced into the load transfer FE model. The fiber interspace is then filled with this equivalent material. This method allows the load transfer between fibers to not be disturbed by variation of local NF density. In the second method, NF networks are effectively created into the fiber interspace. In this case only radial and longitudinal NFs are created, and their position and length are completely randomized.

This crucial step over, the finite element model is developed by considering load transfer between the two CFs under a uniaxial stress field. Load transfer is estimated by comparing the stress field in the CFs between a RVE in which the CFs are unbroken and a RVE in which one of the two fibers is broken at its base. The proposed model is validated by comparing it to the results from the scientific literature.

Finally, the role of NF network on the load transfer has been investigated. The efficiency of NFs is estimated through the ineffective length of the broken CF.

2. Methods

Finite element meshes are generated with the Cast3M software [21]. A mesh is composed of 2 carbon fibers, a matrix area between the two fibers and a NF network located in the matrix. For the sake of efficiency and feasibility, the proposed model is based on a sectional representation (Figure 1).

Figure 1. General characteristics of the model used for the study of load transfer between neighboring fibers.

Figure 1. General characteristics of the model used for the study of load transfer between neighboring fibers.

2.1. Material Behavior

In a finite element analysis of load transfer, Blassiau models the behavior of matrix as elastic, viscoelastic or elastoplastic [18]. From a qualitative point of view, the same tendencies are obtained. In this article, the matrix is modeled as perfectly elastic and isotropic. Matrix Young modulus has been fixed at the value of $E=4.2 \text{GPa}$ and the Poisson coefficient is set at $\nu =0.35$ [7].

CFs and NFs are considered to be purely elastic and transversely isotropic materials. Significantly varying values have appeared in the scientific literature regarding the rigidity of carbon nanotubes. It must be emphasized that the notion of Young modulus used in the continuum mechanic frame is a strong approximation for a material, such as single-wall CNT, which has a thickness of one atom (taking for granted that the notion of thickness is valid for an atom). The value of $1 \text{TPa}$ is commonly accepted for multi-wall CNTs, a value obtained by both experimental measurements [22,23] and by simulations [24,25]. However, based on the work of Byron Pipes [26], due to the low interaction between the multiple shells of a multi-walled carbon nanotube, large multi-wall CNTs should have a much lower rigidity than single-wall CNTs. We have chosen to use the mechanical properties calculated for single-wall CNT by Ashfari [27] ($E_{\mathrm{L}}=580 \text{GPa}$; $E_{\mathrm{T}}=9.4 \text{GPa}$; ${\nu }_{\text{LT}}=0.18$; ${\nu }_{\text{TT}}=0.9$; $G_{\text{LT}}=17.2 \text{GPa}$). Unlike the other values in the literature, this set is completed for a transversely isotropic material. Concerning CFs, mechanical properties are $E_{\mathrm{L}}=297 \text{GPa}$; $E_{\mathrm{T}}=23 \text{GPa}$; ${\nu }_{\text{LT}}=0.02$; ${\nu }_{\text{TT}}=0.35$; $G_{\text{LT}}=30 \text{GPa}$.

2.2. Geometrical Parameters

• Fiber length: constant value, set at 100 μm.
• Fiber diameter: constant value, set at 7 μm.
• NF diameter: variable value, can take the value of $5$, $10$, $20$ or $50 \text{nm}$.
• NF length: variable value, depending on the NF reinforced matrix modeling (homogenized or effective).
• Inter-fiber distance: constant value, set at 0.4 μm, which corresponds to a fiber volume fraction $V_F=70\%$ or $73\%$ respectively for a hexagonal or square distribution (Figure 1). Indeed, this distance depends on fiber volume fraction in the composite. The fiber repartition in the section of a unidirectional composite follows a square or hexagonal distribution. When the fiber volume fraction increases, the hexagonal arrangement is preferred because it increases the compactness of the composite.

2.3. Boundary Conditions

The boundary conditions at the edges of the RVE are fixed according to the following scheme (Figure 1):

• Left and right RVE border: for all the nodes, displacement in the longitudinal direction $U_{\mathrm{L}}$, corresponding to fiber axis, is free; all the nodes on the same border have the same displacement in the radial direction ($U_{\mathrm{R}}$ identical).
• Upper RVE border: radial displacement $U_{\mathrm{R}}$ is free and longitudinal displacement $U_{\mathrm{L}}$ is equal for all the nodes, a force $F=2.5 \mathrm{N}$ is applied uniformly on all the nodes of the upper border in the direction $\overrightarrow{L}$.
• Lower RVE border: $U_{\mathrm{R}}$ free and $U_{\mathrm{L}}=0$ for all the nodes of the left fiber and matrix mesh; for the nodes of the right fiber base, radial displacement $U_{\mathrm{R}}$ is free and longitudinal displacement is free if the fiber is broken, or blocked if the fiber is intact.

These boundary conditions lead to consider that, in the composite material, every other fiber is broken. This model does not correspond to the assumptions used to develop analytical models from the first Shear Lag model [13], where the load transfer between a broken fiber and a fiber in an unbounded region with homogenized properties of the intact composite is considered.

2.4. Modeling of Homogenized Reinforced Matrix

For this first method of modeling the fiber interspace, the matrix area is a simple mesh with a grid of QUA4 square elements. Element size is fixed at $50 \text{nm}$. NF network is not described in the matrix area mesh but is introduced by the virtue of the mechanical properties of this area. The elastic stiffness tensor of NF reinforced matrix is calculated using the numerical process proposed by Leclerc [19,20]. One can obtain the stiffness tensor as a function of NF orientation, NF volume fraction and NF morphological parameters as length and diameter. As an example, evolutions of the Young modulus of homogenized reinforced matrix are plotted on Figure 2. The NF length is fixed for all cases at $400 \text{nm}$. It should be noted that, more than NF diameter and length values, the most relevant geometrical parameter is the NF aspect ratio.

Figure 2. Evolution of the Young modulus of a matrix reinforced by nanofibers in the case of (a) isotropic distribution of nanofibers (NFs) into the matrix; and (b) unidirectional alignment of NFs.

Figure 2. Evolution of the Young modulus of a matrix reinforced by nanofibers in the case of (a) isotropic distribution of nanofibers (NFs) into the matrix; and (b) unidirectional alignment of NFs.

In this CFRC modeling, for all the models, NF length is constant and equal to the inter-fiber distance of $0.4 \text{μm}$. For a given model, NF diameter is constant and can take the value of $5$, $10$, $20$ or $50 \text{nm}$. NF and matrix mechanical properties are given in Section 2.1. Two NF network configurations are studied. In the first one, NFs are randomly oriented. NF reinforced matrix behavior is supposed to be isotropic. In the second one, NFs are strictly parallel to each other. The NF orientation vary from the radial configuration of 0°, where they are perpendicular to fiber axis, to the longitudinal configuration of 90°, where they are parallel with fiber axis. Reinforced matrix behavior is then transverse isotropic.

2.5. Effective Modeling of NF Network Reinforcing Matrix

A second method for modeling of NF reinforced matrix is proposed. Here, fiber interspace is composed of matrix and NFs. NF orientation is not random. NFs can be either oriented in the CF direction or oriented perpendicularly to the CF and able to connect CFs to each other. These two NF families are named respectively longitudinal NFs and radial NFs. In this modeling, for a given model, NF lengths are not constant and vary for each NF, as detailed in Section 2.5.1. NF diameter is constant and can take the value of $5$, $10$, $20$ or $50 \text{nm}$.

2.5.1. NF Generating Method

The method used for NF generation is explained below for radial NF network. The same method is used for longitudinal NFs. It is based on random sampling of probabilities of NF birth and NF growth. The mesh base is a grid of steps equal to NF diameter. This grid is meshed with QUA4 elements. Matrix mechanical properties are applied to the initial grid elements. Each element of the first mesh column has the possibility to transform into a NF element. To do so, a mutation value is drawn randomly and assigned to each element. Among the first column elements, the mutant elements are those whose mutation value is greater than a threshold set by the software user. The first column is then copied on the second one. Following the birth method, a survival probability is given at each NF. Some NFs continue to grow and see their length increase by a grid element, while others stop growing. As for the first column, some new NFs could appear.

This process is repeated as many times as necessary to cover the entire mesh grid. However, the survival probability of a NF decreases with its length. The longer a NF, the less likely it is to continue to develop. At the end of the longitudinal grid scanning, a part of the initial matrix mesh is changed into a network of longitudinal NFs. These NFs are randomly distributed all over the mesh grid and have random lengths. The set of random draws for NF creation is accessible to the software user. It is possible to restrict the draw spread and to focus them more or less strongly on a given value. The same technic is applied to generate longitudinal NFs by scanning the grid row by row.

2.5.2. Intersection and Overlapping between NFs

The intersection between two NFs is a really complex problem to model. From a physical point of view, during their synthesis NFs are not perfect cylindrical tubes. Depending on the process setting, structure and shape defects may appear. NFs can be forked, interlocked by knots, etc., whereas the structure of a perfect NF is almost known; the structure and the underlying properties of these separating and intersection knots are much less defined. Apart from these NF synthesized with complex forms, during NF mixing with matrix, two independent NFs, that are in contact or that are in an overlapping configuration, do not fuse; they interact by weak bonds like Van der Waals bonds. The proposed 2D model represents a section of the composite material. To be fully comprehensive, in the mesh, intersection elements corresponding to complex NF knots should be distinguished from intersection elements corresponding to overlapping of independent NFs. At any rate, properties of intersecting elements are an open question. NF intersection properties can be the sum of the properties of the two NFs, a mix of the two NFs properties, or those of one of the two NFs. A priority is assigned according to the NF creation history during RVE mesh generation. The intersection between two NFs is similar in nature to the first created NF and the intersection element properties are those of first created NF.

2.5.3. NFs Perpendicular to Mesh Plane

NFs could be generated in the direction perpendicular to the study plane. These NFs, visible through their section, would be meshed by a single QUA4 element. A preliminary study has shown that they have a very low influence on global mechanical properties. Consequently, to simplify the number of parameters, no perpendicular NFs are meshed.

2.5.4. NF Network Mesh Refinement

Once built, the NF network is made of QUA4 elements whose lateral dimension is the NF diameter. To stabilize calculation convergence, a mesh refinement is made by dividing this mesh size. The contours of the initial QUA4 mesh are projected on a new grid of QUA4 elements; the new grid step is equal to NF diameter divided by a factor 2 (Figure 3). Some tests with refinement degrees of 2, 4 and 8 have proved that the results become stable and change only negligibly to a refinement greater than 2.

Figure 3. Examples of NF network and matrix mesh for effective modeling of NF network reinforcing matrix. (a) Initial mesh; (b) Mesh after NF refinement and matrix reconstruction.

Figure 3. Examples of NF network and matrix mesh for effective modeling of NF network reinforcing matrix. (a) Initial mesh; (b) Mesh after NF refinement and matrix reconstruction.

2.5.5. Matrix Mesh

To optimize the time computation/result quality ratio, the QUA4 matrix mesh is reconstructed in faster TRI3 elements (Figure 3). The new matrix mesh is based, on the outside, on the outer matrix borders and, inside, on the NF network mesh contour. To ensure a good interface transfer between matrix and CFs, the size of the elements of the boundaries between matrix and carbon fibers is equal to the refined NF network mesh.

2.6. Carbon Fiber Meshes

Concerning CFs, the mesh is made of TRI3 elements with a higher size on external borders (Figure 4).

Figure 4. Partial views of two different representative volume elements (RVEs) and internal and external border meshes of effective modeling of NF network reinforcing matrix. (a) RVE with long NFs; (b) RVE with short NFs. Red = CFs, yellow = matrix, green = radial NFs, purple = longitudinal NFs.

Figure 4. Partial views of two different representative volume elements (RVEs) and internal and external border meshes of effective modeling of NF network reinforcing matrix. (a) RVE with long NFs; (b) RVE with short NFs. Red = CFs, yellow = matrix, green = radial NFs, purple = longitudinal NFs.

2.7. CF-Matrix, CF-NF and NF-Matrix Interfaces

Bonding between the different phases of NF reinforced CFRC is considered perfect without any defect, decohesion or interfacial transition zone. From a mechanical point of view it means that displacements are continuous from both sides of an interface.

2.8. Definitions of the Different Volume Fractions

The mesh is composed of 3 different phases: matrix, NFs and CFs. The classical volume fractions as fiber volume fraction must be redefined to take into account the presence of NFs (1). It must be noted that what we called volume fraction is, in fact, the surface fraction defined by the ratio between the surfaces of the different phases of the composite.

$$\begin{array}{c}\text{NF/fiber: }{V}_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{F}$}\right.}=\frac{{\text{Surf}}_{\text{NF}}}{{\text{Surf}}_{\text{Fiber}}}\\ \text{NF/matrix: }{V}_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\text{FM}$}\right.}=\frac{{\text{Surf}}_{\text{NF}}}{{\text{Surf}}_{\text{Matrice}}}\\ \text{NF/composite: }{V}_{\text{NF}}=\frac{{\text{Surf}}_{\text{NF}}}{{\text{Surf}}_{\text{Fiber}}+{\text{Surf}}_{\text{Matrice}}+{\text{Surf}}_{\text{NF}}}\\ \text{Fiber/composite: }{V}_{\mathrm{F}}=\frac{{\text{Surf}}_{\text{Fiber}}}{{\text{Surf}}_{\text{Fiber}}+{\text{Surf}}_{\text{Matrice}}+{\text{Surf}}_{\text{NF}}}\end{array}$$

(1)

2.9. An Estimation Method of Load Transfer Efficiency

The goal was to verify if NF networks are able to improve mechanical load transfer between a broken fiber and its intact neighbor. For this, longitudinal stress is determined on all nodes of the right boundary of the mesh, corresponding to the central axis of the fiber, which can be broken. At a distance $L$ from the break, along the axis $\overrightarrow{L}$ (Figure 1), the reloading coefficient $C_{\mathrm{R}}\left(L\right)$ is calculated by the ratio of the longitudinal stresses in broken and intact configurations (2). The ineffective load transfer length $L_{\text{ineffective}}$ is defined as twice the fiber length necessary so that the mechanical load supported by the fiber in broken configuration is equal to 90% of that of the fiber in intact configuration (3) [18]. Figure 5 presents the results of reloading coefficient calculation $C_{\mathrm{R}}\left(L\right)$. The threshold of 90% used to estimate the ineffective length $L_{\text{ineffective}}$ corresponds to the inflection point to the value of 100%, on the $C_{\mathrm{R}}\left(L\right)$ curve.

As the goal was to study the efficiency of NF network to improve load transfer, the gain provided by the network is estimated by comparing the ineffective length obtained for a matrix reinforced by NFs with that obtained with a matrix without NFs (4). The gain $G_L$ depends on the morphology of the modeled NF network and represents its efficiency.

$$C_{\mathrm{R}}\left(L\right)=\frac{{\mathrm{\sigma }}_{\text{LL}}^{\text{broken config}}\left(L\right)}{{\mathrm{\sigma }}_{\text{LL}}^{\text{intact config}}\left(L\right)}, 0\le L\le L_{\text{Right fibre}}$$

(2)

$$L_{\text{ineffective}}=2*L_{C_{\mathrm{R}}\left(L\right)=90\%}$$

(3)

$$G_{\mathrm{L}}=\frac{L_{\text{ineffective}}^{\text{with NFs}}-L_{\text{ineffective}}^{\text{without NFs}}}{L_{\text{ineffective}}^{\text{without NFs}}}$$

(4)

The left fiber of the model is always intact without any break. Depending on the right fiber configuration, the left fiber could be overstressed. The overstress level is defined by the overloading coefficient $C_{\mathrm{S}}\left(L\right)$ in Equation (5). The maximum overloading coefficient $C_{\mathrm{s}}^{\text{max}}$ is achieved near the fiber base.

$$C_{\mathrm{S}}\left(L\right)=\frac{{\mathrm{\sigma }}_{\text{LL}}^{\text{broken config}}\left(L\right)}{{\mathrm{\sigma }}_{\text{LL}}^{\text{intact config}}\left(L\right)}, 0\le L\le L_{\text{Left fibre}}$$

(5)

Figure 5. Evolutions of the reloading coefficient of a broken fiber and of the overloading coefficient of the neighboring fiber with a non-reinforced matrix.

Figure 5. Evolutions of the reloading coefficient of a broken fiber and of the overloading coefficient of the neighboring fiber with a non-reinforced matrix.

3. Method Validation

3.1. Non-Reinforced Matrix

To validate the proposed model, the load transfer between CFs separated by a non-reinforced matrix is studied (Figure 5). The overloading coefficient of the left intact fiber is at its maximum near the base of the broken right fiber and decreases gradually. Unlike the Shear-lag model, in the proposed model, matrix stiffness is taken into account and matrix supports a part of the mechanical loading. Consequently, the mechanical loading is not only supported by the intact left fiber and $C_{\mathrm{S}}^{\text{max}}$ is less than 2.

The higher the fiber volume fraction, the more efficient the load transfer and the broken fiber quickly recovers a substantial level of mechanical loading (Figure 6). In return, the overloading supported by the left intact fiber increases. The obtained values are globally consistent with the literature. With a 3D model at $V_{\mathrm{F}}=40\%$, Blassiau [18] has evaluated $C_{\mathrm{S}}^{\text{max}}=1.41$ and $L_{\text{ineffective}}^{\text{without CNTs}}=67.10\text{ μm}$. With the proposed 2D model, values of $C_{\mathrm{S}}^{\text{max}}=1.38$ and $L_{\text{ineffective}}^{\text{without CNTs}}=99.45\text{ μm}$ are obtained. These differences can be explained partly by the difference of modeling (3D for Blassiau) and on the other part by a higher fiber shear modulus for Blassiau ($G=80\text{ GPa}$).

Figure 6. Overloading coefficient and ineffective length for a non-reinforced matrix as a function of fiber volume fraction.

Figure 6. Overloading coefficient and ineffective length for a non-reinforced matrix as a function of fiber volume fraction.

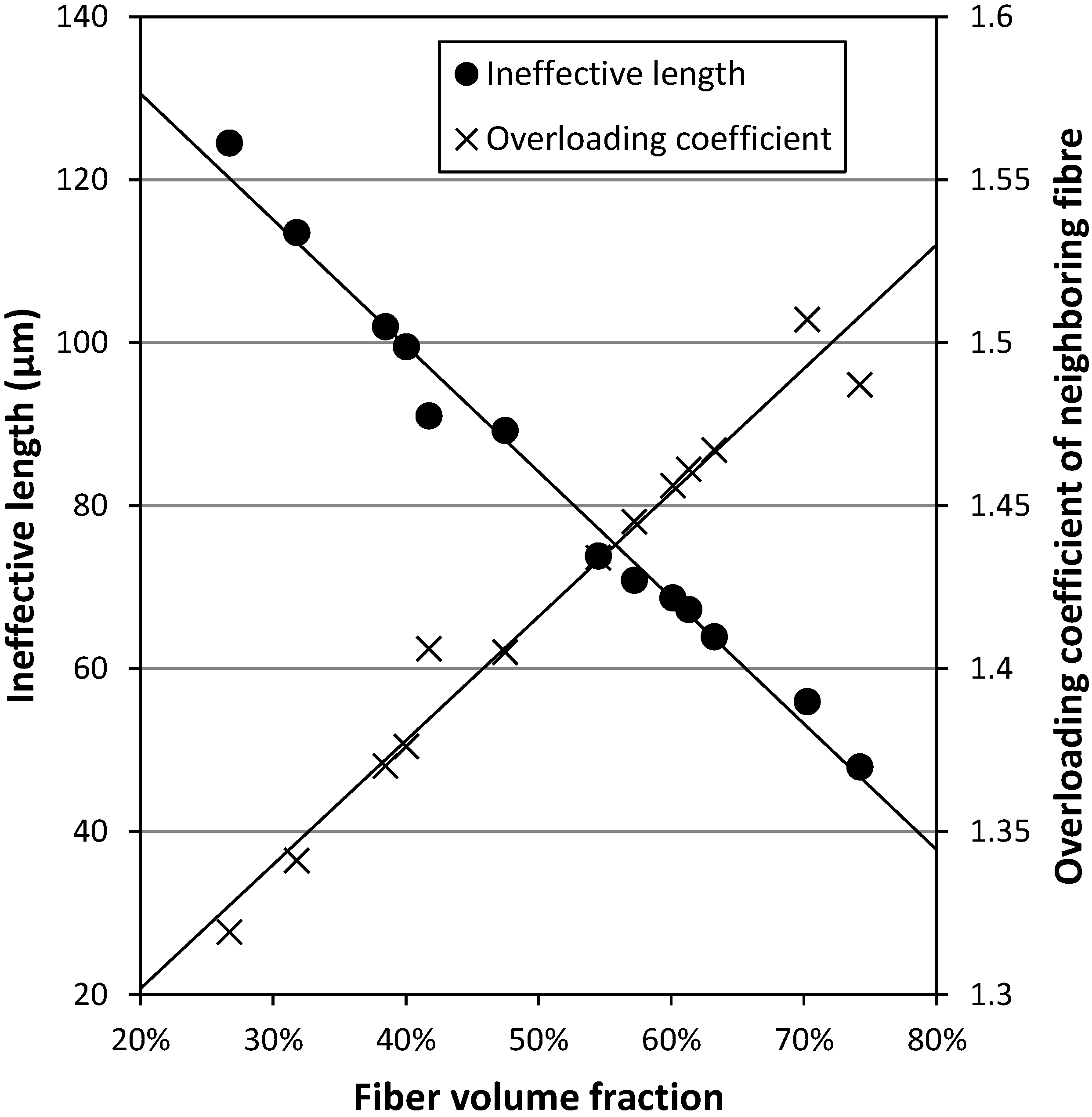
3.2. Result Sensitivity to Mesh

To estimate the sensitivity of results to the reinforced matrix mesh, results obtained with different meshes are compared. The mechanical properties devoted to NF mesh are those of the matrix. It is therefore necessary to determine the evolution of the load transfer between two fibers separated by pure matrix, the only variable being the mesh representing this matrix. For a same fiber volume fraction, the standard deviation on ineffective length and on overloading coefficient is about 5.0% between the different tested meshes. To minimize the mesh influence, the same mesh is used for the configuration with NFs and for the configuration without NFs; only the mechanical properties of the NF mesh are modified depending on the configuration (with or without NFs). The gain on ineffective length provided by a NF network is determined based on the ineffective length calculated for this mesh to which matrix properties are assigned, and not relatively to a unique and standard matrix configuration without meshed NF network.

4. Results and Discussion

4.1. Reinforcement of Matrix Shear Modulus and Load Transfer Efficiency

According to the stress transfer model, the matrix function is to undergo shear to permit a homogenous stress distribution between two neighboring fibers. The mechanical property involved is then the shear modulus. The stiffer the matrix under shear stress, the more efficiently the load transfer between fibers will be done, that means that the ineffective length will be shorter. During local fiber failure, stress concentration in the neighboring fibers is therefore minimized. Cascade propagation of this local fracture is blocked. At the composite level, the ultimate tensile strength is increased.

Evidently, by introducing NFs into the matrix, its mechanical properties are increased. In particular the shear modulus increases [19]. Matrix reinforced by NFs is then more efficient to transfer mechanical loading from a fiber to another one (Figure 7). Gain on ineffective length varies nearly linearly with the volume fraction of NF dispersed into the matrix, a slight inflexion is observed around $V_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{M}$}\right.}=6\%$.

Figure 7. Gain on ineffective length as a function of NF volume fraction, for different NF diameters, with homogenized reinforced matrix.

Figure 7. Gain on ineffective length as a function of NF volume fraction, for different NF diameters, with homogenized reinforced matrix.

With the modeling of homogenized reinforced matrix, efficiency of reinforcing varies slightly with NF diameter. As an example, with NF fraction volume $V_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{M}$}\right.}=10\%$, the values of the ineffective length gain are, respectively, $9.64\%$, $9.64\%$, $11.72\%$, $12.05\%$ for NF diameters of $50, 20, 10 \text{and} 5 \text{nm}$. Indeed, with the modeling of homogenized reinforced matrix, the NF diameter is only taken into account during the estimation of the stiffness tensor of NF reinforced matrix. The mechanical properties of NF reinforced matrix are directly linked to the NF morphology, especially the NF aspect ratio [19]. As in the homogenized matrix modeling, NF length is constant whatever the value of the NF diameter, the NF reinforcing effect is inversely proportional to their diameter. The reinforced matrix shear modulus is then equal to $2.17$, $2.33$, $2.52$ and $2.55 \text{GPa}$, respectively, for NF diameters of $50, 20, 10 \text{and} 5 \text{nm}$.

When NFs are preferentially oriented in one direction, the reinforced matrix is anisotropic. Its shear modulus varies according of NF orientation angle. Ideally, the maximum efficiency should be achieved for a 45° orientation, and be strictly equal for radial (0°) and longitudinal (90°) orientations. However, matrix filling the fiber interspace does not only undergo shear stress, its bears also part of the axial loading in addition to the reinforcing carbon fibers. The maximum efficiency is then obtained for an orientation around 55°, depending on the axial stiffness of the reinforced matrix (Figure 8).

Figure 8. Gain on ineffective length as a function of NF orientation with homogenized reinforced matrix and for $V_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{M}$}\right.}=15\%$.

Figure 8. Gain on ineffective length as a function of NF orientation with homogenized reinforced matrix and for $V_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{M}$}\right.}=15\%$.

4.2. Importance of NF Network Morphology

Ideally, NFs must have an orientation around $45°$ relative to fibers, which is, to date, practically impossible to achieve. Regardless of the method used to introduce NFs into CFRC (NF chemical anchoring, NF dispersion into matrix prior to CF fiber fabric impregnation, in-situ CVD growth of NFs onto CF surface, etc.), NF network morphology is highly difficult to control. For example, SEM observations reveal that the NFs chemically anchored onto the CF are oriented in all the directions [6]. In the best case, successful introduction of radial (0°) or longitudinal (90°) NFs should be achievable. Radial NFs are anchored on left and/or right carbon fibers by their tips. Longitudinal NFs are NFs that have not been anchored onto CF and that have been oriented along fiber axis by the flow of the polymer matrix during carbon fiber fabric impregnation.

With effective modeling of NF network, given a NF volume fraction, the gain on ineffective length is generally lower compared to the values obtained with homogenized reinforced matrix (Figure 9). The mean values of the ineffective length gain calculated with NF fraction volume $V_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{M}$}\right.}=10\%$ are equal to $10.13\%, 6.21\%, 5.12\%$ and $4.31\%$, respectively, for NF diameters equal to $50, 20, 10 \text{and} 5 \text{nm}$. This confirms the necessity of NF orientation around 45° relative to fibers.

Figure 9. Gain on ineffective length as a function of NF volume fraction, for different NF diameters, with effective modeling of NF network reinforcing matrix.

Figure 9. Gain on ineffective length as a function of NF volume fraction, for different NF diameters, with effective modeling of NF network reinforcing matrix.

With effective modeling of NF network, NFs with diameter of $50 nm$ are generally more efficient to reinforce matrix load transfer than smaller diameter of $20, 10 \text{or} 5 \text{nm}$ (Figure 9). Moreover, with bigger NFs, $50$ and $20 \text{nm}$ in diameter, for two identical NF fraction volumes, gain $G_L$ values are not equal (Figure 9) and the gain on ineffective length does not vary linearly with NF volume fraction as for homogenized reinforced matrix. Moreover some negative values can be observed, which mean that, with some NF network morphologies, reinforced matrix is less efficient to transfer mechanical loading from a fiber to its neighbor. In contrast, gain value may be twice or three times the average value. With smaller NFs, $10\text{ nm}$ in diameter, the gain values are less dispersed. With the smallest NFs, $5 \text{nm}$ in diameter, the gain seems to vary linearly with NF volume fraction. With effective modeling of the NF network, as NF are generated following a random process, NF local density is not constant in the fiber interspace. With smallest NFs, NFs are better dispersed all over the matrix and local density varies slightly unlike matrix reinforced with network of large NFs.

To complete the hypothesis of a local action of NF network, the efficiency of some reinforced matrix with NF network dispersed locally has been calculated (Figure 10). In this study, NFs are not present throughout the fiber, but only in the area around the fracture of the fiber. A fiber length anchored with NFs of $15 \text{μm}$ means that NFs are present only on the first $15 \text{μm}$ of the fiber interspace starting from the fiber failure. In the matrix area reinforced by NFs, NF volume fraction is equal to $V_{\raisebox{1ex}{$\text{NF}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{M}$}\right.}=13\%$. Beyond $30 \text{μm}$ after the fiber failure, NFs do not improve load transfer (Figure 10). This coincides with half of the ineffective length (about $30 \text{μm}$). NF action is then located around the fiber failure area. Once the broken fiber returns to the level of mechanical loading of the non-broken fiber, NF networks are no longer useful to reinforce matrix. NF network acts like a bandage that helps the matrix to support mechanical overloading due to a fiber local breakage.

Figure 10. Gain on the ineffective length with a partial distribution of NF network in the fiber interspace, with effective modeling of NF network reinforcing matrix.

Figure 10. Gain on the ineffective length with a partial distribution of NF network in the fiber interspace, with effective modeling of NF network reinforcing matrix.

5. Conclusions

Dispersion of NFs into CF preform is known to increase CRFC mechanical properties. Among all the assumptions considered to explain this improvement, the action of the NF network on the mechanical load transfer between fibers seems the most consistent. This hypothesis was explored with a finite element model representing two carbon fibers separated by a layer of a NF reinforced matrix. It appears that the role of the NF is to strengthen the matrix by increasing matrix shear rigidity, and thus to improve the load transfer between the carbon fibers.

To optimize NF reinforcement, they must have an orientation around 45° relative to fibers. In this way the matrix shear modulus is maximal, and allows an efficient load transfer between neighboring fibers. At present, the different dispersion processes are not able to ensure this NF orientation. The easiest orientations to be obtained are radial (90°) and longitudinal (0°) relative to fibers. In these cases, the performance of NF network is drastically reduced, with a limited improvement of load transfer efficiency.

NF network efficiency increases with NF diameter but with a greater variation in performance, due to a less inhomogeneous spatial distribution of the NF reinforcement.

To accurately analyze the role of NF network morphology, the global NF volume fraction is not sufficient and additional morphological descriptors should be used.