Abstract
This paper presents a compact structure of recursive discrete Fourier transform (RDFT) with prime factor (PF) and common factor (CF) algorithms to calculate variable-length DFT coefficients. Low-power optimizations in VLSI implementation are applied to the proposed RDFT design. In the algorithm, for 256-point DFT computation, the results show that the proposed method greatly reduces the number of multiplications/additions/computational cycles by 97.40/94.31/46.50% compared to a recent approach. In chip realization, the core size and chip size are, respectively, 0.84 × 0.84 and 1.38 × 1.38 mm2. The power consumption for the 288- and 256-point DFT computations are, respectively, 10.2 (or 0.1051) and 11.5 (or 0.1176) mW at 25 (or 0.273) MHz simulated by NanoSim. It would be more efficient and more suitable than previous works for DRM and DRM+ applications.
1. Introduction
Recently, the rapid growth of multimedia and wireless communication technologies has enabled the integration of various audio coding standards in a multimedia platform for audio applications. Digital Radio Mondiale (DRM) [1] is a digital broadcasting system for radio frequencies of below 30 MHz. DRM Plus (DRM+) is the technology extending the DRM system to the VHF bands up to 174 MHz. It is a new standard of the European Telecommunication Standards Institute (ETSI ES 201 980). DRM offers the possibility to use various audio codecs, such as High Efficiency Advanced Audio Coding (HE-AAC), MPEG-4 Code-excited linear prediction (CELP), MPEG-4 Harmonic Vector Excitation Coding (HVXC), and MPEG Surround, etc., to their broadcasting system. The discrete Fourier transform (DFT) and inverse modified cosine transform (IMDCT) have been, respectively, applied to realize the coded orthogonal frequency division multiplexing (COFDM) and the synthesis filterbank of advanced audio coding (AAC) in DRM specification. In a DRM and DRM+ receiver, the COFDM adopts the non-power-of-two and power-of-two DFT whose transform lengths are specified to 288, 256, 176, 112, and 27. For a HE-AAC decoder, it also requires 1920- and 240-point IMDCT computations.
Previously, the issue of a common architecture design of fast Fourier transform (FFT) and IMDCT has been developed in [2,3,4,5] for a digital audio broadcasting (DAB) system [6,7]. The specified transform lengths of both FFT and IMDCT are all power of two, and it is very suitable for parallel design to implement the common architecture of FFT and IMDCT [2,3,4] or FFT-based IMDCT [5]. However, it would be a great challenge to design a flexible FFT or IMDCT accelerator with the transform lengths of power-of-two and non-power-of-two. Currently, Lai et al. [8] propose a recursive DFT (RDFT) to compute IMDCT coefficients. Due to the nature of recursive structure, Lai et al.’s hardware accelerator can arbitrarily switch transform length between power-of-two and non-power-of-two without any extra hardware processing units. Additionally, the results indicate that it achieves lower computational complexity than recursive DCT-based designs [9,10,11,12,13,14,15,16,17,18]. Since the FFT (or RDFT) can be further used for computing the IMDCT, the transform length of IMDCT is shortened from N to N/4. It exactly reduces the iteration loops for recursively computing IMDCT coefficients; however, compared with Lei et al.’s IMDCT [19], this method, which adopted one-dimension (1-D) RDFT as a unified kernel, would not gain better performance. This implies that it still has a bottleneck on using a 1-D RDFT to compute the IMDCT coefficients.
In 2004, Wolkotte et al. [20] presented a detailed analysis for computational complexity in a DRM receiver and clearly showed that the DFT block took 50.51% of all computations. To meet the specification that requires non-power-of-two transform lengths, RDFT approaches [21,22,23,24,25,26,27,28,29,30,31,32] and recursive IMDCT approaches [9,10,11,12,13,14,15,16,17,18] have been suggested for area-efficient implementations. The major limitation of RDFT is on the issue of long computational cycle, i.e., long processing time. To overcome this shortcoming, a 2-D RDFT structure design with prime factor algorithm has been presented in [30,31,32]. Compared with other RDFT approaches [21,22,23,24,25,26], Lai et al. [29,30,31,32] have a greater improvement in terms of computational complexity and latency. However, the computational complexity of 256-point RDFT based on Lai et al.’s algorithm [32] still takes more multiplications and additions, because the transform length only has one prime factor so that we only can adopt three 1-D RDFT hardware accelerators to simultaneously compute all 256-point DFT coefficients. Another issue that arises in [30,32] is that, in order to decompose the N-point RDFT into c- and m-point sub-RDFTs, a great number of register files would be inserted between the first-stage and second-stage RDFTs for buffering temporal data. It makes the chip size become much larger, and consumes much power on memory access. Recently, a FFT design consisted of memory, control unit, and various mixed-radix butterfly modules has been presented in [33]. Hsiao et al. merge prime factor and common factor concepts to realize the proposed accelerator, and propose an efficient address generator to avoid the memory access conflict. However, it still requires many radix-r processing units to support the FFT computations. Due to the nature of RDFT, we can apply the variable-length and low-cost advantages to save these processing units. Thus, high-performance RDFT architecture is proposed to enhance our previous works [29,30,31,32] in this paper.
The rest of this paper is organized as follows: Section 2 takes an overview for our previous works [29,30,31,32] first, and then proposes a new concept to integrate them by applying the common factor DFT (CF-DFT) algorithm. Section 3 demonstrates the compact architecture design of the proposed RDFT, and then Section 4 introduces the low-power optimizations of VLSI implementation for the proposed hardware accelerator. Section 5 compares and contrasts the differences in performance for various approaches. Finally, conclusions are outlined in Section 6.
2. The Proposed Compact RDFT with Prime Factor and Common Factor Algorithms
The N-point DFT formula is defined as Equation (1). According to the derivation of Lai et al. [29], it can be found that the transfer function 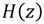 is obtained as Equation (2).
is obtained as Equation (2).
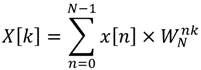
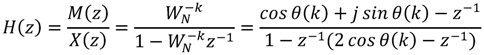
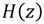 is obtained as Equation (2).
is obtained as Equation (2).
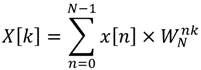
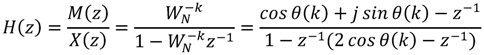
Equation (2) can be easily mapped into a hardware accelerator. To reduce the number of multiplications, both coefficients of 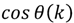 and
and 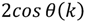 can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [23,24,26,29,30,31,32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai et al. [29] can be further improved. Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in Figure 1b.
can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [23,24,26,29,30,31,32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai et al. [29] can be further improved. Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in Figure 1b.
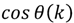 and
and 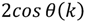 can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [23,24,26,29,30,31,32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai et al. [29] can be further improved. Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in Figure 1b.
can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [23,24,26,29,30,31,32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai et al. [29] can be further improved. Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in Figure 1b.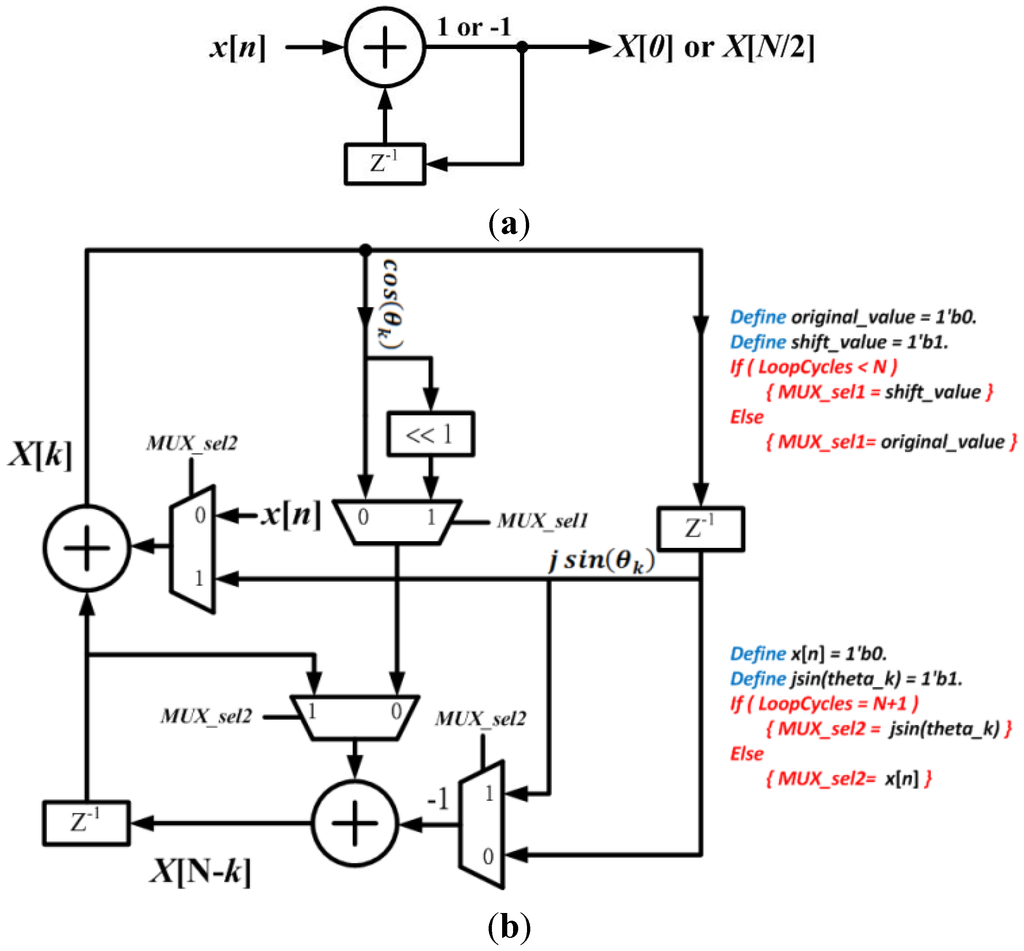
Figure 1.
Proposed compact architecture of recursive discrete Fourier transform (RDFT) module. (a) The computational circuit of X[0] and X[N/2]; (b) The computational circuit design of X[1] to X[N/2 − 1].
Compared with our previous work [29], this design only takes eight multiplexers, four adders and two multipliers in RDFT implementation. To lower the computational complexity and cycle, Lai et al. proposed a new algorithm using the Chinese Reminder Theorem (CRT), i.e., prime factor algorithm, in [30,31,32]. In this algorithm, the input sequence length (N) can be factored into two mutually prime factors (c and m), and then the change of the variables is computed as Equation (3), where 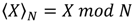 .
.
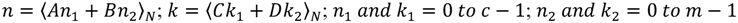
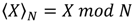 .
.
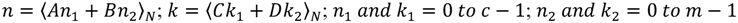
For this mappings to be unique, the condition A, B, C, and D are chosen such that:
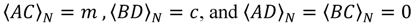
Thus, the DFT algorithm with the CRT scheme, which is also called the prime factor DFT (PF-DFT) algorithm, can be defined as
By adopting the RDFT in Figure 1 to the Equation (5), the low-cost and reconfigurable two-dimension RDFT algorithm can be easily obtained. For a DRM system, the transform length of 288 (N) can be divided into 32 (c) and 9 (m) where factors of c and m are co-prime. The conditions of (A, B, C, D) are then chosen as (9, 32, 64, 225). Similarly, the conditions of (A, B, C, D) for the frame size of 176, 112, 480, 60 can be chosen as (11, 16, 33, 144), (7, 16, 49, 64), (15, 32, 225, 256), and (5, 12, 25, 36), respectively. Note that the details for the selection of these conditions are introduced in the section III of Lai et al. [30]. However, the PF-DFT algorithm cannot be applied to compute the 256-point DFT coefficients, because the transform length only has one prime, i.e., 256 = 28. Thus, we should adopt an efficient method called the CF-DFT algorithm to solve this problem. Assume that the input sequence length (N) can be also factored into two common factors (c and m), and
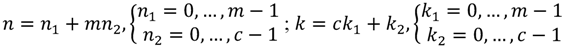
By taking Equation (6) into Equation (1), we can obtain the CF-DFT algorithm as Equation (7):
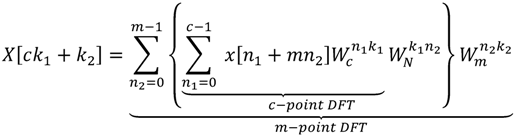

The difference between Equations (5) and (7) is the twiddle factor 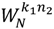 . It implies that the computation between c-point DFT and m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai et al. proposes a coefficient-free algorithm in [31,32]. The two major coefficients in Equation (2), i.e.,
. It implies that the computation between c-point DFT and m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai et al. proposes a coefficient-free algorithm in [31,32]. The two major coefficients in Equation (2), i.e.,  and
and 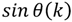 , can be respectively calculated by using the trigonometric identities Equations (9,10) [31]. The detailed computations have been introduced in section 2.C of Lai et al.’s paper [31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.
, can be respectively calculated by using the trigonometric identities Equations (9,10) [31]. The detailed computations have been introduced in section 2.C of Lai et al.’s paper [31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.
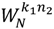 . It implies that the computation between c-point DFT and m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai et al. proposes a coefficient-free algorithm in [31,32]. The two major coefficients in Equation (2), i.e.,
. It implies that the computation between c-point DFT and m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai et al. proposes a coefficient-free algorithm in [31,32]. The two major coefficients in Equation (2), i.e., 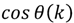 and
and 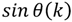 , can be respectively calculated by using the trigonometric identities Equations (9,10) [31]. The detailed computations have been introduced in section 2.C of Lai et al.’s paper [31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.
, can be respectively calculated by using the trigonometric identities Equations (9,10) [31]. The detailed computations have been introduced in section 2.C of Lai et al.’s paper [31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.3. The Proposed Compact RDFT Architecture Design
In the previous section, a compact and low-cost RDFT circuit has been presented in detail. Due to the nature of RDFT, we can apply this design to implement PF-DFT and CF-DFT with variable transform-length DFT computations. Figure 2 demonstrates that the proposed compact RDFT architecture design. The proposed DFT processor can be briefly composed of two memory units, one controller unit, one RDFT unit, and some multiplexers.
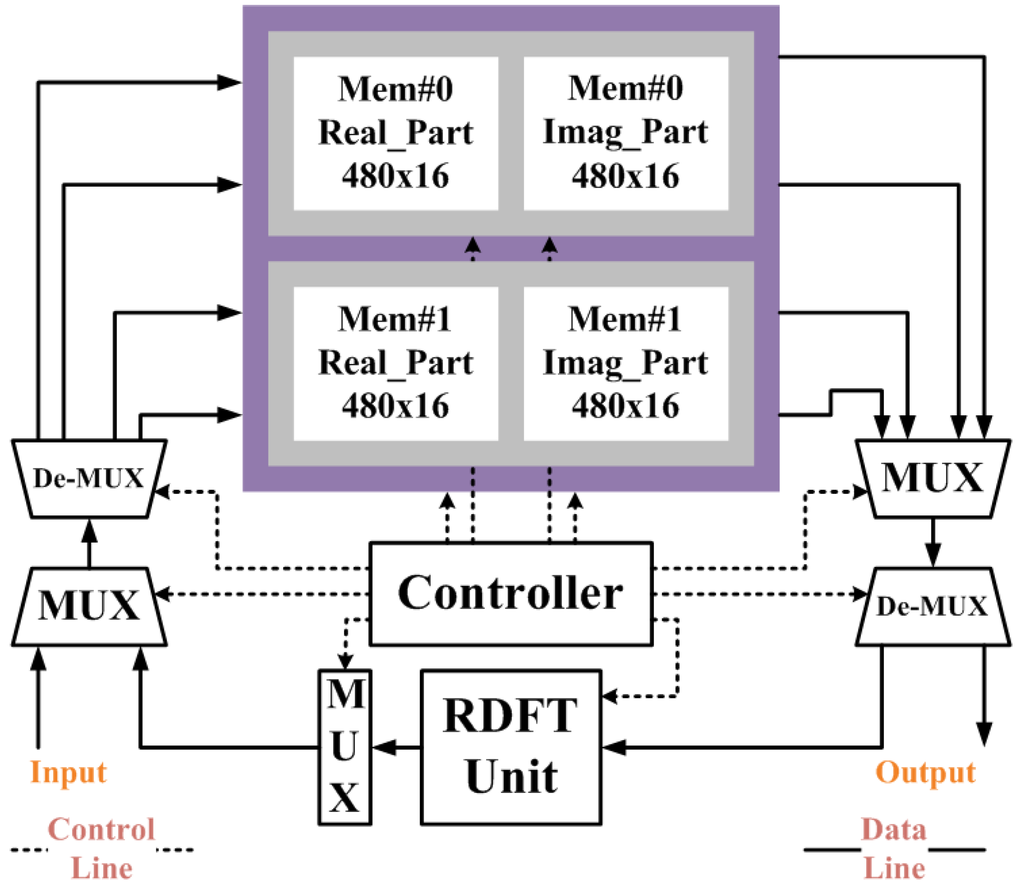
Figure 2.
Proposed compact RDFT architecture design.
The time-domain sequence can be fed into the Mem#0 through the 32-bit input port with real and image parts. The data transmission time is corresponding to the transform length of DFT, and it takes N clock cycles for data transmission. While the input data storing in Mem#0 is ready, the c-point DFT computation can be started. First, the controller unit generates the address for the memory to access the required data, and then the read-out data are further fed into the RDFT unit. Due to the characteristic of the proposed RDFT circuit, two coefficients, i.e., X[k] and X [N − k], can be obtained, and thus we require two 32-bit single port RAMs (16-bit for real part and 16-bit for image part) to alternately switch for storing the temporal data. While the RDFT figures the results out, the controller unit would send a signal for MUX unit to make these two parallel DFT coefficients be sequentially stored back to the Mem#1. After it finishes m times c-point DFT computations, the Mem#1 will fully store all data for the further m-point DFT computation. Hence, we can repeat the above computational flow to generate the m-point DFT coefficients, and then fed the results into Mem#0. Finally, the controller unit will send a signal to the multiplexer and makes the all frequency-domain sequence be transferred to 32-bit output port through the Mem#0. It will also take N clock cycles for data transmission. Note that the twiddle factor multiplications are computed by the same RDFT module, if the CF-DFT algorithm is adopted.
4. Low Power VLSI Implementation
In this section, we will introduce some low-power and optimized schemes applied for the proposed design and further demonstrate the implementation results in detail.
4.1. Low-Power Optimizations
The power consumption has become a critical issue for VLSI design in recent years. For most designs, all designers try their best to minimize the power consumption of chip by using some low-power optimizations such as (1) Clock gating; (2) Operand isolation; and (3) Voltage scaling. For clock gating scheme, it is a method that often used in low power designs, and provides a way to selectively close the clock. It forces the original circuit to make no transition whenever the computation carrying out at the next clock cycle is redundant. In other words, the clock signal is disabled according to the idle conditions of the logic network. We use this gated clock mechanism on the memory module since the memories need to access frequently and it may cause higher power consumption. However, in our design, the number of memory access is processed in an interleaved manner, and the RDFT module needs c or m cycles for each computation. It implies that the storage data will be not updated every cycle, and we can therefore close the clock to reduce power consumption. The idea of operand isolation is to identify redundant operations and uses special isolation circuitry to prevent switching activity from propagating into a module whenever it is to perform a redundant operation [34]. Therefore, the transition activity of the internal nodes of the modules can be significantly reduced, and thus it has lower power consumption. However, the operand isolation technique needs to add extra logic, and may cause some overhead for systems. In the proposed design, the power consumption is dominated on the memory and the RDFT modules. The inputs of RDFT module is coming from memory so that we can isolate the memory output by using a chip enable pin. This method is good for operand isolation since we only need to add some combination circuit to control the enable signal. For the voltage scaling scheme, the traditional dynamic power dissipation equation is defined as
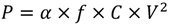 where α is the switching activity, f is the operating frequency, C is loading capacitance, and V is the supply voltage. The supply voltage affects dynamic power by a square term so that to decrease power supply on designs is an efficient way to reduce the power dissipation. Figure 3 shows the power dissipation of the proposed design for 288-point DFT computations at different supply voltages. It clearly shows that the voltage scaling technique can decrease the power consumption by 29.5%.
where α is the switching activity, f is the operating frequency, C is loading capacitance, and V is the supply voltage. The supply voltage affects dynamic power by a square term so that to decrease power supply on designs is an efficient way to reduce the power dissipation. Figure 3 shows the power dissipation of the proposed design for 288-point DFT computations at different supply voltages. It clearly shows that the voltage scaling technique can decrease the power consumption by 29.5%.
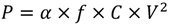
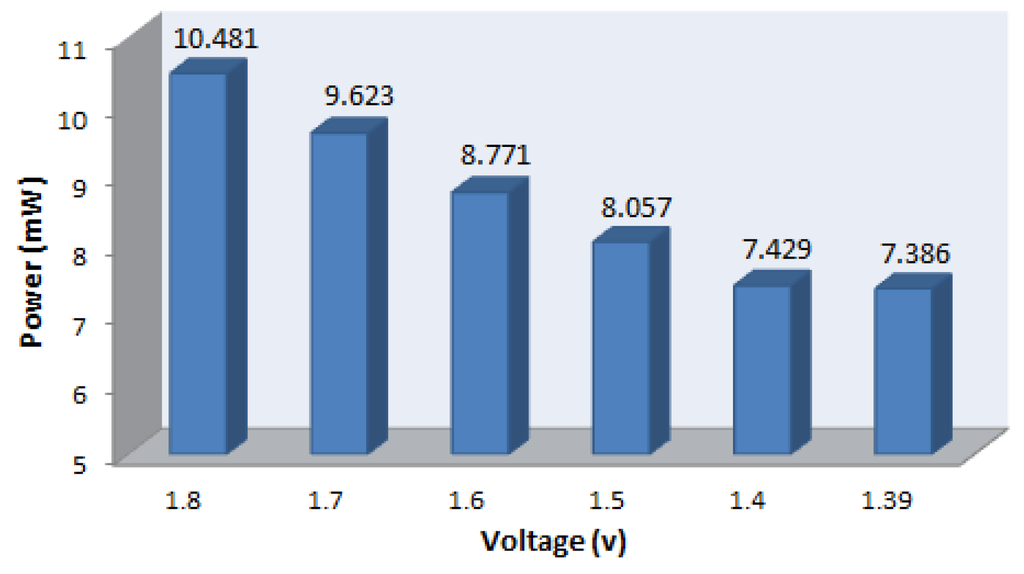
Figure 3.
Power dissipation of 288-point DFT computation at different supply voltages for the proposed RDFT design.
4.2. Implementation Results
The proposed RDFT processor is implemented by using the cell-based design flow with the TSMC 0.18 μm 1P6M CMOS technology. The input and output word lengths are both set to 16-bit format. The internal and coefficient word lengths are both set to 24 bits. Each memory block, i.e., a register file, is generated by Artisan’s Memory Compiler. The verilog code is simulated using Verilog-XL and then is synthesized using the Design Compiler. Finally, it is floorplaned for layout using SoC-encounter. According to the simulation result, the number of gate count of Memory/RDFT/Controller/MUXs is 31,332/13,594/13,451/1,218. Figure 4 shows the percentage of gate count for each module in the proposed design. Figure 5 demonstrates the layout of the proposed RDFT chip.
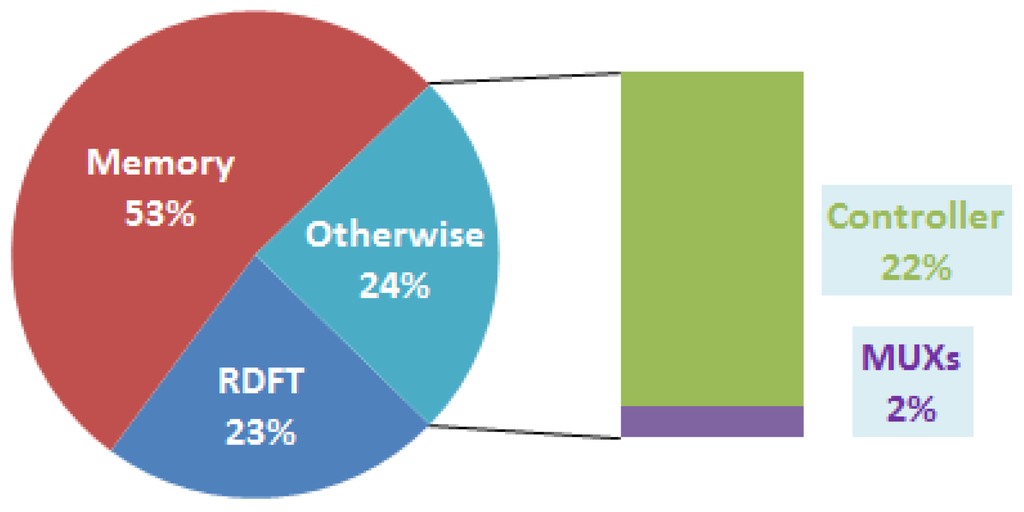
Figure 4.
Percentage of gate count for the proposed design.
The core area and chip area are 0.85 × 0.84 and 1.38 × 1.37 mm2, respectively. The power consumption for 288- and 256-point computation without adopting voltage scaling scheme are, respectively, 10.48 mW and 11.44 mW @25MHz simulated by Nanosim. In fact, the proposed RDFT processor can operate at 273 kHz to meet the real-time requirement of DRM standard. It implies that the power dissipation of the proposed design can be, respectively reduced to 105.1 and 117.6 μW for 288- and 256-point computation. Since the proposed design employs the voltage scaling scheme, the power consumption of the proposed design is reduced from 10.48 mW down to 7.39 mW.
Figure 5.
Chip layout of the proposed RDFT processor.
5. Comparison and Discussion
In this section, we make a completed comparison for various performance evaluations in terms of computational complexity, computational cycle, time cost per transformation (TCPT), and hardware costs. Since the proposed method adopted CF and PF algorithms to speed up the traditional RDFT computation, the factor selection would be greatly impact on the performance of the proposed RDFT. Here, we compare all lists of the required DFT transform lengths in the OFDM of DRM standard, i.e., 288, 256, 176, 112, and 27. Table 1 lists the suitable c and m factors for the proposed RDFT. Both c and m factors are corresponding to the number of computational complexity and the number of computational cycle. To avoid the twiddle factor multiplications in the proposed hardware design, the transform lengths of 288, 176, and 112 are calculated by PFA. Only 256- and 27-point DFT are computed by CFA.

Table 1.
Factor selection for the proposed RDFT.
| Length | 288 | 256 * | 176 | 112 | 27 * | 480 | 60 |
|---|---|---|---|---|---|---|---|
| c | 32 | 16 | 16 | 16 | 9 | 32 | 12 |
| m | 9 | 16 | 11 | 7 | 3 | 15 | 5 |
| A | 9 | 1 | 11 | 7 | 1 | 15 | 5 |
| B | 32 | m | 16 | 16 | m | 32 | 12 |
| C | 64 | c | 144 | 64 | c | 256 | 36 |
| D | 255 | 1 | 33 | 49 | 1 | 255 | 25 |
Note: * common factor only.
Table 2 demonstrates a comparison of computational complexity for various RDFTs with different transform lengths. Van et al.’s method [26] takes (2N2 + 6N) multiplications and (4N2 + 8N) additions to compute N-point DFT coefficients. On the other hand, Lai et al. [9] proposes a much simpler structure, and it takes (N2 – N − 2) multiplications and (2N2 + 7N − 2) additions in N-point DFT computation. Furthermore, Lai et al. proposed two low-complexity methods [30,32] to reduce the numbers of multiplication and addition. It only takes [2N(m + c + 2)] multiplications and [4N(m + c + 2)] additions in [30]. For the proposed PF-RDFT algorithm, i.e., in case of 288-point DFT computations, the number of multiplications would, respectively, take [2m(c + 1)(c/2 − 1)] and [2c(m + 1)(m − 1)/2] for c-point and m-point RDFT computations as shown in (5), where (c/2 − 1) and [(m − 1)/2] are the corresponding number of recursive loops, respectively, for even and odd-point RDFT. In addition, [2m(c + 1)] and [2c(m + 1)] are respectively the number of multiplications per recursive loop, where the scale “2” means the multiplication required for complex input sequence. The total number of additions would, respectively, take [4N(c/2 − 1) + 4c] and [4N(m − 1)/2 + 4m] for c-point and m-point RDFT computations, where (4N) is the number of additions per recursive loop in Figure 1b, and (4c) is the total number of additions only for Figure 1a under consideration of the case of c-point RDFT computations. About the proposed CF-RDFT algorithm, i.e., in case of 256-point DFT computations as shown in Equation (7), it requires extra multiplications and additions for the twiddle factor operation more than that of the proposed PF-RDFT algorithm. However, the twiddle factor operation only takes (4N) multiplications and (2N) additions.
Since the proposed method has a compact and high-throughput RDFT circuit as well as our previous work [32], we can further calculate the desired coefficients with much lower complexity by combining PF and CF algorithms with RDFT. The result shows that the proposed method can, respectively, reduce the numbers of multiplications and additions by 97.40% and 94.31% for 256-point DFT computation while the CFA is adopted.

Table 2.
Computational complexity of various RDFT algorithms for 288- and 256-point computations.
| Method | Multiplications | Additions | ||
|---|---|---|---|---|
| N = 288 | N = 256 | N = 288 | N = 256 | |
| [26] * | 167,616 | 132,608 | 334,080 | 264,192 |
| [27] | 41,464 | 32,760 | 85,658 | 67,946 |
| [29] | 82,654 | 65,278 | 167,902 | 132,862 |
| [30] | 24,768 | 332,928 | 49,536 | 263,168 |
| [32] | 12,704 | 332,928 | 25,984 | 263,168 |
| Proposed | 11,470 | 8,640 | 22,034 | 14,976 |
Note: * pre-processing excluded.
To evaluate the latency of various algorithms, we make a comparison of computational cycle with five transform lengths specified in DRM system. Van et al. [26] and Lai et al. [29] require (N2/2) and [(N2 – N − 1)/2] cycles, respectively, to compute the N-point DFT coefficients. In Table 3, Meher et al. [27] has the lowest computational cycle but requires most hardware resources to implement the systolic structure. Since PFA can be applied to speed up the conventional RDFT and makes the N-point DFT to be c- and m-point sub-DFTs, Lai et al. [30,32] have a lower latency in computation. For example, Lai et al. [30] only requires [(c + 1)N + (m + 1)m] cycles to calculate all coefficients for 288, 176, and 112 transform lengths. Due to the difference of RDFT kernel design, the result shows that the number of computational cycle for our previous works [30,32] is relatively different. In this work, we propose a memory-based structure with a single and compact RDFT processing unit to compute variable-length transform. The results show that the proposed method has a lower latency compared with previous works [26,29,30]. Compared to [32], although the proposed method requires more latency for 288-, 176-, 112-, and 27-point DFT, it still shows a greater performance in terms of 256-point DFT computation, and dramatically reduces the computational cycle by 46.50%. In addition, the hardware costs of this work can be greatly improved, as shown in Table 4.

Table 3.
Computational cycle of various RDFT algorithms.
| Method | Transform length | ||||
|---|---|---|---|---|---|
| 288 | 256 | 176 | 112 | 27 | |
| [26] | 41,472 | 32,768 | 15,488 | 6,272 | N/A |
| [27] | 431 | 383 | 263 | 167 | N/A |
| [29] | 41,327 | 32,639 | 15,399 | 6,215 | 364 |
| [30] | 9,594 | 32,896 | 3,124 | 1,960 | N/A |
| [32] | 4,842 | 11,137 | 1,594 | 1,006 | N/A |
| Proposed | 6,693 | 5,958 | 2,865 | 1,609 | 346 |
For hardware cost comparison, we use items such as a multiplier, adder, buffer, coefficient-ROM, and data throughput per transformation (DTPT) to evaluate the existing RDFT designs in Table 4. For the temporal buffer, Meher et al. [27] require (N/4 − 2) latch cells and each latch cell takes four latches to store the data. By the way, Lai et al. [30] and [32], respectively, require (4 × 11) and (8 × 15) register files. On the other hand, for the number of coefficients stored in the ROM, Van et al. [26] and Lai et al. [29], respectively require (N) and (N − 2) coefficients for each N-point DFT computation, but Meher et al. [27] require (3N − 2) coefficients. It can be observed that Lai et al. [32] have more hardware costs than previous works [26,29,30] do; however, the complexity and latency of [32] have a better improvement according to Table 2, Table 3. To make the design balance in realization, i.e., cost and performance, the proposed method adopts only one RDFT module to implement the memory-based DFT processor. Thus, it does not require extra buffer for temporal data as is the case with Meher et al. [27] and Lai et al. [30,32]. Additionally, we adopt on-line coefficient generator [31,32] to avoid coefficient-ROM using in chip implementation and maintain the same DTPT as well as [29]. The overall comparisons and considerations are clearly indicated that the proposed solution would be a low-cost and high-performance design for variable-length DFT computations.

Table 4.
Hardware cost for various RDFT algorithms.
| Method | Multiplier | Adder | Buffer | ROM | DTPT |
|---|---|---|---|---|---|
| [26] | 10 | 17 | No | Yes | 1 |
| [27] | N + 4 | N + 18 | Yes | Yes | 4 |
| [29] | 2 | 13 | No | Yes | 2 |
| [30] | 4 | 8 | Yes | Yes | 1 |
| [32] | 6 | 18 | Yes | No | 4 |
| Proposed | 2 | 4 | No | No | 2 |
The time cost per transformation (TCPT) of various-length DFTs specified by DRM standard is summarized in Table 5. Based on the results of Table 3, the TCPT of the proposed design can be estimated while the operating frequency rate is set to 25 MHz. In addition, the RAM access time per transformation (RAM_ATPT) is used to calculate the data loading into DFT accelerator and storing back to the system bus, since the proposed design would be an IP in a system. The results show that it can easily achieve real-time requirement of DRM standard and saves over 98.91% of time cost. It implies that we can adjust the operation frequency down to 273 kHz to achieve the requirement of low power consumption. According to NanoSim simulation results, the power consumption for the 288- and 256-point DFT computations are, respectively, 0.105 mW and 0.1176 mW at 273 kHz.

Table 5.
Time cost per transformation for the proposed method.
| Length | 288 | 256 | 176 | 112 | 27 |
|---|---|---|---|---|---|
| DRM Spec. (ms) | <26.7 | <26.7 | <20 | <16.7 | <2.5 |
| Proposed (us) | 267.72 | 238.32 | 114.60 | 64.36 | 13.84 |
| RAM_ATPT(us) | 23.04 | 20.48 | 14.08 | 8.96 | 2.16 |
| Reduction (%) | 98.91 | 99.03 | 99.36 | 99.56 | 99.36 |
Table 6 summarizes the comparisons between the proposed design and other RDFT processors for DRM receiver in the literature. For the purpose of fair comparison with different process technologies, we employ Baas’ normalization Equations (9) and (10) [35] to normalize the area and DFTs/Energy.
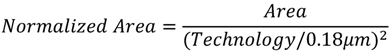
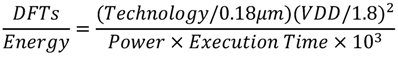
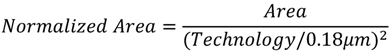
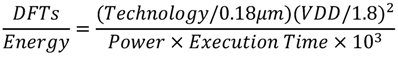

Table 6.
Comparison of chip feature for previous works and this work.
| Design | [29 | [30 | [33] | This work | |
|---|---|---|---|---|---|
| Technology | 0.18 μm | 0.18 μm | 0.18 μm | 0.18 μm | |
| Internal/Coeff. word lengths | 24/24 (bits) | 21/16 (bits) | 24/24 (bits) | 24/24 (bits) | |
| Data Memory (bits) | Excluded | Excluded | Excluded | 2 × 480 × 32 | |
| Coefficient Memory | Excluded | Coeff.-free | Coeff.-free | Coeff.-free | |
| Supply Voltage | 1.98 v | 1.98 v | 1.98 v | 1.7 v (opt.) | |
| Clock Rate | 25 MHz | 25 MHz | 25 MHz | 25 MHz | |
| Supporting DFT | 288, 256, 176, | 288, 256, 176, | 288, 256, 176, | 288, 256, 176, | |
| Transform-Length | 112, 212, 106 | 112 | 112, 480, 60 | 112, 480, 60 | |
| Executing Time for 288-point | 1.65 ms | 384 μs | 193.68 μs | 267.72 μs | |
| Power Consumption | Circuit | 5.98 mW | 8.44 mW | 14.3 mW | 9.62 mW(opt.) |
| Data Memory | 5.53 mW * | 5.53 mW* | 5.53 mW * | ||
| Core Area | Circuit | 0.154 mm2 | 0.265 mm2 | 0.746 mm2 | 0.714 mm2 |
| Data Memory | 0.347 mm2 | 0.347 mm2 | 0.347 mm2 | ||
| Normalized DFTs/Energy | 63.71 | 225.56 | 315.05 | 346.34 (opt.) | |
Note: * estimated by this work.
Note that the memory unit excluded in these literatures. Van et al.’s algorithm [26] has a number of N2/2 computational cycles as well as Lai et al.’s [29], but the implementation chip of Van et al. is only designed to DTMF application. For DRM applications, previous works [30,32] have a better performance in terms of normalized DFTs per energy; however, these designs do not include the data memory to buffer the input and out sequence. This implies that these two designs would occupy most bandwidth of system bus, since they are hard intellectual properties (IPs) in an embedded system. Form the system view to consider this problem, the area and power consumption of data memory (RAM) should not be neglected. Table 2 clearly shows that the proposed design is a smaller than previous work [32], although it seems to lose its advantage in power consumption. Here, we also provide a power consumption result simulated by NanoSim. The result shows that the proposed design consumes 10.693 mW @ 25 MHz. The percentage of power dissipation is as shown in Figure 6. We can see that it consumes the most of power in RDFT module, and the power consumption of memory module is 1.925 mW. Based on Figure 4, Figure 6, we know that the memory module consumes approximately a fifth of total power, and takes more chip area over 50% of total gate counts.
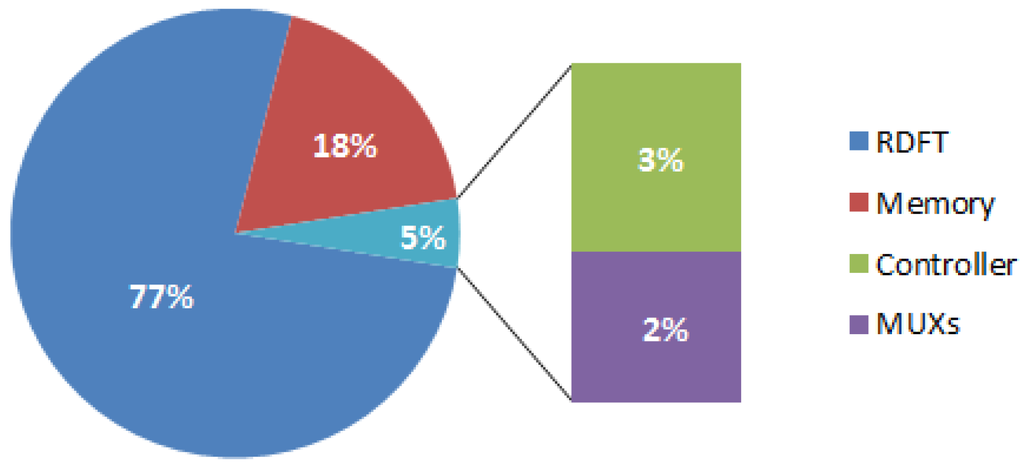
Figure 6.
Percentage of power dissipation for the proposed design by Prime Power.
6. Conclusions
This paper presented a high-performance design for variable-length DFT computations for a DRM and DRM+ receiver by using the low-power and optimized VLSI schemes in implementation. In addition, the compact RDFT kernel integrates prime factor and common factor algorithms into one structure, and only costs a smaller area than previous designs. Therefore, it would be a regular, flexible, and compact design for a VLSI realization in many future variable-length DFT and IMDCT computations.
Acknowledgments
This work was supported in part by the National Science Council, Taiwan under Grant No. 101-2218-E006-005 and 101-2221-E006-271.
References
- Digital Radio Mondiale; System Specification; ES 201 980 V3.1.1; European Telecommunications Standards Institute (ETSI): Nice, France, August 2009.
- Tai, S.C.; Wang, C.C.; Wang, J.L. Circuit-Sharing Design between FFT and IMDCT with Pipeline Structure for DAB Receiver. In Proceedings of the 17th International Conference on Advanced Information Networking and Applications, Xi’an, China, 27–29 March 2003; pp. 768–773.
- Tai, S.C.; Wang, C.C.; Lin, C.Y. FFT and IMDCT circuit sharing in DAB receiver. IEEE Trans. Broadcast. 2003, 49, 124–131. [Google Scholar] [CrossRef]
- Wang, C.C.; Lin, C.Y. An Efficient FFT processor for DAB receiver using circuit-sharing pipeline design. IEEE Trans. Broadcast. 2007, 53, 670–677. [Google Scholar] [CrossRef]
- Kim, B.E.; Chung, J.Y.; Hwang, S.Y. An efficient fixed-point IMDCT algorithm for high-resolution audio appliances. IEEE Trans. Consum. Electron. 2008, 54, 1867–1872. [Google Scholar] [CrossRef]
- Radio Broadcasting System: Digital Audio Broadcasting to Mobile Portable and Fixed Receiver; ETS 300 401; European Telecommunications Standards Institute (ETSI): Nice, France, January 2006.
- Digital Audio Broadcasting (DAB): Transport of Advanced Audio Coding (AAC) Audio; ETSI TS 102 563; European Telecommunications Standards Institute (ETSI): Nice, France, February 2007.
- Lai, S.C.; Lei, S.F.; Luo, C.H. Low-Cost and Shared Architecture Design of Recursive DFT/IDFT/IMDCT Algorithms for Digital Radio Mondiale System. In Proceedings of IEEE International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP-2010), Darmstadt, Germany, 15–17 October 2010; pp. 276–279.
- Chiang, H.C.; Liu, J.C. Regressive implementations for the forward and inverse MDCT in MPEG audio coding. IEEE Signal Process. Lett. 1996, 3, 116–118. [Google Scholar] [CrossRef]
- Nikolajevic, V.; Fettweis, G. Computation of forward and inverse MDCT using Clenshaw’s recurrence formula. IEEE Trans. Signal Process. 2003, 51, 1439–1444. [Google Scholar] [CrossRef]
- Chen, C.G.; Liu, B.D.; Yang, J.F. Recursive architectures for realizing modified discrete cosine transform and its inverse. IEEE Trans. Circuits Syst. II 2003, 50, 28–45. [Google Scholar]
- Nikolajevič, V.; Fettweis, G. New Recursive Algorithms for the Forward and Inverse MDCT. In Proceedings of the IEEE Workshop on Signal Processing Systems: Design and Implementation (SiPS’2001), Antwerp, Belgium, 26–28 September 2001; pp. 51–57.
- Nikolajevič, V.; Fettweis, G. New recursive algorithms for the unified forward and inverse MDCT/MDST. J. VLSI Signal Process. Syst. 2003, 34, 203–208. [Google Scholar] [CrossRef]
- Fox, W.; Carriera, A. Goertzel Implementations of the Forward and Inverse Modified Discrete Cosine Transform. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (CCECE’2004), Niagara Falls, Canada, 2–5 May 2004; pp. 2371–2374.
- Chen, C.H.; Wu, C.B; Liu, B.D.; Yang, J.F. Recursive Architectures for the Forward and Inverse Modified Discrete Cosine Transform. In Proceedings of the IEEE Workshop on Signal Processing Systems: Design and Implementation (SiPS’2000), Lafayette, LA, USA, 11–13 October 2000; pp. 50–59.
- Cheng, Z.Y.; Chen, C.H.; Liu, B.D.; Yang, J.F. Unified Selectable Fixed-Coefficient Recursive Structures for Computing DCT, IMDCT and Subband Synthesis Filtering. In Proceedings of the IEEE International Symposium on Circuits and Systems, Vancouver, Canada, 23–26 May 2004; pp. 557–560.
- Lei, S.F.; Lai, S.C.; Hwang, Y.T.; Luo, C.H. A High-Precision Algorithm for the Forward and Inverse MDCT Using the Unified Recursive Architecture. In Proceedings of the IEEE International Symposium on Consumer Electronics, Vilamoura, Algarve, 14–16 April 2008; pp. 1–4.
- Lai, S.C.; Lei, S.F.; Luo, C.H. Common architecture design of novel recursive MDCT and IMDCT algorithms for application to AAC, AAC in DRM, and MP3 codecs. IEEE Trans. Circuits Syst. II 2009, 56, 793–797. [Google Scholar] [CrossRef]
- Lei, S.F.; Lai, S.C.; Cheng, P.Y.; Luo, C.H. Low complexity and fast computation for recursive MDCT and IMDCT algorithms. IEEE Trans. Circuits Syst. II 2010, 57, 571–575. [Google Scholar] [CrossRef]
- Wolkotte, P.T.; Smit, G.J.M.; Smit, L.T. Partitioning of a DRM Receiver. In Proceedings of the 9th International OFDM-Workshop, Dresden, Germany, 15–16, September 2004; pp. 299–304.
- Goertzel, G. An algorithm for the evaluation of finite trigonometric series. Am. Math. 1958, 65, 34–35. [Google Scholar] [CrossRef]
- Yang, J.F.; Chen, F.K. Recursive discrete Fourier transform with unified IIR filter stluclures. Signal Process. 2002, 82, 31–41. [Google Scholar] [CrossRef]
- Van, L.D.; Yang, C.C. High-Speed Area-Efficient Recursive DFT/IDFT Architectures. In Proceedings of the IEEE International Symposium Circuits and System, Vancouver, Canada, 23–26 May 2004; pp. 357–360.
- Van, L.D.; Yu, Y.C.; Huang, C.N.; Lin, C.T. Low Computation Cycle and High Speed Recursive DFT/IDFT: VLSI Algorithm and Architecture. In Proceedings of the IEEE Workshop on Signal Processing Systems, Athens, Greece, 2–4 November 2005; pp. 579–584.
- Fan, C.P.; Su, G.A. Efficient recursive discrete Fourier transform design with low round-off error. Int. J. Electr. Eng. 2006, 13, 9–20. [Google Scholar]
- Van, L.D.; Lin, C.T.; Yu, Y.C. VLSI architecture for the low-computation cycle and power-efficient recursive DFT/IDFT design. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2007, E90-A, 1644–1652. [Google Scholar]
- Meher, P.K.; Patra, J.C.; Vinod, A.P. Novel Recursive Solution for Area-Time Efficient Systolization of Discrete Fourier Transform. In Proceedings of the IEEE International Symposium on Signals, Circuits and Systems, Lasi, Romania, 12–13 July 2007; pp. 193–196.
- Meher, P.K.; Patra, J.C.; Vinod, A.P. Efficient systolic designs for 1- and 2-dimensional DFT of general transform-lengths for high-speed wireless communication applications. J. Signal Process. Syst. 2010, 60, 1–14. [Google Scholar] [CrossRef]
- Lai, S.C.; Lei, S.F.; Chang, C.L.; Lin, C.C.; Luo, C.H. Low computational complexity, low power, and low area design for the implementation of recursive DFT and IDFT algorithms. IEEE Trans. Circuits Syst. II 2009, 56, 921–925. [Google Scholar] [CrossRef]
- Lai, S.C.; Juang, W.H.; Chang, C.L.; Lin, C.C.; Luo, C.H.; Lei, S.F. Low-computation cycle, power-efficient, and reconfigurable design of recursive DFT for portable digital radio mondiale receiver. IEEE Trans. Circuits Syst. II 2010, 57, 647–651. [Google Scholar] [CrossRef]
- Lai, S.C.; Lei, S.F.; Juang, W.H.; Luo, C.H. A low-cost, low-complexity and memory-free architecture of novel recursive DFT and IDFT algorithms for DTMF application. IEEE Trans. Circuits Syst. II 2010, 57, 711–715. [Google Scholar] [CrossRef]
- Lai, S.C.; Juang, W.H.; Lin, C.C.; Luo, C.H.; Lei, S.F. High-throughput, power-efficient, coefficient-free and reconfigurable green design for recursive DFT in a portable DRM receiver. Int. J. Electr. Eng. 2011, 18, 137–145. [Google Scholar]
- Hsiao, C.F.; Chen, Y.; Lee, C.Y. A generalized mixed-radix algorithm for memory-based FFT processors. IEEE Trans. Circuits Syst. II 2010, 57, 26–30. [Google Scholar] [CrossRef]
- Munch, M.; Wurth, B.; Mehra, R.; Sproch, J.; Wehnl, N. Automating RT-Level Operand Isolation to Minimize Power Consumption in Datapaths. In Proceedings of the IEEE Design Automation and Test, Paris, France, 27–30 March 2000; pp. 624–631.
- Baas, B.M. A low-power, high-performance, 1024-Point FFT processor. IEEE J. Solid-State Circuits 1999, 34, 380–387. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).