Antenna Array with TEM-Horn for Radiation of High-Power Ultra Short Electromagnetic Pulses

Abstract

An antenna array with short shielded transverse electromagnetic horns (S-TEM-horns) for emitting high-power radiation of ultra-short electromagnetic pulses (USEMP) has been created and researched. The antenna unit consists of an ultra-wideband antenna array with four S-TEM horns, with each connected to a two-wire HF transmission line, and these four lines are connected to an antenna feeder. This feeder is connected to a semiconductor generator with the following parameters: a 50 Ohm connector, 10–100 kV high-voltage monopolar pulses, a rise time of about 0.1 ns, FWHM = 0.2–1 ns, and pulse repetition rates of 1–100 kHz. The antenna array was designed and optimized to achieve a high efficiency of about 100% for the antenna aperture by using a 2 × 2 array with S-TEM-horns, with shielding rectangular plates for the return current. The transient responses were studied by simulation using the electromagnetic 3D code “KARAT” at the time domain and experimentally with the use of our stripline sensor for measurement of the impulse electrical field with a 0.03 ns rise time and a 7 ns duration at the traveling wave. The radiators were emitting USEMP waves with a hyperband frequency spectrum of 0.1–6 GHz. The radiation with an amplitude of 5–30 kV/m of the E-field strength at a distance of up to 20 m was successfully applied to test the electronics for immunity to electromagnetic interference.

1. Introduction

The widespread use of artificial intelligence or robotics as the base of digital microelectronics with autonomous and radio remote control in civil and military infrastructures may be accompanied by problems in their correct functioning due to high levels of electromagnetic interference (EMI) from ordinary sources and possible intentional electromagnetic interference (IEMI). Test methods of checking immunity to IEMI, with the goal to increase the reliable operation of equipment and systems, have been developed continually in many countries and by the International Electrotechnical Commission (IEC) [1]. For the testing of any device, as a rule, high-power electromagnetic pulse radiators (HPEM) are used as IEMI simulators. The operating range for modern digital equipment occupies a spectrum in the 0.1–6 GHz frequency band. The HPEM radiators emitting ultra-short electromagnetic pulses with a rise time of about 0.1 ns and with quasi-mono-polar waveforms create EMI waves with such a spectral frequency band. It is a so-called hyperband spectrum with a band ratio of f_h/f_l > 10 for the high and low frequencies, between which there is 90% of the impulse energy [1].

Examples of two types of successful HPEM sources with hyperband spectrums in electromagnetic (EM) pulse waves are in [2,3,4,5,6,7,8,9]. One type of such sources was developed in US laboratories, and it was based on using high-voltage monopolar pulsed generators, which excited the antenna of a half-reflector type (HIRA) with a large diameter (3.1 m in [2], 1.2 m in [3], and 1.8 m in [4]). A large diameter was a necessary attribute of these antennae so that they effectively emitted EM waves with frequencies in the lower range of 0.05–0.2 GHz [2]. Mobile autonomous radiators with relatively non-large sizes (L ~ 0.6 m) as the HPEM sources with hyperband spectrums were developed in our Laboratory of Powerful Electromagnetic Impacts of the JIHT RAS [5,6,7,8,9]. These radiators contained the ultra-wideband (UWB) antenna array with four short shielded transverse electromagnetic horns (S-TEM-horns), which were excited by high-voltage (HV) monopolar pulses from a semiconductor pulser, DC power source, and control unit.

The antenna array was built with four S-TEM horns with shielding of rectangular plates. Each TEM horn was connected to its two-wire HF transmission line, and these four were joined to the antenna feeder. The first such successful antennae with high-efficiency apertures were created in 2008 with an aperture size of 16 cm × 16 cm [5]. The antenna coaxial feeder was connected to the semiconductor pulsers, which were developed by FID Technology [10,11] and fabricated by FID Technics. They had the following parameters: 50 Ohm impedance of HV-HF coaxial connector, monopolar pulses with HV amplitudes of 10–100 kV, rise time of about 0.1 ns, and FWHM of 0.2–1 ns. The pulse repetition rates were up to 100 kHz for the 10 kV version, 5 kHz for the 40 kV version, and 1 kHz for the 100 kV version. The DC power consumption was 200–300 W. The time jitter between the sync and HV impulses was ~0.02 ns. This allows build the active array radiators with the effective radiation potential ER ~1–10 MV. Here, E is the peak field strength in the far field at a distance R.

Transient responses of the antennae were studied by simulations using the electromagnetic 3D code KARAT at the time domain [12] and experimentally with the use of our strip-line sensors for measurements of the impulse E field strength with a 0.03 ns rise time and 7 ns duration of the traveling EM waves [13]. Estimation of the radiation parameters from the radiators was also being done by using analytical models [6,14].

Several advantages and defects concerning the testing of electronics for immunity to the EMI by the HPEM radiators emitting USEMP waves will be discussed below. Typically, the USEMP waves are formed by the pulsed electromagnetic fields with an ultra-wide spectrum of frequencies with a band ratio f_h/f_l > 10. This quality of the USEMP radiator allows its use in the case of the IEMI testing of any device with one simulator instead of several with relatively limited frequency bands [1]. A widening of the spectrum for pulses of the mesoband type was suggested and realized in [15] by the method of summa in a free space of waves with various central frequencies emitted by several synchronous sources. In these cases, a problem of synchronizing of different radiation impulses arose. The advantage of the HPEM radiators with antennae, which are excited by bipolar high-voltage impulses like in [15], is the relatively high factor of conversion of electrical pulse energy in pulsed EM radiation. The antennae are excited by monopolar high-voltage impulses, and the factor of conversion is about two times lower [14]. An obvious defect of the EM pulse with a broader spectrum is the lower spectral density of power in any frequency range. It may be compensated by using a radiated pulse with a higher amplitude of E-field strength on the device under testing. Extreme testing of a device often requires high amplitudes of impact for the E-field strength (≥10 kV/m) and also a relatively high repetition rate of the pulses (~10³ Hz and more) [16,17]. The USEMP high-power radiation creates a flow of the EMI waves with a non-high level of intensity, because the typical sequence of pulses is characterized by a small value of the duty factor (<10⁻⁴). The latter gives less of a danger of soiling ether by the EM pulses in the case of testing outside the shielding chambers, as well as a low probability of irreversible failure of the equipment under testing. At last, the frequency spectrum of waves from the USEMP radiator can be changing if the device under testing will be positioned under various angles toward the axis of the antenna. The bigger angular deviation does lowers the frequency in the spectrum boundary [6] (see Section 3.2 below).

Schematics of the S-TEM-Horn Antennae and Advantages for Radiations within 0.1–6 GHz Frequencies

Figure 1 shows the general design of the antenna array with four S-TEM-horns in 3D and 2D views. Figure 1a shows the structure of the two-story antenna of a 2 × 2 array. Figure 1b shows a side view of the picture in Figure 1a. There is two S-TEM-horns, and the others behind the picture were connected in parallel with the feeder of the antenna.

This simple design for a two-story antenna structure has been used in antennae with an aperture height H_in ≥ 30 cm and pulse repetition rate of its excitation of 1 kHz. In the case of fast antenna excitation, we used plates between the upper and lower story with insulation plate between them [13]. The rear side of the actual antennae was a metallic plate with damper resistors in the circuit of the electric current. The outer shielding plates in the antenna array (upper and lower plates in Figure 1) were intended for flow of the return electric current from the face edges of the horns. These rectangular plates were made with the same width of the antenna aperture, some parts could be a little more than the width of the aperture. These qualities of the shielding plates in the antenna structure played a main role in decreasing the parasitic radiation from any lateral surface of the antenna and in increasing the direct radiation from the antenna aperture.

Each of the four TEM horns was connected to an individual two-wire transmission line. The impedance of the line was about 180 ohms, and it was matched with the impedance of one TEM horn of antenna array. Four lines were connected to the 50 ohm feeder of the antenna.

Our radiators [6,7,8,9,13,14] were emitting waves of the USEMP sub-nanosecond duration in the frequency range 0.1–6 GHz and with an effective voltage potential ER = 20–400 kV. These impulse waves, as simulators of EM interference with a peak strength of 5–30 kV/m, were successfully used for testing electronic devices for EM compatibility or immunity to the EMI. The repetition rate of emitted pulses was up to 100 kHz for the 10 kV version and 1 kHz for the 100 kV version of the pulser for antenna excitation. Mobile autonomous radiators were supplied by a DC power source with an accumulator assembly. The total weight of the radiator was about 10 kg.

This article presents analyses of the results of our works [6,7,8,9,13,14] concerning the creation and optimization of the high-power radiators for ultra-short electromagnetic pulse waves with a linear polarization E-field and quasi-monopolar impulses. Below, we give analyses of the physical processes in classical and shielded TEM horn antennae. In Section 2.1, it is shown that the classical TEM horn antenna has lower radiation parameters of emission than the shielded TEM horn in frequency range of 0.1–6 GHz. In Section 3, the instrument for measurement of the E-field strength in the pulsed traveling EM waves with a spectral band of 0.1–10 GHz is presented. Analyses of the results and problems regarding the optimization and reliability of the high-power radiators for emitting the USEMP waves with a high repetition rate of pulses are given in Section 4. Comparisons with other HPEM radiators for the emission of pulsed waves with a hyper-band spectrum are given in Section 4.1.

2. Calculations and Experiments on Aperture Antennae Based on Classical and Shielded TEM Horns

Well-known high-power microwave (HPM) narrowband sources as impulse radiators with aperture antennae, such as pyramidal horns and parabolic reflectors, have been operating successfully for many decades in radar applications. In particular, the radiators with reflectors, which are excited by magnetrons [18], were used with a high success rate since 1940. Intensive development and application of the pulsed high-power UWB radiators has a history of about 20 years, and it connects with the need for testing of modern electronic equipment for electromagnetic compatibility [1].

The typical estimated aperture efficiency for a parabolic reflector is η_a,_eff ≈ 55% [19] (ch.1-3). The aperture efficiency is estimated usually by the factor η_a,_eff = A_a,eff/A_a, where A_a,eff is the estimated surface area of the aperture in receiver mode of the antenna and A_a is the physical surface area of the aperture. According to the known principle of reciprocity for electrical linear systems, including antennae with pulsed signals, the effective area of the antenna A_a,eff and the transient responses of the antenna units will be identical in two antenna modes (regimes) as a transmitter (T_x) or as a receiver (R_x) [19,20] (ch.1-4, ch.5-1).

Below, we give analyses of the physical processes in some applications of TEM horn antennae in classical and shielded modifications.

2.1. Classical TEM Horn Antenna

For analysis of the time domain characteristics for antennae with TEM horns in receiver mode (R_x), we used the 3D fully electromagnetic code KARAT (the first version was created in 1992 by V.P. Tarakanov [21]).

The TEM half-horn antenna is one half of the TEM horn antenna. It is widely used as a simple sensor for direct measurements of a pulsed E-field in traveling EM waves [22,23,24,25,26,27]. A simple TEM half-horn antenna with an impedance of 50 ohms has a low aperture efficiency (η_a,eff ≈ 0.34) [26], and therefore it is unattractive for use in high-power radiators. A TEM half-horn antenna with an impedance of about 100 ohms has approximately two times the aperture efficiency but bad transient response (which will be shown below).

A numerical 3D simulation of the TEM half-horn antenna (named 1) was conducted. Antenna 1 was placed into a counting region with the following dimensions: width Δx = 27 cm, height Δy = 20 cm, and length Δz = 60 cm. Figure 2 shows the middle cross-section of the counting region in the (Y,Z) plane (x₀ = 13.5 cm). The counting region was composed of the count mesh with 570 × 490 × 1100 nodes along the (X,Y,Z) axis. The counting region coincided with the dimensions of the simulation’s gauge cell-line, which is a model of an actual TEM gauge line section. Such cell-lines are used as a rule for the calibration of antenna sensors [28]. The red lines in Figure 2 at the top and bottom present the upper and lower flat electrodes of the simulation’s gauge cell-line. The external TEM plane wave with an electric component E_y = 500 V/cm, magnetic component B_x = 1.32 A/cm, and front rise time 0.1 ns was launched in an entrance window (z = 0) into the gap between these electrodes at a time moment of T = 0 ns. This TEM wave propagated inside the cell-line along the z-axis and left the cell-line through the output window without reflection. Antenna 1, placed into the region of the cell line, was the object for the creation of some reflected EM waves. The boundary conditions for the reflected EM waves in the simulation region of the cell line were as follows: the bottom and top were conductor plates (electric component E_x(t) = 0 and E_z(t) = 0, magnetic component B_y(t) = 0), and the input and output side surfaces were transparent for transverse waves.

Figure 2 shows the schema of the elements of antenna 1 in the middle (Y,Z) plane and the counting picture of the vectors for the E-field distribution of external EM waves at time moment 2 ns when the wave front arrives at coordinate z = 60 cm.

The violet arrows in Figure 2 are schematic drawings of the E-field vectors of the EM wave. The greater the length of the arrow, the more the module value of the E-field. A small density in arrow distribution shows the regions with low E-field strength values. In Figure 2, such a region occurred inside the antenna gap for the z-coordinate between 7 cm and 25 cm.

The signal electrode was the conducting plate of a triangular shape in the (X,Z) plane with a width of W_1,in = 9 cm at z = 6 cm, and it was placed over the base electrode with an angular separation β₁ = 14.5° (blue line in Figure 2). In any cross section of antenna 1, the width of the electrode (W₁) and height over the base electrode (H₁) were approximately equal. The horn length was L_s = 33 cm. The acute edge of the signal electrode was connected to the stripline (Figure 2, coordinate z = 39 cm). The other end of the strip-line (z = 49 cm) was connected to the antenna coaxial feeder, which transmitted the receiver signal to a recorder.

The point R₁ with coordinates x = 13.5 cm, y = 3 cm, z = 14 cm was set inside the antenna for observation. The calculation results are presented in Figure 3 as waveforms of the pulses.

Figure 3a shows the waveforms of the EM field (curve 1 = E_y,ext(t; z = 6 cm) at the incoming wave; curve 2 = E_y(t; R₁); curve 3 = magnetic field B_x(t; R₁)). Figure 3b shows the external power flow P_a1,in(t; z = 6 cm) throughout the antenna aperture A_a1 = 9 × 8.5 = 76.5 cm² (curve 1). Its value was P_a1,in ≈ 50 kW. Curve 2 is the calculated received power P_a1,Rec(t; z = 53 cm). This power was being sent from the TEM half-horn antenna to the coaxial feeder. Curve 3 is the antenna factor K_H(t) = h_a,eff/H_in. Its maximum value was 0.5.

Using the data of the input and output power flows, one could perform an approximation for the output power and aperture efficiency of the antenna with Equation (1). The calculated aperture efficiency η_a1,_eff had a maximum value of 0.7 and a time decay τ_a1 ≈ 1.6 ns:

$$P_{a1,\mathrm{in}}=A_{a1}{E}_{\mathrm{ext}}^2/Z_0=50.7\mathrm{kW};P_{a1,\mathrm{Rec}}(t\ge 1.95\mathrm{ns})=35(1-(t-1.95)/1.6)\mathrm{kW};{\eta }_{a1,\mathrm{eff}}(t\ge 1.95\mathrm{ns})\approx 0.7(1-(t-1.95)/1.6)$$

(1)

The main disadvantage of the TEM half-horn antennae and sensors is the short time duration of the received pulses without distortions [23,26]. This is on account of the triangular shape of the transient response of the TEM half-horn antenna on impact of the step-like pulse of the external E-field. The work time gap defined on the 0.9V_max level would be equal to ΔT_pw ≈ 0.2(L_s + H_1in)/c₀ (c₀ = 30 cm/ns, light velocity). Application of a complicated horn profile gave an extension of the frequency band, as in [27].

Another method of E-field measurement used the stripline sensor with an approximately constant cross-section along its axis. It had a constant transient response during $\Delta T_{\mathrm{pw},\mathrm{st}}\approx 2\sqrt{{\mathsf{\epsilon }}_{\mathrm{eff}}}{L}_{\mathrm{s}}/c_0$ [23]. Such sensors were used in our past works [5,6,7,8,9,26,28].

The half-horn sensors in the experiments [23,24,25,26] were made with the impedance of 50 ohms (W_1/H₁ = 5) in order to match with the cable impedance. In measurements of the pulsed E-field, a parameter such as an effective length (or height) of the antenna h_a,eff is often used to estimate the electrical field strength by a simple ratio E(t) = V_s(t)/h_a,eff, where V_s(t) is the recorded voltage of the matched load. The authors of [23,25] used an effective length h_a,eff of the TEM half-horn sensors with the air dielectric as a parameter, which characterized it sensibility. We could estimate the aperture efficiency η_a,_eff = A_a,eff/A_a for the half-horn sensor data by using a balance of power(Z₀ = 120π = 377 ohms of impedance of the free space):

$$P_{a,\mathrm{Rec}}={\eta }_{a,\mathrm{eff}}{P}_{a,\mathrm{in}}={\eta }_{a,\mathrm{eff}}{H}_{\mathrm{in}}{W}_{\mathrm{in}}{E}_{\mathrm{in}}^2/Z_0={(K_{\mathrm{H}}{H}_{\mathrm{in}})}^2{E}_{\mathrm{in}}^2/Z$$

(2)

$${\eta }_{a,\mathrm{eff}}=K_{\mathrm{H}}^2(H_{\mathrm{in}}/W_{\mathrm{in}})Z_0/Z;A_{a,\mathrm{eff}}={(K_{\mathrm{H}}{H}_{\mathrm{in}})}^2{Z}_0/Z;L_{a,\mathrm{eff}}=\sqrt{A_{a,\mathrm{eff}}}.$$

(3)

$$K_{\mathrm{H}}=\sqrt{{\eta }_{a,\mathrm{eff}}(W_{\mathrm{in}}/H_{\mathrm{in}})(Z/Z_0)}$$

(4)

According to the calculation by Equation (3), the TEM half-horn sensor in [25] with K_H = 0.5, (H_in/W_in) = 0.2, and Z = 50 ohms had an aperture efficiency of only η_a,eff = 0.377. For comparison, antenna 1 with (H_1/W₁) ≈ 1, Z₁ = 120 ohms had a relatively high aperture efficiency, reaching a maximum of η_a1,_eff ≈ 0.7 according to Equation (1) and the simulation data. It was two times more than that of the sensor in [25]. The antenna factor K_H, estimated by Equation (4) for antenna 1, was equal to the previous K_H,in = 0.47, and this was near the value of K_H for the 50 ohm half-horn in [25].

These results allowed us to take the antenna factor K_H,max ≈ 0.5 as an invariant value in R_x mode for the classic TEM horn antenna [23,24]. It is necessary to note that some problems in applying these formulas for the TEM half-horn antennae with large angular divergences of electrodes or with large ratios of the H/W > 1 may have arisen. The latter were used in radiators of the IRA (HIRA) type [2,3,4]. In cases where H/W > 1, the power flow in the EM wave coming into the aperture of the TEM half-horn antenna would be localized, as is well known, mainly around the signal electrode rather than in the region between the antenna electrodes.

The electrical E_y(t; z-tc₀) and magnetic B_x(t; z-tc₀) fields in the incoming wave excited the electrical current on the inner and outer surfaces of the signal electrode. The inner current, at a direct wave inside the TEM half-horn, was transported along the z-axis without reflections. The induced outer current had an opposite value compared with the induced inner current (a summa of these currents was approximately zero on the input edge of the signal electrode). The magnitude of the induced current wave on the outer surface of the electrode with an increase of the z-coordinate decreased on account of reducing the electrode width. An excess of this outer current was leaking inside the gap of antenna 1, and it separated on two waves with direct and inverse directions. As a result, some direct and inverse waves moved into the gap of the classical TEM horn line antenna sensors because of the transient response of the half-horn sensor having a triangular shape in mode R_x of the antenna. In accordance with the principle of reciprocity, this transient response with a triangular shape would be applied to the classical TEM horn line antenna in a regime as a radiator.

The noted defects of the classical TEM horn antennae are that it is practically unattractive for use in high-power radiators for the effective emission of EM waves with a hyperband spectrum.

2.2. Calculations and Experiments for the UWB Antenna with S-TEM-Horns with Shielding Plates

Numerical 3D simulations by the KARAT code were conducted on a model with one S-TEM half-horn antenna, named antenna 2.

Antenna 2 was placed in a counting region (Figure 4) that coincided with a region of the cell-line section with the following dimensions: width Δx_c = 28 cm, gap Δy_c = 20 cm, and length Δz_c = 60 cm.

This picture gives a 2D view of a cross-section of the cell line in a plane (Y,Z) at x₀ = 14 cm (middle of the cell line). The plane electrode of the shielding plate (y_sh = 8.7 cm) of the TEM half-horn has a red color, representing the base electrode (y_bs = 0.2 cm). The design of the signal electrodes was approximately the same as in antenna 1, except in the region at z ≈ 6 cm, the input edge of the signal electrode was partially rounded with a radius of about 1 cm in order to contact with the shielding rectangular plate under a straight angle. The strip-line between 39 cm and 49 cm on the z-axis was simulated as one two-wire line that connected to the antenna feeder. The parameters of the external TEM plane wave and the boundary conditions for the simulation region were the same as in the cell-line in Figure 2.

A comparison of the moment distribution of the EM fields in the case of antennae 1 and 2 showed very different pictures. In the case of antenna 2, one can see the external EM waves did not penetrate the region between the shielding electrode and the outer surface of the signal electrode (Figure 4 and Figure 5). As a result, the received power was transported to the coaxial antenna feeder without losses. The calculated results are shown in Figure 6.

Figure 6b shows the following. Curve 1 is the P_a2,in(t) external power flow through the aperture A_a2 = H_2,in × W_2,in = 8.5 × 9 = 76.5 cm². This was the same as for antenna 1 (≈ 50 kW). Curve 2 is the received power P_a2,rec(t; z = 53 cm), and the aperture efficiency (η_a2,_eff)_max = P_a2,rec/P_a2,in = 1.14. Curve 3 is the local impedance at the point R₂. This impedance was equal to the ratio of the electric and magnetic field values Z(t; R₂) = E_y(t; R₂)/B_x(t; R₂).

The received EM power P_a2,rec(t) was calculated (Figure 6b, curve 2) inside the coaxial feeder of the antenna at the coordinate z = 53 cm, and it was equal to about 56 kW. Thus, the aperture efficiency of antenna 2 was more than η_a2,_eff(t) ≈ 1.1 during the interval from 1.9 ns to 2.5 ns (see curve 2 on Figure 6b). The result of η_a2,_eff > 1 showed that the receiving area (or effective area) aperture for antenna 2 was about 10% more than the geometric rectangular area of the aperture, which was estimated by the value of A_a2 = H_2,in × W_2,in for the aperture shape with a ratio of (H_2,in/W_2,in) = 1, where H_2,in is the height and W_2,in is the width for the signal electrode on the aperture of antenna 2.

It is necessary to note first that the calculated results of some large values of the receiving power into the coaxial feeder could be due to a limited accuracy on account of the limited sizes of the calculated mesh. Secondly, the effect of η_a2,_eff > 1 could be connected with using these estimations of the aperture area by the geometric rectangular aperture area of A_a2 = H_2,in × W_2,in. Problems in using this approximation will be clearer if the antenna is studied in mode T_x. In this case, a flux of the EM wave in a TEM line with high impedance or for sizes (H₂/W₂) ≈ 1 will be transported along the line with some part of the wave flux outside of the geometric area of A₂ = H₂ × W₂. According to this result, the actual receiving aperture A_a2,rec in antenna 2 could be more than the geometric rectangular aperture area of A_a2 = H_2,in × W_2,in, which was limited by means of the H_2,in height and W_2,in width by the signal electrode on the aperture of antenna 2.

Note that the good result of the aperture efficiency of antenna 2, based on the S-TEM half-horn, could be explained by the transient response with a nearly rectangular shape at an interval of about ΔT_pw,A2 ≈ 0.7 ns (see curve 2 in Figure 6b). The rise time for the external pulse flow was equal to T_f,in ≈ 0.072 ns, and for output pulse flow, it was T_f,out,2 ≈ 0.08 ns. By comparing these T_f values, we could estimate for antenna 2 the rise time of the transient response as T_f,a2 ≤ 0.05 ns. The simulation results of the transient response for antenna 2 showed a high aperture efficiency from the S-TEM horn antenna in mode R_x. According to the principle of reciprocity, this high aperture efficiency would also be applied to the S-TEM horn antenna in the regime as a radiator with an exciting source and with pulses with a rise time of about 0.1 ns and impulse duration of about 0.7 ns.

2.3. Analysis of the Simulations: Analytical Model for Pulsed Radiation from a Phased Antenna Aperture

The simulated antenna 2 was modeled as one eighth of an actual antenna array with four S-TEM horns with shielding plates. Antenna 3, with two S-TEM-half-horn antennae, was simulated as double antenna 2 with an aperture height H_a,3 = 8.5 cm and a total aperture width W_a,3 = 18 cm and with a shielding total plate size of 18 × 54 cm. The results of the calculations for antenna 3 showed high aperture efficiency and good transient response, which was the same as for antenna 2. These simulations confirmed the high efficiency of our antenna array on the basis of four S-TEM horns with shielding rectangular plates. The antennae were used in high-power radiators emitting EM waves of sub-nanosecond durations in a frequency band of 0.1–6 GHz [6,7,8,9,13].

The calculations of antennae 1–3 and other antenna models were simulated on a PC (CPU-4.0 GHz, DRAM-64 GB, 64-bit) by the 3D time domain code KARAT for 10–80 hours, depending on the complexity of the design and a range of geometric sizes in the studied models. The results of the complicated simulations were used in the development of analytical simplified antenna models, which were based on the good known approximation of the Huygens–Kirchhoff as a quasi-optic approach [19,20] (ch.2-2, ch.8-2). The analytic code developed by V. Ye. Ostashev (first versions in 2010 in [29] and next in 2017 in [14]) was used on personal computers. Using this program with the input data of the antenna sizes and time domain data of the exciting generator impulse, we could obtain the main characteristics of the radiation impulse in a few minutes. The approximation in Equation (5) for the radiation potential E(t; φ)R in the far zone for the radiator with uniform excitation and the phased aperture at a distance R in the direction with an angle φ to the antenna axis is given below:

$$E(t;\phi ;R)R\approx \frac{L_{a,\mathrm{eff}}}{4\pi c_0}\sqrt{\frac{Z_0}{Z_a}}\left(\frac{\partial }{\partial t}{\displaystyle {\iint }_{A}V\left(t-(R-({\mathbf{e}}_R,{\mathbf{r}}_a))/c_0\right)\frac{dA}{A}}\right)[1+({\mathbf{e}}_R,{\mathbf{n}}_a)]$$

(5)

where Z_a is the impedance of the antenna feeder that is matched with the impedance of the excitation generator, commonly Z_a = 50 ohms; L_a,eff = (η_a,eff A)^0.5 is the linear size of the effective aperture area A_eff, η_a,eff = (0.9–1) for our antennae; e_R = R/R is the unit vector at the direction R; n_a is the unit vector of the normal to plane aperture A; r_a is the radius vector between the center of aperture A and the radiation element of dA; and V(t−T_RA) is the pulse voltage of a pulser with corrections by convolution with the function F_A(t) of the antenna A transient response and including the time delay of the time-off flight for the radiated waves T_RA = R/c₀.

3. Calibrated Antenna of the Stripline Sensor: Principle of Reciprocity in Applications

3.1. StF4 Stripline Sensor Antenna

Measurement of the E-field strength in a frequency spectrum of 0.1–10 GHz was organized with the use of E-Dot on the basis of the strip-line antenna sensors as the directional wave coupler [7,8,26,28]. The E-Dot of the StF4 was made like a nonsymmetrical two-wire line with a kernel from a plastic thin slat with the dielectric constant ε = 16. It had a small cross-section of an aperture A_a,St = d_st × b_st = 1.5 mm × 1.5 mm and length L_St = 46 cm. This thin and long strip as a two-wire line was placed on a base brass plate (0.5 mm thickness, 6 cm width, and 50 cm length (Figure 7)).

A coaxial cable with an impedance Z_S = 50 ohms and length of 1.5 m was the sensor load. The central wire of the cable was connected to the input end of the upper electrode of the stripline. The other end of the upper electrode was shorted to the base plate. The external shell of the cable had electrical contact with the base plate. The E-Dot was contained in a foam plastic box 1.9 cm thick, 8 cm wide, and 70 cm long.

The transient response of the E-Dot was measured in the traveling EM waves inside the gauge TEM line cell (Figure 8).

The dimensions of the TEM line cell were as follows: 2 cm gap, 8.3 cm width of the signal (upper) electrode, 12 cm width of the base (lower) electrode, and 70 cm length of the region for measurements [7]. The base electrodes of the E-Dot sensor and TEM line cell were in electrical contact. The smallest cross section of the E-Dot sensor compared with the cross-section of the line cell gave the possibility of measuring the transient response of the sensor with high accuracy [28]. Impedance of the gauge line cell was measured with the use of a reflectometer. The line did not distort the impulse with a rise time of about 0.03 ns.

Some defect of the strip-line E-Dot was of a relatively low sensitivity compared with the TEM half-horn sensor and the limit of the time duration of correct measurement. This is a principal defect of the directional wave couplers for usage in pulsed UWB signals.

The transient response of the stripline E-Dot was researched in our past works [7,8,26,28] by simulation with a 3D electromagnetic code with time domain analysis and an experimental study with the use of line cells.

3.2. Application of the Reciprocity Principle for StripLine E-Dot and A16 Pulsed Antenna Types

As was remarked above, the reciprocity theorem predicts that in linear electrical systems, the received short signals will be identical when in the radiator–receiver composition. We rearranged the generator of excitation in places and the recorder of received signal. In the case of experiments with impulse signals, some conditions should be provided: (1) the cables connecting the antennae with a generator and with a signal recorder should be of a sufficient length and have the same impedance (50 ohms in our experiments); (2) there should be a sufficiently large free space R_free > 0.5T_p × c₀ (T_p = pulse duration) around each antenna for decreasing parasitic reflections. In our case, the minimal radius was R_free = 1.1 m.

The experiments were done in the following conditions: (1) a TMG40R generator of antenna excitation [30] generating a step-pulsed voltage 45 V (pulse rise time T_f ≈ 25 ps, pulse repetition rate ≤ 100 kHz); (2) a DSA8200 digital oscilloscope with 80E07-09 remote modules (0–20 GHz, 12 bit); (3) A16 antennae (16 cm× 16 cm aperture size) and an StF4 strip-line antenna sensor; (4) a distance between the antennae of R_A-S = 3.5 m; and (5) the axis of these antennas were coincided or deflected by an angle of 30⁰ relative to the R_A-S –axis of a ray between the two centers of antenna apertures in various experiments.

Figure 9 shows the results of the experiments. For the best view, we shifted the curves to 0.3 ns. The signals were similar, except for a jump at time t ≈ 5.4 ns as result of parasitic reflection from nearby objects. The data presented in Figure 9 confirm that our measurements did not contradict the theorem of reciprocity.

The two maximum peaks in the E(t)R curves in Figure 9b can be explained by the structure of the A16 antenna. This was caused by two columns of the four TEM horns in a 2 × 2 array of the antenna. Each TEM horn had an aperture size of 8 cm× 8 cm. The two peaks in waveforms for E(t)R were separated by a time interval Δt ≈ 0.14 ns. This interval in accuracy corresponded to a time delay of a signal from the adjacent column of the TEM horns (Δt ≈ 8sin(30°)/c₀ ≈ 0.14 ns).

Figure 10 shows the energy spectrum density of the signals, which were presented on Figure 9.

A large decrease in magnitude of the spectrum density in the high frequency part of the spectrum can be seen. Antenna A16 with an angle of deflection φ = 30° gave average radiated pulses at time interval L_A × sin(30°)/c₀ ≈ 0.27 ns (L_A = size of the aperture in its H-plane). The high frequency boundary of the cutting of the power flow for the waves with the length λ_b ≤ 10 cm is shown on Figure 10b. One may compare this length λ_b ≈ 10 cm with the average distance ΔL_A = A × sinφ = 16 × sin(30°) = 8 cm, and as a result, it had an approximation of λ_b ≈ 1.3 L_A × sinφ for other experiments.

Similar results were obtained in our work [6] in the study of the patterns of peak power pulse radiation for the Ant24 + Gp40 radiator.

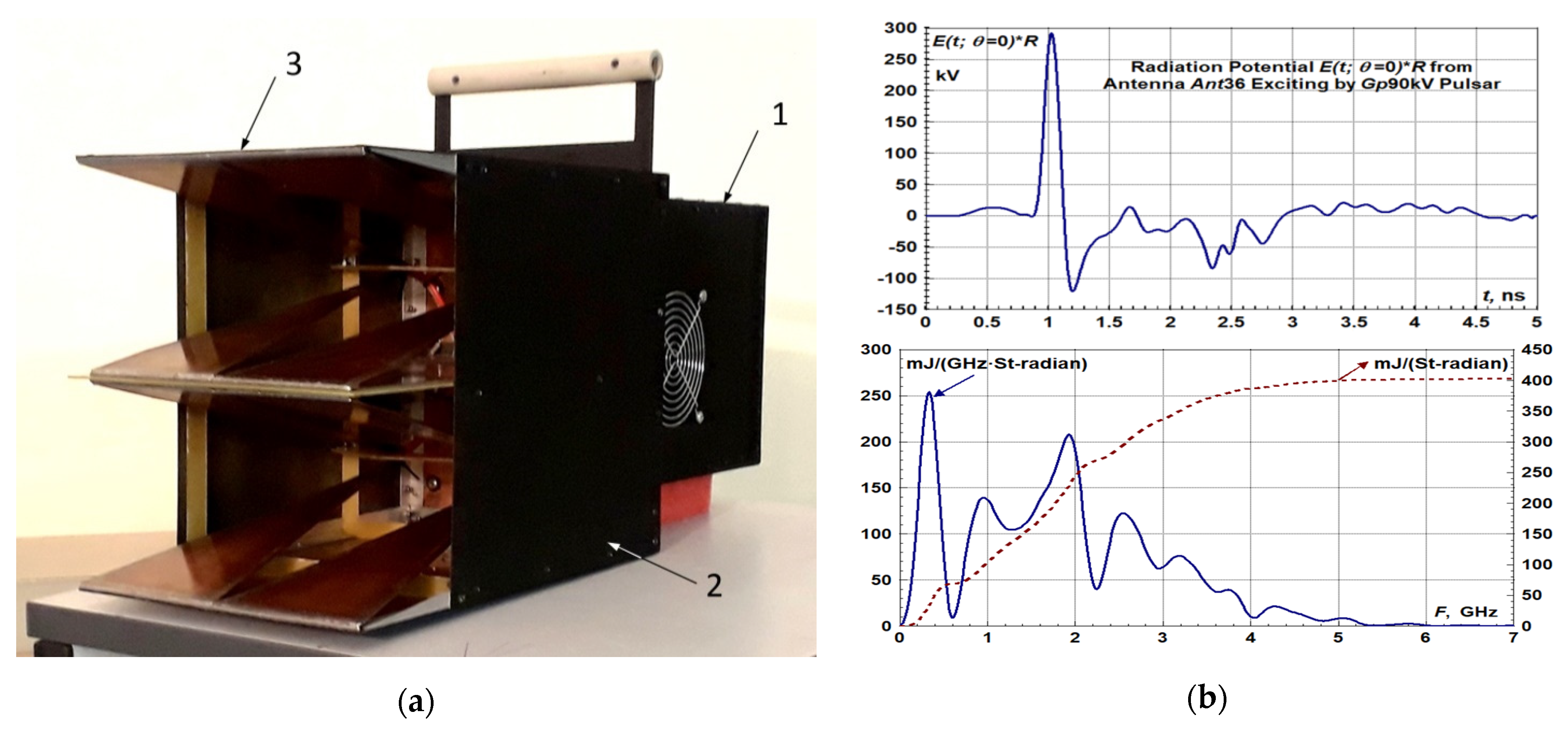
4. High-Power Radiators for the USEMP Waves

We built a series of autonomous HPEM radiators of various sizes with a high aperture efficiency η_a,_eff ≈ 1 on the basis of the 2 × 2 UWB S-TEM-horn array with shielding plates [5,6,7,8,9,13,26,28]. Figure 11 shows a photo of the autonomous radiator with an aperture size L_A = 30 cm and its radiation parameters.

The effective radiation potential of this device was about 300 kV, and the corresponding value of the equivalent isotropic radiated power of the impulse was (ER)²/30 ≈ 3 GW. In the frequency interval of 0.2–3 GHz, the average value of the spectral density of the radiated energy flux at the distance R = 10 m and on the antenna axis was equal to about 1 W/(m²GHz) if the pulse repetition frequency was 10³ Hz.

Figure 12 shows the radiator with an aperture size L_A = 32 cm and a solid-state pulser with a peak amplitude of 100 kV (R-32 cm/100 kV).

Figure 12b shows the radiated potential E(t)R on the axis of the radiator ((ER)_max = 340 kV). The width of the pulse frequency spectrum was 0.1–6 GHz. The frequency band was limited by a TDS-6604B recorder.

The energy’s radiant flux (dotted curve, normalized on the R × R area) along the axis for one impulse versus frequencies up to 7 GHz is shown. In standing, the radiator at a distance of 15 m on a testing place with a radiation intensity of ~0.35 W/(m²GHz) in the frequency band of 0.3–5 GHz at a pulse repetition rate 10³ Hz would be produced.

The autonomous module included the UWB antenna array with four shielded TEM horns, and they were being excited by HV pulses from the semiconductor pulser. Each TEM horn was connected to its two-wire line, and then four these lines were connected to the matched HV-HF antenna coaxial feeder with a 50 ohm line impedance. The work of the pulsed high-power radiators with a high repetition rate of pulses was being met with the problem of suppressing the electric corona discharges around these two-wire HV-HF lines. We solved this problem by using Teflon tape insulation of up to 4 mm swathed around the outer wire diameters. Additionally, we used special silicon grease for filling any pores. The antenna feeder connectors were made with various sizes of inner insulators, with diameters from 7 mm (plug, similar N-type) for the 10 kV pulse voltage and up to 26 mm (plug, M39 × 1.5) for the 100 kV pulse voltages. The antenna feeder was connected with the same connector in the pulser. As mentioned above, all used pulsers were developed by FID Technology and fabricated by FID Technics.

Our early samples of the 2 × 2 antenna array with the S-TEM horns had aperture shapes with a form factor ratio (H_in/W_in) ≈ 1, and the late samples were made with the ratio (H_in/W_in) = (1–2). The radiator in Figure 11 had a ratio of (H_in/W_in) ≈ 1. The radiator in Figure 12 had the ratio (H_in/W_in) ≈ 1.4 and the greater aperture efficiency value. The results of the simulations for the aperture areas with form factor ratios of 1.4…2 for the S-TEM horn antennae are given above in Section 2.2.

4.1. Comparison of Experimental Results with Analytical Estimations and Comparison with Other Pulsed Radiators

The estimations of the radiation potential E(t)R by Equation (5) for the Ant36 and Ant32 radiators with aperture efficiencies ≈ 0.9 and 1.0, respectively, gave the same waveforms as the experimental results in Figure 11 and Figure 12.

In the Ant32 radiator, the 2 × 2 antenna array with S-TEM horns was used. The pulser produced an impulse with an amplitude V_G,max = 98 kV, which had a pre-impulse of 0.1 V_G,max (the amplitude of the pure pulse step was V_G,f = 89 kV) and a rise time T_f,G ≈ 0.1 ns. The transient response of the antenna transport line had a rise time T_f,A ≈ 0.06 ns. The total rise time for the exciting pulse voltage could be estimated by formula τ_f = ((T_f,G)² + (T_f,A)²)^0.5 ≈ 0.12 ns. The effective radiated potential for the Ant32 radiator could be calculated by using Equation (5) as

$$E(R)R\approx 0.44\frac{A_{\mathrm{eff}}}{c_0{\tau }_f}{V}_{\mathrm{G}}\approx 350\mathrm{kV}$$

(6)

The experimental data was 340 kV (see Figure 12b).

We will compare our mobile radiators with the radiators based on reflector-type antennae, such as the HIRA180 radiator, which was studied in [4]. In the radiator [4], the high-voltage monopolar pulse generator (V_G,max = 9.6 kV, τ_f ≈ 0.1 ns, Z_g = 50 ohm) was used. This generator was connected by means of a 100 ohm impedance adapter with the impedance of the antenna feedpoint. The latter was connected to the two tapered transmission lines like two half-horn antennae, with a 200 ohm impedance for each. These half-horn antennae were illuminating and excited the antenna of the half-parabolic reflector with a diameter of 1.8 m. In [4], the measured data of the radiation fields in different standings were presented. In particular, the measured peak amplitude in [4] was equal to E ≈ 1.5 kV/m on the axis in a radiation beam at a distance R = 12 m, in accordance with the effective radiation potential ER ≈ 18 kV.

For comparing the pulse radiators, we used such well-known parameters as the antenna gain factor (directivity) and gain factor of the radiator [14,19,20], which show the ability of the antenna with the generator to radiate directed radiation. The antenna directivity D and gain factor of radiator G are defined as

$$D=\frac{{(RE)}^2}{30P_A}\left(\mathrm{a}\right);G=\frac{{(RE)}^2}{30P_{\mathrm{g}}}=\frac{Z_{\mathrm{g}}}{30}{\left(\frac{RE}{V_{\mathrm{g}}}\right)}^2\left(\mathrm{b}\right)$$

(7)

where P_A is the pulse power supplied to the aperture, P_g is the generator peak power, V_g is the peak amplitude of the pulse voltage, and Z_g is the generator impedance (commonly, Z_g = 50 Ohm).

One can apply Equation (7b) for the HIRA180 radiator [4] and get the following result: G = 1.67(18/9.6)² ≈ 5.9. Possible reasons for the non-large radiation parameters for the HIRA180 radiator in [4] are, perhaps, the mismatching in the generator–antenna line and also the use for excitation of the half-reflector antenna and two half-horn antennae with a large impedance of ≈200 ohm for each. In Section 2.1, it was shown for the classical TEM horn (and for the same half-horn) antenna types that they have low radiation parameters for the effective emission of pulsed waves with a hyperband spectrum in the 0.1–6 GHz range.

As noted in Section 1, realization of the HPEM radiation with a 0.1–6 GHz frequency spectrum in accordance with IEC standards [1] is possible by using few synchronous radiators emitting damped sinusoidal signals with different central frequencies. However, realizations of such radiators are met with the problem of synchronizing several sources. The HPEM radiation in the spectral band of 0.1–1 GHz from two synchronous sources operating with relatively low repetition rate pulses of 100 Hz was realized in [15] with an effective radiation potential of 220 kV. In [15], the combined antenna KA array was used, which was excited by bipolar HV voltage pulses.

The other two examples of HPEM sources for pulsed radiation with a hyperband spectrum with average frequencies of 0.5 GHz and 1 GHz were built according to the traditional scheme [31,32]. These works used antennae of the TEM horn line type with line impedance, which increased toward the output aperture. A generator with spark switches produced high-voltage pulses with a sub-nanosecond rise time, and these pulses were transmitted along the horn line to the antenna aperture. The transport horn line of this antenna was built for the H_H gap and W_H width of a two-electrode line, with an increase in the H_H/W_H ratio in the direction of the aperture of the TEM horn antenna to increase the aperture efficiency (see Equation (3) in Section 2.1). In [31], an effective radiation potential of 90 kV was obtained with a pulse spectrum in the frequency range of 0.15–1 GHz and a radiator gain factor with G ≈ 1.22(90/100)² ≈ 1. In [32], an effective radiation potential of 217 kV was obtained, with a pulse spectrum in the frequency range of 0.2–2 GHz and a repetition rate of 100 Hz.

Our Ant32 radiator with an aperture size of 32 cm, which was excited by an impulse source (V_G,max = 98 kV, τ_f ≈ 0.1 ns, Z_g = 50 ohms), produced an ER = 340 kV with a pulse spectrum in the frequency range of 0.1–6 GHz and a pulse repetition rate of 1 kHz according to the experimental results (see Figure 12b). Using these data and Equation (7b), one can estimate the gain factor of the radiator as G ≈ 1.67(340/98)² ≈ 20.

5. Conclusions

Autonomous mobile HPEM radiators emitting ultra-short electromagnetic pulses with quasi-monopolar waveforms are presented above. The studies of these radiators were carried out by simulations with the time domain electromagnetic 3D code KARAT and experimentally with the use of a stripline E-Dot, which measured in the frequency band of 0.1–10 GHz. The received results were consent with the calculations and reciprocity theorem.

This research has given a basis for creating a pulsed UWB S-TEM-horn antenna. The main properties of this antenna are the impedance of the input feeder of 50 ohms, an aperture efficiency of ≈1, a frequency range of 0.1–6 GHz, and compactness.

A line of compact wearable radiators was created. They contained the S-TEM horn antenna array and also the DC power source with accumulator assembly and the triggering and control systems. The antennae were excited by monopolar impulses, which were of an amplitude of 10–100 kV, rise time ≈ 0.1 ns, FWHM ≈ 0.5 ns, and a repetition rate of 1–100 kHz. The impulses were generated by solid-state pulsers.

The USEMP radiators with a UWB frequency spectrum in the range of 0.1–6 GHz in the case of testing electronics for immunity to electromagnetic interferences allow the use of one source instead of several radiators with relatively narrow frequency bands, such as sinusoidal and damped sinusoidal signals.