A Circuit-Based Wave Port Boundary Condition for the Nodal Discontinuous Galerkin Time-Domain Method

Abstract

Waveguide-like transmission line (WLTL) structures, including rectangular waveguides, circular waveguides, and coaxial lines, have been widely used in microwave engineering. Determining how to efficiently model WLTLs has become vital for the design of various WLTL-based devices. In this paper, a circuit-based wave port boundary condition (CWPBC) is developed and applied in the discontinuous Galerkin time-domain (DGTD) method to accurately simulate these structures for the first time. In the CWPBC, modal voltages and currents of a WLTL are defined, and circuits based on modal voltages and currents are introduced. By co-simulating the modal circuit and the WLTL modeled using the DGTD method, various modal fields can be excited in the WLTL, and at the same time, the WLTL can be terminated without reflections. No extra costs or approximations are used in the proposed CWPBC, and there is no requirement of either the extension of the computational domains widely used in perfectly matched layer (PML) termination or the longitudinal field continuity used in the reported DGTD method. The proposed method can easily obtain the postprocessing parameters, including S-parameters and port power. Numerical results, including rectangular waveguide filters, circular waveguide horns, and coaxial-fed electromagnetic bandgaps (EBG), are given to validate the effectiveness of the proposed CWPBC.

1. Introduction

In recent years, the discontinuous Galerkin time-domain (DGTD) method, as a transient solver with high performance, has attracted much attention [1,2,3,4,5,6,7,8,9,10,11,12]. The DGTD method can be regarded as a combination of the finite element method (FEM) and the finite volume method (FVM) because it has inherited the advantages of both methods, such as a flexible modeling ability, good solution accuracy, elementwise solutions, and a natural parallelization ability. Therefore, the DGTD method has been widely used to analyze various complex electromagnetic problems, for instance, electromagnetic/circuit co-simulation [6], graphene-based devices [7], and multiscale complex electromagnetic problems [10,11].

Waveguide-like transmission lines (WLTLs), including rectangular waveguides, circular waveguides, and coaxial lines, have many important applications in microwave engineering, for instance, in filters, couplers, antennas, and feeding structures [13]. For the simulation of these structures, truncation boundary conditions without reflections need to be introduced. One of the most commonly employed techniques for truncation is the use of perfectly matched layers (PMLs) [14]. PMLs can absorb incoming waves without reflections. However, the implementation of PMLs requires an extra computational domain, thus resulting in more computational costs. In addition to PMLs, the waveguide port boundary condition (WPBC) has been widely used to accurately truncate WLTLs in terms of analytical modal expansions. Two kinds of methods for the good absorption of modal fields have been developed. One is to couple a 3D WLTL with an auxiliary 1D transmission line with the same dispersive property [15,16,17,18,19]. However, in order to avoid reflections from the termination of the 1D transmission line, a long enough 1D transmission line is required, thus resulting in extra computational burdens [19]. The other method is to express transverse modal fields using the longitudinal modal fields in FEM [20,21,22]. When the WPBC is applied in the DGTD method, longitudinal field continuity at the port is implemented [23,24]. However, it is unnecessary for the DGTD method to guarantee longitudinal field continuity, which possibly affects the performance of the conventional DGTD method.

In this paper, a reflection-free circuit-based WPBC (CWPBC) boundary condition is proposed for the first time to terminate WLTLs. A modal circuit representing the modal voltage and the modal current is introduced. The co-simulation of the modal circuit and the WLTL solved using the DGTD method is implemented. With the modal circuit, modal fields can be excited and absorbed without reflections. With the proposed CWPBC, the parameters, including S-parameters and port power, can be easily obtained. The proposed field-circuit cooperative implementation avoids not only some of the extra computations caused by the PML region in [14] and the auxiliary 1D transmission line in [19] but also the unnecessary longitudinal field continuity in [23,24]. Therefore, the proposed CWPBC method has higher computational efficiency with better computational accuracy. This paper is organized as follows: In Section 2, a brief overview of the DGTD method is given, followed by the modal circuit-based CWPBC for WLTLs in Section 3. The co-simulation of the modal circuit and the WLTL is implemented in Section 4. Three numerical examples are discussed in Section 5. Conclusions are given in Section 6.

2. The DGTD Method

A 3D computational domain Ω with permittivity ε and permeability μ is considered. A group of tetrahedrons Ω_k with surfaces ∂Ω_k (k = 1, …, K₀) is used to discretize Ω. In each tetrahedron, the electric field E^k and the magnetic field H^k are expanded in terms of the Nth-order Lagrange scalar functions, which are defined on the N_p Legendre–Gauss–Lobatto (LGL) quadrature points. Here, N_p = (N + 1)(N + 2)(N + 3)/6. Specifically,

$$E^k(x)={\left\{e\right\}}_{k}l(x),$$

(1)

$$H^k(x)={\left\{h\right\}}_{k}l(x),$$

(2)

in which $l(x)={\left\{l_1^k(x),l_2^k(x),\dots ,l_{N_p}^k(x)\right\}}^T$ with the jth Lagrange polynomial $l_j^k(x)$, and ${\left\{u\right\}}_k={\left\{u_x^k,u_y^k,u_z^k\right\}}^T$ (u = e,h) with $u_s^k={\left\{u_{s,1}^k,u_{s,2}^k,\dots ,u_{s,Np}^k\right\}}^T$ (u = E,H; s = x,y,z). Here, $u_{s,i}^k$ denotes the value of $u_s^k$ at the ith interpolation point $x_i$.

By inserting Equations (1) and (2) into two Maxwell curl equations, and by performing the Galerkin spatial testing procedure and the Gauss theorem twice with the resultant equation, one obtains the semi-discrete form as follows:

$$\epsilon {\left[M\right]}_k\frac{\partial {\left\{e\right\}}_k}{\partial t}={\left[S\right]}_k{\left\{h\right\}}_k+\frac{1}{2}{\displaystyle \sum _{f=1}^{N_f}{\left[F\right]}_{k,f}\left\{{\hat{n}}_f\times {\left[\left[{\left\{h\right\}}_k\right]\right]}_f\right\}},$$

(3)

$$\mu {\left[M\right]}_k\frac{\partial {\left\{h\right\}}_k}{\partial t}=-{\left[S\right]}_k{\left\{e\right\}}_k-\frac{1}{2}{\displaystyle \sum _{f=1}^{N_f}{\left[F\right]}_{k,f}\left\{{\hat{n}}_f\times {\left[\left[{\left\{e\right\}}_k\right]\right]}_f\right\}},$$

(4)

where ${\hat{n}}_f$ is the outward normal unit vector across face f, and ${\left[\left[{\left\{e\right\}}_k\right]\right]}_f={\left\{e\right\}}_{k,f}^{+}-{\left\{e\right\}}_{k,f}$ and ${\left[\left[{\left\{\left\{h\right\}\right\}}_k\right]\right]}_f={\left\{h\right\}}_{k,f}^{+}-{\left\{h\right\}}_{k,f}$ denote the jumps of the numerical traces between the kth element and its adjacent element. Here, superscript “+” represents the neighboring element of the kth element, and N_f is the number of neighboring elements. Note that in the derivations of Equations (3) and (4), the center flux is used. The mass matrix [M]_k, the stiffness matrix [S]_k, and the flux matrix [F]_k,f are given, respectively, as

$$\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}{\left[M\right]}_k=\left[\begin{array}{ccc}\left[M_k\right]& & \\ & \left[M_k\right]& \\ & & \left[M_k\right]\end{array}\right],\hfill & {\left[F\right]}_{k,f}=\left[\begin{array}{ccc}\left[F_{k,f}\right]& & \\ & \left[F_{k,f}\right]& \\ & & \left[F_{k,f}\right]\end{array}\right],\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}{\left[S\right]}_k=\left[\begin{array}{ccc}& -\left[S_{z,k}\right]& \left[S_{y,k}\right]\\ \left[S_{z,k}\right]& & -\left[S_{x,k}\right]\\ -\left[S_{y,k}\right]& \left[S_{x,k}\right]& \end{array}\right],\hfill & \end{array}$$

(5)

where

$$\begin{array}{l}{\left[M_k\right]}_{ij}={\displaystyle {\int }_{{\Omega }_k}{l}_i^k}(x)l_j^k(x)dV,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\left[F_{k,f}\right]}_{ij}={\displaystyle {\int }_{\partial {\Omega }_k}{l}_i^k}(x)l_j^{k^{+}}(x)dS,\\ {\left[S_{u,k}\right]}_{ij}={\displaystyle {\int }_{{\Omega }_k}{l}_i^k}(x)\frac{\partial l_j^k(x)}{\partial s}dV\hspace{1em}\left(s=x,y,z\right).\end{array}$$

(6)

With the approximation of the leap-frog scheme for the time derivative, the full-discrete form can be given as

$$\epsilon {\left[M\right]}_k\frac{{\left\{e\right\}}_k^{n+1}-{\left\{e\right\}}_k^n}{\Delta t}={\left[S\right]}_k{\left\{h\right\}}_k^{n+1/2}+\frac{1}{2}{\displaystyle \sum _{f=1}^{N_f}{\left[F\right]}_{k,f}\left\{{\hat{n}}_f\times {\left[\left[{\left\{h\right\}}_k^{n+1/2}\right]\right]}_f\right\}},$$

(7)

$$\mu {\left[M\right]}_k\frac{{\left\{h\right\}}_k^{n+3/2}-{\left\{h\right\}}_k^{n+1/2}}{\Delta t}=-{\left[S\right]}_k{\left\{e\right\}}_k^{n+1}-\frac{1}{2}{\displaystyle \sum _{f=1}^{N_f}{\left[F\right]}_{k,f}\left\{{\hat{n}}_f\times {\left[\left[{\left\{e\right\}}_k^{n+1}\right]\right]}_f\right\}},$$

(8)

where superscript “n” is the nth time.

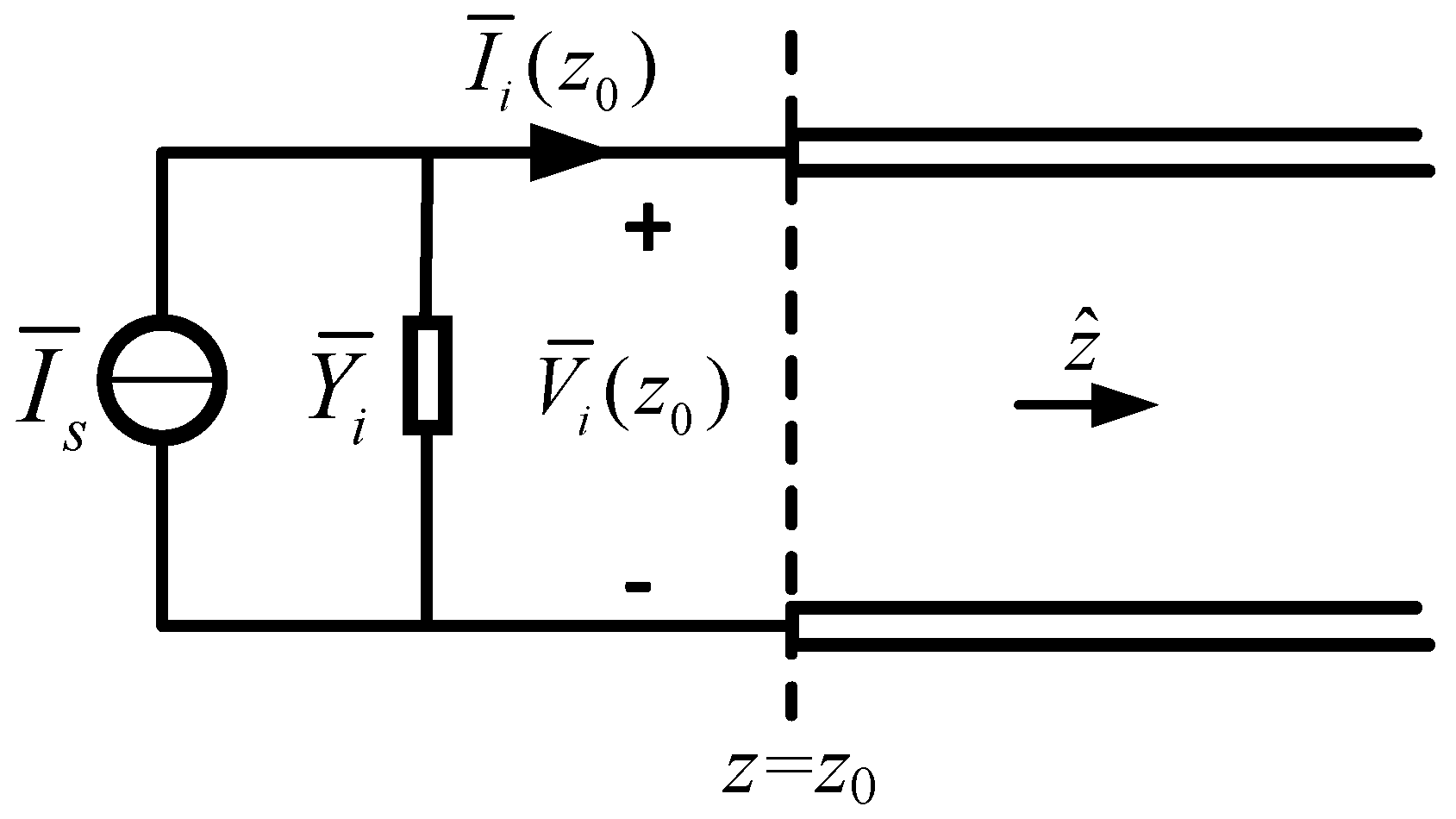
3. The Modal Circuit-Based WPBC

In a uniform WLTL, whose cross-section is of arbitrary shape and remains unchanged along the longitudinal direction, e.g., z., as shown in Figure 1, electromagnetic fields can be decomposed into the transverse magnetic (TM) mode and the transverse electric (TE) mode along the transmission direction. The TE and TM longitudinal modal functions can be obtained according to the 2D Helmholtz equation with different boundary conditions, respectively, as [25]

$$({\nabla }_t^2+k_{cm}^2){\varphi }_m^{TE/TM}(x)=0,\hspace{1em}x\in S$$

(9)

$$\{\begin{array}{c}\frac{\partial {\varphi }_m^{TE}(x)}{\partial n}=0\\ {\varphi }_m^{TM}(x)=0\end{array},\hspace{1em}x\in \partial S$$

(10)

where ${\nabla }_t$ represents the transverse Nabla operator, $k_{cm}$ denotes the cutoff frequency, and S is the cross-section of the waveguide with the contour $\partial S$. With ${\phi }_m^{\mathrm{TE}/\mathrm{TM}}$ solved, the transverse modal fields can be solved as

$$\{\begin{array}{l}{e}_m^{TE}=\hat{z}\times {\nabla }_t{\varphi }_m^{TE}\\ h_m^{TE}=\hat{z}\times e_m^{TE}\end{array}, \mathrm{for} \mathrm{TE} \mathrm{mode}$$

(11)

and

$$\{\begin{array}{l}{e}_m^{TM}=-{\nabla }_t{\varphi }_m^{TM}\\ h_m^{TM}=\hat{z}\times e_m^{TM}\end{array}, \mathrm{for} \mathrm{TM} \mathrm{mode}.$$

(12)

For convenience, the transverse modal fields of $e_m^{TE}$ ($h_m^{TE}$) and $e_m^{TM}$ ($h_m^{TM}$) are sorted in ascending order according to their cutoff frequencies, and the superscripts “TE” and “TM” are omitted. Note that the transverse modal fields are orthonormal, i.e.,

$${\displaystyle {\int }_S{e}_i\cdot e_j}dS={\displaystyle {\int }_S{h}_i\cdot h_j}dS=\{\begin{array}{l}1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=j\\ 0,\hspace{0.17em}\hspace{0.17em}i\ne j\end{array}.$$

(13)

Moreover, the relationship between the transverse modal electric fields and the transverse modal magnetic fields is

$$h_i=\hat{z}\times e_i$$

(14)

Therefore, the transverse components of the frequency-domain fields in the WLTL can be expressed in terms of the transverse modal fields as

$${\overline{E}}_t={\displaystyle \sum _i{e}_i(x,y){\overline{V}}_i(z)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{H}}_t={\displaystyle \sum _i{h}_i(x,y){\overline{I}}_i(z)},$$

(15)

in which the expansion coefficients of the transverse components of the electromagnetic fields ${\overline{V}}_i(z)$ and ${\overline{I}}_i(z)$ are solved as

$${\overline{V}}_i(z)={\displaystyle {\int }_S{\overline{E}}_t\cdot e_{i}dS},\hspace{1em}{\overline{I}}_i(z)={\displaystyle {\int }_S{\overline{H}}_t}\cdot h_{i}dS.$$

(16)

By inserting Equation (15) into the following transverse Maxwell’s equations in the WLTL [25]

$$\hat{z}\times \frac{\partial {\overline{E}}_t}{\partial z}=-j\omega \mu \left({\overline{H}}_t+A_1\frac{1}{k^2}{\nabla }_t^2{\overline{H}}_t\right),\hspace{1em}\frac{\partial {\overline{H}}_t}{\partial z}\times \hat{z}=-j\omega \epsilon \left({\overline{E}}_t+A_2\frac{1}{k^2}{\nabla }_t^2{\overline{E}}_t\right),$$

(17)

and by applying the testing procedure in Equation (17) using transverse modal fields $e_i$ and $h_i$, respectively, one obtains

$$\frac{d{\overline{V}}_i}{dz}=-j\omega \mu \left(1-A_{1,i}\frac{k_{ci}{}^2}{k^2}\right){\overline{I}}_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{d{\overline{I}}_i}{dz}=-j\omega \epsilon \left(1-A_{2,i}\frac{k_{ci}{}^2}{k^2}\right){\overline{V}}_i,$$

(18)

where the constants A₁ and A₂ related to the modes are

$$\{\begin{array}{ll}{A}_1=0,A_2=1\hfill & \mathrm{for}\hspace{0.17em}\mathrm{TE}\hspace{0.17em}\mathrm{mode}\hfill \\ A_1=1,A_2=0\hfill & \mathrm{for}\hspace{0.17em}\mathrm{TM}\hspace{0.17em}\mathrm{mode}\hfill \\ A_1=A_2=0\hfill & \mathrm{for}\hspace{0.17em}\mathrm{TEM}\hspace{0.17em}\mathrm{mode}\hfill \end{array}$$

(19)

Note that in deriving Equation (18), the condition that the transverse components of the electromagnetic fields satisfy the 2D Helmholtz equation is applied, i.e.,

$$({\nabla }_t^2+k_{ci}^2){\overline{E}}_t=0,\hspace{1em}({\nabla }_t^2+k_{ci}^2){\overline{H}}_t{}_t=0$$

(20)

.

Furthermore, (18) is rewritten as

$$\frac{d{\overline{V}}_i}{dz}=-j{\beta }_i{\overline{Z}}_i{\overline{I}}_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{d{\overline{I}}_i}{dz}=-j{\beta }_i{\overline{Y}}_i{\overline{V}}_i,$$

(21)

in which ${\beta }_i=\sqrt{k^2-k_{ci}^2}$ is the mode propagation constant, and ${\overline{Z}}_i=1/{\overline{Y}}_i$ is the mode characteristic impedance with the following expression:

$${\overline{Z}}_i=\{\begin{array}{l}\omega \mu /{\beta }_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}\mathrm{TE}\hspace{0.17em}\mathrm{mode}\\ {\beta }_i/\omega \epsilon \hspace{1em} \mathrm{for}\hspace{0.17em}\mathrm{TM}\hspace{0.17em}\mathrm{mode}\hspace{0.17em}\end{array}$$

(22)

It can be seen from Equation (21) that ${\overline{V}}_i$ and the ${\overline{I}}_i$ satisfy the telegraph’s equation governing the voltage and the current on the transmission line, and, thus, ${\overline{V}}_i$ and ${\overline{I}}_i$ are called the modal voltage and modal current, respectively.

The solution of Equation (21) can be expressed as the superposition of the incident and reflection modal voltages/currents. At z = z₀, the relationship between ${\overline{V}}_i$ and ${\overline{I}}_i$ can be obtained as

$${\overline{I}}_i(z_0)={\overline{I}}_s-{\overline{Y}}_i{\overline{V}}_i(z_0)$$

(23)

where ${\overline{I}}_s=2{\overline{I}}_{inc,i}$ is the modal current source, and ${\overline{I}}_{inc,i}$ is the incident modal current. According to Equation (23), the equivalent modal circuit describing the modal voltage ${\overline{V}}_i$ and the modal current ${\overline{I}}_i$ can be given, as seen in Figure 2. At the port of z = z₀, the ith modal field in the WLTL is excited by the modal circuit with the modal current source ${\overline{I}}_s$.

When transforming Equation (23) into the time domain, one obtains

$$I_i(t)=I_s(t)-Y_i(t)*V_i(t),$$

(24)

in which I_i(t) and V_i(t) are counterparts in the time domain of ${\overline{V}}_i$ and ${\overline{I}}_i$, respectively; “*” represents the convolution operation; and the characteristic admittance Y_i is

$$Y_i(t)=\frac{1}{\eta }\left(c{k}_{c,i}{\displaystyle {\int }_0^t\frac{1}{\tau }{J}_1(c{k}_{c,i}\tau )d\tau }+\delta (t)\right) \mathrm{for} \mathrm{TE} \mathrm{mode},$$

(25)

and

$$Y_i(t)=\frac{1}{\eta }\left(-c{k}_{c,i}{J}_1(c{k}_{c,i}t)+\delta (t)\right) \mathrm{for} \mathrm{TM} \mathrm{mode},$$

(26)

where $\eta =\sqrt{\mu /\epsilon }$, J₁ is the 1st-order Bessel function of the first kind, $\delta (t)$ denotes the Dirac function, and c is the speed of light.

By inserting Equation (25) or (26) into (24) and by performing the time discretization, one obtains

$$I_i^{n+1}+\frac{1}{\eta }{V}_i^{n+1}=2I_{inc,i}^{n+1}+{\mathrm{Conv}}_i^n,$$

(27)

where ${\mathrm{Conv}}_i^n$ denotes the convolution term in Equation (24) at the nth time.

When the modal circuit shown in Figure 2 is implemented at the port of z = z₀, the ith mode field in the waveguide can be well excited. However, when the modal circuit without the modal current source, i.e., the load Y_i, is connected to the waveguide, the ith mode field can be absorbed without reflections. The resulting truncation boundary condition for the WLTL is called the CWPBC.

4. Co-Simulation of Modal Circuit and WLTL

4.1. Field-Circuit Co-Simulation

In order to implement the CWPBC, the co-simulation of the modal circuit and waveguide is introduced, as shown in Figure 3.

It is considered that the port plane is located at z = z₀ and that the WLTL is placed in the region of z > z₀. The modal equivalent circuit is connected to the WLTL at z = z₀. In order to truncate the computational domain at z = z₀ to reduce unnecessary computation, a truncation boundary condition is placed. The common boundary conditions in the DGTD method include a perfect magnetic conductor (PMC), a perfect electric conductor (PEC), and a first-order absorbing boundary condition (ABC). For the PMC, the jumps of the numerical traces are only related to the magnetic fields. For the PEC, the jumps are only related to the electric fields. By comparison, the jumps of the numerical traces of the ABC simultaneously involve the electric fields and the magnetic fields. Therefore, the computational costs of the PMC and the PEC are less than those of the ABC. Considering that the modal equivalent circuit is based on the modal current source given by Equation (23), the PMC boundary is used. This is because the radiations cannot be generated by the electric currents placed on the surface of the PEC. Note that the modal equivalent circuit can be also given in terms of the modal voltage source by the dual transformation of Equation (23), and, accordingly, the PEC is employed for the truncation.

When the PMC boundary is used at z = z₀, the corresponding jumps of the numerical traces become

$$\hat{n}\times {〚{\left\{e\right\}}_k〛}_f=0,\hspace{1em} \hat{n}\times {〚{\left\{h\right\}}_k〛}_f=2\hat{n}\times \left({\left\{h\right\}}_{k,f}^{+}-{\left\{h\right\}}_{k,f}\right)$$

(28)

It is worth pointing out that the jumps of the magnetic fields in (28) are obtained according to Huygens’ principle, which are twice as much as those widely used in the DGTD method.

Due to the zero jumps of the electric fields in Equation (28), (8) can be explicitly solved for ${\left\{h\right\}}_k^{n+3/2}$. However, Equation (7) is solved using the field-circuit co-simulation. In this scenario, the term $\hat{n}\times {\left\{h\right\}}_{k,f}^{+}$ in Equation (28) is expressed in terms of the modal currents as

$$\hat{n}\times {\left\{h\right\}}_{k,f}^{+}=\hat{n}\times {\displaystyle \sum _{i=1}^{N_m}{\left\{h_i\right\}}_{k,f}{I}_i}=-{\displaystyle \sum _{i=1}^{N_m}{\left\{e_i\right\}}_{k,f}{I}_i},$$

(29)

in which N_m is the total number of modes absorbed by the CWPBC. When using the central approximation, $\hat{n}\times {\left\{h\right\}}_{k,f}^{+}$ at the (n + 1/2) th time is obtained as

$$\hat{n}\times {\left\{h\right\}}_{k,f}^{+,n+1/2}=-{\displaystyle \sum _{i=1}^{N_m}{\left\{e_i\right\}}_{k,f}\cdot \left(\frac{I_i^n+I_i^{n+1}}{2}\right)}$$

(30)

By inserting Equations (28) and (30) into (7), one obtains

$${\left\{e\right\}}_k^{n+1}+\frac{\Delta t}{2}{\displaystyle \sum _{i=1}^{N_m}\left[C_{I,k,i}\right]I_i^{n+1}}=\mathrm{RHS}{\left\{e\right\}}_k^n-\frac{\Delta t}{2}{\displaystyle \sum _{i=1}^{N_m}\left[C_{I,k,i}\right]I_i^n},$$

(31)

where

$$\begin{array}{l}\mathrm{RHS}{\left\{e\right\}}_k^n={\left\{e\right\}}_k^n+\Delta t{\epsilon }^{-1}{\left[M\right]}_k{}^{-1}\left\{{\left[S\right]}_k{\left\{h\right\}}_k^{n+1/2}-{\displaystyle \sum _{f=1}^{N_f}{\left[F\right]}_{k,f}\left(\hat{n}\times {\left\{h\right\}}_{k,f}^{n+1/2}\right)}\right\}\\ \left[C_{I,k,i}\right]={\epsilon }^{-1}{\left[M\right]}_k{}^{-1}{\left\{e_i\right\}}_{k,f}{\left[F\right]}_{k,f}\end{array}$$

(32)

However, according to the first equation in (16), we have

$$V_i^{n+1}={\displaystyle {\int }_S{E}^{k,n+1}(x)\cdot e_i}dS={\displaystyle \sum _{k=1}^{N_e}\left[C_{V,k,i}\right]{\left\{e\right\}}_k^{n+1}},$$

(33)

where N_e denotes the number of elements at the port plane, and

$$\left[C_{V,k,i}\right]={\left[{\left\{e_i\right\}}_{k,f}\right]}^T{\left[F\right]}_{k,f}.$$

(34)

By combining Equations (27), (31), and (33), the coupled matrix equation for the CWPBC can be obtained as

$$\left[\begin{array}{ccc}I& 0& \frac{dt}{2}{\tilde{C}}_I\\ 0& \frac{1}{\eta }I& I\\ -{\tilde{C}}_V& I& 0\end{array}\right]\left[\begin{array}{c}{\tilde{e}}^{n+1}\\ {\tilde{V}}^{n+1}\\ {\tilde{I}}^{n+1}\end{array}\right]=\left[\begin{array}{c}\mathrm{RHS}\left\{{\tilde{e}}^n\right\}-\frac{dt}{2}{\tilde{C}}_I{\tilde{I}}^n\\ {\tilde{I}}_{inc}^{n+1}+{\widetilde{Conv}}^n\\ 0\end{array}\right],$$

(35)

in which

$${\tilde{C}}_V=\left[\begin{array}{ccc}\left[C_{V,1,1}\right]& \cdots & \left[C_{V,1,N_m}\right]\\ ⋮& \ddots & ⋮\\ \left[C_{V,N_e,1}\right]& \cdots & \left[C_{V,N_e,N_m}\right]\end{array}\right],\hspace{1em} {\tilde{C}}_I=\left[\begin{array}{ccc}\left[C_{I,1,1}\right]& \cdots & \left[C_{I,1,N_m}\right]\\ ⋮& \ddots & ⋮\\ \left[C_{I,N_e,1}\right]& \cdots & \left[C_{I,N_e,N_m}\right]\end{array}\right],$$

(36)

$$\begin{array}{c}{\tilde{e}}^n=\left[{\left\{e\right\}}_1^n,\dots ,{\left\{e\right\}}_{N_e}^n\right],\hspace{1em} {\tilde{V}}^n={\left[V_1^n,\dots ,V_{N_m}^n\right]}^T,\hspace{1em}{\tilde{I}}^n={\left[I_1^n,\dots ,I_{N_m}^n\right]}^T\\ {\tilde{I}}_{inc}^n={\left[I_{inc,1}^n,\dots ,I_{inc,N_m}^n\right]}^T,\hspace{1em} {\widetilde{Conv}}^n={\left[{\mathrm{Conv}}_1^n,\dots {\mathrm{Conv}}_{N_m}^n\right]}^T\end{array}$$

(37)

By explicitly solving Equation (35), ${\left\{e\right\}}_k^{n+1}$, $I_i^{n+1}$, and $V_i^{n+1}$ can be obtained. Note that without the modal voltage and current, (35) is reduced to the governing equation of the electric field in the conventional DGTD method, i.e., (7). It is worth pointing out that the stability condition of the DGTD method with the CWPBC can be theoretically derived according to the matrix decomposition-based eigenvalue solution method [11]. We also find through the vast numerical examples that the time step is not reduced with the use of the CWPBC.

4.2. S-Parameters and Port Power

Once the electromagnetic fields, the modal voltages, and the modal currents are obtained, the postprocessing parameters, including S-parameters and port power, can be easily obtained. The scattering parameter S (m:i, n:j) between the ith mode reflecting wave at port m, i.e., ${\overline{b}}_i^m$, and the jth mode incident excitation at port n, i.e., ${\overline{a}}_j^n$, is calculated using

$$S(m:i,n:j)=\frac{{\overline{b}}_i^m}{{\overline{a}}_j^n},$$

(38)

in which

$${\overline{a}}_j^n=\sqrt{{\overline{Y}}_j^n}{\overline{I}}_{inc,j}^n,\hspace{1em} {\overline{b}}_i^m=\sqrt{{\overline{Y}}_i^m}\left({\overline{I}}_{inc,i}^m-{\overline{I}}_i^m\right).$$

(39)

However, the computation of the port power can be simply obtained according to the canonical orthogonality properties of the modal fields. For port n with M modes, the input power is solved as

$${\overline{P}}_{in}^n=\frac{1}{2}\mathrm{Re}\left[{\displaystyle {\int }_S{\overline{E}}^n\times {\overline{H}}^{n*}\cdot dS}\right].$$

(40)

By inserting Equation (15) into (40), one obtains

$${\overline{P}}_{in}^n=\frac{1}{2}\mathrm{Re}\left[{\displaystyle \sum _{j=1}^M{\overline{V}}_j^n{\overline{I}}_j^{n*}}\right].$$

(41)

5. Results and Discussion

In this section, three numerical examples are given to show the validity and the effectiveness of the proposed CWPBC. The port of the WLTL is assumed to be a closed homogenous port with an arbitrary cross-section.

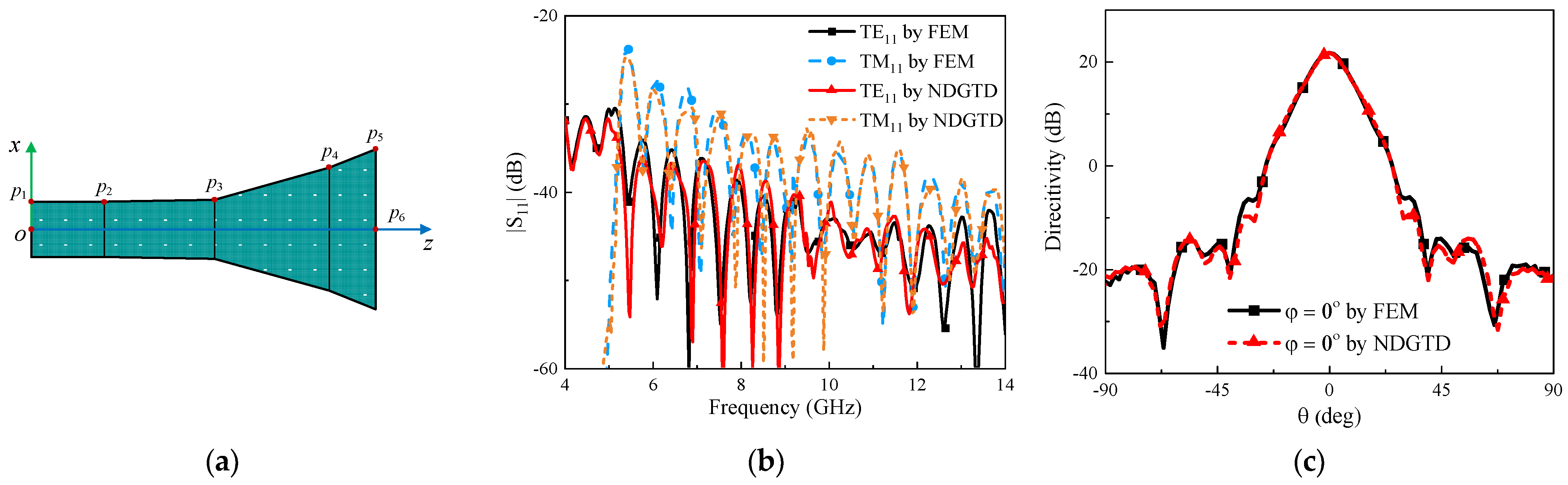
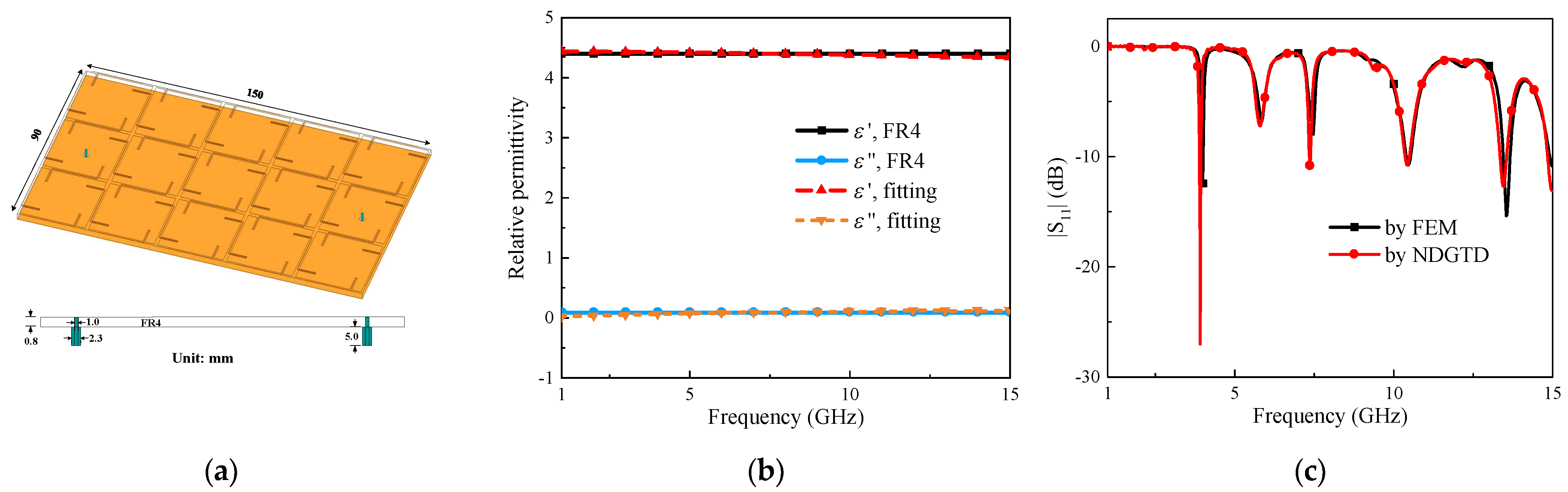
5.1. Performance Validation

In the first example, a WR90 rectangular waveguide with a size of 22.86 mm × 10.16 mm × 40 mm is considered to validate the performance of the proposed CWPBC, as shown in Figure 4a. The waveguide is discretized by elements with an average size of 1/6 λ_10GHz, and, thus, the number of elements is 448. The time step of 4.59 × 10⁻¹³ s is used. For comparison, an unsplit PML with a thickness of 8/10 λ_10GHz is also used to terminate the two ends of the waveguide. In the PML region, the average size of the discretization element is 1/10 λ_10GHz, and in the waveguide, the average size of the discretization element is 1/6 λ_10GHz, thus resulting in 3621 elements. The time step is chosen as 1.67 × 10⁻¹³ s. The transient mode current source I_s = 2I_inc is enforced to excite the TE₁₀ mode, and the waveform of the incident mode current I_inc is shown in Figure 4b. The transient waveforms of the excited mode currents at ports 1 and 2 are plotted in Figure 4b. It can be seen that the waveform of the mode current at port 1 coincides with that of the incident mode current, and the waveform of the mode current at port 2 is the same as that at port 1, with a time delay caused by wave propagation in the waveguide.

A performance comparison between the proposed CWPBC and the PML is presented in Figure 4c. The S₁₁ of the proposed CWPBC is better than that of the PML. Note that, compared with the proposed CWPBC, more elements and unknowns are required due to the introduction of the PML region. In addition, the frequency-domain FEM with the wave port method is adopted, and the corresponding results are shown in Figure 4c. In the lower band, the FEM result is better than the result obtained using the proposed CWPBC, while in the higher band, the FEM result is worse than the result obtained using the proposed CWPBC.

Furthermore, a comparison of CPU time consumption among the PML, the WPBC, and the proposed CWPBC is presented in

Table 1. Comparison of CPU time consumption among PML, WPBC, and the proposed CWPBC.

	PML	WPBC	CWPBC
CPU time Time Ratio	134.76 s 1	10.51 s 0.078	9.84 s 0.073

. Here, 1000 time steps are performed to calculate the CPU time. In Table 1, it can be seen that the proposed CWPBC method consumes less computational time than the PML and the WPCB. The ratio of the computational time consumed by the proposed CWPBC method to that of the PML is 0.073.

5.2. Waveguide Filter

In the second example, a seventh-order rectangular waveguide filter is provided to demonstrate the accuracy of the proposed CWPBC. The geometry of the filter is shown in Figure 5a. Two rectangular ports with a size of 28.5 mm × 12.63 mm, called port 1 and port 2, are used to truncate the computational region. Since the filter only operates in the dominant mode, i.e., the TE₁₀ mode, the modal circuit related to the dominant mode is used in this example. The ports are discretized by tetrahedrons with an average edge length of 1/20 λ_7.5GHz, the iris and slot parts are discretized by tetrahedrons with an average edge length of 1/40 λ_7.5GHz, and the remaining part is discretized by tetrahedrons with an average edge length of 1/10 λ_7.5GHz, thus resulting in 76,800 elements. The second-order basis functions are used to expand the unknown electric and magnetic fields. The time step ∆t = 6.9 × 10⁻¹⁴ s is employed for the stable solution. The S-parameters, including S₁₁ and S₂₁, are solved using the proposed method, and they are compared with those of the FEM results, as shown in Figure 5b,c. A good agreement between them is observed.

5.3. Circular Horn Antenna

In this section, a dual-mode circular horn antenna is considered. Figure 6a gives the dimensions of the horn antenna. When the dominant mode of the horn, i.e., the TE₁₁ mode, is excited, the TE₁₁ mode can be converted to the TM₁₁ mode, and two modes can be radiated at the same time. In this example, the modal circuit related to the first 10 modes is used. The whole computational domain with a size of 0.26 m × 0.26 m × 0.49 m is terminated by the first-order ABC boundary condition. The region close to the horn is discretized by elements with an average size of the 1/10 λ_10GHz, and the remaining region is discretized by elements of an average size of 1/4 λ_10GHz. At the port, an element with an average size of 1/20 λ_10GHz is used. A total of 617571 elements with second-order basis functions are implemented, and the time step ∆t = 1.0 × 10⁻¹⁴ s is chosen. Figure 6b presents the S₁₁ curves of the TE₁₁ mode and the TM₁₁ mode solved using the proposed method and the FEM, and they are in good agreement with each other. Figure 6c presents a comparison of directivity at 10 GHz in the xoz plane between the proposed method and the FEM. A good agreement between the two results is observed

5.4. Electromagnetic Bandgap (EBG) Structure

Finally, a uniplanar compact EBG structure with L-bridges and slits (LBS-EBG) is considered for the application of the ground bounce noise (GBN), as shown in Figure 7a. The EBG with 3 × 5 unit cells is fabricated on an FR4 substrate with a relative permittivity of 4.4 and a loss tangent of 0.02. Two coaxial probes with the characteristic impedance of 50 Ω are inserted in the LBS-EBG. The dominant mode, i.e., transverse electromagnetic (TEM) mode, is excited by the coaxial port. The detailed dimensions of the unit cell can be found in [26].

In the DGTD method, a vector-fitting technique is used to approximate the relative permittivity of the substrate in the band of 1~15 GHz as a partial fraction in terms of real and/or complex-conjugate pole–residue pairs [7], as shown in Figure 7b. The discretization mesh sizes at the port and near the port are 1/75 λ_10GHz and 1/60 λ_10GHz, respectively, and the mesh size of the remaining region is set as 1/30 λ_10GHz. A total of 673254 tetrahedrons are generated, and second-order basis functions are used. The time step ∆t = 3.5 × ⁻¹⁵ s is chosen. S₁₁ is solved using the proposed method and the FEM. A good agreement is obtained, as shown in Figure 7c.

6. Conclusions

This paper develops a circuit-based wave port boundary condition for the nodal discontinuous Galerkin time-domain method. A modal-equivalent circuit in terms of the modal voltage and the modal current is proposed, and a co-simulation between the field and the circuit is implemented to achieve the excitation of the modal fields and the truncation of the waveguide-like transmission line without reflections. Numerical examples, including the rectangular waveguide, the circular waveguide, and the coaxial port, are given to demonstrate the feasibility of proposed method in the solution of practical electromagnetic problems.

It is worth pointing out that the proposed circuit-based wave port boundary condition can accurately truncate waveguide-like transmission lines with frequency-invariant modal fields. The extension of the proposed method to transmission lines with dispersive modal fields is our future research direction.