A Low-Power, Fast-Transient Output-Capacitorless LDO with Transient Enhancement Unit and Current Booster
Abstract
:1. Introduction
2. Proposed LDO Topology
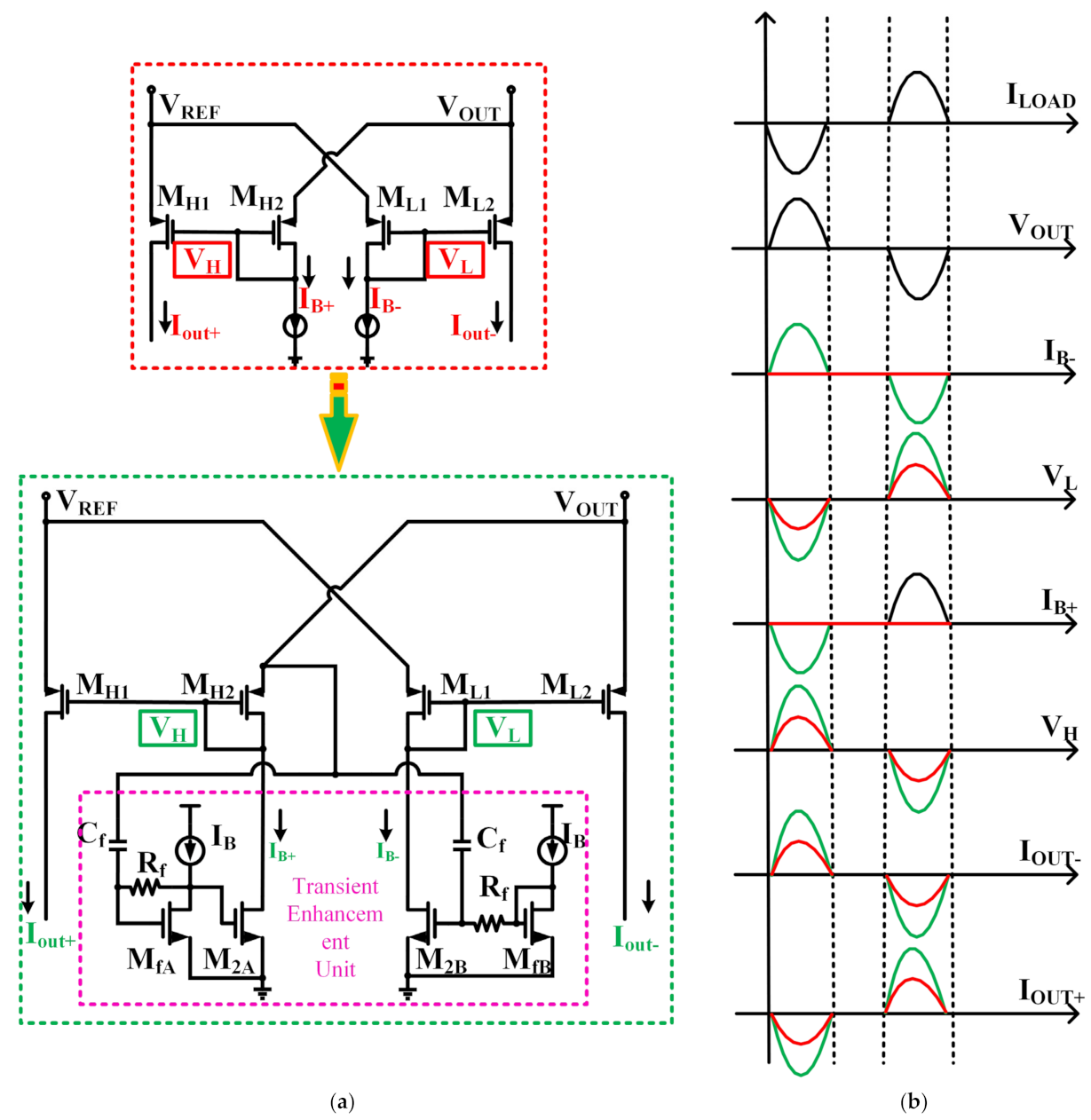
2.1. Transient Enhancement Unit (TEU)
2.2. Current Booster
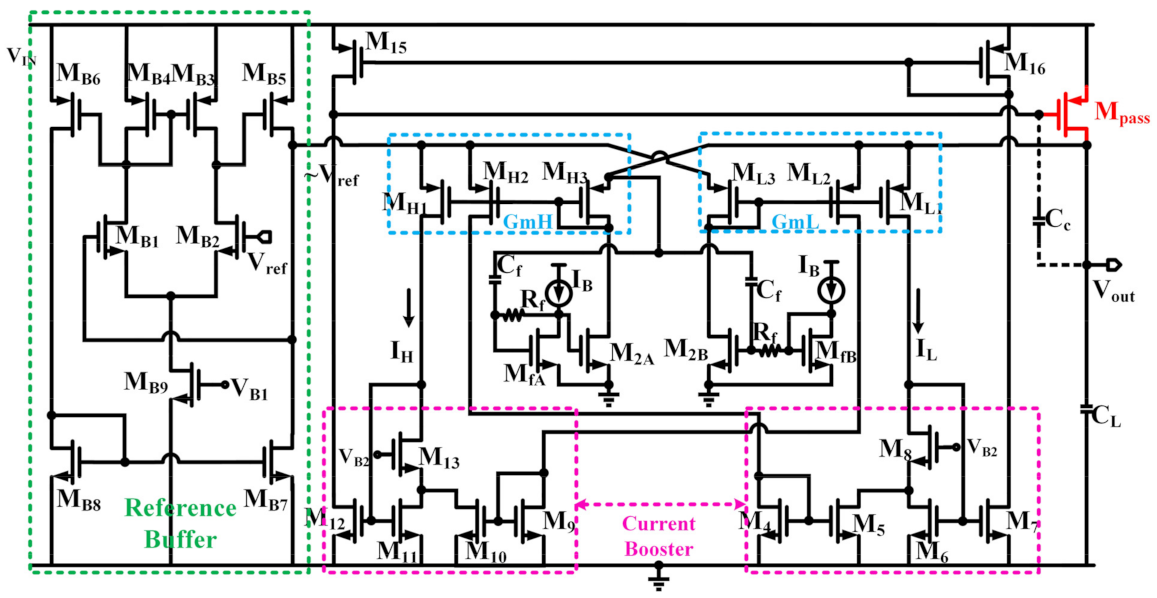
2.3. Circuit Implementation
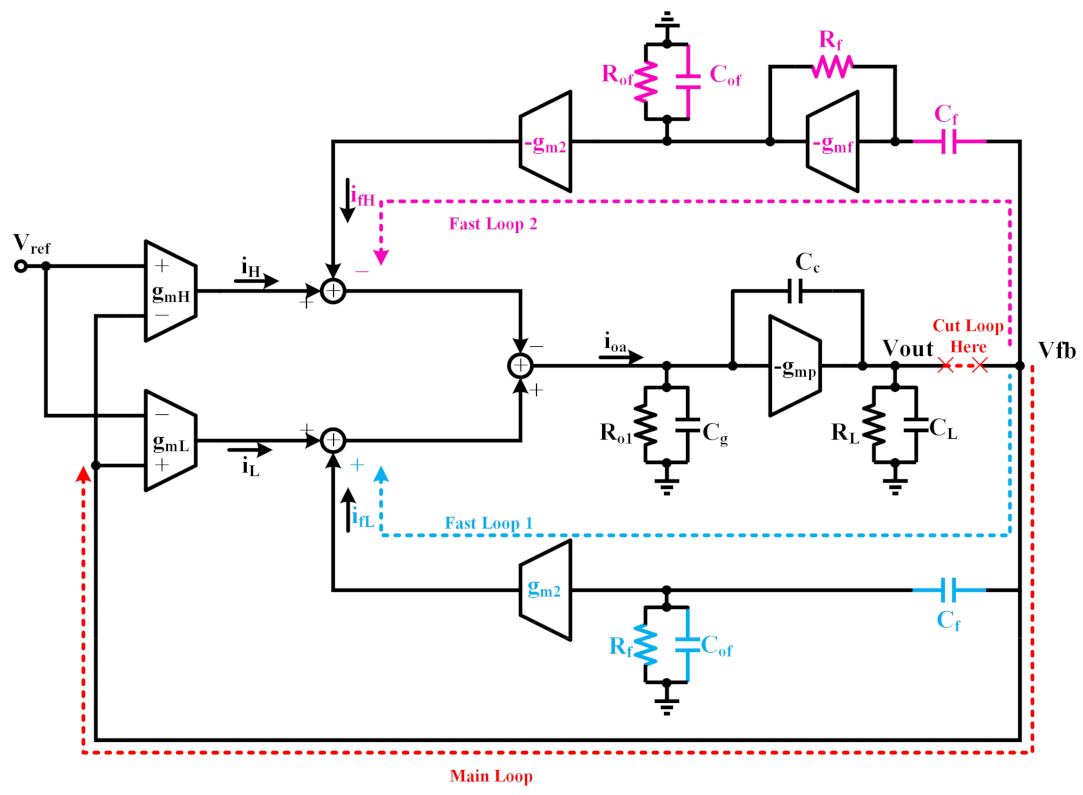
2.4. Stability Analysis
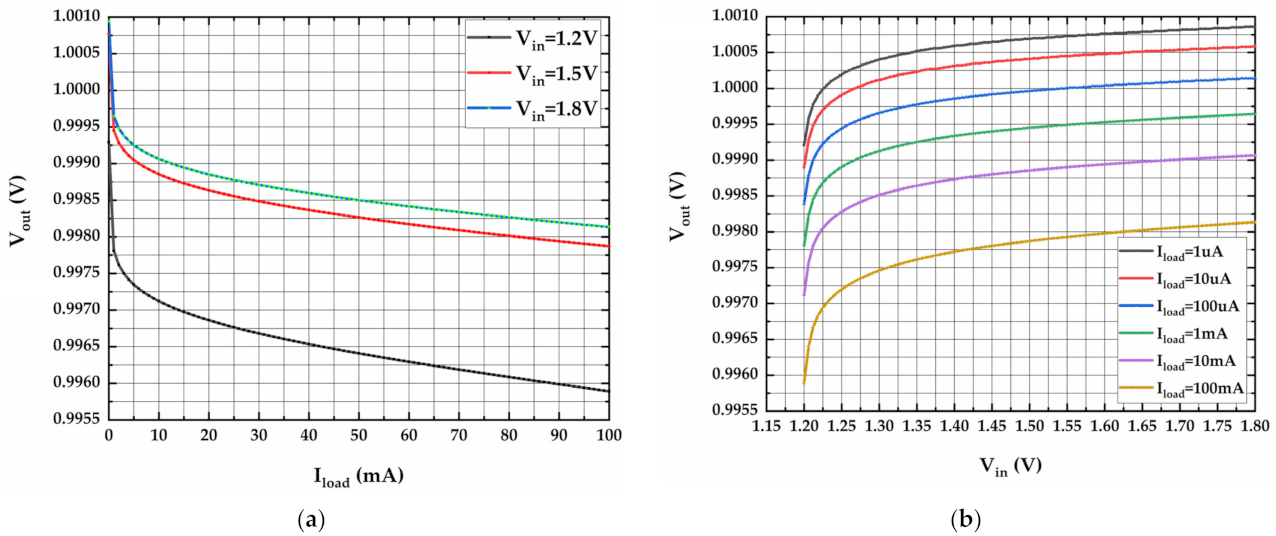
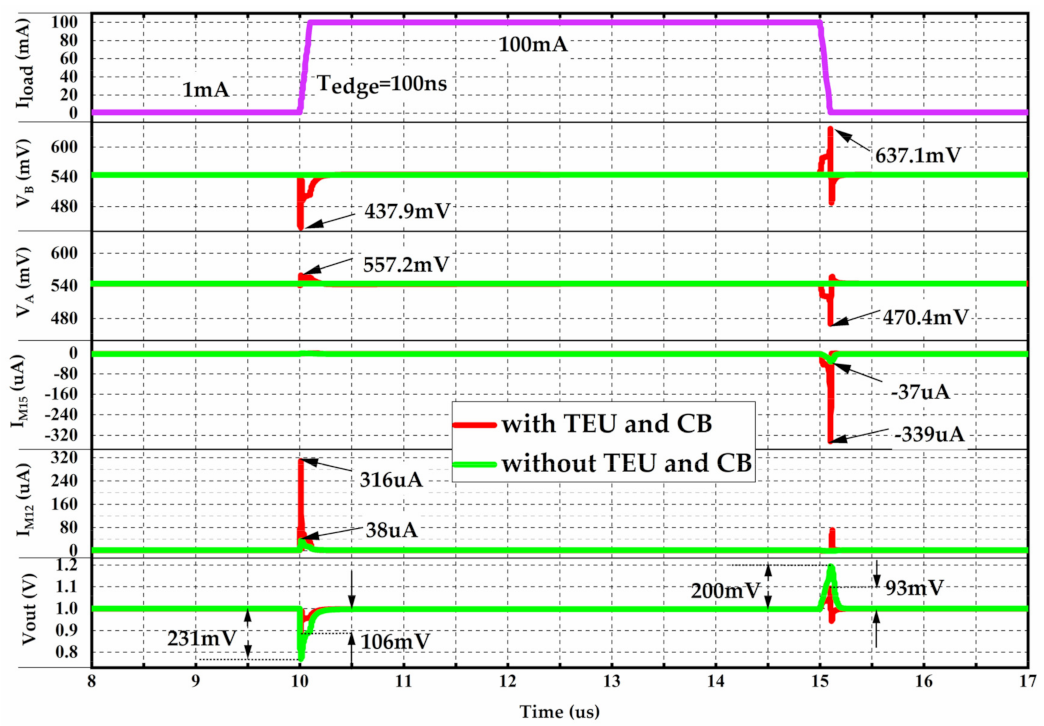
3. Simulation Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Man, T.Y.; Leung, K.N.; Leung, C.Y.; Mok, P.K.T.; Chan, M. Development of single-transistor-control LDO based on flipped voltage follower for SoC. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1392–1401. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Wang, Y.; Pan, Q.; Ki, W.-H.; Yue, C.P. A Fully-Integrated Low-Dropout Regulator With Full-Spectrum Power Supply Rejection. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 707–716. [Google Scholar] [CrossRef]
- Perez-Bailon, J.; Marquez, A.; Calvo, B.; Medrano, N. A 0.18 um CMOS LDO Regulator for an On-Chip Sensor Array Impedance Measurement System. Sensors 2018, 18, 1405. [Google Scholar] [CrossRef] [Green Version]
- Choe, Y.-J.; Nam, H.; Park, J.-D. A Low-Dropout Regulator with PSRR Enhancement through Feed-Forward Ripple Cancellation Technique in 65 nm CMOS Process. Electronics 2020, 9, 146. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Lu, Y.; Li, Q. A Fully Integrated LDO With 50-mV Dropout for Power Efficiency Optimization. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 67, 725–729. [Google Scholar] [CrossRef]
- Qu, X.; Zhou, Z.-K.; Zhang, B.; Li, Z.-J. An Ultralow-Power Fast-Transient Capacitor-Free Low-Dropout Regulator With Assistant Push Pull Output Stage. IEEE Trans. Circuits Syst. II-Express Briefs 2013, 60, 96–100. [Google Scholar] [CrossRef]
- Or, P.Y.; Leung, K.N. An Output-Capacitorless Low-Dropout Regulator With Direct Voltage-Spike Detection. IEEE J. Solid State Circuits 2010, 45, 458–466. [Google Scholar] [CrossRef]
- Wen, K.; Liu, S.B.; Li, Y.Y. A voltage-adjustable output-capacitorless LDO regulator with split-length current mirror compensation and overshoot/undershoot reduction. Analog. Integr. Circuits Signal. Process. 2020, 105, 459–470. [Google Scholar] [CrossRef]
- Milliken, R.J.; Silva-Martinez, J.; Sanchez-Sinencio, E. Full On-Chip CMOS Low-Dropout Voltage Regulator. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 1879–1890. [Google Scholar] [CrossRef]
- Ka Nang, L.; Mok, P.K.T. A capacitor-free cmos low-dropout regulator with damping-factor-control frequency compensation. IEEE J. Solid State Circuits 2003, 38, 1691–1702. [Google Scholar] [CrossRef]
- Lau, S.K.; Mok, P.K.T.; Leung, K.N. A low-dropout regulator for SoC with Q-reduction. IEEE J. Solid State Circuits 2007, 42, 658–664. [Google Scholar] [CrossRef]
- Lu, Y.; Ki, W.-H.; Yue, C.P. 17.11 A 0.65ns-Response-Time 3.01ps FOM Fully-Integrated Low-Dropout Regulator with Full-Spectrum Power-Supply-Rejection for Wideband Communication Systems. In Proceedings of the 1st IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 306–307. [Google Scholar]
- Bu, S.; Guo, J.; Leung, K.N. A 200-ps-Response-Time Output-Capacitorless Low-Dropout Regulator With Unity-Gain Bandwidth > 100 MHz in 130-nm CMOS. IEEE Trans. Power Electron. 2018, 33, 3232–3246. [Google Scholar] [CrossRef]
- Tan, X.L.; Chong, S.S.; Chan, P.K.; Dasgupta, U. A LDO Regulator With Weighted Current Feedback Technique for 0.47 nF–10 nF Capacitive Load. IEEE J. Solid State Circuits 2014, 49, 2658–2672. [Google Scholar] [CrossRef]
- Hong, S.-W.; Cho, G.-H. High-Gain Wide-Bandwidth Capacitor-Less Low-Dropout Regulator (LDO) for Mobile Applications Utilizing Frequency Response of Multiple Feedback Loops. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 46–57. [Google Scholar] [CrossRef]
- Yun, S.J.; Kim, J.S.; Kim, Y.S. Capless LDO Regulator Achieving-76 dB PSR and 96.3 fs FOM. IEEE Trans. Circuits Syst. II-Express Briefs 2017, 64, 1147–1151. [Google Scholar] [CrossRef]
- Sung, E.-T.; Park, S.; Baek, D. A Fast-Transient Output Capacitor-Less Low-Dropout Regulator Using Active-Feedback and Current-Reuse Feedforward Compensation. Energies 2018, 11, 688. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Chen, D. A Transient-Enhanced Output-Capacitorless LDO With Fast Local Loop and Overshoot Detection. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3422–3432. [Google Scholar] [CrossRef]
- Manikandan, P.; Bindu, B. A transient enhanced cap-less low-dropout regulator for wide range of load currents and capacitances. Microelectron. J. 2021, 115, 105207. [Google Scholar] [CrossRef]
- Pérez-Bailón, J.; Calvo, B.; Medrano, N. A Fully-Integrated 180 nm CMOS 1.2 V Low-Dropout Regulator for Low-Power Portable Applications. Electronics 2021, 10, 2108. [Google Scholar] [CrossRef]
- Xin, M.; Ze-kun, Z.; Bo, Z. A low-power ultra-fast capacitor-less LDO with advanced dynamic push-pull techniques. In Proceedings of the 2011 IEEE/IFIP 19th International Conference on VLSI and System-on-Chip, Kowloon, China, 3–5 October 2011; pp. 54–59. [Google Scholar]
- Zhan, C.; Ki, W.-H. An Output-Capacitor-Free Adaptively Biased Low-Dropout Regulator With Subthreshold Undershoot-Reduction for SoC. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 1119–1131. [Google Scholar] [CrossRef]
- Tang, J.; Lee, J.; Roh, J. Low-Power Fast-Transient Capacitor-Less LDO Regulator With High Slew-Rate Class-AB Amplifier. IEEE Trans. Circuits Syst. II-Express Briefs 2019, 66, 462–466. [Google Scholar] [CrossRef]
- Man, T.Y.; Mok, P.K.T.; Chan, M. A high slew-rate push-pull output amplifier for low-quiescent current low-dropout regulators with transient-response improvement. IEEE Trans. Circuits Syst. II-Express Briefs 2007, 54, 755–759. [Google Scholar] [CrossRef]
- Li, K.; Yang, C.; Guo, T.; Zheng, Y. A Multi-Loop Slew-Rate-Enhanced NMOS LDO Handling 1-A-Load-Current Step With Fast Transient for 5G Applications. IEEE J. Solid State Circuits 2020, 55, 3076–3086. [Google Scholar] [CrossRef]
- Li, K.; Xiao, X.; Jin, X.; Zheng, Y. A 600-mA, Fast-Transient Low-Dropout Regulator With Pseudo-ESR Technique in 0.18-mu m CMOS Process. IEEE Trans. Very Large Scale Integr. Syst. 2020, 28, 403–413. [Google Scholar] [CrossRef]
- Galan, J.A.; Lopez-Martin, A.J.; Carvajal, R.G.; Ramirez-Angulo, J.; Rubia-Marcos, C. Super Class-AB OTAs with adaptive biasing and dynamic output current scaling. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 449–457. [Google Scholar] [CrossRef]
- Degrauwe, M.G.; Rijmenants, J.; Vittoz, E.A.; Deman, H.J. Adaptive biasing CMOS amplifiers. IEEE J. Solid State Circuits 1982, 17, 522–528. [Google Scholar] [CrossRef]
- Hazucha, P.; Karnik, T.; Bloechel, B.A.; Parsons, C.; Finan, D.; Borkar, S. Area-efficient linear regulator with ultra-fast load regulation. IEEE J. Solid State Circuits 2005, 40, 933–940. [Google Scholar] [CrossRef]
- Ming, X.; Li, Q.; Zhou, Z.-K.; Zhang, B. An Ultrafast Adaptively Biased Capacitorless LDO With Dynamic Charging Control. IEEE Trans. Circuits Syst. II-Express Briefs 2012, 59, 40–44. [Google Scholar] [CrossRef]









| Zeros | Poles |
|---|---|
| [6] | [14] | [16] | [17] | [18] | [19] | [20] | This Work | |
|---|---|---|---|---|---|---|---|---|
| Year | 2013 | 2014 | 2017 | 2018 | 2020 | 2021 | 2021 | 2021 |
| Technology (nm) | 350 | 65 | 180 | 130 | 65 | 130 | 180 | 180 |
| Chip Area (mm2) | 0.04 | 0.0133 | 0.033 | 0.0252 | 0.01 | 0.029 | 0.103 | 0.01524 |
| Input Voltage (V) | 1.2–1.5 | 0.75–1.2 | 1.8 | 1.4–2.7 | 1.05–1.2 | 1.2 | 1.297–3.3 | 1.2–1.8 |
| Output Voltage (V) | 1.0–1.3 | 0.55 | 1.6 | 1.2–2.5 | 0.9 | 1 | 1.2 | 1 |
| Maximum Output Current (mA) | 100 | 50 | 100 | 50 | 20 | 50 | 50 | 100 |
| Quiescent Current (μA) | 1.2–14 | 15.9–487 | 71–101 | 65.8 | 65 | 95 | 8.6 | 10.3 |
| Current Efficiency (%) | 99.99 | 99.03 | 99.93 | 99.87 | 99.68 | 99.81 | 99.99 | 99.99 |
| Load Regulation (mV/mA) | - | 0.18 | N/A | 0.048 | - | 0.009 | 0.006 | 0.034 |
| Line Regulation (mV/V) | - | 4 | 131 | 1.23 | - | 5 | 0.065 | 2.74 |
| On-chip Capacitor (pF) | 0 | 4.1 | 12.7 | 2.6 | 1.4 | 10 | 6.1 | 7.5 |
| Output Capacitor (pF) | 0–100 | 470–10000 | 100 | 0–100 | 0–100 | 0–2000 | 0–50 | 0–100 |
| Settling Time (μs) | 2.7 | 0.25 | 0.2 | 0.69 | 0.3 | 0.2 | 3.6 | 0.19 |
| FOM (ns) | 0.0324 | 0.0795 | 0.202 | 0.90804 | 0.975 | 0.38 | 0.310 | 0.01957 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Wang, L.; Wang, S.; Cui, M.; Zheng, Z.; Li, Y. A Low-Power, Fast-Transient Output-Capacitorless LDO with Transient Enhancement Unit and Current Booster. Electronics 2022, 11, 701. https://doi.org/10.3390/electronics11050701
Jiang Y, Wang L, Wang S, Cui M, Zheng Z, Li Y. A Low-Power, Fast-Transient Output-Capacitorless LDO with Transient Enhancement Unit and Current Booster. Electronics. 2022; 11(5):701. https://doi.org/10.3390/electronics11050701
Chicago/Turabian StyleJiang, Yongchao, Lixin Wang, Shixin Wang, Mengyao Cui, Zhuoxuan Zheng, and Yuanzhe Li. 2022. "A Low-Power, Fast-Transient Output-Capacitorless LDO with Transient Enhancement Unit and Current Booster" Electronics 11, no. 5: 701. https://doi.org/10.3390/electronics11050701





