A 220 GHz to 325 GHz Grounded Coplanar Waveguide Based Periodic Leaky-Wave Beam-Steering Antenna in Indium Phosphide Process
Abstract
:1. Introduction
2. Antenna Design
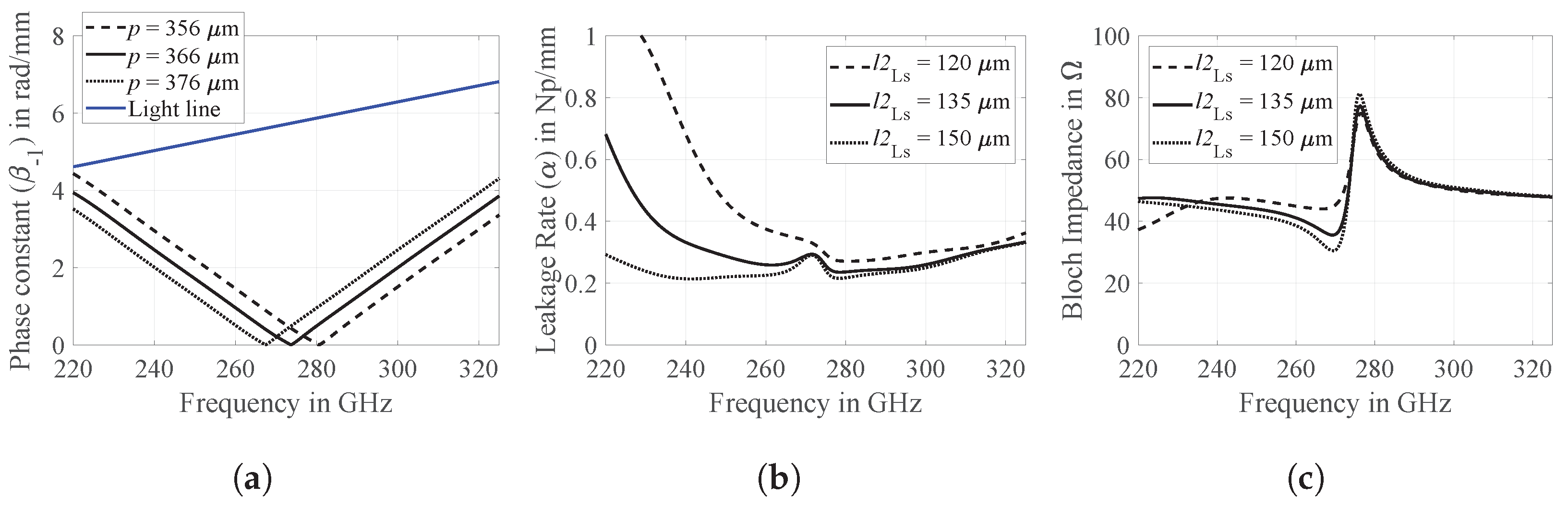
2.1. GCPW Leaky-Wave UC Analysis
2.2. GCPW Leaky-Wave Antenna: Full EM Simulation vs. Ideal Model
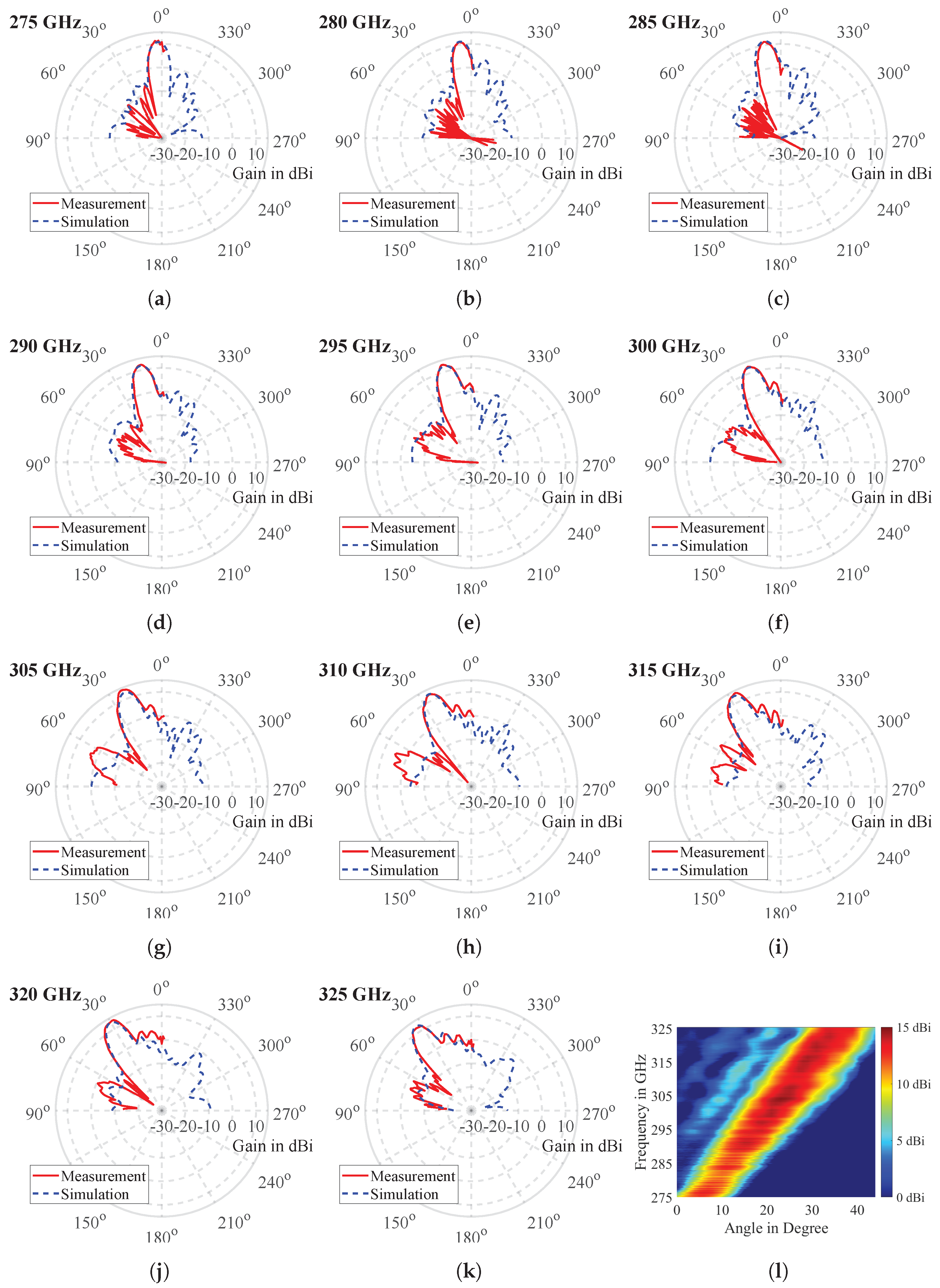
3. Probe-Based Antenna Measurement Results
4. Comparison with State-of-the-Art THz Beam-Steering Antennas and Future Outlook
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CPW | Coplanar waveguide |
| EM | Electromagnetic |
| GCPW | Grounded coplanar waveguide |
| GSG | Ground Signal Ground |
| IMT | International mobile telecommunication |
| InP | Indium Phosphide |
| THz | Terahertz |
| UC | Unit cell |
| UTC | Uni traveling carrier |
References
- Future Technology Trends of Terrestrial International Mobile Telecommunications Systems towards 2030 and Beyond. Available online: https://www.itu.int/dms_pub/itu-r/opb/rep/R-REP-M.2516-2022-PDF-E.pdf (accessed on 14 July 2023).
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications Above 100 GHz: Opportunities and Challenges for 6G and Beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Buckwalter, J.F.; Rodwell, M.J.W.; Ning, K.; Ahmed, A.; Arias-Purdue, A.; Chien, J.; O’Malley, E.; Lam, E. Fundamental Limits of High-Efficiency Silicon and Compound Semiconductor Power Amplifiers in 100—300 GHz Bands. ITU J. Future Evol. Technol. 2021, 2. Available online: https://www.itu.int/dms_pub/itu-s/opb/jnl/S-JNL-VOL2.ISSUE7-2021-A04-PDF-E.pdf (accessed on 14 July 2023).
- Zhang, Y.P.; Liu, D. Antenna-on-Chip and Antenna-in-Package Solutions to Highly Integrated Millimeter-Wave Devices for Wireless Communications. IEEE Trans. Antennas Propag. 2009, 57, 2830–2841. [Google Scholar] [CrossRef]
- Sarkas, I.; Laskin, E.; Hasch, J.; Chevalier, P.; Voinigescu, S.P. Second generation transceivers for D-band radar and data communication applications. In Proceedings of the 2010 IEEE MTT-S International Microwave Symposium, Anaheim, CA, USA, 23–28 May 2010; pp. 1328–1331. [Google Scholar] [CrossRef]
- Müller, D.; Reiss, S.; Massler, H.; Tessmann, A.; Leuther, A.; Zwick, T.; Kallfass, I. A H-band reflective-type phase shifter MMIC for ISM-Band applications. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Lu, P.; Haddad, T.; Sievert, B.; Khani, B.; Makhlouf, S.; Dülme, S.; Estévez, J.F.; Rennings, A.; Erni, D.; Pfeiffer, U.; et al. InP-Based THz beam-steering Leaky-Wave Antenna. IEEE Trans. Terahertz Sci. Technol. 2021, 11, 218–230. [Google Scholar] [CrossRef]
- Haddad, T.; Biurrun-Quel, C.; Lu, P.; Kaya, H.; Mohammad, I.; Stöhr, A. Suppressing Open Stopband for Terahertz Periodic Microstrip Leaky-wave Antennas. In Proceedings of the 2023 17th European Conference on Antennas and Propagation (EuCAP), Florence, Italy, 26–31 March 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Sarabandi, K.; Jam, A.; Vahidpour, M.; East, J. A Novel Frequency Beam-Steering Antenna Array for Submillimeter-Wave Applications. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 654–665. [Google Scholar] [CrossRef]
- Dancila, D.; Beuerle, B.; Shah, U.; Oberhammer, J.; Rydberg, A. Leaky Wave Antenna at 300 GHz in Silicon Micromachined Waveguide Technology. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Guerboukha, H.; Shrestha, R.; Neronha, J.; Ryan, O.; Hornbuckle, M.; Fang, Z.; Mittleman, D.M. Efficient leaky-wave antennas at terahertz frequencies generating highly directional beams. Appl. Phys. Lett. 2020, 117, 261103. [Google Scholar] [CrossRef]
- Guerboukha, H.; Shrestha, R.; Neronha, J.; Fang, Z.; Mittleman, D.M. Conformal leaky-wave antennas for wireless terahertz communications. Commun. Eng. 2023, 2, 17. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Tofani, S.; Zografopoulos, D.C.; Baccarelli, P.; Burghignoli, P.; Beccherelli, R.; Galli, A. Systematic Design of THz Leaky-Wave Antennas Based on Homogenized Metasurfaces. IEEE Trans. Antennas Propag. 2018, 66, 1169–1178. [Google Scholar] [CrossRef]
- Grbic, A.; Eleftheriades, G.V. Leaky CPW-based slot antenna arrays for millimeter-wave applications. IEEE Trans. Antennas Propag. 2002, 50, 1494–1504. [Google Scholar] [CrossRef]
- Wang, H.; Sun, S.; Xue, X. A Periodic CPW Leaky-Wave Antenna With Enhanced Gain and Broadside Radiation. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 676–680. [Google Scholar] [CrossRef]
- Rouvalis, E.; Renaud, C.C.; Moodie, D.G.; Robertson, M.J.; Seeds, A.J. Continuous Wave Terahertz Generation From Ultra-Fast InP-Based Photodiodes. IEEE Trans. Microw. Theory Tech. 2012, 60, 509–517. [Google Scholar] [CrossRef]
- Makhlouf, S.; Dülme, S.; Grzeslo, M.; Estévez, J.L.F.; Rymanov, V.; Lackmann, J.; Stöhr, A. Monolithically Integrated THz Photodiodes With CPW-to-WR3 E-Plane Transitions for Photodiodes Packages With WR3-Outputs. J. Light. Technol. 2021, 39, 7804–7812. [Google Scholar] [CrossRef]
- Dyck, A.; Rösch, M.; Tessmann, A.; Leuther, A.; Kuri, M.; Wagner, S.; Gashi, B.; Schäfer, J.; Ambacher, O. A Transmitter System-in-Package at 300 GHz With an Off-Chip Antenna and GaAs-Based MMICs. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 335–344. [Google Scholar] [CrossRef]
- Hejase, J.A.; Paladhi, P.R.; Chahal, P.P. Terahertz Characterization of Dielectric Substrates for Component Design and Nondestructive Evaluation of Packages. IEEE Trans. Components Packag. Manuf. Technol. 2011, 1, 1685–1694. [Google Scholar] [CrossRef]
- Indium Phosphide, Michigan State University, Terahertz Systems Laboratory. Available online: https://www.egr.msu.edu/~tesla-web/tesla/TESLA/Indium_Phosphide_table.html (accessed on 14 July 2023).
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 381–386. [Google Scholar]
- Oliner, A.A. Leaky-Wave Antennas. Antenna Engineering Handbook, 3rd ed.; McGraw Hill, Inc.: New York, NY, USA, 1993; pp. 292–294. [Google Scholar]
- Beer, S.; Zwick, T. Probe based radiation pattern measurements for highly integrated millimeter-wave antennas. In Proceedings of the Fourth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–5. [Google Scholar]
- Gulan, H.; Beer, S.; Diebold, S.; Rusch, C.; Leuther, A.; Kallfass, I.; Zwick, T. Probe based antenna measurements up to 325 GHz for upcoming millimeter-wave applications. In Proceedings of the 2013 International Workshop on Antenna Technology (iWAT), Karlsruhe, Germany, 4–6 March 2013; pp. 228–231. [Google Scholar] [CrossRef]
- Reniers, A.C.F.; van Dommele, A.R.; Smolders, A.B.; Herben, M.H.A.J. The Influence of the Probe Connection on mm-Wave Antenna Measurements. IEEE Trans. Antennas Propag. 2015, 63, 3819–3825. [Google Scholar] [CrossRef]
- Boehm, L.; Hitzler, M.; Roos, F.; Waldschmidt, C. Probe influence on integrated antenna measurements at frequencies above 100 GHz. In Proceedings of the 2016 46th European Microwave Conference (EuMC), London, UK, 4–6 October 2016; pp. 552–555. [Google Scholar] [CrossRef]





| w | s | wg | p | |||
|---|---|---|---|---|---|---|
| 70 μm | 71 μm | 100 μm | 366 μm | 41 μm | 135 μm | 28 μm |
| 30 μm | 23 μm | 63 μm | 364 μm | 20 μm | 95 μm | 46 μm | 1.8 mm | 6.8 mm |
| Reference | Frequency Range | Relative Bandwidth | Antenna Type | Realized Gain | Beam-Steering Range | Electrical Length |
|---|---|---|---|---|---|---|
| [7] | 230 GHz–330 GHz | Microstrip | 11 dBi | to | ≈ | |
| [9] | 230 GHz–245 GHz | Rectangular Waveguide | 29 dBi | to | ||
| [10] | 288 GHz–306 GHz | Slotted Waveguide | 15 dBi * | - | ||
| [11] | 150 GHz–300 GHz | Parallel-plate Waveguide | 24.3 dBi * | to | ≫15 | |
| This work | 220 GHz–325 GHz | GCPW | 13.5 dBi | to |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhutani, A.; Kretschmann, M.; Dittmer, J.; Lu, P.; Stöhr, A.; Zwick, T. A 220 GHz to 325 GHz Grounded Coplanar Waveguide Based Periodic Leaky-Wave Beam-Steering Antenna in Indium Phosphide Process. Electronics 2023, 12, 3482. https://doi.org/10.3390/electronics12163482
Bhutani A, Kretschmann M, Dittmer J, Lu P, Stöhr A, Zwick T. A 220 GHz to 325 GHz Grounded Coplanar Waveguide Based Periodic Leaky-Wave Beam-Steering Antenna in Indium Phosphide Process. Electronics. 2023; 12(16):3482. https://doi.org/10.3390/electronics12163482
Chicago/Turabian StyleBhutani, Akanksha, Marius Kretschmann, Joel Dittmer, Peng Lu, Andreas Stöhr, and Thomas Zwick. 2023. "A 220 GHz to 325 GHz Grounded Coplanar Waveguide Based Periodic Leaky-Wave Beam-Steering Antenna in Indium Phosphide Process" Electronics 12, no. 16: 3482. https://doi.org/10.3390/electronics12163482
APA StyleBhutani, A., Kretschmann, M., Dittmer, J., Lu, P., Stöhr, A., & Zwick, T. (2023). A 220 GHz to 325 GHz Grounded Coplanar Waveguide Based Periodic Leaky-Wave Beam-Steering Antenna in Indium Phosphide Process. Electronics, 12(16), 3482. https://doi.org/10.3390/electronics12163482







