Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System
Abstract
:1. Introduction
2. Modeling and Characteristic Analysis of the Harmonic Current of the Inverter
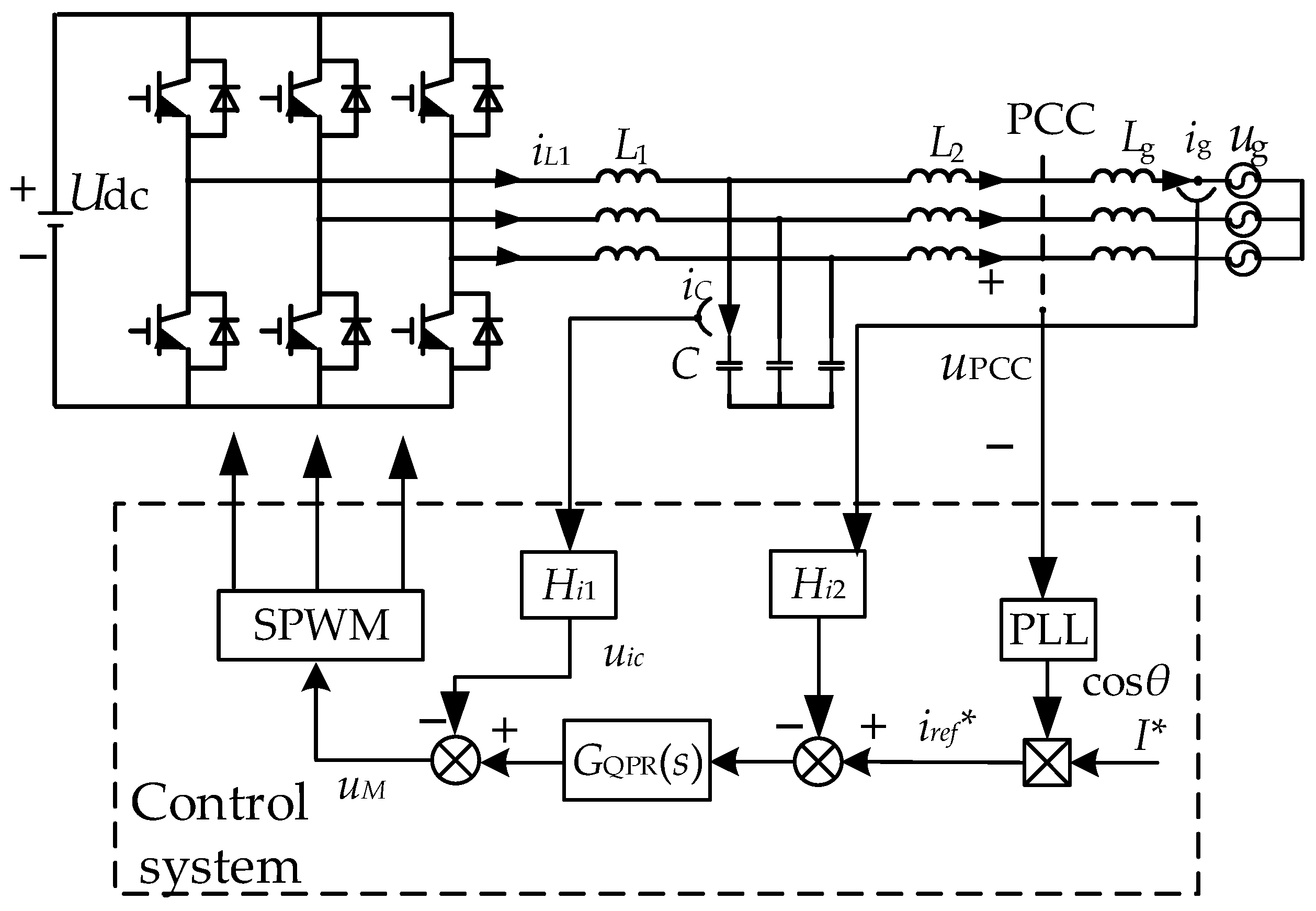
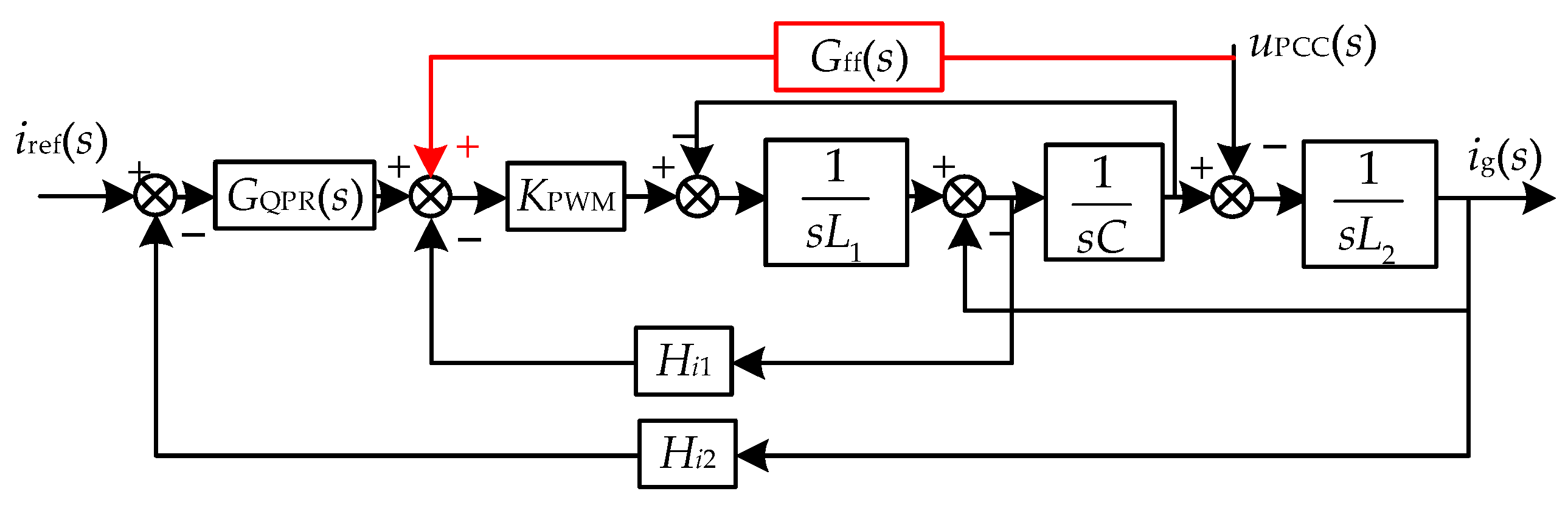
2.1. Structure and Control of the Inverter
2.2. Parameterization of LCL Filter
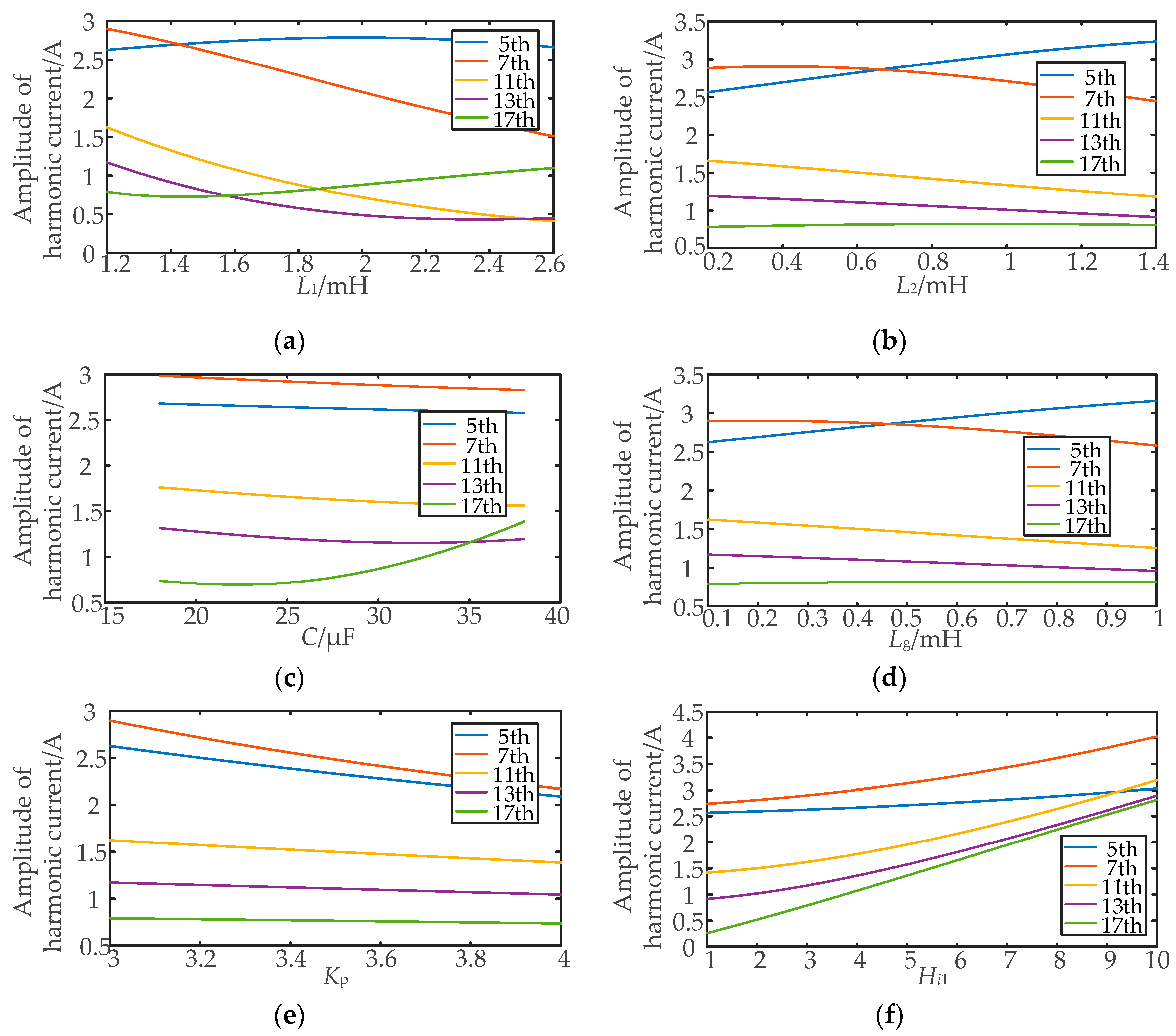
2.2.1. Parameter of Inverter Side Inductor L1
2.2.2. Parameter of Filter Capacitor C
2.2.3. Parameter of Grid-Side Inductor L2
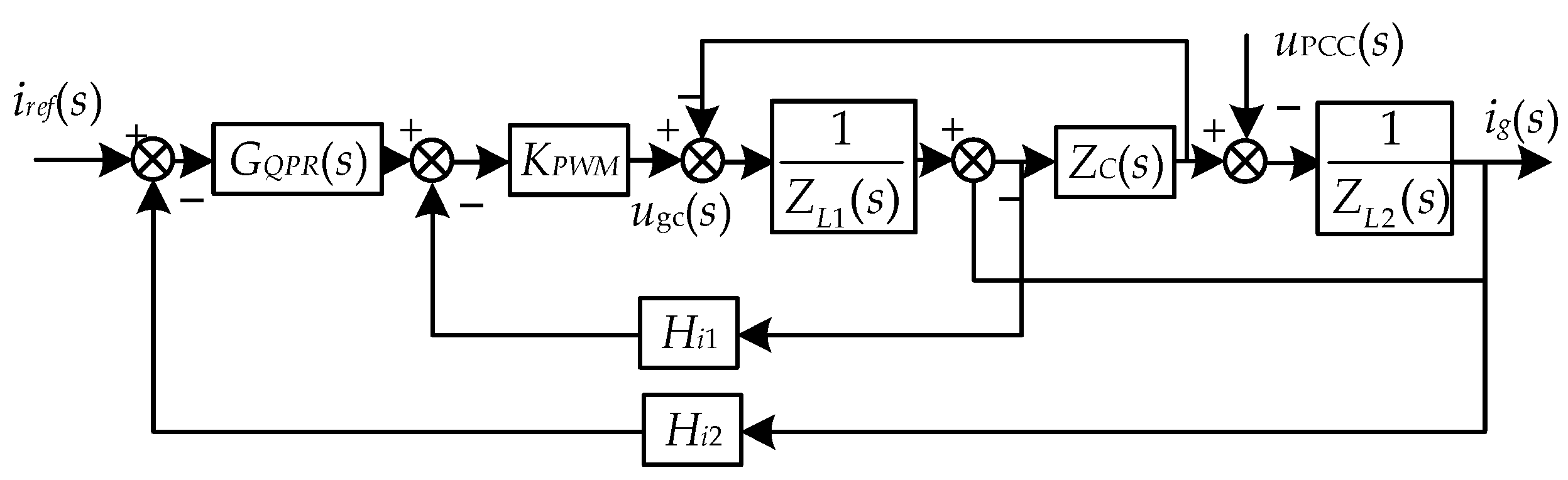
2.3. Modeling of Harmonic Current of Inverter
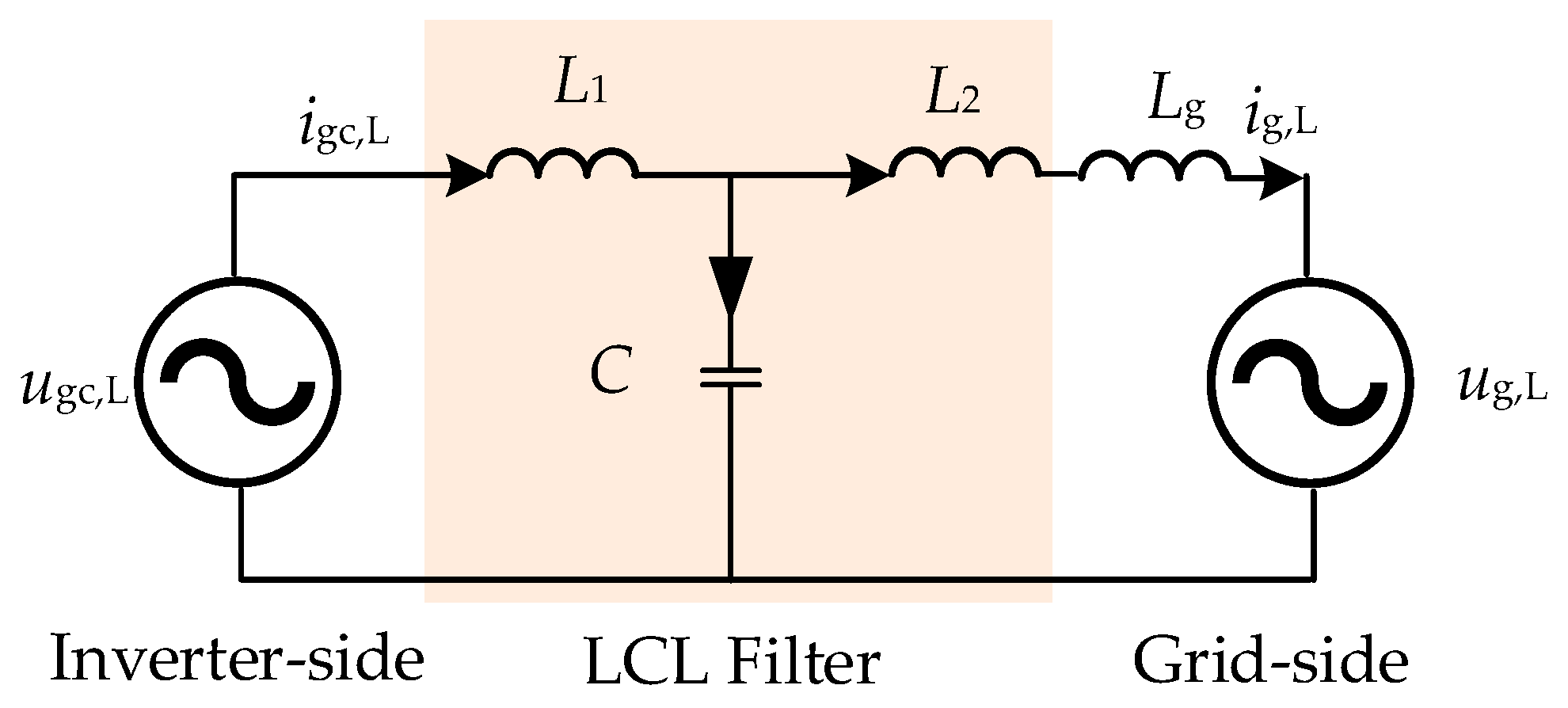
2.3.1. Low-Frequency Harmonics Caused by External Harmonic Sources
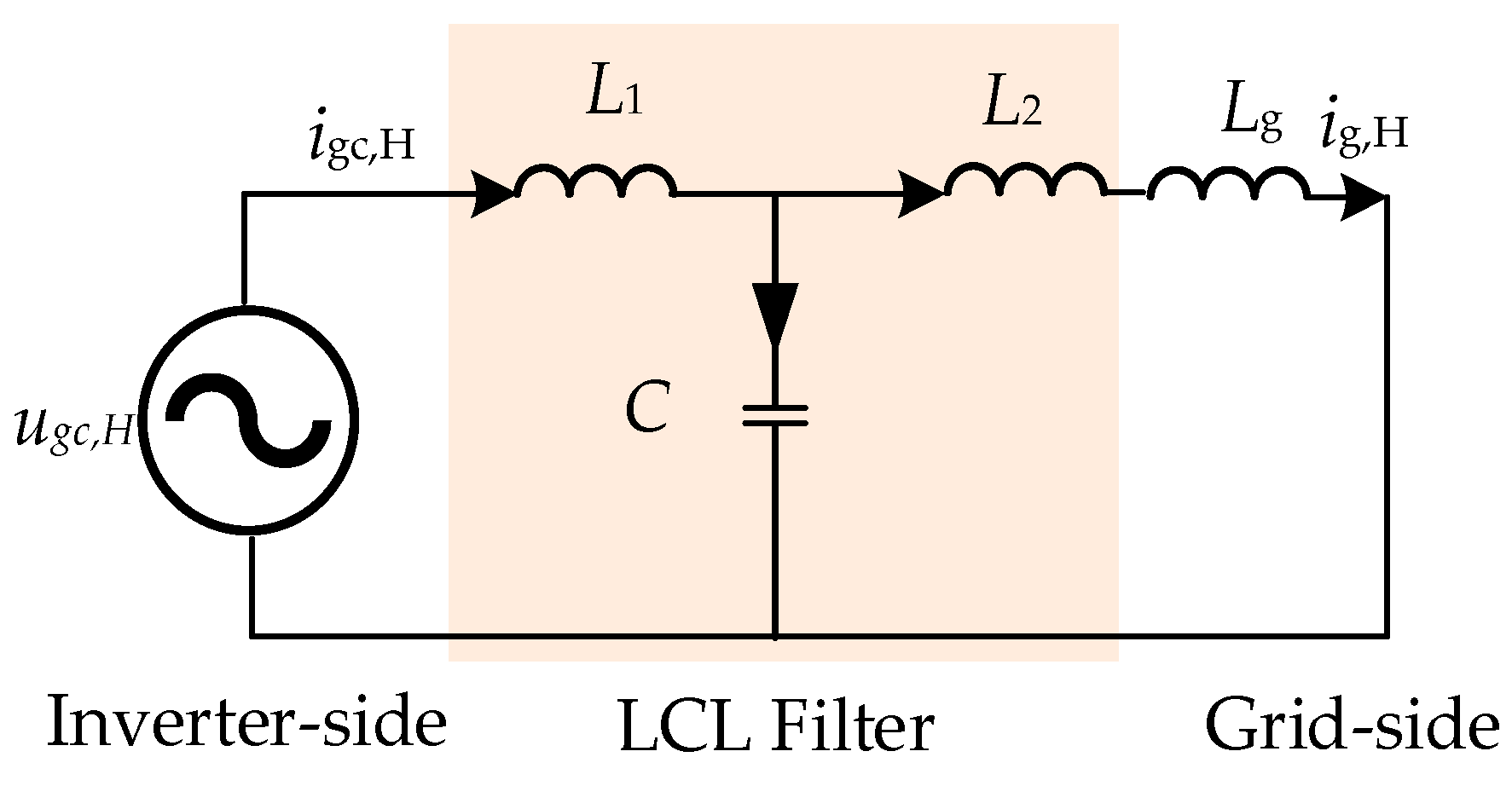
2.3.2. High Harmonic Caused by Internal Harmonic Sources
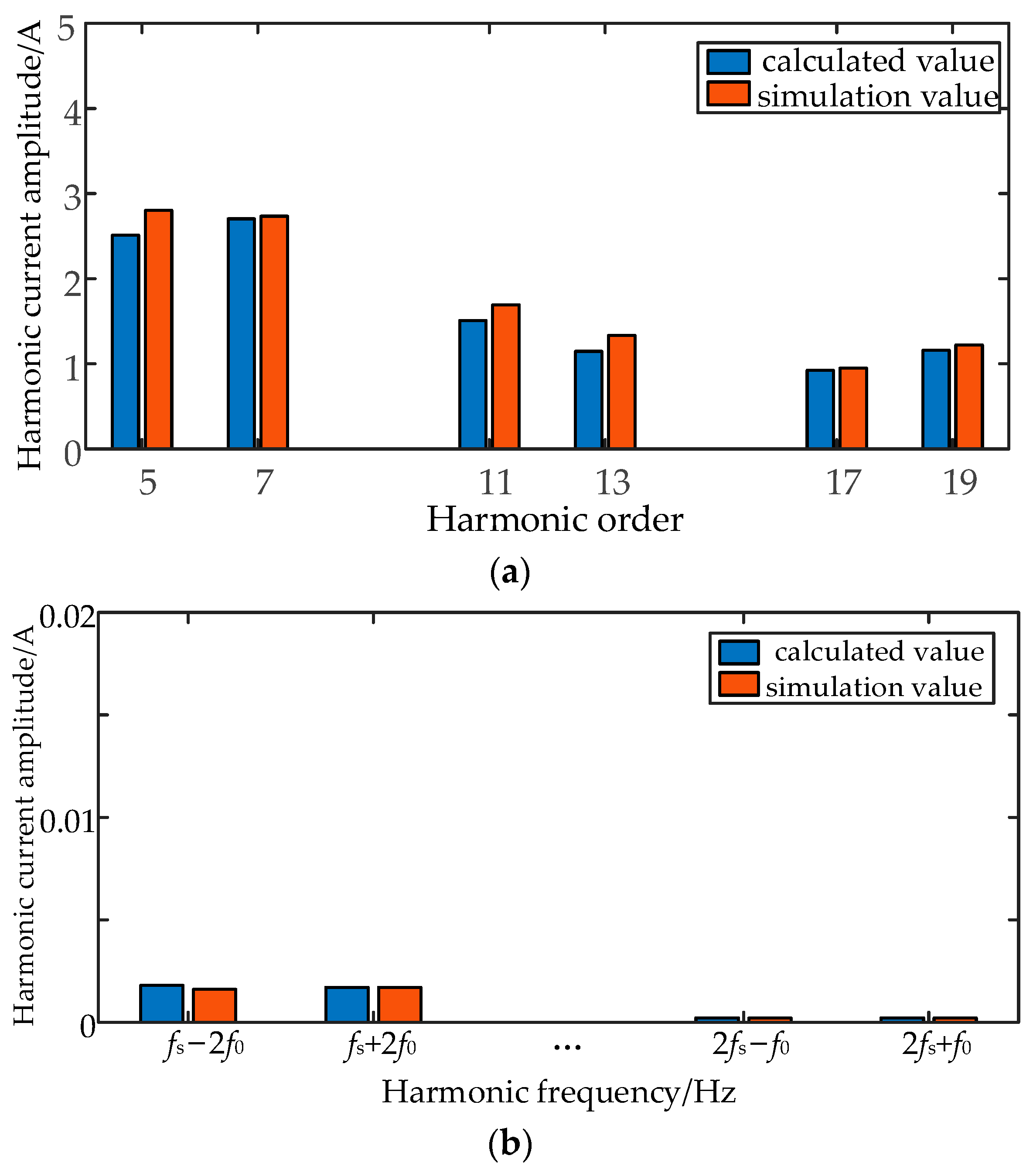
2.3.3. Simulation Validation
2.4. Characteristic Analysis of Harmonic Current
3. Analysis of Inverter Resonance Mechanism
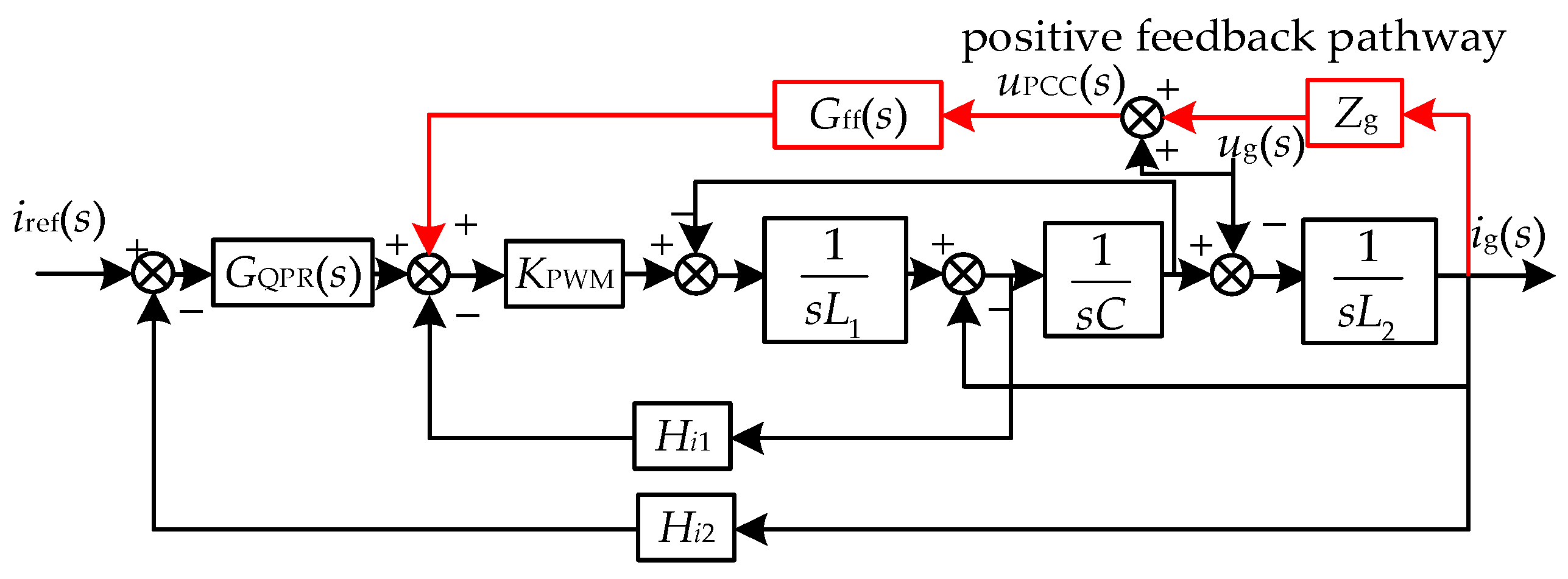
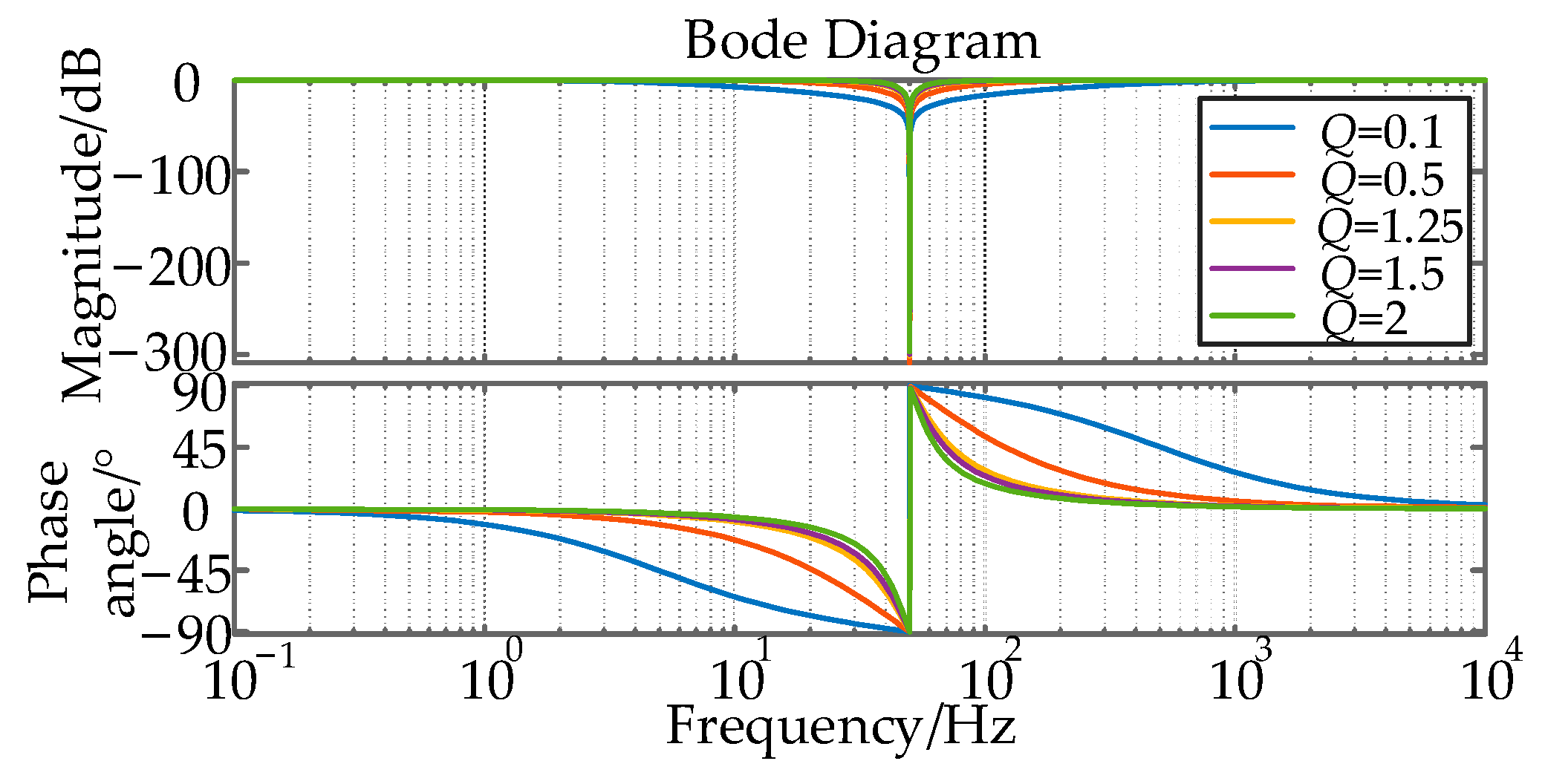
3.1. Mechanism of Resonance Induced by Grid Voltage Feed-Forward Links
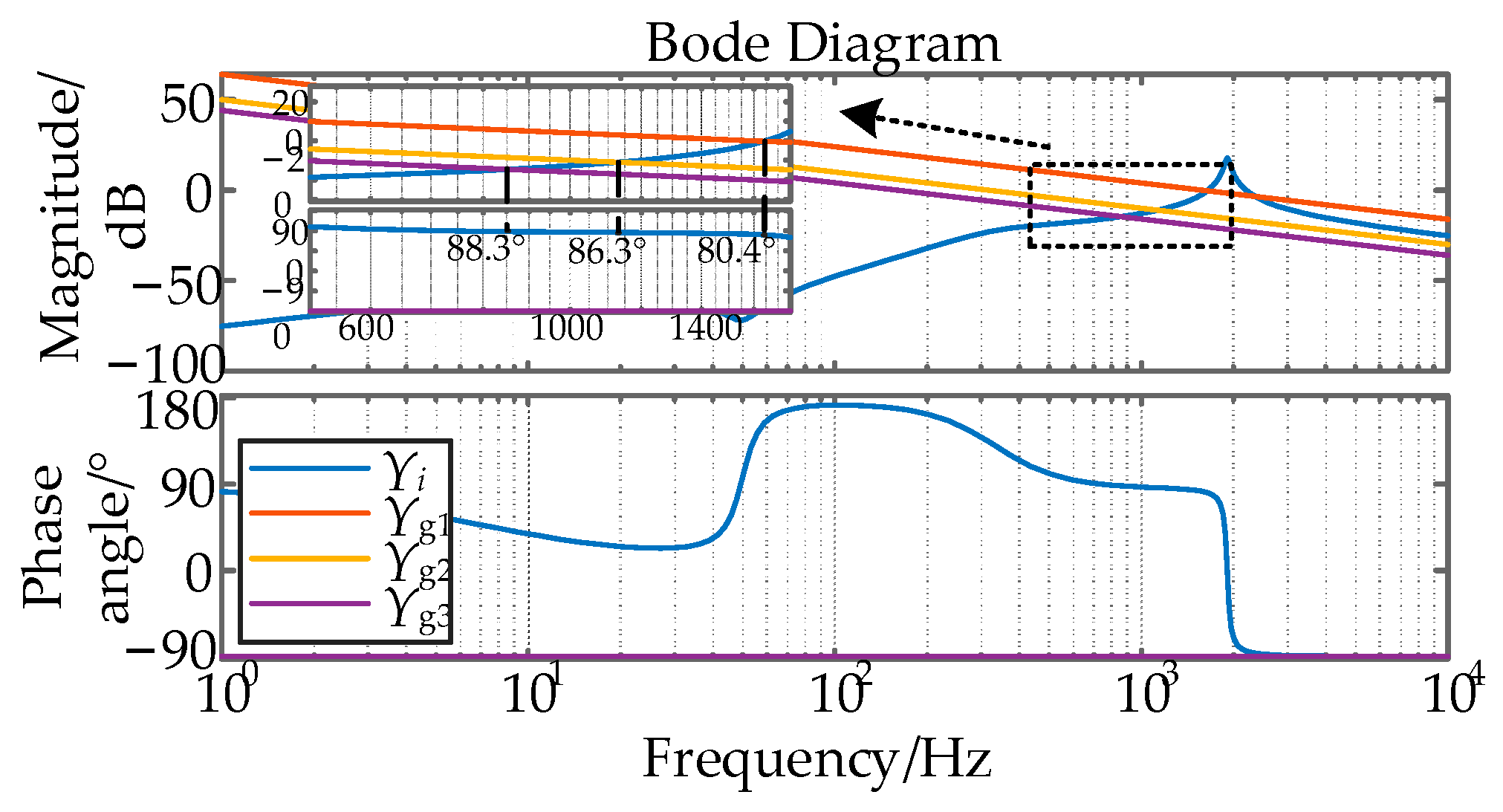
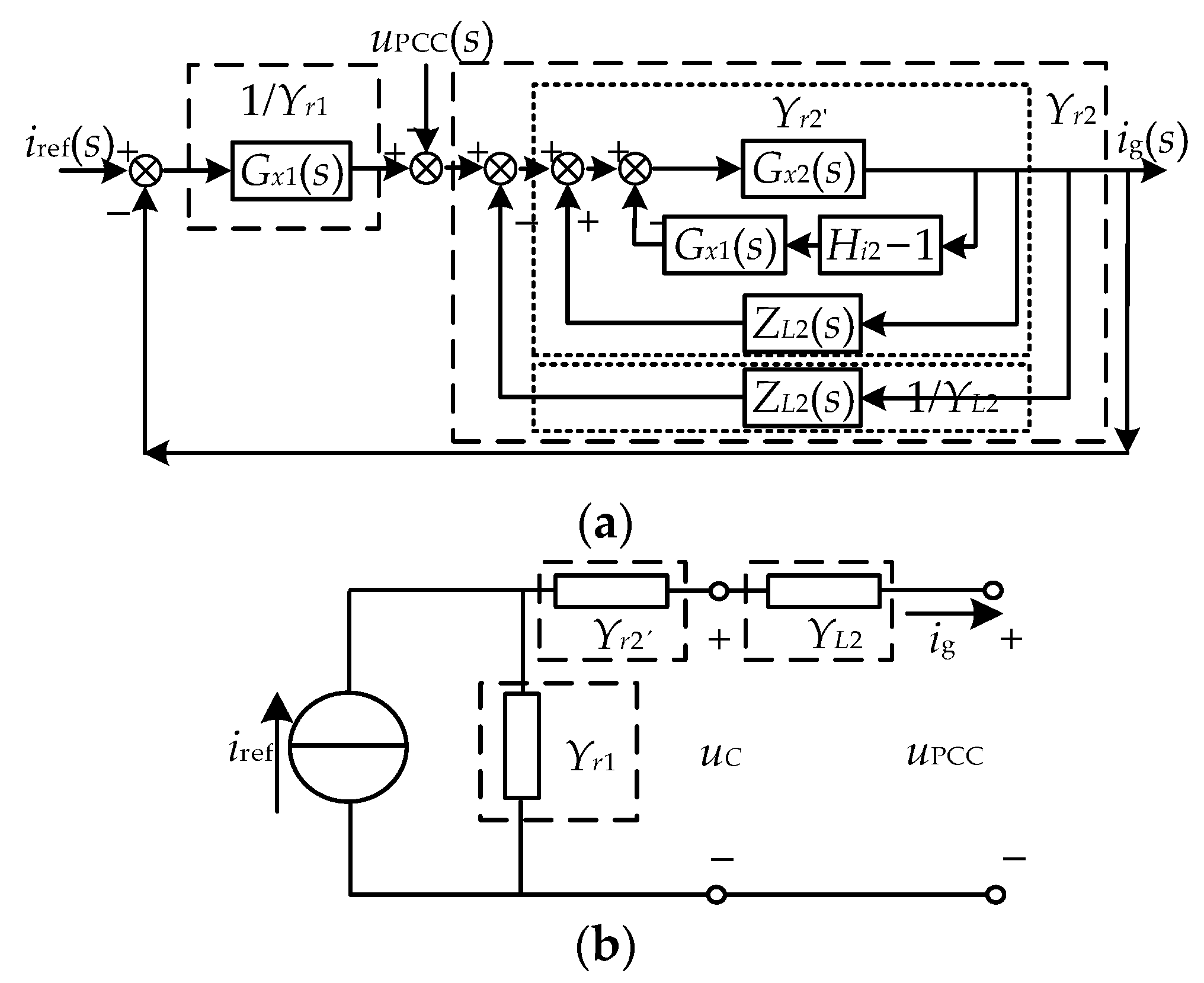
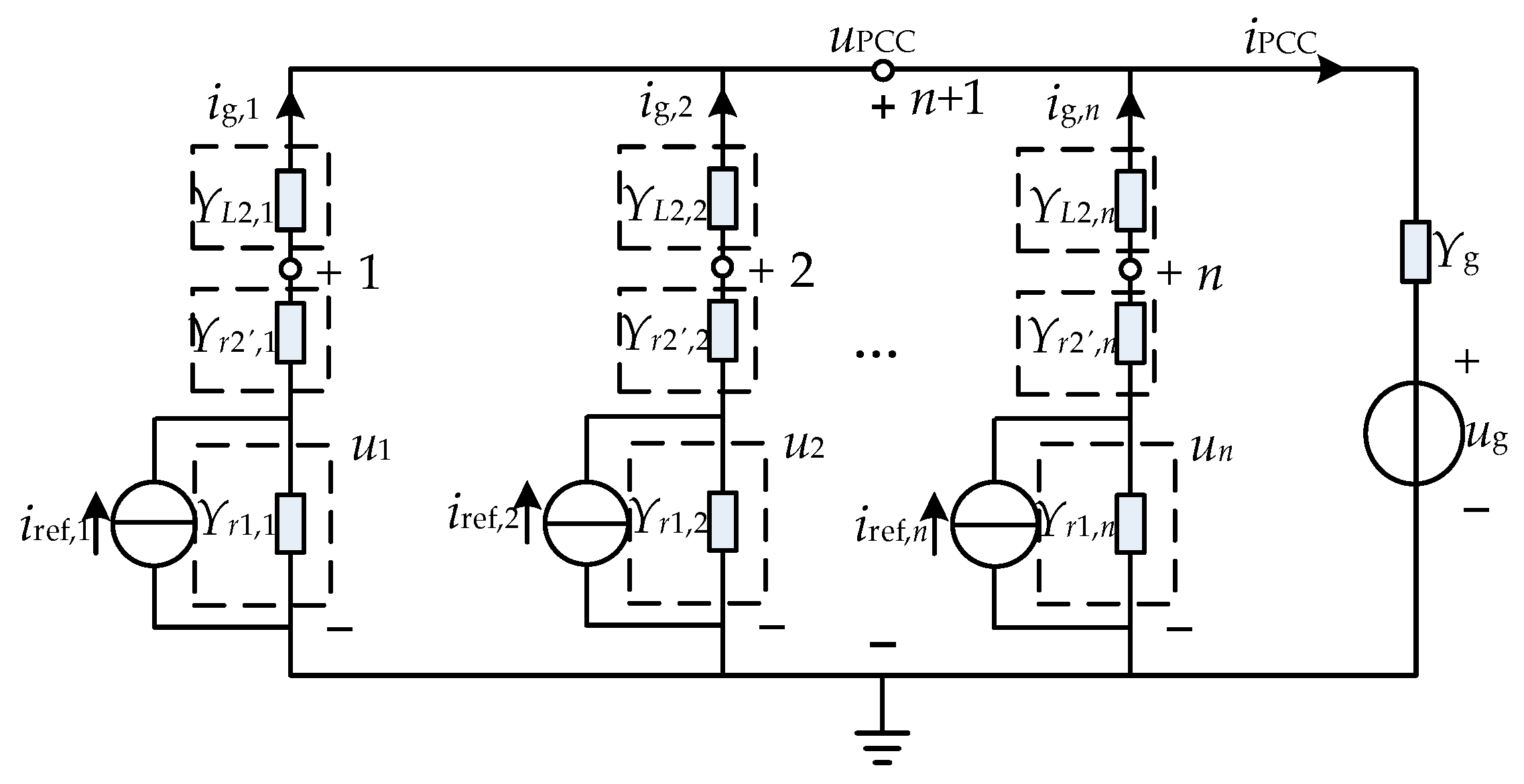
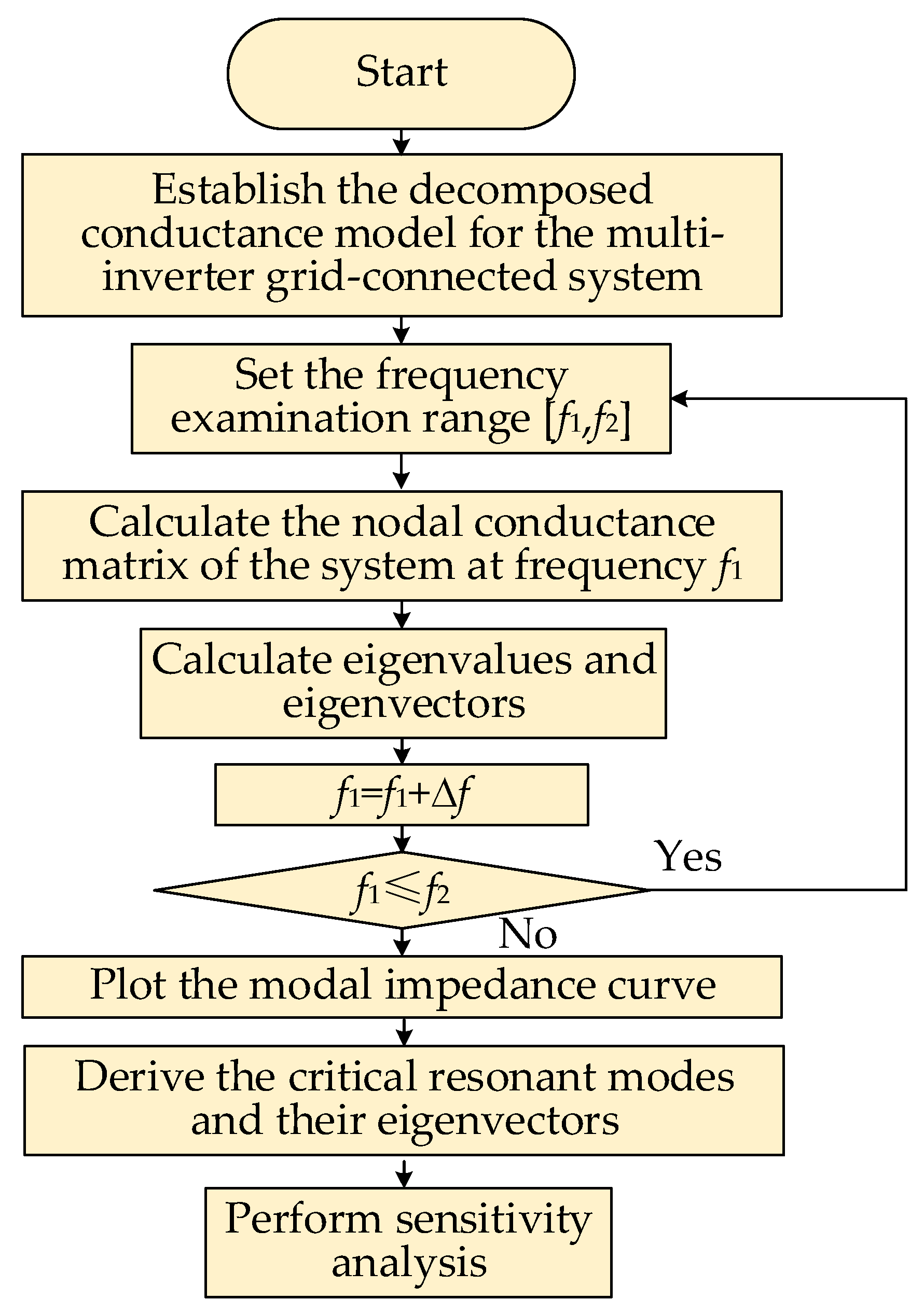
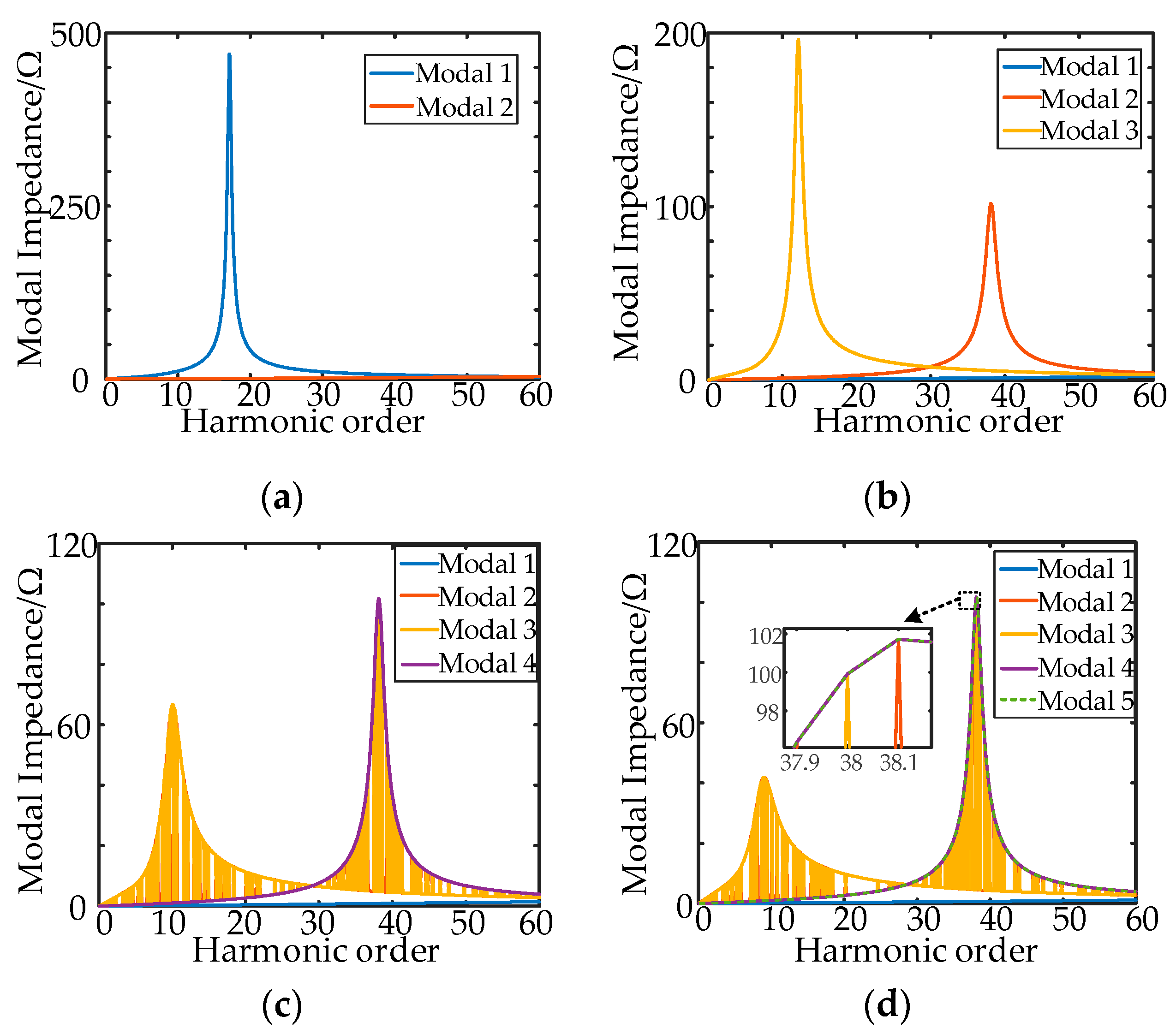
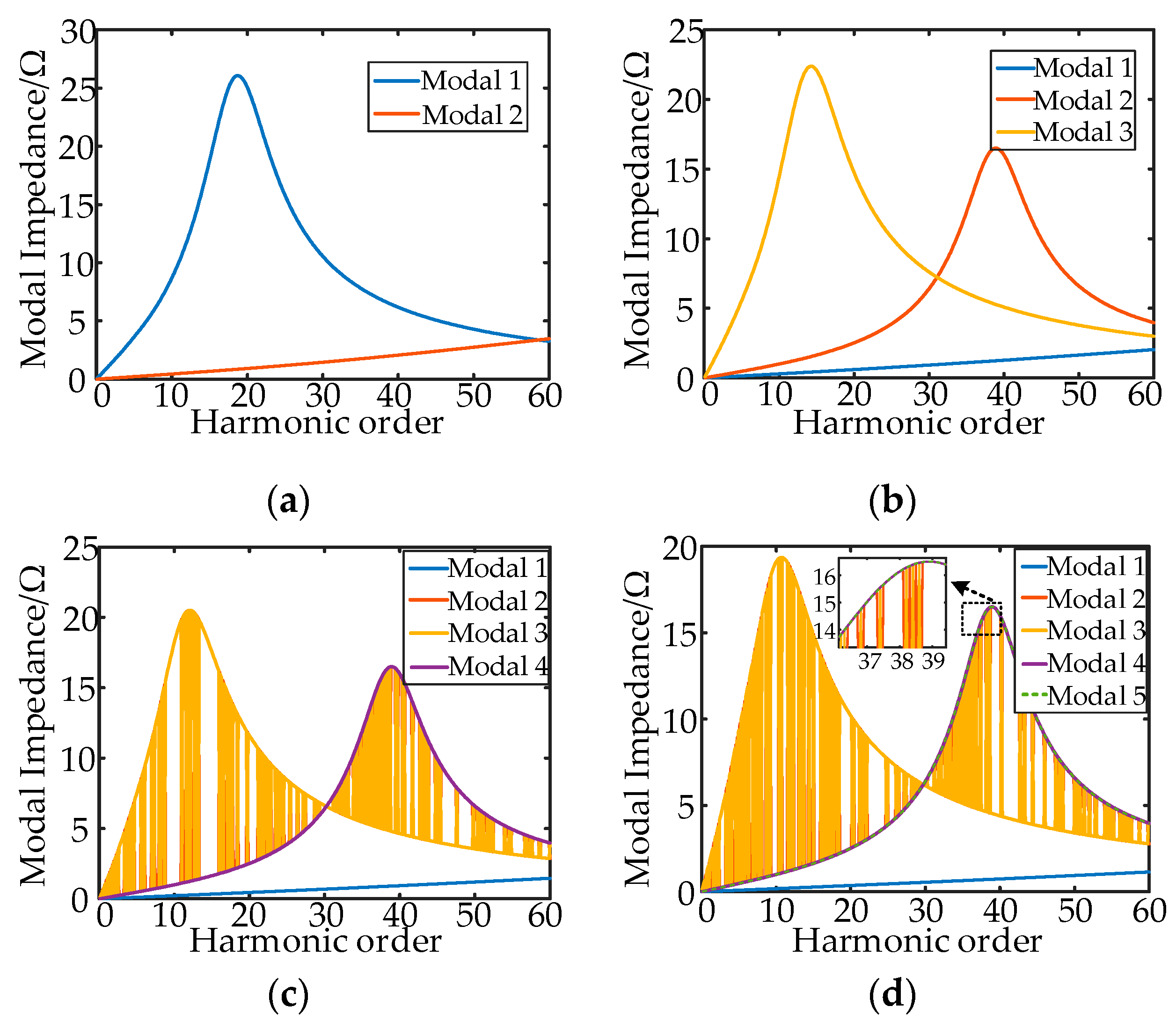
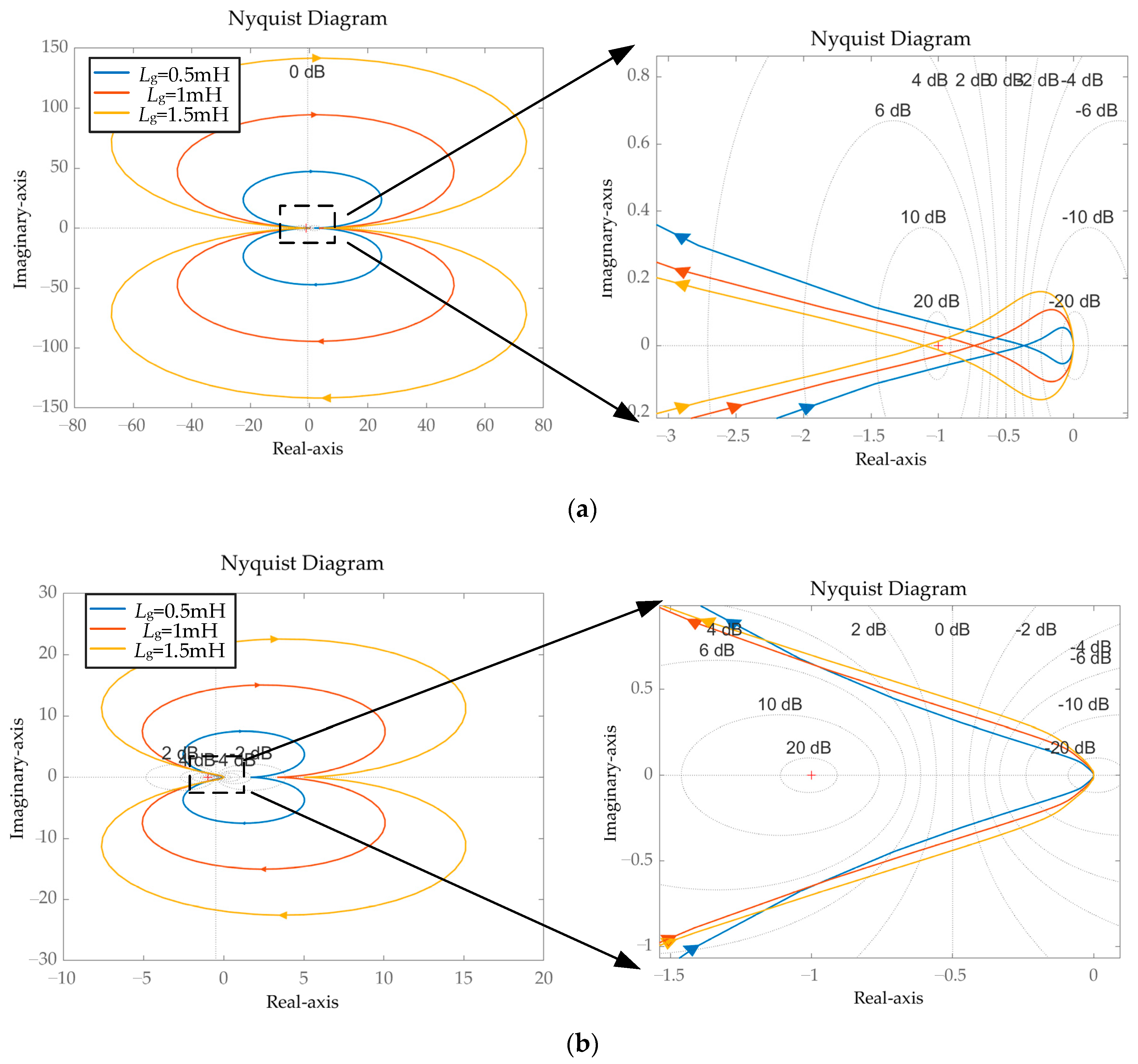
3.2. Impedance Modeling and Resonance Analysis of Multi-Inverter Grid-Connected Systems
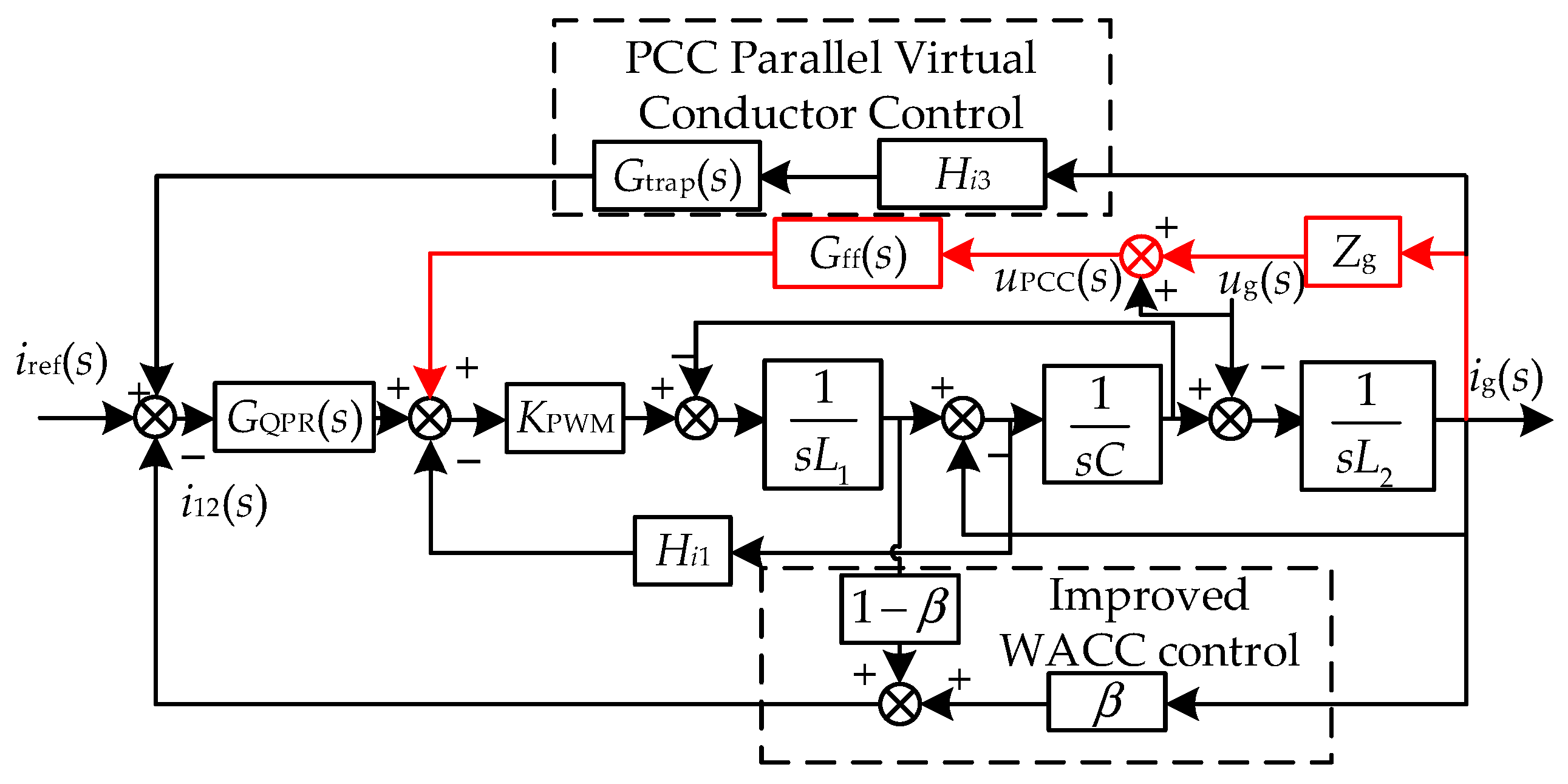
4. Impedance Remodeling Harmonic Resonance Suppression Method for Multi-Inverter Grid-Connected Systems
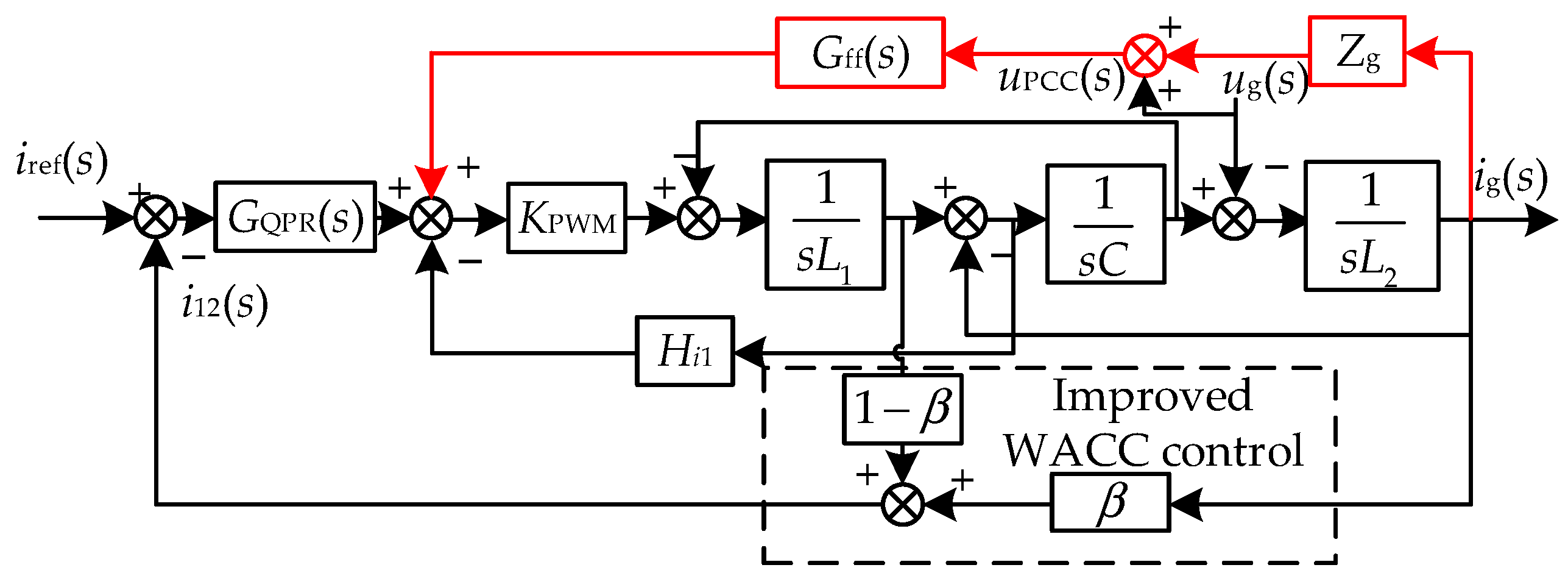
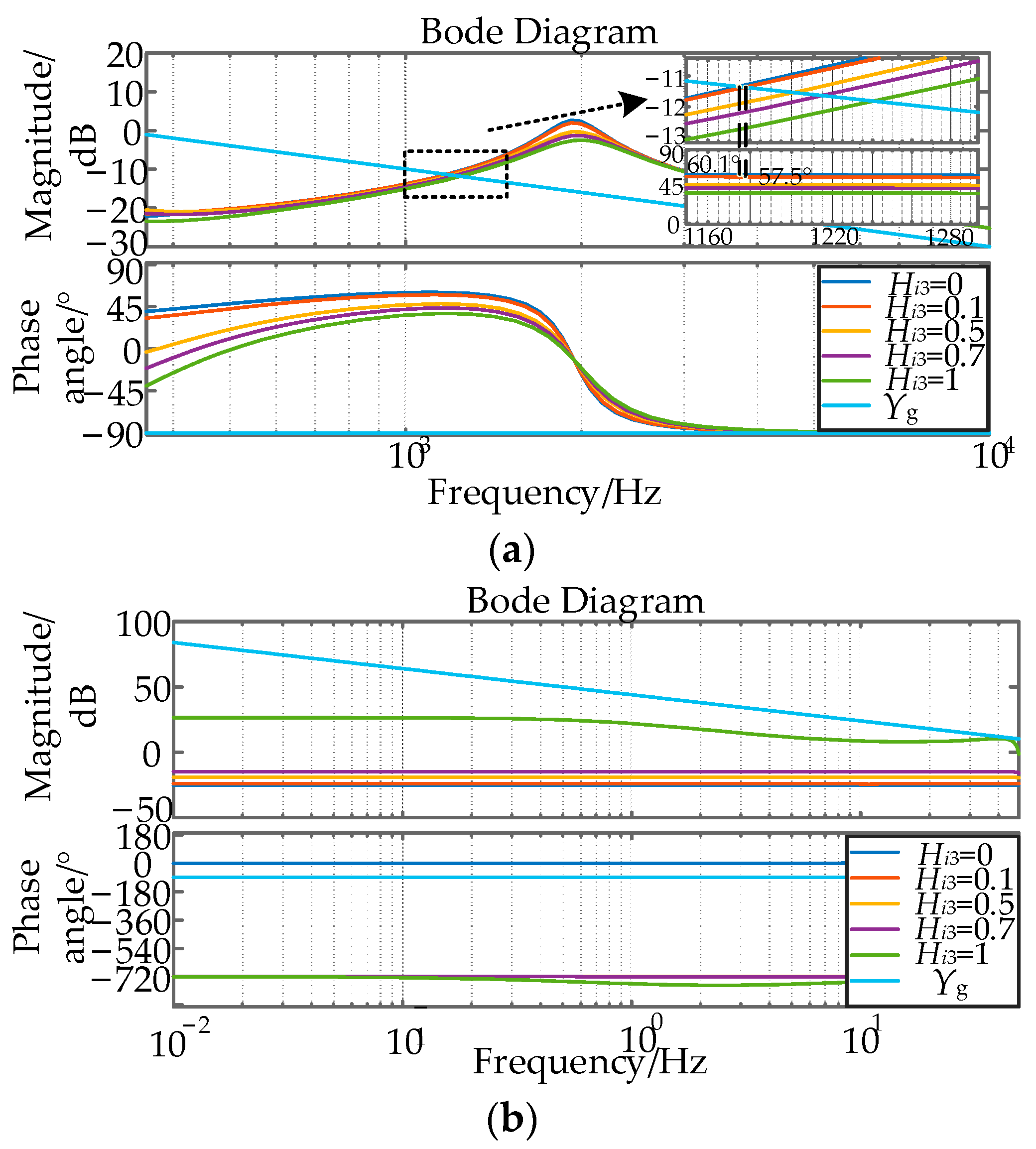
4.1. Improved WACC Current Control Strategy
4.2. PCC Point-Parallel Virtual Conductance Strategy
4.3. Comparison of the Effects of Different Methods
5. Simulation Verification
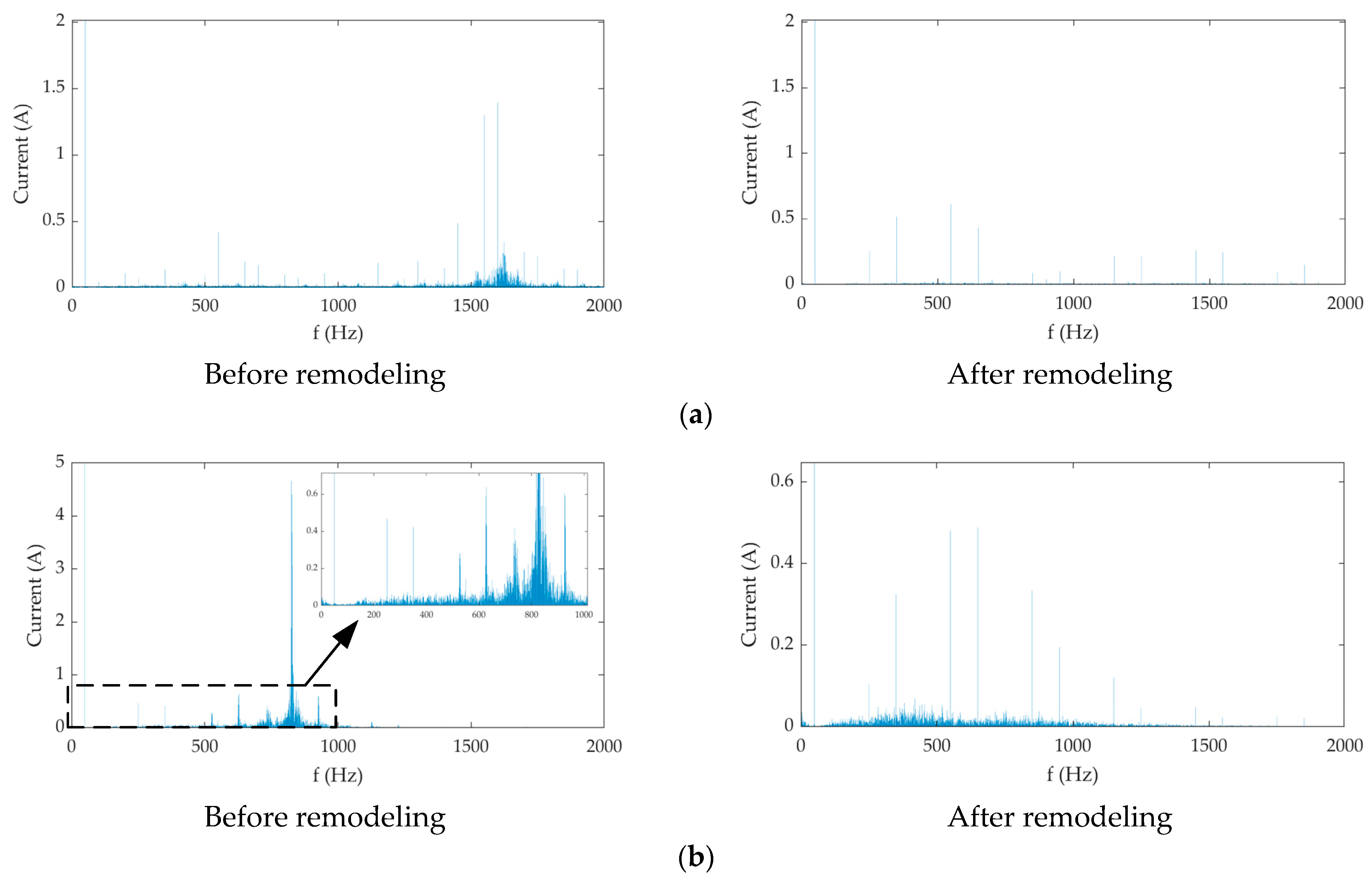
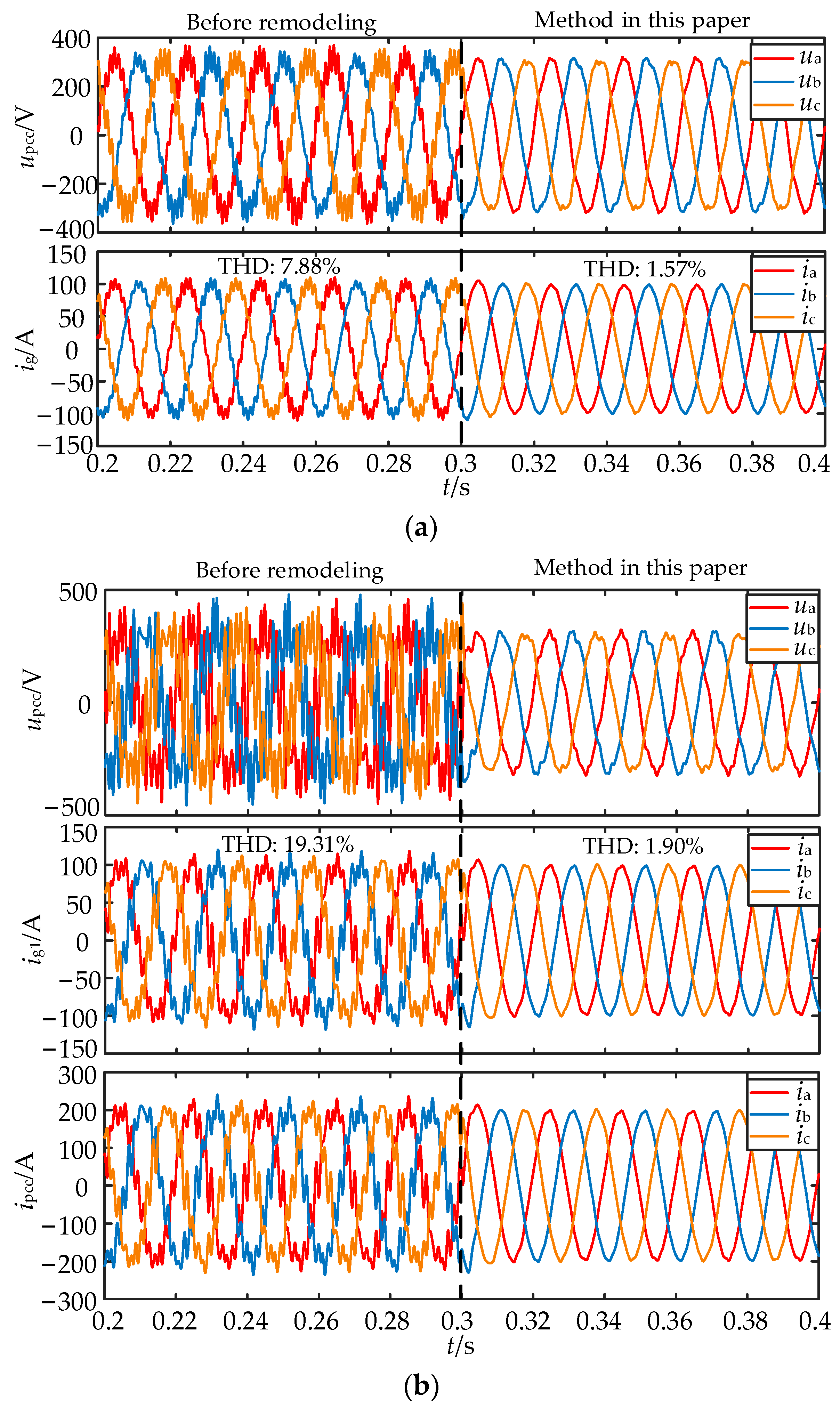
5.1. Verification of Single Inverter Operating Conditions without Background Harmonics
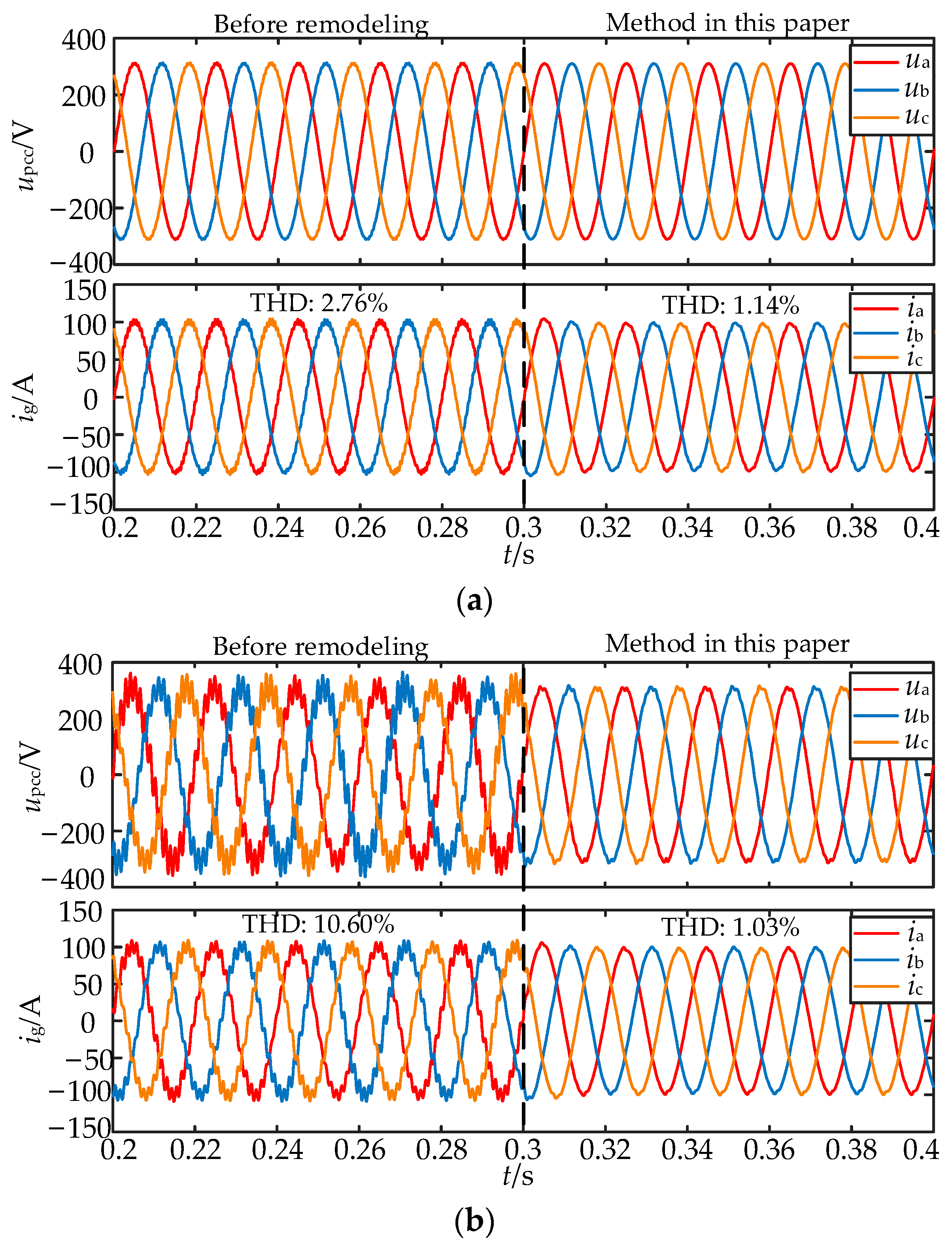
5.2. Verification of Single and Multiple Inverter Operating Conditions with Background Harmonics
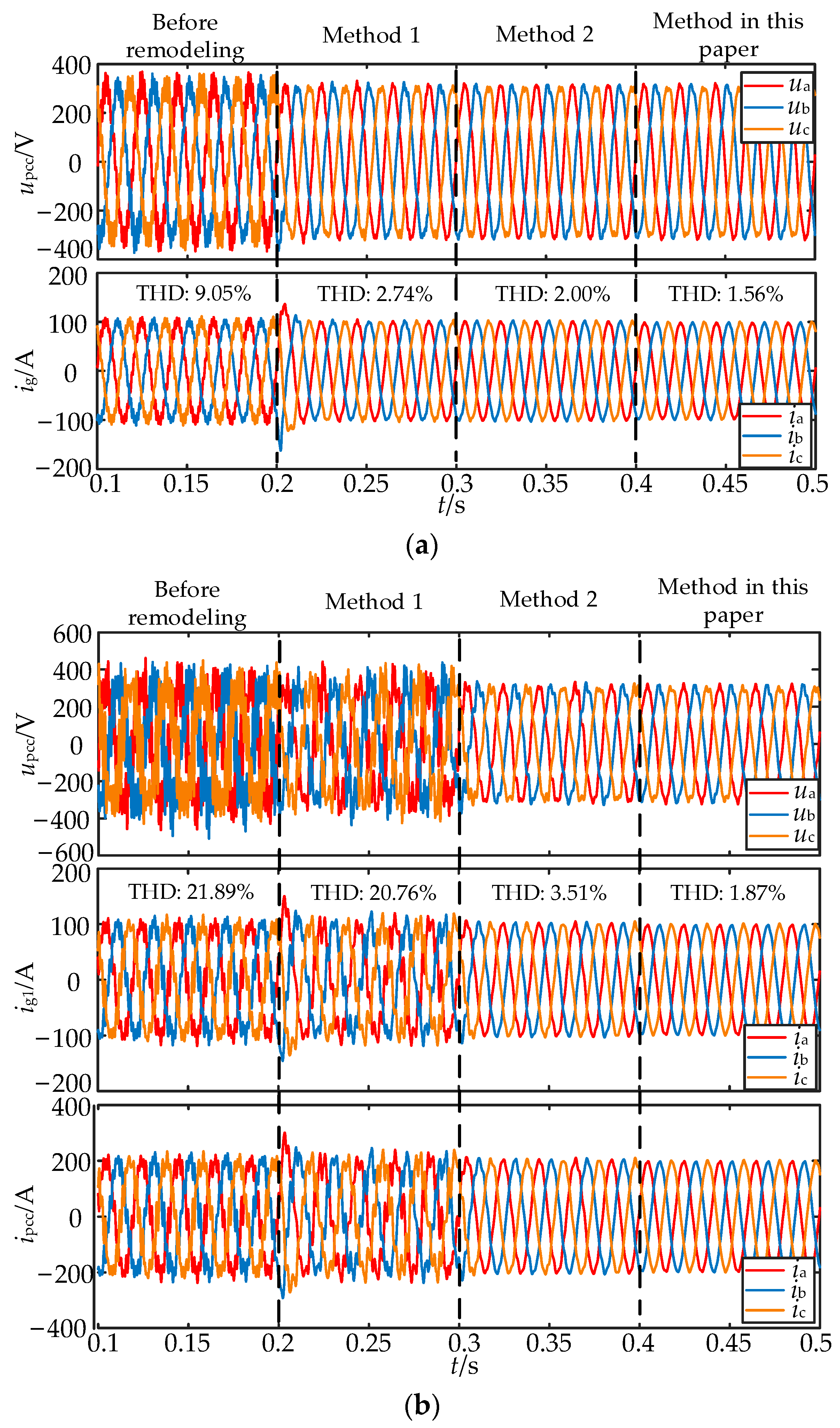
5.3. Comparison and Verification of Different Strategies
6. Conclusions
- (1)
- The high-frequency characteristics of the inverter tend to be filtered by the LCL filter to very small values until they are negligible. The harmonics of the inverter are mainly distributed at low frequencies.
- (2)
- The decomposed conductance model is more suitable for the modal analysis method for system resonance characterization than the traditional Norton circuit model, which can better reflect the response characteristics between the inverter and the grid. The modal analysis method can reflect the resonance information of the multi-inverter system.
- (3)
- The impedance remodeling method proposed in this paper is more suitable for resonance suppression of multi-inverter grid-connected systems in background harmonic scenarios than other schemes, and it can further reduce the output harmonic currents while meeting the engineering requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, E.; Zhang, N.; Hodge, B.; Wang, Q.; Kang, C.; Kroposk, B.; Xia, Q. The role of concentrating solar power toward high renewable energy penetrated power systems. IEEE Trans. Power Syst. 2018, 33, 6630–6641. [Google Scholar] [CrossRef]
- Hosseinzadeh, N.; Aziz, A.; Mahmud, A.; Gargoom, A.; Rabbani, M. Voltage stability of power systems with renewable-energy inverter-based generators: A review. Electronics 2021, 10, 115. [Google Scholar] [CrossRef]
- Joan, R.; Alvaro, L.; Frede, B. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar]
- Yu, J.; Lin, X.; Song, D.; Yu, R.; Li, Y.; Mei, S. Harmonic instability and amplification for grid-connected inverter with voltage harmonics compensation considering phase-locked loop. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3944–3959. [Google Scholar] [CrossRef]
- Zhong, P.; Sun, J.; Zhen, T.; Huang, M.; Yu, P.; Zha, X. An improved impedance measurement method for grid-connected inverter systems considering the background harmonics and frequency deviation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4236–4247. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A.M.; Ribeiro, P.F. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters. IEEE Trans. Power Electron. 2011, 26, 786–797. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Zou, R.; Li, Y. Harmonic resonance characteristic of large-scale PV plant: Modelling, analysis, and engineering case. IEEE Trans. Power Deliv. 2022, 37, 2359–2368. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, C.; Xu, Y.; Dong, Z.; Zhang, R. Multi-objective hierarchically-coordinated volt/var control for active distribution networks with droop-controlled PV inverters. IEEE Trans. Smart Grid 2022, 13, 998–1011. [Google Scholar] [CrossRef]
- Batzelis, E.I.; Papathanassiou, S.A. A method for the analytical extraction of the single-diode PV model parameters. IEEE Trans. Sustain. Energy 2016, 7, 504–512. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Q.; Li, Z.S. A dynamic bayesian network control strategy for modeling grid-connected inverter stability. IEEE Trans. Reliab. 2022, 71, 75–86. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Espin, F.G.; Figueres, E.; Garcera, G. An adaptive synchronous-reference-frame phase-locked loop for power quality improvement in a polluted utility grid. IEEE Trans. Power Electron. 2012, 59, 2718–2731. [Google Scholar]
- Mohammed, N.; Zhou, W.; Bahrani, B. Comparison of PLL-Based and PLL-Less Control Strategies for Grid-Following Inverters Considering Time and Frequency Domain Analysis. IEEE Access 2022, 10, 80518–80538. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Liserre, M. An active damper for stabilizing power-electronics-based AC systems. IEEE Trans. Power Electron. 2014, 29, 3318–3329. [Google Scholar] [CrossRef]
- Cao, W.; Ma, Y.; Wang, F. Sequence-impedance-based harmonic stability analysis and controller parameter design of three-phase inverter-based multibus AC power systems. IEEE Trans. Power Electron. 2017, 32, 7674–7693. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R. Inverse Nyquist stability criterion for grid-tied inverters. IEEE Trans. Power Electron. 2017, 32, 1548–1556. [Google Scholar] [CrossRef]
- Nie, C.; Lei, W.; Wang, Y.; Wang, H.; Feng, G. Resonance analysis of multi-paralleled converter systems and research on optimal virtual resistor damping methods. Proc. CSEE 2017, 37, 1467–1478. [Google Scholar]
- Chen, L.; Xu, Y.; Tao, S.; Wang, T.; Sun, S. Multi-inverter resonance modal analysis based on decomposed conductance model. Electronics 2023, 12, 1251. [Google Scholar] [CrossRef]
- Zou, C.; Liu, B.; Duan, S.; Li, R. Influence of delay on system stability and delay optimization of grid-connected inverters with LCL filter. IEEE Trans. Ind. Inf. 2014, 10, 1775–1784. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, X.; Liu, S.; Tse, C.K. Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics. IEEE Trans. Power Electron. 2010, 25, 3119–3127. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Yang, Z. Improved WACC weighted coefficient method for LCL grid-connected inverter considering the influence of voltage feedforward. Proc. CSEE 2018, 38, 5158–5166. [Google Scholar]
- Xu, J.; Cao, X.; Hao, Z. A Harmonic-current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage. Tran. China Electrotech. Soc. 2022, 37, 2018–2029. [Google Scholar]
- He, N.; Xu, D.; Zhu, Y.; Zhang, J.; Shen, G.; Zhang, Y.; Ma, J.; Liu, C. Weighted average current control in a three-phase grid inverter with an LCL filter. IEEE Trans. Power Electron. 2013, 28, 2785–2797. [Google Scholar] [CrossRef]
- Xu, J.; Xie, S.; Huang, R. A Robust current control strategy for grid-connected inverters with LCL filtered. Autom. Electr. Power Syst. 2012, 36, 99–104. [Google Scholar]
- Bonaldo, J.P.; Tofoli, F.L.; Monteiro, R.V.A.; Morales-Paredes, H.K. Comparative analysis of techniques for the limitation of compensation currents in multifunctional grid-tied inverters. Int. J. Electr. Power Energy Syst. 2021, 126, 106574. [Google Scholar] [CrossRef]
- Chilipi, R.; Sumaiti, A.A.; Singh, B. Control of Grid-Tied Multiple Distributed Generation Systems with Cooperative Compensation Capabilities. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 821–833. [Google Scholar] [CrossRef]
- Herbert, L.G.; Czarnecki, L.S. An Optimization based method for selection of resonant harmonic filter branch parameters. IEEE Trans. Power Deliv. 2006, 21, 1445–1451. [Google Scholar]
- Yang, T.D.; Ruan, X.; Wu, H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, A.; Hu, N. Resonance suppression strategy for multi-parallel grid-connected inverters. South. Power Syst. Technol. 2022, 16, 87–96. [Google Scholar]
- Li, S.; Lin, H. Passivity enhancement-based general design of capacitor current active damping for LCL-type grid-tied inverter. IEEE Trans. Power Electron. 2023, 38, 8223–8236. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Wang, S.; Yang, C.; Zhao, X. A Digital Delay Compensation Method to Improve the Stability of LCL Grid-Connected Inverters. Energies 2021, 14, 2730. [Google Scholar] [CrossRef]
- Domenico, S.; Silas, A.S.; Tofolib, F.L.; Leãoa, R.P.S.; Sombraa, A.K.R. An integrated design approach of LCL filters based on nonlinear inductors for grid-connected inverter applications. Electr. Power Syst. Res. 2020, 186, 106389. [Google Scholar]





| Methods | Realization | Advantages | Drawbacks |
|---|---|---|---|
| Passive damping method [22] | This is accomplished by connecting resistors in series or parallel to the inductive or capacitive branches of the LCL filter. | It is simple, easy to implement and effective | Energy losses due to passive damping resistors cannot be avoided. |
| Active damping method [29] | It is the virtualization of the damping resistor through the control algorithm that ensures the damping effect and avoids the energy consumption of the damping resistor. | A good suppression effect is achieved without additional energy loss. | The requirements for the inverter control circuit are very high. |
| Active damper method [30] | Active dampers are additional devices independent of the grid-connected inverter system. | It can be set independently without affecting the work of other inverters. | Research in resonance detection is not advanced enough to require additional construction and maintenance costs. |
| Impedance remodeling method [28] | Changing the system impedance destroys the resonance conditions of the system and thus acts as a resonance suppressor. | It will not add extra energy loss and can achieve a better suppression effect. | The algorithm is complex and demanding on the inverter control circuit. |
| Parameters | Symbol | Value |
|---|---|---|
| Power grid voltage | Ug/V | 220 |
| Power grid impedance | Lg/mH | 0.1 |
| Inverter side inductor | L1/mH | 1.2 |
| Grid-side inductance | L2/mH | 0.3 |
| Filter capacitor | C/μF | 28 |
| Quasi-proportional resonance controller parameters | kp | 3 |
| ki | 100 | |
| ωi/rad·s−1 | 5 | |
| Capacitive current feedback coefficient | Hi1 | 3 |
| Grid-connected current feedback coefficient | Hi2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Wang, J.; Zhang, S.; Gao, L.; Guo, X.; Chen, L.; Xu, Y. Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System. Electronics 2023, 12, 3684. https://doi.org/10.3390/electronics12173684
Zhang M, Wang J, Zhang S, Gao L, Guo X, Chen L, Xu Y. Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System. Electronics. 2023; 12(17):3684. https://doi.org/10.3390/electronics12173684
Chicago/Turabian StyleZhang, Min, Jinhao Wang, Shifeng Zhang, Le Gao, Xiangyu Guo, Lin Chen, and Yonghai Xu. 2023. "Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System" Electronics 12, no. 17: 3684. https://doi.org/10.3390/electronics12173684
APA StyleZhang, M., Wang, J., Zhang, S., Gao, L., Guo, X., Chen, L., & Xu, Y. (2023). Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System. Electronics, 12(17), 3684. https://doi.org/10.3390/electronics12173684





