Abstract
In view of the unstable electromagnetic performance of the air gap magnetic field caused by the torque ripple and harmonic interference of a multi-slot and multi-pole low-speed, high-torque permanent magnet synchronous motor, we propose a simplified model of double-layer permanent magnets. The model is divided into an upper and a lower subdomain, with the upper subdomain being an ideal circular ring and the lower subdomain being a segmented sector ring. Moreover, we develop an exact analytical model of the motor that predicts the magnetic field distribution based on Laplace’s and Poisson’s equations, which is solved using the method of separating variables. Taking a 40p168s low-speed, high-torque permanent magnet synchronous motor as an example, the accuracy of the model is verified by comparison with an ideal circular ring model, a segmented sector ring model, and the finite element method. Based on the proposed simplified model, three combined permanent magnets considering both edge-cutting and polar arc cutting structures are proposed, which are chamfered, rounded, and rectangular combinations. Under the premise of a consistent edge-cutting amount, the electromagnetic characteristics of the three combination types of permanent magnets are compared using the finite element method. The results show that the electromagnetic characteristics of the chamfered combination PM are superior to those of the other two combinations. Finally, a prototype is manufactured and tested to validate the theoretical analysis.
1. Introduction
Direct-drive, low-speed, and high-torque permanent magnet synchronous motors (LHPMSMs) are increasingly used in industrial applications, such as wind power generation, hydro generators, and mine transportation, due to the advantages of high efficiency, low energy consumption, and high power density [1,2,3]. However, LHPMSMs also have multiple poles and multiple slots, as well as low assembly accuracy [4,5,6]. Therefore, in the motor design process, larger design margins are often needed to compensate for the performance losses caused by these errors. This inevitably leads to an increase in effective material usage and manufacturing costs.
An Integrated LHPMSM for a mine hoist was proposed in [7]. The mechanical transmission structure of the motor does not adopt a reducer and coupling. Consequently, the volume and assembly cost of the motor can be significantly reduced. However, the motor has a large outer diameter and axial length, which will give rise to a multi-pole and axial segmented arrangement to improve the utilization of permanent magnets (PMs). Moreover, the outer diameter of the stator core will also be large to reduce magnetic leakage. Therefore, the shapes of PMs and stator slots have more significant impacts on the electromagnetic performance of the system, such as through cogging torque, torque ripple, and eddy current loss compared to small- and medium-sized motors.
Many optimization methods for PMs have been developed to reduce cogging torque. These can be summarized into two categories: the spatial arrangement of PMs and the shape design of PMs. For the former, the segmented skewed magnetic pole is an effective method by which to reduce cogging torque and torque ripple [8], but the function will be greatly weakened as the degree of motor saturation increases, and this can have a negative effect [9]. Therefore, it is also essential to optimize both the tilt angle and the current phase lead angle so that an effective result can be obtained. In [10], an axial arrangement model of PMs with unequal pole arc coefficients was studied. A calculation model for the cogging torque of uniformly segmented PMs and axially unequal pole arc coefficient segmented PMs was proposed based on the analytical method. The effects of different combinations of skewed angles and pole arc coefficients on the cogging torque were compared, and the results show that the latter can significantly reduce the fundamental wave component of the cogging torque. However, the assembly cost of this method will rise evidently with the number of PMs. In this article, congruent PMs with a uniformly segmented axis are adopted.
The shape design of the PMs can be summarized into two types: pole arc cutting and pole edge cutting. In respect of the former, an analytical model for cogging torque was established in [11], which implied that the amplitude of the cogging torque is positively correlated with the fifth power of the ratio of the actual thickness of PMs to their maximum thickness. Therefore, a concentric tile-shaped PM has the maximum cogging torque. Namely, the cogging torque can be effectively reduced by changing the magnetization thickness of the PM. In [12], outer arc eccentric pole-shaped PMs and inner arc eccentric pole-shaped PMs were presented, and it was suggested that the thickness of the PM can change the amplitude of the air gap flux density, while the eccentricity can affect its spatial distribution. However, the relationship between the two parameters was not clarified. In [13], the eccentric PM subdomain is equivalent to a multi-segment ideal circular ring with radial non-uniform thickness, and a magnetic field prediction model is established based on the SD method. However, this model is more suitable for situations where the number of PMs is small, the width is large, and the pole arc coefficient is large. In [14], an eccentric PM magnetic field prediction model with regular edges is established using an improved conformal mapping method, which can significantly improve the calculation accuracy of the armature reaction magnetic field and the load air gap magnetic field. However, this method is only applicable to the case of parallel magnetization of PMs. Moreover, when the edge lines of the PM are irregular, it will be difficult to represent the coordinates of the mapping points. In [15], an eccentric surface-inset Halbach magnet is proposed for solving the magnetic fields in a brushless permanent magnet. Using a subdomain model with an equivalently split method, the 2D magnetic fields in the surface-inset PM machine with eccentric Halbach magnets are analytically derived. Compared with the finite element model, the magnetic field prediction model obtained using the equivalently split method has high accuracy. In [16], a hybrid analytical model combining the subdomain method is presented. The rectangular spoke magnets, eccentric magnetic poles, and rotor slots are approximated using multiple layers of ideal arc-shaped subdomains. The analytical results match well with the FEM and experiment results, and the error of the calculation is less than 5%. In [17], an eccentric PM with parallel edges is studied based on the aforementioned two types of PMs. The effects of the magnetization angle, pole arc width, and inner arc radius on the electromagnetic characteristics are studied using the multi-objective optimization design method, and it is shown that the cogging torque, unbalanced magnetic pull (UMP), and torque ripple can be effectively suppressed by the proposed PM. In [18], a PM cutting structure with the same radius of the inner arc and the outer arc is proposed. It is suggested that when the eccentric distance is equal to the maximum magnetization thickness of the PM, not only can the amount of PMs be reduced, but the total harmonic distortion (THD) of the air gap flux density and the cogging torque can also be significantly weakened. In addition, other methods, such as sine cutting [19,20], inverse cosine cutting [21], and third harmonic cutting [22,23], can also improve the air gap magnetic flux density waveform toward a sinusoidal distribution, thereby reducing its low harmonic content and decreasing the cogging torque and torque ripple. However, for a multi-pole LHPMSM, the complex shape of PMs will greatly increase the production cost, with a large amount of material waste. Therefore, the eccentric PM described in [17,18] is suitable for an integrated LHPMSM. Nevertheless, the cutting amount of the PM will decrease if the magnetization thickness of the PM is much smaller than the diameter of the inner and outer arcs so that the weakening effect on the cogging torque will also be reduced.
In terms of PM edge cutting, three types of PM with different edge shapes, i.e., chamfered cutting, circular internal cutting, and rounded cutting, are proposed in [24]. The influence of the key parameters of the three structures on the cogging torque is analyzed. The results show that the chamfered PM has the best weakening effect on the cogging torque. In [25], it is shown that a tile-shaped PM with chamfered edges can effectively reduce the torque ripple under different load conditions. However, a magnetic field model of the PMs is not established, which is essential to the design and optimization. In [15,26,27], the eccentric magnetic pole is equivalent to N segments of micro-units with equal thickness and equal electrical angle, and the magnetization strength of the PM can be obtained using the superposition method. Then, the magnetic vector potential of the PM subdomain can be derived. The same method is applied to a chamfered PM in [28]. Since the relative permeability of the PM is close to that of air, the PM subdomain is usually regarded as an ideal circular ring when calculating the magnetic vector potential. For eccentric magnetic poles, geometric relationships are usually employed to calculate the magnetization thickness of the PM as a function of the electrical angle, and then the air gap magnetic flux density function is derived using the air gap magnetic permeability method. Therefore, in this article, we consider a situation where the arc diameter of the PM in an LHPMSM is much larger than the magnetization thickness, and a simple model of the magnetization thickness function is proposed.
The rest of this paper is organized as follows. Section 2 introduces the structure of the LHPMSM, as well as the exact SD model of the motor. Section 3 describes the modeling process of magnetic fields in double-layer subdomains, as well as the rest of the SD model. In Section 4, the accuracy of the analytical model in Section 3 is verified using the finite element method (FEM). Next, in Section 5, three composite cutting PMs that meet the requirements of the simplified model are proposed, and the electromagnetic characteristics of the three structures are compared. Moreover, the influence of the composite structural parameters of the PM is analyzed, and the optimal structure is obtained under the same cutting amount condition. The fabrication and testing of a 40-pole/168-slot prototype is discussed in Section 6. Conclusions are drawn in Section 7.
2. Structure and Analytical Model
2.1. The Structural Composition of LHPMSM
Figure 1 shows the three-dimensional (3D) structure of a 168-slot/40-pole LHPMSM for a mine hoist. The rotor system consists of rollers, support structures, and bearings. There are four sets of brakes on both sides of the rotor system. The stator system consists of a stator core, a main shaft, and an adapter flange. The two sides of the main shaft adopt hexagonal anti-torsion structures with interference fitting, which are assembled with a bearing seat that is fixed on the ground. Two air-cooled channels are installed on one side of the stator system. Figure 2 depicts the axial segmented arrangement and the permanent magnet fixed with non-magnetic wedge blocks. Figure 3 displays the shape of the stator slot.
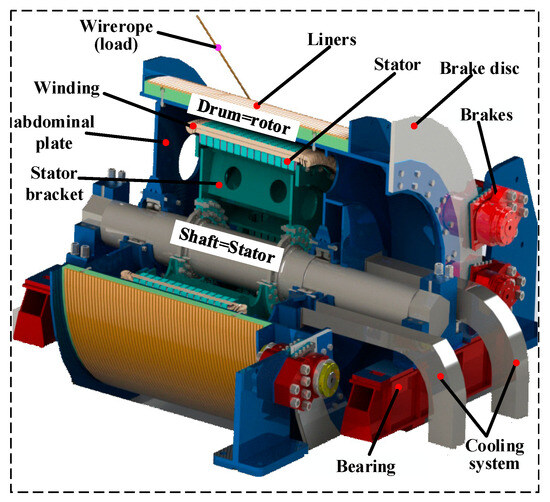
Figure 1.
Three-dimensional structure of the LHPMSM.

Figure 2.
Axial uniform segmented PMs in the LHPMSM.

Figure 3.
Stator slots of the LHPMSM.
2.2. Analytical Model
Figure 4a presents the eccentric cutting of the outer pole arc PM model for which the radius of the outer arcs RA and the inner arcs RB of the PMs are equal. Moreover, the maximum radial magnetization thickness hm and eccentricity eAB of the PM are equal. It is clear that the magnetization thickness ab of the PM varies with θpm, which can be given by
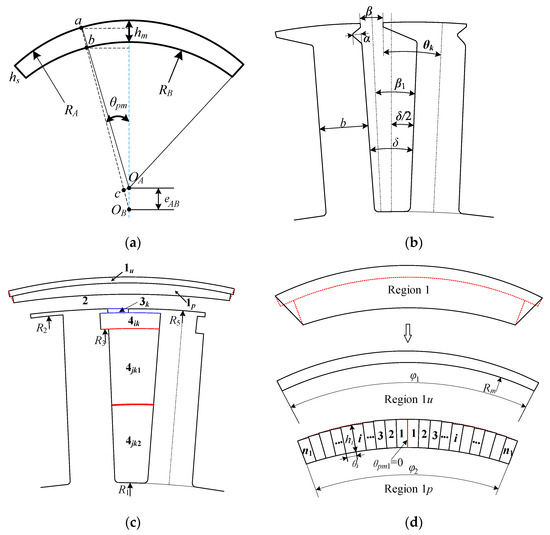
Figure 4.
Several PM models. (a) PM for eccentric cutting of outer pole arc; (b) single asymmetric stator slot model; (c) solution domain of the motor; (d) simplified model of the PM region.
The arc diameter RA is much larger than the magnetization thickness hm or the eccentricity eAB, RA >> eAB. Therefore, Equation (1) can be equivalent to a simple sine function related to eAB and θpm:
Figure 4b depicts the single stator slot parametric model, which has a semi-open slot structure. The slot opening and the slot body for installing magnetic slot wedges comprise the asymmetric structure. As shown in Figure 4c, to facilitate modeling, the irregular region in the slot is simplified as the sector annular area and we define the asymmetry of the slot opening λ and the asymmetry of the inside slot ξ, which can be expressed as in [7].
where α is the angle of the U-shaped groove inside the slot, °; δ is the slot angle, °.
Figure 4c shows the subdomains of the motor, which including five regions: PMs, air gap, asymmetric slot opening, asymmetric slot body, and symmetrical slot body, denoted by subdomains 1u, 1p, 2, 3k, 4ik, 4jk1, 4jk2. The parameters in the model are the radius of the slot bottom, R1, inner radius of the slot opening, R2, outer radius of the symmetrical slot body, R3, inner radius of PMs, RB, outer radius of the slot opening, R5, outer radius of the PMs, RA, and the initial position of the kth slot, θk.
Furthermore, considering the edge cutting of PMs, there is not always an ideal fan-ring structure. We divided the PM region into double-layer subdomains, with the upper layer being an ideal fan ring and the lower layer being a pole arc cutting structure without considering edge cutting. However, the center angles of the two regions are different. As shown in Figure 4a,d, the intersection points of the Region 1u and Region 1p edges are OA, and the center angles are φ1 and φ2, respectively. Region 1p can be divided into 2n1 segments with equal center angles θi, the thickness of the ith segment is hi, and θ and hi are satisfied:
where αp is the pole arc coefficient of Region 1p; Rm is the inner arc radius of Region 1u, mm.
3. Modeling and Analysis of Magnetic Fields
To simplify the analysis process, the following assumptions have been made: (1) the end effect is neglected; (2) the PMs adopt radial magnetization; (3) the permeability of the stator iron is infinite; (4) the saturation effect is neglected. According to (3) and (4), θk and β can be rewritten as
The sth region magnetic vector potential As satisfies the following control function as
where μ0, Mrs, and Js are the permeability of the vacuum, the radial component of magnetization in the PM region, and the current density in the slot region, respectively.
The analytical solutions of As can be expressed as follows [29]:
where As0, Bs0, Asn, Bsn, Csn, and Dsn are integral constants; fsa and fsb are functions of r; θs is the angle of the sth subdomain and θs = θ − θs0, where θs0 is the initial phase angle of the sth subdomain, °; ηs is the Fourier series period. The fsa, fsb, and ps can be expressed as follows
where RsO and RsI are the outside semidiameter and inside semidiameter of the sth regions, mm, respectively.
3.1. PM Region
According to (10), the magnetic vector potential A1u expressions of Region 1u are given by
where Mru is the radial component of the magnetization vectors in Region 1u, A/m, which can be expressed by
The PM in Region 1p is segmented into 2n1 uniform pieces. The magnetic vector potential A1pi expressions of Region 1p can be expressed by
The magnetization vectors of the ith piece can be expressed by
where Mrpi is the radial component of the magnetization vectors of the ith piece in Region 1p, A/m; n/p = 1, 3, 5, …; αpi is the pole arc coefficient of the ith piece, αpi = αp/2n.
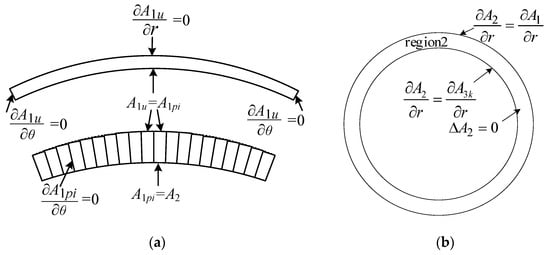
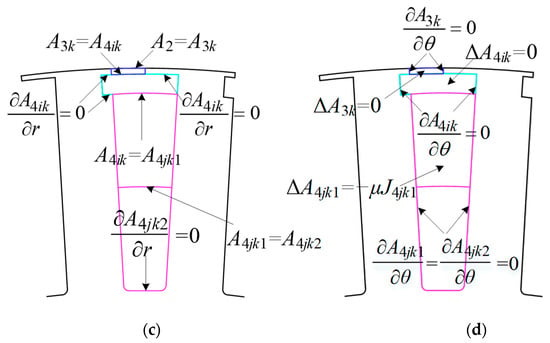
Figure 5.
Boundary conditions. (a) PM region; (b) air gap region; (c) radial asymmetric slot opening and slot body region; (d) circumferential asymmetric slot opening and slot body region.
The analytical solutions of A1u and A1pi can be derived as
3.2. The Other Regions
According to (9), the magnetic vector potential expressions of the air gap subdomain, the asymmetric slot opening subdomain, the asymmetric slot body region, and the symmetrical slot body region can be expressed as follows:
where J4jk1 and J4jk2 denote the current density, A/m2.
In Figure 5b–d, the boundary conditions of Region 2, Region 3k, Region 4ik, Region 4jk1, and Region 4jk2 can be written as
where , mm.
On the basis of (10), the general solution of vector potentials A2, A3k, A4ik, A4jk1, A4jk2 can be derived as
The integral constants of Region 1u and Region 1p, and Region 1p and Region 2, are shown in Appendix A. The integral constants of the other regions are given in [7].
3.3. Cogging Torque
In the polar coordinate system, the magnetic flux density can be obtained by
where Brs and Bθs are the radial and tangential flux density at the radius r of the sth region, respectively, T.
Based on the Maxwell stress tensor method, a circle with the semidiameter of rag in the air gap region is regard as the path of integration. The cogging torque can be calculated as follows:
where Lef is the axial length of the stator, mm; rag is the semidiameter of the air gap, mm.
4. FEM Results and Comparative Analysis
In order to validate the presented theoretical research, an LHPMSM with outer arc eccentric pole-shaped PMs and asymmetric slots was chosen for the prototype. Three analytical models, the ideal circular ring model (AM1), the direct segmented model (AM2), and the proposed double-layer model (AM3), were adopted to compare the air gap flux density with the FEA models at no-load and on-load conditions. The FEA models of the prototype and mesh density are given in Figure 6. Structural parameters of the prototype are shown in Table 1. Operating parameters of the machine are described in Table 2. The materials of PMs and stator cores are NdFeB35 and DW465-50, respectively. The grade of the PMs is N38SH. The specific simulation process is as follows:
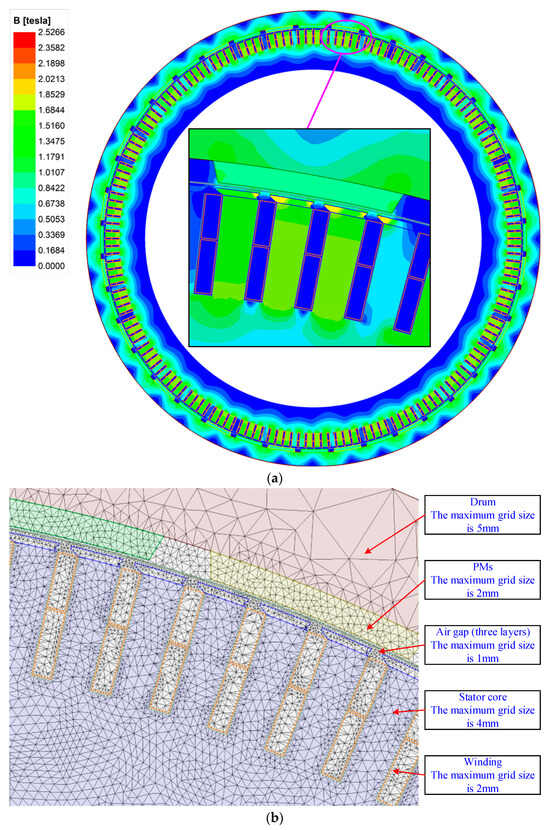
Figure 6.
FEM of prototype. (a) Magnetic flux distribution; (b) mesh density.

Table 1.
Specification of the prototype.

Table 2.
Operating parameters of prototype.
- (1)
- Establish the FEM of the prototype based on the parameters shown in Table 1. Magnetostatic analysis is conducted to obtain the calculation results the air gap flux density under no-load conditions.
- (2)
- During the transient analysis process, set the prototype operating parameters shown in Table 2 and add ideal three-phase alternating current excitation. The radial and tangential air gap magnetic flux density and electromagnetic torque under load conditions can be obtained.
- (3)
- Still conducting the analysis in transient mode, removing the excitation source, modifying the speed to 1 r/s, and dividing the air gap domain into three layers with a maximum grid size of 1 mm, the distribution of the cogging torque can be obtained.
4.1. Air Gap Flux Density
Three sets of AM and FEM results for the radial and tangential flux density at r = 826.5 mm under no-load conditions are illustrated in Figure 7. In Figure 7a,b, the air gap flux density waveforms obtained using the AMs and FEM have a higher degree of coincidence under no-load conditions. Therefore, all three AMs can accurately predict the magnetic field characteristics of the motor. However, the slotting effect can cause distortion of the flux density waveforms. Peaks and troughs of AM1 are slightly higher than those of AM2 and AM3 in some special locations. Due to AM1 not considering the shape of the PM, this gives rise to the radial component of the magnetization vector of the PM being higher than that of AM2 and AM3. In addition, the waveforms of AM2 and AM3 only have differences at the ends of the flat top position of the curve, as the latter takes into account the edge shape of the PM.
where B1 is the fundamental amplitude of the air gap flux density, T; B2ν+1 denotes the (2ν + 1)th harmonic contents of the air gap flux density, T.
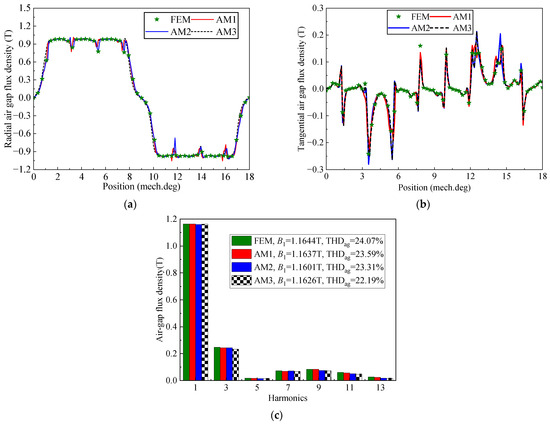
Figure 7.
Air gap flux density of three AMs and FEM under no-load conditions: (a) radial; (b) tangential; (c) harmonic analysis.
The harmonic analysis results of the air gap flux density for the three AM models and FEM under no-load conditions are shown in Figure 7c. The AM1 has the highest fundamental amplitude of the air gap flux density compared to the other three models. The fundamental amplitude and lower harmonic amplitude values of AM2 are similar to the FEM results, which is consistent with the research results in [25]. The harmonic amplitude of the air gap flux density of AM3 is slightly lower than those of the other three models, which is related to the values of Rm and φ2. Therefore, the effects of these two parameters on the electromagnetic characteristics are discussed in Section 5. Furthermore, the total harmonic distortion (THD) rates of the air gap flux density for AM1, AM2, AM3, and the FEM can be calculated using (51); these are 23.59%, 23.31%, 22.19% and 24.07%, respectively. It can be seen that the THD comparison results are consistent with B1.
Figure 8a,b displays the AMs and FEM results for the radial and tangential flux density in the middle of at r = 826.5 mm under on-load conditions. The waveform distortion at the tip of the stator teeth is more severe than under no-load conditions, which is due to the more significant impact of the armature reaction compared to the no-load conditions. The result is also demonstrated in the harmonic analysis of Figure 8c. The THDag values of the air gap flux density for AM1, AM2, AM3, and FEM can be calculated using (51); these are 32.53%, 32.12%, 30.98%, and 31.27%, respectively. Moreover, the B1 under on-load conditions is higher than under no-load conditions.
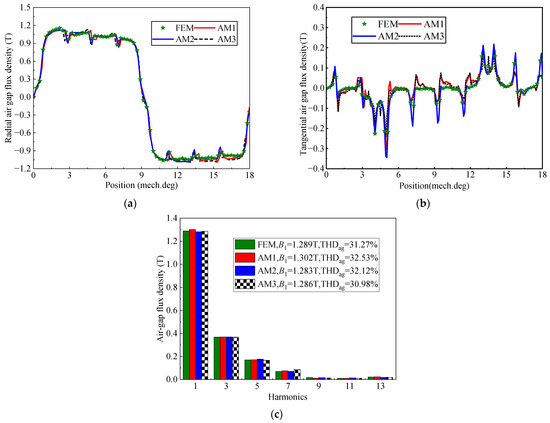
Figure 8.
Air gap flux density of three AMs and FEM under on-load conditions: (a) radial; (b) tangential; (c) harmonic analysis.
4.2. Torque Characteristics
The LHPMSM often bears heavy loading and vibration during operation. Consequently, the motor requires an excellent output stability, which depend on the low torque ripple ratio. However, the cogging torque can bring about significant torque ripple, especially at low speeds.
Figure 9a shows the electromagnetic torque of the three AMs and FEM. The average electromagnetic torques of the AM1, AM2, AM3, and FEM are 2.233 kN·m, 2.146 kN·m, 2.199 kN·m, and 2.199 kN·m, respectively. The corresponding torque ripples of the four models are 2.48%, 2.86%, 2.26%, and 2.73%, respectively.
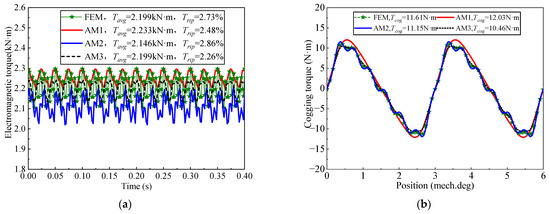
Figure 9.
Electromagnetic characteristics of three AMs and FEM: (a) electromagnetic torque; (b) cogging torque.
Figure 9b depicts the cogging torque of the three AMs and FEM. The peak values of the cogging torque of the AM1, AM2, AM3, and FEM are 11.15 N·m, 11.61 N·m, 10.46 N·m, and 12.03 N·m, respectively. The cogging torque Tcog of the four models are similar to B1.
5. Edge Cutting Models for PM
Three combination models based on AM3 with the eccentric cutting of the outer pole arc PM model are proposed in this article. The structures have the same polar arc coefficient and edge thickness with different cutting shapes at the edges of the inner arc, which are chamfer cutting, rectangular cutting, and fillet cutting. As shown in Figure 10, the chamfer shape in Figure 10a can be approximated as a right-angled triangle, where the cutting angle is θcf and the cutting width is lcf. The chamfer shape in Figure 10b can be regarded as rectangular, where the length and width are lc and lw, respectively. As shown in Figure 10c, the chamfer shape can be considered equivalent to a quarter circle, where the radius is Rcm. The edge cutting amounts of the three types are equal, with the edge structural parameters given by Equation (52). Obviously, there are countless parameter combinations that meet the conditions. However, a magnetic field prediction model with any edge cutting size can be obtained by controlling Rm and φ2 in the proposed model. Therefore, we adopt the multi-objective optimization design method proposed in [30], where Rm and φ2 are set as optimization variables, and the average value of the electromagnetic torque, the peak value of the cogging torque, and the THD of the no-load back electromotive force are set as objective functions. The optimal parameter combination was obtained as φ2 = 7.125°, Rm = 834 mm, and the edge cutting dimensions of the three PMs are shown in Table 3.
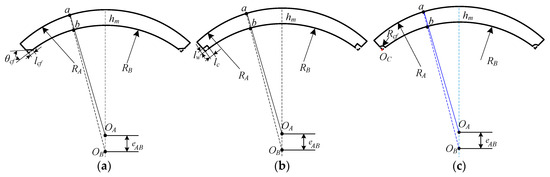
Figure 10.
Edge cutting models for the eccentric cutting of the outer pole arc: (a) chamfer cutting; (b) rectangular cutting; (c) fillet cutting.

Table 3.
Edge cutting parameter combinations of three types of combined PMs.
Figure 11a,b shows the air gap flux density and the harmonic analysis for three types of combined PMs. It can be seen that there are slight differences in the radial and tangential air gap magnetic flux density at the slot opening, with the waveform of the chamfer-cutting PM transitioning smoother compared to the other two types. This is because the change in unit thickness of the chamfer-cutting PM is smoother. The rectangular cutting type has a sudden change in the thickness of the PM, which can cause a deeper “depression” in the waveform at the slot opening, resulting in more severe distortion of the air gap magnetic field. From Figure 11c, the fundamental amplitudes of the air gap flux density for the chamfered cutting, rounded cutting, and rectangular cutting are 1.165 T, 1.165 T, and 1.162 T, respectively. The total harmonic distortion rates (THDag) of the air gap magnetic flux density obtained from Equation (52) are 23.4%, 23.9%, and 24.5%, respectively.
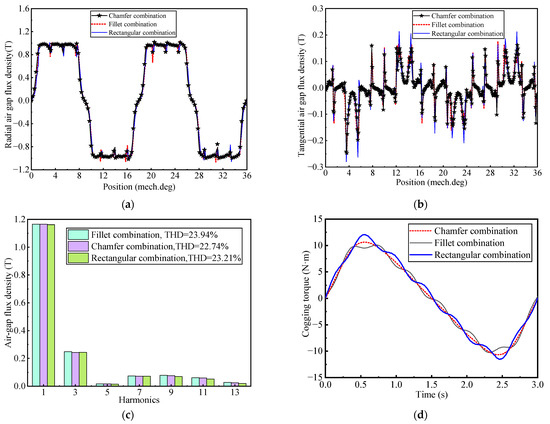
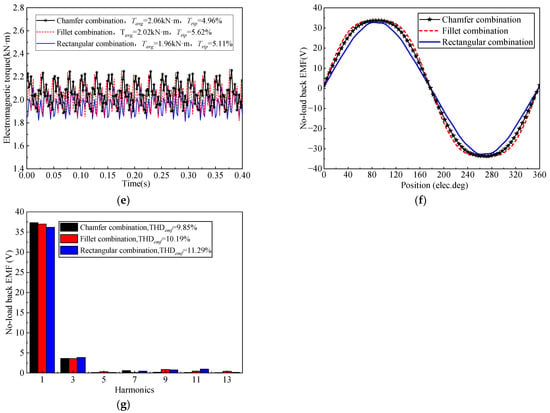
Figure 11.
Electromagnetic characteristics for three types of combined PMs: (a) radial air gap flux density; (b) tangential air gap flux density; (c) harmonic analysis of air gap flux density; (d) cogging torque; (e) electromagnetic torque; (f) no-load back EMF; (g) harmonic analysis of no-load back EMF.
Figure 11d illustrates the electromagnetic torque analysis of three types of combined PMs. It can be observed that the maximum electromagnetic torque of the chamfer cutting is 45.58 kN·m, which is slightly higher than the 44.29 kN·m of the fillet cutting and the 44.21 kN·m of the rectangular cutting. Meanwhile, the torque ripple of the chamfer cutting is 4.96%, which is also slightly lower than those of the other two types. This proves that the chamfer-cutting PM can yield higher electromagnetic torque and have lower torque ripple under the same usage.
Figure 11e depicts a comparative analysis of the cogging torque of three types of combined PMs. As can be seen, the peak values of cogging torque that are derived from the chamfer cutting, rectangular cutting, and fillet cutting are 10.09 N·m, 12.06 N·m, and 10.46 N·m, respectively. This is mainly because the change in magnetic field energy on both sides of the chamfer cutting PM is relatively gentle compared to the other two types. The magnetic field energy of the edges of the rectangular-cutting PM undergoes sudden change. The magnetic field energy changes more sharply at the edges of the fillet-cutting PM. Therefore, the lowest cogging torque is generated by the chamfer-cutting PM under the same usage.
Figure 11f shows the no-load back EMF results of three types of combined PMs. It can be seen that the amplitudes of chamfer cutting, rectangular cutting, and fillet cutting are 33.81 V, 33.69 V, and 32.76 V, respectively. In addition, the harmonic analysis results are shown in Figure 11g; the THD values of the no-load back EMF for three types of combined PMs are 9.85%, 10.19%, and 11.29%, respectively.
In summary, comparisons of electromagnetic characteristics for three types of combined PMs are shown in Table 4.

Table 4.
Comparison of electromagnetic characteristics for three types of combined PMs.
6. Experimental Results
To confirm electromagnetic characteristics of the motor, a prototype of LHPMSM was manufactured according to Table 1 and the optimized results. As predicted in Figure 12, the experimental platform consists of the prototype, worktop, hydraulic system, electric source, frequency transformer, power analyzer, current Sensor, and encoder.

Figure 12.
Testing platform of the LHPMSM prototype.
The outer surface of the rotor was not winding the steel wire rope, which could be regarded as no-load working conditions. The chamfered combination PMs was adopted. The frequency transformer was set to the LOCAL mode, and signal were transmitted to the computer through a Bluetooth interface; the encoder signals were received, filtered, and converted by the control board to the oscilloscope through an Ethernet cable.
The LHPMSM was operated at 26.5 r/min and the no-load back-EMF can be seen in Figure 13. It was found that the proposed chamfered combination PM has sinusoidal and symmetric no-load back EMF. Therefore, the measured waveform confirms the simulation result given in Figure 11f.
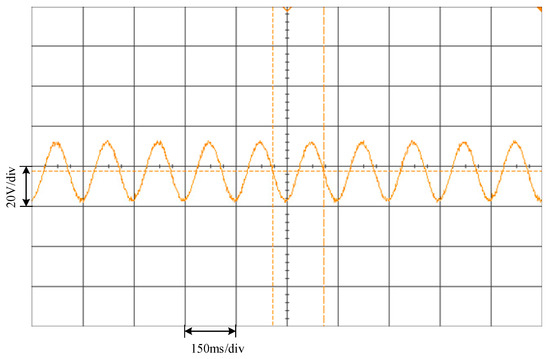
Figure 13.
Measured no-load back EMF at 26.5 r/min (phase A).
In Figure 14, it can be seen that the amplitude of phase current is 60 A. The electromagnetic torque test results of the motor are described in Figure 15, with the torque ripple is about 5.15% during the stable operation of the prototype. The error between the simulation result and the experimental result is about 3.6%, which verifies the correctness of the FEA result.
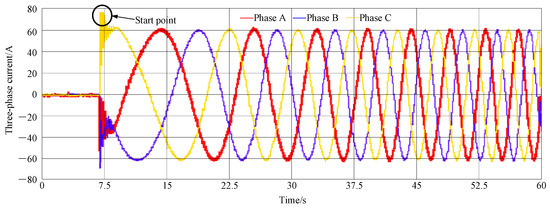
Figure 14.
Measured three-phase currents.
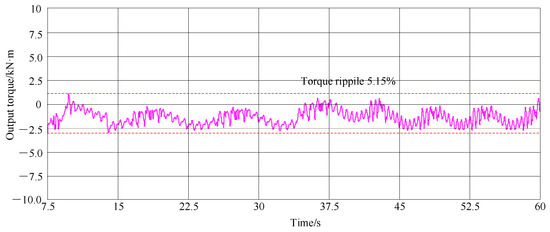
Figure 15.
Measured electromagnetic torque under no-load conditions.
7. Conclusions
A dual-layer simplified model for the eccentric cutting of an outer pole arc PM was proposed, which can simplify the irregular boundaries of the PM into upper and lower regular edges. By optimizing the inner ring radius of the upper subdomain and the center angle of the lower subdomain, a simplified model with any edge shape can be obtained. Compared with traditional ideal circular ring, segmented fan ring, and finite element models, this model also has high accuracy in magnetic field prediction. Three application forms based on this simplified model were presented, including three combined chamfer, fillet, and rectangle shapes with an eccentric cutting of the outer pole arc PM. The electromagnetic characteristics of the three types of PMs were compared using the FEM, and the results show that the chamfer combination PM is the best choice. The prototype was manufactured and the theoretical analysis was validated through experiments. The following conclusions were obtained:
- (1)
- Compared to the ideal circular ring model (AM1) and segmented circular ring model (AM2), the dual-layer permanent magnet simplified model (AM3) shows a higher degree of agreement with the FEM. Its average electromagnetic torque is equal to the FEM calculation result, but the torque ripple is the lowest among the four models (the average electromagnetic torque values for AM1, AM2, AM3, and FEM are 2.233 kN·m, 2.146 kN·m, 2.199 kN·m, and 2.199 kN·m, respectively; the torque ripple values are 2.48%, 2.86%, 2.26%, and 2.73%, respectively). Moreover, the THD of the air gap flux density of AM3 is the lowest under both no-load and load conditions.
- (2)
- Under the premise of the same amount of PM usage, the chamfered combination PM has superior electromagnetic characteristics. Specifically, the THD of the air gap flux density is 2% and 4% lower than the fillet and rectangular combinations, the average electromagnetic torque is higher by 1.9% and 4.8%, the torque ripple is lower by 11.7% and 2.9%, and the cogging torque is lower by 16.3% and 5.1%.
Author Contributions
S.K.: Simulation, writing review and editing, Visualization. Z.K.: Conceptualization, Supervision, Methodology, Funding acquisition, Project administration; J.W.: Funding acquisition, Project administration; Y.W.: Formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (grant no. 52274156), National Natural Science Foundation of China (grant no. 52205120), Guizhou science and technology support plan projects (grant no. Guizhou science and technology cooperation support (2022) general 004), Shanxi province raised funds to support the scientific research projects of the returned overseas person (grant no. 2021-049).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Appendix A. Integration Constants
- (1)
- Region 1u and Region 1p
On the basis of (11)–(14) and (16), the following expression can be derived:
Interface condition (17) can be rewritten as
According to (11)~(14) and (A2), the following equations can be obtained:
- (2)
- Region 1p and Region 2
On the basis of (13), (14), (20), (23), (24) and (42), the following equations can be obtained:
where
The Boundary condition (21) can be expanded as
where μr is the relative permeability.
According to (23), (24) and (A6), (A4) and (A5) can be simplified as
where
References
- Lu, E.; Li, W.; Yang, X.F.; Xu, S.Y. Composite Sliding Mode Control of a Permanent Magnet Direct-Driven System for a Mining Scraper Conveyor. IEEE Access 2017, 5, 22399–22408. [Google Scholar] [CrossRef]
- Tlali, P.M.; Wang, R.J.; Gerber, S.; Botha, C.D.; Kamper, M.J. Design and Performance Comparison of Vernier and Conventional PM Synchronous Wind Generators. IEEE Trans. Ind. Appl. 2020, 56, 2570–2579. [Google Scholar] [CrossRef]
- Sheng, L.C.; Li, W.; Wang, Y.Q.; Fan, M.B.; Yang, X.F. Sensorless Control of a Shearer Short-Range Cutting Interior Permanent Magnet Synchronous Motor Based on a New Sliding Mode Observer. IEEE Access 2017, 5, 18439–18450. [Google Scholar] [CrossRef]
- Crider, J.M.; Sudhoff, S.D. An Inner Rotor Flux-Modulated Permanent Magnet Synchronous Machine for Low-Speed High-Torque Applications. IEEE Trans. Energy Convers. 2015, 30, 1247–1254. [Google Scholar] [CrossRef]
- Popescu, M.; Staton, D.A.; Jennings, S.; Schnüttgen, J.; Barucki, T. A Line-Fed Permanent-Magnet Motor Solution for Drum-Motor and Conveyor-Roller Applications. IEEE Trans. Ind. Appl. 2013, 49, 832–840. [Google Scholar] [CrossRef]
- Song, Y.D.; Zhang, Z.Y.; Yu, S.Y.; Zhang, F.G.; Zhang, Y. Analysis and Reduction of Cogging Torque in Direct-Drive External-Rotor Permanent Magnet Synchronous Motor for Belt Conveyor Application Cogging Torque Reduction of ERPMSM. IET Electr. Power Appl. 2021, 15, 668–680. [Google Scholar] [CrossRef]
- Kou, S.K.; Kou, Z.M.; Wu, J.; Wang, Y.D. Modeling and Simulation of a Novel Low-Speed High-Torque Permanent Magnet Synchronous Motor with Asymmetric Stator Slots. Machines 2022, 10, 1143. [Google Scholar] [CrossRef]
- Chu, W.Q.; Zhu, Z.Q. Reduction of On-Load Torque Ripples in Permanent Magnet Synchronous Machines by Improved Skewing. IEEE Trans. Magn. 2013, 49, 3822–3825. [Google Scholar] [CrossRef]
- Chu, W.Q.; Zhu, Z.Q. Investigation of Torque Ripples in Permanent Magnet Synchronous Machines with Skewing. IEEE Trans. Magn. 2013, 49, 1211–1220. [Google Scholar] [CrossRef]
- Wang, H.M.; Guan, P.J.; Liu, S.; Wu, S.; Shi, T.N.; Guo, L.Y. Modeling and Analyzing for Magnetic Field of Segmented Surface-Mounted PM Motors with Skewed Poles. J. Electr. Eng. Technol. 2022, 17, 1097–1109. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.H.; Zhang, C.; Liu, L.; Wang, X.Z. Cogging Torque Reduction in External-Rotor Permanent Magnet Torque Motor Based on Different Shape of Magnet. In Proceedings of the 2017 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Ningbo, China, 19–21 November 2017; pp. 304–309. [Google Scholar]
- Chen, Z.F.; Xia, C.L.; Geng, Q.; Yan, Y. Modeling and Analyzing of Surface-Mounted Permanent-Magnet Synchronous Machines with Optimized Magnetic Pole Shape. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Xing, Z.Z.; Wang, X.H.; Zhao, W.L. Electromagnetic Vibration Reduction of Surface-Mounted Permanent Magnet Synchronous Motors Based on Eccentric Magnetic Poles. J. Electr. Eng. Technol. 2023, 18, 3603–3614. [Google Scholar] [CrossRef]
- Ding, Z.A.; Wu, X.Z.; Chen, C.T.; Yuan, X.B. Magnetic Field Analysis of Surface-Mounted Permanent Magnet Motors Based on an Improved Conformal Mapping Method. IEEE Trans. Ind. Appl. 2023, 59, 1689–1698. [Google Scholar] [CrossRef]
- Ni, Y.Y.; Chen, K.; Xiao, B.X.; Qian, W.; Wang, Q.J. Analytical Modeling of PM Electrical Machines with Eccentric Surface-Inset Halbach Magnets. IEEE Trans. Magn. 2021, 57, 1–9. [Google Scholar] [CrossRef]
- Kong, X.H.; Hua, Y.T.; Zhang, Z.R.; Wang, C.; Liu, Y. Analytical Modeling of High-Torque-Density Spoke-Type Permanent Magnet In-Wheel Motor Accounting for Rotor Slot and Eccentric Magnetic Pole. IEEE Trans. Transp. Electrif. 2021, 7, 2683–2693. [Google Scholar] [CrossRef]
- Wang, H.M.; Liu, S.; Wu, S.; Guo, L.Y.; Shi, T.N. Optimal Design of Permanent Magnet Structure to Reduce Unbalanced Magnetic Pull in Surface-Mounted Permanent-Magnet Motors. IEEE Access 2020, 8, 77811–77819. [Google Scholar] [CrossRef]
- Pang, Y.; Zhu, Z.Q.; Feng, Z.J. Cogging Torque in Cost-Effective Surface-Mounted Permanent-Magnet Machines. IEEE Trans. Magn. 2011, 47, 2269–2276. [Google Scholar] [CrossRef]
- Chai, F.; Liang, P.X.; Pei, Y.L.; Cheng, S.K. Magnet Shape Optimization of Surface-Mounted Permanent-Magnet Motors to Reduce Harmonic Iron Losses. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, F.Q.; Ruan, Z.B.; Liu, Y.; Lai, H.K. The Modified Analytical Model of Sine Pole-Shaping Surface-Mounted PM Motor. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 1346–1354. [Google Scholar] [CrossRef]
- Liu, C.; Xu, Y.; Zou, J.; Yu, G.; Zhuo, L. Systems, Permanent Magnet Shape Optimization Method for PMSM Air Gap Flux Density Harmonics Reduction. CES Trans. Electr. Mach. Syst. 2021, 5, 284–290. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Z.Q.; Ombach, G. Torque Enhancement of Surface-Mounted Permanent Magnet Machine Using Third-Order Harmonic. IEEE Trans. Magn. 2014, 50, 104–113. [Google Scholar] [CrossRef]
- Hu, P.F.; Wang, D. Analytical Average Torque Optimization Method of Parallel MagnetizedSurface-Mounted Permanent-MagnetMachine withThird-OrderHarmonic Shaping Method. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1377–1383. [Google Scholar] [CrossRef]
- Chabchoub, M.; Salah, I.B.; Krebs, G.; Neji, R.; Marchand, C. PMSM Cogging Torque Reduction: Comparison Between Different Shapes of Magnet. In Proceedings of the 2012 First International Conference on Renewable Energies and Vehicular Technology (REVET), Hammamet, Tunisia, 26–28 March 2012. [Google Scholar]
- Zhu, H.Q.; Xu, Y. Permanent Magnet Parameter Design and Performance Analysis of Bearingless Flux Switching Permanent Magnet Motor. IEEE Trans. Ind. Appl. 2021, 68, 4153–4163. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Chen, C. Analytical Calculation of Air Gap Magnetic Field for Permanent Magnet Machines Based on Pole Partition Processing. Proc. CSEE 2021, 41, 6390–6398. [Google Scholar]
- Wang, K.; Sun, H.; Zhu, S.; Liu, C. Airgap Magnetic Field Reconstruction for Torque Ripple Mitigation of Permanent Magnet Machines. Proc. CSEE 2023, 43, 2563–2572. [Google Scholar]
- Yu, Z.Y.; Li, Y.; Jing, Y.T.; Du, J.M.; Wang, Z.C. Analytical model for magnetic field calculation of SPMSM with chamfered pole considering iron core saturation. IET Electr. Power Appl. 2020, 14, 1856–1864. [Google Scholar] [CrossRef]
- Hu, H.Z.; Zhao, J.; Liu, X.D.; Guo, Y.G. Magnetic Field and Force Calculation in Linear Permanent-Magnet Synchronous Machines Accounting for Longitudinal End Effect. IEEE Trans. Ind. Appl. 2016, 63, 7632–7643. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, Y.; Pan, W.; Diao, X.; Zhu, H. Multi-objective Optimization Design of Bearingless Permanent Magnet Synchronous Motor Using Improved Particle Swarm Optimization Algorithm. Proc. CSEE 2023, 43, 4443–4451. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).