Robust Nonsingular Terminal Sliding Mode Control of a Buck Converter Feeding a Constant Power Load

Abstract

In recent years, DC microgrid systems feeding constant power loads (CPLs) have been given a particular focus due to their effect on the overall system stability caused by their electrical characteristics behaving as negative incremental impedance. To address this issue, this paper investigates the stabilization of a DC bus voltage in a DC microgrid (MG) feeding a CPL. The output voltage of the main DC bus is stabilized by using a robust nonsingular terminal sliding mode controller that is characterized by the elimination of the singularity problem that arises from the conventional terminal sliding mode controller. The CPL is emulated by a boost converter where its output voltage is tightly regulated. The system is investigated in terms of voltage following and disturbance rejection. The robustness and effectiveness of the proposed control strategy are assessed against input voltage fluctuations and power demand variations. The proposed controller is validated through simulations and an experimental setup.

1. Introduction

In recent years, there has been increased interest in developing new and innovative ways of producing and distributing electrical energy. The main reasons for this have been the desire to move towards more efficient and reliable energy infrastructures and accelerating the deployment of renewable energy sources. This approach allows not only to promote a more efficient energy mix but also to have an energy production close to the end user. Moreover, the advanced state of maturity of power electronics converters and digital controllers have boosted the interest in distributed generation and the emergence of the microgrid (MG) concept. An MG is defined as a combination of interconnected distributed energy sources, energy storage systems and loads acting as a single controllable unit. The most attractive feature of an MG is its ability to operate in both grid-connected and stand-alone modes. This results in increased security in terms of power delivery [1,2,3]. Although AC microgrids have been extensively explored, due to the nature of the grid utility, DC microgrids have been considered as a very promising alternative. This is mainly due to the features of DC microgrids such as high reliability, ease of integration and cost-effectiveness. In addition, the inherent issues of AC microgrids, such as harmonic content, synchronization problems, reactive power and control complexity are additional factors that reinforce the attractiveness of DC MGs [4].

However, despite the above-mentioned advantages of DC MGs, there are still some challenges to be overcome. For example, the proliferation of new types of loads based on static converter interfaces can impact the overall stability of the DC MG. Constant power loads (CPLs), constant voltage loads (CVLs) and constant current loads (CCLs) are examples of these type of loads. In particular, CPLs can be a source of instability of the MG when an inappropriate control is applied. This situation can be encountered in a topology that cascades two DC converters, one playing the role of a source and the other playing the role of a load. Practical CPLs can be found in aircraft, electric vehicles, ships, spacecraft, telecommunication networks and residential DC loads and many others [5].

CPLs are nonlinear loads that act as a negative incremental impedance. This behavior of this type of load arises from simultaneous increases/decreases in output current with decreases/increases in output voltage [6,7,8]. This characteristic is a challenge from the control point of view to ensure the stability of a common DC bus.

Many investigations have addressed the negative impact of a CPL via different control methods. For example, passivity damping, proposed in [9,10,11], uses additional passive elements in the DC-DC power converter to increase the damping factor. Solutions based on active damping have been proposed in [12,13,14]. In these approaches, the authors suggested the adjustment of the closed-loop controller of the system through the inclusion of virtual impedance. The feedback linearization technique, proposed in [15], suggests the pole placement technique by linearizing the system. The control technique proposed in [16,17] uses the Backstepping algorithm and a nonlinear disturbance observer to estimate the behavior of a DC-DC converter with a variable constant power load. Sliding mode control is addressed in [6,18,19,20], where the emphasis is on the stabilization of the DC output voltage under disturbances with the presence of a CPL. In [21,22], the authors propose a passivity-based control approach where the disturbance rejection is performed using disturbance estimation techniques. Pulse width adjustment, proposed in [23], introduces a new fixed frequency technique to guarantee the stability of a DC converter feeding a constant power load. The authors in [24] investigated a compensation strategy to improve the stability of the MG in the presence of a CPL using Middlebrook’s Nyquist impedance criterion. In [25,26], the authors used a predictive controller to provide a compensating action for a DC-DC converter powering a CPL. Other techniques are based on Lyapunov and Bryaton–Mayer’s, which is a theory of equilibrium point stability, and an estimation of the region of attraction is applied for a cascaded system [27]. In [28], the authors investigated the stability influence of the Bidirectional DC-DC power converter (BDC) with CPLs and derived the control parameter determination method for BDC interfaced storage systems.

Table 1. Control methods summary.

Methods	Advantages	Drawbacks
Passive damping [9,10,11]	Simple to implement	Reduced effectiveness
Active damping [12,13,14]	Overcomes the disadvantages of passive damping techniques	Closed-loop control is altered The performance of the control system may deteriorate
Backstepping and passivity-based control [16,17,21,22]	The ability to deal with uncertainty to a certain extent Lyapunov-based stability and design procedure Asymptotic convergence	Requires information on all system states Calculation burden Gives rise to a higher magnitude of the control signal Steady-state error
Model predictive control (MPC) [25,26]	A strong control strategy for DC/DC converters. The system’s stability is ensured with this technique.	Calculation burden
Sliding mode control (SMC) [6,18,19,20]	Insensitive to external disturbances Controller structure is simple and easily tunable Robustness and ability to handle nonlinearities Stability is guaranteed by the Lyapunov function	Chattering effect Sensor drift caused by high-frequency noise Nonfinite time convergence
The feedback linearization technique [15]	Powerful technique for nonlinear systems Transform the nonlinear system dynamics into a fully or partially linearized system.	Most of the time, such data is unavailable.= Reduced effectiveness
Pulse width adjustment [23]	It is extremely simple This digital control requires only a few logic gates and comparators to implement.	The presence of steady-state error Decreases the efficiency

highlights the benefits and downsides of several approaches used to mitigate the impact of CPLs. Although the above-mentioned control techniques have been effective in dealing with the characteristics of CPL and its negative effects, they still have some weaknesses, namely: low efficiency, due to the additional passive components, and computational burden due to the complexity of the algorithms.

This paper investigates the stabilization issues of the common DC bus voltage in a DC microgrid feeding a constant power load. The output voltage of the main DC bus is stabilized by using a robust nonsingular terminal sliding mode controller that is characterized by the elimination of the singularity problem that arises from the conventional terminal sliding mode controller. The CPL is emulated by a boost converter where its output voltage is tightly regulated. The system is investigated in terms of voltage following and disturbances rejection. The robustness and effectiveness of the proposed control strategy are assessed against input voltage fluctuations and power demand variations. The proposed controller is validated through simulations and an experimental setup.

The major contributions of this paper are summarized hereafter:

• Eliminating the negative effect of the CPL caused by the interaction between the DC-DC buck converter and a voltage-controlled boost converter acting as a CPL.
• Avoiding the singularity problem caused by the conventional terminal sliding mode controller.
• Experimental validation of the suggested controller.

The remainder of the paper is organized as follows: Section 2 presents the effect of a CPL and the instability concerns that may arise due to the negative incremental impedance. Section 3 introduces the basics of the traditional terminal sliding mode controller. The design of the robust nonsingular terminal sliding mode controller is presented in Section 4. Simulation and experimental results, and real-time implementation setup are discussed in Section 5. Section 6 concludes the paper.

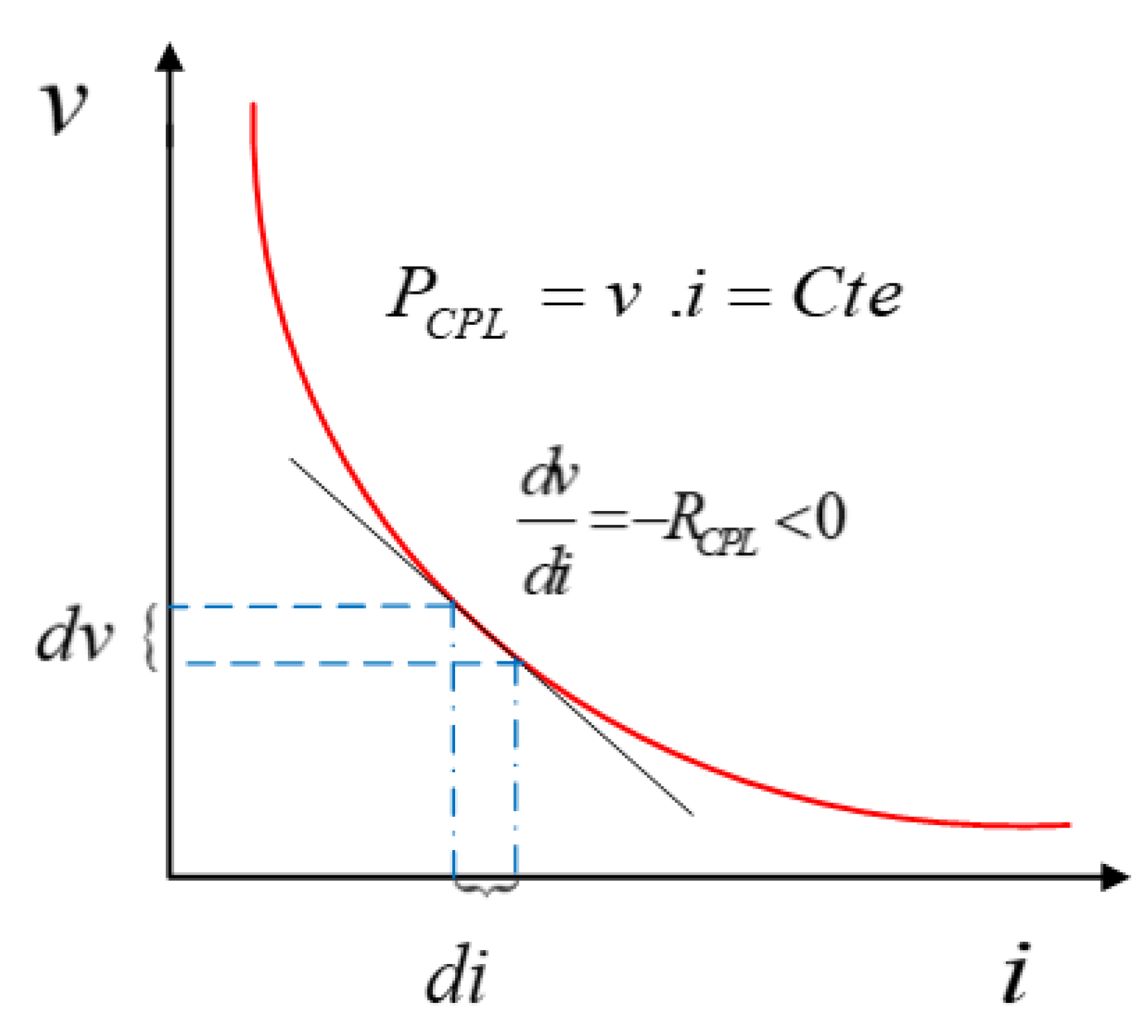
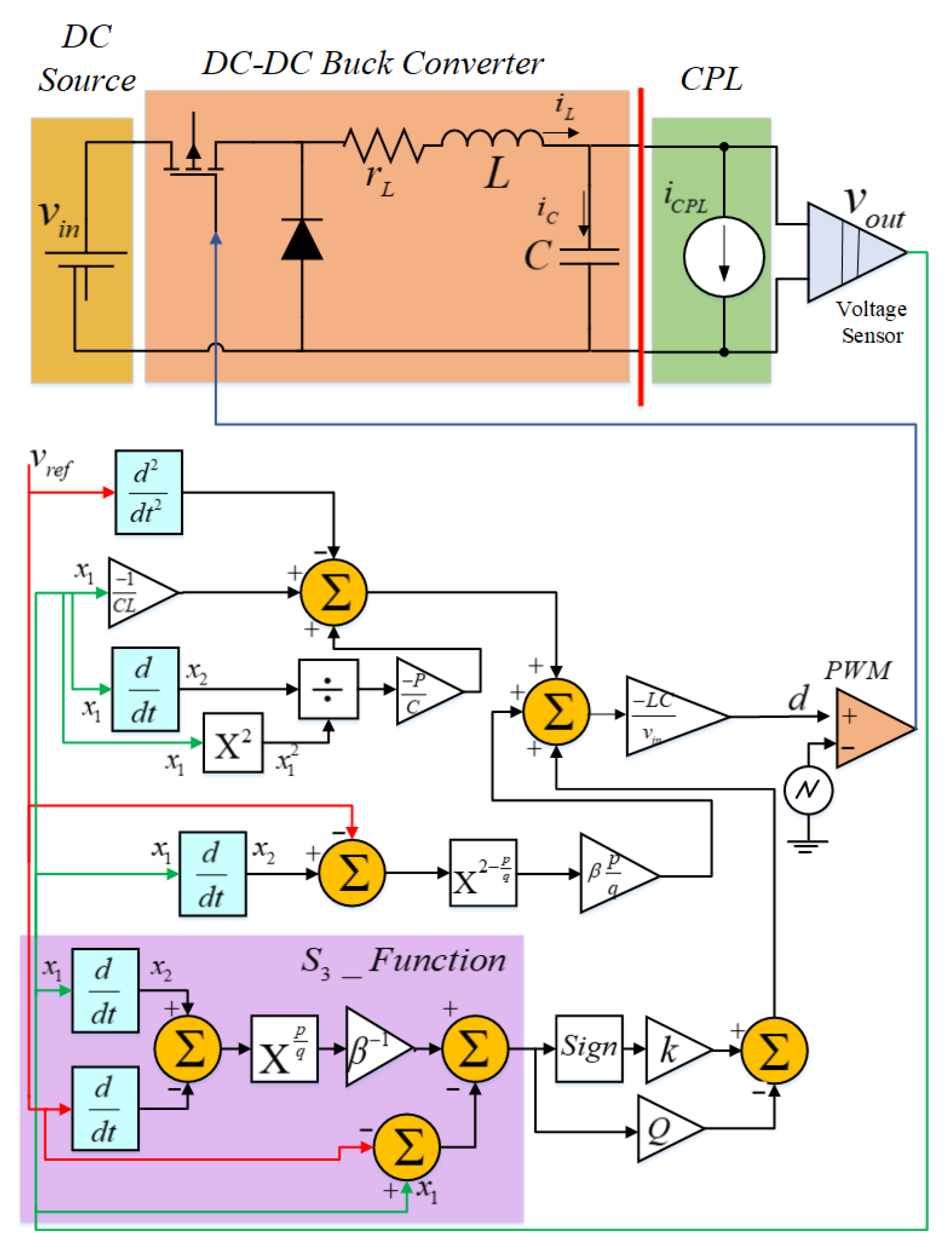
2. System Description and Problem Statement

A typical DC microgrid feeding AC and DC loads is illustrated in Figure 1. Meanwhile, Figure 2 depicts the cascaded architecture of power electronic interfaces. The cascaded topology includes a DC source, a DC-DC buck converter (upstream converter), and a voltage-regulated boost converter acting as a CPL. The interaction between these power electronic interfaces creates large oscillations that may cause instability [6,7].

Figure 3 shows the equivalent circuit model of the studied system where the load converter is modeled by a controlled current source. We note that the required power is constant, as expected by the CPL characteristics. The buck converter is represented by its input voltage $v_{in}$ and the second-order LC filter.

In the continuous condition mode (CCM), the boost converter can function as a CPL if its output voltage is tightly regulated. When the frequency is lower than the voltage loop cut-off frequency of the DC-DC buck converter, the input impedance is equivalent to a negative resistance. When the frequency exceeds the cut-off frequency, the input impedance becomes equivalent to inductance [6,29].

The consumed power for a CPL is constant throughout the controller bandwidth, and its relationship is provided by:

$$P_{CPL}=v_{}·i=Cte$$

(1)

where:

$P_{CPL}$ is the power absorbed by the CPL, $v$ is the input voltage and $i$ stands for the consumed current.

Deriving the current of the CPL with respect to its voltage and inverting the result yields to the expression of the incremental negative impedance of a CPL, as follows:

$$\frac{dv}{di}=-\frac{v}{i}=-\frac{P_{CPL}}{i^2}=-\frac{v^2}{P_{CPL}}$$

(2)

Thus:

$$\frac{dv}{di}=-R_{CPL}<0$$

(3)

Equation (3) demonstrates that a CPL has incremental negative impedance (INI), as illustrated in Figure 4. From an automatic point of view, this negative incremental impedance exhibits a −180° phase lag in the Bode diagram. Therefore, if the output impedance module of the source converter intersects with the input impedance module of the CPL, while the cut-off frequency of the source converter is lower than the CPL one, instability occurs. Moreover, power quality and overall system performance are affected by the INI characteristic [6,7,29]. Figure 5 depicts the simulation results of an open loop operation of a buck converter feeding a CPL. As can be seen, the output voltage and the inductor current are oscillating due to the INI effect of the load.

To overcome the above-mentioned issue, many researchers have proposed various methods, such as adding passive loads parallel to the CPL in order to eliminate the INI characteristic and increase the damping factor [19,21].

Figure 6 shows the simulation result of the studied system before and after adding a passive load in parallel with the CPL. The parameters used in this example are given as follows: (v_in = 28 V, C = 220 uF, L = 2.7 mH, P_CPL = 20 W, and d = 0.5).

Therefore, an appropriate approach is required to avoid the INI effect and increase the damping factor without adding the passive loads. In addition, the suggested control approach must stabilize the overall system against power load changes and input voltage variation. In the following, the system modeling of a buck converter feeding a CPL is investigated.

When the buck converter feeding a CPL operates in a CCM, the system can be represented as follows:

$$\{\begin{array}{l}\frac{d{i}_L}{dt}=\frac{1}{L}\left(v_{in}-v_o\right)\\ \frac{d{v}_o}{dt}=\frac{1}{C}\left(i_L-\frac{P}{v_o}\right)\end{array}\mathrm{for}0<t<dT$$

(4a)

$$\{\begin{array}{l}\frac{d{i}_L}{dt}=\frac{1}{L}\left(-v_o\right)\\ \frac{d{v}_o}{dt}=\frac{1}{C}\left(i_L-\frac{P}{v_o}\right)\end{array}\mathrm{for}dT<t<T$$

(4b)

By using the state-space averaging technique, the dynamic model of a buck converter feeding a CPL can be written as follows:

$$\{\begin{array}{l}\frac{d{i}_L}{dt}=\frac{1}{L}\left(v_{in}d-v_o\right)\\ \frac{d{v}_o}{dt}=\frac{1}{C}\left(i_L-\frac{P}{v_o}\right)\end{array}$$

(5)

To minimize the number of states variables, a transformation method is used. To achieve this requirement, the output voltage and its derivative are chosen as the state variables of the overall system as follows:

$$\{\begin{array}{l}{x}_1=v_0\\ x_2=\frac{d{v}_0}{dt}\end{array}$$

(6)

By substituting the selected state variables given by Equation (6) in Equation (5), the new state space model characterizing the system is given below:

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\frac{v_{in}}{CL}d-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}\end{array}$$

(7)

where:

$x_1$ is the output voltage and $x_2$ its derivative.

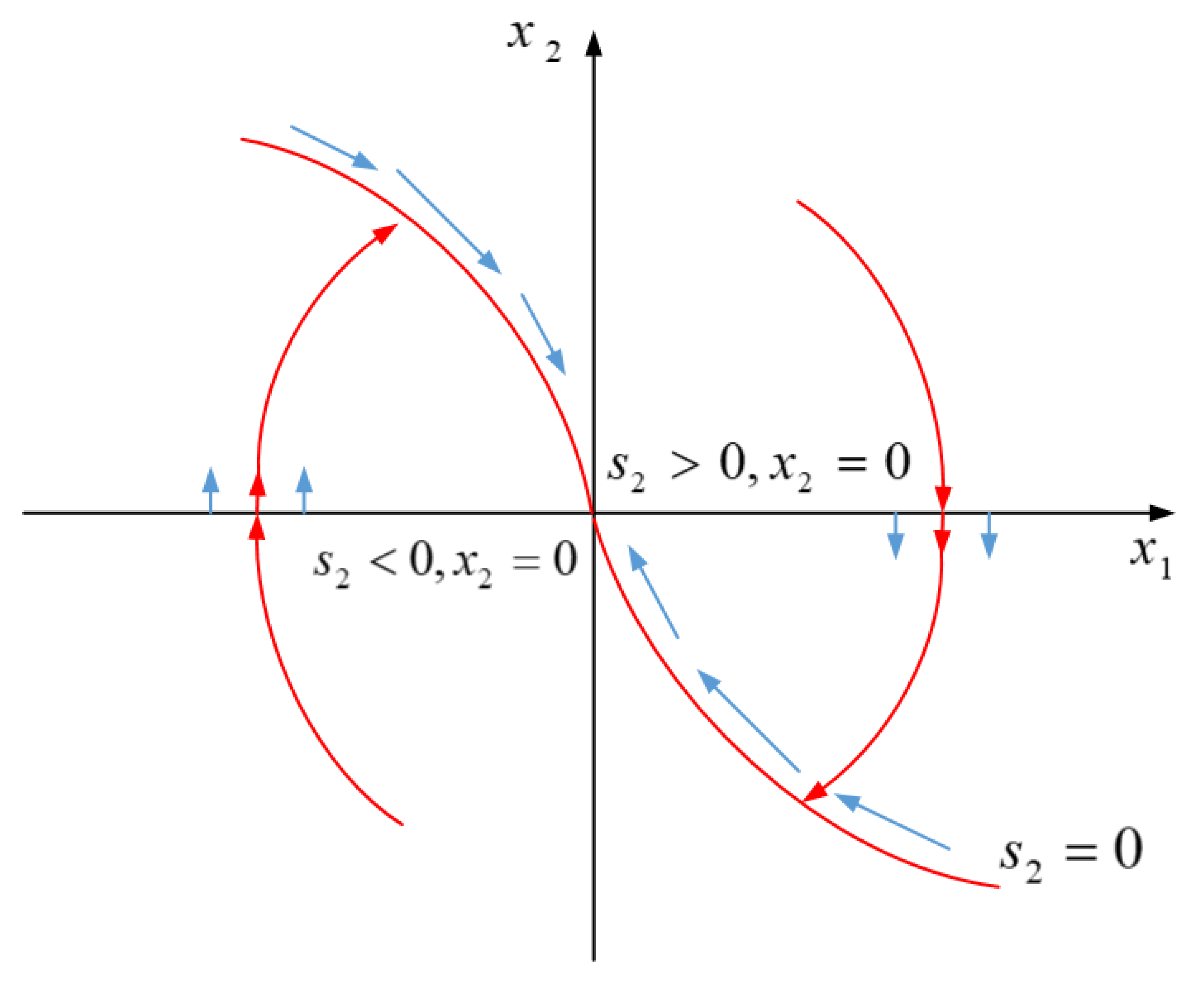
3. Basics of Terminal Sliding Mode Controller

The terminal sliding mode controller (TSMC) has become a very popular robust, nonlinear control approach in recent years. This control technique is widely used in many applications such as aircraft, motor drives, robots, and so on. The TSM controller provides fast time convergence, high precision and improved robustness [30,31,32,33]. Furthermore, the TSM controller is a highly effective method for dealing with external disturbances and uncertainties. It is worth mentioning that Lyapunov theory is critical for demonstrating the overall system’s asymptotic stability. This section provides an overview of the TSM controller’s state of the art. Let us consider the nonlinear second-order system given by the following equations:

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=f\left(x\right)+b\left(x\right)u+g\left(x\right)\end{array}$$

(8)

where:

${\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]}^T$ represents the states variables, $f(x)$ and $b(x)$ are smooth nonlinear functions of x and $g(x)$ expresses the uncertainties in the overall system, including disturbances, which is assumed to satisfy $\left|g(x)\right|\le I_G$, where $I_G>0$. The variable u represents the control law of the system. The conventional TSM is characterized by a first-order sliding mode surface given by the following expression:

$$s_1=x_2+\beta x_1^{q/p}$$

(9)

where:

β > 0 is a constant in this equation and p and q are odd integers greater than zero that satisfy: $p>q$.

The time derivative of Equation (9) is computed as:

$${\dot{s}}_1=f\left(x\right)+b\left(x\right)u+g\left(x\right)+\beta \frac{q}{p}{x}_2 x_1{}^{\frac{q}{p}-1}$$

(10)

Let us suppose the candidate Lyapunov function as:

$$V_1=\frac{1}{2}{s}_1^2$$

(11)

The time derivative of Equation (11) is given by:

$${\dot{V}}_1=s_1{\dot{s}}_1$$

(12)

According to Equations (10) and (12), the control laws u is given as:

$$u=-b^{-1}(x)\left[f(x)+\beta \frac{q}{p}{x}_1{}^{\frac{q}{p}-1}{x}_2+I_g+\eta \mathrm{sgn}({\mathrm{s}}_1)\right]$$

(13)

where:

η > 0 is a design constant.

It is clear that if $s_1(0)\ne 0$, the dynamic of the system states track the sliding surface at $s_1=0$ for a finite and time $t_r$. The time $t_r$ satisfies the following condition:

$$t_r\le \frac{\left|s_1(0)\right|}{\eta }$$

(14)

Furthermore, when the sliding mode reaches $s_1=0$, the system dynamics are determined by the following nonlinear differential equation:

$$x_2+\beta x_1{}^{q/p}={\dot{x}}_1+\beta x_1{}^{q/p}=0$$

(15)

where $x_1=0$ is the terminal attractor of the system given in Equation (15).

The limited time $t_s$ required to pass from $x_1(t_r)\ne 0$ to $x_1(t_s+t_r)=0$ is given by the following expression:

$$t_s=-{\beta }^{-1}{\displaystyle \underset{x_1(t_r)}{\overset{0}{\int }}\frac{d{x}_1}{x_1^{q/p}}=}\frac{p}{\beta (p-q)}{\left|x_1(t_r)\right|}^{1-\frac{q}{p}}$$

(16)

Therefore, in the TSM manifold given in Equation (15), the state variables $x_1,x_2$ converge to zero in a determined period of time.

The TSM control given by Equation (13) demonstrates that if $x_2\ne 0$ while $x_1=0$, the second part involving $x_1^{(q/p)-1}{x}_2$ may cause a singularity problem. When $s_1=0$, Equation (9) can be written as follows:

$$x_2=-\beta x_1{}^{\frac{q}{p}}$$

(17)

By inserting Equation (17) into Equation (13), the control law u can be rewritten as follows:

$$u=-b^{-1}(x)\left[f(x)-{\beta }^2\frac{q}{p}{x}_1{}^{\left((2q-p)/p\right)}+I_g+\eta \mathrm{sgn}({\mathrm{s}}_1)\right]$$

(18)

As a result, in the ideal sliding mode $s_1=0$, the singularity problem does not occur.

Therefore, it is mandatory to deal with the singularity problem in classic TSM systems in the section that follows.

4. NTSM Controller Applied to a Buck Converter Feeding a CPL

In this section, a nonsingular terminal sliding mode (NTSM) controller is applied to avoid the singularity issue that occurs with conventional TSM controllers [33]. Using the NTSM, the system states may be assured to approach a defined TSM manifold in finite time and then converge to the origin in finite time. The proof of the stability of the NTSM systems is also given in this section. The NTSM controller has various advantages, including less steady-state error, faster finite-time convergence, and a low control energy cost. The proposed NTSM controller is then applied to the control of a cascaded buck converter with a tightly voltage-regulated boost converter (acting as a CPL). The proposed controller eliminates the negative CPL effect and attenuate the external disturbances. Simulations and experimental setups have been carried out to validate the suggested control approach. In this work, the suggested NTSM surface is defined as follows [33]:

$$s_2=x_1+\frac{1}{\beta }{x}_2{}^{p/q}$$

(19)

It can be easily seen that when $s_2=0$, the surface of NTSM given in Equation (19) is equal to the surface given in Equation (9). Thus, the period required to reach the equilibrium point, $x_1=0$, is the same as in Equation (16). It is important to note that when using Equation (19), the time derivative of $s_2$ along the system given in Equation (8) does not result in negative fractional powers. The NTSM controller is further discussed in the following theorem:

Theorem 1. 

For the system given in Equation (8) with the NTSM surface defined by Equation (19), if the control is designed as

$$u=-b^{-1}(x)\left\{f(x)+\beta \frac{q}{p}{x}_2{}^{2-p/q}+I_g+\eta \mathrm{sgn}(s_2)\right\}$$

(20)

where 1 < p/q < 2 and η > 0, then the surface of NTSM given in Equation (19) will be reached at a finite time. In addition,$x_1,x_2$will reach zero in a finite time.

Proof of Theorem 1. 

For the surface of NTSM given in Equation (19), its derivative along the system dynamics defined by Equation (8) is

$${\dot{s}}_2=x_2+\frac{1}{\beta }\frac{p}{q}{x}_2{}^{p/q-1}\left(f(x)+g(x)+b(x)u\right)$$

(21)

The candidate Lyapunov function is defined as follows:

$$V_2=\frac{1}{2}{s}_2{}^2$$

(22)

The derivative of Equation (22) with respect to time is given as

$${\dot{V}}_2=s_2{\dot{s}}_2$$

(23)

$${\dot{V}}_2=s_2\left(x_2+\frac{1}{\beta }\frac{p}{q}{x}_2{}^{p/q-1}\left(f(x)+g(x)+b(x)u\right)\right)$$

(24)

The above-mentioned control law u given in Equation (20) is computed using Equations (23) and (21).

By substituting Equation (20) into Equation (24), we obtain

$${\dot{V}}_2=s_2{\dot{s}}_2=s_2\left(-\frac{1}{\beta }\frac{p}{q}{x}_2{}^{p/q-1}\eta \mathrm{sgn}(s_2)\right)$$

(25)

This yields

$${\dot{V}}_2=-s_2\left(\frac{1}{\beta }\frac{p}{q}\eta x_2{}^{p/q-1}\left|s_2\right|\right)<0$$

(26)

where:

$1<p/q<2$, and $x_2{}^{p/q-1}>0$.

Let us assume that

$$\rho (x_2)=(1/\beta )(p/q)\eta x_2{}^{p/q-1}$$

(27)

Thus,

$$\{\begin{array}{l}{\dot{V}}_2\le -\rho (x_2)\left|s_2\right|\\ \rho (x_2)>0\end{array}\mathrm{for}{x}_2\ne 0$$

(28)

Therefore, Lyapunov stability condition is satisfied when $x_2\ne 0$. The system states can reach the sliding mode $s_2=0$ within a finite time. □

4.1. Application of an NTSM Controller to a Buck Converter Supplying a CPL

According to the equivalent circuit of the buck converter given in Section 2 and its derived model, given in Equation (7), the first step in designing the NTSM controller is to provide a stable surface. In this work, the desired surface is defined by the one given by Equation (29). It is worth noting that this defined surface depends on β and p/q.

$$s_3=e+\frac{1}{\beta }{\dot{e}}^{\frac{p}{q}}=\left(x_1-x_{1r}\right)+\frac{1}{\beta }{\left(x_2-{\dot{x}}_{1r}\right)}^{\frac{p}{q}}$$

(29)

where:

β > 0, p and q are odd number integers greater than zero that perform the conditions p = 2m + 1, m = 1, 2, ….., where 1 < p/q < 2.

Assuming that the desired reference of the output voltage is denoted by x_1r, then the tracking error of the output voltage and its derivative are expressed as follows:$e=x_1-x_{1r},\dot{e}=x_2-{\dot{x}}_{1r}$.

Assume the time between $s_3(0)\ne 0$ and $s_3(0)=0$ is $t_r$, and $t_s$ is the time to reach the equilibrium point. When the system reaches the sliding surface $s_3$_, then it can be written as

$$s_3=e+\frac{1}{\beta }{\dot{e}}^{\frac{p}{q}}=0$$

(30)

The mentioned equation can be obtained by transforming Equation (30) as follows:

$$\dot{e}=-{\beta }^{\frac{q}{p}}{e}^{\frac{q}{p}}$$

(31)

Then, by solving the deferential equation given in Equation (31), $t_s$ is given by the following expression:

$$t_s=\frac{p}{{\beta }^{\frac{q}{p}}\left(p-q\right)}{\left|e(t_r)\right|}^{1-\frac{q}{p}}$$

(32)

The system can achieve a steady state during t_s by adapting p, q, and β.

In order to obtain the required control law $u(t)$ of the NTSM controller, the switching control law of SMC is defined as follows:

$$u_{sw}=-Q{s}_3-ksign(s_3)=\{\begin{array}{l}{\dot{s}}_3>0\_if\_s_3<0\\ {\dot{s}}_3<0\_if\_s_3>0\end{array}$$

(33)

where:

Q > 0 and k > 0.

To prove the existence of the sliding mode, the derivative of the function s₃ is required to validate the function defined in Equation (33). First, the time derivative of s₃ based on Equation (29) is calculated as follows:

$${\dot{s}}_3=\dot{e}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\left(\ddot{e}\right)=\left({\dot{x}}_1-{\dot{x}}_{1r}\right)+\frac{p}{\beta q}{\left({\dot{x}}_1-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left({\ddot{x}}_1-{\ddot{x}}_{1r}\right)$$

(34)

Depending on the dynamic model given in Equation (7), the first and second time derivative tracking errors for the output voltage can be represented as follows:

$$\dot{e}={\dot{v}}_o-{\dot{x}}_{1r}$$

(35)

$$\ddot{e}=\frac{v_{in}}{CL}d-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}-{\ddot{x}}_{1r}$$

(36)

Substituting Equations (35) and (36) in Equation (34) yields

$${\dot{s}}_3=\left({\dot{x}}_1-{\dot{x}}_{1r}\right)+\frac{p}{\beta q}{\left({\dot{x}}_1-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left(\frac{v_{in}}{CL}d-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}-{\ddot{x}}_{1r}\right)$$

(37)

Hence, to guarantee the stability and convergence of the phase space trajectory to the desired sliding surface, a Lyapunov function is defined as

$$V_3=\frac{1}{2}{s}_3{}^2$$

(38)

The switching control law given by Equation (33) should therefore ensure that the derivative of $V_3(s_3)$, when $s_3\ne 0$, remains less than zero; thus:

$${\dot{V}}_3(s_3)=s_3{\dot{s}}_3<0$$

(39)

Therefore, two conditions are obtained by substituting Equation (33) in Equation (37), resulting in $s_3{\dot{s}}_3<0$:

(1)

If $s_3>0$, ${\dot{s}}_3$ must be smaller than 0, which yields:

$${\dot{s}}_3=\left({\dot{x}}_1-{\dot{x}}_{1r}\right)+\frac{p}{\beta q}{\left({\dot{x}}_1-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left(\frac{v_{in}}{CL}d-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}-{\ddot{x}}_{1r}\right)<0$$

(40)

(2)

If $s_3>0$, ${\dot{s}}_3$ must be greater than 0, which yields:

$${\dot{s}}_3=\left({\dot{x}}_1-{\dot{x}}_{1r}\right)+\frac{p}{\beta q}{\left({\dot{x}}_1-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left(\frac{v_{in}}{CL}d-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}-{\ddot{x}}_{1r}\right)>0$$

(41)

4.2. Control Design and Stability Analysis of NTSM Controller

The control law u(t) has two parts: The first term represents the equivalent control u_eq to keep ${\dot{s}}_3=0$, and the second part represents the discontinuous control u_sw, as given below.

$$u=u_{eq}+u_{sw}$$

(42)

The time derivative of Equation (38) is given by:

$${\dot{V}}_3=s_3{\dot{s}}_3=s_3\left[\left({\dot{x}}_1-{\dot{x}}_{1r}\right)+\frac{p}{\beta q}{\left({\dot{x}}_1-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left(\frac{v_{in}}{CL}d-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}-{\ddot{x}}_{1r}\right)\right]$$

(43)

As the control variable in a DC-DC converter is known as the duty cycle d, then according to Equation (43), the control input d (i.e.,: u=d) is given by the following expression:

$$d=-\frac{LC}{v_{in}}\left(-\frac{x_1}{CL}-\frac{P{x}_2}{C{x}_1^2}-{\ddot{x}}_{1r}+\beta \frac{p}{q}{\left(x_2-{\dot{x}}_{1r}\right)}^{2-\frac{p}{q}}+ksign(s_3)+Q{s}_3\right)$$

(44)

Substituting Equation (44) into Equation (43) yields:

$${\dot{V}}_3=s_3{\dot{s}}_3=-s_3\left(\frac{p}{\beta q}{\left(x_2-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left(Q{s}_3+ksign(s_3)\right)\right)$$

(45)

knowing that

$$1<p/q<2$$

(46)

then

$$0<\frac{p}{q}-1<1$$

(47)

When $(x_1-{\dot{x}}_{1r})\ne 0$, and $x_{1r}$ is defined as a constant, resulting that ${\dot{x}}_{1r}=0$, then:

$${\left(x_2-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}>0$$

(48)

Thus,

$${\dot{V}}_3<-s_3\left(\frac{p}{\beta q}{\left(x_2-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}\left(Q{s}_3+ksign(s_3)\right)\right)$$

(49)

Simplifying Equation (49) yields

$${\dot{V}}_3\le -s_3\left[\lambda \left(Q{s}_3+ksign\left(s_3\right)\right)\right]<0$$

(50)

where

$$\lambda =\frac{p}{\beta q}{\left(x_2-{\dot{x}}_{1r}\right)}^{\frac{p}{q}-1}>0$$

(51)

Therefore, the Lyapunov stability condition is satisfied. Figure 7 depicts the phase plot of the investigated system with the NTSM controller.

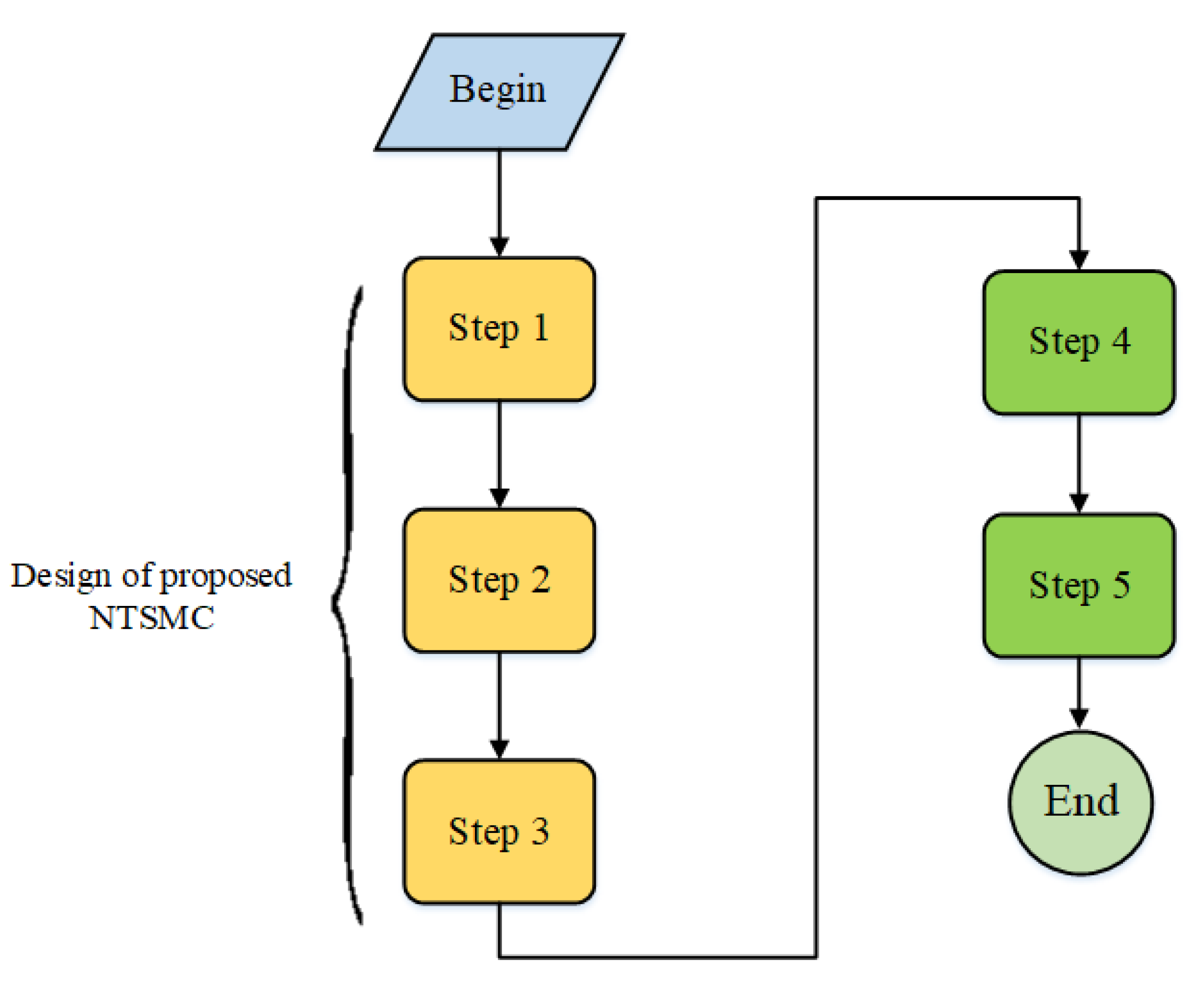
4.3. Implementation of the Proposed NTSM Controller

The proposed robust nonsingular terminal sliding mode (NTSM) controller is implemented using PSIM software. Using the transformation method suggested in Equations (6) and (7), the proposed NTSM controller for a buck converter supplying a CPL is depicted by the block diagram shown in Figure 8.

The design process of the robust NTSM controller (see Figure 9) can be summarized by the following the steps:

• Step 1: defining the studied state variables $v_o,i_L$ of the system;
• Step 2: Selecting new state variables $x_1,x_2$;
• Step 3: Performing the new model design by using $x_1,x_2$;
• Step 4: Constructing NTSM control with the new model;
• Step 5: Lyapunov condition test in order to ensure the stability.

5. Results and Discussion

In this section, the proposed NTSM controller of a buck power converter feeding a voltage-controlled boost converter (CPL) was tested in the PSIM program and experimentally validated. The parameters of the system are summarized in

Table 2. Buck converter parameters values.

Variable	Measure	Unit
Voltage Reference	14	V
Inductance	6	mH
Input Voltage	28	V
Capacitance	2	mF
CPL Power	10	W
Switching Frequency	25	kHz

. In order to verify the ability of the proposed controller to stabilize the DC bus voltage in front of CPL changes and input voltage fluctuations, two scenarios were considered:

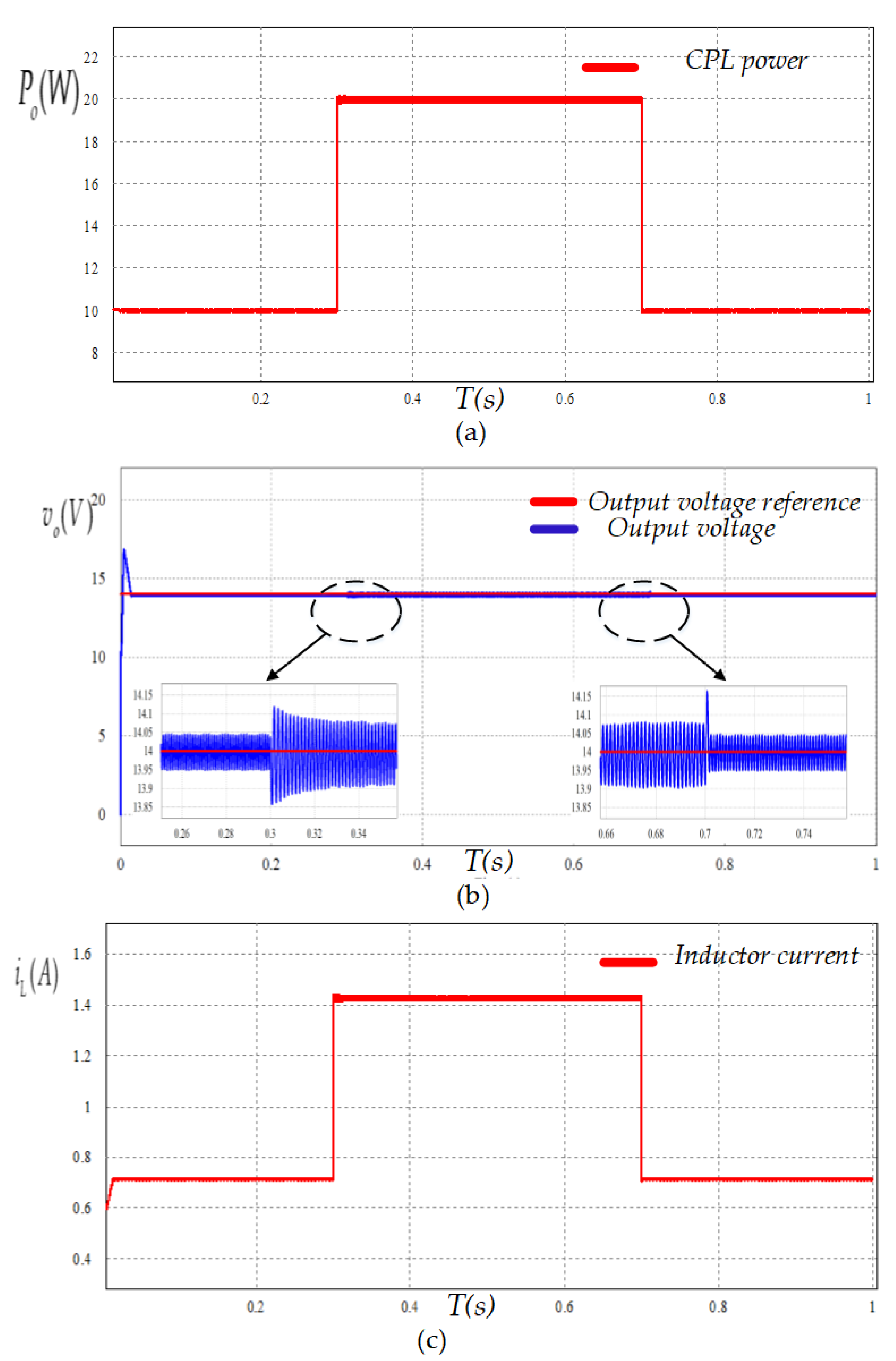
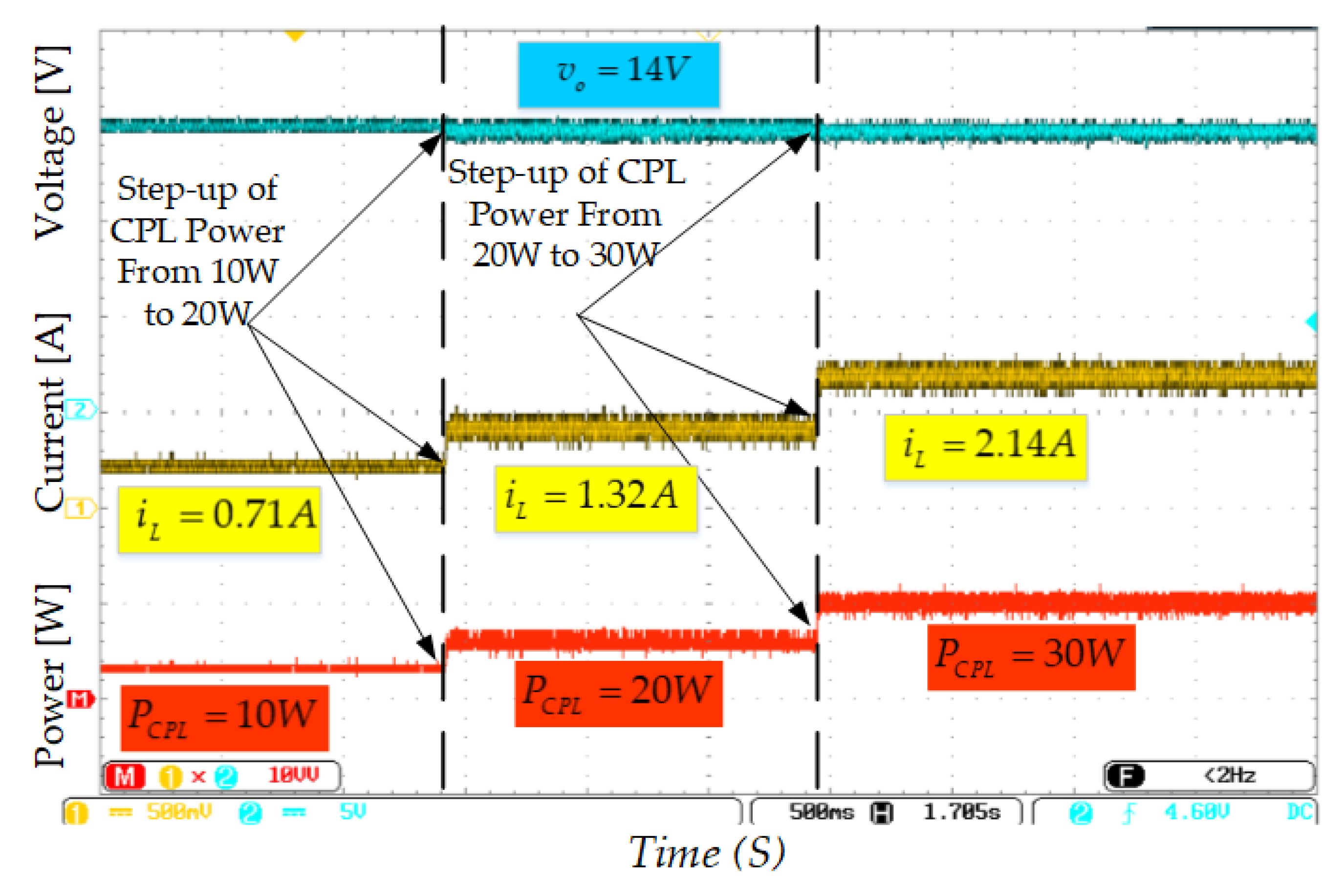
(Case 1)

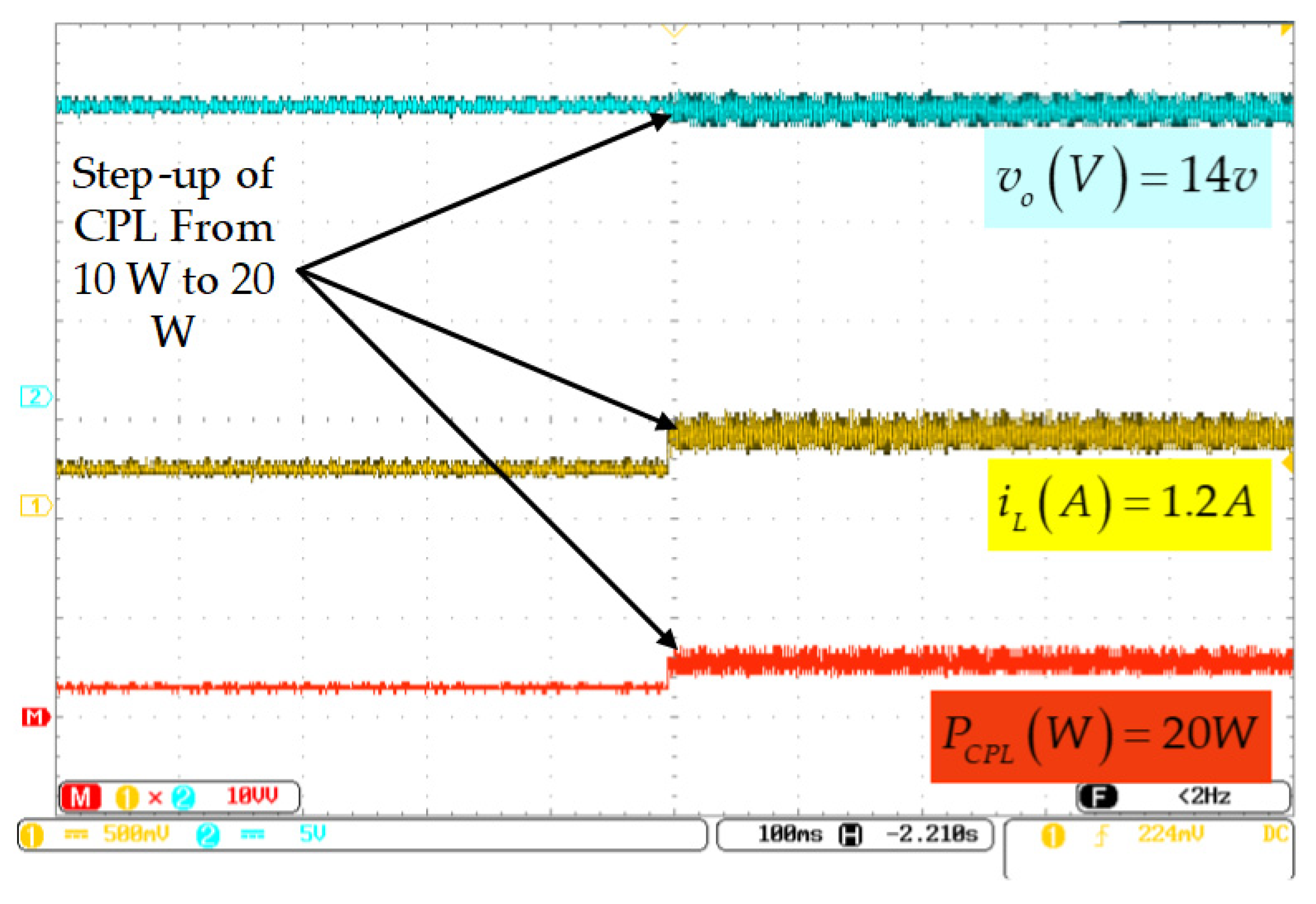
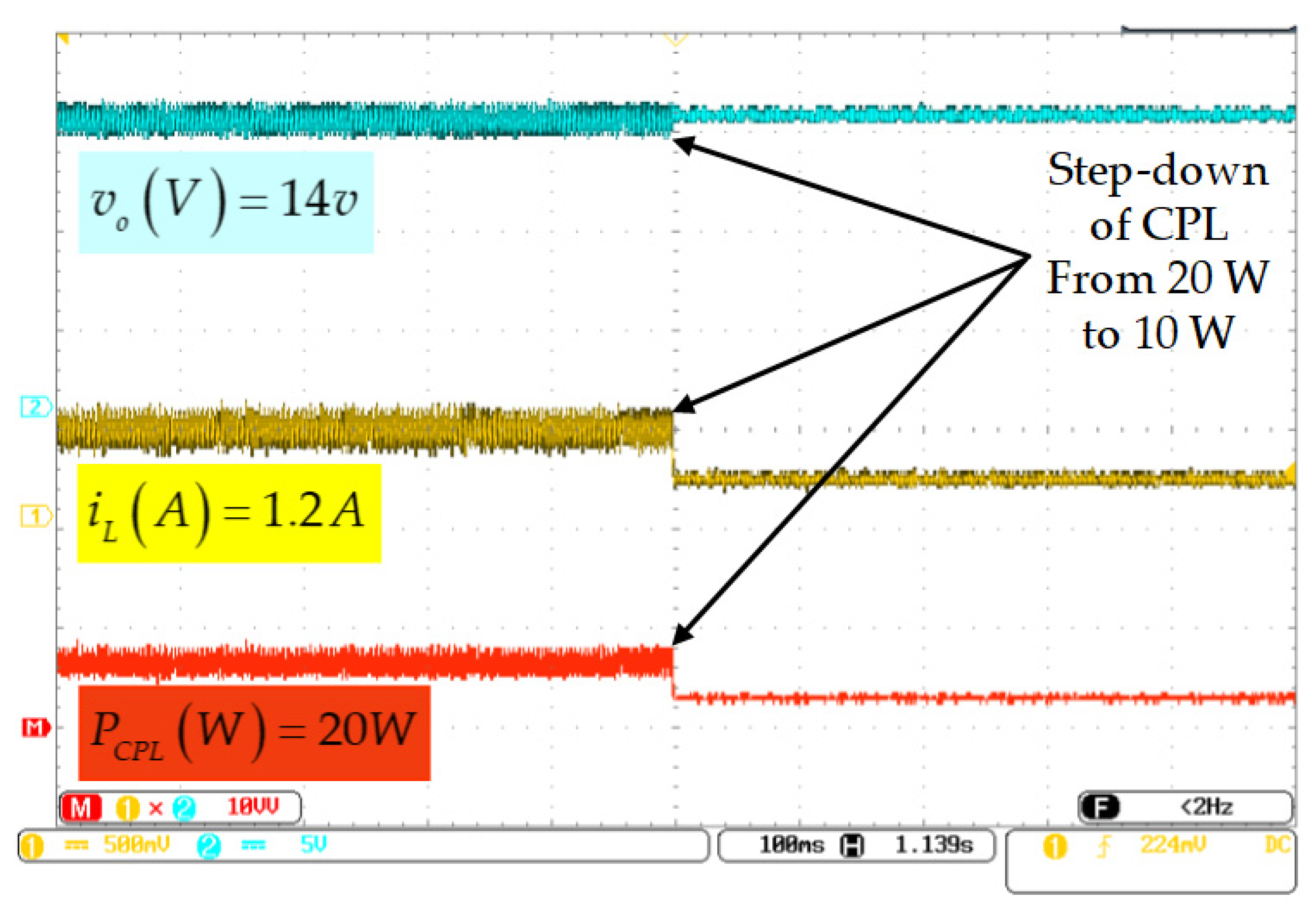
Response to sudden changes in the power consumed by the CPL.

(Case 2)

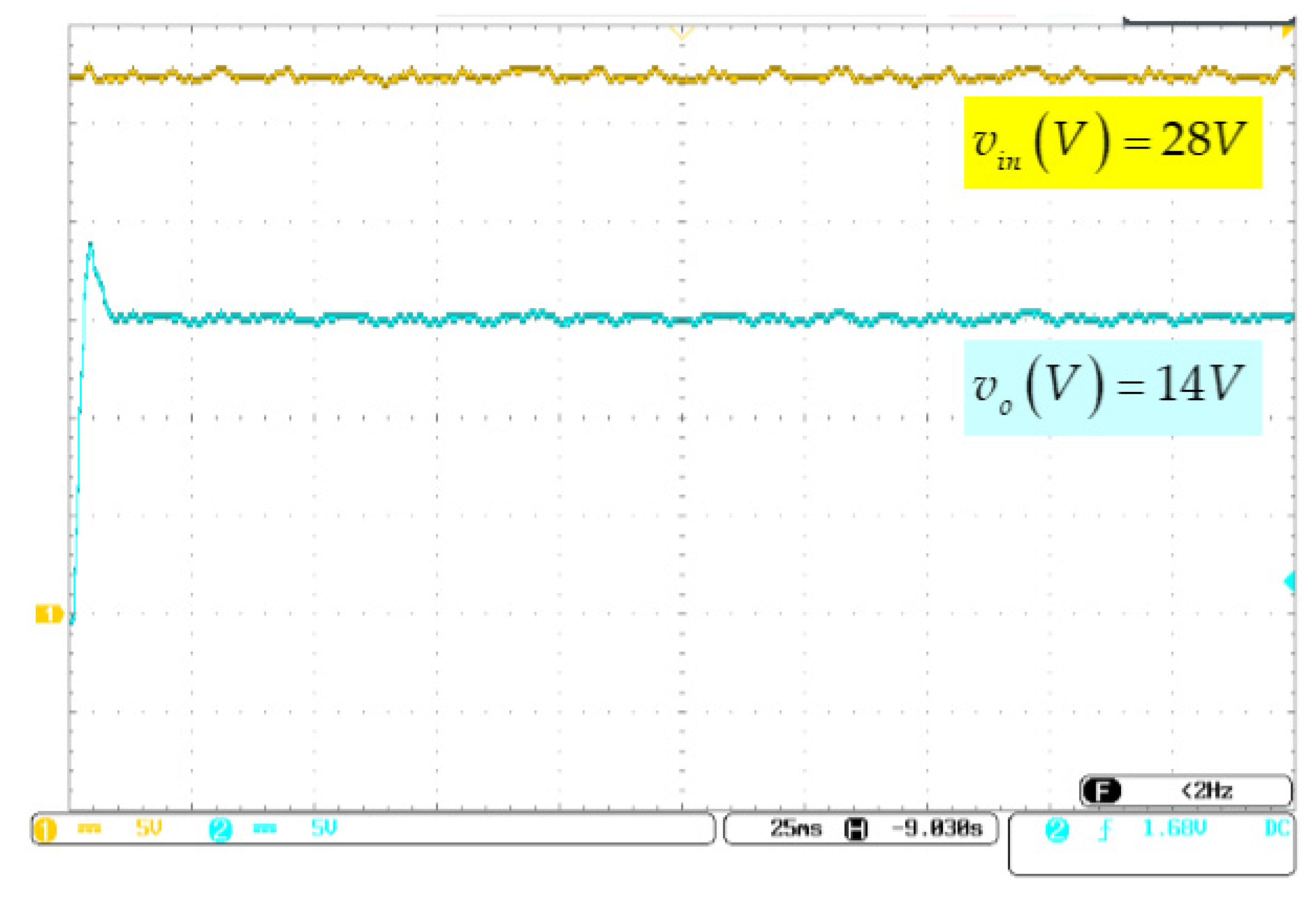
Response against input voltage fluctuations.

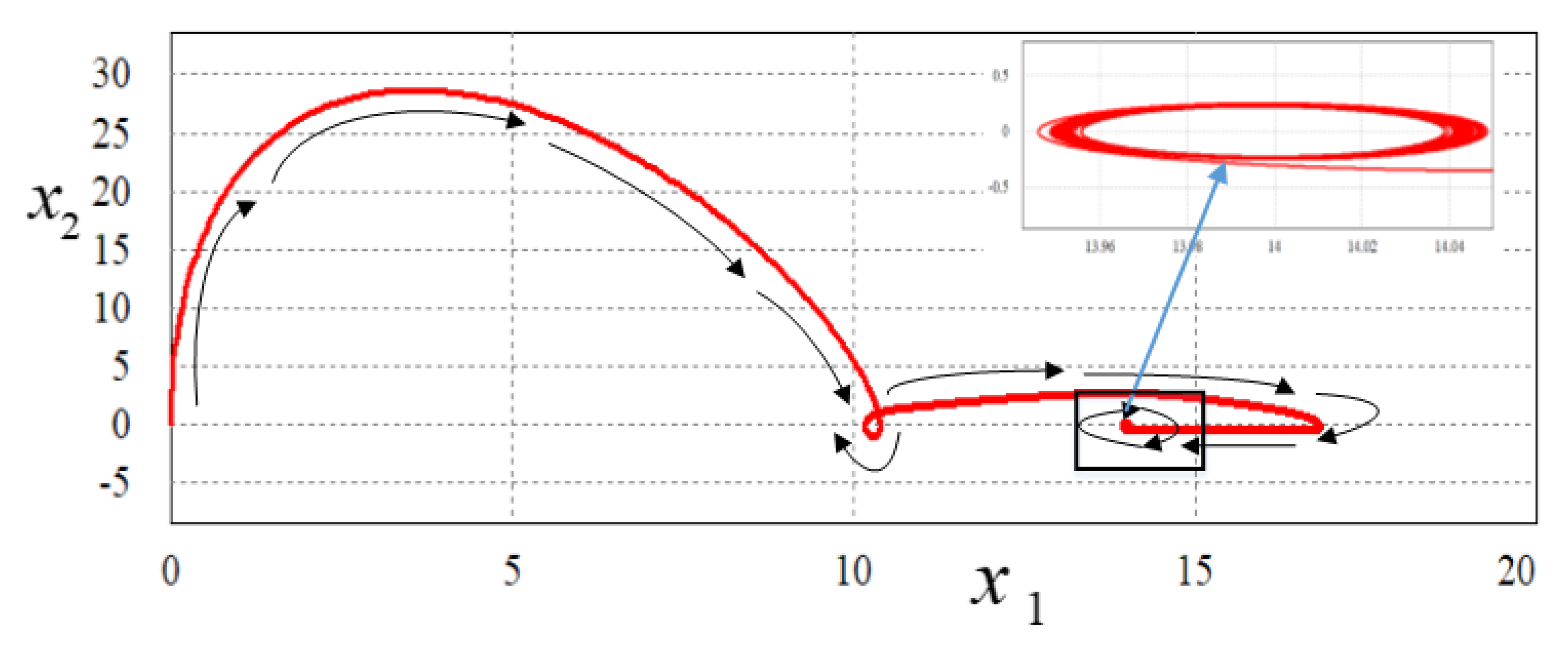
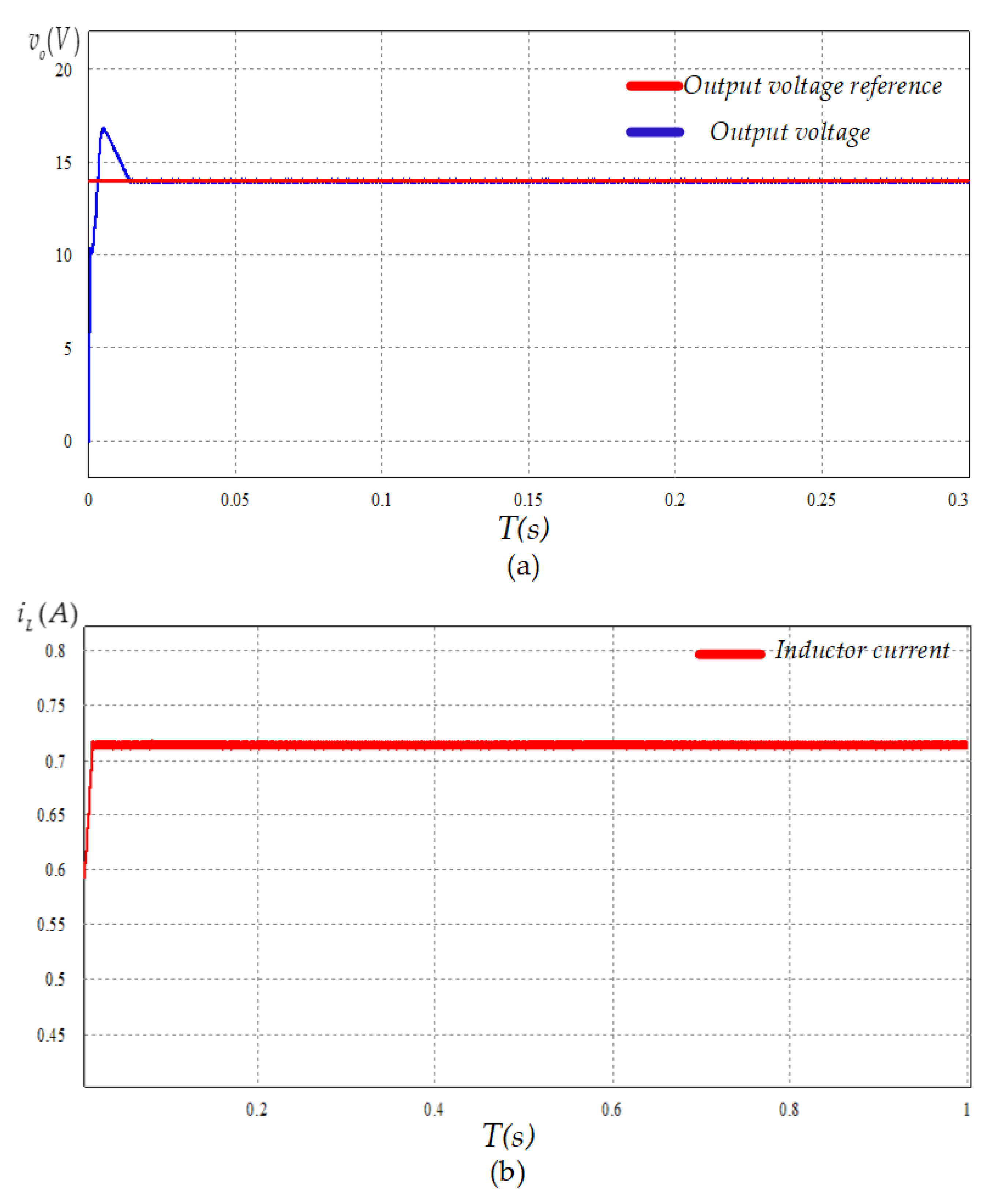
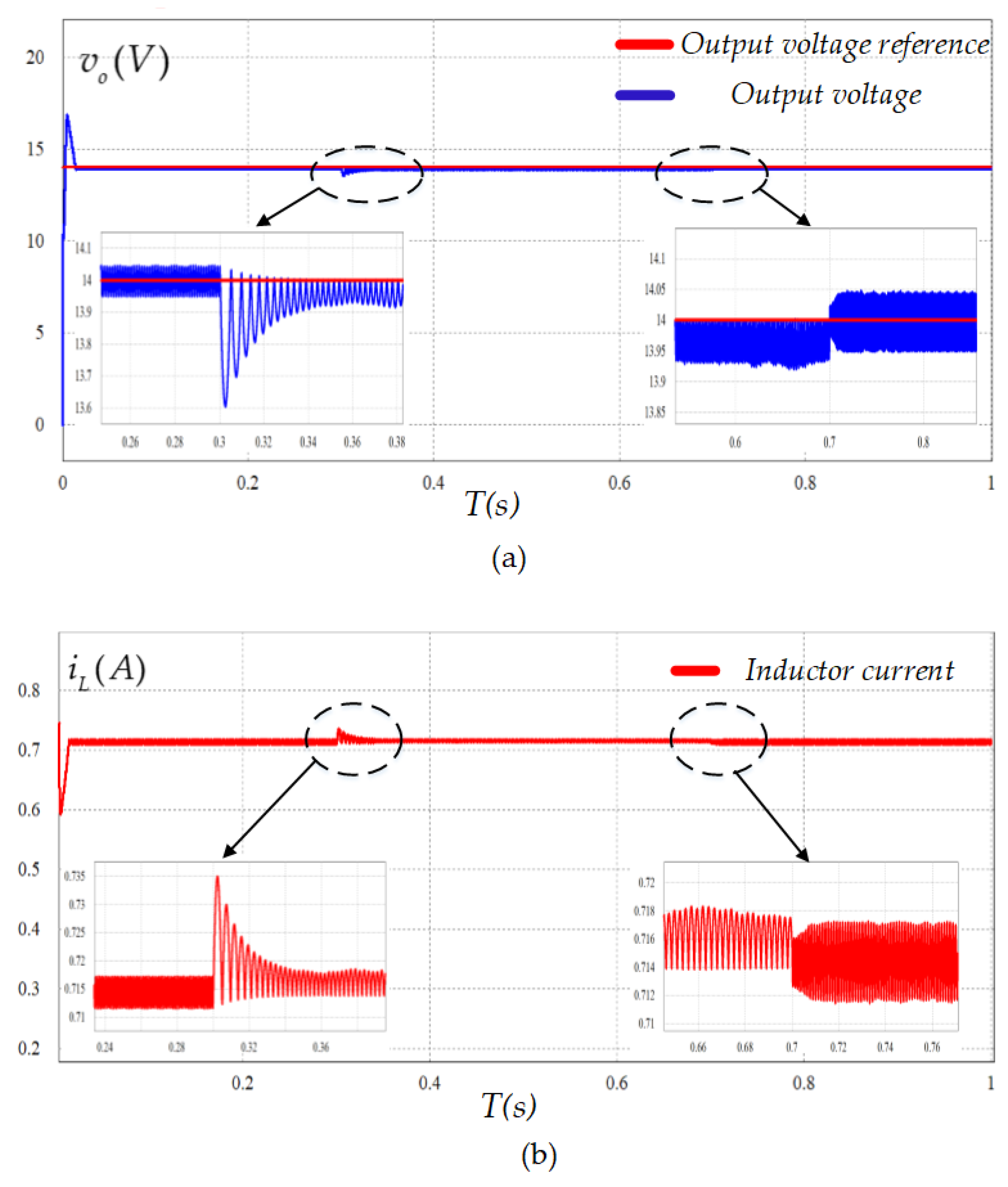
5.1. Simulation Results

The simulation study was carried out in the PSIM environment. In this section, the simulation results of the proposed controller in case 1 and case 2 are presented in Figure 10, Figure 11 and Figure 12.

5.1.1. Power Demand Variation Test

The responses of the studied system with the suggested controller are shown in Figure 10 and Figure 11. These responses have a short settling time of 0.01 s, a small overshoot and track the output voltage to achieve a zero steady state. The proposed controller rejects all disturbances, despite the variation in the power required by the CPL, as shown in Figure 11.

The experiment of the power load demand test was performed as follows: the overall system consumed 10 W from 0 s to 0.3 s. From 0.3 s to 0.7 s, we carried out a sudden increase in the power demand by the CPL to 20 W. After that, we performed a sudden decrease of 10 W (original value) for the rest of the time, as shown in Figure 11a.

5.1.2. Input Voltage Fluctuation Test

To test the effectiveness and robustness of the suggested approach against input voltage, fluctuations were performed in the input voltage, as shown in Figure 12. The input voltage passes from 28 V to 23 V and then returns to the nominal value. Based on the obtained results, it can be seen that the output voltage tracks the desired reference value with no significant variation observed. The proposed controller produces negligible variations in the inductor current response under input voltage fluctuation.

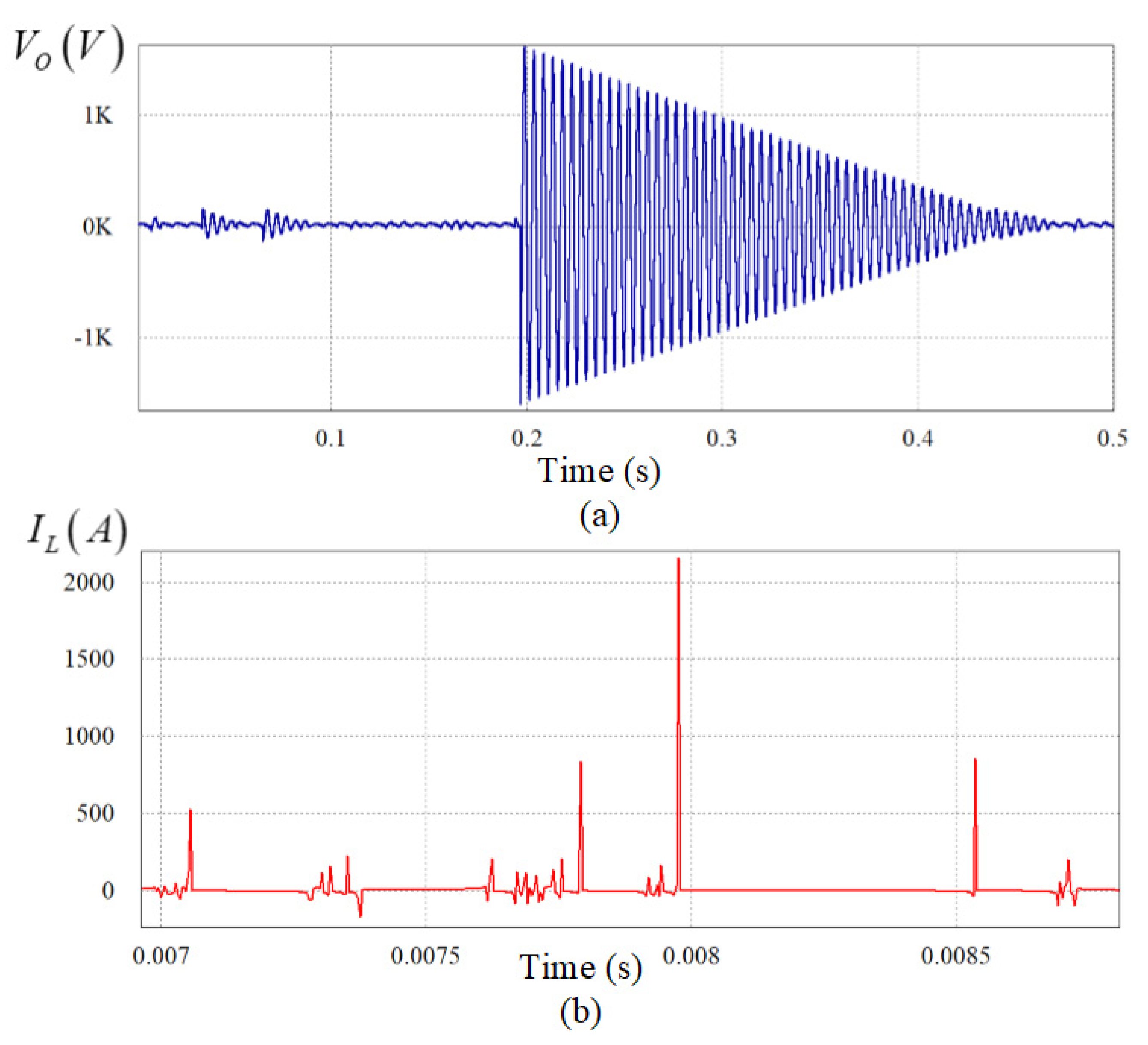
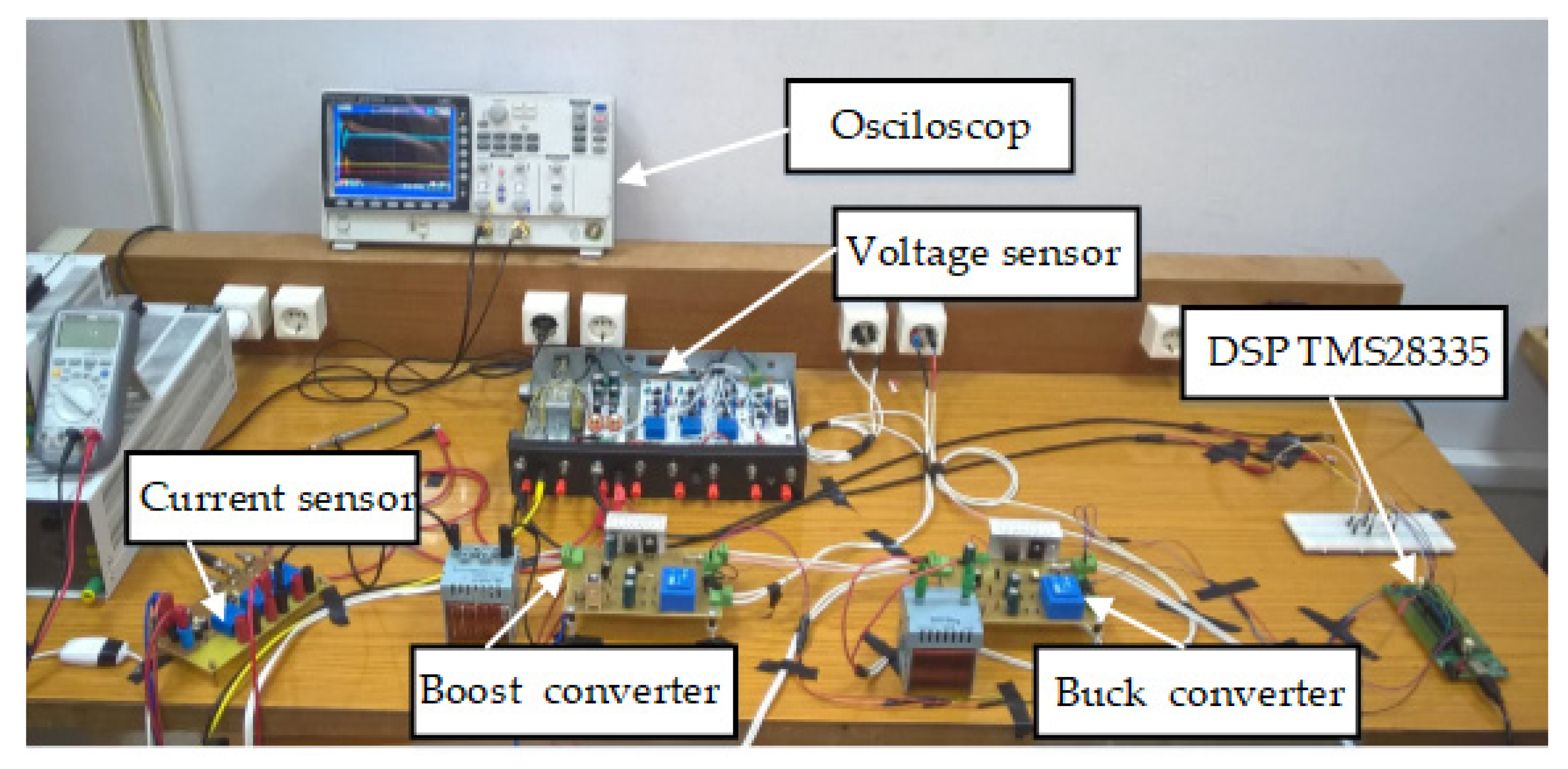
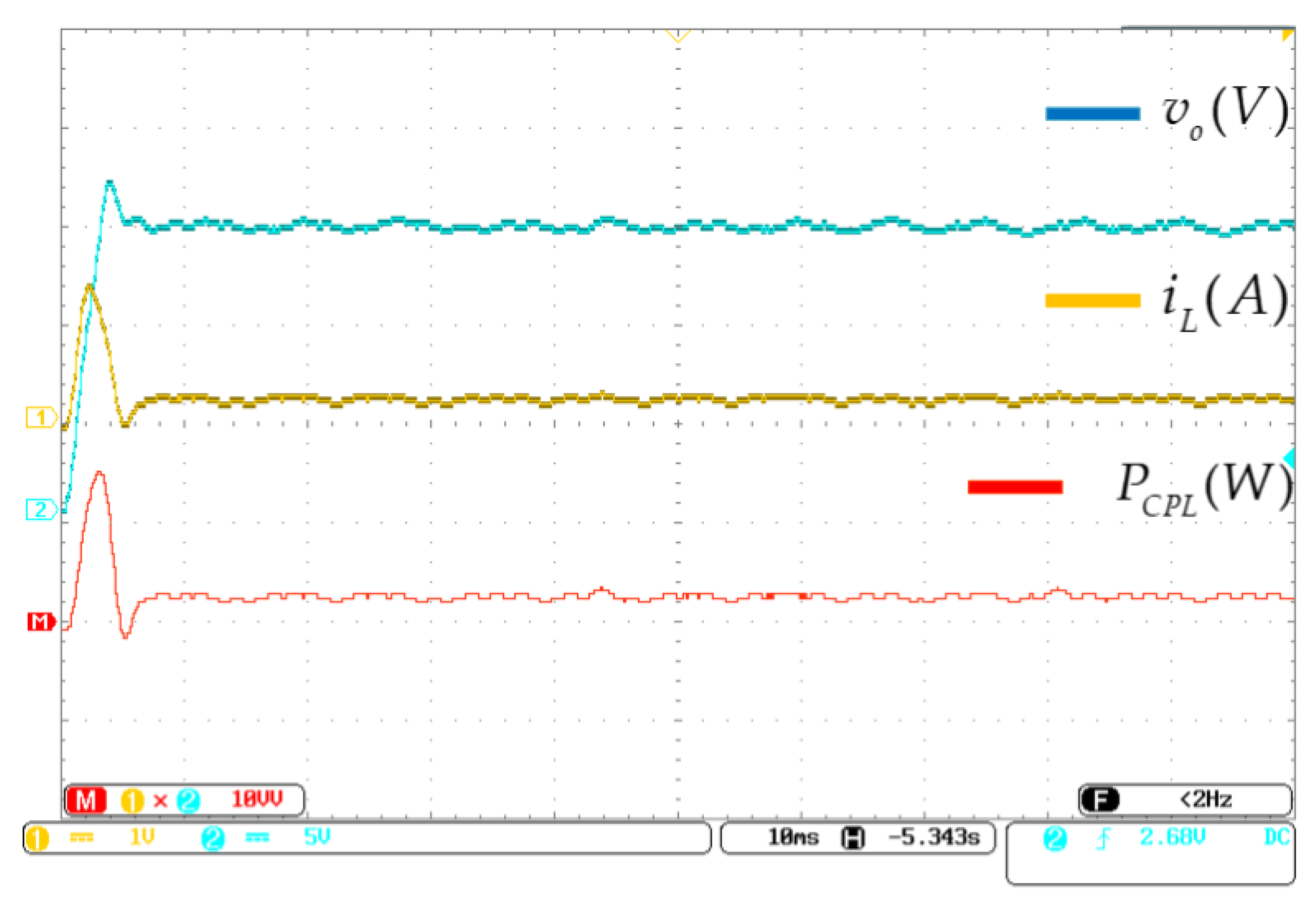
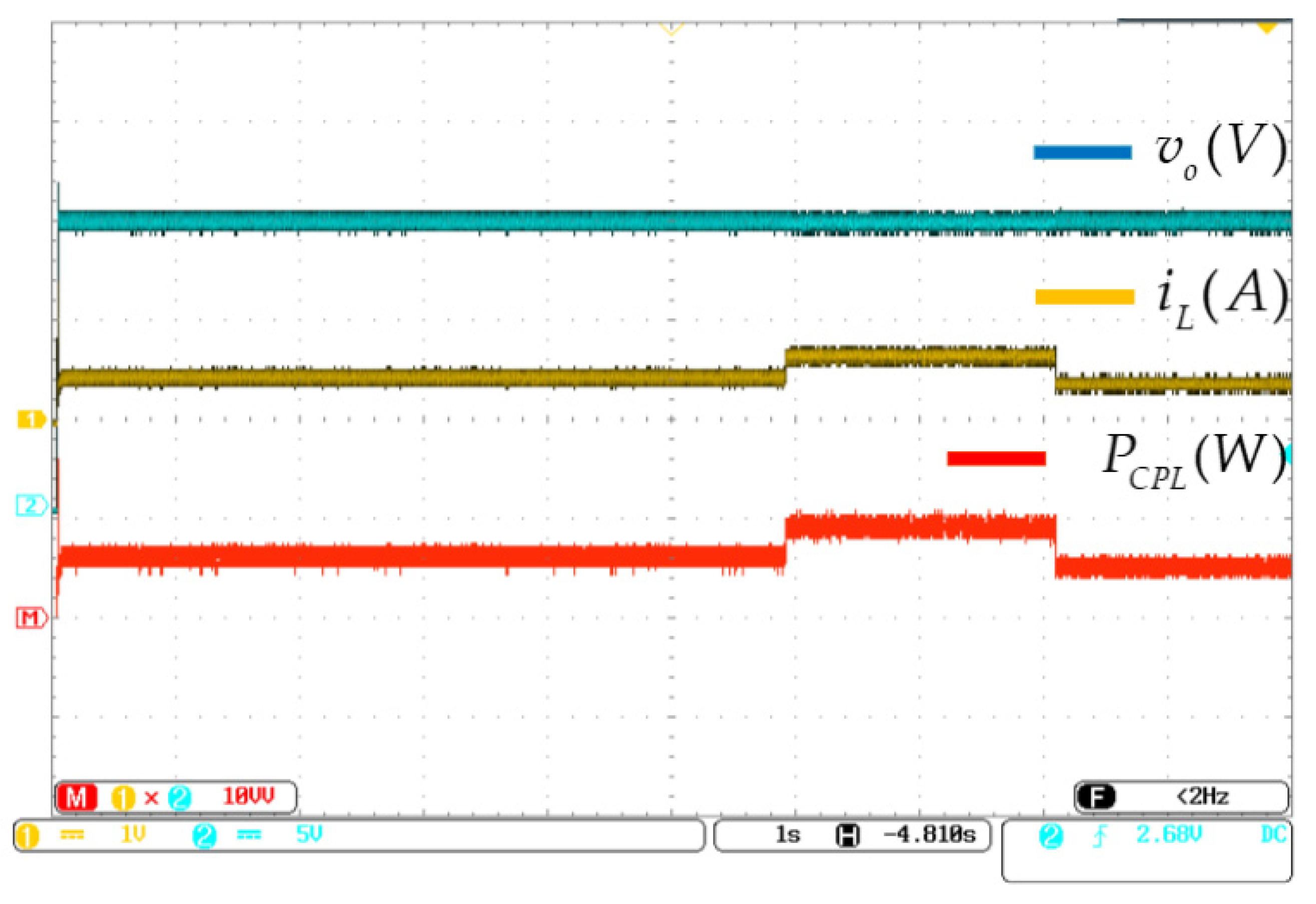
5.2. Experimental Results and Discussion

To verify the system modeling and the proposed controller, an experimental setup was carried out based on the generated code C of the PSIM software. In this experiment, a voltage-controlled boost converter (acting as a CPL) was supplied by a buck converter. The experimental platform is shown in Figure 13. The effectiveness of the suggested controller was tested considering two scenarios. The power demand variation test was carried out by adjusting the resistive load of the voltage-regulated boost converter, while input voltage variations were made by varying the DC source. It is worth mentioning that despite the fact that the parameters listed in Table 2 are not similar to the values used in the implementation, all the experimental results show perfect tracking performance and disturbance rejection.

The experimental setup was built by using a DC source (VDC = 28 V), a buck converter, a voltage-controlled boost converter (load converter), a TMS28335 microcontroller, voltage sensor LA25-NP (717087), and current sensor LV25-P (714227). Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 show the experimental results. We note that all the experimental equipment are listed in

Table A1. Equipment used in the experimental setup.

N	The Equipment
1	DC-DC buck converter
2	DC-DC boost converter
3	DC source giving a 28 V
4	DSP TMS28335 C2000 microcontroller
5	Voltage sensor LA25-NP (717087)
6	Current sensor LV25-P (714227)
7	Buck converter’s inductance L = 2.7 mH
8	Boost converter’s inductance Lb = 0.52 mH
9	Buck converter’s capacitance C = 470 uF
10	Boost converter’s capacitance Cb = 470 uF
11	Boost converter’s resistive load RLoad = 30 Ω
12	Code Composer Studio software (CCS)
13	PSIM software

in the Appendix A.

The buck converter’s parameter values utilized in this implementation are: v_in = 28 V, v_o = 14 V, C = 470 uF, L = 2.7 mH, r_L = 0.8 Ω, P_CPL = 10 W and f_sw = 25 kHz.

The parameters of the boost converter are: v_{in_b} = 14 V, v_{o_b} = 20 V, C_b = 470 uF, L_b = 0.52 mH, r_{L_b} = 0.52 Ω, R_Load = 30 Ω and f_sw = 25 kHz.

5.2.1. CPL Changing Experiment

This experiment study assessed the effectiveness of the proposed control against the sudden power demand of the CPL. In this experiment, the power load demand was changed from 10 W to 20 W and to 10 W again. The experimental results are presented in Figure 15, Figure 16 and Figure 17.

Figure 15 shows the experimental waveforms for both output current and output voltage for a buck converter when the power demand varies. We note that the input voltage remains fixed at v_in = 28 V. As can be remarked through the experimental results, the suggested controller ensures the output voltage follows its desired reference v_in = 14 V with a fast settling time of less than 0.02 s and a short overshoot. Figure 18 shows that even when a power load is changed with sequential variations, the output voltage remains constant.

5.2.2. Input Voltage Variation Test

Input voltage variation is one of the most serious power quality issues because it can damage electronic systems and cause significant systemic problems. In addition, fluctuations in input voltage decrease the quality of electronic equipment and cause the instability of internal voltages and currents.

In this experiment, the robustness of the proposed approach was assessed by applying a 10% sequential variation in the input voltage of the buck converter, as shown in Figure 20.

The input voltage of the buck converter changed with a rate of 3 V as follows: 28 V toward 25 V and returns to 28 V, respectively. In this experiment, the CPL power was kept constant at 10 W. Figure 19 and Figure 20 show the response of the output voltage before and after applying sequential variations in the input voltage.

Based on the experimental results, it can be seen that the behavior of the output voltage response remains unchanged at v_o = 14 V. The effect of fluctuating input voltage on the output voltage of the buck converter feeding a CPL is almost nonexistent. The proposed controller rejects the fluctuations caused in the input voltage.

6. Conclusions

In this paper, a nonsingular terminal sliding mode controller has been investigated to control a DC-DC buck converter supplying a tightly voltage-regulated boost converter which acts as constant power load. CPL loads are known as loads that can be seen as negative impedance, which bring stability issues to the overall system. In order to adapt this nonlinear control technique to this particular case, first, the singularity problem, which is the main weakness of the terminal sliding mode, has been solved by suggesting a new sliding surface in which negative fractional terms are removed from the control law. In the second step, the system model of the DC-DC back converter with the CPL has been transformed in order to be adapted to the derived nonsingular sliding mode controller. This approach allowed us to avoid the passive load and virtual impedance used in several works.

The effectiveness of the proposed controller has been confirmed by simulation and experimental setups. Two case studies have been carried out to assess its effectiveness. The first test was against the variation in the power demand and the second one against input voltage fluctuations. These two tests are common situations in DC or AC microgrids. As a result, good performance tracking and disturbance rejection were found. The experimental results have also proven these two features of the proposed controller. As a perspective, the authors plan to apply this control strategy to another constant power load such as an AC motor drive with constant speed.