AI-Based Real-Time Star Tracker
Abstract
1. Introduction
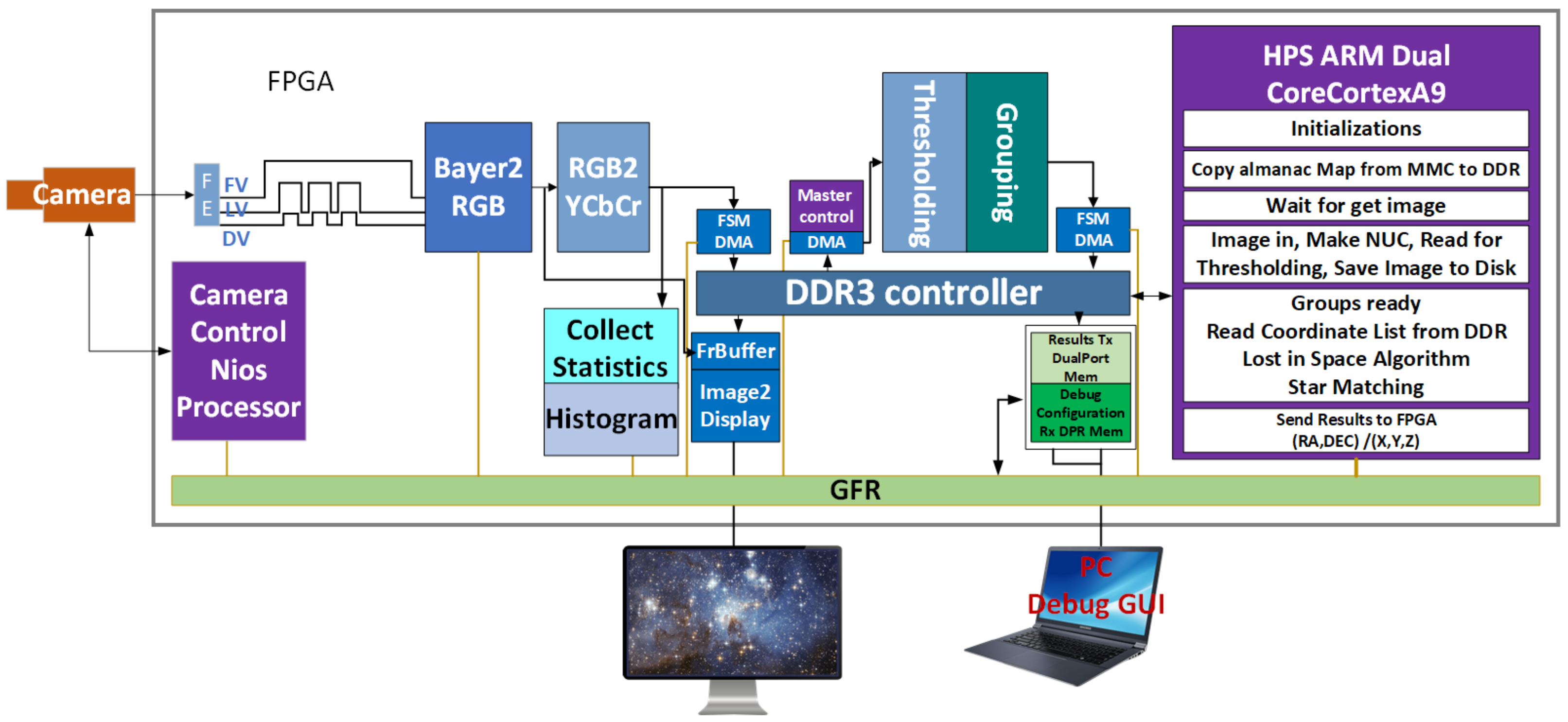
2. Materials and Methods
- A high-sensitivity VIS camera [14];
- A DE1 evaluation board with Cyclone V FPGA-SOC with an ARM cortex A9 Dual Core processor [15];
- A screen that displays the captured image at 60 FPS;
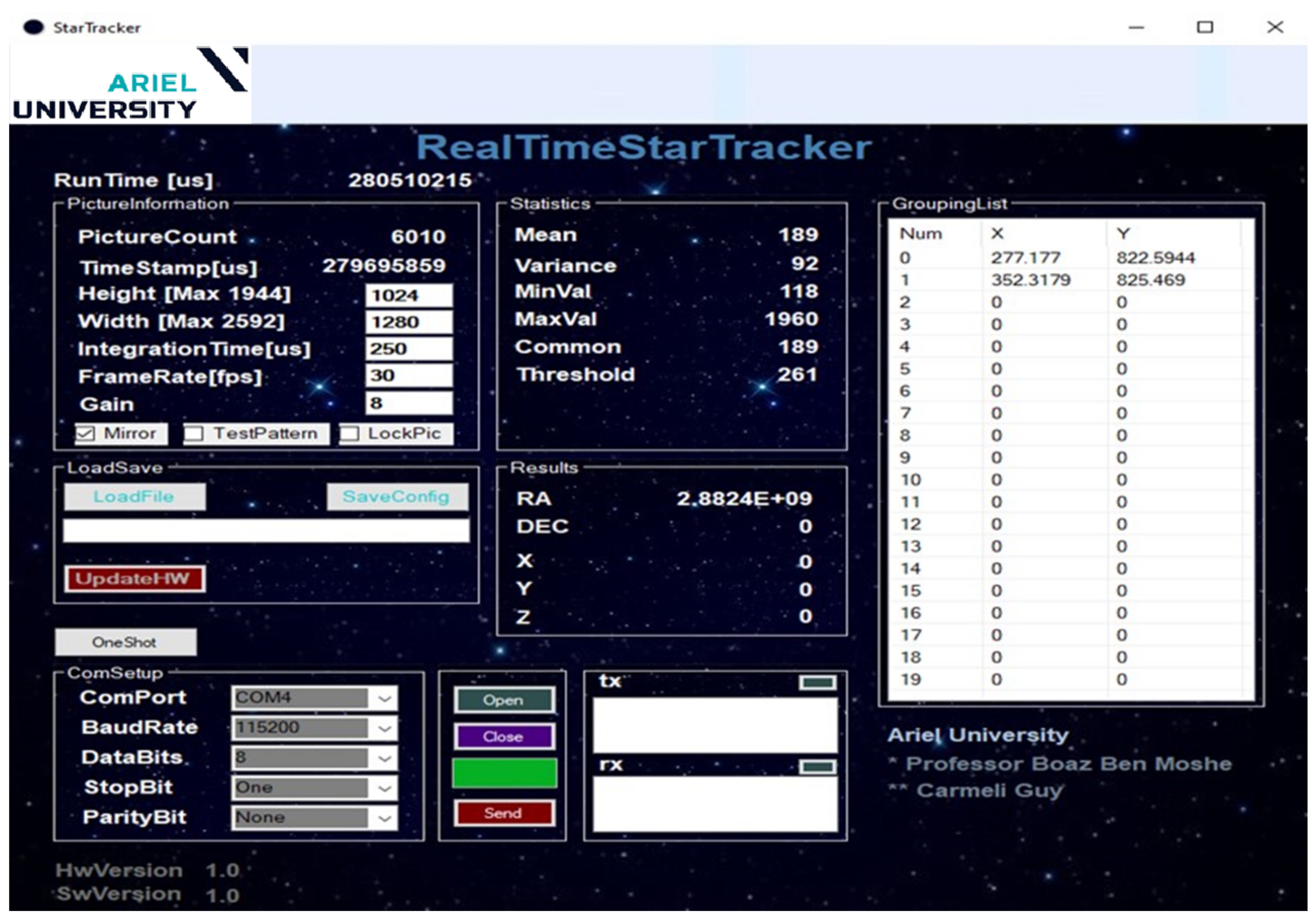
- A GUI application that allows a convenient interface with the camera for testing purposes during the study and for displaying the results after the image has been processed.
2.1. Optical Sensor and Image Capture
2.2. Image Processing
- Image average, STD, and variance, which are used to calculate parameters for the thresholding process;
- Pixel min/max value, range: max–min, which can be used for image enhancement of the display, such as stretching the histogram of the image;
- Building a histogram and finding the parameters: common1, number of pixels in common1, common2, number of pixels in common2, saturation signal (actively high when 20% of the pixels are above 90% of brightness), and the number of pixels above the saturation value. The FPGA looks for two common values, one on the left side of the histogram for dark pictures and the other on the right side of the histogram for images with either the sun or the moon. The common value is used for the threshold calculation and for the exposure-time control mechanism. This process is performed on every single frame.
2.2.1. Non-Uniformity Calibration and Statistical Thresholding
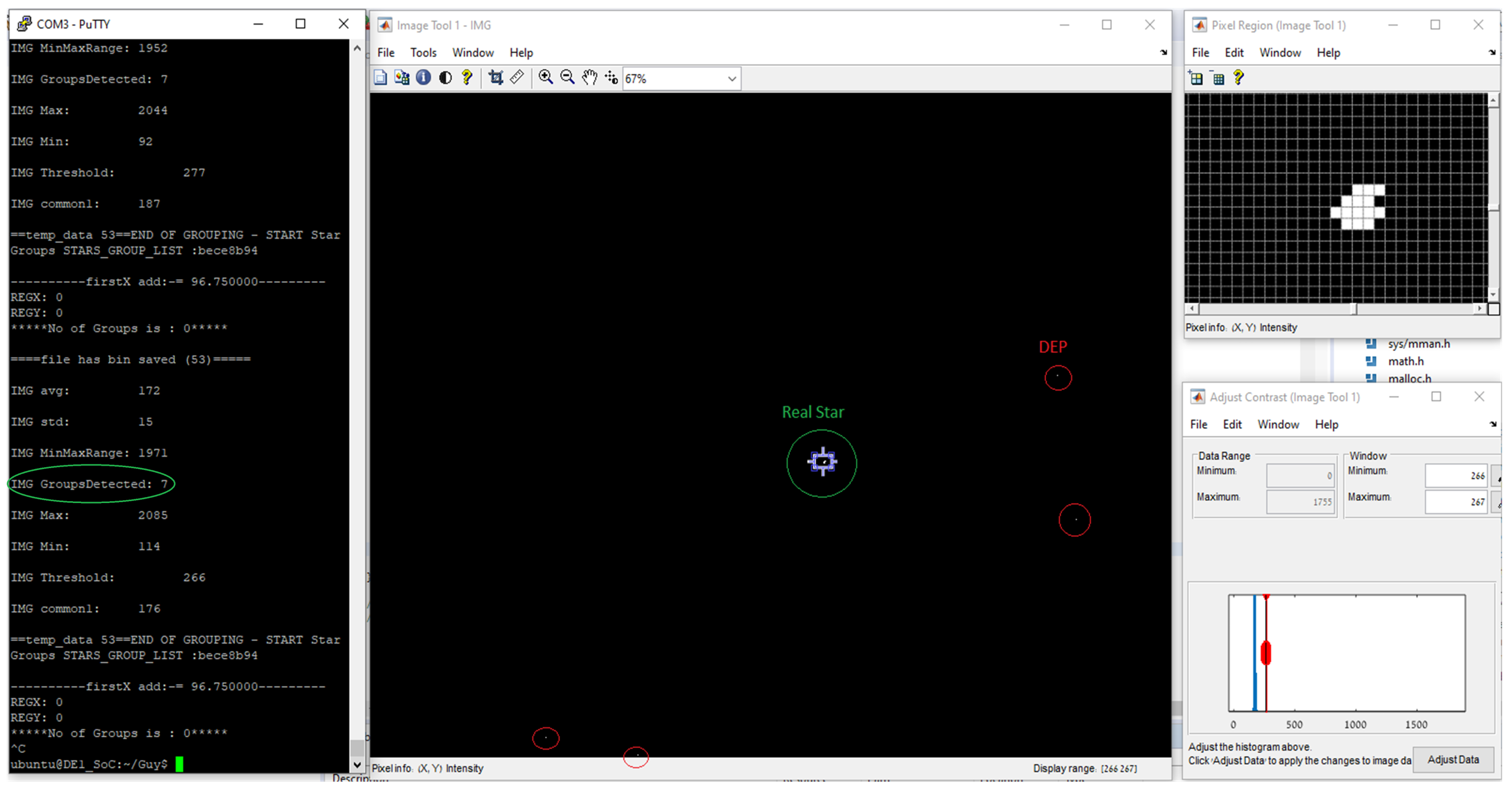
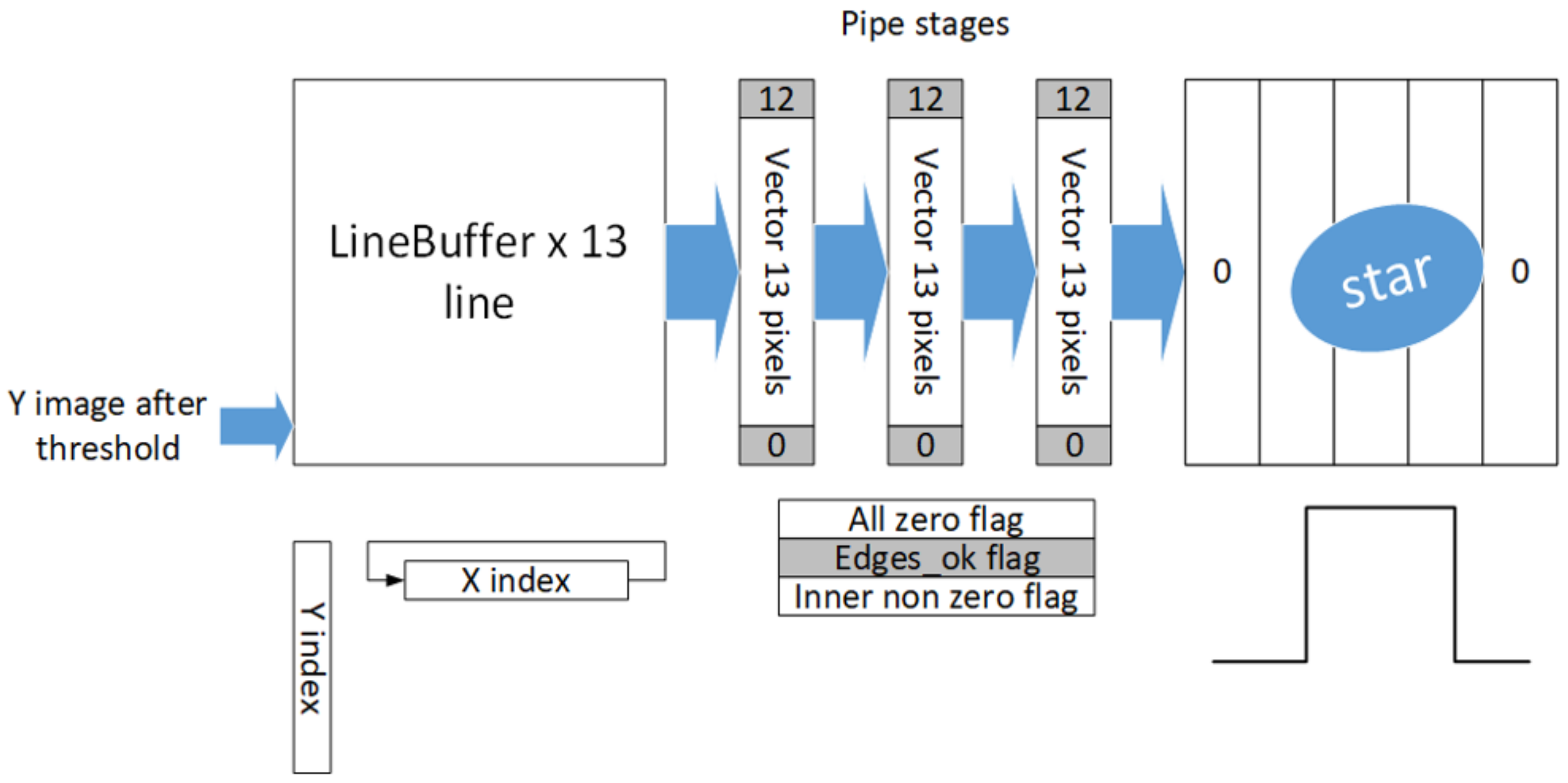
2.2.2. Clustering Detection and Saving Groups to Memory
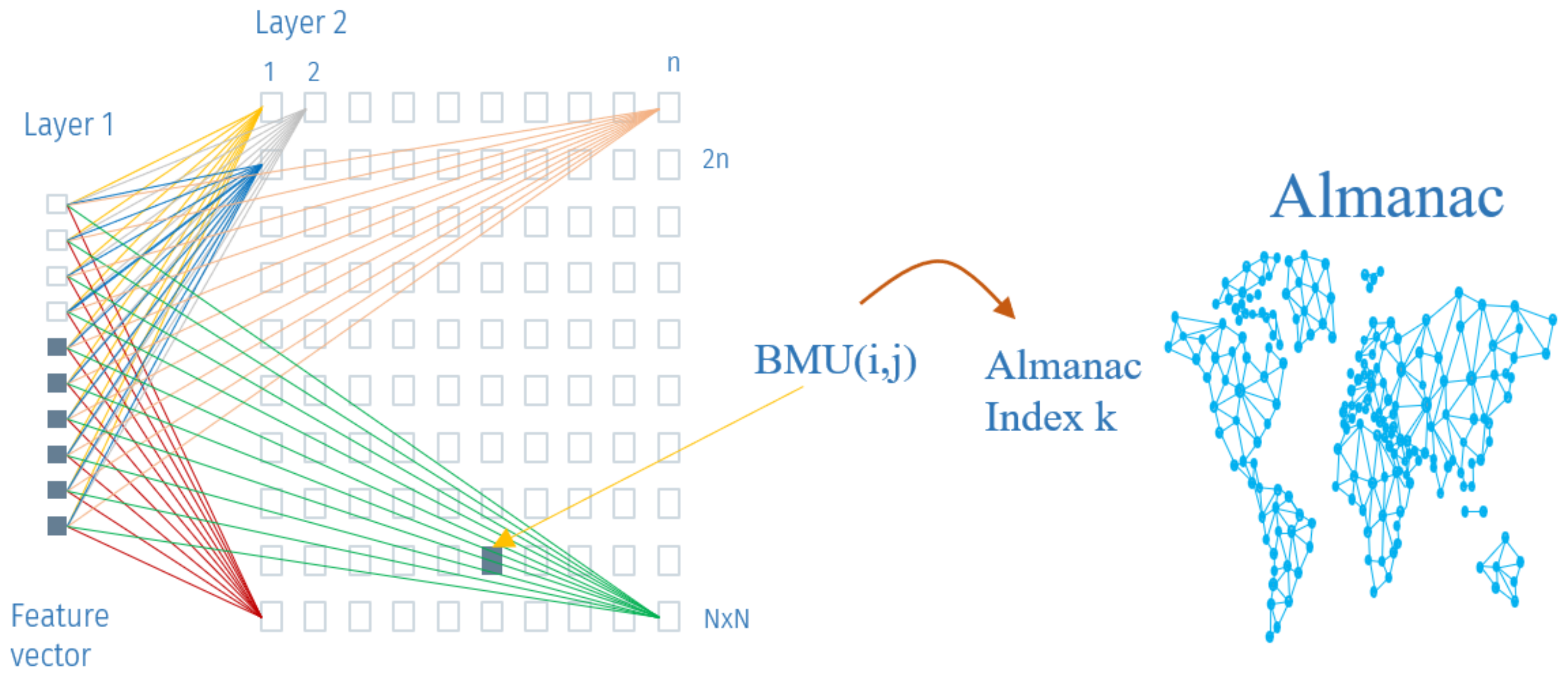
2.3. Star Pattern Recognition Related to Almanac
| Algorithm 1 ARM preparatory actions for pattern matching using an AI Kohonen map [1] |
|

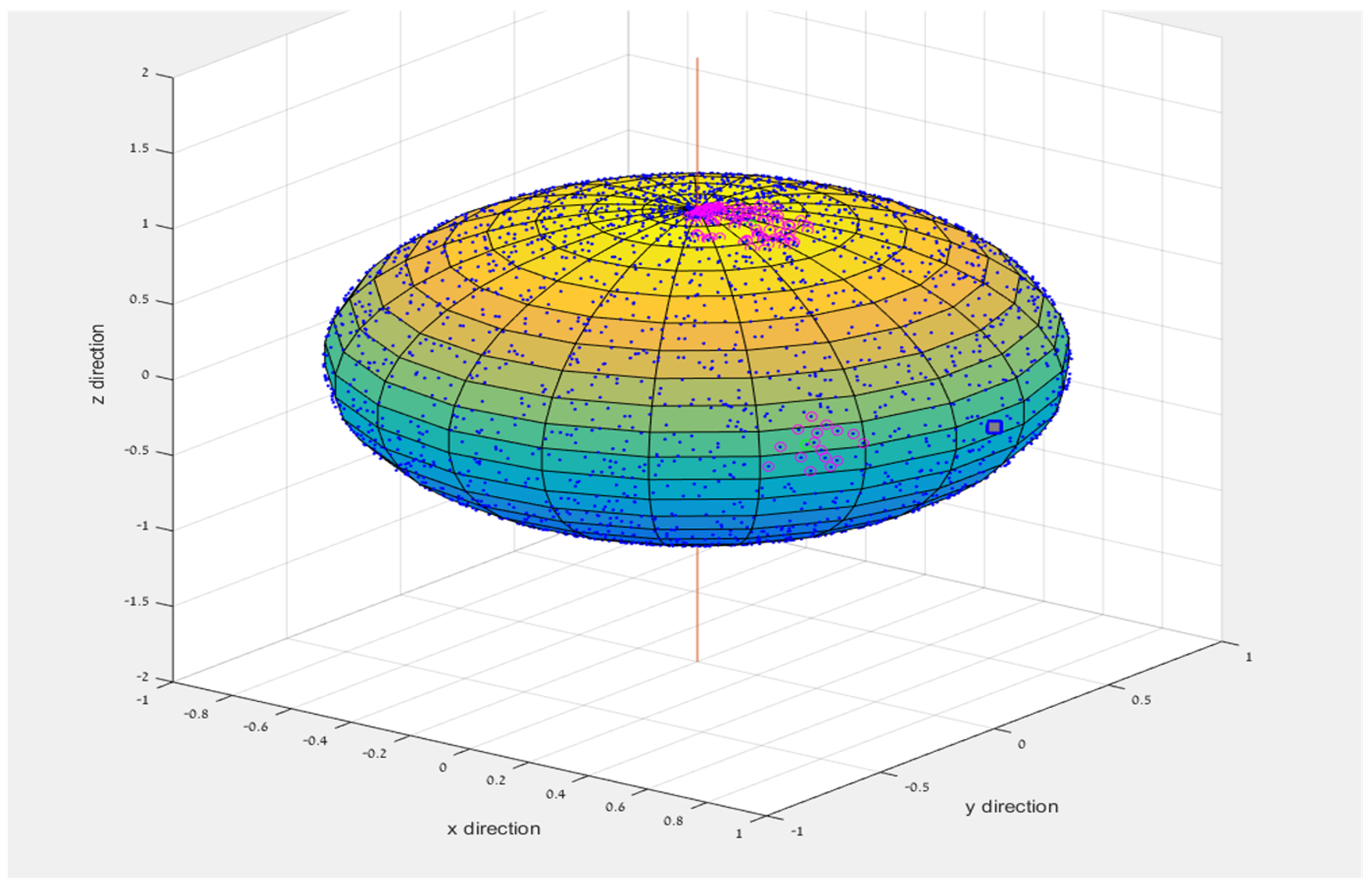
2.3.1. Building the Database Using Camera Sensitivity in a Given FOV, for NN Training
- 1.
- Select the radius in a FOV; in our case, radius R = 7.5 deg.
- 2.
- From the Tycho2 2018 almanac, a sensitivity of magnitude 6 is selected. The database is filtered accordingly and then sorted by intensity from high to low. The map is now reduced to 4642 stars out of over two million.
- 3.
- For each star, we take the four brightest neighboring stars, for which the minimum distance between the main star and the nearest neighbor is 0.85 degrees.
- 4.
- Find the distances between any two stars in a five-star group. We gather all 10 distance combinations. Neighbors are chosen in such way that they are not closer than 20 pixels (angular distance) to another star.
- 5.
- The angular distances are sorted in ascending order and constitute the features vector of the SOM.
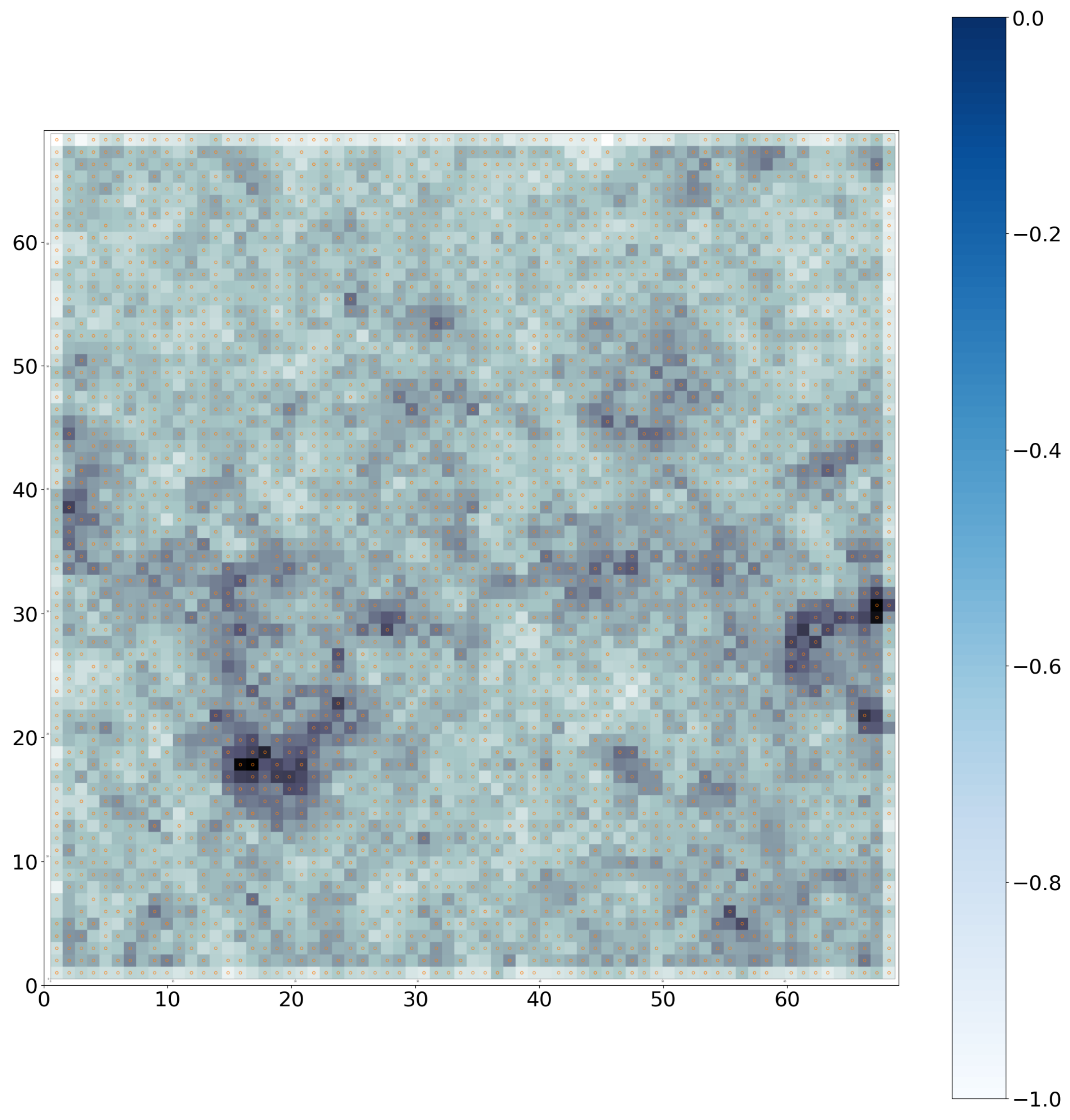
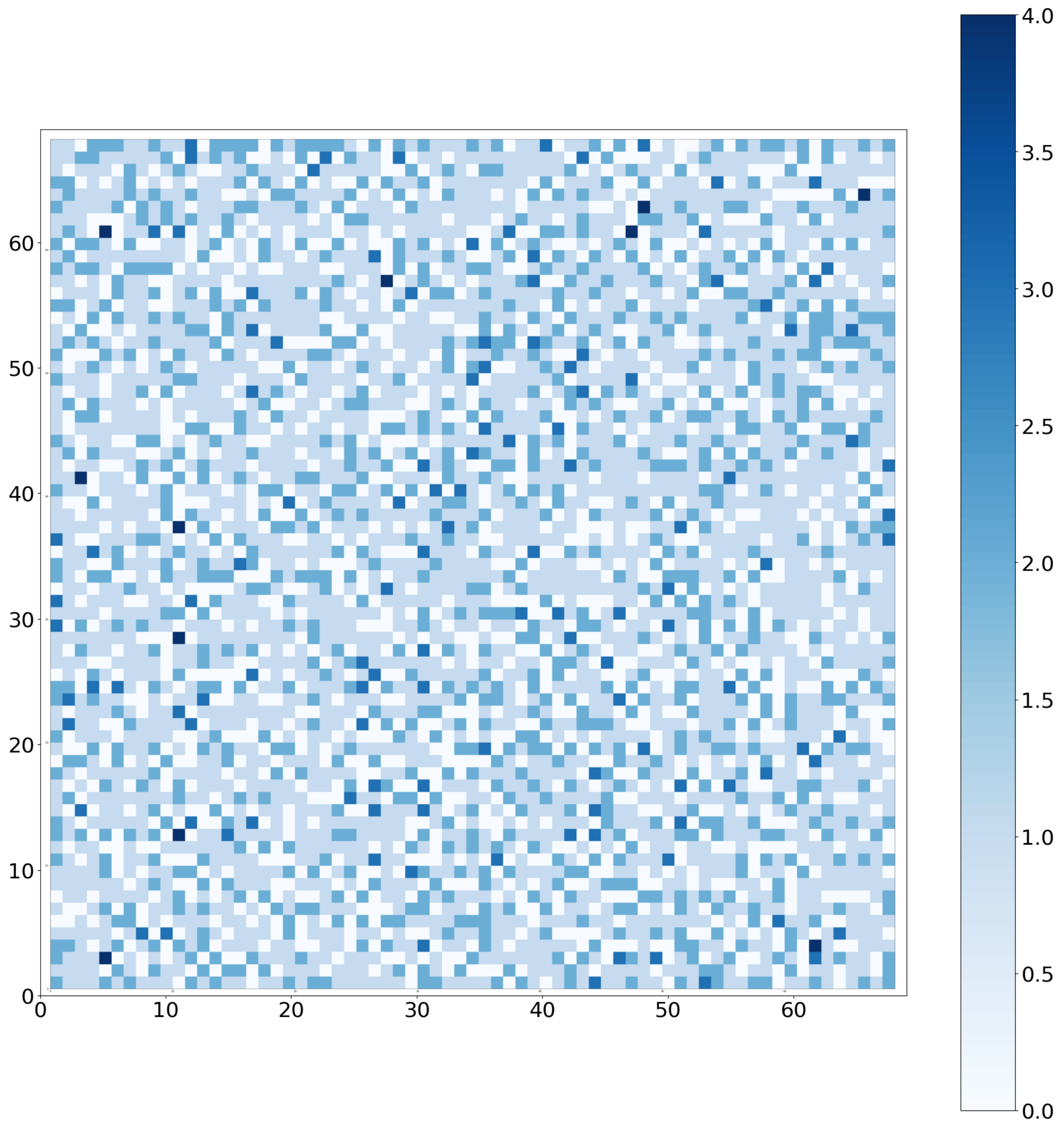
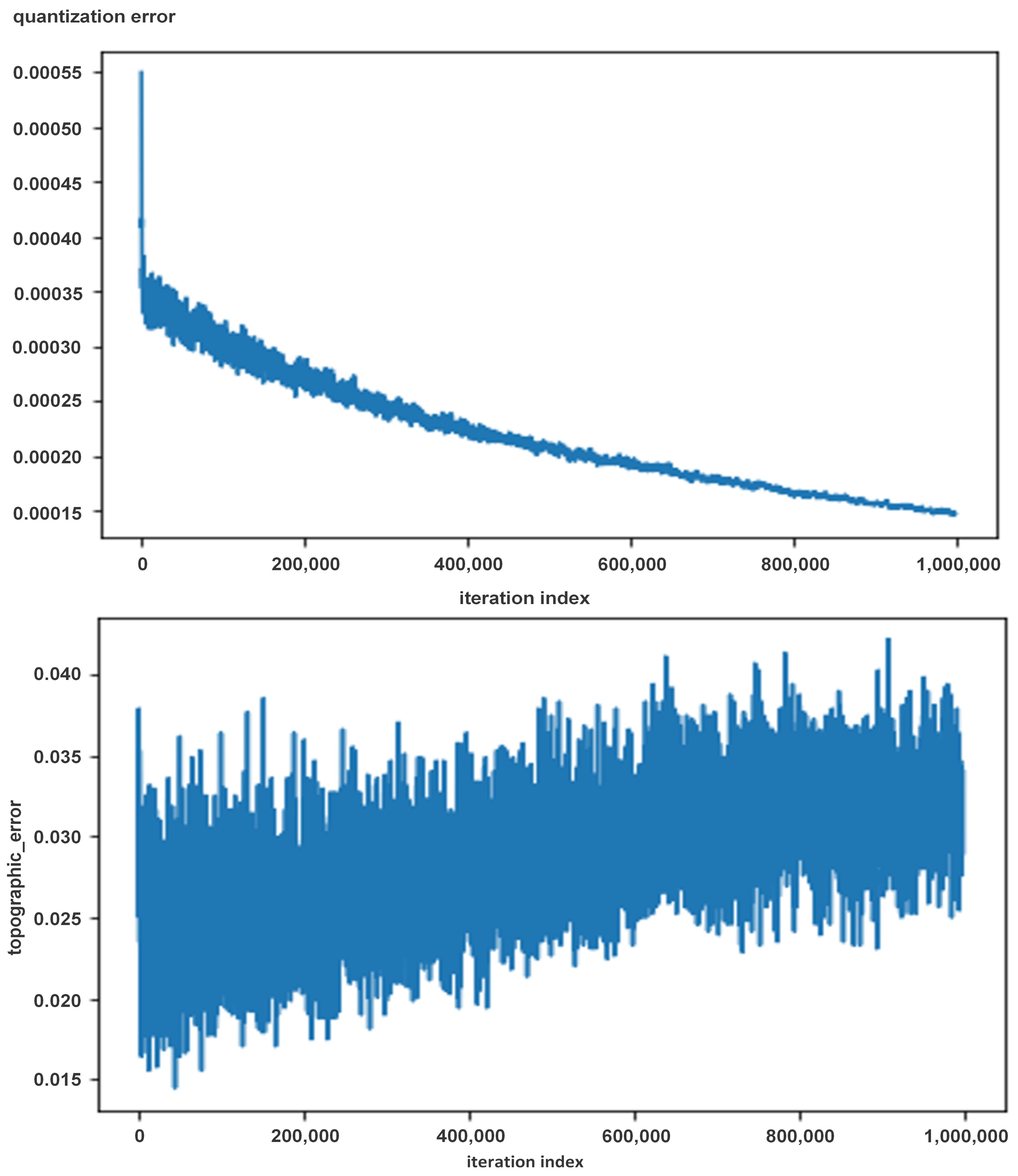
2.3.2. Building a Self-Organizing Map Network—Kohonen Map
- Size: 69 × 69;
- Features vector: 10;
- Clusters output: 4642;
- Sigma: 3;
- Learning rate: 0.7;
- Neighborhood function: Gaussian;
- Train batch: 1 M.
| Algorithm 2 Apply the self organizing map (SOM) algorithm: repeat the following procedure until the map converges1. |
|
1 whereby:
|
3. Results
4. Timing and Performance
Expected Pointing Accuracy
5. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, G.; Zhang, G. Star Identification Utilizing Neural Networks; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Gose, E.; Johnsonbaugh, R.; Jost, S. Pattern Recognition and Image Analysis; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Mantas, J. Methodologies in pattern recognition and image analysis—A brief survey. Pattern Recognit. 1987, 20, 1–6. [Google Scholar] [CrossRef]
- Salomon, P.M.; Glavich, T.A. Image signal processing in sub-pixel accuracy star trackers. In Proceedings of the 24th Annual Technical Symposium, San Diego, CA, USA, 29 July–1 August 1980; Volume 252, pp. 64–74. [Google Scholar]
- Liebe, C.C. Accuracy performance of star trackers-a tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Wang, B.; Wang, H.; Jin, Z. An Efficient and Robust Star Identification Algorithm Based on Neural Networks. Sensors 2021, 21, 7686. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, T.; Feng, G.; Ni, M.; Ou, S. A fuzzy C-means clustering algorithm based on spatial context model for image segmentation. Int. J. Fuzzy Syst. 2021, 23, 816–832. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Terasic. DE1-SoC Development Kit User Manual; DE1-SoC Manual; Terasic: Hsinchu, Taiwan, 2016. [Google Scholar]
- Rockett, L.; Patel, D.; Danziger, S.; Cronquist, B.; Wang, J. Radiation hardened FPGA technology for space applications. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, Montana, 3–10 March 2007; pp. 1–7. [Google Scholar]
- Wirthlin, M. High-reliability FPGA-based systems: Space, high-energy physics, and beyond. Proc. IEEE 2015, 103, 379–389. [Google Scholar] [CrossRef]
- Anjankar, S.C.; Kolte, M.T.; Pund, A.; Kolte, P.; Kumar, A.; Mankar, P.; Ambhore, K. FPGA based multiple fault tolerant and recoverable technique using triple modular redundancy (FRTMR). Procedia Comput. Sci. 2016, 79, 827–834. [Google Scholar] [CrossRef]
- Terasic. Terasic TRDB D5M, 5 Mega Pixel Digital Camera Development Kit; USer Manual; Terasic: Hsinchu, Taiwan, 2017. [Google Scholar]
- Support Intel. Intel SoC FPGA Embedded Development Suite User Guide; ug-1137; Support Intel: Santa Clara, CA, USA, 2019. [Google Scholar]
- Minervini, M.; Rusu, C.; Tsaftaris, S.A. Computationally efficient data and application driven color transforms for the compression and enhancement of images and video. In Color Image and Video Enhancement; Springer International Publishing: Cham, Switzerland, 2015; pp. 371–393. [Google Scholar]
- Sunex. Lens—Sunex DSL901j-NIR-F3.0. 2017. Available online: http://www.optics-online.com/OOL/DSL/DSL901.PDF (accessed on 4 April 2023).
- Padgett, C.; Kreutz-Delgado, K. A grid algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 202–213. [Google Scholar] [CrossRef]
- Mortari, D.; Samaan, M.A.; Bruccoleri, C.; Junkins, J.L. The pyramid star identification technique. Navigation 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Aghaei, M.; Moghaddam, H.A. Grid star identification improvement using optimization approaches. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2080–2090. [Google Scholar] [CrossRef]
- Luo, L.Y.; Xu, L.P.; Zhang, H.; Sun, J.R. Improved autonomous star identification algorithm. Chin. Phys. B 2015, 24, 064202. [Google Scholar] [CrossRef]



| Subject | Parameters | Our Case |
|---|---|---|
| Active Matrix [mm] | 5.7H × 4.28V 1 | 2.81H × 2.25V |
| Active pixels | 2592H × 1944V | 1280H × 1024V |
| Pixel size | 2.2 × 2.2 m | |
| Bit depth Global shutter | 12 bit | |
| Gain A/D | 1–16 Analog, Digital | 16 Analog |
| FOV [deg] | According to lens | 13.38H × 10.72V |
| Feature | Value |
|---|---|
| Sensor | MT9P001 |
| Lens: SUNEX | DSL901j-NIR-F3.0 |
| Focal length | 12 mm |
| F# | 3 |
| Aperture | 4 mm |
| SensorActiveArea-X | 0.002816 m |
| SensorActiveArea-Y | 0.0022528 m |
| X | 1280 Pixels |
| Y | 1024 Pixels |
| Pixel Size | 2.2 m |
| Fov(x) | = |
| Fov(Y) | = |
| deg/Pixel(x) | = 0.01045 |
| deg/Pixel(y) | = 0.01046 |
| deg/Pixel(avg) |
| DDR addr | Base | ++4h | ++8h | ++Ch | ++10h |
|---|---|---|---|---|---|
| Variable | Total groups | ||||
| Group No. | – | Group1 | – | – | Group2 |
| MainStar Index | Feature1 | Fea.2 | Fea.3 | Fea.4 | Fea.5 | Fea.6 | Fea.7 | Fea.8 | Fea.9 | Feature10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.4423 | 0.5401 | 0.5713 | 1.7155 | 2.2265 | 2.2459 | 2.3442 | 3.5961 | 3.9351 | 4.1632 |
| 2 | 1.1573 | 1.6522 | 2.0266 | 2.4743 | 2.7054 | 2.7343 | 4.0751 | 4.3159 | 5.1978 | 6.5945 |
| 3 | 0.169 | 1.269 | 2.5161 | 2.7003 | 2.866 | 3.2137 | 4.6179 | 4.7815 | 5.658 | 5.8259 |
| 4 | 0.1473 | 0.9652 | 1.7718 | 1.836 | 1.9854 | 2.5176 | 2.8021 | 2.8488 | 3.6899 | 3.719 |
| … | … | … | … | … | … | … | … | … | … | … |
| 4642 | 2.6456 | 4.3696 | 6.0897 | 6.2987 | 6.6346 | 6.7552 | 7.0136 | 7.8045 | 9.025 | 12.6147 |
| Main Star Index | N1 | N2 | N3 | N4 1 |
|---|---|---|---|---|
| 21 | 423 | 449 | 446 | 70 |
| Star Index 21 Feature Vector [0–9] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3.1083 | 4.3947 | 5.0128 | 5.0412 | 6.1340 | 6.6687 | 6.6815 | 8.7224 | 9.4316 | 9.6025 |
| Main Star Index | N1 | N2 | N3 | N4 1 |
|---|---|---|---|---|
| 423 | 449 | 21 | 539 | 373 |
| Star Index 423 Feature Vector [0–9] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3.1083 | 4.3947 | 4.6086 | 5.0128 | 5.4160 | 6.1670 | 8.0109 | 8.3438 | 9.2132 | 9.5359 |
| Feature | Performance 1 |
|---|---|
| Exposure time | Varies as needed 100 ms to 500 ms. Camera dependent |
| Reading the image from the sensor (3 × 12 bit), Performing image processing and memory retention | ∼14 ms (Read image from sensor takes 13.6 ms Clk = 96 Mhz, Resolution 1280 × 1024) |
| Bayer To RGB-YCbC | latency 166 us: done on the fly |
| Building a histogram & collecting statistics | 0 delay, done on the fly, in parallel. |
| Nuc—Clear DEPs | 78 us , Done by HPS processor |
| Threshold and Clusters Detection, save groups to MeM | ∼14 ms (reading image from memory takes 13.1 ms, Clk = 100 Mzh, resolution 1280 × 1024) |
| AI Neural Network result | 870 us |
| Algorithm Identification | Time | Memory Consumption |
|---|---|---|
| Proposed algorithm | 870 us | 249 KB |
| NN Based algorithm [6] | 32.7 ms | 1920.6 KB |
| Pyramid algorithm [19] | 341.2 ms | 2282.3 KB |
| Optimized Grid algorithm [20] | 178.7 ms | 348.1 KB |
| Modified LPT algorithm [21] | 65.4 ms | 313.5 KB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carmeli, G.; Ben-Moshe, B. AI-Based Real-Time Star Tracker. Electronics 2023, 12, 2084. https://doi.org/10.3390/electronics12092084
Carmeli G, Ben-Moshe B. AI-Based Real-Time Star Tracker. Electronics. 2023; 12(9):2084. https://doi.org/10.3390/electronics12092084
Chicago/Turabian StyleCarmeli, Guy, and Boaz Ben-Moshe. 2023. "AI-Based Real-Time Star Tracker" Electronics 12, no. 9: 2084. https://doi.org/10.3390/electronics12092084
APA StyleCarmeli, G., & Ben-Moshe, B. (2023). AI-Based Real-Time Star Tracker. Electronics, 12(9), 2084. https://doi.org/10.3390/electronics12092084










