Optimization Decomposition of Monthly Contracts for Integrated Energy Service Provider Considering Spot Market Bidding Equilibria
Abstract
1. Introduction
- (1)
- Given the difficulties in the connection between the medium- and long-term market and the spot market and the volatility and uncertainty of the price and quantity of the spot market transactions, this paper designs a medium- and long-term monthly contract optimization decomposition strategy that can stabilize the bidding space in the spot market and reduce the fluctuation in the demand of spot bidding by considering the equilibrium of the bidding space in the spot market to ensure the smooth connection between the medium- and long-term market and the spot market;
- (2)
- To ensure the effective execution of the mid-and long-term contract decomposition results daily and reduce the contract decomposition deviation, this paper constructs a day-ahead scheduling model of the IES that accounts for the coupling of multiple energy flows, takes into account the substitution and cross-complementary characteristics of electricity, gas, and heat of multi-energy resources, and carries out the optimal scheduling of various types of resources based on the daily decomposition results of the mid-and long-term contracts;
- (3)
- To effectively alleviate the pressure of energy supply at the energy supply point and realize the efficient interconnection and interaction of electricity, gas, and heat networks in the IES, this paper considers the dynamic pipe storage characteristics of the gas network and realizes the low storage and high generation of the gas network. The results show that the method can effectively reduce the dispatch operation cost.
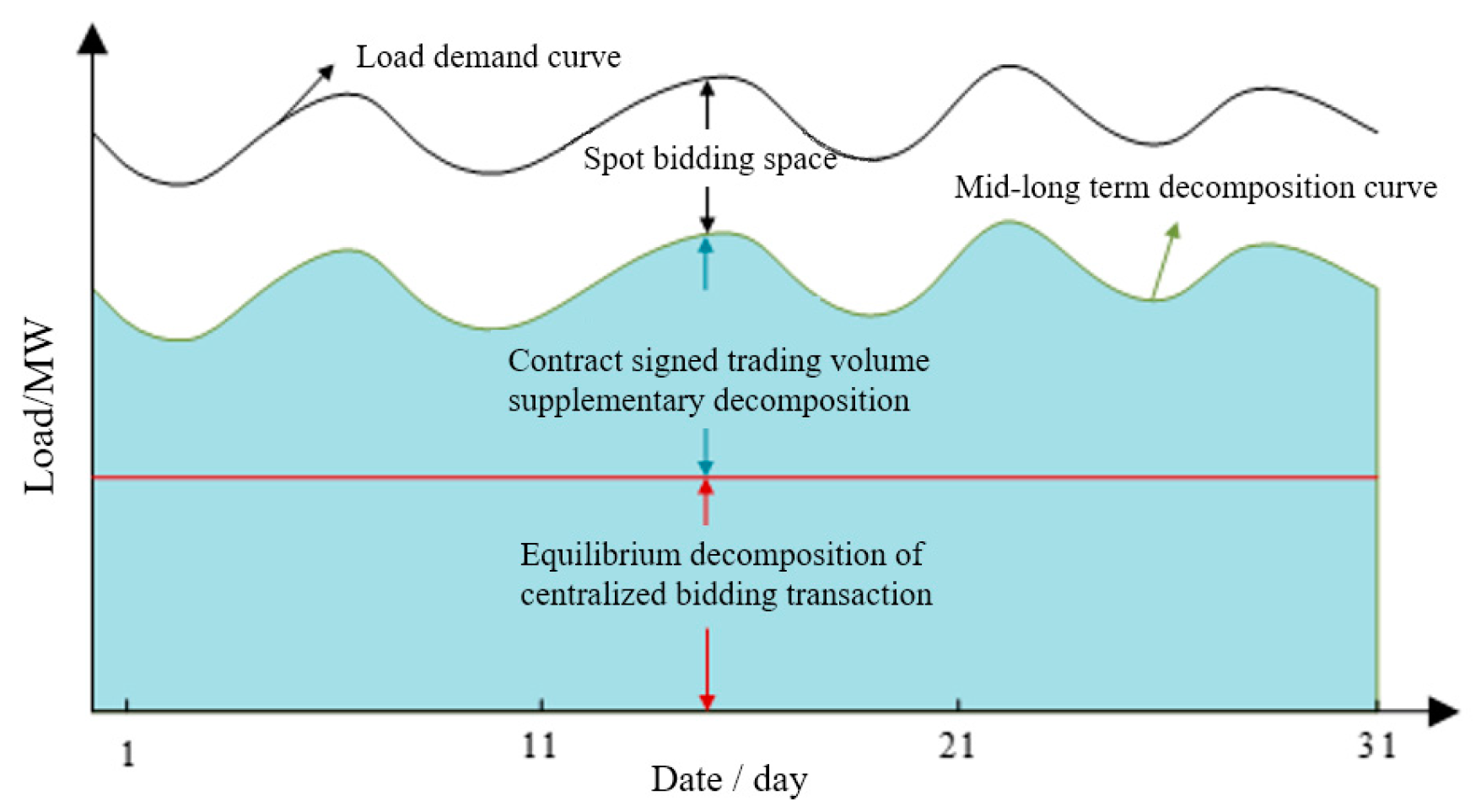
2. The Connection Process of Multi-Energy Transactions between the Medium- and Long-Term Market and the Spot Market
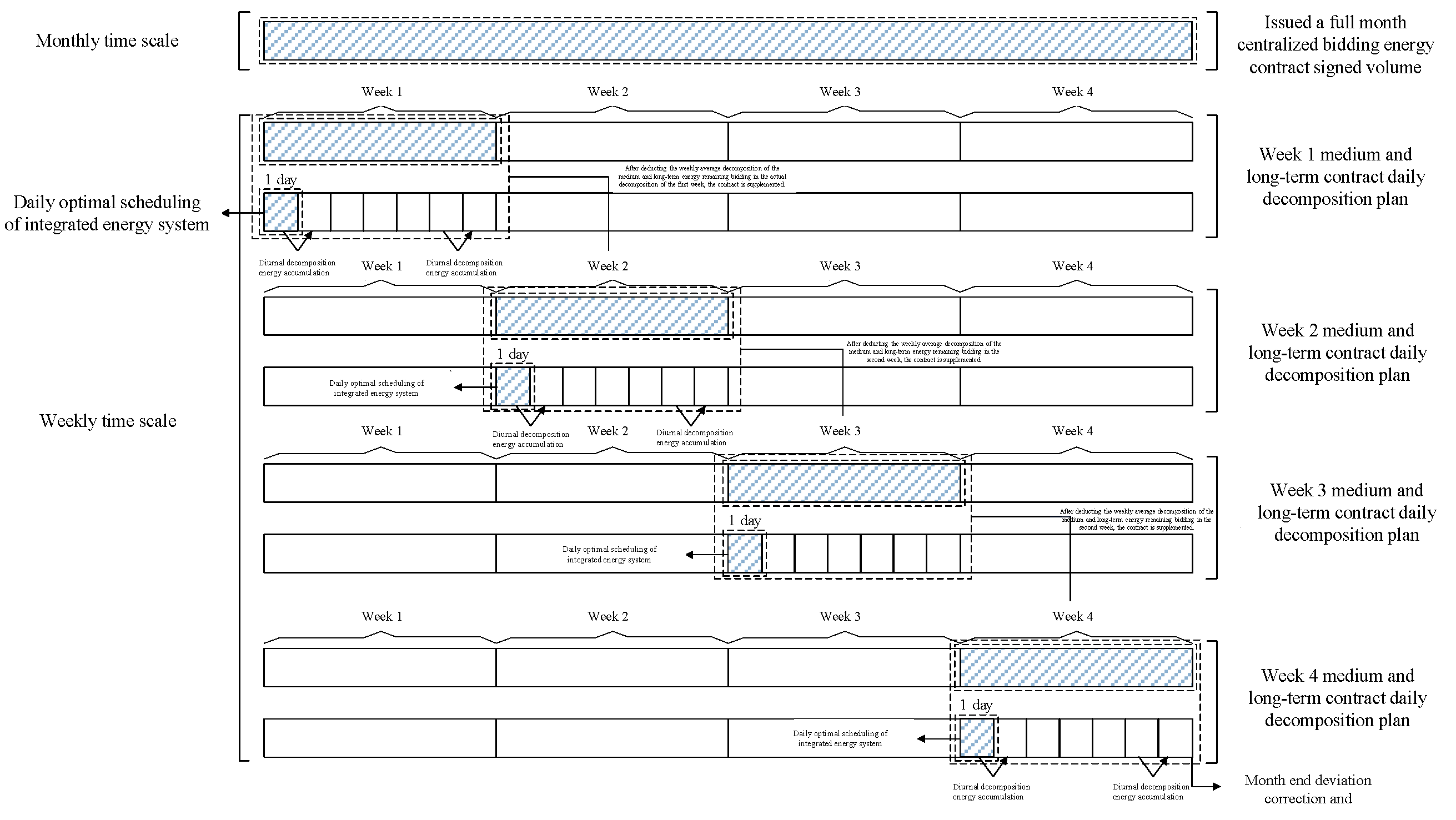
3. Daily Decomposition of Monthly Medium- and Long-Term Contracts Considering Spot Bid Equalization
3.1. Monthly Contract Optimization Decomposition Model
3.1.1. Objective Function
3.1.2. Restrictive Condition
4. A Day-Ahead Scheduling Model for IESs Accounting for Multiple Energy Flow Coupling
4.1. Objective Function
4.2. Restrictive Condition
4.2.1. Grid Operation Constraints
4.2.2. Gas Network Operational Constraints
4.2.3. Thermal Network Operational Constraints
4.2.4. Source Hub Constraint
4.3. Model Solving Steps
5. Calculus Analysis
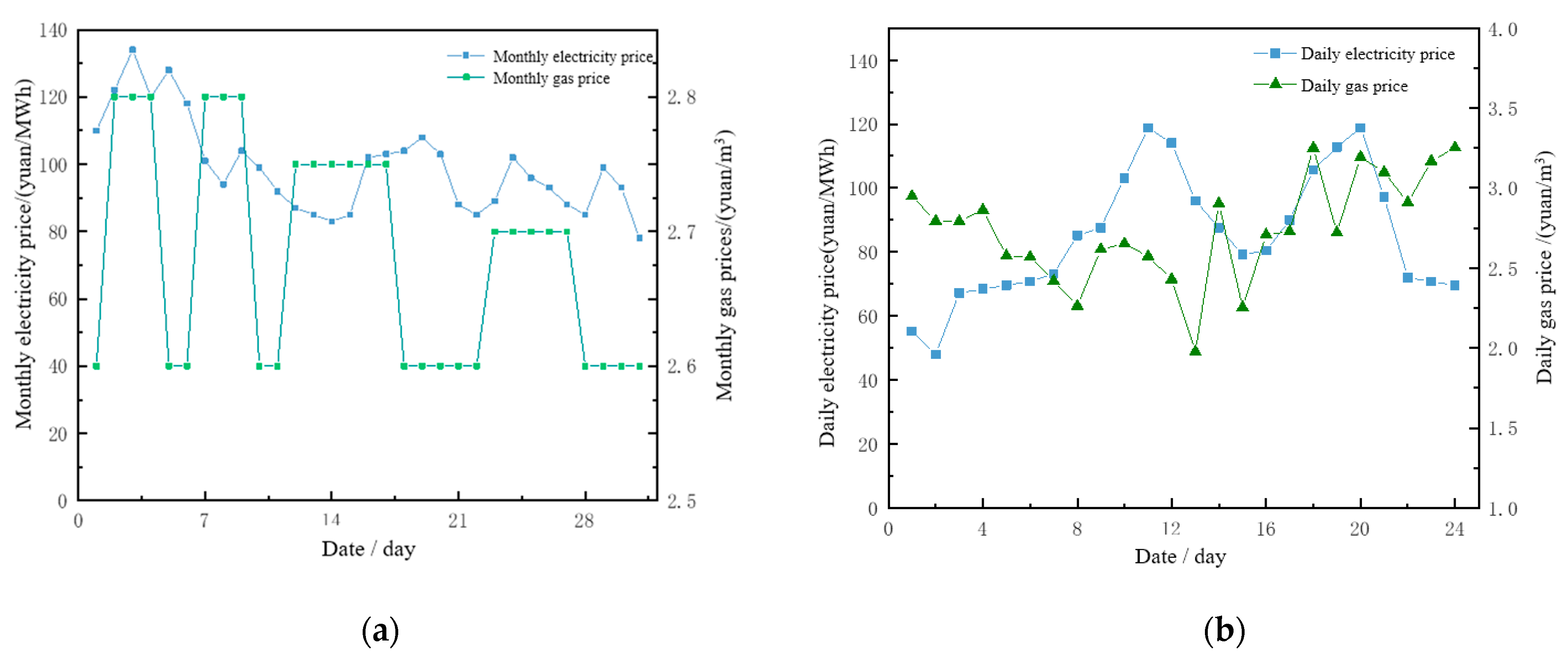
5.1. Basic Data
5.2. Analysis of the Effectiveness of the Monthly Contract Equalization Decomposition Method
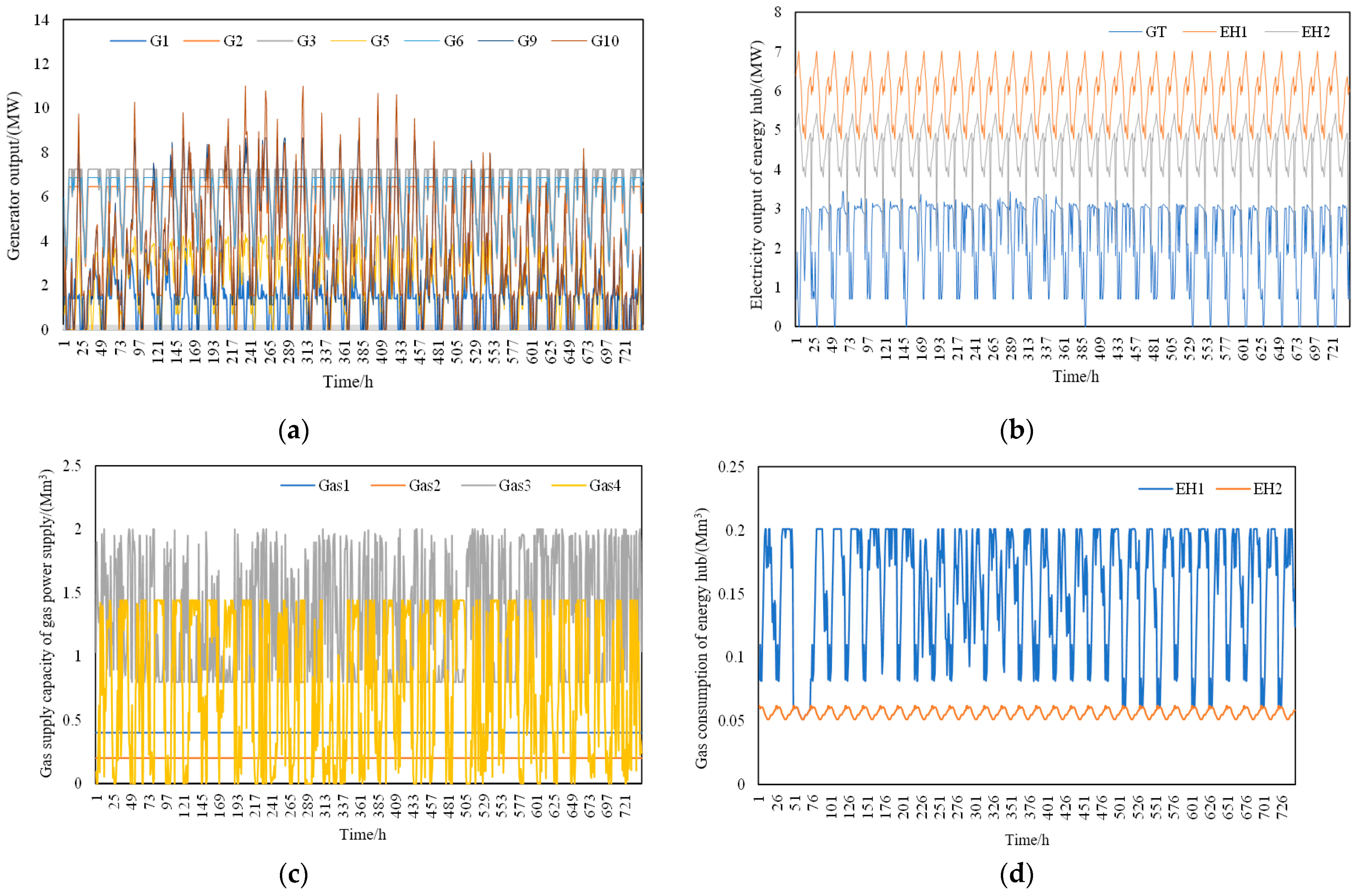
5.3. Analysis of the Actual Daily Performance of Monthly Contracts
6. Conclusions
- (1)
- The proposed method in this chapter considers the equilibrium decomposition of the centralized bidding volume as well as the equalization of the spot bidding space, which reduces the contract decomposition cost by about USD 0.33 million compared to the contract decomposition cost without considering the equilibrium decomposition, and the spot energy purchase variance also decreases by about 4.64%; at the same time, the consideration of the spot bidding variance can also effectively alleviate the fluctuation in the spot market and achieve smooth convergence of the spot market with the medium- and long-term market;
- (2)
- In this chapter, the daily operation plan of the IES is formulated based on the preliminary decomposition of the contract, which ensures that the deviation in daily energy supply and output does not exceed 3% in response to the assessment index at the end of the month, and then the optimized decomposition of the attributed amount of the medium- and long-term contract and the spot purchase plan is carried out so that the daily decomposition of the contract can maximize the operating income of each supplier;
- (3)
- Considering that the dynamic pipe storage characteristics of the gas network trim the overall daily operating cost of IES by 2.01% compared to the scenario without this consideration, the noteworthy cost reduction is predominantly in the gas network, lowered by approximately 6.4%. Simultaneously, the gas source point’s output exhibits a smoother trend. This substantiates the effectiveness of gas network pipe storage characteristics in easing energy supply pressure at the energy supply point and achieving efficient interconnection of the electricity, gas, and heat networks in the IES.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haaskjold, K.; Pedrero, R.A. Long-term optimization of the Norwegian energy system under the influence of the European power market. In Proceedings of the 2023 19th International Conference on the European Energy Market (EEM), Lappeenranta, Finland, 6–8 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gomez, T.; Herrero, I.; Rodilla, P.; Escobar, R.; Lanza, S.; de la Fuente, I.; Llorens, M.L.; Junco, P. European Union Electricity Markets: Current Practice and Future View. IEEE Power Energy Mag. 2019, 17, 20–31. [Google Scholar] [CrossRef]
- Lu, T.; Zhang, W.; Wang, Y.; Xie, H.; Ding, X. Medium and Long-term Trading Strategies for Large Electricity Retailers in China’s Electricity Market. Energies 2022, 15, 3342. [Google Scholar] [CrossRef]
- Wang, K.; Wang, X.; Jia, R.; Dang, J.; Liang, Y.; Du, H. Research on Coupled Cooperative Operation of Medium and Long-term and Spot Electricity Transaction for Multi-Energy System: A Case Study in China. Sustainability 2022, 14, 10473. [Google Scholar] [CrossRef]
- Manjunatha, H.M.; Purushothama, G.K.; Nanjappa, Y.; Deshpande, R. Auction-Based Single-Sided Bidding Electricity Market: An Alternative to the Bilateral Contractual Energy Trading Model in a Grid-Tied Microgrid. IEEE Access 2024, 12, 48975–48986. [Google Scholar] [CrossRef]
- Kohansal, M.; Samani, E.; Mohsenian-Rad, H. Understanding the Structural Characteristics of Convergence Bidding in Nodal Electricity Markets. IEEE Trans. Ind. Inform. 2021, 17, 124–134. [Google Scholar] [CrossRef]
- Cui, M.Y.; Xuan, M.Y.; Lu, Z.G.; He, L.C. Operation optimization strategy of multi-integrated energy service companies based on cooperative game theory. Proc. CSEE 2022, 42, 3548–3564. [Google Scholar] [CrossRef]
- Li, T.; Gao, C.; Chen, T.; Jiang, Y.; Feng, Y. Medium and long-term electricity market trading strategy considering renewable portfolio standards in the transitional period of electricity market reform in Jiangsu, China. Energy Econ. 2022, 107, 105860. [Google Scholar] [CrossRef]
- Huang, Y.; Qu, K.; Li, C.; Si, G. Research on Modeling Method of Medium-and long-term Wind Power Time Series Based on K-means MCMC Algorithm. Power Syst. Technol. 2019, 43, 2469–2476. [Google Scholar]
- Li, C.; Hu, Y.; Zhao, H.; Li, X. General Model and Algorithm for Contract Energy Decomposition. Power Syst. Autom. 2007, 31, 26–30. [Google Scholar]
- Wang, Y.; Zhang, P.; Shu, J.; Yang, Y. The economic distribution of contract trading volume and bidding trading volume in the daily plan. Power Syst. Autom. 2002, 26, 45–48. [Google Scholar]
- Huang, Y.; Wang, X.; Zhang, W.; Cao, C. Energy decomposition of long and middle term contract in multi-energy system. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3735–3740. [Google Scholar]
- Guntermann, C.; Tebbenjohanns, P.; Moser, A. Price convergence in an integrated simulation of the electricity and the gas market. In Proceedings of the 2023 19th International Conference on the European Energy Market (EEM), Lappeenranta, Finland, 6–8 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Sotiropoulos, E.; He, Y.; Hildmann, M.; Andersson, G. Modeling of electricity load for forward contract pricing. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Li, L.; Wang, N.; Chen, Y. Research on the Trial Operation of Mid-term and Long-term Transactionsthe Southern Electricity Spot Market Environment. Price Theory 2020, 2, 47–50. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, C.; Zhang, B.; Han, J.; Yang, Y.; Zhang, T.; Chen, Y. Design of Bilateral Trading Mechanism for Gansu Electricity Spot Market. Glob. Energy Interconnect. 2020, 3, 441–450. [Google Scholar]
- Cao, H.; Qiu, Z.; Xiang, J.; Hao, Q.; Gui, W. Wind Power Accommodation Model Considering the Link of Medium and Long-term Transactions with Short-term Dispatch. Power Grid Technol. 2020, 44, 4200–4210. [Google Scholar] [CrossRef]
- Yucekaya, A. Electricity trading for coal-fired power plants in Turkish power market considering uncertainty in spot, derivatives and bilateral contract market. Renew. Sustain. Energy Rev. 2022, 159, 112189. [Google Scholar] [CrossRef]
- EPEX SPOT. PCR Project Main Features. [EB/OL]. [2020-4-1]. Available online: https://www.EPEXSPOT.com (accessed on 3 January 2024).
- Xu, C.; Pang, K.; Wen, F.; Palu, I.; Gong, J.; Xie, Y.; Chen, C. Decomposition model of contract for difference considering market power mitigation. In Proceedings of the2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe(EEEIC/I& CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–5. [Google Scholar]
- Nie, Z.; Gao, F.; Wu, J.; Guan, X.; Liu, K. Contract for difference energy decomposition model for maximizing social benefit in the electricity market. In Proceedings of the World Congress on Intelligent Control and Automation, Guilin, China, 12–15 June 2016; pp. 2449–2454. [Google Scholar]
- Samani, E.; Mohsenian-Rad, H. A Data-Driven Study to Discover, Characterize, and Classify Convergence Bidding Strategies in California ISO Energy Market. In Proceedings of the 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–18 February 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Miao, S.; Luo, B.; Shen, J.; Cheng, C.; Li, G.; Sun, Y. Short-Term Multi-Objective Hydro-Thermal Generation Dispatch Considering Electricity Market Transition and Mid-and Long-Term Contract Decomposition. Power Grid Technol. 2018, 42, 2221–2231. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S.; Wang, Y.; Wu, B. A distributionally robust optimization model for power generators’ medium and long-term contracted energy decomposition. Power Syst. Prot. Control. 2023, 51, 71–80. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Liu, Z. Decomposition of Yearly Bided Volume Based on Rol-uniformization of Monthly Competitive Bidding Spaces. Power Syst. Autom. 2006, 30, 24–2764. [Google Scholar]
- Chen, Q.; Zhang, W.; Teng, F.; Guo, H.; Liu, X.; Jiang, N. Transmission Mechanisms and Coupling Approaches in European Transnational Electricity Markets. Glob. Energy Interconnect. 2020, 3, 423–429. [Google Scholar] [CrossRef]
- Borisovsky, P.A.; Eremeev, A.V.; Grinkevich, E.B.; Klokov, S.A.; Vinnikov, C.V. Trading hubs construction for electricity markets. In Optimization in the Energy Industry; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Xu, S.; Liu, J. Decomposition of Yearly Bided Volume Based on Roll-uniformization of Monthly Competitive Bidding Spaces. Modern Electric Power. 2023, 40, 505–513. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Staudt, P.; Garttner, J.; Weinhardt, C. Trading on local energy markets: A comparison of market designs and bidding strategies. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, J.; Hu, J.; Liao, S.; Ke, D.P.; Wang, Y.L.; Sun, R.F. Collaborative optimization of integrated energy system considering network dynamic characteristics and integrated demand response. Power Syst. Autom. 2021, 45, 40–48. [Google Scholar]
- Wu, G.; Liu, J.; Xiang, Y.; Shen, X.D.; Ma, Y.H. Day-ahead optimal scheduling of integrated electricity and natural gas system with medium and long-term e electricity contract decomposition and wind power uncertainties. Power Syst. Autom. Equip. 2019, 39, 246–253. [Google Scholar]









| Scene | Contract Decomposition Cost/(USD) | Spot Purchase Energy Variance |
|---|---|---|
| S1 | 45,871,627 | 24.5681 |
| S2 | 44,302,449 | 87,193.68 |
| S3 | 45,534,180 | 23.4273 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Wei, Z.; Jiang, X.; Huang, Y.; Fan, D. Optimization Decomposition of Monthly Contracts for Integrated Energy Service Provider Considering Spot Market Bidding Equilibria. Electronics 2024, 13, 1945. https://doi.org/10.3390/electronics13101945
Wu C, Wei Z, Jiang X, Huang Y, Fan D. Optimization Decomposition of Monthly Contracts for Integrated Energy Service Provider Considering Spot Market Bidding Equilibria. Electronics. 2024; 13(10):1945. https://doi.org/10.3390/electronics13101945
Chicago/Turabian StyleWu, Chen, Zhinong Wei, Xiangchen Jiang, Yizhen Huang, and Donglou Fan. 2024. "Optimization Decomposition of Monthly Contracts for Integrated Energy Service Provider Considering Spot Market Bidding Equilibria" Electronics 13, no. 10: 1945. https://doi.org/10.3390/electronics13101945
APA StyleWu, C., Wei, Z., Jiang, X., Huang, Y., & Fan, D. (2024). Optimization Decomposition of Monthly Contracts for Integrated Energy Service Provider Considering Spot Market Bidding Equilibria. Electronics, 13(10), 1945. https://doi.org/10.3390/electronics13101945






