A New Safety Distance Model Based on Braking Process Considering Adhesion Coefficient
Abstract
:1. Introduction
- We introduce a novel safety distance model that takes into account the real-time changes in the adhesion coefficient during the braking process. Simulation results demonstrate that this model improves the accuracy of calculated safety distance by at least 14.99% compared to traditional methods.
- We analyze the entire reaction braking process and find that the traditional safety distance model fails to ensure overall safety.
- The proposed model’s safety and stability are validated through simulation of a car-following process involving a motorcade of five cars.
2. Preliminaries
2.1. Description of Parameters
2.2. Traditional Safety Distance Model
3. Proposed Safety Distance Model
3.1. Proposed Safety Distance
3.1.1. Minimum Safety Distance
3.1.2. Expected and Maximum Safety Distance
3.2. The Control Strategy of Proposed Car-Following Model
3.3. The Stability Analysis
4. Results and Discussion
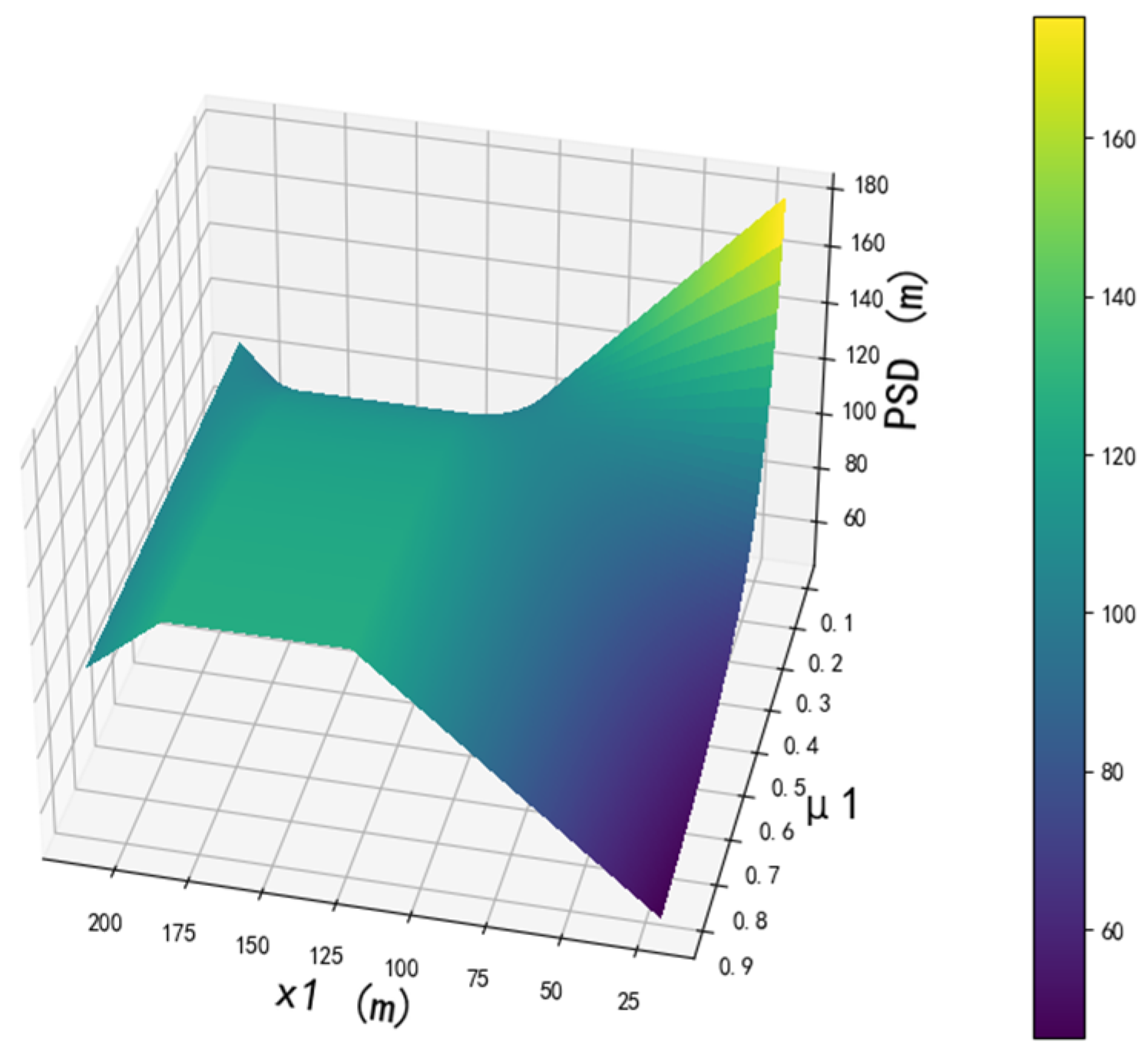
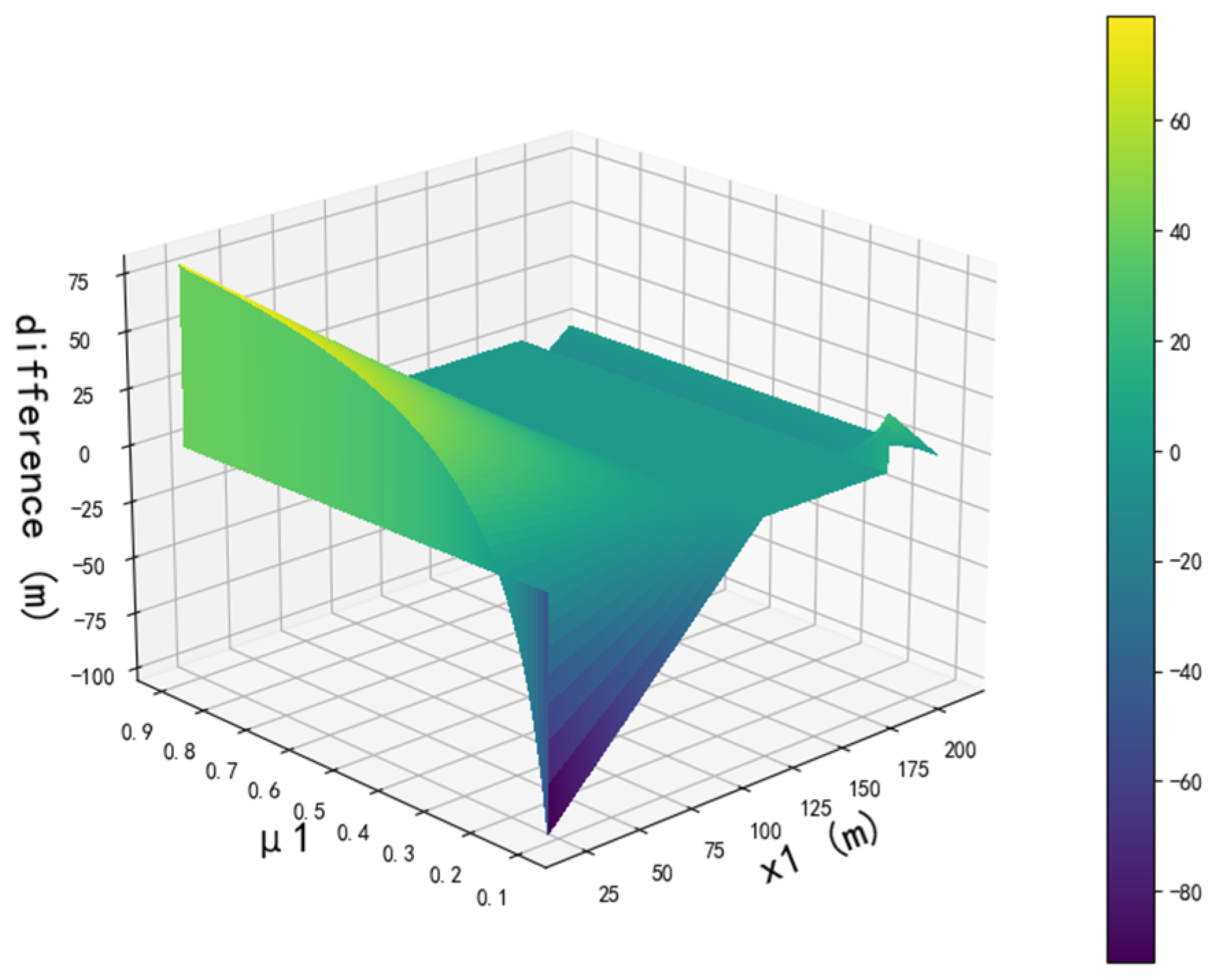
4.1. Comparison with Traditional Safety Distance
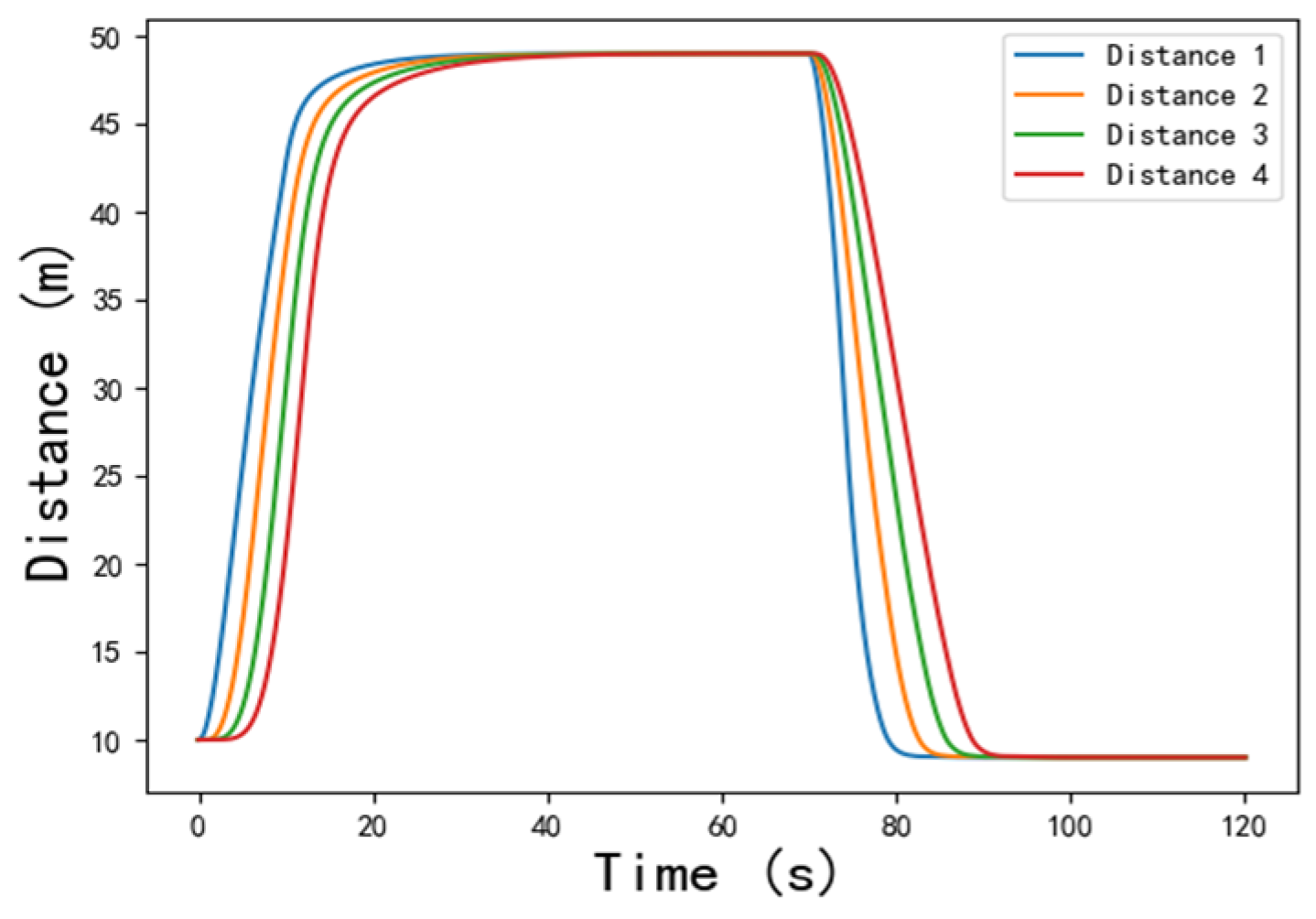
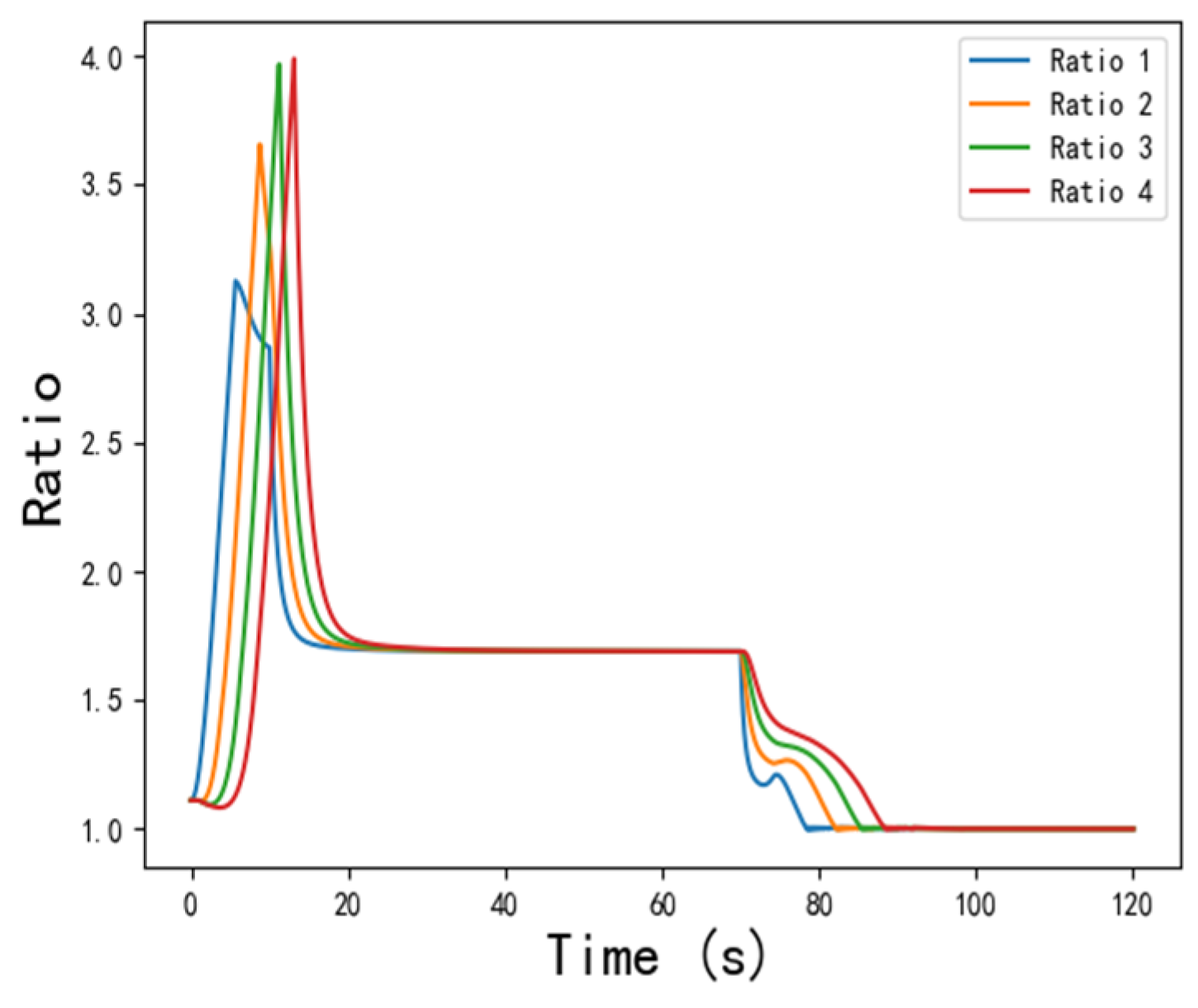
4.2. Analysis of Car-following Process
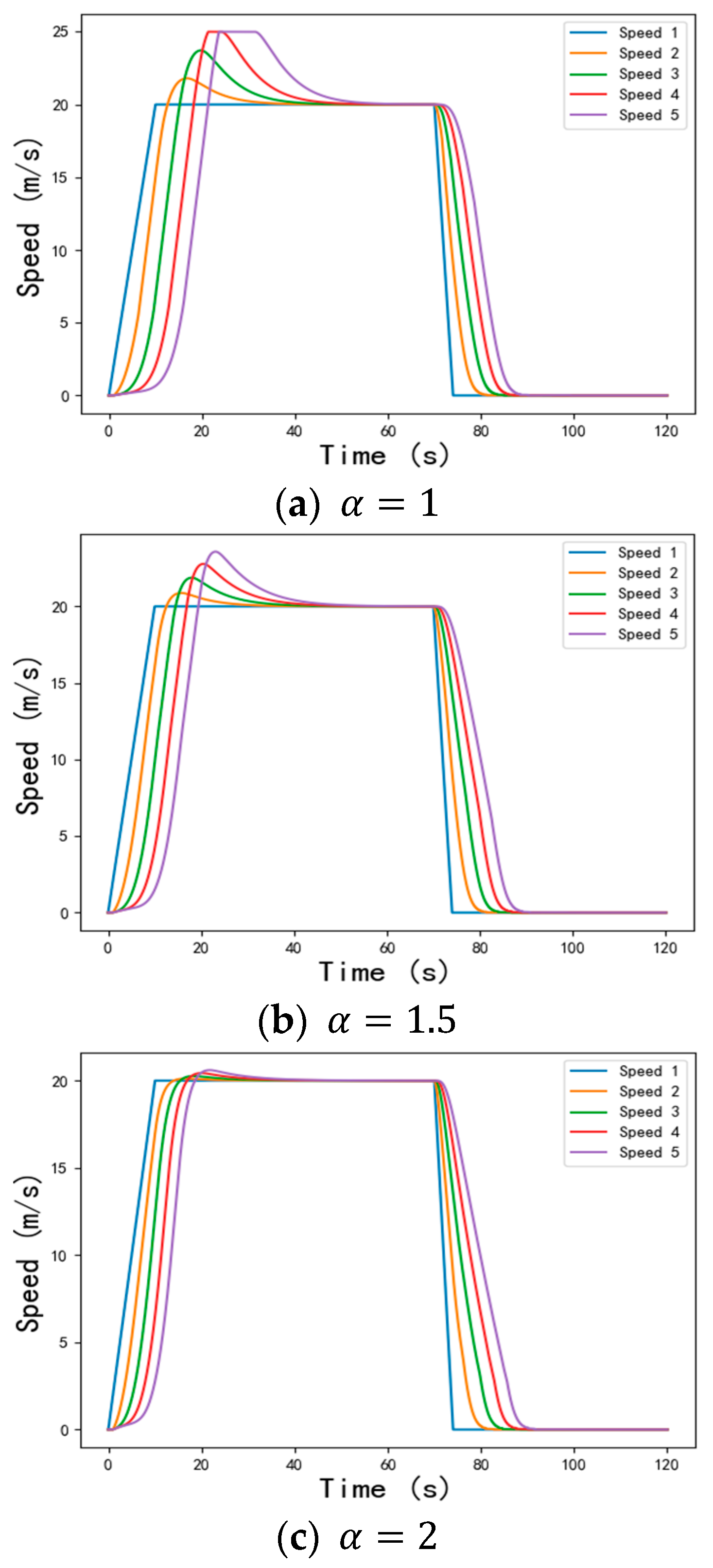
4.2.1. Stability Analysis
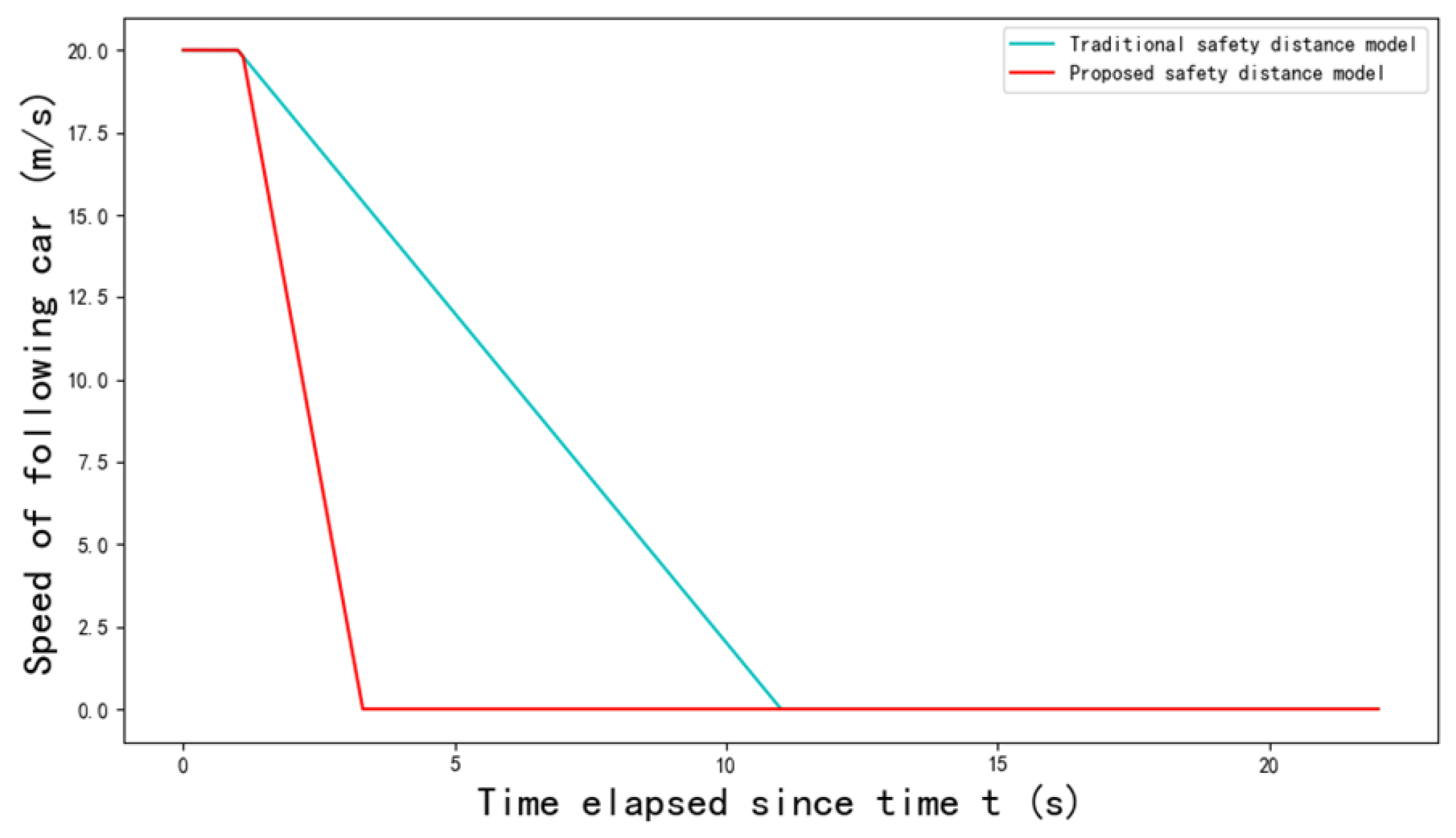
4.2.2. Safety Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jafaripournimchahi, A.; Hu, W.; Sun, L. Nonlinear stability analysis for an anticipation-memory car following model in the era of autonomous and connected vehicles. In Proceedings of the 2020 International Conference on Urban Engineering and Management Science (ICUEMS), Zhuhai, China, 24–26 April 2020; pp. 409–413. [Google Scholar]
- Zeng, Y.; Zhang, N. Review and new insights of the traffic flow lattice model for road vehicle traffic flow. In Proceedings of the 2014 IEEE International Conference on Control Science and Systems Engineering, Yantai, China, 29–30 December 2014; pp. 100–103. [Google Scholar]
- Yu, Y.; He, Z.; Qu, X. On the Impact of Prior Experiences in Car-Following Models: Model Development, Computational Efficiency, Comparative Analyses, and Extensive Applications. IEEE Trans. Cybern. 2023, 53, 1405–1418. [Google Scholar] [CrossRef] [PubMed]
- Abdelhalim, A.; Abbas, M. A Real-Time Safety-Based Optimal Velocity Model. IEEE Open J. Intell. Transp. Syst. 2022, 3, 165–175. [Google Scholar] [CrossRef]
- Xing, H.; Zhang, L.; Liu, Y. Effect of altruistic scenarios for individual car-following behavior. J. Tsinghua Univ. (Sci. Technol.) 2018, 58, 1000–1005. [Google Scholar]
- Li, X.; Luo, X.; He, M.; Chen, S. An improved car-following model considering the influence of space gap to the response. Phys. A Stat. Mech. Its Appl. 2018, 509, 536–545. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Lu, G. Influence of Driving Behaviors on the Stability in Car Following. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1081–1098. [Google Scholar] [CrossRef]
- Kometani, E.; Sasaki, T. Dynamic Behavior of Traffic with a Nonlinear Spacing-speed Relationship. In Proceedings of the Symposium on Theory of Traffic Flow; Elsevier: New York, NY, USA, 1959; pp. 105–119. [Google Scholar]
- Park, M.; Kim, Y.; Yeo, H. Development of an Asymmetric Car-Following Model and Simulation Validation. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3513–3524. [Google Scholar] [CrossRef]
- Gipps, P.G. A behavioural car-following model for computer simulation. Transp. Res. B Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wang, S.-C.; Wang, C.-A. Study on vehicle safety distance warning system. In Proceedings of the 2008 IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008; pp. 1–6. [Google Scholar]
- Feng, G.; Wang, W.; Feng, J.; Tan, H.; Li, F. Modelling and Simulation for Safe Following Distance Based on Vehicle Braking Process. In Proceedings of the 2010 IEEE 7th International Conference on E-Business Engineering, Shanghai, China, 10–12 November 2010; pp. 385–388. [Google Scholar]
- Luo, Q.; Xun, L.; Cao, Z.; Huang, Y. Simulation analysis and study on car-following safety distance model based on braking process of leading vehicle. In Proceedings of the 2011 9th World Congress on Intelligent Control and Automation, Taipei, Taiwan, 21–25 June 2011; pp. 740–743. [Google Scholar]
- Duan, S.; Zhao, J. A model based on hierarchical safety distance algorithm for ACC control mode switching strategy. In Proceedings of the 2017 2nd International Conference on Image, Vision and Computing (ICIVC), Chengdu, China, 2–4 June 2017; pp. 904–908. [Google Scholar]
- Xia, F.; Li, S.; Li, H. Autonomous Obstacle Avoidance Control Strategy for Intelligent Vehicle Based on Lateral and Longitudinal Safety Distance Model. In Proceedings of the 2021 IEEE International Conference on Emergency Science and Information Technology (ICESIT), Chongqing, China, 22–24 November 2021; pp. 509–513. [Google Scholar]
- Lin, D.; Li, L. An Efficient Safety-Oriented Car-Following Model for Connected Automated Vehicles Considering Discrete Signals. IEEE Trans. Veh. Technol. 2023, 72, 9783–9795. [Google Scholar] [CrossRef]
- Erd, A.; Jaśkiewicz, M.; Koralewski, G.; Rutkowski, D.; Stokłosa, J. Experimental research of effectiveness of brakes in passenger cars under selected conditions. In Proceedings of the 2018 XI International Science-Technical Conference Automotive Safety, Častá, Slovakia, 18–20 April 2018; pp. 1–5. [Google Scholar]
- Lian, Y.; Zhao, Y.; Hu, L.; Tian, Y. Longitudinal Collision Avoidance Control of Electric Vehicles Based on a New Safety distance Model and Constrained-Regenerative-Braking-Strength-Continuity Braking Force Distribution Strategy. IEEE Trans. Veh. Technol. 2016, 65, 4079–4094. [Google Scholar] [CrossRef]
- Sevil, A.O.; Canevi, M.; Soylemez, M.T. Development of an Adaptive Autonomous Emergency Braking System Based on Road Friction. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; pp. 815–819. [Google Scholar]
- Guo, C.; Wang, X.; Su, L. Safety distance model for longitudinal collision avoidance of logistics vehicles considering slope and road adhesion coefficient. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 498–512. [Google Scholar] [CrossRef]
- Castillo, J.J.; Cabrera, J.A.; Guerra, A.J.; Simón, A. A Novel Electrohydraulic Brake System with Tire–Road Friction Estimation and Continuous Brake Pressure Control. IEEE Trans. Ind. Electron. 2016, 63, 1863–1875. [Google Scholar] [CrossRef]
- Guan, R.; Fang, J.; Liu, J. Based on Binocular Identification Technology of Automobile Active Braking Safety Distance Model Research. In Proceedings of the 2016 International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 355–357. [Google Scholar]
- Cheng, J.; Du, F.; Qi, L.; Zhang, S.; Du, Q.; Ji, P. Research on Vehicle Cruise Control Strategy Based on Fixed Distance. In Proceedings of the 2022 International Conference on Mechanical and Electronics Engineering (ICMEE), Xi’an, China, 21–23 November 2022; pp. 122–126. [Google Scholar]
- Teng, C.; Ligang, G.; Zexu, W.; Qin, S.; Hao, N. Car Following Model Based on Driving Risk Field for Vehicle Infrastructure Cooperation. In Proceedings of the 2022 6th CAA International Conference on Vehicular Control and Intelligence (CVCI), Nanjing, China, 28–30 October 2022; pp. 1–6. [Google Scholar]
- Chen, C.-H. A Cell Probe-Based Method for Vehicle Speed Estimation. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2020, 103, 265–267. [Google Scholar] [CrossRef]
- Surya, H.R.; Raju, N.; Arkatkar, S.S. Stability Analysis of Mixed Traffic Flow using Car-Following Models on Trajectory Data. In Proceedings of the 2021 International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 5–9 January 2021; pp. 656–661. [Google Scholar]
- Jin, H.; Hao, H.; Yang, X. Continuous and Discrete Analysis of Local Stability for Car-Following Model with Speed-Based Desired-Headway. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5374–5386. [Google Scholar] [CrossRef]
- Ngoduy, D. Analytical studies on the instabilities of heterogeneous intelligent traffic flow. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2699–2706. [Google Scholar] [CrossRef]
- Wang, M.; Hoogendoorn, S.P.; Daamen, W.; van Arem, B.; Shyrokau, B.; Happee, R. Delay-compensating strategy to enhance string stability of adaptive cruise controlled car followings. Transp. B Transp. Dyn. 2018, 6, 211–229. [Google Scholar]
- Li, Y.; Tang, C.; Peeta, S.; Wang, Y. Nonlinear Consensus-Based Connected Vehicle Platoon Control Incorporating Car-Following Interactions and Heterogeneous Time Delays. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2209–2219. [Google Scholar] [CrossRef]
- Jia, B.; Yang, D.; Zhang, X.; Wu, Y.; Guo, Q. Car-following model considering the lane-changing prevention effect and its stability analysis. Eur. Phys. J. B 2020, 93, 153. [Google Scholar] [CrossRef]
- Wan, N.; Zhang, C.; Vahidi, A. Probabilistic Anticipation and Control in Autonomous Car Following. IEEE Trans. Control. Syst. Technol. 2019, 27, 30–38. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Li, X.-G.; Zhang, Y.; Niculescu, S.-I.; Çela, A. Stability Analysis of Car-Following Systems with Uniformly Distributed Delays Using Frequency-Sweeping Approach. IEEE Access 2021, 9, 69747–69755. [Google Scholar] [CrossRef]




| Symbol | Parameter Description |
|---|---|
| Position of the car numbered n at time t | |
| Speed of the car numbered n at time t | |
| Acceleration of the car numbered n at time t | |
| Driver’s reaction time | |
| Maximum deceleration of the car numbered n at time t | |
| Maximum comfortable acceleration of the car numbered n | |
| Maximum allowable driving speed on the road | |
| Adhesion coefficient at position x | |
| The acceleration of gravity | |
| Length of the car numbered n |
| Scene No. | (m/s) | (m/s) | (m) | |
|---|---|---|---|---|
| Scene 1 | 10 | 20 | 0.2 | 185 |
| Scene 2 | 10 | 20 | 0.8 | 185 |
| Scene 3 | 10 | 10 | 0.2 | 40 |
| Scene 4 | 10 | 10 | 0.8 | 20 |
| Scene 5 | 20 | 20 | 0.2 | 110 |
| Scene 6 | 20 | 20 | 0.8 | 40 |
| Combination Number | (m) | |
|---|---|---|
| Combination 1 | 0.9 | 20.2 |
| Combination 2 | 0.9 | 119.8 |
| Combination 3 | 0.1 | 20.2 |
| Combination 4 | 0.1 | 119.8 |
| Time to Steady State (s) | Speed Error (m/s) | Distance Error (m/s2) | |
|---|---|---|---|
| 1 | 62.29 | 0.0176 | 0.0882 |
| 1.5 | 56.90 | 0.0073 | 0.0365 |
| 2 | 43.76 | 0.0013 | 0.0067 |
| 2.5 | 42.11 | 0.0009 | 0.0039 |
| 3 | 47.92 | 0.0023 | 0.0107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, R.; Ma, M.; Hei, X.; Yang, L.; Li, A.; Qiu, Y. A New Safety Distance Model Based on Braking Process Considering Adhesion Coefficient. Electronics 2024, 13, 421. https://doi.org/10.3390/electronics13020421
Fei R, Ma M, Hei X, Yang L, Li A, Qiu Y. A New Safety Distance Model Based on Braking Process Considering Adhesion Coefficient. Electronics. 2024; 13(2):421. https://doi.org/10.3390/electronics13020421
Chicago/Turabian StyleFei, Rong, Mengyang Ma, Xinhong Hei, Lu Yang, Aimin Li, and Yuan Qiu. 2024. "A New Safety Distance Model Based on Braking Process Considering Adhesion Coefficient" Electronics 13, no. 2: 421. https://doi.org/10.3390/electronics13020421






