Nonlinear Magnetic Model of IPMSM Based on the Frozen Permeability Technique Utilized in Improved MTPA Control
Abstract
1. Introduction
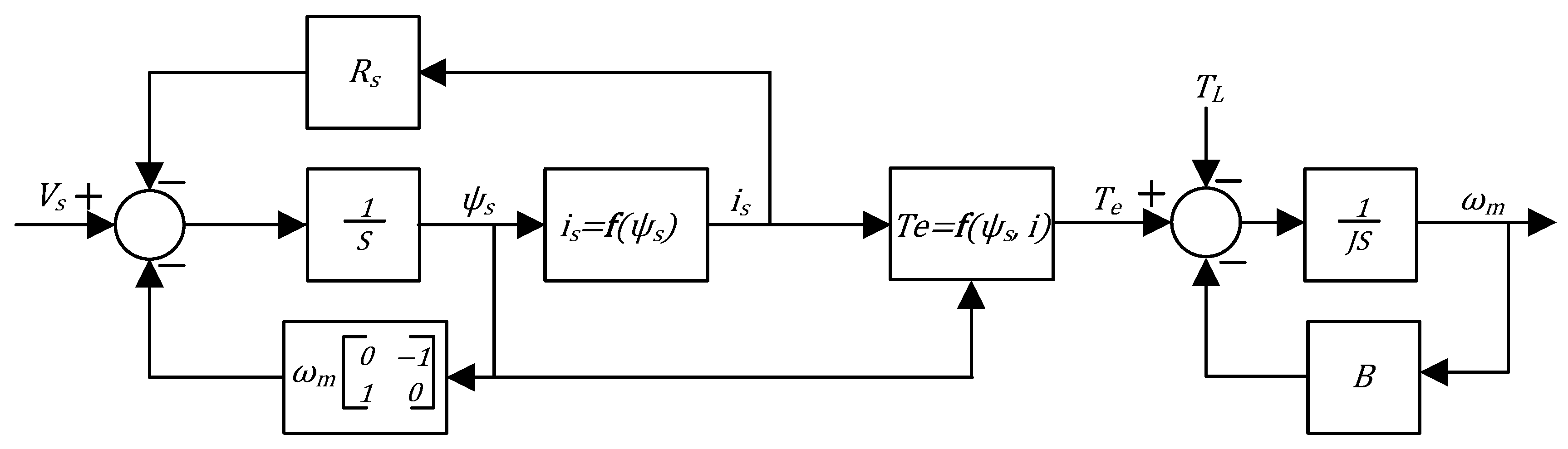
2. State-Space Nonlinear Model of IPMSM
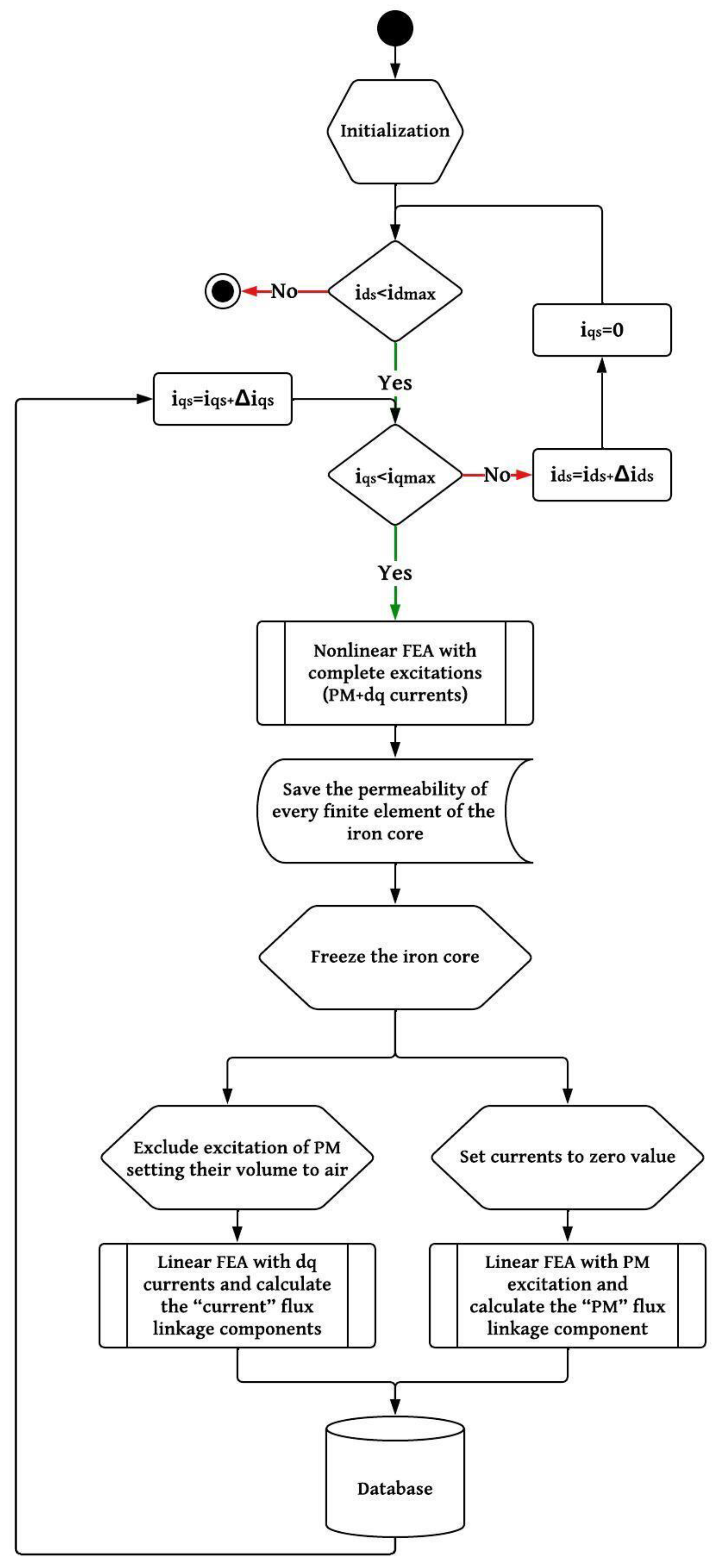
3. Frozen Permeability Technique for FEA Modeling of IPMSM
3.1. The Low Voltage Highly Utilized IPMSM for EV Traction Drive
3.2. Basic Principle of Frozen Permeability Technique
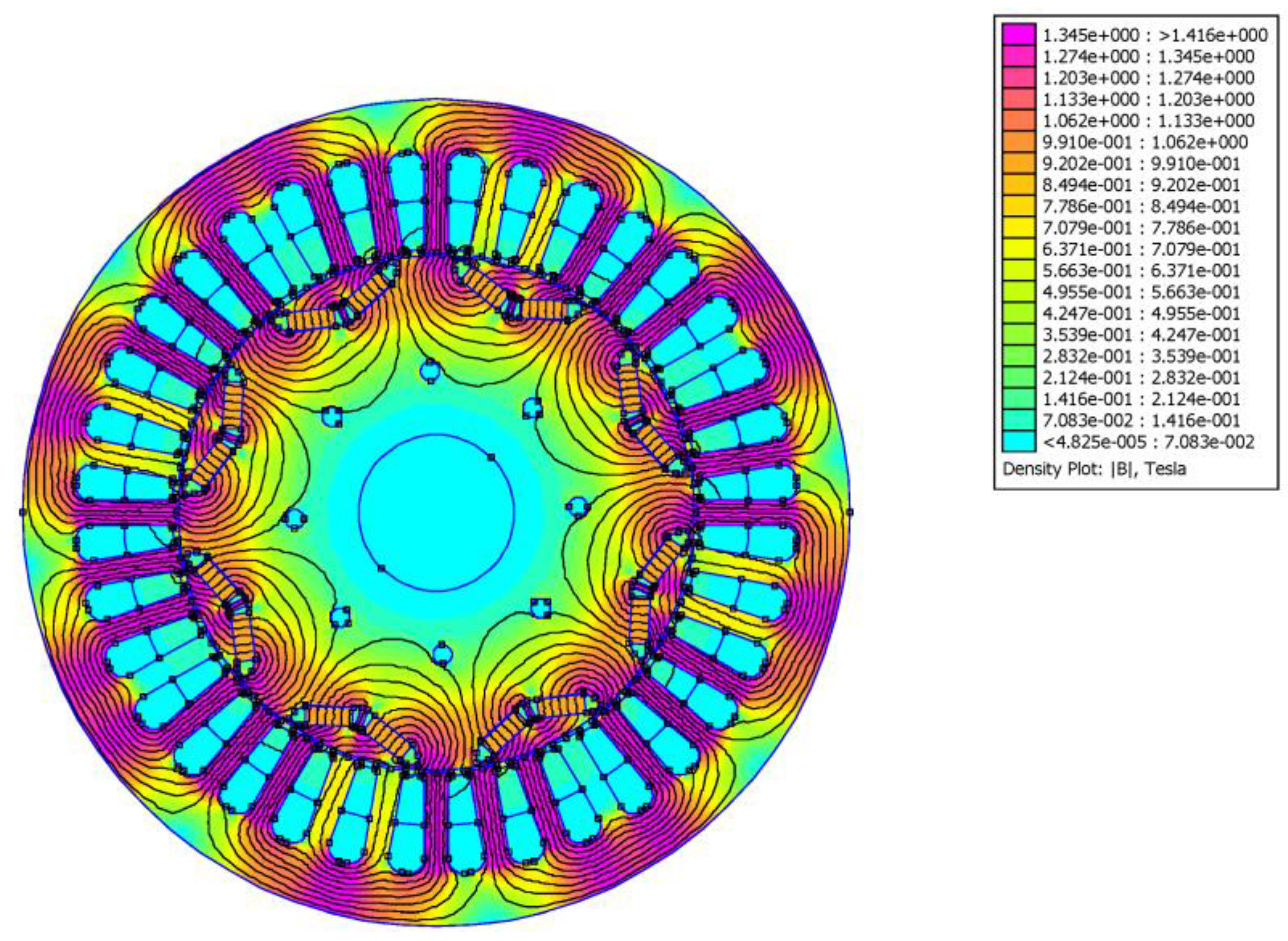
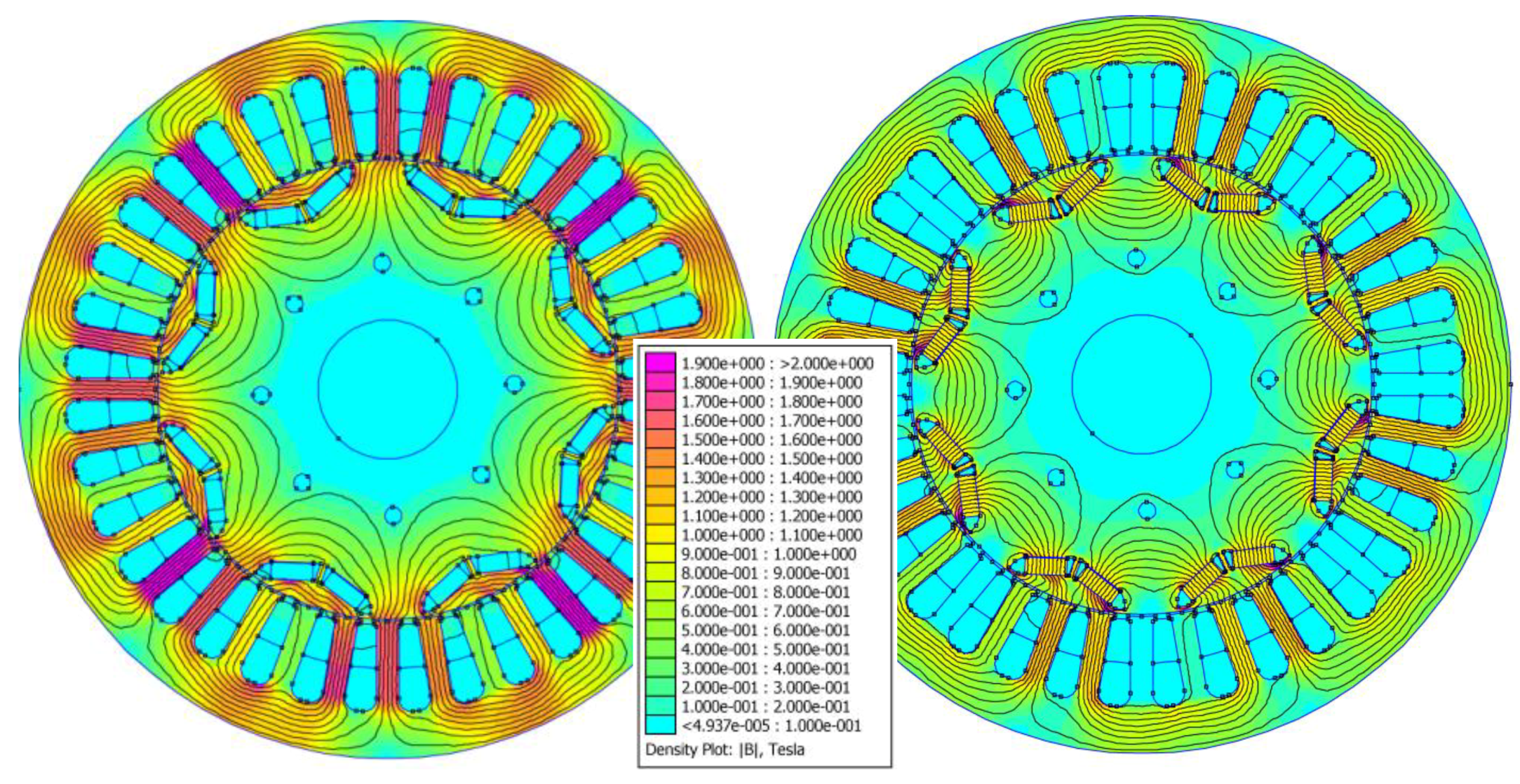
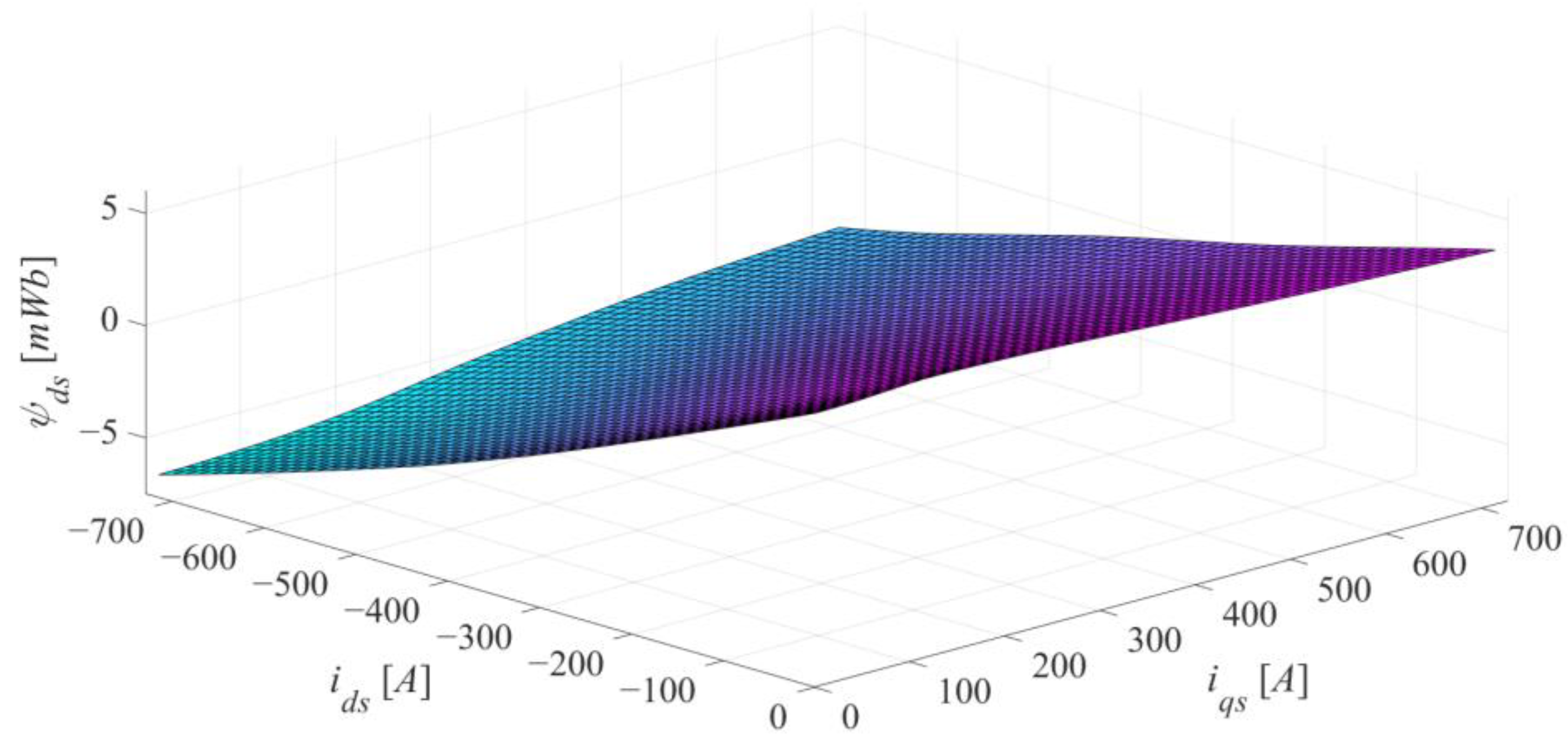
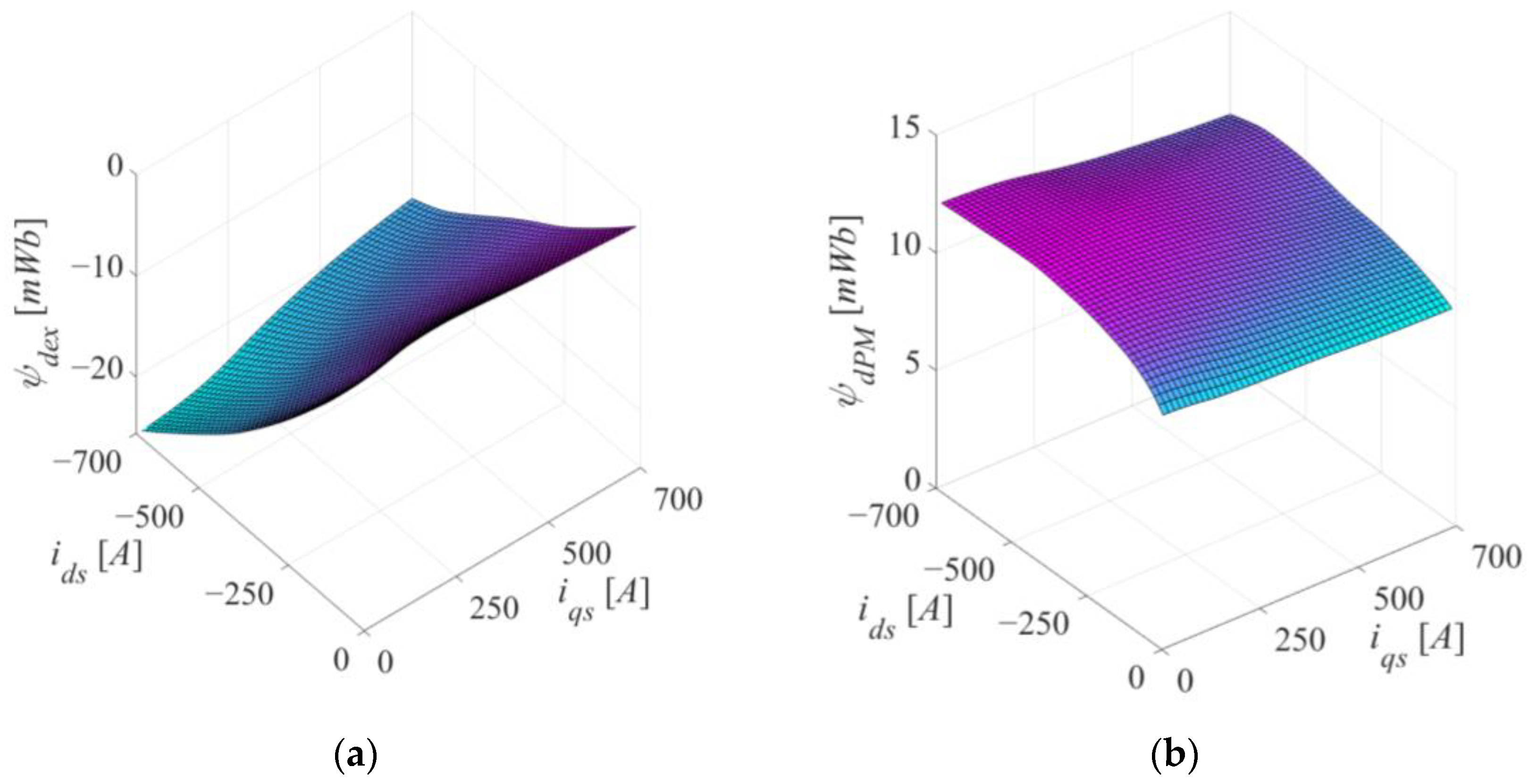
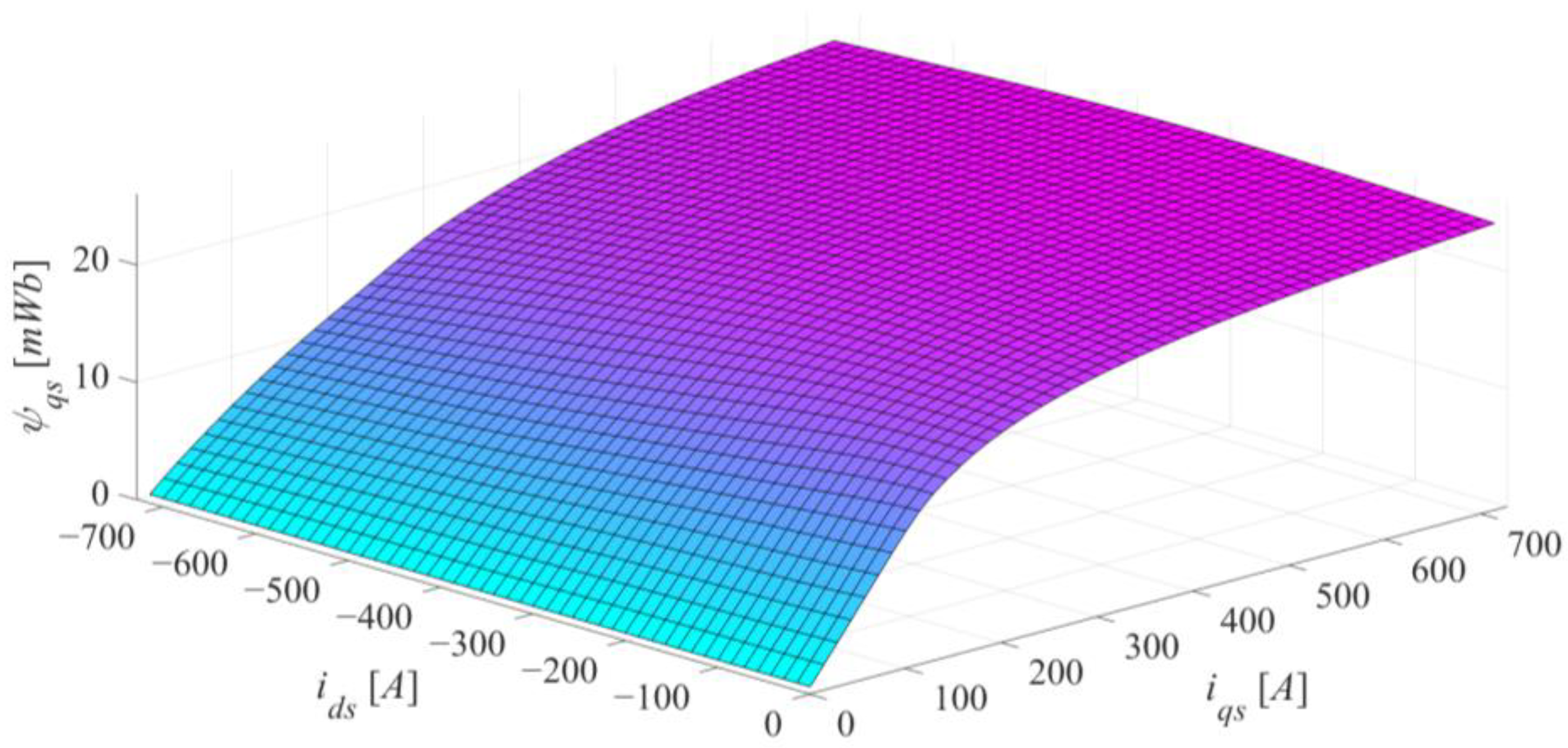
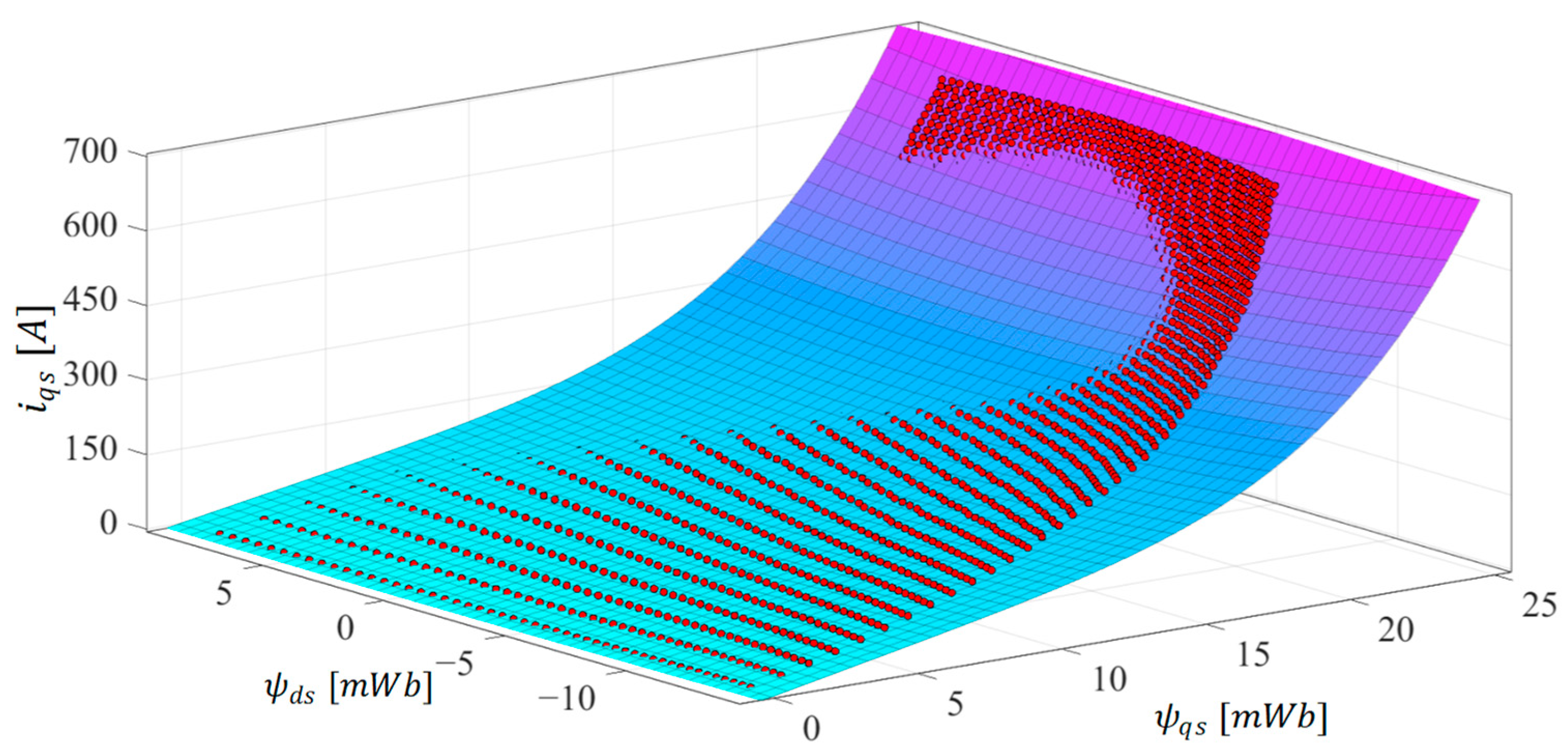
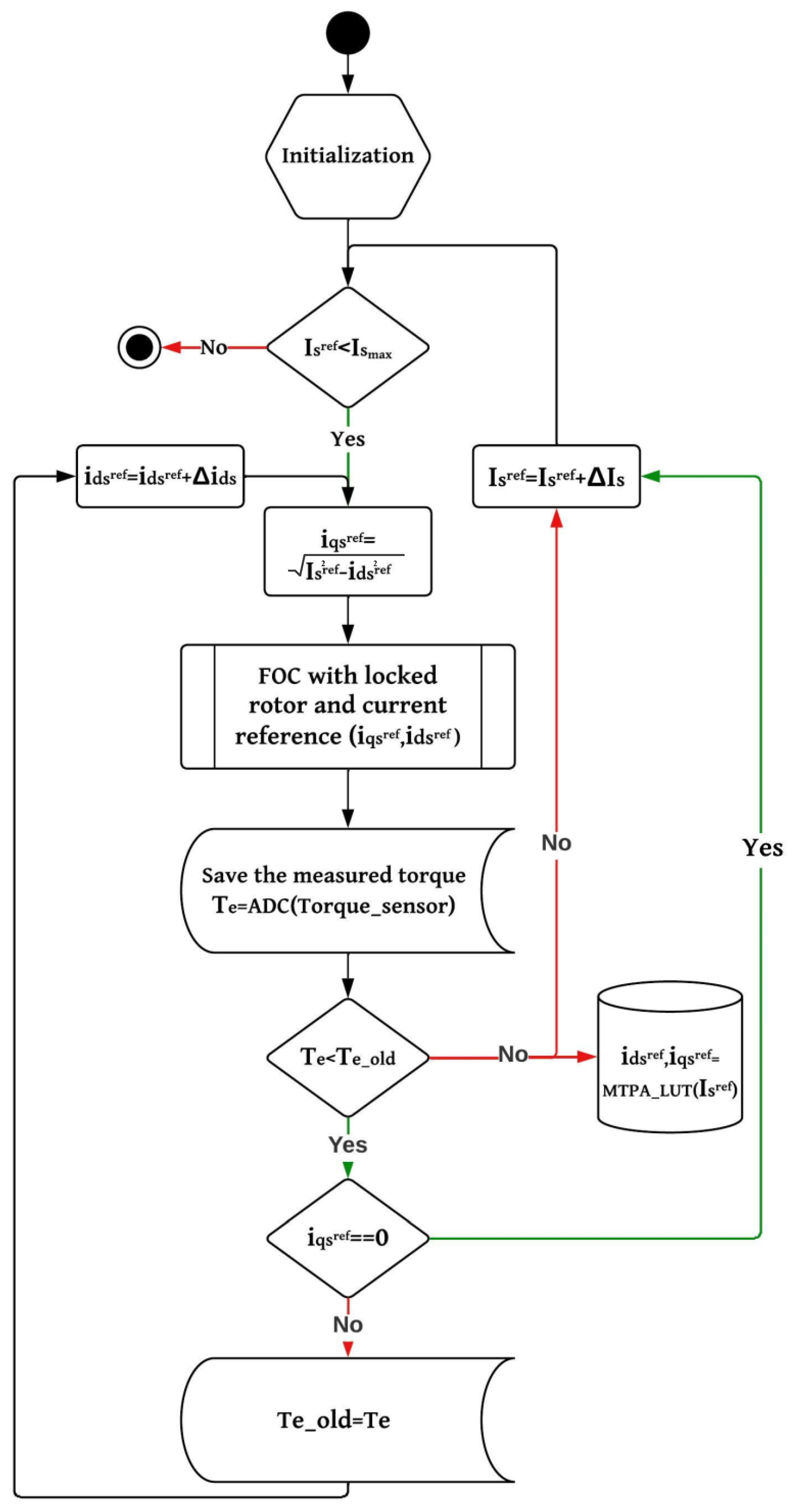
3.3. Results of the Frozen Permeability Technique
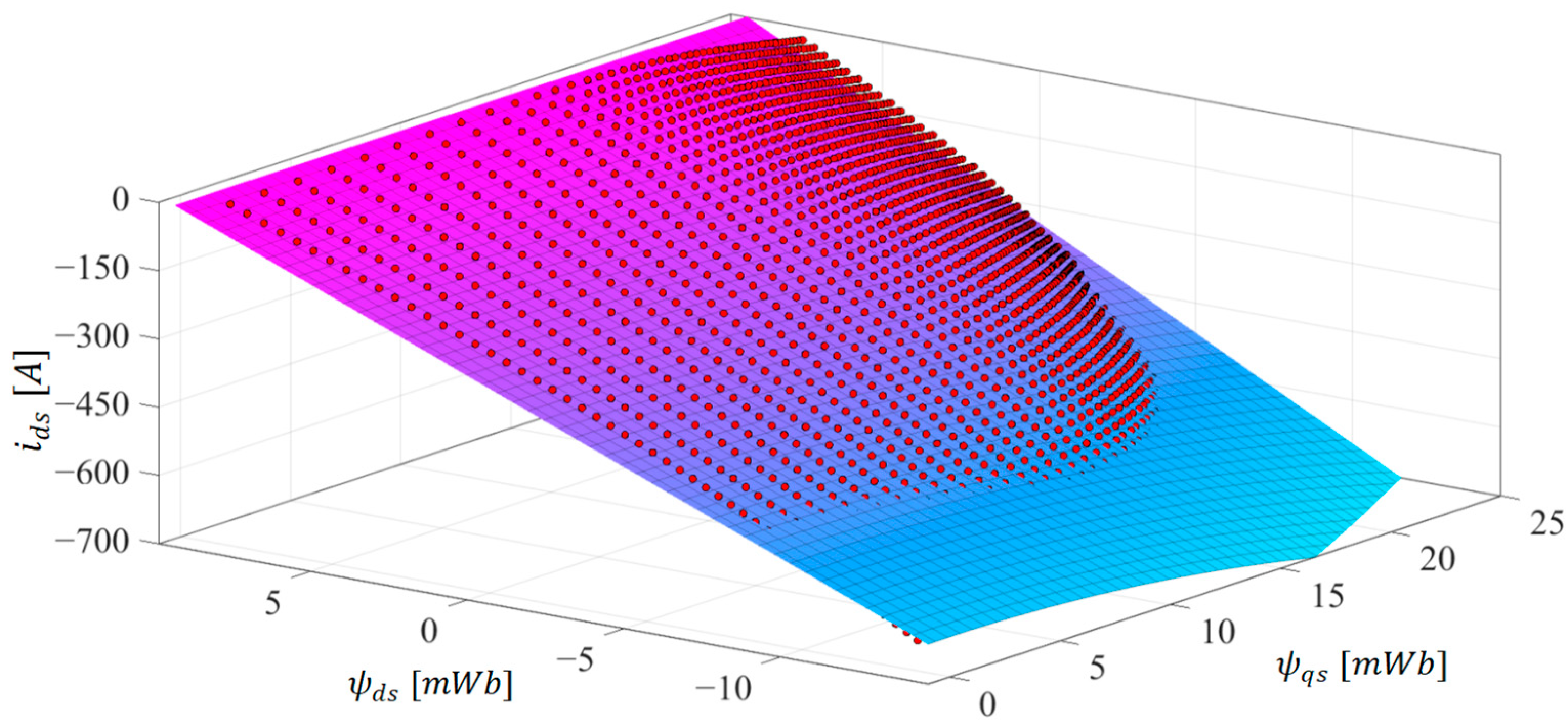
4. Algebraic Magnetic Model Representation
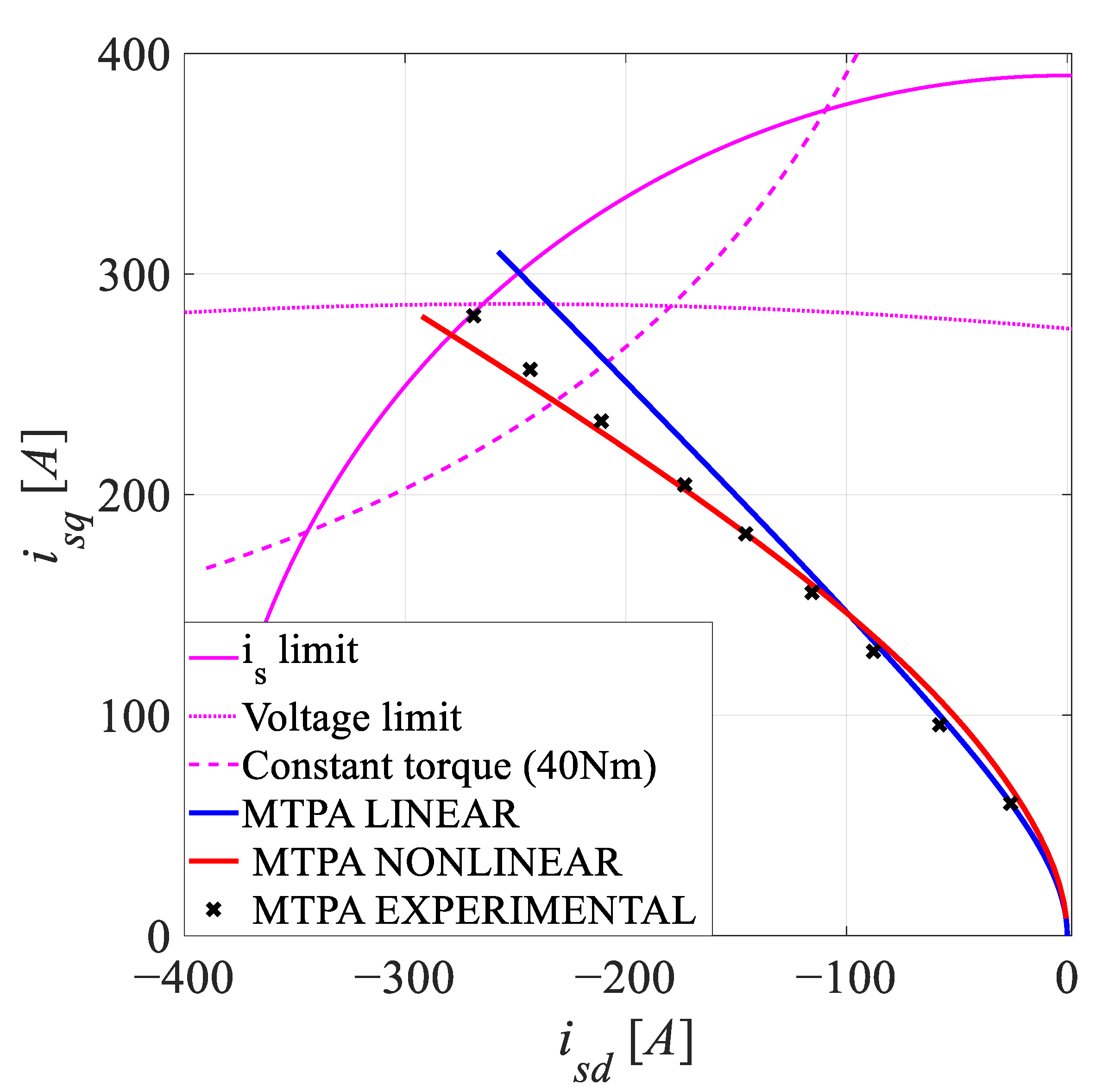
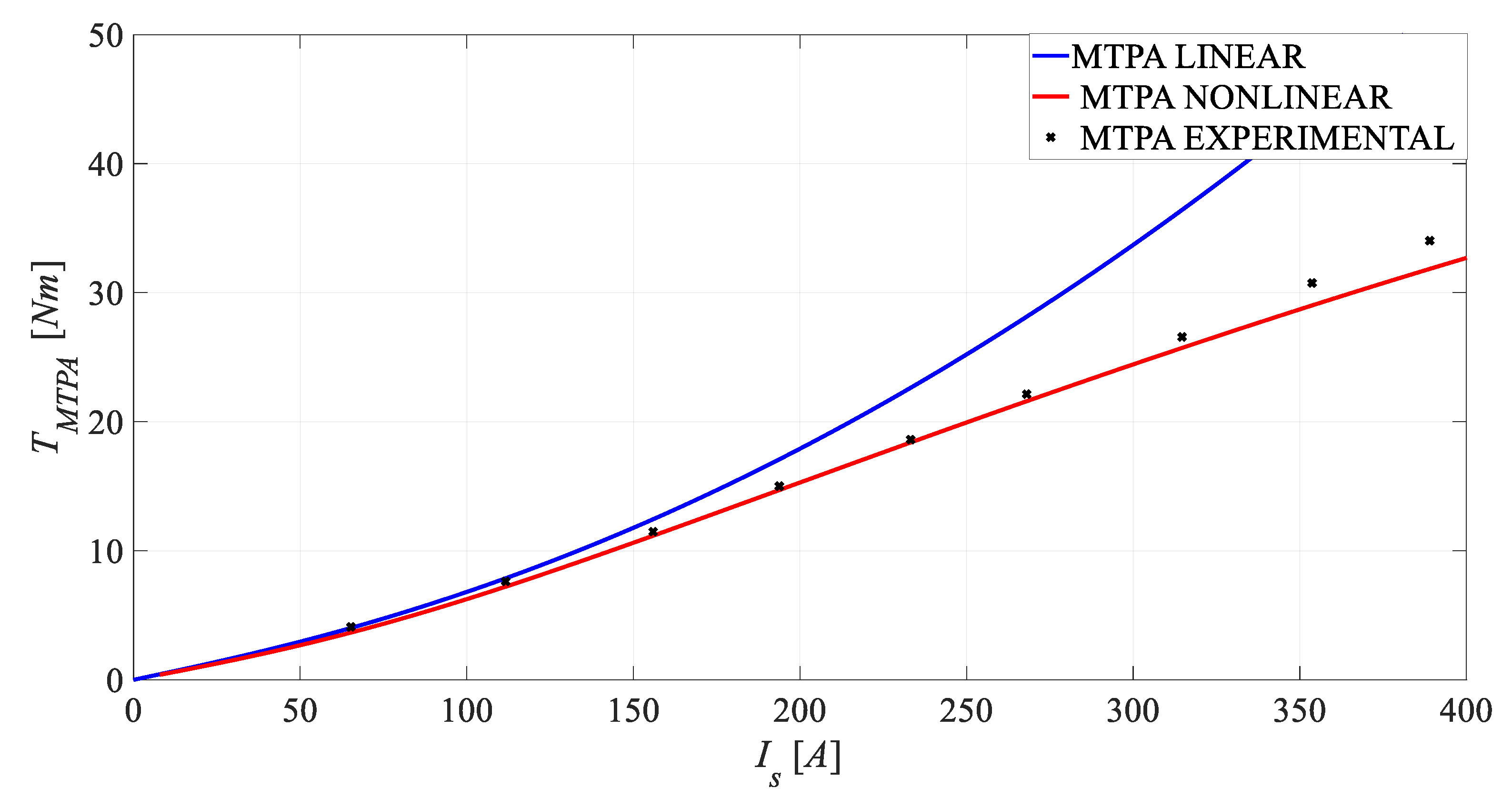
5. MTPA Control Based on the Proposed Magnetic Model
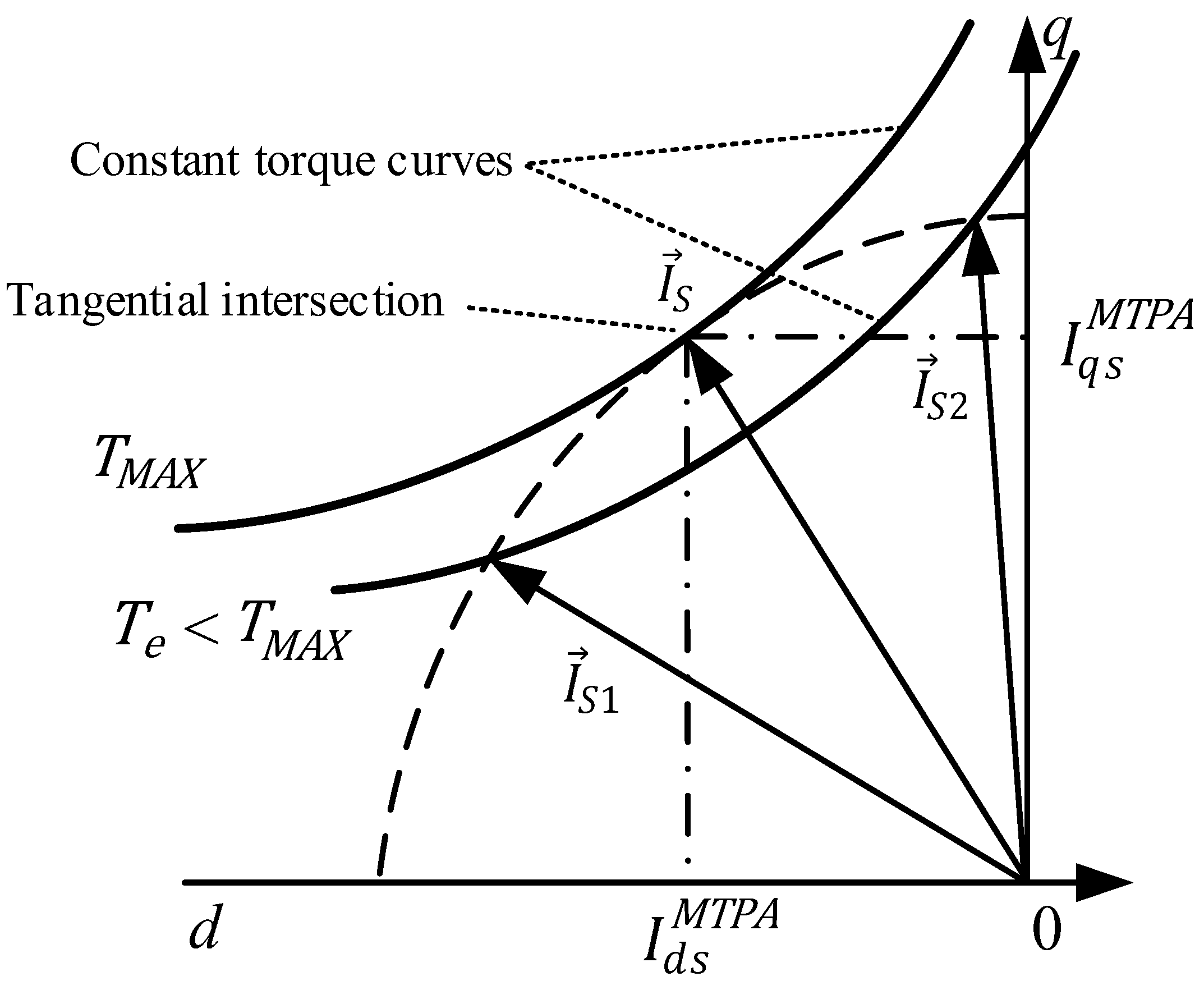
5.1. MTPA Linear Strategy Based on IPMSM’s Constant Parameters
5.2. MTPA Nonlinear Strategy Based on the Proposed Magnetic Model
6. Validation of the Proposed Nonlinear Magnetic Model Utilized in the Improved MTPA Control Strategy
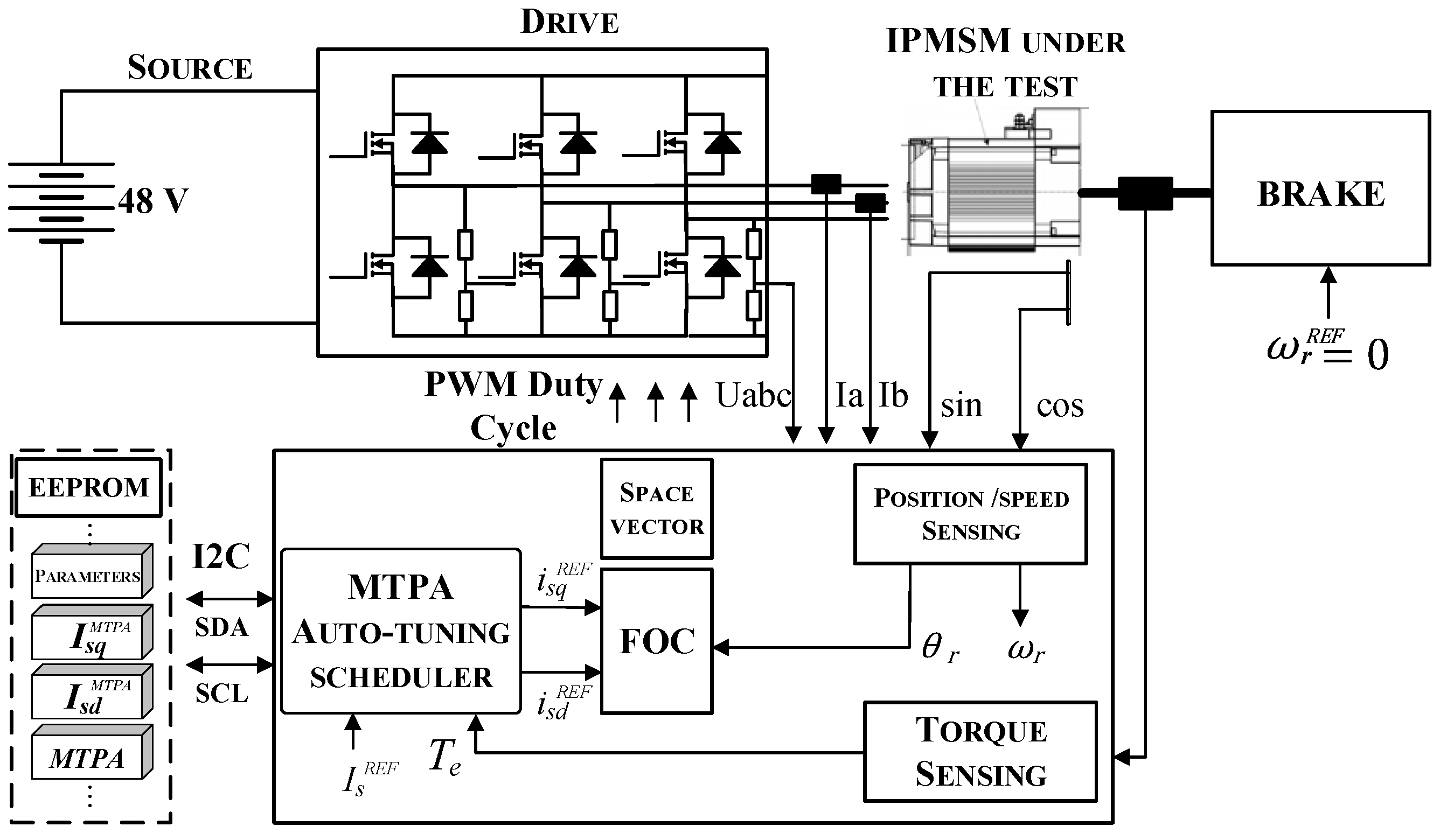
6.1. Experimental Test Workbench
6.2. Experimental Results and Disccusion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gundogdu, T.; Zhu, Z.-Q.; Chan, C.C. Comparative Study of Permanent Magnet, Conventional, and Advanced Induction Machines for Traction Applications. World Electr. Veh. J. 2022, 13, 137. [Google Scholar] [CrossRef]
- Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the Performances and Parameters of Interior PMSM Used for Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
- Yang, Y.; Castano, S.M.; Yang, R.; Kasprzak, M.; Bilgin, B.; Sathyan, A.; Dadkhah, H.; Emadi, A. Design and Comparison of Interior Permanent Magnet Motor Topologies for Traction Applications. IEEE Trans. Transp. Electrif. 2017, 3, 86–97. [Google Scholar] [CrossRef]
- Stumberger, B.; Stumberger, G.; Dolinar, D.; Hamler, A.; Trlep, M. Evaluation of Saturation and Cross-Magnetization Effects in Interior Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2003, 39, 1264–1271. [Google Scholar] [CrossRef]
- Meessen, K.J.; Thelin, P.; Soulard, J.; Lomonova, E.A. Inductance Calculations of Permanent-Magnet Synchronous Machines Including Flux Change and Self- and Cross-Saturations. IEEE Trans. Magn. 2008, 44, 2324–2331. [Google Scholar] [CrossRef]
- Li, C.; Zhang, W.; Gao, J.; Huang, S. Permanent Magnet Flux Linkage Analysis and Maximum Torque per Ampere (MTPA) Control of High Saturation IPMSM. Energies 2023, 16, 4717. [Google Scholar] [CrossRef]
- Lai, C.; Feng, G.; Mukherjee, K.; Kar, N.C. Investigations of the Influence of PMSM Parameter Variations in Optimal Stator Current Design for Torque Ripple Minimization. IEEE Trans. Energy Convers. 2017, 32, 1052–1062. [Google Scholar] [CrossRef]
- Bianchini, C.; Bisceglie, G.; Torreggiani, A.; Davoli, M.; Macrelli, E.; Bellini, A.; Frigieri, M. Effects of the Magnetic Model of Interior Permanent Magnet Machine on MTPA, Flux Weakening and MTPV Evaluation. Machines 2023, 11, 77. [Google Scholar] [CrossRef]
- Miao, Q.; Li, Q.; Xu, Y.; Lin, Z.; Chen, W.; Li, X. Virtual Constant Signal Injection-Based MTPA Control for IPMSM Considering Partial Derivative Term of Motor Inductance Parameters. World Electr. Veh. J. 2022, 13, 240. [Google Scholar] [CrossRef]
- Su, S.-W.; Hackl, C.M.; Kennel, R. Analytical Prototype Functions for Flux Linkage Approximation in Synchronous Machines. IEEE Open J. Ind. Electron. Soc. 2022, 3, 265–282. [Google Scholar] [CrossRef]
- Wendel, S.; Karamanakos, P.; Dietz, A.; Kennel, R. Flux Linkage-Based Model Predictive Current Control for Nonlinear PMSM Drives. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3051–3056. [Google Scholar]
- Liu, K.; Feng, J.; Guo, S.; Xiao, L.; Zhu, Z.-Q. Identification of Flux Linkage Map of Permanent Magnet Synchronous Machines Under Uncertain Circuit Resistance and Inverter Nonlinearity. IEEE Trans. Ind. Inform. 2018, 14, 556–568. [Google Scholar] [CrossRef]
- Bedetti, N.; Calligaro, S.; Petrella, R. Stand-Still Self-Identification of Flux Characteristics for Synchronous Reluctance Machines Using Novel Saturation Approximating Function and Multiple Linear Regression. IEEE Trans. Ind. Appl. 2016, 52, 3083–3092. [Google Scholar] [CrossRef]
- Ortombina, L.; Tinazzi, F.; Zigliotto, M. Magnetic Modeling of Synchronous Reluctance and Internal Permanent Magnet Motors Using Radial Basis Function Networks. IEEE Trans. Ind. Electron. 2018, 65, 1140–1148. [Google Scholar] [CrossRef]
- Chen, B.; Wu, J.; Sun, Q.; Wu, H.; Zhang, L. FEA-Based Mathematical Modeling and Simulation for IPMSM Drive with Consideration of Saturation and Cross-Coupling Influence. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Ge, M.; Li, J.; Qu, R.; Lu, Y.; Chen, J. A Synthetic Frozen Permeability Method for Torque Separation in Hybrid PM Variable-Flux Machines. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Elsherbiny, H.; Szamel, L.; Ahmed, M.K.; Elwany, M.A. High Accuracy Modeling of Permanent Magnet Synchronous Motors Using Finite Element Analysis. Mathematics 2022, 10, 3880. [Google Scholar] [CrossRef]
- Woo, T.-G.; Lee, S.-H.; Lee, H.-J.; Yoon, Y.-D. Flux Weakening Control Technique without Look-Up Tables for SynRMs Based on Flux Saturation Models. Electronics 2020, 9, 218. [Google Scholar] [CrossRef]
- Awan, H.A.A.; Song, Z.; Saarakkala, S.E.; Hinkkanen, M. Optimal Torque Control of Saturated Synchronous Motors: Plug-and-Play Method. IEEE Trans. Ind. Appl. 2018, 54, 6110–6120. [Google Scholar] [CrossRef]
- Jun, S.-B.; Kim, C.-H.; Cha, J.; Lee, J.H.; Kim, Y.-J.; Jung, S.-Y. A Novel Method for Establishing an Efficiency Map of IPMSMs for EV Propulsion Based on the Finite-Element Method and a Neural Network. Electronics 2021, 10, 1049. [Google Scholar] [CrossRef]
- Wendel, S.; Karamanakos, P.; Gebhardt, P.; Dietz, A.; Kennel, R. Flux Linkage-Based Direct Model Predictive Current Control for Synchronous Machines. IEEE Trans. Power Electron. 2021, 36, 14237–14256. [Google Scholar] [CrossRef]
- Hall, S.; Marquez-Fernandez, F.J.; Alakula, M. Dynamic Magnetic Model Identification of Permanent Magnet Synchronous Machines. IEEE Trans. Energy Convers. 2017, 32, 1367–1375. [Google Scholar] [CrossRef]
- Li, H.; Gao, J.; Huang, S.; Fan, P. A Novel Optimal Current Trajectory Control Strategy of IPMSM Considering the Cross Saturation Effects. Energies 2017, 10, 1460. [Google Scholar] [CrossRef]
- Lee, H.; Woldesemayat, M.L.; Nam, K. Zero Torque Control for EV Coasting Considering Cross-Coupling Inductance. IEEE Trans. Ind. Electron. 2017, 64, 6096–6104. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Pescetto, P.; Molsa, E.; Saarakkala, S.E.; Pellegrino, G.; Bojoi, R. Sensorless Self-Commissioning of Synchronous Reluctance Motors at Standstill Without Rotor Locking. IEEE Trans. Ind. Appl. 2017, 53, 2120–2129. [Google Scholar] [CrossRef]
- Vagati, A.; Pastorelli, M.; Scapino, F.; Franceschini, G. Impact of Cross Saturation in Synchronous Reluctance Motors of the Transverse-Laminated Type. IEEE Trans. Ind. Appl. 2000, 36, 1039–1046. [Google Scholar] [CrossRef]
- Carbonier, M.; Soong, W.L.; Mahmoudi, A.; Bianchi, N. Fast Flux Mapping of PM and Synchronous Reluctance Machines: Method Description and Comparison with Full FEA Approach. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 3724–3730. [Google Scholar]
- Wu, Q.; Li, W.; Feng, G.; Zhang, B. Optimization Control of Canned Electric Valve Permanent Magnet Synchronous Motor. Electronics 2023, 12, 2433. [Google Scholar] [CrossRef]
- Morimoto, S.; Tong, Y.; Takeda, Y.; Hirasa, T. Loss Minimization Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Electron. 1994, 41, 511–517. [Google Scholar] [CrossRef]
- Popovic, V.; Vujkov, B.; Vuckovic, M.; Vasic, V.; Marcetic, D.; Oros, D. MAPT Strategy for IPMSM with Parameter Sensitivity Analysis. In Proceedings of the 2020 International Symposium on Industrial Electronics and Applications (INDEL), Banja Luka, Bosnia and Herzegovina, 4–6 November 2020; pp. 1–4. [Google Scholar]
- Odhano, S.A.; Pescetto, P.; Awan, H.A.A.; Hinkkanen, M.; Pellegrino, G.; Bojoi, R. Parameter Identification and Self-Commissioning in AC Motor Drives: A Technology Status Review. IEEE Trans. Power Electron. 2019, 34, 3603–3614. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Base power | 4.4 kW | Stator slots | 36 |
| Rated voltage | 48 V | Stack length | 80 mm |
| Peak current | 390 A | Rotor pole number | 8 |
| Duty | S2-60 min | Frequency | 66.66 Hz |
| Stator outer diameter | 175 mm | Air-gap length | 0.5 mm |
| Stator inner diameter | 110 mm | Magnet dimensions | 2 × (4 × 10) mm |
| Rotor outer diameter | 109 mm | Magnet material | N35UH |
| Rotor inner diameter | 33 mm | Magnetic steel material | M250-35A |
| Parameter | Value | Parameter | FEA | FP-FEA |
|---|---|---|---|---|
| A | 0 | 35 × 10−6 | 37 × 10−6 | |
| B | 0 | 110 × 10−6 | 111 × 10−6 | |
| C = E | 2 | 246.59 | 251.57 | |
| D | 4 | 5.928 × 10−6 | 6.175 × 10−6 | |
| F | 0 | 0.9800 | 0.9896 | |
| 1 | 1.004 × 10−14 | 1.279 × 10−14 | ||
| 0 | 1.886 × 10−6 | 2.058 × 10−6 |
| d Axis Flux Linkage Map Fit | q Axis Flux Linkage Map Fit | ||||
|---|---|---|---|---|---|
| Parameter | FEA | FP-FEA | Parameter | FEA | FP-FEA |
| SSE | 2.866 × 105 | 9.441 × 104 | SSE | 3.525 × 105 | 1.547 × 105 |
| R-square | 0.9878 | 0.9960 | R-square | 0.9850 | 0.9934 |
| RMSE | 13.06 | 7.494 | RMSE | 14.48 | 9.597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vučković, M.; Popović, V.; Jerkan, D.; Jarić, M.; Banović, M.; Vasić, V.; Marčetić, D. Nonlinear Magnetic Model of IPMSM Based on the Frozen Permeability Technique Utilized in Improved MTPA Control. Electronics 2024, 13, 673. https://doi.org/10.3390/electronics13040673
Vučković M, Popović V, Jerkan D, Jarić M, Banović M, Vasić V, Marčetić D. Nonlinear Magnetic Model of IPMSM Based on the Frozen Permeability Technique Utilized in Improved MTPA Control. Electronics. 2024; 13(4):673. https://doi.org/10.3390/electronics13040673
Chicago/Turabian StyleVučković, Mladen, Vladimir Popović, Dejan Jerkan, Milica Jarić, Milica Banović, Veran Vasić, and Darko Marčetić. 2024. "Nonlinear Magnetic Model of IPMSM Based on the Frozen Permeability Technique Utilized in Improved MTPA Control" Electronics 13, no. 4: 673. https://doi.org/10.3390/electronics13040673
APA StyleVučković, M., Popović, V., Jerkan, D., Jarić, M., Banović, M., Vasić, V., & Marčetić, D. (2024). Nonlinear Magnetic Model of IPMSM Based on the Frozen Permeability Technique Utilized in Improved MTPA Control. Electronics, 13(4), 673. https://doi.org/10.3390/electronics13040673







