Two-Timescale Design for RIS-Aided Multicell MIMO Systems with Transceiver Hardware Impairments

Abstract

This paper investigates the reconfigurable intelligent surface (RIS)-aided uplink multicell massive multiple-input multiple-output (mMIMO) communication system with transceiver hardware impairments (THWIs), and the practical and feasible two-timescale scheme is used to design the phase shifts of the RIS. We consider the Rician channel model and use maximal-ratio combining (MRC) technology to process the received signal at the base stations (BS). The expression of the uplink achievable rate is derived and analyzed. Moreover, the genetic algorithm (GA) is used to optimize the phase shifts of the RIS to maximize the data rate. Finally, the accuracy of the derived results is verified. The simulation results show that appropriately increasing the number of RIS reflecting elements can compensate for the performance loss caused by inter-cell interference and THWIs and reduce the demand for BS antennas, which can significantly reduce the hardware costs at the BS.

1. Introduction

The explosive growth of mobile data, as well as the emergence of innovative technologies such as virtual reality and holographic communication, requires future wireless communication systems with extremely high data rates, seamless coverage, and ultra-high reliability [1]. In the past few years, wireless communication systems have expanded the coverage and increased the user rate by continuously increasing the size of the base station (BS) antennas, which will lead to inter-antenna interference and carries great hardware costs. Fortunately, reconfigurable intelligent surfaces (RISs) can enable future wireless communication systems to meet these requirements [2,3,4]. Therefore, RISs have been widely studied [5,6,7,8,9,10]. The authors in [5] focused on the RIS-aided multicell multiple-input single-output (MISO) system and maximized the minimum weighted signal-to-interference-plus-noise ratio (SINR) by jointly optimizing the transmit beamforming vectors at the BS and the reflective beamforming vector of the RIS. The authors in [6] investigated a RIS backscatter-based uplink coordinated transmission strategy and aimed to maximize the weighted sum rate (WSR). In [7], the authors suggested an RIS be deployed at the boundaries of multiple cells to mitigate inter-cell interference and assist cell-edge users in communicating with the BS, aiming to maximize the WSR by jointly optimizing the phase shifts of the RIS and the precoding matrix at the BS. In [8], the authors considered the phase shift design of the RIS and joint user scheduling in RIS-aided multicell downlink systems. The authors in [9] studied an intelligent omni-surface-aided multicell MIMO communication system and designed a distributed hybrid beamforming scheme to maximize the sum rate. In [10], besides considering the joint beamforming problems for an RIS-aided multicell MISO system, the authors further considered the SINR balancing beamforming design to enhance the fairness of users by maximizing the minimum SINR among all users.

However, most of the contributions mentioned above are based on the instantaneous CSI scheme, which will lead to an extremely high estimation overhead and computational complexity [11,12,13] and ignore the existence of transceiver hardware impairments. In this work, we adopt the two-timescale design scheme to avoid these problems caused by the instantaneous CSI-based scheme. The two-timescale design scheme refers to the design adopting instantaneous CSI and statistical CSI at the BS and RIS, respectively [14]. The reason for adopting statistical CSI at the RIS is that the locations and the angles of the arrival and departure of the users concerning the BS and the RIS barely change in a coherence interval. Many contributions have been devoted to the two-timescale design scheme and have proven its efficiency [15,16,17,18,19]. The RIS-aided mMIMO system with imperfect CSI based on the two-timescale design scheme was analyzed in [15], and the authors not only offered analytical insights into the power scaling laws but also compared the two-timescale scheme and the conventional instantaneous CSI scheme. The result in [15] showed that the adoption of the two-timescale scheme can effectively increase the system performance. The authors of [16] focused on the RIS-aided cell-free mMIMO system based on the two-timescale scheme and proved the superiority of the two-timescale scheme. Double-RIS-aided multi-user communication was researched in [17], and the authors adopted a novel multi-user two-timescale channel estimation protocol in the slow time-varying channel to minimize the pilot overhead. The authors of [18] compared the proposed two-timescale-based beam training algorithm with the empirical beam training algorithm, and they proved that the proposed two-timescale-based beam training algorithm achieved better performance with significantly lower training and feedback overheads. In simultaneously transmitting and reflecting reconfigurable intelligent surface-aided NOMA systems, the authors of [19] proposed two efficient two-timescale (TTS) transmission protocols for different channel setups to maximize the respective average achievable sum rate, and the simulation results showed that the proposed transmission protocols could reduce the channel estimation overhead as compared to the instantaneous CSI-based scheme.

Moreover, it is meaningful to consider the existence of transceiver hardware impairments (THWIs) in the RIS-aided communication system, which will lead to oscillator phase noise, non-linearities, and quantization errors [20]. There has been a lot of work to prove the necessity of considering the THWIs in models and the effect of THWIs on RIS-aided communication systems [21,22,23,24]. The authors of [21] investigated an RIS-aided device-to-device communication system with THWIs and analyzed the influence of the THWIs on the system by considering two special cases, i.e., no RIS hardware impairments and no transceiver hardware impairments. Meanwhile, [22] revealed the impact of the phase shift error (PSE) and THWIs on the RIS-aided wireless-powered IoT network; the authors started with a scenario where only the PSE was considered, and then moved toward a scenario where the PSE and THWIs were both considered. A robust design for an RIS-aided wireless communication system based on imperfect CSI and THWIs was studied in [23], and the simulation results proved that increasing the RIS elements can effectively reduce the influence of THWIs on the communication system. In [24], THWIs were also considered. The authors proposed a modified ON/OFF estimation (MOE) with a moderate pilot overhead to improve the accuracy of the direct estimation (DE) scheme, and the benefits of introducing RISs into hardware-impaired cell-free massive MIMO systems were also illustrated.

In addition, this work also takes the cascaded Rician channel into account, which is vital due to the installation height of the base station and RIS. Most of the current in-depth work has focused on the cascaded Rician channel, such as [25,26,27]. They focused on RIS-aided communication systems with cascaded Rician fading channels and gave some useful analysis. In [25], the authors derived the closed-form expressions of several performance metrics in terms of the exact outage probability, ergodic capacity, and average bit error rate (BER). In [26], the authors derived the closed-form expression of the outage probability determined by the distribution of the RIS-based composite channel and an asymptotic outage probability expression in a specific case. Similarly to [26], the authors of [26] derived new accurate closed-form approximations for several performance measures and derived an asymptotic expression for the outage probability at high signal-to-noise ratio (SNR) values; they also provided closed-form expressions for the system diversity order and coding gain.

To the best of our knowledge, the performance of RIS-aided multicell massive MIMO systems with THWIs has not been considered. In particular, the more practical and feasible two-timescale design scheme is adopted in this work. We derive the closed-form expression of the uplink achievable data rate, which will facilitate the investigation of how the RIS improves the performance of the proposed model. Moreover, some analytical results are given based on these derived expressions. Then, the genetic algorithm (GA) with low complexity is adopted to optimize the phase shifts, because this algorithm does not need to calculate the first-order derivative of the objective function when compared with the gradient descent method. Finally, a simulation validates our derivations and shows that appropriately increasing the number of RIS-reflecting elements can compensate for the performance loss caused by inter-cell interference and THWIs and also reduce the demand for BS antennas in the RIS-aided multicell mMIMO system with THWIs, which can significantly reduce the hardware costs at the BS.

Our main contributions are summarized as follows:

• The two-timescale scheme is adopted to design the beamforming at the BS and RIS, respectively, based on instantaneous CSI and statistical CSI, for less computational complexity and less channel estimation overhead.
• We derive the closed-form achievable rate expression, which holds for an arbitrary number of BS antennas and RIS elements under Rician fading. The properties of the achievable rate in different cases are analyzed to draw useful insights.
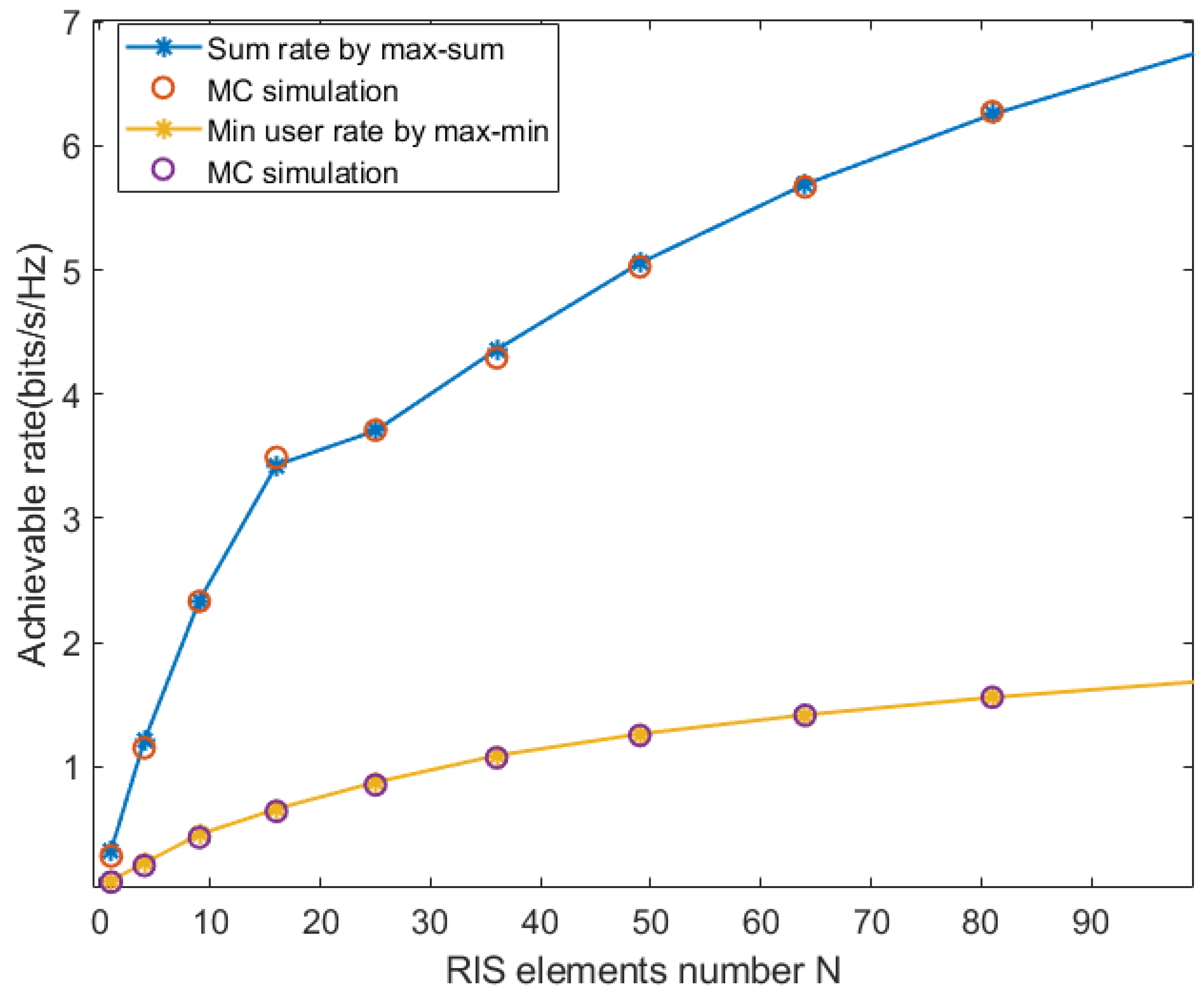
• The GA method is applied to maximize the sum rate and the minimum user rate by optimizing the phase shifts of the RIS.
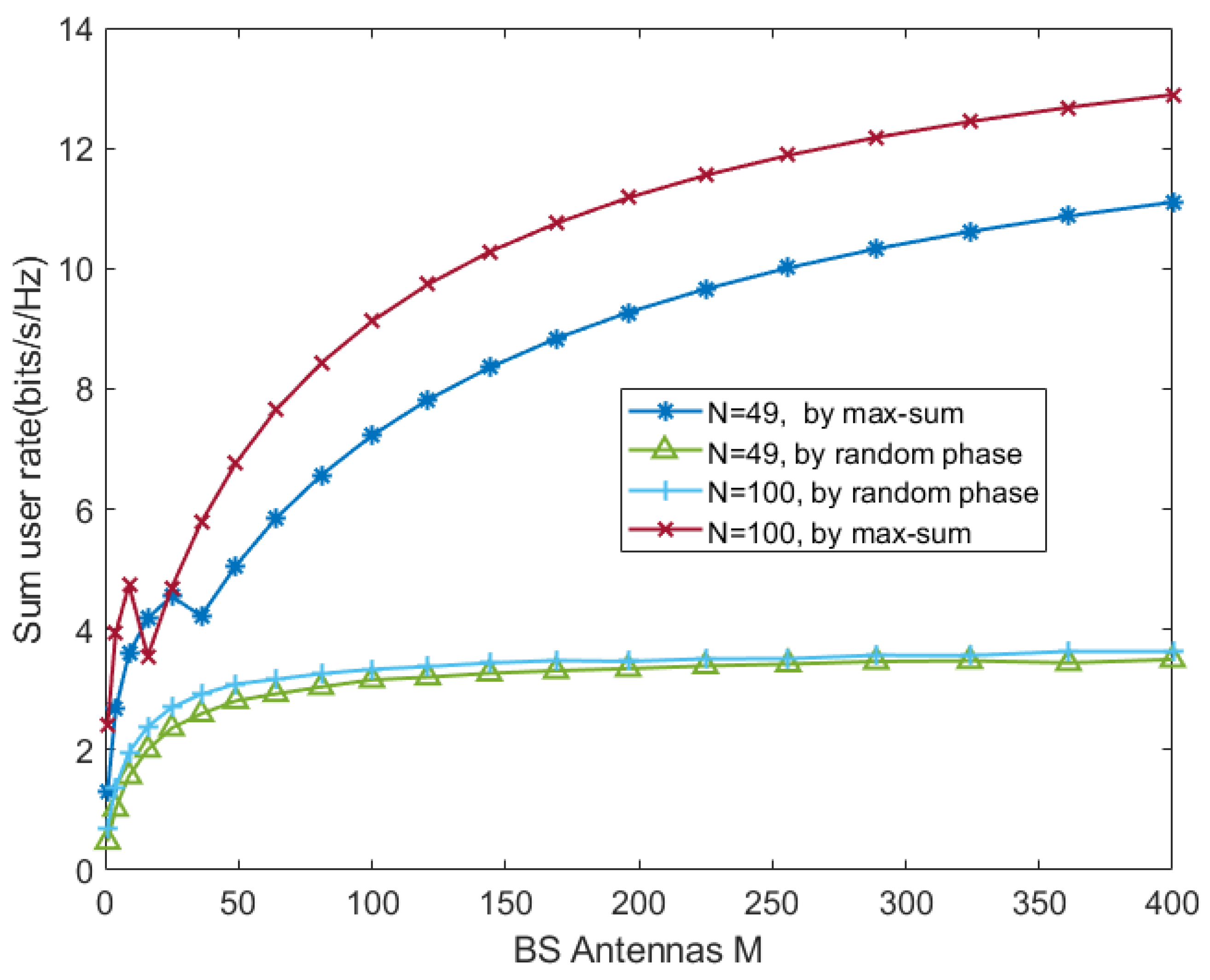
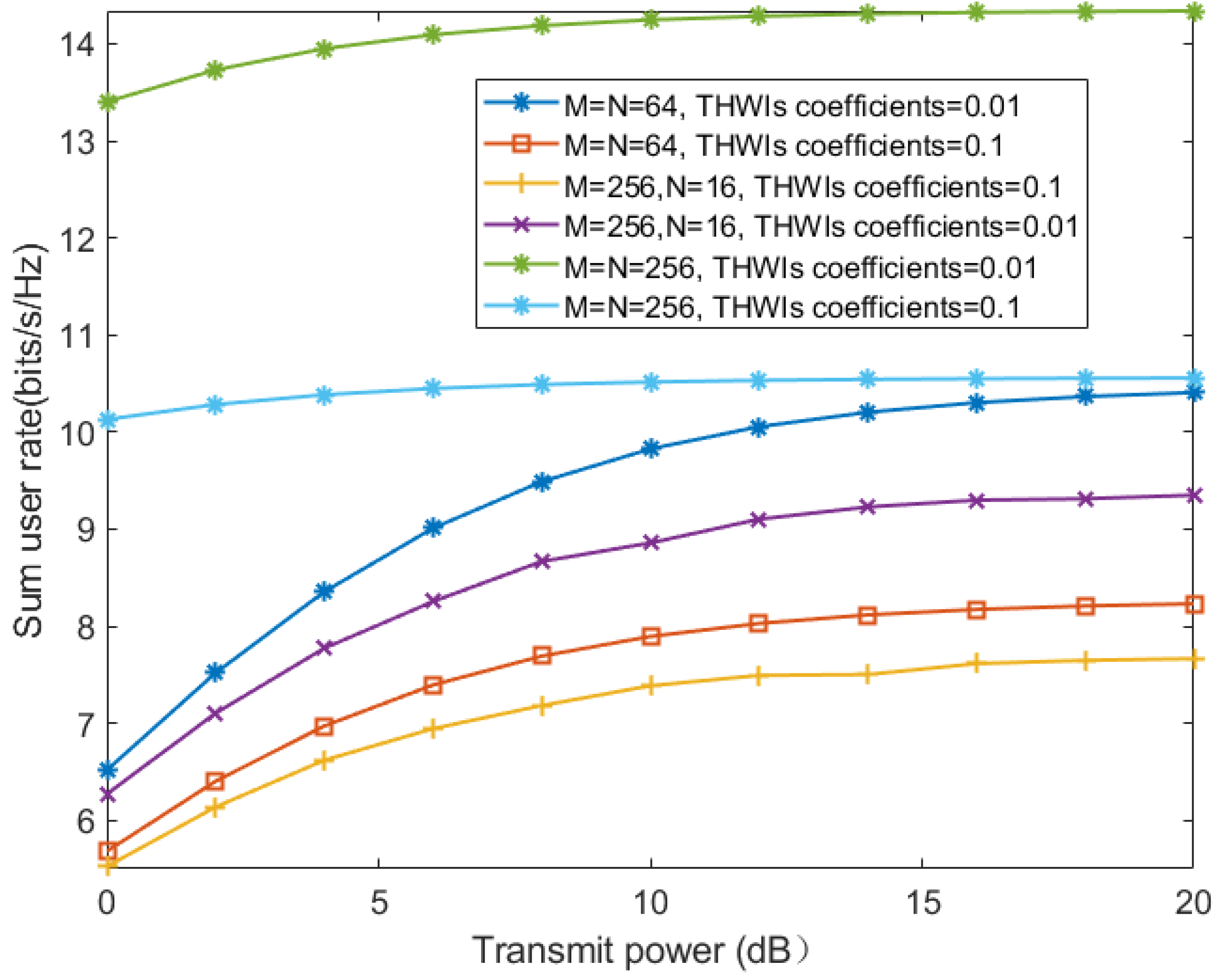
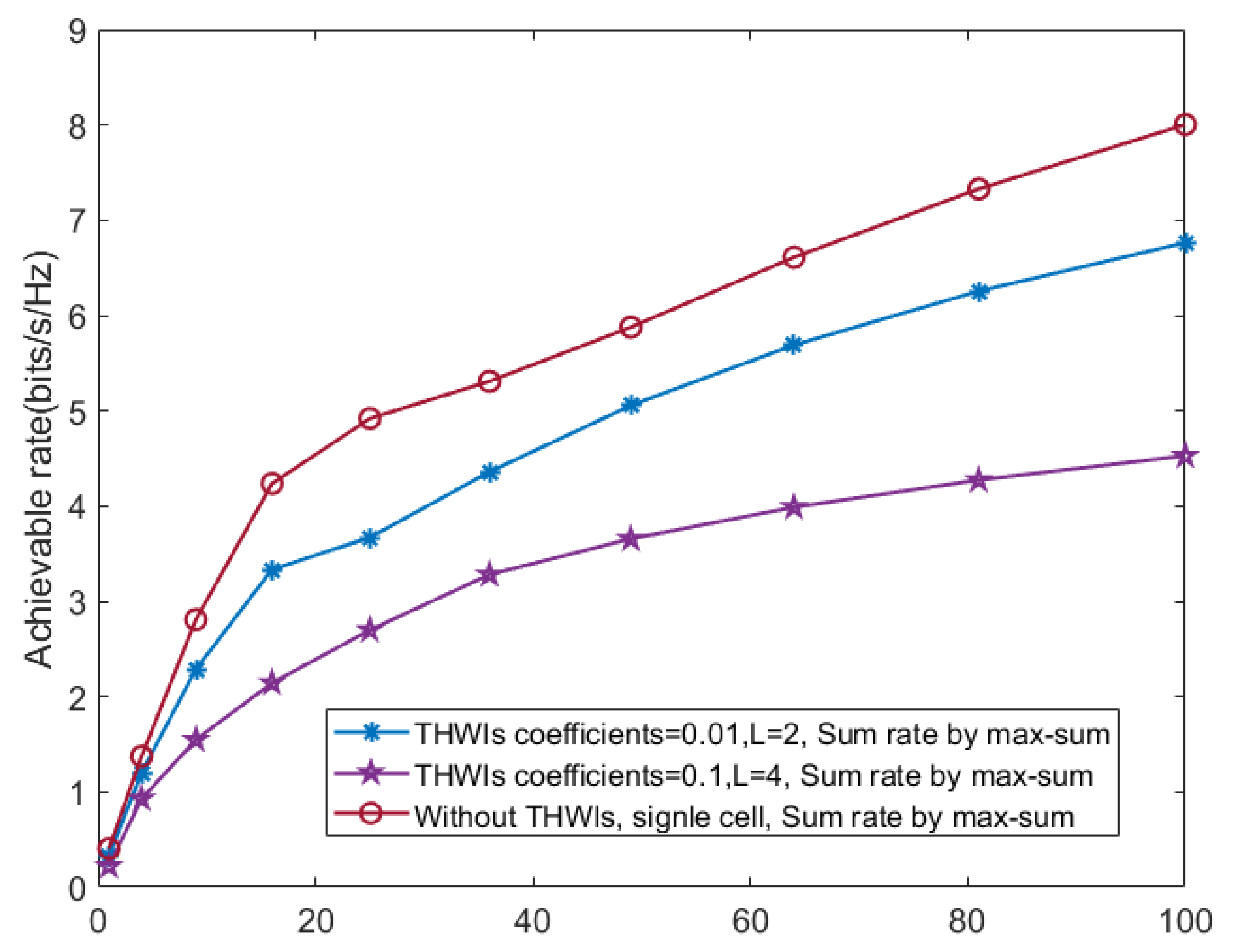
• Finally, numerical results validate our analytical conclusions and reveal that increasing the number of RIS elements can compensate for the influence of THWIs and effectively reduce the costs of the communication hardware.

2. System Model

As shown in Figure 1, we consider an RIS-aided uplink multicell mMIMO communication system. The number of cells is L, and the RIS comprises N reflecting elements. The base station (BS) in each cell is equipped with M antennas. In each cell, the direct link between users and the BS is blocked by obstacles, K single-antenna users can only communicate with the BS through the RIS, and both the transmitters and receivers have hardware impairments.

The phase shifts matrix of the RIS is $\mathbf{\Theta }=\mathrm{diag}\left\{e^{j{\theta }_1},\dots ,e^{j{\theta }_n},\dots ,e^{j{\theta }_N}\right\}$, where ${\theta }_n\in [0,2\pi )$, $n=1,\dots ,N$, ${\theta }_n$ represents the phase shift of the n-th element. In the l-th cell, the channel from the users to the RIS is denoted by ${\mathbf{H}}_{l,ur}=\left[{\mathbf{h}}_{l,1},\dots ,{\mathbf{h}}_{l,k},\dots ,{\mathbf{h}}_{l,K}\right]\in {\mathbb{C}}^{N\times K}$, $l=1,\dots ,L$, where ${\mathbf{h}}_{l,k}$ represents the channel from the k-th user to the RIS. The channel from the RIS to the BS is denoted by ${\mathbf{H}}_{l,rb}\in {\mathbb{C}}^{M\times N}$. The expressions of ${\mathbf{H}}_{l,rb}$ and ${\mathbf{h}}_{l,k}$ are

$$\begin{array}{cc}\hfill {\mathbf{H}}_{l,rb}=& \sqrt{{\nu }_l}\left(\begin{array}{c}\sqrt{\frac{{\rho }_l}{{\rho }_l+1}}{\overline{\mathbf{H}}}_{l,rb}+\sqrt{\frac{1}{{\rho }_l+1}}{\tilde{\mathbf{H}}}_{l,rb}\end{array}\right),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mathbf{h}}_{l,k}=& \sqrt{{\mu }_{l,k}}\left(\begin{array}{c}\sqrt{\frac{{ϵ}_{l,k}}{{ϵ}_{l,k}+1}}{\overline{\mathbf{h}}}_{l,k}+\sqrt{\frac{1}{{ϵ}_{l,k}+1}}{\tilde{\mathbf{h}}}_{l,k}\end{array}\right),\hfill \end{array}$$

(2)

where ${\nu }_l$ and ${\mu }_{l,k}$ are large-scale path loss factors, ${\rho }_l$ and ${ϵ}_{l,k}$ are Rician factors, and ${\tilde{\mathbf{H}}}_{l,rb}$ and ${\tilde{\mathbf{h}}}_{l,k}$ are the none-line-of-sight (NLoS) components of the channel, whose elements are independent and identical distribution (i.i.d.) random variables following $\mathcal{C}\mathcal{N}\left(0,1\right)$.

${\overline{\mathbf{H}}}_{l,rb}$ and ${\overline{\mathbf{h}}}_{l,k}$ are the LoS components of the channel, and the expressions are

$$\begin{array}{cc}\hfill {\overline{\mathbf{H}}}_{l,rb}=& {\mathbf{a}}_M\left(\begin{array}{c}{\psi }_{l,rb}^a,{\psi }_{l,rb}^e\end{array}\right){\mathbf{a}}_N^H\left(\begin{array}{c}{\varphi }_{l,rb}^a,{\varphi }_{l,rb}^e\end{array}\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\overline{\mathbf{h}}}_{l,k}=& {\mathbf{a}}_N\left(\begin{array}{c}{\psi }_{l,kr}^a,{\psi }_{l,kr}^e\end{array}\right).\hfill \end{array}$$

(4)

where ${\psi }_{l,rb}^a$, ${\psi }_{l,rb}^e$, respectively, represent the arrival azimuth and elevation angles from the RIS to the BS in the l-th cell. ${\varphi }_{l,rb}^a$, ${\varphi }_{l,rb}^e$, respectively, represent the departure azimuth and elevation angles from the RIS to the BS in the l-th cell. ${\psi }_{l,kr}^a$, ${\psi }_{l,kr}^e$, respectively, represent the arrival azimuth and elevation angles from user k to the RIS in the l-th cell.

In addition, we adopt the uniform square planar array to express ${\mathbf{a}}_M\left(\begin{array}{c}{\psi }_{l,rb}^a,{\psi }_{l,rb}^e\end{array}\right)$, and it can be written as

$$\begin{array}{cc}\hfill {\mathbf{a}}_M\left({\psi }_{l,rb}^a,{\psi }_{l,rb}^e\right)=& \left[1,\dots ,e^{j\frac{2\pi d}{\lambda }(p{sin\psi }_{l,rb}^a{sin\psi }_{l,rb}^e+q{cos\psi }_{l,rb}^e)},\right.\hfill \\ \hfill & {\left.\dots ,e^{j\frac{2\pi d}{\lambda }(\sqrt{M}-1){sin\psi }_{l,rb}^a{sin\psi }_{l,rb}^e+(\sqrt{M}-1){cos\psi }_{l,rb}^e}\right]}^T,\hfill \end{array}$$

(5)

where $0\le p,q\le \sqrt{M}-1$, d represents the element spacing, and $\lambda$ represents the wavelength.

Based on the above definitions, the cascaded channel in the l-th cell can be denoted by ${\mathbf{G}}_l={\mathbf{H}}_{l,rb}\mathbf{\Theta }{\mathbf{H}}_{l,ur}=\left[{\mathbf{g}}_{l,1},\dots {\mathbf{g}}_{l,k},\dots {\mathbf{g}}_{l,K}\right]$, where ${\mathbf{g}}_{l,k}={\mathbf{H}}_{l,rb}\mathbf{\Theta }{\mathbf{h}}_{l,k}$. In the l-th cell, the transmit distortion of users is denoted by ${\mathbf{z}}_{l,t}={\left[z_{l,1},\dots z_{l,k},\dots ,z_{l,K}\right]}^T$, where $z_{l,k}$ represents the transmit distortion of the user k. The receive distortion of the BS is denoted by ${\mathbf{z}}_{l,r}$.

Therefore, the signal received by the BS of the l-th cell is

$$\begin{array}{cc}\hfill {\mathbf{y}}_l=& {\mathbf{G}}_l\left({\mathbf{P}}_l{\mathbf{x}}_l+{\mathbf{z}}_{l,t}\right)+{\mathbf{z}}_{l,r}+{\mathbf{n}}_l=\sum _{i=1}^K{\mathbf{g}}_{l,i}\left(\sqrt{p_{l,i}}{x}_{l,i}+z_{l,i}\right)+{\mathbf{z}}_{l,r}+{\mathbf{n}}_l,\hfill \end{array}$$

(6)

where ${\mathbf{P}}_l=\mathrm{diag}\left(\sqrt{p_{l,1}},\dots ,\sqrt{p_{l,K}}\right)$ is the transmit power of users. ${\mathbf{x}}_l=\left[x_{l,1},\dots ,x_{l,K}{]}^T\right.$ is the signal vector of users, and $\mathbb{E}\left\{|x_{l,i}{|}^2\right\}=1$. ${\mathbf{n}}_l\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }^2{\mathbf{I}}_N\right)$ represents the additive white Gaussian noise (AWGN). The transceiver distortions are described in terms of conditional distributions with respect to the channel realizations as $z_{l,i}\sim \mathcal{C}\mathcal{N}\left(0,k_{l,u}{p}_{l,i}\right)$ and ${\mathbf{z}}_{l,r}\sim \mathcal{C}\mathcal{N}\left(0,k_{l,b}{\displaystyle \sum _{j=1}^L}{\displaystyle \sum _{i=1}^K}{p}_{j,i}{\mathbf{I}}_M{\mathbf{g}}_{j,i}{\displaystyle {\mathbf{g}}_{j,i}^H}\right)$, where $k_{l,u}$ and $k_{l,b}$ represent the severity of the residual impairments of the transceiver.

Then, we employ the MRC technology, and the received signal at the BS can be expressed as

$$\begin{array}{cc}\hfill {\mathbf{r}}_l=& {\mathbf{G}}_l^H\left(\begin{array}{c}{\displaystyle \sum _{i=1}^K}{\mathbf{g}}_{l,i}\left(\sqrt{p_{l,i}}{x}_{l,i}+z_{l,i}\right)+{\mathbf{z}}_{l,r}+{\mathbf{n}}_l\end{array}\right).\hfill \end{array}$$

(7)

Therefore, in the l-th cell, the k-th user’s signal received by the BS can be expressed as

$$\begin{array}{cc}\hfill r_{l,k}=& {\mathbf{g}}_{l,k}^H\left(\sum _{i=1}^K{\mathbf{g}}_{l,i}\left(\sqrt{p_{l,i}}{x}_{l,i}+z_{l,i}\right)+\sum _{j=1,j\ne l}^L\sum _{i=1}^K{\mathbf{g}}_{j,i}\left(\sqrt{p}{x}_{j,i}+z_{j,i}\right)+{\mathbf{z}}_{l,r}+{\mathbf{n}}_l\right)\hfill \\ \hfill =& \underset{\mathrm{Signal}}{\underbrace{{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{l,k}\sqrt{p_{l,k}}{x}_{l,k}}}+\underset{\mathrm{Intra}\text{-}\mathrm{cell}\mathrm{interference}}{\underbrace{{\displaystyle \sum _{i=1,i\ne k}^K}{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{l,i}\sqrt{p_{l,i}}{x}_{l,i}}}+\underset{\mathrm{Inter}\text{-}\mathrm{cell}\mathrm{interference}}{\underbrace{\sum _{j=1,j\ne l}^L\sum _{i=1}^K{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{j,i}\sqrt{p_{j,i}}{x}_{j,i}}}\hfill \\ \hfill +& \underset{\mathrm{Total}\mathrm{THWIs}}{\underbrace{\sum _{j=1}^L\sum _{i=1}^K{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{j,i}{z}_{j,i}+{\mathbf{g}}_{l,k}^H{\mathbf{z}}_{l,r}}}+\underset{\mathrm{Noise}}{\underbrace{{\mathbf{g}}_{l,k}^H{\mathbf{n}}_l}}.\hfill \end{array}$$

(8)

3. Analysis of Uplink Achievable Rate

The uplink data rate of user k can be denoted by $R_{l,k}=\mathbb{E}\left\{{log}_2(1+{\mathrm{SINR}}_{l,k})\right\}$, where ${\mathrm{SINR}}_{l,k}$ is the signal-to-interference-plus-noise ratio (SINR) of the user k in the l-th cell. The expression of ${\mathrm{SINR}}_{l,k}$ is given as

$$\begin{array}{c}\hfill {\mathrm{SINR}}_{l,k}=\frac{p_{l,k}{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{l,k}\right|}^2}{{\displaystyle \sum _{i=1,i\ne k}^K}{p}_{l,i}{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{l,i}\right|}^2+{\displaystyle \sum _{j=1,j\ne l}^L}{\displaystyle \sum _{i=1}^K}{p}_{j,i}{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{j,i}\right|}^2+{\displaystyle \sum _{j=1}^L}{\displaystyle \sum _{i=1}^K}{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{j,i}{\mathbf{z}}_{j,i}\right|}^2+{\left|{\mathbf{g}}_{l,k}^H{\mathbf{z}}_r\right|}^2+{\sigma }^2{∥{\mathbf{g}}_{l,k}∥}^2},\end{array}$$

(9)

Theorem 1.

In the RIS-aided uplink multicell mMIMO communication system with THWIs, $R_{l,k}$ can be approximated as $R_{l,k}\approx {log}_2\left(1+{\mathrm{SINR}}_{l,k}\right)$, where

$$\begin{array}{c}\hfill {\mathrm{SINR}}_{l,k}=\frac{p_{l,k}{\mathbb{E}}_{\mathit{signal}}^{l,k}}{{\displaystyle \sum _{i=1,i\ne k}^K}{p}_{l,i}{\mathbb{E}}_{\mathit{intra}}^{l,i}+{\displaystyle \sum _{j=1,j\ne l}^L}{\displaystyle \sum _{i=1}^K}{p}_{j,i}{\mathbb{E}}_{\mathit{inter}}^{j,i}+{\mathbb{E}}_{\mathit{thwis}}^{l,k}+{\sigma }^2{\mathbb{E}}_{\mathit{noise}}^{l,k}},\end{array}$$

(10)

where ${\mathbb{E}}_{\mathit{signal}}^{l,k}=\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{l,k}\right|}^2\right\}$, ${\mathbb{E}}_{\mathit{intra}}^{l,i}=\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{l,i}\right|}^2\right\}$, ${\mathbb{E}}_{\mathit{inter}}^{j,i}=\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{j,i}\right|}^2\right\}$, ${\mathbb{E}}_{\mathit{noise}}^{l,k}=\mathbb{E}\left\{{∥{\mathbf{g}}_{l,k}∥}^2\right\}$, and ${\mathbb{E}}_{\mathit{thwis}}^{l,k}=\mathbb{E}\left\{{\displaystyle \sum _{j=1}^L}{\displaystyle \sum _{i=1}^K}{\left|{\mathbf{g}}_{l,k}^H{\mathbf{g}}_{j,i}{z}_{j,i}\right|}^2+{\left|{\mathbf{g}}_{l,k}^H{\mathbf{z}}_{l,r}\right|}^2\right\}$.

The expressions of ${\mathbb{E}}_{\mathrm{signal}}^{l,k}$, ${\mathbb{E}}_{\mathrm{intra}}^{l,k}$, ${\mathbb{E}}_{\mathrm{inter}}^{j,i}$, ${\mathbb{E}}_{\mathrm{noise}}^{l,k}$ and ${\mathbb{E}}_{\mathrm{thwis}}^{l,k}$ are, respectively, given by (11)–(15), where $a_{l,k}=\frac{{\nu }_l{\mu }_{l,k}}{\left({\rho }_l+1\right)\left({ϵ}_{l,k}+1\right)}$, ${\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)={\mathbf{a}}_N^H\left({\varphi }_{l,rb}^a,{\varphi }_{l,rb}^e\right)\mathbf{\Theta }{\stackrel{-}{\mathbf{h}}}_{l,k}$, ${\mathbf{g}}_{l,k_m}$ is the m-th element of ${\mathbf{g}}_{l,k}$.

$$\begin{array}{cc}\hfill & {\mathbb{E}}_{\mathrm{signal}}^{l,k}=M{a}_{l,k}^2\times \left\{M{\rho }_l^2{{ϵ}_{l,k}}^2{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^4+M{N}^2\left(2{\rho }_l^2+{ϵ}_{l,k}^2+2{\rho }_l{ϵ}_{l,k}+2{\rho }_l+2{ϵ}_{l,k}+1\right)+2{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\right.\hfill \\ \hfill & \left(2MN{\rho }_l+MN{ϵ}_{l,k}+MN+2M+N{ϵ}_{l,k}+N+2\right)+N^2\left({ϵ}_{l,k}^2+2{\rho }_l{ϵ}_{l,k}+2{\rho }_l+2{ϵ}_{l,k}+1\right)+(M+1)N\left(2{\rho }_l+2{ϵ}_{l,k}+1\right)\},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & {\mathbb{E}}_{\mathrm{intra}}^{l,i}=M{a}_{l,k}{a}_{l,i}\left\{M{\rho }_l^2{ϵ}_{l,k}{ϵ}_{l,i}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2{\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2\right.+{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\left({\rho }_{l}MN+N{ϵ}_{l,i}+N+2M\right)+{\rho }_l{ϵ}_{l,i}{\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & \left(N\left({\rho }_{l}M+{ϵ}_{l,k}+1\right)+2M\right)+MN\left(2{\rho }_l+{ϵ}_{l,i}+{ϵ}_{l,k}+1\right)+N^2\left(M{\rho }_l^2+{\rho }_l\left({ϵ}_{l,i}+{ϵ}_{l,k}+2\right)+\left({ϵ}_{l,k}+1\right)\left({ϵ}_{l,i}+1\right)\right)\hfill \\ \hfill & \left.+M{ϵ}_{l,k}{ϵ}_{l,i}{\left|{\overline{\mathbf{h}}}_{l,k}^H{\overline{\mathbf{h}}}_{l,i}\right|}^2+2M{\rho }_l{ϵ}_{l,k}{ϵ}_{l,i}\mathrm{Re}\{{\mathbf{\Phi }}_{l,k}^H\left(\mathbf{\Theta }\right){\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\left.{\overline{\mathbf{h}}}_{l,i}^H{\overline{\mathbf{h}}}_{l,k}\right\}\right\},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & {\mathbb{E}}_{\mathrm{inter}}^{j,i}=M{a}_{l,k}{a}_{j,i}\times \left\{M{\rho }_l^2{ϵ}_{l,k}{ϵ}_{j,i}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2{\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2\right.+{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\left({\rho }_{l}MN+N{ϵ}_{j,i}+N+2M\right)+{\rho }_l{ϵ}_{j,i}{\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & \left(N\left({\rho }_{l}M+{ϵ}_{l,k}+1\right)+2M\right)+MN\left(2{\rho }_l+{ϵ}_{j,i}+{ϵ}_{l,k}+1\right)+N^2\left(M{\rho }_l^2+{\rho }_l\left({ϵ}_{j,i}+{ϵ}_{l,k}+2\right)+\left({ϵ}_{l,k}+1\right)\left({ϵ}_{j,i}+1\right)\right)\hfill \\ \hfill & \left.+M{ϵ}_{l,k}{ϵ}_{j,i}{\left|{\overline{\mathbf{h}}}_{l,k}^H{\overline{\mathbf{h}}}_{j,i}\right|}^2+2M{\rho }_l{ϵ}_{l,k}{ϵ}_{j,i}\mathrm{Re}\{{\mathbf{\Phi }}_{l,k}^H\left(\mathbf{\Theta }\right){\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\left.{\overline{\mathbf{h}}}_{j,i}^H{\overline{\mathbf{h}}}_{l,k}\right\}\right\},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\mathbb{E}}_{\mathrm{noise}}^{l,k}=M{a}_{l,k}\left({ϵ}_{l,k}{\rho }_l{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2+N{ϵ}_{l,k}+N{\rho }_l+N\right),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\mathbb{E}}_{\mathrm{thwis}}^{l,k}=k_{l,u}{p}_{l,k}{\mathbb{E}}_{\mathrm{signal}}^{l,k}+k_{l,u}\sum _{i=1,i\ne k}^K{p}_{l,i}{\mathbb{E}}_{\mathrm{intra}}^{l,i}+\sum _{j=1,j\ne l}^L{k}_{j,u}\sum _{i=1}^K{p}_{j,i}{\mathbb{E}}_{\mathrm{inter}}^{j,i}+k_{l,b}M\left(p_{l,k}\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k_m}\right|}^4\right\}+\sum _{i=1,i\ne k}^K{p}_{l,i}\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}\right.\hfill \\ \hfill & \left.+\sum _{j=1,j\ne l}^L\sum _{i=1}^K{p}_{j,i}\mathbb{E}\left\{{\left|{\mathbf{g}}_{j,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k_m}\right|}^4\right\}=a_{l,k}^2{\rho }_l^2{ϵ}_{l,k}^2{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^4+4a_{l,k}^2{\rho }_l{ϵ}_{l,k}\left[\left(N\left({\rho }_l+{ϵ}_{l,k}+1\right)+2\right){\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2+N^2\right]+2a_{l,k}^{2}N\left({\rho }_l^{2}N+{ϵ}_{l,k}^{2}N+N+1\right)\hfill \\ \hfill & +4a_{l,k}^{2}N(N+1)\left({\rho }_l+{ϵ}_{l,k}\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{{\left|{\mathbf{g}}_{l,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}=a_{l,k}{a}_{l,i}{\rho }_l\left(N+{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\right)\left({\rho }_l{ϵ}_{l,i}{\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2+{\rho }_{l}N+{ϵ}_{l,i}N\right)+a_{l,k}{a}_{l,i}{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & +a_{l,k}{a}_{l,i}{\rho }_{l}N\left(\left({ϵ}_{l,k}+{ϵ}_{l,i}\right){\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2+2\right)+a_{l,k}{a}_{l,i}N+a_{l,k}{a}_{l,i}{\rho }_l{N}^2+a_{l,k}{a}_{l,i}N\left({ϵ}_{l,k}+1\right)\left(\left({\rho }_l+1\right)N+{ϵ}_{l,i}(N+1)\right)\hfill \\ \hfill & +2a_{l,k}{a}_{l,i}{\rho }_l\left({ϵ}_{l,i}{ϵ}_{l,k}\mathrm{Re}\left\{{\mathbf{\Phi }}_{l,k}^H\left(\mathbf{\Theta }\right){\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right){\overline{\mathbf{h}}}_{l,k}^H{\overline{\mathbf{h}}}_{l,i}\right\}+{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2+{ϵ}_{l,i}{\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{{\left|{\mathbf{g}}_{j,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}=a_{l,k}{a}_{j,i}{\rho }_l\left(N+{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\right)\left({\rho }_l{ϵ}_{j,i}{\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2+{\rho }_{l}N+{ϵ}_{j,i}N\right)+a_{l,k}{a}_{j,i}{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & +a_{l,k}{a}_{j,i}{\rho }_{l}N\left(\left({ϵ}_{l,k}+{ϵ}_{j,i}\right){\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2+2\right)+a_{l,k}{a}_{j,i}N+a_{l,k}{a}_{j,i}{\rho }_l{N}^2+a_{l,k}{a}_{j,i}N\left({ϵ}_{l,k}+1\right)\left(\left({\rho }_l+1\right)N+{ϵ}_{j,i}(N+1)\right)\hfill \\ \hfill & +2a_{l,k}{a}_{j,i}{\rho }_l\left({ϵ}_{j,i}{ϵ}_{l,k}\mathrm{Re}\left\{{\mathbf{\Phi }}_{l,k}^H\left(\mathbf{\Theta }\right){\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right){\overline{\mathbf{h}}}_{l,k}^H{\overline{\mathbf{h}}}_{j,i}\right\}+{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2+{ϵ}_{j,i}{\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2\right).\hfill \end{array}$$

(18)

Proof of Theorem 1.

Please refer to Appendix A. □

By observing (10), we find that the closed-form expression is independent of the NLoS components, including ${\tilde{\mathbf{d}}}_{\chi }$, ${\tilde{\mathbf{h}}}_{\chi }$, $\tilde{\mathbf{H}}$, and the phase shift term ${\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)$ is always related to the Rician factors and path loss factors, i.e., ${\rho }_l$, ${ϵ}_{l,k}$, ${ϵ}_{l,i}$, which barely change in a coherence interval. This means that the two-timescale scheme can greatly reduce the computational complexity and power consumption due to the slowly varying CSI, i.e., Rician factors and path loss factors.

Moreover, based on this analysis, we can conclude that if the channel in this system is a fully Rayleigh channel, namely ${\rho }_l={ϵ}_{l,k}={ϵ}_{l,i}=0$, $\forall l,k,i$, the performance of this system will be independent of the phase shifts and only depends on the number of RIS elements N and BS antennas M. Hence, it is important to reveal the relation between the system performance and the number of RIS elements N and BS antennas M. In the following, we will focus on two special cases where the BS antennas M and the RIS elements N tend to be infinite, respectively.

Corollary 1.

In the RIS-aided uplink multicell mMIMO communication system with THWIs, when $N\to \infty$ and the phase shifts of the RIS are random, we can approximate the rate as $R_{l,k}\to {log}_2\left(1+{\mathrm{SINR}}_N\right)$, and the ${\mathrm{SINR}}_N$ is given as

$$\begin{array}{c}\hfill {\mathrm{SINR}}_N=\frac{p_{l,k}{a}_{l,k}{\mathbf{A}}_1}{{\displaystyle \sum _{i=1,i\ne k}^K}{p}_{l,i}{a}_{l,i}{\mathbf{A}}_2+{\displaystyle \sum _{j=1,j\ne l}^L}{\displaystyle \sum _{i=1}^K}{p}_{j,i}{a}_{j,i}{\mathbf{A}}_3+{\mathbf{A}}_4},\end{array}$$

(19)

where

$$\begin{array}{cc}\hfill & {\mathbf{A}}_1=2M{\rho }_l^2{{ϵ}_{l,k}}^2+M\left(2{\rho }_l^2+{ϵ}_{l,k}^2+2{\rho }_l{ϵ}_{l,k}+2{\rho }_l+2{ϵ}_{l,k}+1\right)\hfill \\ \hfill & +2{\rho }_l{ϵ}_{l,k}\left(2M{\rho }_l+M{ϵ}_{l,k}+M+{ϵ}_{l,k}+1\right)+\left({ϵ}_{l,k}^2+2{\rho }_l{ϵ}_{l,k}+2{\rho }_l+2{ϵ}_{l,k}+1\right),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & {\mathbf{A}}_2=M{\rho }_l^2{ϵ}_{l,k}{ϵ}_{l,i}+{\rho }_l{ϵ}_{l,k}\left({\rho }_{l}M+{ϵ}_{l,i}+1\right)+{\rho }_l{ϵ}_{l,i}\left({\rho }_{l}M+{ϵ}_{l,k}+1\right)+M{\rho }_l^2+{\rho }_l\left({ϵ}_{l,i}+{ϵ}_{l,k}+2\right)\hfill \\ \hfill & +\left({ϵ}_{l,k}+1\right)\left({ϵ}_{l,i}+1\right),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & {\mathbf{A}}_3=M{\rho }_l^2{ϵ}_{l,k}{ϵ}_{j,i}+{\rho }_l{ϵ}_{l,k}\left({\rho }_{l}M+{ϵ}_{j,i}+1\right)+{\rho }_l{ϵ}_{j,i}\left({\rho }_{l}M+{ϵ}_{l,k}+1\right)+\left(M{\rho }_l^2+{\rho }_l\left({ϵ}_{j,i}+{ϵ}_{l,k}+2\right)\right.\hfill \\ \hfill & +\left.\left({ϵ}_{l,k}+1\right)\left({ϵ}_{j,i}+1\right)\right),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & {\mathbf{A}}_4=k_{l,u}{p}_{l,k}{a}_{l,k}{\mathbf{A}}_1+k_{l,u}\sum _{i=1,i\ne k}^K{p}_{l,i}{a}_{l,i}{\mathbf{A}}_2+\sum _{j=1,j\ne l}^L{k}_{j,u}\sum _{i=1}^K{p}_{j,i}{a}_{j,i}{\mathbf{A}}_3\hfill \\ \hfill & +k_{l,b}\left(p_{l,k}\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k_m}\right|}^4\right\}+\sum _{i=1,i\ne k}^K{p}_{l,i}\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}+\sum _{j=1j\ne l}^L\sum _{i=1}^K{p}_{j,i}\mathbb{E}\left\{{\left|{\mathbf{g}}_{j,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}\right),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k_m}\right|}^4\right\}=2a_{l,k}{\rho }_l^2{ϵ}_{l,k}^2+4a_{l,k}{\rho }_l{ϵ}_{l,k}\left({\rho }_l+{ϵ}_{l,k}+1\right)+4a_{l,k}{\rho }_l{ϵ}_{l,k}+2a_{l,k}^2\left({\rho }_l^2+{ϵ}_{l,k}+1\right)\hfill \\ \hfill & +4a_{l,k}\left({\rho }_l+{ϵ}_{l,k}\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{{\left|{\mathbf{g}}_{l,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}=a_{l,i}{\rho }_l\left[\left(1+{ϵ}_{l,k}\right)\left({\rho }_l{ϵ}_{l,i}+{\rho }_l+{ϵ}_{l,i}\right)+\left({ϵ}_{l,k}+{ϵ}_{l,i}\right)+1\right]\hfill \\ \hfill & +a_{l,i}\left({ϵ}_{l,k}+1\right)\left({\rho }_l+{ϵ}_{l,i}+1\right),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{{\left|{\mathbf{g}}_{j,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}=a_{j,i}{\rho }_l\left[\left(1+{ϵ}_{l,k}\right)\left({\rho }_l{ϵ}_{l,i}+{\rho }_l+{ϵ}_{l,i}\right)+\left({ϵ}_{l,k}+{ϵ}_{j,i}\right)+1\right]\hfill \\ \hfill & +a_{j,i}\left({ϵ}_{l,k}+1\right)\left({\rho }_l+{ϵ}_{j,i}+1\right).\hfill \end{array}$$

(26)

Proof of Corollary 1.

Similar to the derivation method in ([12], Corollary 3), we can remove the terms that are not on the order of $\mathcal{O}\left(N^2\right)$ when $N\to \infty$. Moreover, it is noted that the phase shift terms such as ${\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)$ can be replaced in line with expectation. □

It can be seen that the noise term ${\mathbb{E}}_{\mathrm{noise}}^{l,k}$ is not included in Equation (19), and the rate will tend to be constant. This shows that in the RIS-aided uplink multicell mMIMO communication system with THWIs, when $N\to \infty$ and the phase shifts of the RIS are random, we can eliminate the effect of noise. Moreover, on this basis, if the number of BS antennas also becomes infinite, the rate will also be constant. The order of all terms, which includes the signal power terms, interference terms, and the terms caused by THWIs, is on the order of $\mathcal{O}\left(M\right)$ when the number of BS antennas also becomes infinite.

Corollary 2.

In the RIS-aided uplink multicell mMIMO communication system with THWIs, when $M\to \infty$, we can approximate the rate as $R_{l,k}\to {log}_2\left(1+{\mathrm{SINR}}_M\right)$, and the ${\mathrm{SINR}}_M$ is given as

$$\begin{array}{c}\hfill {\mathrm{SINR}}_M=\frac{p_{l,k}{a}_{l,k}^2{\mathbf{B}}_1}{{\displaystyle \sum _{i=1,i\ne k}^K}{p}_{l,i}{a}_{l,k}{a}_{l,i}{\mathbf{B}}_2+{\displaystyle \sum _{j=1,j\ne l}^L}{\displaystyle \sum _{i=1}^K}{p}_{j,i}{a}_{l,k}{a}_{j,i}{\mathbf{B}}_3+{\mathbf{B}}_4},\end{array}$$

(27)

where

$$\begin{array}{cc}\hfill & {\mathbf{B}}_1={\rho }_l^2{{ϵ}_{l,k}}^2{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^4+N^2\left(2{\rho }_l^2+{ϵ}_{l,k}^2+2{\rho }_l{ϵ}_{l,k}+2{\rho }_l+2{ϵ}_{l,k}+1\right)+2{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & \left(2N{\rho }_l+N{ϵ}_{l,k}+N+2\right)+N\left(2{\rho }_l+2{ϵ}_{l,k}+1\right),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & {\mathbf{B}}_2={\rho }_l^2{ϵ}_{l,k}{ϵ}_{l,i}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2{\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2+{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\left({\rho }_{l}N+2\right)+{\rho }_l{ϵ}_{l,i}{\left|{\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & \left(N{\rho }_l+2\right)+N\left(2{\rho }_l+{ϵ}_{l,i}+{ϵ}_{l,k}+1\right)+N^2{\rho }_l^2+{ϵ}_{l,k}{ϵ}_{l,i}{\left|{\overline{\mathbf{h}}}_{l,k}^H{\overline{\mathbf{h}}}_{l,i}\right|}^2\hfill \\ \hfill & +2{\rho }_l{ϵ}_{l,k}{ϵ}_{l,i}\mathrm{Re}\left\{{\mathbf{\Phi }}_{l,k}^H\left(\mathbf{\Theta }\right){\mathbf{\Phi }}_{l,i}\left(\mathbf{\Theta }\right){\overline{\mathbf{h}}}_{l,i}^H{\overline{\mathbf{h}}}_{l,k}\right\},\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {\mathbf{B}}_3={\rho }_l^2{ϵ}_{l,k}{ϵ}_{j,i}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2{\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2+{\rho }_l{ϵ}_{l,k}{\left|{\mathbf{\Phi }}_{l,k}\left(\mathbf{\Theta }\right)\right|}^2\left({\rho }_{l}N+2\right)+{\rho }_l{ϵ}_{j,i}{\left|{\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right)\right|}^2\hfill \\ \hfill & \left(N{\rho }_l+2\right)+M\left(2{\rho }_l+{ϵ}_{j,i}+{ϵ}_{l,k}+1\right)+N^2{\rho }_l^2+{ϵ}_{l,k}{ϵ}_{j,i}{\left|{\overline{\mathbf{h}}}_{l,k}^H{\overline{\mathbf{h}}}_{j,i}\right|}^2\hfill \\ \hfill & +2{\rho }_l{ϵ}_{l,k}{ϵ}_{j,i}\mathrm{Re}\left\{{\mathbf{\Phi }}_{l,k}^H\left(\mathbf{\Theta }\right){\mathbf{\Phi }}_{j,i}\left(\mathbf{\Theta }\right){\overline{\mathbf{h}}}_{j,i}^H{\overline{\mathbf{h}}}_{l,k}\right\},\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & {\mathbf{B}}_4=k_{l,u}{p}_{l,k}{a}_{l,k}^2{\mathbf{B}}_1+k_{l,u}\sum _{i=1,i\ne k}^K{p}_{l,i}{a}_{l,k}{a}_{l,i}{\mathbf{B}}_2+\sum _{j=1,j\ne l}^L{k}_{j,u}\sum _{i=1}^K{p}_{j,i}{a}_{l,k}{a}_{j,i}{\mathbf{B}}_3\hfill \\ \hfill & +k_{l,b}\left(p_{l,k}\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,k_m}\right|}^4\right\}+\sum _{i=1,i\ne k}^K{p}_{l,i}\mathbb{E}\left\{{\left|{\mathbf{g}}_{l,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}+\sum _{j=1,j\ne l}^L\sum _{i=1}^K{p}_{j,i}\mathbb{E}\left\{{\left|{\mathbf{g}}_{j,i_m}\right|}^2{\left|{\mathbf{g}}_{l,k_m}\right|}^2\right\}\right).\hfill \end{array}$$

(31)

Proof of Corollary 2.

Similarly to the derivation of Corollary 1, we can remove the terms that are not on the order of $\mathcal{O}\left(M^2\right)$. □

As in Corollary 1, when the number of BS antennas M tends to be infinite, the rate of this system will tend to be constant, and the effect of noise can be ignored.

4. Phase Shift Optimization

By observing (10), we find that the rate only depends on the statistical CSI, including the Rician factors, the LoS components of the channel, and the path loss coefficients. Therefore, we can optimize the phase shifts of the RIS based on statistical CSI.

Algorithm 1: Mutation Algorithm

for $s=1:S_3$ do

for $n=1:N$ do $r=rand\left(1\right)$;

if $r<0.1$ then

The n-th chromosome of individual mutates to $2\pi *r$;

end if

end for

end for

Specifically, we formulate two optimization problems: the sum rate maximization problem to guarantee overall system performance and the minimum user rate maximization problem to guarantee fairness between users—see (27) and (28).

$$\begin{array}{c}\hfill \underset{\mathbf{\Theta }}{max}\sum _{l=1}^L\sum _{k=1}^K{R}_{l,k}\end{array}$$

(32)

$$\begin{array}{c}\hfill \mathrm{or}\underset{\mathbf{\Theta }}{max}\underset{k}{min}{R}_{l,k}\end{array}$$

(33)

$$\begin{array}{c}\hfill s.t.{\theta }_n\in [0,2\pi ),\forall n\end{array}$$

(34)

where $R_{l,k}$ is given in (10).

Due to the complexity of the rate expression, the existing gradient descent method and convex optimization method cannot solve this problem. The genetic algorithm (GA) does not need to calculate the first-order derivative of the objective function as the conventional gradient descent method does. Instead, we only need to calculate the objective function in each iteration, so we use GA. The detailed steps of the algorithm are as follows.

Initialize population: Generate S individuals, and each individual has N chromosomes randomly generated from $[0,2\pi )$, corresponding to the phase shift matrix of the RIS.

Calculate fitness: In the current population, we first calculate the fitness of each individual through the objective function of the optimization problem (32) or (33). Then, we sort them in descending order according to fitness.

Select elite: We select the top $S_1$ individuals as elites and pass them to the next generation.

Mutation: We select the last $S_3$ individuals as parents and mutate them with a probability of 0.1 to generate $S_3$ offspring. The mutation algorithm is shown in Algorithm 1.

Crossover: We use stochastic universal sampling to generate $2S_2$ parents from the remaining $S_2=S-S_1-S_3$ individuals. Then, we use the two-point crossover method to generate $S_2$ offspring from $2S_2$ parents. The two-point crossover method is shown in Algorithm 2.

Finally, we combine $S_1$ elites and $S_2+S_3$ offspring to generate the next-generation population. When the change value of the average fitness is less than the preset value or the number of iterations reaches the preset maximum number of iterations, the algorithm stops. In the current population, the chromosome of the individual with the highest fitness corresponds to the optimal phase shift of the RIS.

Algorithm 2: Two-Point Crossover Algorithm

Initialize $c=1$;

for $s=1:S_2$ do;

Select the c-th and $(c+1)$-th parents from the $2S_2$ parents;

Randomly generate integers $a,b$ from $[1,N-1]$ and satisfy $a<b$;

Generate the s-th offspring, and the N chromosomes of the s-th offspring are the $[1:a]$

chromosomes of the c-th parent, the $[a+1:b]$ chromosomes of the $(c+1)$-th parent, the

$[b+1:N]$ chromosomes of the c-th parent;

$c=c+2$

end for

5. Simulation Results

In this section, we provide simulation results to validate the derived expressions and analyze various system parameters. The parameter settings are derived from [7,13]. Unless otherwise stated, we set them as follows: $N=49$, $L=2$, $M=49$, $K=4$, $p_{l,k}=30$ dBm, ${\sigma }^2=-104$ dBm, ${\rho }_l=1,{ϵ}_{l,k}=10,\forall l,k$. Different from [7,13], we consider not only the RIS-aided multi-cell mMIMO system but also the THWIs. Hence, the THWI coefficients need to be set additionally, namely $k_{l,u}=k_{l,b}=0.01$. We assume that the distance from the RIS to the BS is $d_{rb}=800$ m, $\forall l$, and users are distributed on a circle with the RIS as the center and a radius of $d_{ur}=30$ m. Therefore, ${\nu }_l={10}^{-3}{d}_{rb}^{-2.5}$, ${\mu }_{l,k}={10}^{-3}{d}_{ur}^{-2},\forall l,k$. In addition, the element spacing of $d=\lambda /2$ is set to avoid spatial correlation. The various angles at the BS and RIS are randomly generated from $[0,2\pi ]$ and fixed after initial generation.

As shown in Figure 2, we plot the achievable rate obtained from optimization problems (32) and (33) and carry out MC simulation for verification. The MC simulation results are consistent with the derived results, which shows the accuracy of the derived results.

In Figure 3, we verify that the optimization problem (33) can ensure the users’ fairness. The relationship between the two vertical coordinates is four times, and the two curves coincide with each other, while the number of users $K=4$, which means that the minimum user rate reaches the average user rate, i.e., all users have the same rate.

Figure 4 depicts the achievable rate in different scenarios. As shown in Figure 4, scheme ‘$N=49$, Sum rate by max-sum’ is superior to scheme ‘$N=100$, Sum rate by random phase’, and, as N increases, the performance gap between the two will become larger. This is consistent with our Corollary 2, i.e., the rate will tend to be constant when BS antennas $M\to \infty$. Moreover, it indicates that it is necessary to optimize the phase shifts of the RIS.

In Figure 5, we plot the achievable rate versus the Rician factor of the RIS–BS channel. As ${\rho }_l$ increases, the sum and minimum user rates decrease. This is because, with the increase in ${\rho }_l$, the channels between users have a stronger correlation, which reduces the spatial multiplexing gain and also increases the interference between users.

In Figure 6, we plot the achievable rate with different THWI coefficients. As the transmit power increases, the sum rate and minimum user rate gradually increase and tend towards a limit value. In addition, with the increase in power, the performance gap between the two THWI scenarios also widens because the THWIs are tightly coupled with the transmitted signal and become stronger as the THWI coefficients $k_{l,u},k_{l,b}$ increase.

Figure 7 depicts the achievable rate under different schemes. Through comparison, we find that the rate performance of scheme ‘$M=256$, $N=16$’ is the same as that of scheme ‘$M=N=64$’. This means that we can significantly reduce the demand for the number of BS antennas by appropriately increasing the number of RIS-reflecting elements, effectively reducing the hardware cost at the BS.

To ensure the accuracy of the scheme comparison, we further draw Figure 8. In Figure 8, the scheme ‘$M=N=64$’ is superior to the scheme ‘$M=256$, $N=16$’ in different THWI and power scenarios, which shows the accuracy of the scheme comparison.

In Figure 9, we plot the sum rate for three scenarios. In scenario $k_{l,u}=k_{l,b}=0.1,L=4$, Sum rate by max-sum’, the impact of inter-cell interference and THWIs can be compensated for by increasing the number of components. This is meaningful because increasing N is more cost-effective and practical compared to replacing the transceivers and reducing the number of cells.

6. Conclusions

This paper has focused on an RIS-aided uplink multicell mMIMO communication system with THWIs. We have derived and analyzed the achievable rate expression, and the phase shifts of the RIS have been optimized based on the two-timescale design scheme. Through simulation, the correctness of the derived expression has been verified, and the following conclusion has been obtained. In the RIS-aided uplink multicell mMIMO communication system with THWIs, we can compensate for the performance loss caused by the inter-cell interference and THWIs by appropriately increasing the number of RIS-reflecting elements, and we also significantly reduce the demand for BS-receiving antennas, which will effectively reduce the hardware cost at the BS.