Time Delay Extraction from Frequency Domain Data Using Causal Fourier Continuations for High-Speed Interconnects

Abstract

We present a new method for time delay estimation using band limited frequency domain data representing the port responses of interconnect structures. The approach is based on the spectrally accurate method for causality characterization that employs SVD-based causal Fourier continuations, which was recently developed by the authors. The time delay extraction is constructed by incorporating a linearly varying phase factor to the system of equations that determines the Fourier coefficients. The method is capable of determining the time delay using data affected by noise or approximation errors that come from measurements or numerical simulations. It can also be employed when only a limited number of frequency responses is available. The technique can be extended to multi-port and mixed-mode networks. Several analytical and simulated examples are used to demonstrate the accuracy and strength of the proposed technique.

1. Introduction

Identification and extraction of time delay is an important research problem in signal processing and has applications in many fields, including radar [1], sonar [2,3], ultrasonics [4], microwave imaging [5], geophysics [6], seismology [7,8], wireless communications [9], as well as modeling of passive structures in electronic systems, in particular transmission line modeling [10,11], transient simulation of interconnects [12] and co-simulation of passive structures with active devices in a time domain using SPICE. Passive structures in electronic systems have been traditionally analyzed in the frequency domain, while transient simulations are performed in the time domain using suitable models that accurately capture the relevant electromagnetic phenomena. The models are obtained from either direct measurements or electromagnetic simulations. Interconnect models are typically approximated by rational transfer functions using the vector fitting algorithm in various implementations [13,14,15,16,17,18,19], which is the standard macromodeling approach. As clock frequencies increase, the size of passive structures becomes of the same order as the signal wavelength at the operating frequency, which causes the distributed effects, such as the time delay, to play a significant role in the time domain simulations. For this reason, time delay has to be included in macromodeling, in particular when causality is analyzed. The connection between causality and time delay is in fact that time delays can pull a non-causal signal into the causal region or vice versa pull a causal signal into the non-causal region, while causality, in turn, can be expressed in terms of the Hilbert transform [20,21,22]. Several approaches can be used to extract delays in the frequency domain, for example using the Hilbert transform [23,24,25], the minimum phase all-pass decomposition [12,26,27], incorporating an optimal time delay into the vector fitting algorithm [10,11], employing a modified Lie approximation to develop a passive and compact macromodel [28], using a Gabor transform to develop delayed rational function macromodels for long interconnects [19,29] or conducting a probabilistic analysis of the cepstrum in the presence of noise [30]. In the time domain, delayed rational functions [31,32] can be employed to extract delays. In this paper, a novel approach is proposed in which time delay is determined in the frequency domain using a causality argument. Causality is verified using the SVD-based causal Fourier continuation method developed by the authors [33,34], while the time delay presence is incorporated by a linearly-varying phase factor to the system of equations that determines Fourier coefficients. Preliminary results are reported in [35].

The rest of the paper is organized as follows. Section 2 provides a background on causality for linear time translation-invariant systems and dispersion relations. In Section 3, we show the main steps in the derivation of causal Fourier continuations using the truncated singular value decomposition (SVD) method that was developed to access causality. We also provide error estimates that take into account a possible presence of noise in the data. Section 4 extends the causality characterization method to develop a technique for time delay extraction. The proposed method is tested in Section 5 using several analytic and simulated examples. We also analyze the performance of the algorithm when only a limited number of frequency responses is available and when noise/approximation errors are present in the data. In Section 6, we present our conclusions. The Appendix section is devoted to the formulation of error bounds for the causality characterization method based on causal Fourier continuations.

2. Causality of Linear Time-Invariant Systems

Consider a linear and time-invariant physical system with the impulse response $h\left(t\right)$ subject to a time-dependent input $f\left(t\right)$, to which it responds by an output $x\left(t\right)$. Denote by:

$$H\left(w\right)={\int }_{-\infty }^{\infty }h\left(\tau \right){\mathrm{e}}^{-iw\tau }d\tau$$

(1)

the Fourier transform of $h\left(t\right)$, which is also called the transfer function.

The system is causal if the output cannot precede the input, i.e., if $f\left(t\right)=0$ for $t<T$, the same must be true for $x\left(t\right)$. This primitive causality condition in the time domain implies $h\left(t\right)=0$, $t<0$. Hence, the domain of integration in Equation (1) can be reduced to $[0,\infty )$.

Assume $H\left(w\right)\in L_2\left(\mathbb{R}\right)$. Then, starting from Cauchy’s theorem and using contour integration, one can show [22] that for any point w on the real axis, $H\left(w\right)$ can be written (please note that we use the opposite sign of the exponent in the definition of the Fourier transform from that in [22]) as:

$$H\left(w\right)=\frac{1}{\pi i}{\sout{\int }}_{-\infty }^{\infty }\frac{H(w\prime )}{w-w\prime }dw\prime ,\text{\hspace{0.5em}real }w$$

(2)

where:

$${\sout{\int }}_{-\infty }^{\infty }=P{\int }_{-\infty }^{\infty }=\underset{ϵ\to 0}{\text{lim}}({\int }_{-\infty }^{w-ϵ}+{\int }_{w+ϵ}^{\infty })$$

(3)

denotes Cauchy’s principal value. Separating the real and imaginary parts of Equation (2), we get:

$$\text{Re }H\left(w\right)=\frac{1}{\pi }{\sout{\int }}_{-\infty }^{\infty }\frac{\text{Im }H(w\prime )}{w-w\prime }dw\prime$$

(4)

$$\text{Im }H\left(w\right)=-\frac{1}{\pi }{\sout{\int }}_{-\infty }^{\infty }\frac{\text{Re }H(w\prime )}{w-w\prime }dw\prime$$

(5)

Equation (4) and (5) are called the dispersion relations or Kramers–Krönig relations. They show that $\text{Re }H$ and $\text{Im }H$ are not independent functions, but instead, they are related to each other: $\text{Re }H$ at one frequency depends on $\text{Im }H$ at all frequencies, and vice versa. This implies that if one of the functions $\text{Re }H$ or $\text{Im }H$ is square integrable and known, then the other one can be completely determined by causality. Recalling the definition of the Hilbert transform,

$$\mathcal{H}\left[u\left(w\right)\right]=\frac{1}{\pi }{\sout{\int }}_{-\infty }^{\infty }\frac{u(w\prime )}{w-w\prime }dw\prime$$

(6)

we see that $\text{Re }H$ and $\text{Im }H$ are Hilbert transforms of each other, i.e.,

$$\text{Re }H\left(w\right)=\mathcal{H}\left[\text{Im }H\right(w\left)\right],\text{Im }H\left(w\right)=-\mathcal{H}\left[\text{Re }H\right(w\left)\right]$$

(7)

In other words, $\text{Re }H$ or $\text{Im }H$ form a Hilbert transform pair. Dispersion relations provide the causality condition in the frequency domain.

Evaluation of the Hilbert transform requires integration on $(-\infty ,\infty )$, which can be reduced to $[0,\infty )$ by the spectrum symmetry of $H\left(w\right)$ if $h\left(t\right)$ is real valued. In practice, only a limited number of discrete values of $H\left(w\right)$ is available on $[w_{min},w_{max}]$. Thus, the domain of integration has to be truncated. This usually causes serious boundary artifacts due to the lack of out-of-band frequency responses. To reduce or even completely remove boundary artifacts, the authors recently developed causality characterization methods based on periodic polynomial continuations [36,37] and causal Fourier continuations [33,34], respectively. The approach was motivated by the example $H\left(w\right)={\mathrm{e}}^{-iaw}$, $a>0$, that is not square integrable, but still satisfies the dispersion relations. The causality characterization method based on causal Fourier continuations allows one to construct highly accurate approximations of a given transfer function on the original frequency interval $[w_{min},w_{max}]$ with the uniform error that decreases as the number of Fourier coefficients increases. The technique is applicable to both baseband and bandpass cases and capable of detecting very small localized causality violations. The method can also be extended to multidimensional cases.

In the next section, for the completeness of presentation, we show the main steps in the derivation of the causal Fourier continuation method that can be used to access the causality of a given transfer function whose values are available at a discrete set of frequencies. We also provide upper bounds of the reconstruction error between the given function and its causal Fourier continuation. We use these error estimates to understand how to extract the time delay when data with different resolutions are available and when data are affected by noise or other approximation errors.

3. Causal Fourier Continuations

Consider a transfer function $H\left(w\right)=\text{Re }H+i\text{ Im }H$, whose N discrete values are available on $[w_{min},w_{max}]$, $w_{min}\ge 0$. For real-valued impulse response functions $h\left(t\right)$, $\text{Re }H$ and $\text{Im }H$ are even and odd functions, respectively. This implies that $H\left(w\right)$ has values on $[-w_{max},-w_{min}]$ by spectrum symmetry. For convenience, we rescale the frequency interval $[-w_{max},w_{max}]$ to $[-0.5,0.5]$ by the substitution $x=\frac{0.5}{w_{max}}w$, so the rescaled transfer function $H\left(x\right)$ is defined on the unit length interval with $\tilde{N}$ values where $\tilde{N}=2N-1$ or $\tilde{N}=2N$ depending on if $H\left(x\right)$ is available at $x=0$ or not. Both baseband and bandpass cases can be considered.

The idea of a causal Fourier continuation is to construct an accurate Fourier series approximation of $H\left(x\right)$ by allowing the Fourier series to be periodic and causal in an extended domain. The result is the Fourier continuation of H that we denote by $\mathcal{C}\left(H\right)$, and it is defined by:

$$\mathcal{C}\left(H\right)\left(x\right)=\sum _{k=-M+1}^M{\alpha }_k{\mathrm{e}}^{-\frac{2\pi i}{b}kx}$$

(8)

for an even number $2M$ of terms, whereas for an odd number $2M+1$ of terms, the index k varies from $-M$ to M. Throughout this paper, we assume that the number M of Fourier coefficients is even, for simplicity. When M is odd, analogous results can be formulated. Here, b is the period of approximation. For SVD-based periodic continuations, b is normally chosen as twice the length of the domain on which function H is given, though the value $b=2$ is not necessarily optimal. The optimal value b depends on a function being approximated. In practice, several values $b\in (1,4)$ may be tried to get a slightly better reconstruction of $H\left(x\right)$ with a Fourier series.

Functions ${\varphi }_k\left(x\right)={\mathrm{e}}^{-\frac{2\pi i}{b}kx}$, $k\in \mathbb{Z}$, form a complete orthogonal basis in $L_2[-\frac{b}{2},\frac{b}{2}]$. It can be shown that $\mathcal{H}\left\{{\varphi }_k\left(x\right)\right\}=i\text{ sgn}\left(k\right){\varphi }_k\left(x\right)$, which implies that functions $\left\{{\varphi }_k\left(x\right)\right\}$ are the eigenfunctions of the Hilbert transform $\mathcal{H}$ with associated eigenvalues $\pm i$ with $x\in [-\frac{b}{2},\frac{b}{2}]$. For a causal periodic continuation, according to Equation (7), we need $\text{Im }\mathcal{C}\left(H\right)\left(x\right)$ to be the Hilbert transform of $-\text{Re }\mathcal{C}\left(H\right)\left(x\right)$. It can be shown [33] that this implies ${\alpha }_k=0$ for $k\le 0$ in Equation (8). Hence, a causal Fourier continuation has the form:

$$\mathcal{C}\left(H\right)\left(x\right)=\sum _{k=1}^M{\alpha }_k{\varphi }_k\left(x\right)$$

(9)

Evaluating $H\left(x\right)$ at points $x_j$, $j=1,\dots ,\tilde{N}$, $x_j\in [-0.5,0.5]$, produces a complex valued system:

$$\sum _{k=1}^M{\alpha }_k{\varphi }_k\left(x_j\right)=H\left(x_j\right)$$

(10)

with $\tilde{N}$ equations for M unknowns ${\alpha }_k$, $k=1,\dots ,M$, $\tilde{N}\ge M$. If $\tilde{N}>M$, System (10) is overdetermined and has to be solved in the least squares sense. When Fourier coefficients ${\alpha }_k$ are computed, Formula (9) provides reconstruction of $H\left(x\right)$ on $[-0.5,0.5]$. The least squares problem is extremely ill-conditioned. However, it can be regularized using a truncated SVD method when singular values below some cutoff tolerance ξ close to the machine precision are being discarded.

Since $\text{Re }H\left(x\right)$ and $\text{Im }H\left(x\right)$ are even and odd functions of x, respectively, the Fourier coefficients:

$${\alpha }_k=\frac{1}{b}{\int }_{-b/2}^{b/2}H\left(x\right)\overline{{\varphi }_k\left(x\right)}dx,k=1,\dots ,M$$

(11)

are real. Here, $\overline{ }$ denotes the complex conjugate. To ensure that numerically computed Fourier coefficients ${\alpha }_k$ are real, instead of solving complex-valued system (10), one can separate the real and imaginary parts of $H\left(x_j\right)$ and its causal Fourier continuation $\mathcal{C}\left(H\right)\left(x_j\right)$ to obtain the real-valued system:

$$\begin{array}{c}{\displaystyle \phantom{-}\sum _{k=1}^M{\alpha }_k\text{Re }{\varphi }_k\left(x_j\right)=\text{Re }H\left(x_j\right)}\hfill \\ {\displaystyle \sum _{k=1}^M{\alpha }_k\text{Im }{\varphi }_k\left(x_j\right)=\text{Im }H\left(x_j\right)}\hfill \end{array}$$

(12)

We show in [33] that the real formulation (12) provides slightly more accurate results than complex. In what follows, we use the real formulation (12).

To have a better control on the ill-conditioning of matrix problem (10) or (12), at least twice more data points $\tilde{N}$ than the Fourier coefficients M should be used [38]. This approach is called the over-collocation. We use $\tilde{N}=2M$ as an effective way to obtain an accurate and reliable approximation of $H\left(x\right)$ over the interval $[-0.5,0.5]$. This relation corresponds (in [33], N denoted the number of points on $[-0.5,0.5]$, while in this work, N is the number of points on $[0,0.5]$ or originally on $[w_{min},w_{max}]$) to $N=M$, where N is the number of data points available originally on $[w_{min},w_{max}]$.

To access the quality of the approximation of $H\left(x\right)$ with its causal Fourier continuation $\mathcal{C}\left(H\right)\left(x\right)$, we introduce reconstruction errors, $E_R\left(x\right)$ and $E_I\left(x\right)$, for real and imaginary parts of $H\left(x\right)$:

$$E_R\left(x\right)=\text{Re }H\left(x\right)-\text{Re }\mathcal{C}\left(H\right)\left(x\right)$$

(13)

$$E_I\left(x\right)=\text{Im }H\left(x\right)-\text{Im }\mathcal{C}\left(H\right)\left(x\right)$$

(14)

on the original interval $[-0.5,0.5]$ where data are available.

The error analysis performed in [33] (see also the Appendix) shows that the error between $H\left(x\right)$ and its causal Fourier continuation $\mathcal{C}(H+\epsilon )$, under the presence of a noise ε, has the following upper bound:

$$\left|\right|H-{\mathcal{C}(H+\epsilon )\left|\right|}_{L_2(\Omega )}\le {ϵ}_F+{ϵ}_n+{ϵ}_T$$

(15)

Here:

$${ϵ}_F=(1+{\Lambda }_2\sqrt{2N(M-K)})\left|\right|H-{\widehat{H}}_M{\left|\right|}_{L_{\infty }(\Omega )}$$

(16)

is the error due to approximation of H with its causal Fourier series. It decays as $\mathcal{O}\left(M^{-k+1}\right)$, where k is the smoothness order of the transfer function $H\left(x\right)$.

$${ϵ}_T={\Lambda }_1\sqrt{K/b}\left|\right|{\widehat{H}}_M{\left|\right|}_{L_{\infty }\left({\Omega }^c\right)}$$

(17)

is the error due to the truncation of singular values. It is typically small and close to the cut-off value ξ.

$${ϵ}_n=(1+{\Lambda }_2\sqrt{2N(M-K)}){\left|\right|\epsilon \left|\right|}_{L_{\infty }(\Omega )}$$

(18)

is the error due to the presence of a noise or approximation errors in the given data, and it shows a level of causality violation. In practice, the size of ${ϵ}_n$ is close to the size of noise in the data. Function ${\widehat{H}}_M$, constants ${\Lambda }_1$, ${\Lambda }_2$ and K, domains Ω and ${\Omega }^c$ are defined in the Appendix. The constants ${\Lambda }_1$, ${\Lambda }_2$ and K depend only on the continuation parameters N, M, b and ξ, as well as the location of discrete points $x_j$ and not on the function H.

The error bound (15) shows that the reconstruction errors $E_R$ and $E_I$ decrease as M increases due to the causal Fourier series approximation error with the error bound ${ϵ}_F$ until either the level ϵ of a noise or level ${ϵ}_T$ due to the truncation of singular values is reached. If only round-off errors are present in the data, the errors will level off at ${ϵ}_T$. If reconstruction errors level off at some value $ϵ>{ϵ}_T$ as the resolution increases, the data are declared non-causal with the error approximately at the order of ϵ. More information about the error analysis for the causality characterization methods based on causal Fourier continuations can be found in [33].

4. Time Delay Estimation

The above approach for causality assessment can be transformed into a delay estimation algorithm by observing the following. Suppose that $h\left(t\right)$ is non-zero only from time $T_0\ge 0$, and we would like to identify the time delay $T_0$. Consider the Fourier transform $H\left(w\right)$ of $h\left(t\right)$:

$$H\left(w\right)={\int }_{t=T_0}^{\infty }{\mathrm{e}}^{-iwt}h\left(t\right)dt={\int }_{t=T_0}^{\infty }{\mathrm{e}}^{-i\frac{x}{a}t}h\left(t\right)dt$$

(19)

where we used the substitution $x=aw$, $a=\frac{0.5}{w_{max}}$. Introducing $\tau =\frac{t}{a}$, we can write:

$$H\left(w\right)=a{\int }_{\frac{T_0}{a}}^{\infty }{\mathrm{e}}^{-ix\tau }h\left(a\tau \right)d\tau$$

(20)

or with $u=\tau -\frac{T_0}{a}$, we obtain:

$$H\left(w\right)=a{\mathrm{e}}^{-ix\frac{T_0}{a}}{\int }_0^{\infty }{\mathrm{e}}^{-ixt}h(T_0+au)du=a{\mathrm{e}}^{-ix\frac{T_0}{a}}G\left(x\right)$$

(21)

where $G\left(x\right)$ is the Fourier transform of a causal function with no time delay. This implies that when $0\le T\le T_0$, the transfer function $H\left(x\right){\mathrm{e}}^{ix\frac{T}{a}}$ is causal, but when $T\ge T_0$, the transfer function $H\left(x\right){\mathrm{e}}^{ix\frac{T}{a}}$ has a non-causal component. Therefore, ${\tilde{T}}_0=T_0/a$ is the time delay for $H\left(x\right)$, and the delay $T_0$ for the original function $H\left(w\right)$ is recovered by multiplying ${\tilde{T}}_0$ by a. Since one can add any integral multiple of $2\pi$ to $xT/a$, it is enough to restrict our investigations to the interval:

$$0\le \frac{T}{a}\le T_{max}=\frac{2\pi }{x_{max}}=\frac{2\pi }{0.5}=4\pi$$

(22)

Then, for each potential time delay $0\le \frac{T}{a}\le T_{max}$, we solve the following modified system:

$$\sum _{k=1}^M{\alpha }_k{\varphi }_k\left(x_j\right)={\mathrm{e}}^{i{x}_j\frac{T}{a}}H\left(x_j\right),j=1,\dots ,\tilde{N}$$

(23)

or its equivalent real-valued formulation. For $T<T_0$, the reconstruction errors $E_R$, $E_I$ should be small and approximately of the same order. As T increases and becomes greater than some critical transition time close to the time delay $T_0$, the reconstruction errors should start to increase. The goal is to approximate $T_0$. The difficulty is that the reconstruction errors grow gradually as $T\ge T_0$, so the transition is not sharp. Moreover, the order of reconstruction errors for $T<T_0$ depends on the resolution of data and threshold ξ used in the truncated SVD method, which, in turn, affects a transition time. In addition, a noise in the data, if present, also affects when reconstruction errors start growing. A similar approach was used in [25] to estimate the time delay for square integrable transfer functions. In this contribution, we extend the approach to more general transfer functions. In addition, we use a different causality measure than in [25] and take into account different resolutions of given data and the possible presence of noise. The approach can be extended to multi-port and mixed-mode networks by applying it to each element of the transfer matrix.

5. Numerical Examples

In this section, we apply the proposed technique to several analytic and simulated examples when the time delay is either known exactly or can be estimated using other techniques. We also consider the effect of noise presence on the accuracy of time delay estimation.

5.1. Four-Pole Example

Consider a transfer function with four poles and time delay $T_0$, defined by:

$$H\left(w\right)={\mathrm{e}}^{-iw{T}_0}\tilde{H}\left(w\right)$$

(24)

with:

$$\tilde{H}\left(w\right)=\frac{r_1}{iw+p_1}+\frac{{\overline{r}}_1}{iw+{\overline{p}}_1}+\frac{r_2}{iw+p_2}+\frac{{\overline{r}}_2}{iw+{\overline{p}}_2}$$

(25)

where $r_1=1+2i$, $p_1=1+3i$, $r_2=\frac{2}{3}+\frac{1}{2}i$, $p_2=\frac{1}{2}+5i$, and $T_0=0.25$. Since the poles of $\tilde{H}\left(w\right)$ are located in the upper half w-plane at $\pm 3+i$ and $\pm 5+\frac{1}{2}i$, this function is causal as a sum of four causal transforms and has no time delay. Therefore, the function $H\left(w\right)$ is a causal function delayed with offset $T_0$. H is sampled on $[0,w_{max}]$ at N frequency points varying from $N=50$ to 1500 with $w_{max}=6$.

The real and imaginary parts of $H\left(w\right)$ are shown in Figure 1. After rescaling with $x=\frac{0.5}{w_{max}}w$ and reflecting to negative frequencies, we obtain a rescaled transfer function $H\left(x\right)$ defined on $x\in [-0.5,0.5]$, for which we construct a causal Fourier continuation $\mathcal{C}\left(H\right)$ defined in Equation (9) using $M=N$ Fourier coefficients. Hence, the number M of Fourier coefficients also varies between 50 and 1500. $\text{Re }H\left(x\right)$ and $\text{Im }H\left(x\right)$ of the rescaled and reflected $H\left(x\right)$ together with their causal Fourier continuations with $M=300$ are depicted in Figure 2. Even though given $H\left(x\right)$ and its causal Fourier continuation approximation look indistinguishable, the actual reconstruction errors $E_R$ and $E_I$ in both the real and imaginary parts, which are defined in (13) and (14), are on the order of ${10}^{-6}$, and they decrease as M increases (with $M=N$). For example, with $M=800$, the errors are on the order of ${10}^{-13}$. Since both errors $E_R$ and $E_I$ are of the same order, it is enough to analyze one of the errors, for example $E_R$. The results using $E_I$ are similar.

Figure 1. $\text{Re }H\left(w\right)$ and $\text{Im }H\left(w\right)$ in the four-pole example.

Figure 1. $\text{Re }H\left(w\right)$ and $\text{Im }H\left(w\right)$ in the four-pole example.

Figure 2. $\text{Re }H\left(x\right)$ and $\text{Im }H\left(x\right)$ of the rescaled and reflected by symmetry transfer function $H\left(x\right)$ in the four-pole example together with their causal Fourier continuations $\text{Re }\mathcal{C}\left(H\right)$ and $\text{Im }\mathcal{C}\left(H\right)$, respectively, with $M=300$ Fourier coefficients.

Figure 2. $\text{Re }H\left(x\right)$ and $\text{Im }H\left(x\right)$ of the rescaled and reflected by symmetry transfer function $H\left(x\right)$ in the four-pole example together with their causal Fourier continuations $\text{Re }\mathcal{C}\left(H\right)$ and $\text{Im }\mathcal{C}\left(H\right)$, respectively, with $M=300$ Fourier coefficients.

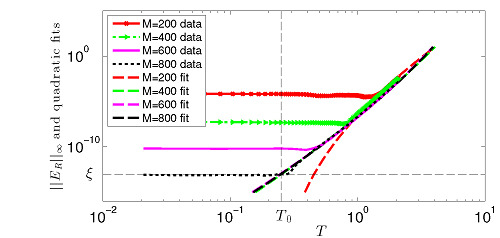
To estimate the time delay, we analyze the evolution of $\left|\right|E_R\left|\right|\infty$, the ∞ norm of $E_R$, shown in Figure 3, for various values M.

Figure 3. Evolution of the reconstruction error $\left|\right|E_R{\left|\right|}_{\infty }$ as a function of T in the four-pole example. The dashed line corresponds to the exact delay $T_0=0.25$.

Figure 3. Evolution of the reconstruction error $\left|\right|E_R{\left|\right|}_{\infty }$ as a function of T in the four-pole example. The dashed line corresponds to the exact delay $T_0=0.25$.

Since the error due to a causal Fourier series approximation decreases with M (see error bound (16)), the reconstruction error between the given transfer function H and its causal Fourier continuation $\mathcal{C}\left(H\right)$ also decreases as M increases until it either reaches the level ξ of filtering of singular values or a level ϵ of noise/causality violations (see error bounds (17) and (18), respectively). For each fixed M, as time T increases, the errors $E_R$ and $E_I$ first are small and about of the same order until some transition time close to the time delay $T_0$ is approached. After that, the errors grow approximately as a power function on the log-log scale. For smaller T, the errors are dominated by a causal Fourier series approximation error. Then for T greater than some transition time, they are dominated by causality violations since this value T provides a large enough negative time delay and shifts a causal function into a non-causal area. A transition value $T=T_c$, we call it a critical time, from a plateau region to a growth region is different for each M. It decreases as the resolution or number of Fourier coefficients increases if the error is dominated by the causal Fourier series approximation error. The critical times $T_c$ approach the time delay $T_0$ as M increases. The goal is to estimate $T_0$ using the error curves shown in Figure 3. Analyzing graphs of the error curves for $M>800$, we observe some non-monotonic behavior at T close to $T_0$. This behavior is due to the filtering of the singular values below the threshold $\xi ={10}^{-13}$ that we used in our experiments. By increasing the value of ξ, the non-monotonic behavior will be present at smaller values of M. This suggests that portions of error curves close to threshold ξ are affected by filtering and may be inaccurate and difficult to use for time delay estimation as we find in our experiments. To estimate critical times $T_c$ of transition from the plateau region to the growth region, we approximate the growing region by a quadratic function on the log-log scale. Specifically, we assume that $lnT\approx a_2{\left(ln\left|\right|E_R{\left|\right|}_{\infty }\right)}^2+a_{1}ln\left|\right|E_R{\left|\right|}_{\infty }+a_0\equiv f(ln||E_R{\left|\right|}_{\infty })$, where coefficients $a_0$, $a_1$ and $a_2$ are determined in the least squares sense. The resulting quadratic function $f(ln|\left|E_R\right|{|}_{\infty })$ is then evaluated at the value of $\left|\right|E_R{\left|\right|}_{\infty }$ at $T=0$ that is assumed to be the “most causal” time. By taking the exponential function of the result, we find a critical transition time $T_c$ for a given M. This procedure produces estimates of the time delay $T_0$ for various values of M. The graph of the critical transition times $T_c$ as a function of M is shown in Figure 4. One can clearly see that the critical times approach the exact time delay $T_0=0.25$ as M increases. A good approximation of $T_0$ is achieved at $M=800$.

Figure 4. Critical transition times $T_c$ in the four-pole example that approach $T_0$ as M increases. The dashed line corresponds to the exact delay $T_0=0.25$.

Figure 4. Critical transition times $T_c$ in the four-pole example that approach $T_0$ as M increases. The dashed line corresponds to the exact delay $T_0=0.25$.

The values of $T_c$ for $M\ge 200$ are presented in Table 1. The results indicate that the approximations become more accurate as M increases. The error with $M=900$ is less than 1%. At the same time, the error with $M=1500$ is about 3%, which is due to the fact that the results in this case are more affected by the filtering of singular values. In the cases when M is high and the resulting error is not flat for $T<T_0$, instead of evaluating a fitted quadratic curve at the value of $\left|\right|E_R{\left|\right|}_{\infty }$ at $T=0$, we evaluate it at ξ, the threshold of filtering singular values, to avoid using results affected by filtering.

Table 1. Critical transition times $T_c$ in the four-pole example that approach $T_0=0.25$ as M increases.

M	$T_c$	M	$T_c$
200	1.4604	700	0.3394
300	1.1294	800	0.2529
400	0.9077	900	0.2497
500	0.6655	1000	0.2472
600	0.4759	1500	0.2576

Table 1. Critical transition times $T_c$ in the four-pole example that approach $T_0=0.25$ as M increases.

M	$T_c$	M	$T_c$
200	1.4604	700	0.3394
300	1.1294	800	0.2529
400	0.9077	900	0.2497
500	0.6655	1000	0.2472
600	0.4759	1500	0.2576

In practice, the number N of samples of the transfer function $H\left(w\right)$ is usually limited, which sets the bound for the number $M=N$ of Fourier coefficients, so it may not always be possible to use large enough M to obtain critical time $T_c$ close enough to the actual time delay $T_0$. A good method should be capable of producing an accurate approximation of $T_0$ even with a small number of data points. We achieve this by employing another approach for time delay estimation. Using the obtained fitted quadratic error curves, we extrapolate them to the value ξ of the filtering of singular values, which is typically chosen to be close to the machine precision. This corresponds to finding time T at which the error reaches the value ξ. This choice is natural, since the errors below ξ are most likely affected by filtering and may not be accurate enough to use. The results of such extrapolation are shown in Figure 5 for $M=200$, 400, 600 and 800. An intersection of the extrapolated curve corresponding to $M=200$ is at a value $T=0.45451$, which is a bit far from the exact $T_0=0.25$. At the same time, intersections of extrapolated curves with higher values of M are much closer; see Table 2 for details.

Figure 5. $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits. The vertical dashed line indicates the exact time delay $T_0=0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Figure 5. $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits. The vertical dashed line indicates the exact time delay $T_0=0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Table 2. Approximations of $T_0$ in the four-pole example using extrapolation. The exact value $T_0=0.25$, averaged value $T_0^{\left(aver\right)}=0.24805$.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	0.45451	700	0.24734
300	0.27235	800	0.24969
400	0.25297	900	0.24974
500	0.25053	1000	0.24724
600	0.24633	1500	0.25759

Table 2. Approximations of $T_0$ in the four-pole example using extrapolation. The exact value $T_0=0.25$, averaged value $T_0^{\left(aver\right)}=0.24805$.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	0.45451	700	0.24734
300	0.27235	800	0.24969
400	0.25297	900	0.24974
500	0.25053	1000	0.24724
600	0.24633	1500	0.25759

Results shown in Table 2 indicate that as M increases, the extrapolated quadratic curve intersects the horizontal line with the value ξ at times closer to $T_0$. Obtained approximations of $T_0$ can be averaged producing $T_0\approx T_0^{\left(aver\right)}=0.24805$. The approach with extrapolation provides a faster convergence and good approximations of $T_0$ even for small values of M, i.e., less data points are needed to approximate $T_0$.

We also consider the effect of noise on the time delay estimation. To study this, we impose a sine perturbation:

$$asin\left(10\pi x\right)$$

(26)

of various amplitudes a that we add to $\text{Re }H$, while keeping $\text{Im }H$ unchanged. We choose $N=800$ and vary a from ${10}^{-10}$–${10}^{-3}$. For the convenience of the reader, the perturbed profiles of $\text{Re }H$ are shown in the left panel of Figure 6 using the signal-to-noise ratio (SNR) format, where we consider ratios of $\text{Re }H+asin\left(10\pi x\right)$ to the amplitude a of the perturbation, presenting them in dB units, i.e., plotting $20·{log}_{10}(\text{Re }H+asin\left(10\pi x\right)/a)$. The reconstruction error $E_R$ with no perturbation for early times $T<T_0$ is of the order of ${10}^{-13}$, as shown in the right panel of Figure 6, that corresponds to the level of the filtering of singular values. When the perturbation is added, the reconstruction errors for $T<T_0$ are higher and approximately of the order of a. Once some critical transition time greater than $T_0$ is passed, reconstruction errors start growing. They grow at the same rate and coincide almost perfectly with each other. This observation suggests that the proposed approach can also be used in the cases when data have a noise, which is typical in real-life applications, when data have either measurement or simulation errors. For noise with a smaller amplitude, the region close to $T_0$ will be less affected by noise, and a bigger growing region will be available for fitting, so we expect better accuracy of time delay estimation in such cases. When more noise in data is present, the less growing region will be available for fitting, and the extrapolation of fitted quadratic error curves may be less accurate. We demonstrate this by considering two cases: with $a={10}^{-5}$ (noisier case) and $a={10}^{-8}$ (less noisy case).

Figure 6. Left panel: profiles of perturbed $\text{Re }H$ in the signal-to-noise ratio (SNR) format, i.e., $(\text{Re }H+asin(10\pi x\left)\right)/a$, plotted in dB. Right panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with added sine perturbation $asin\left(10\pi x\right)$. The vertical dashed line corresponds to the exact delay $T_0=0.25$.

Figure 6. Left panel: profiles of perturbed $\text{Re }H$ in the signal-to-noise ratio (SNR) format, i.e., $(\text{Re }H+asin(10\pi x\left)\right)/a$, plotted in dB. Right panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with added sine perturbation $asin\left(10\pi x\right)$. The vertical dashed line corresponds to the exact delay $T_0=0.25$.

Figure 7. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-5}sin\left(10\pi x\right)$. The dashed line corresponds to the exact delay $T_0=0.25$. Right panel: error curves $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-5}sin\left(10\pi x\right)$ and $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits. The vertical dashed line indicates the exact time delay $T_0=0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Figure 7. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-5}sin\left(10\pi x\right)$. The dashed line corresponds to the exact delay $T_0=0.25$. Right panel: error curves $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-5}sin\left(10\pi x\right)$ and $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits. The vertical dashed line indicates the exact time delay $T_0=0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

The error curves with a higher amplitude $a={10}^{-5}$ are presented in the left panel of Figure 7. It is clear that the error does not become smaller than ${10}^{-5}$ as $M\ge 300$ gets larger because of the noise. We use available growing regions and extrapolate fitted error curves to find their intersection with the horizontal line with value ξ. This gives us time T when the error reaches the value ξ for each considered M. The results of such extrapolation for $M=200$, 400, 600 and 800 are shown in the right panel of Figure 7. Clearly, extrapolated error curves reach value ξ at times around $T_0$, but not close enough to $T_0$ and without established convergence, but rather in a spread-out manner around $T_0$.

Approximations of $T_0$ for the values of M that we investigated are shown in Table 3. Averaging these approximations, we obtain $T_0^{\left(aver\right)}=0.26586$. The extrapolated curves can be made more focused around $T_0$ by narrowing down the fitted region. The results of this procedure are shown in Figure 8. This improves the average time delay to $T_0^{\left(aver\right)}=0.24216$.

Table 3. Approximations of $T_0$ in the four-pole example with perturbation ${10}^{-5}sin\left(10\pi x\right)$ using extrapolations with original fitting regions for various M. The exact value $T_0=0.25$, averaged value $T_0^{\left(aver\right)}=0.26586$.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	0.40158	700	0.39113
300	0.25578	800	0.28392
400	0.19863	900	0.26543
500	0.14311	1000	0.20293
600	0.45358	1500	0.32837

Table 3. Approximations of $T_0$ in the four-pole example with perturbation ${10}^{-5}sin\left(10\pi x\right)$ using extrapolations with original fitting regions for various M. The exact value $T_0=0.25$, averaged value $T_0^{\left(aver\right)}=0.26586$.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	0.40158	700	0.39113
300	0.25578	800	0.28392
400	0.19863	900	0.26543
500	0.14311	1000	0.20293
600	0.45358	1500	0.32837

Figure 8. $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-5}sin\left(10\pi x\right)$ and $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits constructed using more narrow fitting region. The vertical dashed line indicates the exact time delay $T_0$ = $0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by ξ = ${10}^{-13}$.

Figure 8. $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-5}sin\left(10\pi x\right)$ and $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits constructed using more narrow fitting region. The vertical dashed line indicates the exact time delay $T_0$ = $0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by ξ = ${10}^{-13}$.

Next, we show the results when a smaller noise of amplitude $a={10}^{-8}$ is added. The evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ as T increases is shown in the left panel of Figure 9. We can see that the plateau error region in this case is at about the ${10}^{-9}$ level, so the error growth region is bigger than in the previous case, which should make fitting and extrapolation more accurate.

Indeed, extrapolated quadratic curves intersect the horizontal line with value ξ in a more localized region about $T_0$, as shown in the right panel of Figure 9, while averaging of obtained approximations to $T_0$ produces $T_0^{\left(aver\right)}=0.25436$, which is more accurate than in the case with a higher amplitude $a={10}^{-5}$. Approximations of $T_0$ for various M are shown in Table 4.

Figure 9. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-8}sin\left(10\pi x\right)$ of a smaller amplitude. The dashed line corresponds to the exact delay $T_0=0.25$. Right panel: $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-8}sin\left(10\pi x\right)$ and $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits. The vertical dashed line indicates the exact time delay $T_0=0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Figure 9. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-8}sin\left(10\pi x\right)$ of a smaller amplitude. The dashed line corresponds to the exact delay $T_0=0.25$. Right panel: $\left|\right|E_R{\left|\right|}_{\infty }$ in the four-pole example with the added perturbation ${10}^{-8}sin\left(10\pi x\right)$ and $M=200$, 400, 600 and 800 together with their extrapolated quadratic fits. The vertical dashed line indicates the exact time delay $T_0=0.25$, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Table 4. Approximations of $T_0$ in the four-pole example with perturbation ${10}^{-8}sin\left(10\pi x\right)$ using extrapolations for various M. The exact value $T_0=0.25$, averaged value $T_0^{\left(aver\right)}$ = $0.25436$.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	0.46392	700	0.25502
300	0.27635	800	0.26081
400	0.25683	900	0.2444
500	0.26798	1000	0.25582
600	0.26391	1500	0.25292

Table 4. Approximations of $T_0$ in the four-pole example with perturbation ${10}^{-8}sin\left(10\pi x\right)$ using extrapolations for various M. The exact value $T_0=0.25$, averaged value $T_0^{\left(aver\right)}$ = $0.25436$.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	0.46392	700	0.25502
300	0.27635	800	0.26081
400	0.25683	900	0.2444
500	0.26798	1000	0.25582
600	0.26391	1500	0.25292

5.2. Transmission Line Example

We consider a uniform transmission line segment with the following per unit-length parameters: L = $7.574$ nH/inches, $C=2.61166$ pF/inches, $R=16.278$ $m\Omega$/inches, $G=5.58$ μS/inches and length $\mathcal{L}=5$ inches. The frequency is sampled on the interval $(0,5.0]$ GHz. The scattering matrix of the structure is computed using MATLAB function rlgc2s. We consider the element $\tilde{H}\left(w\right)=S_{11}\left(w\right)$ and impose the time delay $T_0=1.25$ ns by multiplying $\tilde{H}\left(w\right)$ by $exp(-iw{T}_0)$ to get the delayed transfer function $H\left(w\right)=exp(-iw{T}_0)\tilde{H}\left(w\right)$. The real and imaginary parts of $H\left(w\right)$ are given in Figure 10.

Figure 10. $\text{Re }H\left(w\right)$ and $\text{Im }H\left(w\right)$ in the transmission line example.

Figure 10. $\text{Re }H\left(w\right)$ and $\text{Im }H\left(w\right)$ in the transmission line example.

The error curves for different M are shown in the left panel of Figure 11, indicating that the reconstruction error decreases quickly as M increases and reaches the level close to machine precision at $M=600$.

Figure 11. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the transmission line example as M varies. The vertical dashed line indicates the time delay $T_0=1.25$ ns. Right panel: estimation of the delay time in the transmission line example using critical transition times $T_c$ as M varies. The dashed line corresponds to the exact delay $T_0=1.25$ ns.

Figure 11. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ in the transmission line example as M varies. The vertical dashed line indicates the time delay $T_0=1.25$ ns. Right panel: estimation of the delay time in the transmission line example using critical transition times $T_c$ as M varies. The dashed line corresponds to the exact delay $T_0=1.25$ ns.

Figure 12. $\left|\right|E_R{\left|\right|}_{\infty }$ in the transmission line example with $M=200$, 400, 600 and 800 together with their quadratic fits. The vertical dashed line indicates the exact time delay $T_0$ = $1.25$ ns, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Figure 12. $\left|\right|E_R{\left|\right|}_{\infty }$ in the transmission line example with $M=200$, 400, 600 and 800 together with their quadratic fits. The vertical dashed line indicates the exact time delay $T_0$ = $1.25$ ns, while the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$.

Constructing fitted quadratic error curves and finding their intersections with $\left|\right|E_R{\left|\right|}_{\infty }$ at $T=0$ or finding times when these fitted error curves reach the value ξ of the error for $M\ge 600$, we get a sequence of critical transition times $T_c$, which we show in the right panel of Figure 11. Clearly, critical times $T_c$ converge to $T_0$ and provide a good approximation of $T_0$ for $M\ge 500$. Using an alternative approach when we extrapolate the fitted quadratic error curves to find their intersections with the error threshold ξ, we also obtain good approximations of $T_0$. Some of these curves for $M=200$, 400, 600 and 800 are depicted in Figure 12.

Approximations of $T_0$ using the extrapolation procedure for various values of M ranging from M = 200 to 1500 are given in Table 5. An accurate approximation of $T_0$ is obtained even with $M=300$. As before, approximations of $T_0$ become better as M increases, but for very large values of $M\ge 1000$ when the reconstruction error falls below the filtering threshold ξ and filtering affects the results more, extrapolation becomes less accurate. Averaging obtained approximations of $T_0$ produces $T_0^{\left(aver\right)}=1.2498$ ns, which is very close to the exact value $T_0=1.25$ ns.

Table 5. Approximations of $T_0$ (in ns) in the transmission line example using extrapolations for various M. The exact value $T_0=1.25$ ns, averaged value $T_0^{\left(aver\right)}=1.2498$ ns.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	$1.5194$	700	$1.2531$
300	$1.3147$	800	$1.2512$
400	$1.2793$	900	$1.2678$
500	$1.2506$	1000	$1.2348$
600	$1.2668$	1500	$1.2242$

Table 5. Approximations of $T_0$ (in ns) in the transmission line example using extrapolations for various M. The exact value $T_0=1.25$ ns, averaged value $T_0^{\left(aver\right)}=1.2498$ ns.

M	$T_0$ Approximation	M	$T_0$ Approximation
200	$1.5194$	700	$1.2531$
300	$1.3147$	800	$1.2512$
400	$1.2793$	900	$1.2678$
500	$1.2506$	1000	$1.2348$
600	$1.2668$	1500	$1.2242$

5.3. Dawson’s Integral Example

We consider here another analytic example [25] modeled by the transfer function:

$$H\left(w\right)={\mathrm{e}}^{-iw{T}_0}\tilde{H}\left(w\right)$$

(27)

where:

$$\tilde{H}\left(w\right)={\mathrm{e}}^{-w^2}-\frac{2i}{\sqrt{\pi }}D\left(w\right)$$

(28)

$D\left(w\right)$ is Dawson’s integral:

$$D\left(w\right)={\mathrm{e}}^{-w^2}{\int }_0^w{\mathrm{e}}^{t^2}dt=\frac{\sqrt{\pi }}{2}{\mathrm{e}}^{-w^2}\text{erfi}\left(w\right)$$

(29)

and $\text{erfi}\left(w\right)$ is the imaginary error function. Since [21] (please note that we use the opposite sign in the definition of the Hilbert transform than that in [21] and [25]):

$$\mathcal{H}\left[\text{Re }\tilde{H}\right]=\mathcal{H}\left({\mathrm{e}}^{-w^2}\right)=\frac{2}{\sqrt{\pi }}D\left(w\right)=-\text{Im }\tilde{H}$$

(30)

function $\tilde{H}\left(w\right)$ is causal. Hence, the function $H\left(w\right)$ is a causal function delayed with offset $T_0$. We use $T_0=0.125$ and sample $H\left(w\right)$ on $[0,w_{max}]$ with $w_{max}=20$ using various numbers of points ranging from $N=100$ to 600. Real and imaginary parts of H are shown in Figure 13.

Figure 13. $\text{Re }H\left(w\right)$ and $\text{Im }H\left(w\right)$ in Dawson’s integral example using $N=300$ sample points.

Figure 13. $\text{Re }H\left(w\right)$ and $\text{Im }H\left(w\right)$ in Dawson’s integral example using $N=300$ sample points.

The evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ for various M is shown in the left panel of Figure 14. It is clear from the graphs that critical transition times $T_c$ approach $T_0$.

Figure 14. Left panel: $\left|\right|E_R{\left|\right|}_{\infty }$ in Dawson’s integral example as M varies. The vertical dashed line indicates the time delay $T_0=0.125$. Right panel: evolution of the relative error $\left|\right|E_R^{rel}{\left|\right|}_{\infty }$ in Dawson’s integral example as M varies. The vertical dashed line indicates the time delay $T_0=0.125$.

Figure 14. Left panel: $\left|\right|E_R{\left|\right|}_{\infty }$ in Dawson’s integral example as M varies. The vertical dashed line indicates the time delay $T_0=0.125$. Right panel: evolution of the relative error $\left|\right|E_R^{rel}{\left|\right|}_{\infty }$ in Dawson’s integral example as M varies. The vertical dashed line indicates the time delay $T_0=0.125$.

Constructing fitted quadratic error curves and extrapolating them to find their intersections with the horizontal line corresponding to the error value ξ produce a set of approximations of $T_0$, shown in Table 6. Averaging obtained approximations of $T_0$ for $M\ge 200$, once some convergence is established, gives $T_0^{\left(aver\right)}=0.12528$.

It is interesting to note the behavior of the relative error $E_R^{rel}$ in this example. The evolution of its ∞ norm is shown in the right panel of Figure 14. It is clear that all profiles, even for small values of M, have a unique local maximum at $T=T_0$. The 2-norm has a similar behavior. Even though the behavior of the relative error $E_R^{rel}$ can be used to determine the time delay in this example, we did not find the same pronounced behavior in the other examples we considered. At the same time, extrapolating fitted quadratic curves of ∞ norms of the absolute error $E_R$ was a robust approach in all examples that we considered.

Table 6. Approximations of $T_0$ in Dawson’s integral example using extrapolations of fitted error curves for various M. The exact value $T_0=0.125$, averaged value is $T_0^{\left(aver\right)}=0.12528$ for M ranging from 200 to 600.

M	$T_0$ Approximation	M	$T_0$ Approximation
150	0.16735	240	0.12362
170	0.13116	300	0.12661
180	0.12964	400	0.12233
200	0.12753	500	0.12578
230	0.12333	600	0.12414

Table 6. Approximations of $T_0$ in Dawson’s integral example using extrapolations of fitted error curves for various M. The exact value $T_0=0.125$, averaged value is $T_0^{\left(aver\right)}=0.12528$ for M ranging from 200 to 600.

M	$T_0$ Approximation	M	$T_0$ Approximation
150	0.16735	240	0.12362
170	0.13116	300	0.12661
180	0.12964	400	0.12233
200	0.12753	500	0.12578
230	0.12333	600	0.12414

5.4. Stripline Example

We simulated an asymmetric stripline modeled in [39] with length $L=8$ in, width $W=14$ mils, distances from the trace to reference planes $H_1=10$ mils, $H_2=20$ mils, substrate dielectric Megtron6-1035, laminate with a dielectric constant ${ϵ}_r=3.45$ using a Cadence software tool with an FEM full-wave field solver. The scattering matrix S is obtained on $[0,w_{max}]$ with $w_{max}=2$ GHz. We analyze element $H\left(w\right)=S_{11}\left(w\right)$ of the transfer matrix. The real and imaginary parts of H are shown in Figure 15.

Figure 15. $\text{Re }H$ and $\text{Im }H$ in the stripline example with $N=1000$.

Figure 15. $\text{Re }H$ and $\text{Im }H$ in the stripline example with $N=1000$.

The evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ for various M is depicted in Figure 16. Even for high values of M, the error in causality does not go to the machine precision or the filtering level ξ and, instead, levels off around ${10}^{-6}$. This indicates that our finite element simulation results are accurate only within ${10}^{-6}$. For causality characterization, this implies that data have noise/approximation errors with an amplitude around ${10}^{-6}$. Graphs of $\left|\right|E_R{\left|\right|}_{\infty }$ suggest that for $M\le 2000$, the error is dominated by Fourier series approximation error, while for higher M, the error is dominated by the noise/approximation errors from the finite element method.

Figure 16. $\left|\right|E_R{\left|\right|}_{\infty }$ in the stripline example for various M. The vertical dashed line indicates the closed form microwave theory time delay approximation $T_0=1.25809$ ns.

Figure 16. $\left|\right|E_R{\left|\right|}_{\infty }$ in the stripline example for various M. The vertical dashed line indicates the closed form microwave theory time delay approximation $T_0=1.25809$ ns.

In this example, the time delay is estimated using a closed form microwave theory approximation as $T_0=8\times 0.0254/(c_0/\sqrt{{ϵ}_r})=1.25809$ ns, where $c_0=3\times {10}^8$m/s is the speed of light and $0.0254$ is a conversion factor to convert from inches to meters. The error curves were fitted to quadratic curves, as explained above. Because of the relatively high errors in the data, the fitted regions are not long enough. Besides, there is more nonlinear behavior of the error curves for high values of $T>T_0$. All this makes it difficult to estimate the time delay, as shown in the left panel of Figure 17. As can be seen, extrapolated quadratic curves do not focus at $T_0$, but instead spread out around $T_0$, similarly to the four-pole example with an imposed noise of relatively large amplitude considered in Section 5.1.

Figure 17. Left panel: extrapolated quadratic curves based on the initial fitting range in the stripline example. Right panel: extrapolated quadratic curves based on a more narrow fitting range in the stripline example. The average time delay is $T_0^{\left(aver\right)}=1.2669$ ns.

Figure 17. Left panel: extrapolated quadratic curves based on the initial fitting range in the stripline example. Right panel: extrapolated quadratic curves based on a more narrow fitting range in the stripline example. The average time delay is $T_0^{\left(aver\right)}=1.2669$ ns.

This problem can be corrected by decreasing the fitting range and going further away from transition regions. The results are shown in the right panel of Figure 17.

The approximations of $T_0$ are given in Table 7. Averaging them for values of M up to 3000 produces $T_0^{\left(aver\right)}=1.2669$ ns, which agrees well with an analytically estimated time delay using a closed form formula. As in other examples, results with very high values of $M>3000$, which are more affected by noise and approximation errors in data, are less accurate.

Table 7. Approximations of $T_0$ (in ns) in the stripline example using extrapolations of fitted quadratic error curves for various M. The closed form approximation of the time delay is $T_0=1.25809$ ns, and the averaged value is $T_0^{\left(aver\right)}=1.2669$ ns for M ranging up to 3000.

M	$T_0$ Approximation	M	$T_0$ Approximation
80	1.266	700	1.1987
100	1.2312	800	1.2179
200	1.2553	900	1.2593
300	1.2797	1000	1.2205
400	1.2826	2000	1.246
500	1.2413	3000	1.5878
600	1.1833	4000	1.0168

Table 7. Approximations of $T_0$ (in ns) in the stripline example using extrapolations of fitted quadratic error curves for various M. The closed form approximation of the time delay is $T_0=1.25809$ ns, and the averaged value is $T_0^{\left(aver\right)}=1.2669$ ns for M ranging up to 3000.

M	$T_0$ Approximation	M	$T_0$ Approximation
80	1.266	700	1.1987
100	1.2312	800	1.2179
200	1.2553	900	1.2593
300	1.2797	1000	1.2205
400	1.2826	2000	1.246
500	1.2413	3000	1.5878
600	1.1833	4000	1.0168

5.5. Finite Element Model of a DDR4 Module with a DRAM Package

In this example, we use a scattering matrix S generated by a finite element modeling of a DDR4 module with a DRAM package (courtesy of Micron Technology, Inc.). The package is attached to the module using ball grid array (BGA) technology. The model includes a no-die DRAM package on a printed circuit board (PCB). The model contains 110 input and output ports. The simulation process is performed for 100 equally spaced frequency points ranging from $w_{min}$=0 to $w_{max}=5$ GHz using ANSYS Electromagnetics Suite. For time delay analysis, we consider a group of address buses A8–A4 from module pins to package die-side pins. The port assignment for this group is as follows. Port 1 is placed at the junction of the package and PCB or the BGA; Port 2 is placed at the die-side pin of the package; and Port 3 is placed at the module pin. Hence, $S_{21}$ represents how the signal is transmitted on the address bus from the BGA to the die; $S_{31}$ shows how the signal is transmitted from the BGA to the module pin; while $S_{32}$ represents how the signal is transmitted from the die to the module pin. The magnitudes of these scattering parameters in a signal-to-noise ratio format are shown in Figure 18 assuming that the data accuracy is ${10}^{-5}$, as justified below.

We chose the element $H\left(w\right)=S_{32}\left(w\right)$ to test the performance of the proposed method. The real and imaginary parts of H are shown in Figure 19. Since the number $N=100$ of data points is fixed in this example, we first use $M=100$ Fourier coefficients. The evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ reveals that the causality for early times is satisfied only within ${10}^{-4}$, suggesting either low data resolution or relatively high approximation errors in the data. Approximating the time delay $T_0$ by extrapolating only one error curve to the filtering threshold $\xi ={10}^{-13}$ may be inaccurate, so we decided to construct causal Fourier series approximations for several numbers M of Fourier coefficients ranging from $M=100$ to 600 while keeping the same resolution with $N=100$ to get several approximations of the time delay $T_0$. Using more than $M=100$ Fourier coefficients did not significantly affect the causality accuracy, as can be seen in the left panel of Figure 20. The results indicate that the data are only accurate within ${10}^{-5}$ at most, which is consistent with the expected accuracy of the finite element simulations of the model. It should be noted that with $M\ge 300$, causal Fourier series approximations become more oscillatory, and the amplitude of the oscillations increases as M increases. In fact, for $M\ge 300$, we construct trigonometric interpolants with very small errors at collocation data points, but large oscillations between the collocation points. The presence of such spurious oscillations is the reason why over-collocation [38] is suggested for SVD-based Fourier continuations. With over-collocation, the number of data points should exceed the number of Fourier coefficients, and it is recommended to use at least twice more collocation data points than the number M of Fourier coefficients. We have $2N$ data points because of the spectrum symmetry, and we use $N=M$ Fourier coefficients to get accurate and non-oscillatory causal Fourier series approximations. Even though using more Fourier coefficients M in this example than the number N of collocation points affected causal Fourier series approximations, the qualitative dynamics of the error curves has not changed. At the same time, having several error curves that can be extrapolated to the level ξ provided several approximations of the time delay $T_0$, which we can use to get an average time delay.

Figure 18. Magnitudes of elements $S_{21}$, $S_{31}$ and $S_{32}$ in dB using the signal-to-noise ratio (SNR) format in the DDR4 module with a DRAM package example with ${10}^{-5}$ data accuracy.

Figure 18. Magnitudes of elements $S_{21}$, $S_{31}$ and $S_{32}$ in dB using the signal-to-noise ratio (SNR) format in the DDR4 module with a DRAM package example with ${10}^{-5}$ data accuracy.

Figure 19. $\text{Re }H$ and $\text{Im }H$ of the element $H\left(w\right)=S_{32}\left(w\right)$ from the DDR4 module with a DRAM package example.

Figure 19. $\text{Re }H$ and $\text{Im }H$ of the element $H\left(w\right)=S_{32}\left(w\right)$ from the DDR4 module with a DRAM package example.

In the right panel of Figure 20, we show several error curves together with their extrapolated quadratic fits. The fits were obtained using a more localized fitting range, since the data have a relatively high level of error.

Figure 20. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ for various M in the DDR4 module with a DRAM package example. The vertical dashed line indicates the time delay $T_0=0.04$ ns estimated using alternative methods. Right panel: error curves $\left|\right|E_R{\left|\right|}_{\infty }$ together with their extrapolated quadratic curves, and the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$. The average time delay is $T_0^{\left(aver\right)}=0.040841$ ns.

Figure 20. Left panel: evolution of $\left|\right|E_R{\left|\right|}_{\infty }$ for various M in the DDR4 module with a DRAM package example. The vertical dashed line indicates the time delay $T_0=0.04$ ns estimated using alternative methods. Right panel: error curves $\left|\right|E_R{\left|\right|}_{\infty }$ together with their extrapolated quadratic curves, and the horizontal dashed line indicates the level of filtering of singular values given by $\xi ={10}^{-13}$. The average time delay is $T_0^{\left(aver\right)}=0.040841$ ns.

The approximation of the time delay $T_0$ using various values of M is shown in Table 8. Averaging them, we obtain $T_0^{\left(aver\right)}=0.040841$ ns.

Table 8. Approximations of $T_0$ (in ns) in the DDR4 module with a DRAM package example using extrapolations of fitted quadratic error curves for various M. An estimate of the time delay obtained using alternative methods is $T_0=0.04$ ns. The average time delay obtained using various numbers of Fourier coefficients ranging from 100 to 600 is $T_0^{\left(aver\right)}=0.040841$ ns.

M	$T_0$ Approximation	M	$T_0$ Approximation
100	$0.034741$	240	$0.038346$
150	$0.038733$	300	$0.042901$
170	$0.039733$	400	$0.0403$
180	$0.036878$	500	$0.04391$
200	$0.044321$	600	$0.046096$

Table 8. Approximations of $T_0$ (in ns) in the DDR4 module with a DRAM package example using extrapolations of fitted quadratic error curves for various M. An estimate of the time delay obtained using alternative methods is $T_0=0.04$ ns. The average time delay obtained using various numbers of Fourier coefficients ranging from 100 to 600 is $T_0^{\left(aver\right)}=0.040841$ ns.

M	$T_0$ Approximation	M	$T_0$ Approximation
100	$0.034741$	240	$0.038346$
150	$0.038733$	300	$0.042901$
170	$0.039733$	400	$0.0403$
180	$0.036878$	500	$0.04391$
200	$0.044321$	600	$0.046096$

For comparison, the time delay $T_0$ is estimated using two other alternative methods. In the first method, since S parameters have units of voltage amplitudes, $S_{32}$ is considered as a minimum-phase transfer function [26]. The plot of the phase of $S_{32}$, shown in the left panel of Figure 21, reveals that the phase of $S_{32}$ is approximately a linear function for the frequencies we consider (for higher frequencies, it is expected to have a more nonlinear behavior). Its slope can be used to approximate the time delay. For example, from DC to 3.939 GHz, the phase of $S_{32}$ has changed −0.9996 radians. This implies that the time delay $T_0\approx \frac{\Delta \theta }{\Delta \omega }=\frac{0.9996}{2\pi *3.939*{10}^9}\approx 0.0404$ ns. Alternatively, the slope of the phase of $S_{32}$ can be approximated by using the linear least squares fitting. We find the slope to be $-0.251567\times {10}^{-9}$. Dividing it by $2\pi$ gives $T_0\approx 0.251567\times {10}^{-9}/\left(2\pi \right)\approx 0.04004$ ns.

Another way to estimate the time delay from S-parameters is by using the time domain transmission (TDT). The input step function is initialized with the sample time $T_s=0.1$ ps and rise time $T_r=1$ ps, and it is shown in the right panel of Figure 21 using a solid blue line. The transfer function $S_{32}$ is fit to a rational function using the vector fitting method implemented in the MATLAB function rationalfit. Since the bandwidth of $S_{32}$ is only 5 GHz and the transfer function does not decay enough, we extend the bandwidth of the fitted rational function to 50 GHz to avoid aliasing according to the Nyquist criterion. Then, we use the inverse fast Fourier transform to compute the response of the system to the unit step function due to $S_{32}$ in the time domain. This response is shown in the right panel of Figure 21 using a dashed red line. Measuring times at which the input step function and the output step response reach $50\%$ of their maximum values and taking their difference, we obtain an approximation to the time delay $T_0\approx 0.04065\mathrm{ns}-0.0006\mathrm{ns}=0.04005\mathrm{ns}$.

The average time delay $T_0^{\left(aver\right)}=0.040841$ ns obtained using the proposed method is consistent with other alternative approximations of the time delay, which demonstrates the robustness of our technique.

Figure 21. Left panel: phase of $S_{32}$ as a function of frequency in the DDR4 module with a DRAM package example. Its slope is $-0.251567\times {10}^{-9}$, which gives an approximation of the time delay $T_0=0.251567\times {10}^{-9}/\left(2\pi \right)\approx 0.04004$ ns.

Figure 21. Left panel: phase of $S_{32}$ as a function of frequency in the DDR4 module with a DRAM package example. Its slope is $-0.251567\times {10}^{-9}$, which gives an approximation of the time delay $T_0=0.251567\times {10}^{-9}/\left(2\pi \right)\approx 0.04004$ ns.

6. Conclusions

We proposed a new method for time delay extraction from tabulated frequency responses. The approach uses the spectrally accurate causality enforcement technique constructed using SVD-based causal Fourier continuations, that was recently developed by the authors. The time delay is incorporated into the causality characterization approach by introducing a linear varying phase factor to the system of equations that defines Fourier coefficients. Varying time until a threshold time, which depends on the maximum frequency at which the transfer function is available, results in the reconstruction error between the given data and their causal Fourier continuations to go from an almost constant small value to a rapidly growing function at some critical transition time. The critical transition times depend on the resolution and approach the time delay as the resolution increases. Several sets of frequency responses with increasing resolution can be used to establish convergence and get an approximation of the time delay. Alternatively, when only a limited number of samples is available, a growing portion of the error curve can be extrapolated to find an approximation of the time delay. The method is applicable to data that have noise or other approximation errors. A few sets of frequency responses can be used to improve the accuracy of time delay approximation by averaging the obtained results. The technique can be extended for multi-port and mixed-mode networks. The performance of the method is demonstrated using several analytic and simulated examples, including data with noise, for which time delay is known exactly or can be estimated using other alternative approaches.