Progress towards Spin-Based Light Emission in Group IV Semiconductors
Abstract
:1. Introduction
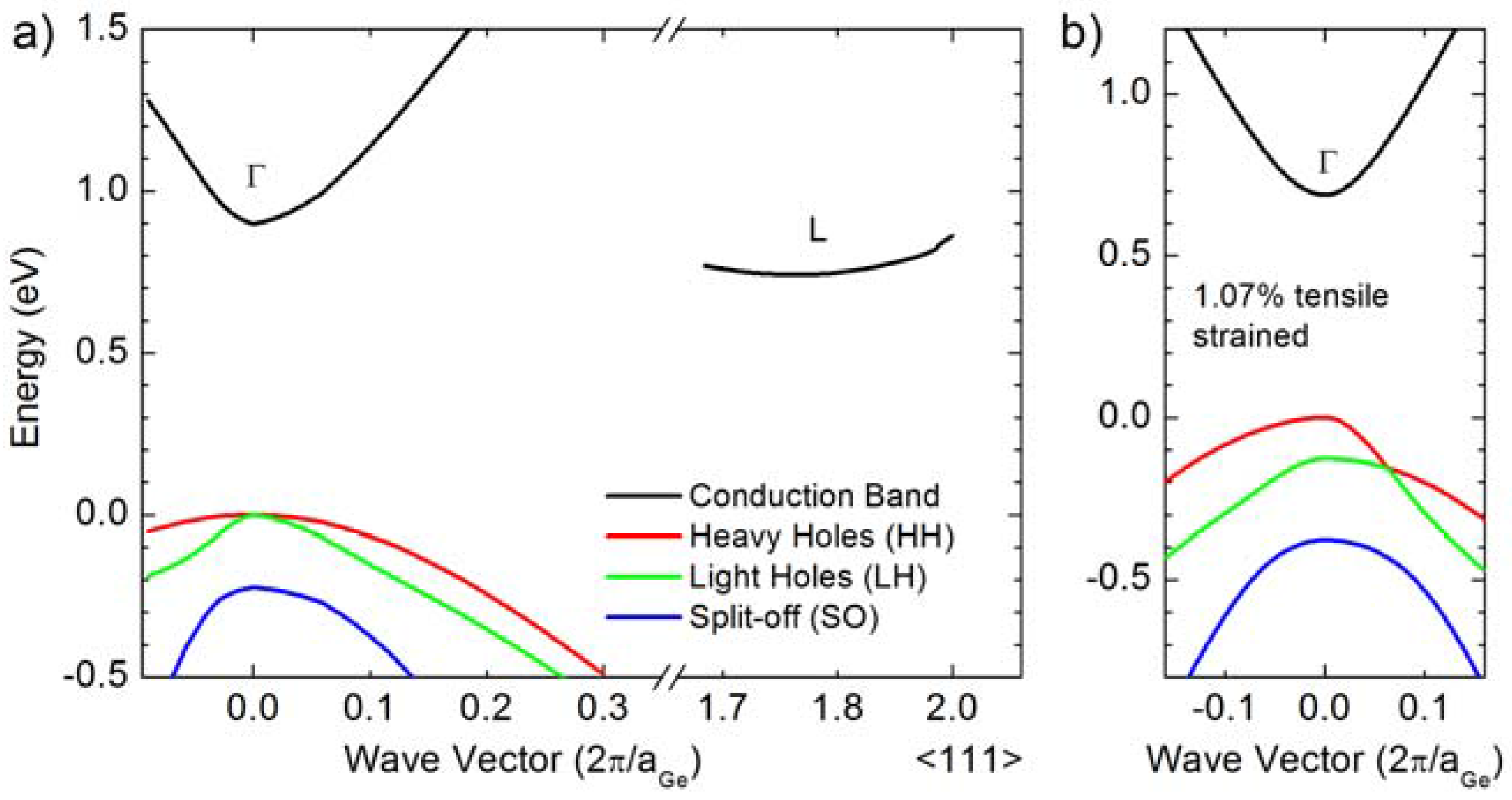
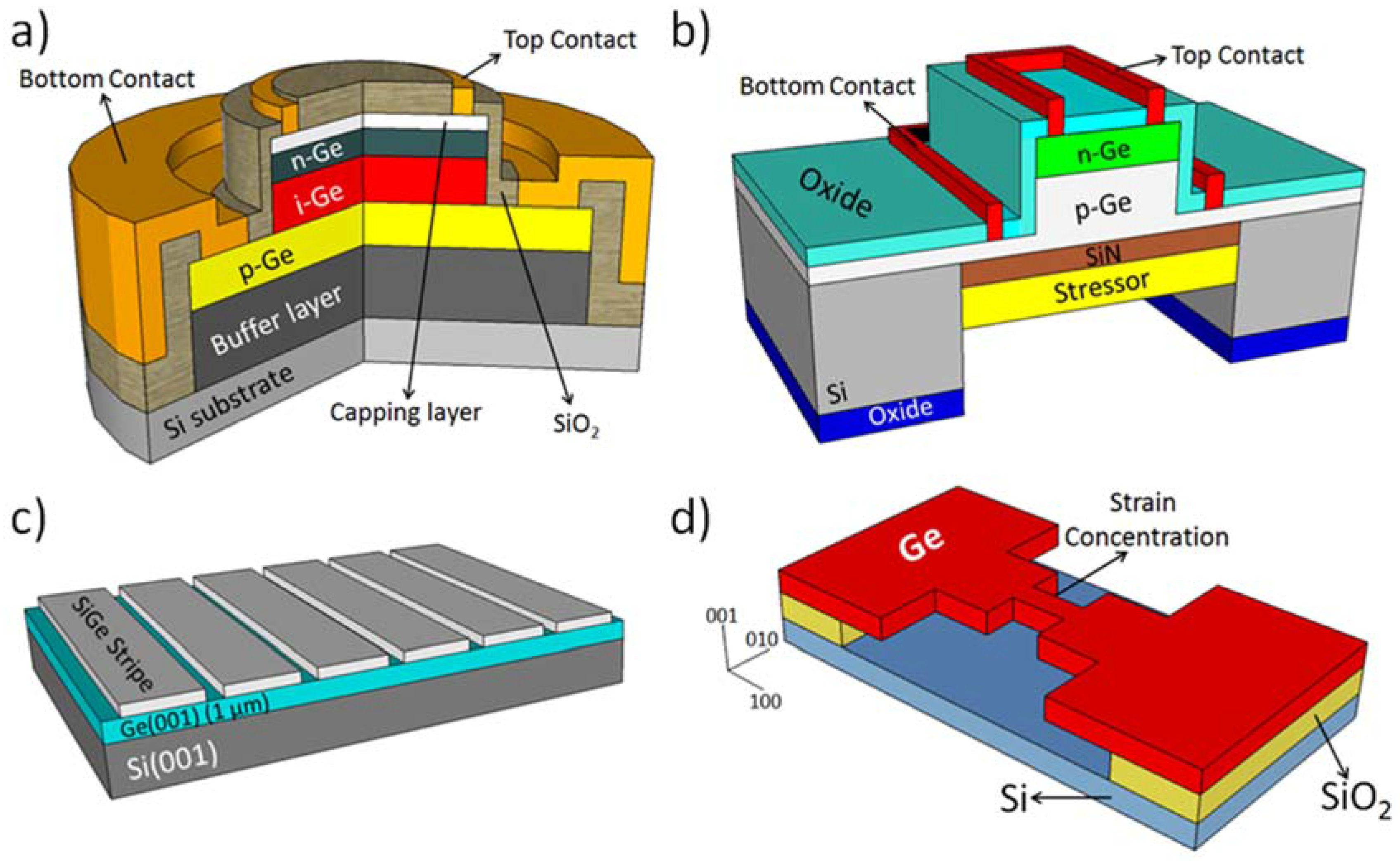
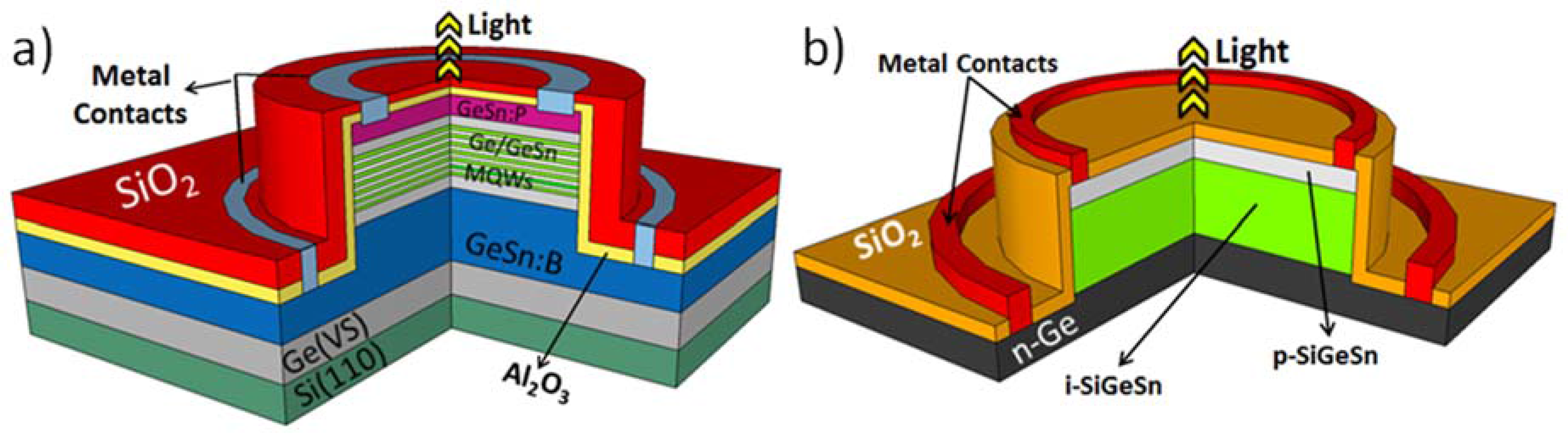
2. Light Emitters Based on Group IV Materials
3. Spintronics Based on Group IV Materials
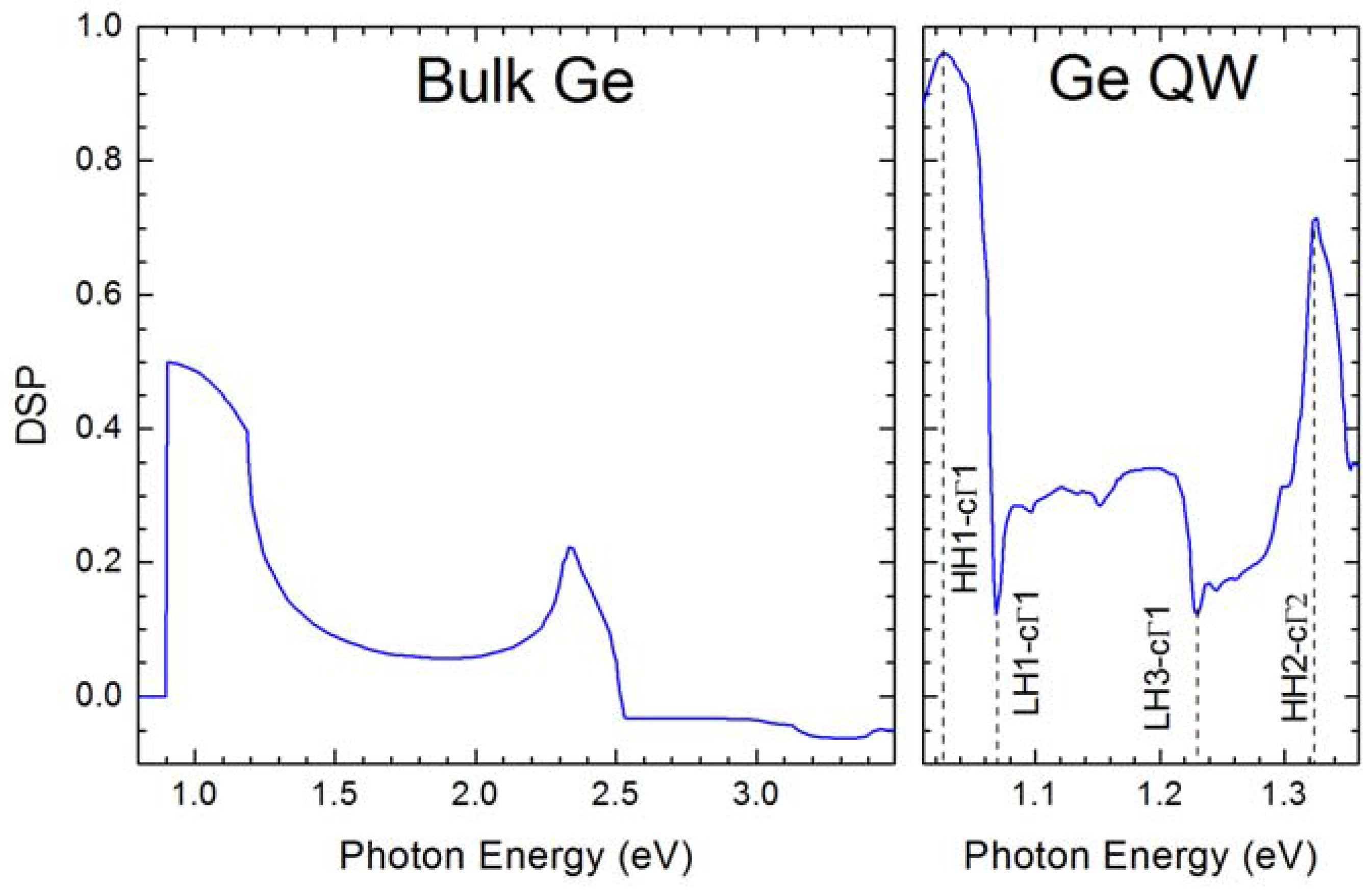
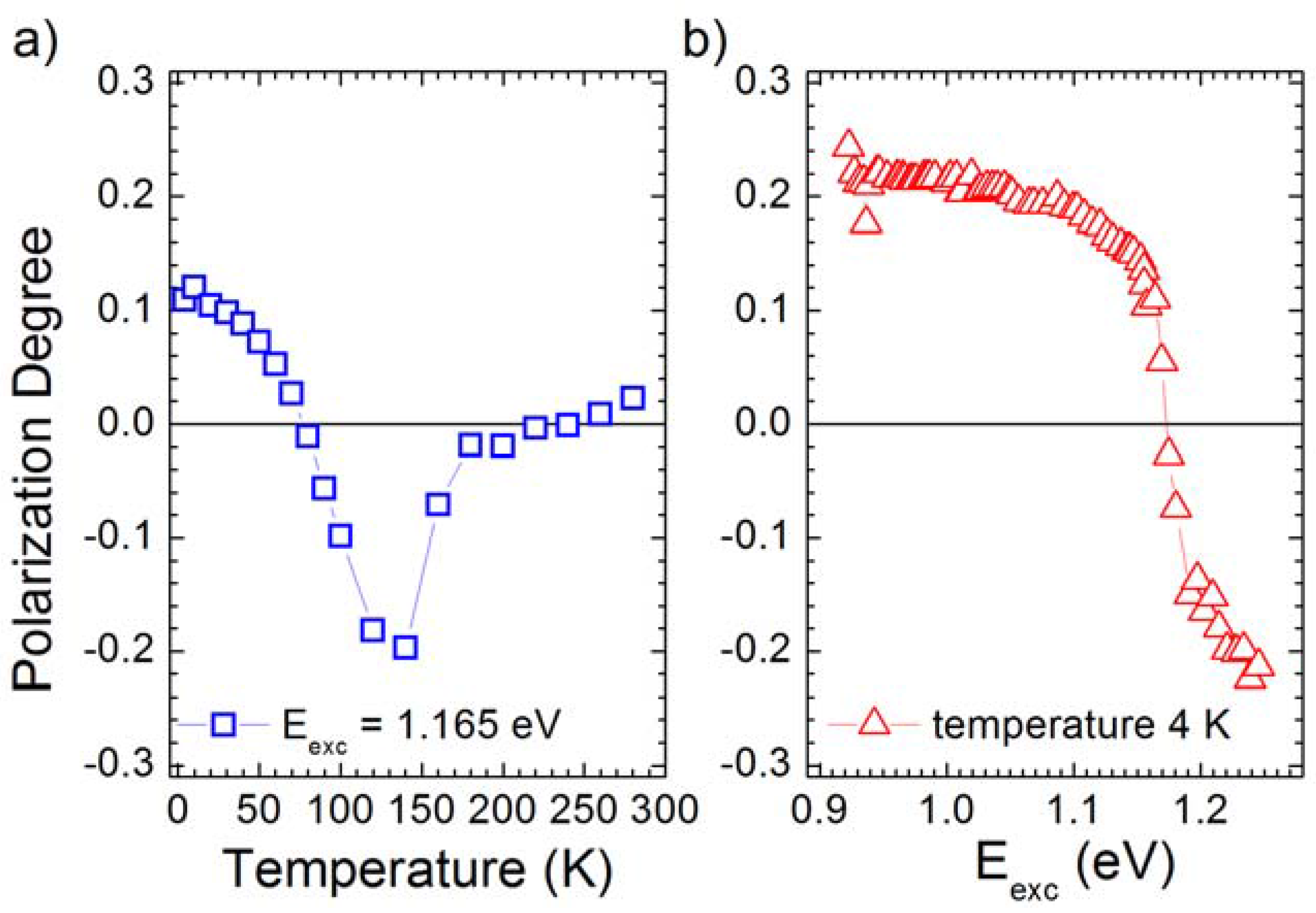
3.1. Optical Investigations of the Spin Physics of Group IV Materials
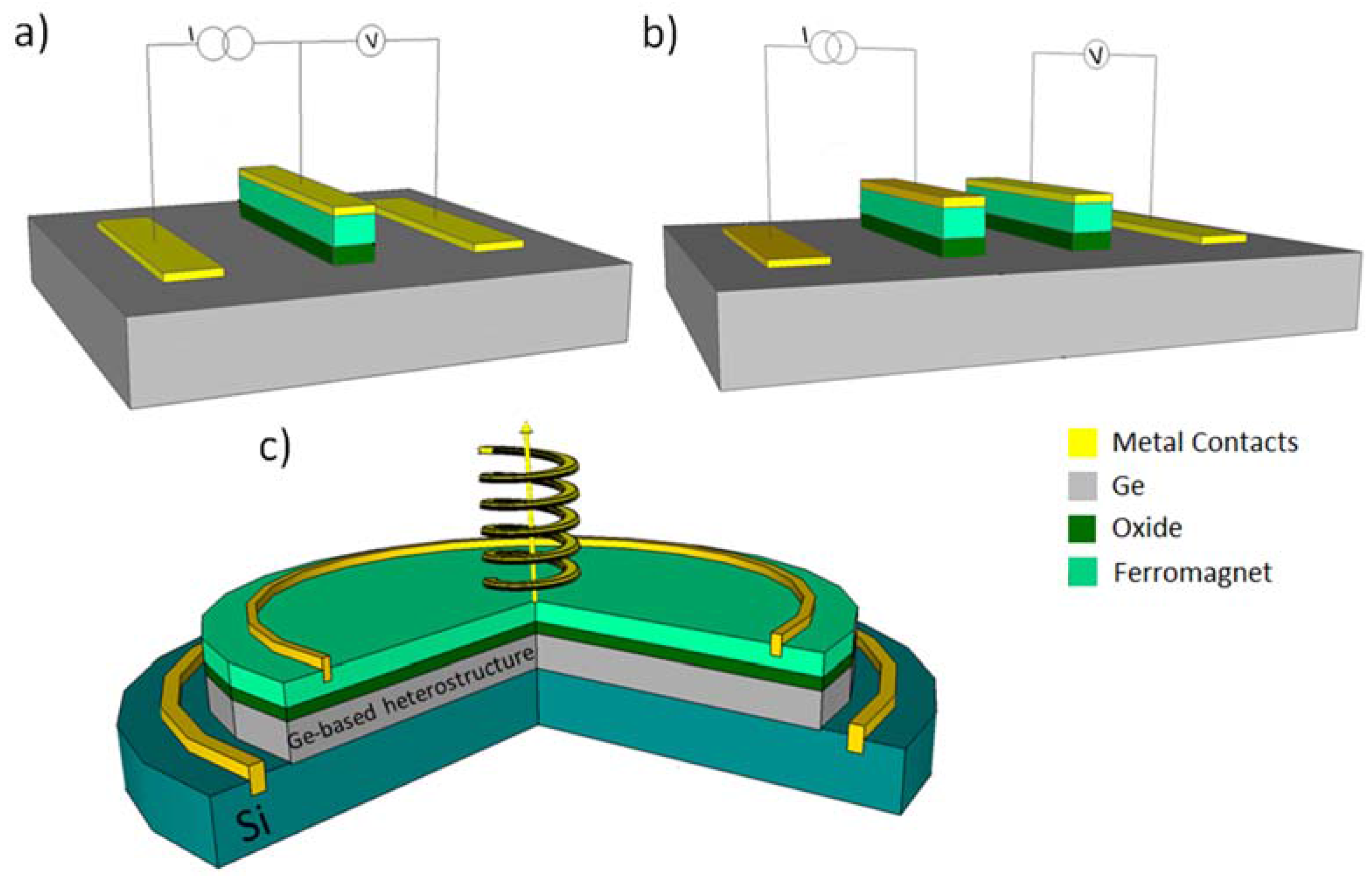
3.2. Electrical Spin Injection in Ge
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Waldrop, M.M. The chips are down for Moore’s law. Nature 2016, 530, 144–147. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnár, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [PubMed]
- Soref, R. The past, present, and future of silicon photonics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1678–1687. [Google Scholar] [CrossRef]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Nguyen Van Dau, F.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39, 4828–4830. [Google Scholar] [CrossRef]
- Awshalom, D.D.; Flatté, M.E. Challenges for semiconductor spintronics. Nat. Phys. 2007, 3, 153–159. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F.; Cibert, J.; Ferrand, D. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
- Dietl, T. A ten-year perspective on diluite magnetic semiconductors and oxides. Nat. Mater. 2010, 9, 965–974. [Google Scholar] [CrossRef] [PubMed]
- Dietl, T.; Ohno, H. Dilute ferromagnetics semiconductors: Physics and spintronics structures. Rev. Mod. Phys. 2014, 86, 187–251. [Google Scholar] [CrossRef]
- Jansen, R. Silicon spintronics. Nat. Mater. 2012, 11, 400–408. [Google Scholar] [CrossRef] [PubMed]
- Morton, J.J.L.; McCamey, D.R.; Eriksson, M.A.; Lyon, S.A. Embracing the quantum limit in silicon computing. Nature 2011, 479, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Dushenko, S.; Koike, M.; Ando, Y.; Shinjo, T.; Myronov, M.; Shiraishi, M. Experimental Demonstration of Room-Temperature Spin Transport in n-Type Germanium Epilayers. Phys. Rev. Lett. 2015, 114, 196602. [Google Scholar] [CrossRef] [PubMed]
- Sigillito, A.J.; Jock, R.M.; Tyryshkin, A.M.; Beeman, J.W.; Haller, E.E.; Itoh, K.M.; Lyon, S.A. Electron spin coherence of shallow donors in natural and isotopically enriched. Phys. Rev. Lett. 2015, 115, 247601. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.A.B. Rationale and challenges for optical interconnects to electronic chips. Proc. IEEE 2000, 88, 728–749. [Google Scholar] [CrossRef]
- O’Brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695. [Google Scholar] [CrossRef]
- O’Brien, J.L.; Pryde, G.J.; White, A.G.; Ralph, T.C.; Branning, D. Demonstration of an all-optical quantum controlled-NOT gate. Nature 2003, 426, 264–267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tiarks, D.; Schmidt, S.; Rempe, G.; Dürr, S. Optical phase shift created with a single-photon pulse. Sci. Adv. 2016, 2, e1600036. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Bowers, J.E. Recent progress in lasers on silicon. Nat. Photonics 2010, 4, 511–517. [Google Scholar] [CrossRef]
- Zhou, Z.; Yin, B.; Michel, J. On-chip light sources for silicon photonics. Light Sci. Appl. 2015, 4, e358. [Google Scholar] [CrossRef]
- Soref, R.A.; Friedman, L. Direct-gap Ge/GeSn/Si and GeSn/Ge/Si heterostructures. Superlattices Microstruct. 1993, 14, 189–193. [Google Scholar] [CrossRef]
- Fitzgerald, E.A.; Freeland, P.E.; Asom, M.T.; Lowe, W.P.; Macharrie, R.A.; Weir, B.E.; Kortan, A.R.; Thiel, F.A.; Xie, Y.H.; Sergent, A.M.; et al. Epitaxially stabilized GeSn diamond cubic alloys. J. Electron. Mater. 1991, 20, 489–501. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Camacho-Aguilera, R.; Kimerling, L.C.; Michel, J. Ge-on-Si laser operating at room temperature. Opt. Lett. 2010, 35, 679–681. [Google Scholar] [CrossRef] [PubMed]
- Wirths, S.; Geiger, R.; von den Driesch, N.; Mussler, G.; Stoica, T.; Mantl, S.; Ikonic, Z.; Luysberg, M.; Chiussi, S.; Hartmann, J.M.; et al. Lasing in direct-bandgap GeSn alloy grown on Si. Nat. Photonics 2015, 9, 88–92. [Google Scholar] [CrossRef]
- Camacho-Aguilera, R.E.; Cai, Y.; Patel, N.; Bessette, J.T.; Romagnoli, M.; Kimerling, L.C.; Michel, J. An electrically pumped germanium laser. Opt. Express 2012, 20, 11316–11320. [Google Scholar] [CrossRef] [PubMed]
- Lampel, G. Nuclear dynamic polarization by optical electronic saturation and optical pumping in semiconductors. Phys. Rev. Lett. 1968, 20, 491–493. [Google Scholar] [CrossRef]
- Loren, E.J.; Ruzicka, B.A.; Werake, L.K.; Zhao, H.; van Driel, H.M.; Smirl, A.L. Optical injection and detection of ballistic pure spin currents in Ge. Appl. Phys. Lett. 2009, 95, 092107. [Google Scholar] [CrossRef]
- Guite, C.; Venkataraman, V. Measurement of Electron Spin Lifetime and Optical Orientation Efficiency in Germanium Using Electrical Detection of Radio Frequency Modulated Spin Polarization. Phys. Rev. Lett. 2011, 107, 166603. [Google Scholar] [CrossRef] [PubMed]
- Pezzoli, F.; Bottegoni, F.; Trivedi, D.; Ciccacci, F.; Giorgioni, A.; Li, P.; Cecchi, S.; Grilli, E.; Song, Y.; Guzzi, M.; et al. Optical Spin Injection and Spin Lifetime in Ge Heterostructures. Phys. Rev. Lett. 2012, 108, 156603. [Google Scholar] [CrossRef] [PubMed]
- Oestreich, M.; Hubner, J.; Hagele, D.; Bender, M.; Gerhardt, N.; Hofmann, M.; Ruhle, W.W.; Kalt, H.; Hartmann, T.; Klar, P.; et al. Spintronics: Spin electronics and optoelectronics in semiconductors. Adv. Solid State Phys. 2001, 41, 173–186. [Google Scholar]
- Holub, M.; Bhattacharya, P. Spin-polarized light-emitting diodes and lasers. J. Phys. D Appl. Phys. 2007, 40, R179–R203. [Google Scholar] [CrossRef]
- Lee, J.; Oszwaldowski, R.; Gothgen, C.; Zutic, I. Mapping between quantum dot and quantum well lasers: From conventional to spin lasers. Phys. Rev. B 2012, 85, 045314. [Google Scholar] [CrossRef]
- Holub, M.; Shin, J.; Saha, D.; Bhattacharya, P. Electrical Spin Injection and Threshold Reduction in a Semiconductor Laser. Phys. Rev. Lett. 2007, 98, 146603. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Bearden, S.; Wasner, E.; Zutic, I. Spin-lasers: From threshold reduction to large-signal analysis. Appl. Phys. Lett. 2014, 105, 042411. [Google Scholar] [CrossRef]
- Hallstein, S.; Berger, J.D.; Hilpert, M.; Schneider, H.C.; Rühle, W.W.; Jahnke, F.; Koch, S.W.; Gibbs, H.M.; Khitrova, G.; Oestreich, M. Manifestation of coherent spin precession in stimulated semiconductor emission dynamics. Phys. Rev. B 1997, 56, R7076–R7079. [Google Scholar] [CrossRef]
- Fiederling, R.; Keim, M.; Reuscher, G.; Ossau, W.; Schmidt, G.; Waag, A.; Molenkamp, L.W. Injection and detection of a spin-polarized current in a light-emitting diode. Nature 1999, 402, 787–790. [Google Scholar]
- Ohno, Y.; Young, D.K.; Beschoten, B.; Matsukura, F.; Ohno, H.; Awschalom, D.D. Electrical spin injection in a ferromagnetic semiconductor heterostructure. Nature 1999, 402, 790–792. [Google Scholar] [CrossRef]
- Jonker, B.T.; Kioseoglou, G.; Hanbicki, A.T.; Li, C.L.; Thompson, P.E. Electrical spin-injection into silicon from a ferromagnetic metal/tunnel barrier contact. Nat. Phys. 2007, 3, 542–546. [Google Scholar] [CrossRef]
- Lee, M.L.; Fitzgerald, E.A.; Bulsara, M.T.; Currie, M.T.; Lochtefeld, A. Strained Si, SiGe, and Ge channels for high-mobility metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2005, 97, 011101. [Google Scholar] [CrossRef]
- Nanver, L.K.; Jovanovic, V.; Biasotto, C.; Moers, J.; Grützmacher, D.; Zhang, J.J.; Hrauda, N.; Stoffel, M.; Pezzoli, F.; Schmidt, O.G.; et al. Integration of MOSFETs with SiGe dots as stressor material. Solid-State Electron. 2011, 60, 75–83. [Google Scholar] [CrossRef]
- Schmidt, O.G.; Eberl, K. Self-Assembled Ge/Si Dots for Faster Field-Effect Transistors. IEEE Trans. Electron. Dev. 2001, 48, 1175–1179. [Google Scholar] [CrossRef]
- Richard, S.; Aniel, F.; Fishman, G. Energy-band structure of Ge, Si and GaAs: A thirty-band k∙p method. Phys. Rev. B 2004, 70, 235204. [Google Scholar] [CrossRef]
- Boztug, C.; Sánchez-Pérez, J.R.; Sudradjat, F.F.; Jacobson, R.B.; Paskiewicz, D.M.; Lagally, M.G.; Paiella, R. Tensilely Strained Germanium Nanomembranes as Infrared Optical Gain Media. Small 2013, 9, 622–630. [Google Scholar] [CrossRef] [PubMed]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 2010, 4, 495–497. [Google Scholar] [CrossRef]
- Soref, R. Group IV photonics: Enabling 2 μm communications. Nat. Photonics 2015, 9, 358–359. [Google Scholar] [CrossRef]
- Fischetti, M.V.; Laux, S.E. Band structure, deformation potentials, and carrier mobility in strained Si, Ge, and SiGe alloys. J. Appl. Phys. 1996, 80, 2234–2252. [Google Scholar] [CrossRef]
- Zhang, F.; Crespi, V.H.; Zhang, P. Prediction that Uniaxial Tension along <111> Produces a Direct Band Gap in Germanium. Phys. Rev. Lett. 2009, 102, 156401. [Google Scholar] [CrossRef] [PubMed]
- El Kurdi, M.; Fishman, G.; Sauvage, S.; Boucaud, P. Band structure and optical gain of tensile-strained germanium based on a 30 band k·p formalism. J. Appl. Phys. 2010, 107, 013710. [Google Scholar] [CrossRef]
- Pizzi, G.; Virgilio, M.; Grosso, G. Tight-binding calculation of optical gain in tensile strained [001]-Ge/SiGe quantum wells. Nanotechnology 2010, 21, 055202. [Google Scholar] [CrossRef] [PubMed]
- Schmid, M.; Oehme, M.; Gollhofer, M.; Körner, R.; Kaschel, M.; Kasper, E.; Schulze, J. Effect of heavy doping and strain on the electroluminescence of Ge-on-Si light emitting diodes. Thin Solid Films 2014, 557, 351–354. [Google Scholar] [CrossRef]
- Schwartz, B.; Klossek, A.; Kittler, M.; Oehme, M.; Kasper, E.; Schulze, J. Electroluminescence of germanium LEDs on silicon: Influence of antimony doping. Phys. Status Solidi C 2014, 11, 1686–1691. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, W.; Li, C.; Li, Y.; Xue, C.; Li, C.; Zuo, Y.; Cheng, B.; Wang, Q. Room temperature direct-bandgap electroluminescence from n-type straincompensated Ge/SiGe multiple quantum wells. Appl. Phys. Lett. 2012, 101, 231108. [Google Scholar]
- Arguirov, T.; Kittler, M.; Oehme, M.; Abrosimov, N.V.; Kasper, E.; Schulze, J. Room Temperature Direct Band-Gap Emission from an Unstrained Ge P-I-N LED on Si. Solid State Phenom. 2011, 178–179, 25–30. [Google Scholar] [CrossRef]
- Oehme, M.; Werner, J.; Kasper, E.; Jutzi, M.; Berroth, M. High bandwidth Ge p-i-n photodetector integrated on Si. Appl. Phys. Lett. 2006, 89, 071117. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Kimerling, L.C.; Michel, J. Tensile-strained, n-type Ge as a gain medium for monolithic laser integration on Si. Opt. Express 2007, 15, 11272–11277. [Google Scholar] [CrossRef] [PubMed]
- Jain, J.R.; Hryciw, A.; Baer, T.M.; Miller, D.A.B.; Brongersma, M.L.; Howe, R.T. A micromachining-based technology for enhancing germanium light emission via tensile strain. Nat. Photonics 2012, 6, 398–405. [Google Scholar] [CrossRef]
- Boucaud, P.; El Kurdi, M.; Sauvage, S.; de Kersauson, M.; Ghrib, A.; Checoury, X. Light emission from strained germanium. Nat. Photonics 2013, 7, 162. [Google Scholar] [CrossRef]
- Cheng, T.-H.; Peng, K.-L.; Ko, C.-Y.; Chen, C.-Y.; Lan, H.-S.; Wu, Y.-R.; Liu, C.W.; Tseng, H.-H. Strain-enhanced photoluminescence from Ge direct transition. Appl. Phys. Lett. 2010, 96, 211108. [Google Scholar] [CrossRef]
- Süess, M.J.; Geiger, R.; Minamisawa, R.A.; Schiefler, G.; Frigerio, J.; Chrastina, D.; Isella, G.; Spolenak, R.; Faist, J.; Sigg, H. Analysis of enhanced light emission from highly strained germanium microbridges. Nat. Photonics 2013, 7, 466–472. [Google Scholar] [CrossRef]
- Lan, H.-S.; Chan, S.-T.; Cheng, T.-H.; Chen, C.-Y.; Jan, S.-R.; Liu, C.W. Biaxial tensile strain effects on photoluminescence of different orientated Ge wafers. Appl. Phys. Lett. 2011, 98, 101106. [Google Scholar] [CrossRef]
- El Kurdi, M.; Kociniewski, T.; Ngo, T.-P.; Boulmer, J.; Débarre, D.; Boucaud, P.; Damlencourt, J.F.; Kermarrec, O.; Bensahel, D. Enhanced photoluminescence of heavilyn-doped germanium. Appl. Phys. Lett. 2009, 94, 191107. [Google Scholar] [CrossRef]
- Sun, X.; Liu, J.; Kimerling, L.C.; Michel, J. Direct gap photoluminescence of n-type tensile-strained Ge-on-Si. Appl. Phys. Lett. 2009, 95, 011911. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Kimerling, L.C.; Michel, J. Direct-gap optical gain of Ge on Si at room temperature. Opt. Lett. 2009, 34, 1738–1740. [Google Scholar] [CrossRef] [PubMed]
- Carroll, L.; Friedli, P.; Neuenschwander, S.; Sigg, H.; Cecchi, S.; Isa, F.; Chrastina, D.; Isella, G.; Fedoryshyn, Y.; Faist, J. Direct-Gap Gain and Optical Absorption in Germanium Correlated to the Density of Photoexcited Carriers, Doping, and Strain. Phys. Rev. Lett. 2009, 109, 057402. [Google Scholar] [CrossRef] [PubMed]
- Virgilio, M.; Manganelli, C.L.; Grosso, G.; Pizzi, G.; Capellini, G. Radiative recombination and optical gain spectra in biaxially strainedn-type germanium. Phys. Rev. B 2013, 87, 235313. [Google Scholar] [CrossRef]
- Virgilio, M.; Manganelli, C.L.; Grosso, G.; Schroeder, T.; Capellini, G. Photoluminescence, recombination rate, and gain spectra in optically excited n-type and tensile strained germanium layers. J. Appl. Phys. 2013, 114, 243102. [Google Scholar] [CrossRef]
- Wen, H.; Bellotti, E. Rigorous theory of the radiative and gain characteristics of silicon and germanium lasing media. Phys. Rev. B 2015, 91, 035307. [Google Scholar] [CrossRef]
- Prost, M.; El Kurdi, M.; Aniel, F.; Zerounian, N.; Sauvage, S.; Checoury, X.; Bœuf, F.; Boucaud, P. Analysis of optical gain threshold in n-doped and tensile-strained germanium heterostructure diodes. J. Appl. Phys. 2015, 118, 125704. [Google Scholar] [CrossRef]
- Pezzoli, F.; Isa, F.; Isella, G.; Falub, C.V.; Kreiliger, T.; Salvalaglio, M.; Bergamaschini, R.; Grilli, E.; Guzzi, M.; von Känel, H.; et al. Ge Crystals on Si Show Their Light. Phys. Rev. Appl. 2014, 1, 044005. [Google Scholar] [CrossRef]
- Huo, Y.; Lin, H.; Chen, R.; Makarova, M.; Rong, Y.; Li, M.; Kamins, T.I.; Vuckovic, J.; Harris, J.S. Strong enhancement of direct transition photoluminescence with highly tensilestrained Ge grown by molecular beam epitaxy. Appl. Phys. Lett. 2011, 98, 011111. [Google Scholar] [CrossRef]
- Jakomin, R.; de Kersauson, M.; El Kurdi, M.; Largeau, L.; Mauguin, O.; Beaudoin, G.; Sauvage, S.; Ossikovski, R.; Ndong, G.; Chaigneau, M.; et al. High quality tensile-strained n-doped germanium thin films grown on InGaAs buffer layers by metal-organic chemical vapor deposition. Appl. Phys. Lett. 2011, 98, 091901. [Google Scholar] [CrossRef]
- Capellini, G.; Reich, C.; Guha, S.; Yamamoto, Y.; Lisker, M.; Virgilio, M.; Ghrib, A.; El Kurdi, M.; Boucaud, P.; Tillack, B.; et al. Tensile Ge microstructures for lasing fabricated by means of a silicon complementary metal-oxide-semiconductor process. Opt. Express, 2014, 22, 399–410. [Google Scholar] [CrossRef] [PubMed]
- Chahine, G.A.; Zoellner, M.H.; Richard, M.-I.; Guha, S.; Reich, C.; Zaumseil, P.; Capellini, G.; Schroeder, T.; Schülli, T.U. Strain and lattice orientation distribution in SiN/Ge complementary metal–oxide–semiconductor compatible light emitting microstructures by quick X-ray nanodiffraction microscopy. Appl. Phys. Lett. 2015, 106, 071902. [Google Scholar] [CrossRef]
- Millar, R.W.; Gallacher, K.; Samarelli, A.; Frigerio, J.; Chrastina, D.; Isella, G.; Dieing, T.; Paul, D.J. Extending the emission wavelenght of Ge nanopillars to 2.25 μm using silicon nitride stressor. Opt. Express 2015, 23, 18193–18202. [Google Scholar] [CrossRef] [PubMed]
- Ghrib, A.; El Kurdi, M.; Prost, M.; Sauvage, S.; Checoury, X.; Beaudoin, G.; Chaigneau, M.; Ossikovski, R.; Sagnes, I.; Boucaud, P. All-around SiN stressor for high and homogeneous tensile strain in germanium microdisk cavities. Adv. Opt. Mater. 2015, 3, 353–358. [Google Scholar] [CrossRef]
- El Kurdi, M.; Prost, M.; Ghrib, A.; Sauvage, S.; Checoury, X.; Beaudoin, G.; Sagnes, I.; Picardi, G.; Ossikovski, R.; Boucaud, P. Direct bandgap germanium microdisks obtained with silicon nitride stressor layer. ACS Photonics 2016, 3, 443–448. [Google Scholar] [CrossRef]
- Nam, D.; Sukhdeo, D.; Roy, A.; Balram, K.; Cheng, S.-L.; Huang, K.C.-Y.; Yuan, Z.; Brongersma, M.; Nishi, Y.; Miller, D.; Saraswat, K. Strained germanium thin film membrane on silicon substrate for optoelectronics. Opt. Express 2011, 19, 25866–25872. [Google Scholar] [CrossRef] [PubMed]
- Nam, D.; Sukhdeo, D.; Cheng, S.-L.; Roy, A.; Huang, K.C.-Y.; Brongersma, M.; Nishi, Y.; Saraswat, K. Electroluminescence from strained germanium membranes and implications for an efficient Si-compatible laser. Appl. Phys. Lett. 2012, 100, 131112. [Google Scholar] [CrossRef]
- Bollani, M.; Chrastina, D.; Gagliano, L.; Rossetto, L.; Scopece, D.; Barget, M.; Mondiali, V.; Frigerio, J.; Lodari, M.; Pezzoli, F.; et al. Local uniaxial tensile strain in germanium of up to 4% induced by SiGe epitaxial nanostructures. Appl. Phys. Lett. 2015, 107, 083101. [Google Scholar] [CrossRef]
- Scopece, D.; Montalenti, F.; Bollani, M.; Chrastina, D.; Bonera, E. Straining Ge bulk and nanomembranes for optoelectronic applications: A systematic numerical analysis. Semicond. Sci. Technol. 2014, 29, 095012. [Google Scholar] [CrossRef]
- Gassenq, A.; Tardif, S.; Guilloy, K.; Dias, G.O.; Pauc, N.; Duchemin, I.; Rouchon, D.; Hartmann, J.-M.; Widiez, J.; Escalante, J.; et al. Accurate strain measurements in highly strained Ge microbridges. Appl. Phys. Lett. 2016, 108, 241902. [Google Scholar] [CrossRef]
- Gassenq, A.; Guilloy, K.; Dias, G.O.; Pauc, N.; Rouchon, D.; Hartmann, J.-M.; Widiez, J.; Tardif, S.; Rieutord, F.; Escalante, J.; et al. 1.9% bi-axial tensile strain in thick germanium suspended membranes fabricated in optical germanium-on-insulator substrates for laser applications. Appl. Phys. Lett. 2015, 107, 191904. [Google Scholar] [CrossRef]
- Guilloy, K.; Pauc, N.; Gassenq, A.; Niquet, Y.-M.; Escalante, J.-M.; Duchemin, I.; Tardif, S.; Dias, G.O.; Rouchon, D.; Widiez, J.; et al. Germanium under High Tensile Stress: Nonlinear Dependence of Direct Band Gap vs. Strain. ACS Photonics 2016, 3, 1907–1911. [Google Scholar] [CrossRef]
- Lim, P.H.; Park, S.; Ishikawa, Y.; Wada, K. Enhanced direct bandgap emission in germanium by micromechanical strain engineering. Opt. Express 2009, 17, 16358–16365. [Google Scholar] [CrossRef] [PubMed]
- El Kurdi, M.; Bertin, H.; Martincic, E.; de Kersauson, M.; Fishman, G.; Sauvage, S.; Bosseboeuf, A.; Boucaud, P. Control of direct bandgap emission of bulk germanium by mechanical tensile strain. Appl. Phys. Lett. 2010, 96, 041909. [Google Scholar] [CrossRef]
- Boztug, C.; Sánchez-Pérez, J.R.; Cavallo, F.; Lagally, M.G.; Paiella, R. Strained-Germanium Nanostructures for Infrared Photonics. ACS Nano 2014, 8, 3136–3151. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Pérez, J.R.; Boztug, C.; Chen, F.; Sudradjat, F.F.; Paskiewicz, D.M.; Jacobson, R.B.; Lagally, M.G.; Paiella, R. Direct-bandgap light-emitting germanium in tensilely strained nanomembranes. Proc. Natl. Acad. Sci. USA 2011, 108, 18893–18898. [Google Scholar] [CrossRef] [PubMed]
- Boztug, C.; Sánchez-Pérez, J.R.; Yin, J.; Lagally, M.G.; Paiella, R. Grating-coupled mid-infrared light emission from tensilely strained germanium nanomembranes. Appl. Phys. Lett. 2013, 103, 201114. [Google Scholar] [CrossRef]
- Kouvetakis, J.; Menendez, J.; Chizmeshya, A.V.G. TIN-BASED GROUP-IV SEMICONDUCTORS: New Platforms for Opto- and Microelectronics on Silicon. Annu. Rev. Mater. Res. 2006, 36, 497–554. [Google Scholar] [CrossRef]
- Fleurial, J.P.; Borshchevsky, A. Si-Ge-Metal Ternary Phase Diagram Calculations. J. Electrochem. Soc. 1990, 137, 2928–2937. [Google Scholar] [CrossRef]
- Ragan, R.; Atwater, H.A. Measurement of the direct energy gap of coherently strained SnxGe1-x/Ge(001) heterostructures. Appl. Phys. Lett. 2000, 77, 3418–3420. [Google Scholar] [CrossRef]
- Kasper, E.; Werner, J.; Oehme, M.; Escoubas, S.; Burle, N.; Schulze, J. Growth of silicon based germanium tin alloys. Thin Solid Films 2012, 520, 3195–3200. [Google Scholar] [CrossRef]
- Schulze, J.; Oehme, M.; Werner, J. Molecular beam epitaxy grown Ge/Si pin layer sequence for photonic devices. Thin Solid Films 2012, 520, 3259–3261. [Google Scholar] [CrossRef]
- Pérez Ladròn de Guevara, H.; Rodrìguez, A.G.; Navarro-Contreras, H.; Vidal, M.A. Ge1-xSnx alloys pseudomorphically grown on Ge(001). Appl. Phys. Lett. 2003, 83, 4942–4944. [Google Scholar] [CrossRef]
- Bauer, M.R.; Taraci, J.; Tolle, J.; Chizmeshya, A.V.G.; Zollner, S.; Smith, D.J.; Menendez, J.; Hu, C.; Kouvetakis, J. Ge-Sn semiconductors for band-gap and lattice engineering. Appl. Phys. Lett. 2002, 81, 2992–2994. [Google Scholar] [CrossRef]
- Bauer, M.R.; Cook, C.S.; Aella, P.; Tolle, J.; Kouvetakis, J.; Crozier, P.A.; Chizmeshya, A.V.G.; Smith, D.J.; Zollner, S. SnGe superstructure materials for Si-based infrared optoelectronics. Appl. Phys. Lett. 2003, 83, 3489–3491. [Google Scholar] [CrossRef]
- D’Costa, V.R.; Fang, Y.-Y.; Tolle, J.; Kouvetakis, J.; Menéndez, J. Tunable Optical Gap at a Fixed Lattice Constant in Group-IV Semiconductor Alloys. Phys. Rev. Lett. 2009, 102, 107403. [Google Scholar] [CrossRef] [PubMed]
- Vincent, B.; Gencarelli, F.; Bender, H.; Merckling, C.; Douhard, B.; Petersen, D.H.; Hansen, O.; Henrichsen, H.H.; Meersschaut, J.; Vandervorst, W.; et al. Undoped and in-situ B doped GeSn epitaxial growth on Ge by atmospheric pressurechemical vapor deposition. Appl. Phys. Lett. 2011, 99, 152103. [Google Scholar] [CrossRef] [Green Version]
- Mathews, J.; Beeler, R.T.; Tolle, J.; Xu, C.; Roucka, R.; Kouvetakis, J.; Menéndez, J. Direct-gap photoluminescence with tunable emission wavelength in Ge1−y Sny alloys on silicon. Appl. Phys. Lett. 2010, 97, 221912. [Google Scholar] [CrossRef]
- Grzybowski, G.; Jiang, L.; Mathews, J.; Roucka, R.; Xu, C.; Beeler, R.T.; Kouvetakis, J.; Menéndez, J. Photoluminescence from heavily doped GeSn:P materials grown on Si(100). Appl. Phys. Lett. 2011, 99, 171910. [Google Scholar] [CrossRef]
- Ryu, M.-Y.; Harris, T.R.; Yeo, Y.K.; Beeler, R.T.; Kouvetakis, J. Temperature-dependent photoluminescence of Ge/Si and Ge1-ySny/Si, indicating possible indirect-to-direct bandgap transition at lower Sn content. Appl. Phys. Lett. 2013, 102, 171908. [Google Scholar] [CrossRef]
- Stange, D.; Wirths, S.; von den Driesch, N.; Mussler, G.; Stoica, T.; Ikonic, Z.; Hartmann, J.M.; Mantl, S.; Grützmacher, D.; Buca, D. Optical Transitions in Direct-Bandgap Ge1−xSnx Alloys. ACS Photonics 2015, 2, 1539–1545. [Google Scholar] [CrossRef]
- Gupta, S.; Magyari-Köpe, B.; Nishi, Y.; Saraswat, K.C. Achieving direct bandgap in germanium through integration of Sn alloying and external strain. J. Appl. Phys. 2013, 113, 073707. [Google Scholar] [CrossRef]
- Pezzoli, F.; Giorgioni, A.; Patchett, D.; Myronov, M. Temperature-Dependent Photoluminescence Characteristics of GeSn Epitaxial Layers. ACS Photonics 2016, 3, 2004–2009. [Google Scholar] [CrossRef]
- Stange, D.; Wirths, S.; Geiger, R.; Schulte-Braucks, C.; Marzban, B.; von den Driesch, N.; Mussler, G.; Zabel, T.; Stoica, T.; Hartmann, J.-M.; et al. Optically Pumped GeSn Microdisk Lasers on Si. ACS Photonics 2016, 3, 1279–1285. [Google Scholar] [CrossRef]
- Al-Kabi, S.; Ghetmiri, S.A.; Margetis, J.; Pham, T.; Zhou, Y.; Dou, W.; Collier, B.; Quinde, R.; Du, W.; Mosleh, A.; et al. An optically pumped 2.5 μm GeSn laser on Si operating at 110 K. Appl. Phys. Lett. 2016, 109, 171105. [Google Scholar] [CrossRef]
- Roucka, R.; Mathews, J.; Beeler, R.T.; Tolle, J.; Kouvetakis, J.; Menéndez, J. Direct gap electroluminescence from Si/Ge1−ySny p-i-n heterostructure diodes. Appl. Phys. Lett. 2011, 98, 061109. [Google Scholar] [CrossRef]
- Gupta, J.P.; Bhargava, N.; Kim, S.; Adam, T.; Kolodzey, J. Infrared electroluminescence from GeSn heterojunction diodes grown by molecular beam epitaxy. Appl. Phys. Lett. 2013, 102, 251117. [Google Scholar] [CrossRef]
- Tseng, H.H.; Wu, K.Y.; Li, H.; Mashanov, V.; Cheng, H.H.; Sun, G.; Soref, R.A. Mid-infrared electroluminescence from a Ge/Ge0.922Sn0.078/Ge double heterostructure p-i-n diode on a Si substrate. Appl. Phys. Lett. 2013, 102, 182106. [Google Scholar] [CrossRef]
- Werner, J.; Oehme, M.; Schmid, M.; Kaschel, M.; Schirmer, A.; Kasper, E.; Schulze, J. Germanium-tin p-i-n photodetectors integrated on silicon grown by molecular beam epitaxy. Appl. Phys. Lett. 2011, 98, 061108. [Google Scholar] [CrossRef]
- Oehme, M.; Kostecki, K.; Arguirov, T.; Mussler, G.; Ye, K.; Gollhofer, M.; Schmid, M.; Kaschel, M.; Körner, R.A.; Kittler, M.; et al. GeSn Heterojunction LEDs on Si Substrates. IEEE Photonics Technol. Lett. 2014, 26, 187–189. [Google Scholar] [CrossRef]
- Zhou, Y.; Dou, W.; Du, W.; Pham, T.; Ghetmiri, S.A.; Al-Kabi, S.; Mosleh, A.; Alher, M.; Margetis, J.; Tolle, J.; et al. Systematic study of GeSn heterostructure-based light-emitting diodes towards midinfrared applications. J. Appl. Phys. 2016, 120, 023102. [Google Scholar] [CrossRef]
- Gallagher, J.D.; Senaratne, C.L.; Sims, P.; Aoki, T.; Menéndez, J.; Kouvetakis, J. Electroluminescence from GeSn heterostructurepindiodes at the indirect to direct transition. Appl. Phys. Lett. 2015, 106, 091103. [Google Scholar] [CrossRef]
- Gallagher, J.D.; Senaratne, C.L.; Xu, C.; Sims, P.; Aoki, T.; Smith, D.J.; Menéndez, J.; Kouvetakis, J. Non-radiative recombination in Ge1−ySny light emitting diodes: The role of strain relaxation in tuned heterostructure designs. J. Appl. Phys. 2015, 117, 245704. [Google Scholar] [CrossRef]
- Senaratne, C.L.; Wallace, P.M.; Gallagher, J.D.; Sims, P.E.; Kouvetakis, J.; Menéndez, J. Direct gap Ge1−ySny alloys: Fabrication and design of mid-IR photodiodes. J. Appl. Phys. 2016, 120, 025701. [Google Scholar] [CrossRef]
- Xie, J.; Tolle, J.; D’Costa, V.R.; Chizmeshya, A.V.G.; Menéndez, J.; Kouvetakis, J. Direct integration of active Ge1−x(Si4Sn)x semiconductors on Si(100). Appl. Phys. Lett. 2009, 95, 181909. [Google Scholar] [CrossRef]
- Moontragoon, P.; Soref, R.A.; Ikonic, Z. The direct and indirect bandgaps of unstrained SixGe1−x−ySny and their photonic device applications. J. Appl. Phys. 2012, 112, 073106. [Google Scholar] [CrossRef]
- Stange, D.; von den Driesch, N.; Rainko, D.; Schulte-Braucks, C.; Wirths, S.; Mussler, G.; Tiedemann, A.T.; Stoica, T.; Hartmann, J.M.; Ikonic, Z.; et al. Study of GeSn based heterostructures: Towards optimized group IV MQW LEDs. Opt. Express 2016, 24, 1358–1367. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Soref, R.A.; Cheng, H.H. Design of an electrically pumped SiGeSn/GeSn/SiGeSn double-heterostructure midinfrared laser. J. Appl. Phys. 2010, 108, 033107. [Google Scholar] [CrossRef]
- Gallagher, J.D.; Xu, C.; Senaratne, C.L.; Aoki, T.; Wallace, P.M.; Kouvetakis, J.; Menéndez, J. Ge1−x−ySixSny light emitting diodes on silicon for mid-infrared photonic applications. J. Appl. Phys. 2015, 118, 135701. [Google Scholar] [CrossRef]
- Parsons, R.R. Band-to-band optical pumping in solids and polarized photoluminescence. Phys. Rev. Lett. 1969, 23, 1152–1154. [Google Scholar] [CrossRef]
- Dyakonov, M.I.; Perel, V.I. Optical Orientation; Meier, F., Zacharchenya, B.P., Eds.; North-Holland: New York, NY, USA, 1984; Chapter 2. [Google Scholar]
- Žutić, I.; Fabian, J.; Erwin, S.C. Spin Injections and Detection in Silicon. Phys. Rev. Lett. 2006, 97, 026602. [Google Scholar] [CrossRef] [PubMed]
- Allenspach, R.; Meier, F.; Pescia, D. Experimental Symmetry Analysis of Electronic States by Spin-Dependent photoemission. Phys. Rev. Lett. 1983, 51, 2148–2150. [Google Scholar] [CrossRef]
- Dyakonov, M.I. Spin Physics in Semiconductors. In Basics of Semiconductor and Spin Physics; Dyakonov, M.I, Ed.; Springer: Berlin, Germany, 2008; pp. 1–28. [Google Scholar]
- Fodor, P.S.; Levy, J. Group IV solid state proposals for quantum computation. J. Phys. Condens. Matter 2006, 18, S745–S766. [Google Scholar] [CrossRef]
- Li, P.; Dery, H. Theory of Spin-Dependent Phonon-Assisted Optical Transitions in Silicon. Phys. Rev. Lett. 2010, 105, 03720. [Google Scholar] [CrossRef] [PubMed]
- Mak, G.J.; van Driel, H.M. Femtosecond transmission spectroscopy at the direct band edge of germanium. Phys. Rev. B 1994, 49, 16817–16820. [Google Scholar] [CrossRef]
- Loren, E.J.; Rioux, J.; Lange, C.; Sipe, J.E.; van Driel, H.M.; Smirl, A.L. Hole spin relaxation and intervalley electron scattering in germanium. Phys. Rev. B 2011, 84, 214307. [Google Scholar] [CrossRef]
- Rioux, J.; Sipe, J.E. Optical injection and control in germanium: Thirty-band k∙p theory. Phys. Rev. B 2010, 81, 155215. [Google Scholar] [CrossRef]
- Nastos, F.; Rioux, J.; Strimas-Mackey, M.; Mendoza, B.S.; Sipe, J.E. Full band structure LDA and k∙p calculations of optical spin-injection. Phys. Rev. B 2007, 76, 205113. [Google Scholar] [CrossRef]
- Hautmann, C.; Surrer, B.; Betz, M. Ultrafast optical orientation and coherent Larmor precession of electron and hole spins in bulk germanium. Phys. Rev. B 2011, 83, 161203. [Google Scholar] [CrossRef]
- Hautmann, C.; Betz, M. Magneto-optical analysis of the effective g tensor and electron spin decoherence in the multivalley conduction band of bulk germanium. Phys. Rev. B 2012, 85, 121203. [Google Scholar] [CrossRef]
- Lohrenz, J.; Paschen, T.; Betz, M. Resonant spin amplification in intrinsic bulk germanium: Evidence for electron spin lifetimes exceeding 50 ns. Phys. Rev. B 2014, 89, 121201. [Google Scholar] [CrossRef]
- Roth, L.M. g Factor and Donor Spin-Lattice Relaxation for Electrons in Germanium and Silicon. Phys. Rev. 1960, 118, 1534–1540. [Google Scholar] [CrossRef]
- Feher, G.; Wilson, D.K.; Gere, E.A. Electron Spin Resonance Experiments on Shallow Donors in Germanium. Phys. Rev. Lett. 1959, 3, 25–28. [Google Scholar] [CrossRef]
- Guite, C.; Venkataraman, V. High sensitivity detection of radio-frequency modulated magnetic moment in semiconductors. Rev. Sci. Instrum. 2011, 82, 103905. [Google Scholar] [CrossRef] [PubMed]
- Guite, C.; Venkataraman, V. Temperature dependence of spin lifetime of conduction electrons in bulk germanium. Appl. Phys. Lett. 2012, 101, 252404. [Google Scholar] [CrossRef]
- Li, P.; Song, Y.; Dery, H. Intrinsic spin lifetime of conduction electrons in germanium. Phys. Rev. B 2012, 86, 085202. [Google Scholar] [CrossRef]
- Pezzoli, F.; Quing, L.; Giorgioni, A.; Isella, G.; Grilli, E.; Guzzi, M.; Dery, H. Spin and energy relaxation in germanium studied by spin-polarized direct-gap photoluminescence. Phys. Rev. B 2013, 88, 045204. [Google Scholar] [CrossRef]
- Giorgioni, A.; Vitiello, E.; Grilli, E.; Guzzi, M.; Pezzoli, F. Valley-dependent spin polarization and long-lived electron spins in germanium. Appl. Phys. Lett. 2014, 105, 152404. [Google Scholar] [CrossRef]
- Li, P.; Trivedi, D.; Dery, H. Spin-dependent optical properties in strained silicon and germanium. Phys. Rev. B 2013, 87, 115203. [Google Scholar] [CrossRef]
- Li, P.; Li, J.; Quing, L.; Dery, H.; Appelbaum, I. Anisotropy-Driven Spin Relaxation in Germanium. Phys. Rev. Lett. 2013, 111, 257204. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.-M.; Collins, B.T.; Flatté, M.E. Electron spin-phonon interaction symmetries and tunable spin relaxation in silicon and germanium. Phys. Rev. B 2012, 85, 045202. [Google Scholar] [CrossRef]
- Song, Y.; Chalaev, O.; Dery, H. Donor-Driven Spin Relaxation in Multivalley Semiconductors. Phys. Rev. Lett. 2014, 113, 167201. [Google Scholar] [CrossRef] [PubMed]
- Qing, L.; Li, J.; Appelbaum, I.; Dery, H. Spin relaxation via exchange with donor impurity-bound electrons. Phys. Rev. B 2015, 91, 241405. [Google Scholar] [CrossRef]
- Pezzoli, F.; Balocchi, A.; Vitiello, E.; Amand, T.; Marie, X. Optical orientation of electron spins and valence-band spectroscopy in germanium. Phys. Rev. B 2015, 91, 201201. [Google Scholar] [CrossRef]
- Bottegoni, F.; Isella, G.; Cecchi, S.; Ciccacci, F. Spin polarized photoemission from strained Ge epilayers. Appl. Phys. Lett. 2011, 98, 242107. [Google Scholar] [CrossRef]
- Bottegoni, F.; Ferrari, A.; Isella, G.; Cecchi, S.; Marcon, M.; Chrastina, D.; Trezzi, G.; Ciccacci, F. Ge/SiGe heterostructures as emitters of polarized electrons. J. Appl. Phys. 2012, 111, 063916. [Google Scholar] [CrossRef]
- Bottegoni, F.; Ferrari, A.; Isella, G.; Finazzi, M.; Ciccacci, F. Enhanced orbital mixing in the valence band of strained germanium. Phys. Rev. B 2012, 98, 245312. [Google Scholar] [CrossRef]
- Ferrari, A.; Bottegoni, F.; Cecchi, S.; Isella, G.; Ciccacci, F. Optical spin orientation in group-IV heterostructures. J. Appl. Phys. 2013, 113, 17C504. [Google Scholar] [CrossRef]
- Ferrari, A.; Bottegoni, F.; Isella, G.; Cecchi, S.; Ciccacci, F. Epitaxial Si1−xGex alloys studied by spin-polarized photoemission. Phys. Rev. B 2013, 88, 115209. [Google Scholar] [CrossRef]
- Vitiello, E.; Virgilio, M.; Giorgioni, A.; Frigerio, J.; Gatti, E.; De Cesari, S.; Bonera, E.; Grilli, E.; Isella, G.; Pezzoli, F. Spin-dependent direct-gap emission in tensile-strained Ge films on Si substrates. Phys. Rev. B 2015, 92, 201203. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Lee, Y.K.; Ge, Y.; Ren, S.; Roth, J.E.; Kamins, T.I.; Miller, D.A.B.; Harris, J.S. Strong quantum-confined Stark effect in germanium quantum-well structures on silicon. Nature 2005, 437, 1334–1336. [Google Scholar] [CrossRef] [PubMed]
- Bonfanti, M.; Grilli, E.; Guzzi, M.; Virgilio, M.; Grosso, G.; Chrastina, D.; Isella, G.; von Känel, H.; Neels, A. Optical transition in Ge/SiGe multiple quantum wells with Ge-rich barriers. Phys. Rev. B 2008, 78, 041407. [Google Scholar] [CrossRef]
- Paul, D.J. 8-band k∙p modeling of the quantum confined Stark effect in Ge quantum wells on Si substrates. Phys. Rev. B 2008, 77, 155323. [Google Scholar] [CrossRef]
- Gatti, E.; Grilli, E.; Guzzi, M.; Chrastina, D.; Isella, G.; von Känel, H. Room temperature photoluminescence of Ge multiple quantum wells with Ge-rich barriers. Appl. Phys. Lett. 2011, 98, 031106. [Google Scholar] [CrossRef] [Green Version]
- Giorgioni, A.; Gatti, E.; Grilli, E.; Chernikov, A.; Chatterjee, S.; Chrastina, D.; Isella, G.; Guzzi, M. Photoluminescence decay of direct and indirect transitions in Ge/SiGe multiple quantum wells. J. Appl. Phys. 2012, 111, 013501. [Google Scholar] [CrossRef]
- Gatti, E.; Isa, F.; Chrastina, D.; Müller Gubler, E.; Pezzoli, F.; Grilli, E.; Isella, G. Ge/SiGe quantum wells on Si(111): Growth, structural, and optical properties. J. Appl. Phys. 2014, 113, 043518. [Google Scholar] [CrossRef]
- Chaisakul, P.; Marris-Morini, D.; Frigerio, J.; Chrastina, D.; Rouifed, M.S.; Cecchi, S.; Crozat, P.; Isella, G.; Vivien, L. Integrated germanium optical interconnects on silicon substrates. Nat. Photonics 2014, 8, 482–488. [Google Scholar] [CrossRef]
- Virgilio, M.; Grosso, G. Optical spin orientation in strained Ge/SiGe quantum wells: A tight-binding approach. Phys. Rev. B 2009, 80, 205309. [Google Scholar] [CrossRef]
- Giorgioni, A.; Pezzoli, F.; Gatti, E.; Cecchi, S.; Inoki, C.K.; Deneke, C.; Grilli, E.; Isella, G.; Guzzi, M. Optical tailoring of carrier spin polarization in Ge/SiGe multiple quantum wells. Appl. Phys. Lett. 2013, 102, 012408. [Google Scholar] [CrossRef]
- Lange, C.; Köster, N.S.; Chatterjee, S.; Sigg, H.; Chrastina, D.; Isella, G.; von Känel, H.; Schäfer, M.; Kira, M.; Koch, S.W. Ultrafast nonlinear optical response of photoexcited Ge/SiGe quantum wells: Evidence for a femtosecond transient population inversion. Phys. Rev. B 2009, 79, 201306. [Google Scholar] [CrossRef]
- Lange, C.; Isella, G.; Chrastina, D.; Pezzoli, F.; Köster, N.S.; Woscholski, R.; Chatterjee, S. Spin band-gap renormalization and hole spin dynamics in Ge/SiGe quantum wells. Phys. Rev. B 2012, 85, 241303. [Google Scholar] [CrossRef]
- Giorgioni, A.; Paleari, S.; Cecchi, S.; Vitiello, E.; Grilli, E.; Isella, G.; Jantsch, W.; Fanciulli, M.; Pezzoli, F. Strong confinement-induced engineering of the g-factor and lifetime of conduction electron spins in Ge quantum wells. Nat. Commun. 2016, 7, 13886. [Google Scholar] [CrossRef] [PubMed]
- Baron, F.A.; Kiselev, A.A.; Robinson, H.D.; Kim, K.W.; Wang, K.L.; Yablonovitch, E. Manipulating the L-valley electron g factor in Si-Ge heterostructures. Phys. Rev. B 2003, 68, 195306. [Google Scholar] [CrossRef]
- Gerhardt, N.C.; Hofmann, M.R. Spin-controlled Vertical-Cavity Surface-Emitting Lasers. Adv. Opt. Technol. 2012, 2012, 268949. [Google Scholar] [CrossRef]
- Chen, T.Y.; Chien, C.L.; Petrovic, C. Enhanced Curie temperature and spin polarization in Mn4FeGe3. Appl. Phys. Lett. 2007, 91, 142505. [Google Scholar] [CrossRef]
- Jaafar, R.; Nehme, Y.; Berling, D.; Bubendorff, J.L.; Mehdaoui, A.; Pirri, C.; Garreau, G.; Uhlaq-Bouillet, C. Room-temperature ferromagnetism in single crystal Fe1.7Ge thin films of high thermal stability grown on Ge(111). Appl. Phys. Lett. 2008, 93, 033114. [Google Scholar] [CrossRef]
- Miyao, M.; Hamaya, K.; Sadoh, T.; Itoh, H.; Maeda, Y. Molecular beam epitaxial growth of ferromagnetic Heusler alloys for group-IV semiconductor spintronic devices. Thin Solid Films 2010, 518, S273–S277. [Google Scholar] [CrossRef]
- Tang, J.; Wang, C.-Y.; Hung, M.-H.; Jiang, X.; Chang, L.-T.; He, L.; Liu, P.-H.; Yang, H.-J.; Tuan, H.-Y.; Chen, L.-J.; et al. Ferromagnetic Germanide in Ge Nanowire Transistors for Spintronics Application. ACS Nano 2012, 6, 5710–5717. [Google Scholar] [CrossRef] [PubMed]
- Le Thanh, V.; Spiesser, A.; Dau, M.-T.; Olive-Mendez, S.F.; Michez, L.A.; Petit, M. Epitaxial growth and magnetic properties of Mn5Ge3/Ge and Mn5Ge3Cx/Ge heterostructures for spintronic applications. Adv. Nat. Sci. Nanosci. Nanotechnol. 2013, 4, 043002. [Google Scholar] [CrossRef]
- Wang, K.L.; Xiu, F. Spintronics of nanostructured manganese germanium (MnGe) dilute magnetic semiconductors. In Silicon-Germanium (SiGe) Nanostructures; Shiraki, Y., Usami, N., Eds.; Woodhead Publishing Limited: Cambridge, UK, 2011; pp. 575–602. [Google Scholar]
- Kasahara, K.; Baba, Y.; Yamane, K.; Ando, Y.; Yamada, S.; Hoshi, Y.; Sawano, K.; Miyao, M.; Hamaya, K. Spin accumulation created electrically in an n-type germanium channel using Schottky tunnel contacts. J. Appl. Phys. 2012, 111, 07C503. [Google Scholar] [CrossRef]
- Hamaya, K.; Baba, Y.; Takemoto, G.; Kasahara, K.; Yamada, S.; Sawano, K.; Miyao, M. Qualitative study of temperature-dependent spin signals in n-Ge-based lateral devices with Fe3Si/n+-Ge Schottky-tunnel contacts. J. Appl. Phys. 2013, 113, 183713. [Google Scholar] [CrossRef]
- Spiesser, A.; Saito, H.; Jansen, R.; Yuasa, S.; Ando, K. Large spin accumulation voltages in epitaxial Mn5Ge3 contacts on Ge without an oxide tunnel barrier. Phys. Rev. B 2014, 90, 205213. [Google Scholar] [CrossRef]
- Kasahara, K.; Fujita, Y.; Yamada, S.; Sawano, K.; Miyao, M.; Hamaya, K. Greatly enhanced generation efficiency of pure spin currents in Ge using Heusler compound Co2FeSi electrodes. Appl. Phys. Express 2014, 7, 033002. [Google Scholar] [CrossRef]
- Hamaya, K.; Takemoto, G.; Baba, Y.; Kasahara, K.; Yamada, S.; Sawano, K.; Miyao, M. Room-temperature electrical creation of spin accumulation in n-Ge using highly resistive Fe3Si/n+-Ge Schottky-tunnel contacts. Thin Solid Films 2014, 557, 382–385. [Google Scholar] [CrossRef]
- Grenet, L.; Jamet, M.; Noé, P.; Calvo, V.; Hartmann, J.-M.; Nistor, L.E.; Rodmacq, B.; Auffret, S.; Warin, P.; Samson, Y. Spin injection in silicon at zero magnetic field. Appl. Phys. Lett. 2009, 94, 032502. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Raghunathan, S.; Wilson, R.J.; Nikonov, D.E.; Saraswat, K.; Wang, S.X. The influence of Fermi level pinning/depinning on the Schottky barrier height and contact resistance in Ge/CoFeB and Ge/MgO/CoFeB structures. Appl. Phys. Lett. 2010, 96, 052514. [Google Scholar] [CrossRef]
- Rojas-Sanchez, J.-C.; Cubukcu, M.; Jain, A.; Vergnaud, C.; Portemont, C.; Ducruet, C.; Barski, A.; Marty, A.; Vila, L.; Attane, J.-P.; et al. Spin pumping and inverse spin Hall effect in germanium. Phys. Rev. B 2013, 88, 064403. [Google Scholar] [CrossRef]
- Gao, L.; Jiang, X.; Yang, S.-H.; Burton, J.D.; Tsymbal, E.Y.; Parkin, S.S.P. Bias Voltage Dependence of Tunneling Anisotropic Magnetoresistance in Magnetic Tunnel Junctions with MgO and Al2O3 Tunnel Barriers. Phys. Rev. Lett. 2007, 99, 226602. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.-C.; Park, S.-Y.; Manchon, A.; Chshiev, M.; Han, J.-H.; Lee, H.-W.; Lee, J.-E.; Nam, K.-T.; Jo, Y.; Kong, Y.-C.; et al. Bias-voltage dependence of perpendicular spin-transfer torque in asymmetric MgO-based magnetic tunnel junctions. Nat. Phys. 2009, 5, 898–902. [Google Scholar] [CrossRef]
- Zhou, Y.; Ogawa, M.; Bao, M.; Han, W.; Kawakami, R.K.; Wang, K.L. Engineering of tunnel junctions for prospective spin injection in germanium. Appl. Phys. Lett. 2009, 94, 242104. [Google Scholar] [CrossRef]
- Jeon, K.-R.; Min, B.-C.; Lee, H.-S.; Shin, I.-J.; Park, C.-Y.; Shin, S.-C. Single crystalline CoFe/MgO tunnel contact on nondegenerate Ge with a proper resistance-area product for efficient spin injection and detection. Appl. Phys. Lett. 2010, 97, 022105. [Google Scholar] [CrossRef]
- Han, W.; Zhou, Y.; Wang, Y.; Li, Y.; Wong, J.J.I.; Pi, K.; Swartz, A.G.; McCreary, K.M.; Xiu, F.; Wang, K.L.; et al. Growth of single-crystalline, atomically smooth MgO films on Ge(001) by molecular beam epitaxy. J. Cryst. Growth 2009, 312, 44–47. [Google Scholar] [CrossRef]
- Cantoni, M.; Petti, D.; Rinaldi, C.; Bertacco, R. Bandstructure line-up of epitaxial Fe/MgO/Ge heterostructures: A combined X-ray photoelectron spectroscopy and transport study. Appl. Phys. Lett. 2011, 98, 032104. [Google Scholar] [CrossRef]
- Petti, D.; Cantoni, M.; Rinaldi, C.; Brivio, S.; Bertacco, R.; Gazquez, J.; Varela, M. Sharp Fe/MgO/Ge(001) epitaxial heterostructures for tunneling junctions. J. Appl. Phys. 2011, 109, 084909. [Google Scholar] [CrossRef]
- Saito, H.; Watanabe, S.; Mineno, Y.; Sharma, S.; Jansen, R.; Yuasa, S.; Ando, K. Electrical creation of spin accumulation in p-type germanium. Solid State Commun. 2011, 151, 1159–1161. [Google Scholar] [CrossRef]
- Dash, S.P.; Sharma, S.; Patel, R.S.; de Jong, M.P.; Jansen, R. Electrical creation of spin polarization in silicon at room temperature. Nature 2009, 462, 491–494. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Louahadj, L.; Peiro, J.; Le Breton, J.C.; Vergnaud, C.; Barski, A.; Beigné, C.; Notin, L.; Marty, A.; Baltz, V.; et al. Electrical spin injection and detection at Al2O3/n-type germanium interface using three terminal geometry. Appl. Phys. Lett. 2011, 99, 162102. [Google Scholar] [CrossRef]
- Iba, S.; Saito, H.; Spiesser, A.; Watanabel, S.; Jansen, R.; Yuasa, S.; Ando, K. Spin Accumulation in Nondegenerate and Heavily Doped p-Type Germanium. Appl. Phys. Express 2012, 5, 023003. [Google Scholar] [CrossRef]
- Sharma, S.; Spiesser, A.; Dash, S.P.; Iba, S.; Watanabe, S.; van Wees, B.J.; Saito, H.; Yuasa, S.; Jansen, R. Anomalous scaling of spin accumulation in ferromagnetic tunnel devices with silicon and germanium. Phys. Rev. B 2014, 89, 075301. [Google Scholar] [CrossRef]
- Song, Y.; Dery, H. Magnetic-Field-Modulated Resonant Tunneling in Ferromagnetic-Insulator-Nonmagnetic Junctions. Phys. Rev. Lett. 2014, 113, 047205. [Google Scholar] [CrossRef] [PubMed]
- Rortais, F.; Vergnaud, C.; Ducruet, C.; Beigné, C.; Marty, A.; Attanè, J.-P.; Widiez, J.; Jaffrès, H.; George, J.-M.; Jamet, M. Electrical spin injection in silicon and the role of defects. Phys. Rev. B 2016, 94, 174426. [Google Scholar] [CrossRef]
- Jeon, K.-R.; Min, B.-C.; Park, Y.-H.; Jo, Y.-H.; Park, S.-Y.; Park, C.-Y.; Shin, S.-C. Effect of spin relaxation rate on the interfacial spin depolarization in ferromagnet/oxide/semiconductor contacts. Appl. Phys. Lett. 2012, 101, 02240. [Google Scholar] [CrossRef]
- Jeon, K.-R.; Min, B.-C.; Jo, Y.-H.; Lee, H.-S.; Shin, I.-J.; Park, C.-Y.; Park, S.-Y.; Shin, S.-C. Electrical spin injection and accumulation in CoFe/MgO/Ge contacts at room temperature. Phys. Rev. B 2011, 84, 165315. [Google Scholar] [CrossRef]
- Hanbicki, A.T.; Cheng, S.-F.; Goswami, R.; van’t Erve, O.M.J.; Jonker, B.T. Electrical injection and detection of spin accumulation in Ge at room temperature. Solid State Commun. 2012, 152, 244–248. [Google Scholar] [CrossRef]
- Spiesser, A.; Watanabe, S.; Saito, H.; Yuasa, S.; Ando, K. Effective Creation of Spin Polarization in p-Type Ge from a Fe/GeO2 Tunnel Contact. Jpn. J. Appl. Phys. 2013, 52, 04CM01. [Google Scholar] [CrossRef]
- Aoki, Y.; Kameno, M.; Ando, Y.; Shikoh, E.; Suzuki, Y.; Shinjo, T.; Shiraishi, M.; Sasaki, T.; Oikawa, T.; Suzuki, T. Investiagation of the inverted Hanle effect in highly doped Si. Phys. Rev. B 2012, 86, 081201. [Google Scholar] [CrossRef]
- Chang, L.-T.; Han, W.; Zhou, Y.; Tang, J.; Fischer, I.A.; Oehme, M.; Schulze, J.; Kawakami, R.K.; Wang, K.L. Comparison of spin lifetimes in n-Ge characterized between three-terminal and four-terminal nonlocal Hanle measurements. Semicond. Sci. Technol. 2013, 28, 015018. [Google Scholar] [CrossRef]
- Uemura, T.; Kondo, K.; Fujisawa, J.; Matsuda, K.-I.; Yamamoto, M. Critical effect of spin-dependent transport in a tunnel barrier on enhanced Hanle-type signal observed in three-terminal geometry. Appl. Phys. Lett. 2012, 101, 132411. [Google Scholar] [CrossRef]
- Zhou, Y.; Han, W.; Chang, L.-T.; Xiu, F.; Wang, M.; Oehme, M.; Fischer, I.A.; Schulze, J.; Kawakami, R.K.; Wang, K.L. Electrical spin injection and transport in germanium. Phys. Rev. B 2011, 84, 125323. [Google Scholar] [CrossRef]
- Jain, A.; Vergnaud, C.; Peiro, J.; Le Breton, J.C.; Prestat, E.; Louahadj, L.; Portemont, C.; Ducruet, C.; Baltz, V.; Marty, A.; et al. Electrical and thermal spin accumulation in germanium. Appl. Phys. Lett. 2012, 101, 022402. [Google Scholar] [CrossRef]
- Jain, A.; Rojas-Sanchez, J.-C.; Cubukcu, M.; Peiro, J.; Le Breton, J.C.; Prestat, E.; Vergnaud, C.; Louahadj, L.; Portemont, C.; Ducruet, C.; et al. Crossover from Spin Accumulation into Interface States to Spin Injection in the Germanium Conduction Band. Phys. Rev. Lett. 2012, 109, 106603. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Rojas-Sanchez, J.-C.; Cubukcu, M.; Peiro, J.; Le Breton, J.-C.; Vergnaud, C.; Augendre, E.; Vila, L.; Attané, J.-P.; Gambarelli, S.; et al. Transition from spin accumulation into interface states to spin injection in silicon and germanium conduction bands. Eur. Phys. J. B 2013, 86, 140. [Google Scholar] [CrossRef]
- Yu, T.; Wu, M.W. Hot-electron effect in spin relaxation of electrically injected electrons in intrinsic Germanium. J. Phys. Condens. Matter 2015, 27, 255001. [Google Scholar] [CrossRef] [PubMed]
- Ando, K.; Saitoh, E. Observation of the inverse spin Hall effect in silicon. Nat. Commun. 2012, 3, 629. [Google Scholar] [CrossRef] [PubMed]
- Oyarzun, S.; Nandy, A.K.; Rortrais, S.; Rojas-Sanchez, J.C.; Dau, M.-T.; Noel, P.; Laczkowski, P.; Pouget, S.; Okuno, H.; Vila, L.; et al. Evidence for spin-to-charge conversion by Rashba coupling in metallic states at the Fe/Ge(111) interface. Nat. Commun. 2016, 7, 13857. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, C.; Cantoni, M.; Petti, D.; Sottocorno, A.; Leone, M.; Caffrey, N.M.; Sanvito, S.; Bertacco, R. Ge-Based Spin-Photodiodes for Room-Temperature Integrated Detection of Photon Helicity. Adv. Mater. 2012, 24, 3037–3041. [Google Scholar] [CrossRef] [PubMed]
- Iba, S.; Saito, H.; Yuasa, S.; Yasutake, Y.; Fukatsu, S. Fabrication of Ge-based light-emitting diodes with a ferromagnetic metal/insulator tunnel contact. Jpn. J. Appl. Phys. 2015, 54, 04DM02. [Google Scholar] [CrossRef]
- Rojas-Sánchez, J.-C.; Oyarzún, S.; Fu, Y.; Marty, A.; Vergnaud, C.; Gambarelli, S.; Vila, L.; Jamet, M.; Ohtsubo, Y.; Taleb-Ibrahimi, A.; et al. Spin to Charge Conversion at Room Temperature by Spin Pumping into a New Type of Topological Insulator: α-Sn Films. Phys. Rev. Lett. 2016, 116, 096602. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Cesari, S.; Vitiello, E.; Giorgioni, A.; Pezzoli, F. Progress towards Spin-Based Light Emission in Group IV Semiconductors. Electronics 2017, 6, 19. https://doi.org/10.3390/electronics6010019
De Cesari S, Vitiello E, Giorgioni A, Pezzoli F. Progress towards Spin-Based Light Emission in Group IV Semiconductors. Electronics. 2017; 6(1):19. https://doi.org/10.3390/electronics6010019
Chicago/Turabian StyleDe Cesari, Sebastiano, Elisa Vitiello, Anna Giorgioni, and Fabio Pezzoli. 2017. "Progress towards Spin-Based Light Emission in Group IV Semiconductors" Electronics 6, no. 1: 19. https://doi.org/10.3390/electronics6010019
APA StyleDe Cesari, S., Vitiello, E., Giorgioni, A., & Pezzoli, F. (2017). Progress towards Spin-Based Light Emission in Group IV Semiconductors. Electronics, 6(1), 19. https://doi.org/10.3390/electronics6010019





